Theoretical and experimental investigations of the crossover phenomenon in micromachined arch resonator: part II—simultaneous 1:1 and 2:1 internal resonances

Abstract

We investigate in a silicon micromachined arch beam the activation of a one-to-one internal resonance between the first symmetric and first antisymmetric modes simultaneously with the activation of a two-to-one internal resonance between these modes and the second symmetric mode. The arch is excited electrically, using an antisymmetric partial electrode to activate both modes of vibrations, and tuned electrothermally via Joule’s heating. Theoretically, we explore the dynamics of the beam using the Galerkin and multiple timescales methods. The simulation results are shown to have good agreement with the experimental data. The results show the merging of both modes at crossing, after which the first antisymmetric mode exchanges the nonlinear behavior with the first symmetric mode. The nonlinear behavior of the arch beam is demonstrated and analyzed experimentally and theoretically as experiencing the simultaneous 2:1 and 1:1 internal resonances.

1 Introduction

Energy transfer via internal resonance among various modes of vibration of micro and nano-electromechanical structures (MEMS and NEMS) has been explored for several potential applications, such as timing/synchronization [1, 2], energy harvesting [3, 4], mass sensing [5], and frequency stabilization [6, 7]. Internal resonance, also called auto-parametric resonance, represents a nonlinear mechanism for energy leakage from the targeted vibration mode to another mode. One necessary condition to activate internal resonance is to have an integer ratio between the involved modes. Commonly, the 1:1 [8, 9], 2:1 [7, 10,11,12,13], 3:1 [6, 7, 9, 11], and 4:1 [7] internal resonance types are investigated.

In the classical structural dynamic, several studies demonstrated and explored different types of internal resonances experimentally and theoretically, mainly in cables [14,15,16,17], curved [18,19,20], and cantilever beams [21, 22].

Various studies have been conducted on internal resonance in M/NEMS resonators either for fundamental understanding or for implementation in different potential applications. One of the early works is that of Antonio et al. [6] who showed that the oscillation frequency of a nonlinear self-sustained MEMS resonator could be stabilized by coupling different modes of vibration through 3:1 internal resonance. The same group [1] has recently shown a novel technique to realize a self-sustained oscillation, via internal resonance, to compensate for energy losses. In electrothermally tuned MEMS arch resonator [7, 9, 11, 12, 23], 2:1 and 3:1 internal resonances were explored experimentally and theoretically among the first two symmetric vibrational modes. Rich complex dynamics were shown, such as Hopf bifurcation, limit cycle instabilities, and chaotic behavior. At the nanoscale, Samanta et al. [8] studied the activation of 1:1 internal resonance in 2D materials in $\hbox {MoS}_{{2}}$ NEMS structures.

The one-to-one internal resonance has also been studied theoretically among the first symmetric and antisymmetric modes for arch MEMS resonators known by their rich and complex dynamical behavior [9]. As shown in the presented work in [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)], as tuning the stiffness of the arch beam (increasing the compressive load via electrothermal voltage), the first symmetric mode frequency shows higher sensitivity (increases with high slope) to the stiffness change compared to the first antisymmetric mode frequency (slowly decreases) due to the stretching. Hence, both modes cross a critical load, which enhances the potential to activate 1:1 internal resonance due to the break of symmetry by the electrostatic excitation with the antisymmetric electrode configuration. The linear coupling between both involved modes at crossing has been in-depth investigated in [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)]. As both modes cross, they possess a ratio 2:1 with the second symmetric mode. This offers a condition for the activation of simultaneous 1:1 and 2:1 internal resonances.

In the classical structural dynamics, the simultaneous 2:1 and 1:1 internal resonances among the second symmetric mode and both first symmetric and antisymmetric modes were in-depth investigated in suspended cables [14, 15]. In [14, 15], the 2:1 internal resonance, which is for the in-plane motion, is coupled to the out-of-plane 1:1 internal resonance and analytically solved via the method of multiple timescales (MTS). Another recent example on shallow suspended cables is the work of Wang and Zhao [24], in which they investigated the 3:1 internal resonance between the first and third in-plane symmetric modes coupled with a 1:1 internal resonance between the in-plane and out-of-plane third modes. Cylindrical shells are another classical structure where simultaneous internal resonances are observed [25,26,27]. In cylindrical shells, coupling occurs between the first and third axisymmetric modes via 2:1 internal resonance while more than one asymmetric modes are in the 1:1 internal resonance with the first axisymmetric mode. This results in a coupled four-degree-of-freedom system that is solved and analyzed using MTS. Other classical examples where simultaneous internal resonances occur are in rotating strings [28], liquid sloshing in storage systems [29], coupled beams [30], and beams with cruciform cross section under the influence of shear deformation [31]. In most of these works, the simultaneous internal resonance is activated due to the coupling between a planer and non-planner modes, which is analyzed via perturbation methods. More examples of these internal resonances can be found in [32].

Here, the investigation presented in [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)] is extended to study the nonlinear coupling among the first two symmetric and first antisymmetric modes of the initially curved beam, which leads to simultaneous activation of the 1:1 and 2:1 internal resonances. The theoretical study will be based on the Galerkin and MTS methods, which will be validated with the experimental data based on a silicon-based initially curved beam.

The rest of the paper is organized as follows. Modeling using MTS is presented in Sect. 2. A discussion of the dynamic results is presented in Sect. 3. The main conclusions are summarized in Sect. 4.

2 Modeling: perturbation analysis

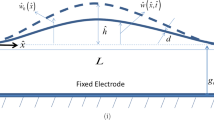
We conduct the analysis on a curved beam separated from a stationary electrode (with antisymmetric configuration) with a transduction gap of width d. The curved beam is actuated electrostatically by a DC bias voltage $V_{\mathrm{DC}}$ and an AC harmonic voltage of amplitude $V_\mathrm{AC}$ and frequency $\hat{{\varOmega }}$ and subjected to viscous damping of coefficient $\hat{c}$. A DC voltage, $V_{\mathrm{Th}}$, is applied between the anchors of the arch beam controlling its induced axial load, and hence stiffness, via Joule’s heating effect. The curved beam under consideration is of length $700\,\upmu \hbox {m}$, thickness $2\,\upmu \hbox {m}$ (h), depth $30\,\upmu \hbox {m}$ (b), and initial rise at the midpoint $2.6\,\upmu \hbox {m}$.

The problem formulation and the Galerkin procedure are presented in [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)]. Here, the multiple time scales procedure will be detailed. The frequency of the first symmetric mode of the arch beam makes a ratio 2:1 with that of the second symmetric mode as crossing with the first antisymmetric mode, which affects the linear eigenvalue problem. Hence, we consider analyzing the multiple internal resonances by directly attacking the dimensionless nonlinear partial differential equation [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)], which is expressed as

$$\begin{aligned}&\frac{\partial ^{2}w}{\partial t^{2}}+\frac{\partial ^{4}w}{\partial x^{4}}+c\frac{\partial w}{\partial t}\nonumber \\&\quad =\left( \left( {\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \right. \nonumber \\&\qquad \left. \left[ {N+\alpha _1 \mathop {\int }\limits _0^1 {\left[ {\frac{\partial w}{\partial x}^{2}+2\frac{\partial w}{\partial x}\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right] \mathrm{d}x} } \right] \right) \nonumber \\&\qquad +\,\alpha _2 \frac{(V_{\mathrm{DC}} +V_\mathrm{AC} \cos (\varOmega t))^{2}}{\left( {1-w-w_0 } \right) ^{2}}u(x-0.5) \end{aligned}$$

(1)

where the nondimensional variables above are defined as follows: w is the deflection, x is the position, t is time, $w_0$ is the initial static deflection, and $u(x-0.5)$ is the Heaviside function to account for the influence of partial electrode electrostatic excitation. The nondimensional axial applied load N, nondimensional viscous damping coefficient c, frequency of excitation $\varOmega$, and the parameters $\alpha _1$ and $\alpha _2$ are defined as below

$$\begin{aligned}&\alpha _1 =6\frac{\mathrm{d}^{2}}{h^{2}};\quad N=N_0 +S_{\mathrm{Th}};\nonumber \\&N_0 =\frac{l^{2}}{EI}\hat{{N}}_0 ;\quad S_{\mathrm{Th}} =\frac{l^{2}}{EI}\hat{{S}}_{\mathrm{Th}} ;\nonumber \\&\alpha _2=\frac{6\varepsilon l^{4}}{Eh^{3}\mathrm{d}^{3}};\quad c=\frac{l^{4}}{EIT_s }\hat{{c}};\quad \varOmega =T_s \hat{{\varOmega }} \end{aligned}$$

(2)

where $\upvarepsilon$ represents the dielectric constant of the medium and $T_s =\sqrt{{\rho bhl^{4}}/{EI}}$ is the timescale. The arch beam has Young’s modulus E, material density $\rho$, and a moment of inertia ${I= bh}^{3}/12$. The arch beam is subjected to an axial load that is a combination of $\hat{N}_0$, arising from the fabrication process (positive for tensile), and $\hat{S}_{\mathrm{Th}}$, denoting the thermal compressive load induced by $V_{Th }$ [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)].

First, the equation governing the static displacement $w_{\mathrm{st}} (x)$ is obtained by dropping the time-dependent terms in Eq. (1) yielding

$$\begin{aligned}&\frac{\mathrm{d}^{4}w_{\mathrm{st}} }{\mathrm{d}x^{4}}=\left( \left( {\frac{\mathrm{d}^{2}w_{\mathrm{st}} }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \right. \nonumber \\&\quad \left. \left[ {N+\alpha _1 \mathop {\int }_0^1 {\left[ {\frac{\mathrm{d}w_{\mathrm{st}} }{\mathrm{d}x}^{2}+2\frac{\mathrm{d}w_{\mathrm{st}} }{\mathrm{d}x}\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right] \mathrm{d}x} } \right] \right) \nonumber \\&\quad +\,\alpha _2 \frac{V_{\mathrm{DCeff}}^2 }{\left( {1-w_{\mathrm{st}} -w_0 } \right) ^{2}}u(x-0.5) \end{aligned}$$

(3.1)

where $V_{\mathrm{DCeff}}$ is defined as $V_{\mathrm{DCeff}}^2 =V_{\mathrm{DC}} ^{2}+1/2V_\mathrm{AC} ^{2}$. The boundary value problem of Eq. (3.1) is solved using the shooting method [33, 34]. Then, we perturb Eq. (1) around the static solution by adding the dynamic displacement $w_d (x,t)$ as

$$\begin{aligned} w(x,t)=w_{\mathrm{st}} (x)+w_d (x,t) \end{aligned}$$

(3.2)

Equation (3.2) is substituted in Eq. (1). Then expanding the electrostatic force term in Taylor series and dropping the static terms of Eq. (3.1) yield

$$\begin{aligned}&\frac{\partial ^{2}w_d }{\partial t^{2}}+\frac{\partial ^{4}w_d }{\partial x^{4}}+c\frac{\partial w_d }{\partial t} =\left( {\frac{\mathrm{d}^{2}w_{\mathrm{st}} }{\mathrm{d}x^{2}}+\frac{\mathrm{d}^{2}w_0 }{\mathrm{d}x^{2}}} \right) \nonumber \\&\quad \left[ {\alpha _1 \mathop {\int }\limits _0^1 {\left[ {2\left( {\frac{\mathrm{d}w_{\mathrm{st}} }{\mathrm{d}x}+\frac{\mathrm{d}w_0 }{\mathrm{d}x}} \right) \frac{\partial w_d }{\partial x}+\left( {\frac{\partial w_d }{\partial x}} \right) ^{2}} \right] \mathrm{d}x} } \right] \nonumber \\&\quad +\,\left( {\frac{\partial ^{2}w_d }{\partial x^{2}}} \right) \left[ N+\alpha _1 \mathop {\int }\limits _0^1 \left[ \left( {\frac{\mathrm{d}w_{\mathrm{st}} }{\mathrm{d}x}+\frac{\partial w_d }{\partial x}} \right) ^{2}\right. \right. \nonumber \\&\quad \left. \left. +\,2\left( {\frac{\mathrm{d}w_{\mathrm{st}} }{\mathrm{d}x}+\frac{\partial w_d }{\partial x}} \right) \frac{\mathrm{d}w_0 }{\mathrm{d}x} \right] \mathrm{d}x \right] \nonumber \\&\quad +\,\alpha _2 \left[ \frac{V(t)}{\left( {1-w_s -w_0 } \right) ^{2}}\right. \nonumber \\&\quad \left. +\,2\frac{V_{\mathrm{DCeff}}^2 +V(t)}{\left( {1-w_{\mathrm{st}} -w_0 } \right) ^{3}}w_d \right] u(x-0.5) \nonumber \\&\quad +\,\alpha _2 \left[ {3\frac{V_{\mathrm{DCeff}}^2 +V(t)}{\left( {1-w_{\mathrm{st}} -w_0 } \right) ^{4}}w_d ^{2}+HOT} \right] u(x-0.5)\nonumber \\ \end{aligned}$$

(3.3)

where HOT denotes higher-order terms and the electrostatic forcing term V(t) is defined as $V(t)=2V_\mathrm{AC} V_{\mathrm{DC}} \cos \left( {\varOmega t} \right) +\frac{V_\mathrm{AC} ^{2}}{2}\cos \left( {2\varOmega t} \right)$. The influence of the second term in the electrostatic frequency excitation results in a primary resonance in the case of a two-to-one frequency ratio. We note in Eq. (3.3) the cubic stretching nonlinearities in addition to the quadratic terms from the curvature and the electrostatic force. On that basis, we seek a third-order expansion of the form

$$\begin{aligned}&w_d (x,t;\varepsilon )=\varepsilon w_1 (x,T_0 ,T_1 ,T_2 )\nonumber \\&\quad +\,\varepsilon ^{2}w_2 (x,T_0 ,T_1 ,T_2 )+\,\varepsilon ^{3}w_3 (x,T_0 ,T_1 ,T_2 ) \end{aligned}$$

(4)

where $T_{i}= \varepsilon ^{i}t$, $\varepsilon$ is a bookkeeping parameter that is introduced to segregate the different nonlinear scales. As such, the chosen scale in Eq. (4) determines that the quadratic nonlinearity is at $\varepsilon ^{2}$ and the cubic nonlinearity is at $\varepsilon ^{3}$. Then, the forcing and damping terms are scaled, based on the simultaneous one-to-one and two-to-one internal resonance, as $\varepsilon ^{2}V(t)$ and $\varepsilon {c}$, respectively. We substitute Eq. (4) in Eq. (3.3) to obtain

$$\begin{aligned}&\varepsilon ^{1}:\ell (w_1 )=D_0 ^{2}w_1 +w_1 ^{iv}\nonumber \\&\quad -\left( {N+ \alpha _1 \mathop {\int }\limits _0^1 \left( {w_s ^{\prime }} \right) ^{2}-\left( {w_0 ^{\prime }} \right) ^{2}\hbox {d}x} \right) w_1 ^{\prime \prime }\nonumber \\&\quad -2\alpha _1 w_s ^{\prime \prime }\left( {\mathop {\int }\limits _0^1 w_s ^{\prime }w_1 ^{\prime }\hbox {d}x} \right) \nonumber \\&\quad -\frac{2\alpha _2 V_{\mathrm{DCeff}}^2 }{\left( {1-w_s } \right) ^{3}}w_1 =0 \end{aligned}$$

(5)

$$\begin{aligned}&\varepsilon ^{2}:\ell (w_2 )=-2D_0 D_1 w_1 -cD_0 w_1 \nonumber \\&\quad +\,\alpha _1 w_s ^{\prime \prime }\left( {\mathop {\int }\limits _0^1 \left( {w_1 ^{\prime }} \right) ^{2}\hbox {d}x} \right) +2\alpha _1 w_1 ^{\prime \prime }\left( {\mathop {\int }\limits _0^1 w_s ^{\prime }w_1 ^{\prime }\hbox {d}x} \right) \nonumber \\&\quad +\,\frac{3\alpha _2 V_{\mathrm{DCeff}}^2 }{\left( {1-w_s } \right) ^{4}}w_1 ^{2}+\frac{2\alpha _2 V_\mathrm{AC} V_{\mathrm{DC}} }{\left( {1-w_s } \right) ^{2}}\cos \left( {\varOmega T_0 } \right) \nonumber \\&\quad +\,\frac{\alpha _2 V_\mathrm{AC}^2 }{2\left( {w_s \left( x \right) -1} \right) ^{2}}\cos \left( {2\varOmega T_0 } \right) \end{aligned}$$

(6)

$$\begin{aligned}&\varepsilon ^{3}:\ell (w_3 )=-2D_0 D_2 w_1 -2D_0 D_1 w_2 -D_1 ^{2}w_1 \nonumber \\&\quad -\,cD_1 w_1 -cD_0 w_2 \nonumber \\&\quad +\,\frac{4\alpha _2 V_\mathrm{AC} V_{\mathrm{DC}} }{\left( {1-w_s } \right) ^{3}}\cos \left( {T_0 \varOmega } \right) w_1 \nonumber \\&\quad +\,\frac{\alpha _2 V_\mathrm{AC}^2 }{\left( {1-w_s } \right) ^{3}}\cos \left( {2\varOmega T_0 } \right) w_1 +\frac{6\alpha _2 V_{\mathrm{DCeff}}^2 }{\left( {1-w_s } \right) ^{4}}w_1 w_2 \nonumber \\&\quad +\,2\alpha _1 w_s ^{\prime \prime }\left( {\mathop {\int }\limits _0^1 w_1 ^{\prime }w_2 ^{\prime }\hbox {d}x} \right) +2\alpha _1 w_2 ^{\prime \prime }\left( {\mathop {\int }\limits _0^1 w_s ^{\prime }w_1 ^{\prime }\hbox {d}x} \right) \nonumber \\&\quad +\,2\alpha _1 w_1 ^{\prime \prime }\left( {\mathop {\int }\limits _0^1 w_s ^{\prime }w_2 ^{\prime }\hbox {d}x} \right) \nonumber \\&\quad +\,\alpha _1 w_1 ^{\prime }\left( {\mathop {\int }\limits _0^1 \left( {w_1 ^{\prime }} \right) ^{2}\hbox {d}x} \right) \end{aligned}$$

(7)

where the total static deflection is given by $w_s =w_{\mathrm{st}} +w_0$, the derivatives are defined as $D_j ^{i}=\frac{\partial }{\partial T_j ^{i}}$, and $()'$ denotes the derivative with respect to x. For simplicity, we introduce

$$\begin{aligned} \varGamma (f_1 (x,t),f_2 (x,t))=\mathop {\int }\limits _0^1 {\frac{\partial f_1 }{\partial x}\frac{\partial f_2 }{\partial x}\hbox {d}x} \end{aligned}$$

(8)

Equation (5) is the linear eigenvalue problem taking into consideration the influence of the electrostatic actuation. Hence, it can be solved using, for example, the Galerkin method [35].

For coupled mode interaction of the modes contributing to the internal resonances, we assume the solution to be of the form

$$\begin{aligned} w_1= & {} A_m (T_1 ,T_2 )\phi _m (x)e^{i\omega _m T_0 }\nonumber \\&+\,A_n (T_1 ,T_2 )\phi _n (x)e^{i\omega _n T_0 }\nonumber \\&+\,A_k (T_1 ,T_2 )\phi _k (x)e^{i\omega _k T_0 }+\hbox {c.c.} \end{aligned}$$

(9)

where $A_{m}, A_{n}, A_{k}$ represent the amplitudes of modes m, n, and k, ${\phi }_{m} , \phi _{n}, \phi _{k}$ represent their mode shapes, ${\omega }_{m}, \omega _{n} , \omega _{k}$ represent their frequencies, and c.c. denotes complex conjugate where the amplitudes are represented by $\bar{A}_{m} , \bar{A}_{n}, \bar{A}_{k}$. First, we consider the interaction at the second order, where a two-to-one internal resonance occurs, by assuming the excitation to be around the first natural frequency, i.e., ${\varOmega =\omega }_{m}+{\varepsilon }\sigma _{1}$, and the one-to-one and two-to-one internal resonances activation conditions are given by $\omega _{n} = \omega _{m} +\varepsilon \sigma _{2}$ and $\omega _{k}=2{\omega }_{n}+ \varepsilon \sigma _{3}$. Substituting Eq. (9) into Eq. (6) while considering the activation conditions and multiplying the result with the adjoint of each mode $\phi _m \left( x \right) \hbox {e}^{\pm i\omega _m T_0 }$,$\,\phi _n \left( x \right) \hbox {e}^{\pm i\omega _n T_0 }$, and $\phi _k \left( x \right) \hbox {e}^{\pm i\omega _k T_0 }$ yields the solvability conditions at the second order as

$$\begin{aligned} 2i{\omega _m}{D_1}{A_m}= & {} - 2i\mu {\omega _m}{A_m} + {R_{{m_1}}}{A_k}{\bar{A}_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {2{\sigma _2} + {\sigma _3}} \right) {T_1}}} \nonumber \\&+\, {R_{{m_2}}}{A_k}{\bar{A}_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _2} + {\sigma _3}} \right) {T_1}}} + {F_{{m_1}}}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _1}{T_1}}}\end{aligned}$$

(10.1)

$$\begin{aligned} 2i{\omega _n}{D_1}{A_n}= & {} - 2{\mathrm{i}}\mu {\omega _n}{A_n} + {R_{{n_1}}}{A_k}{\bar{A}_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _2} + {\sigma _3}} \right) {T_1}}} \nonumber \\&+\, {R_{{n_2}}}{A_k}{\bar{A}_n}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _3}{T_1}}} + {F_{{n_1}}}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _1} - {\sigma _2}} \right) {T_1}}} \end{aligned}$$

(10.2)

$$\begin{aligned} 2i\omega _k D_1 A_k= & {} -2i\mu \omega _k A_k +R_{k_1 } A_m^2 \hbox {e}^{-\hbox {i}\left( {2\sigma _2 +\sigma _3 } \right) T_1 }\nonumber \\&+\,R_{k_3 } A_n^2 \hbox {e}^{-\hbox {i}\sigma _3 T_1 }\nonumber \\&+\,R_{k_2 } A_m A_n \hbox {e}^{-\hbox {i}\left( {\sigma _2 +\sigma _3 } \right) T_1 } \nonumber \\&+\,F_{k_1 } \hbox {e}^{\mathrm {i}\left( {2\left( {\sigma _1 -\sigma _2 } \right) -\sigma _3 } \right) T_1 } \end{aligned}$$

(10.3)

where the coefficients $\mu$, $R_{m_1 }$, $R_{m_2 }$, $F_{m_1 }$, $R_{n_1 }$, $R_{n_2 }$, $F_{n_1 }$, $R_{k_1 }$, $R_{k_2 }$, $R_{k_3 }$ and $F_{k_1 }$ are defined in “Appendix A.” Next, we consider the particular solution at the second order, which is written as

$$\begin{aligned} {w_2}= & {} {\phi _m}\left( x \right) {B_m}\left( {{T_1},{T_2}} \right) {{\mathrm{e}}^{{\mathrm{i}}{\omega _m}{T_0}}} \nonumber \\&+\,{\phi _n}\left( x \right) {B_n}\left( {{T_1},{T_2}} \right) {{\mathrm{e}}^{{\mathrm{i}}{\omega _n}{T_0}}}\nonumber \\&+\, {\phi _k}\left( x \right) {B_k}\left( {{T_1},{T_2}} \right) {{\mathrm{e}}^{{\mathrm{i}}{\omega _k}{T_0}}} \nonumber \\&+\,{\psi _{km}}\left( x \right) {A_k}{A_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\omega _k} + {\omega _m}} \right) {T_0}}} \nonumber \\&+\,{\psi _{kn}}\left( x \right) {A_k}{A_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\omega _k} + {\omega _n}} \right) {T_0}}}\nonumber \\&+\, {\psi _{mn}}\left( x \right) {{\bar{A}}_m}{A_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\omega _n} - {\omega _m}} \right) {T_0}}} \nonumber \\&+\,{\psi _{mm}}\left( x \right) {A_m}{{\bar{A}}_m} + {\psi _{nn}}\left( x \right) {A_n}{{\bar{A}}_n} \nonumber \\&+\, {\psi _{kk}}\left( x \right) {A_k}{{\bar{A}}_k} + {\psi _{{k_2}}}\left( x \right) A_k^2{{\mathrm{e}}^{2{\mathrm{i}}{\omega _k}{T_0}}} + {\mathrm{c}}{\mathrm{.c}}{\mathrm{.}}\nonumber \\ \end{aligned}$$

(11)

The homogenous terms in Eq. (11) with amplitudes $B_m$, $B_n$, and $B_k$ are introduced to satisfy the Lagrangian formulation at the third order following the detailed procedure in [36, 37]. The functions $\psi _{km}$, $\psi _{kn}$, $\psi _{mn}$, $\psi _{mm}$, $\psi _{nn}$, $\psi _{kk}$, and $\psi _{k_2 }$ are obtained by solving the boundary value problems given by

$$\begin{aligned}&\psi _{km} (x):{H}[\omega _k +\omega _m ]=\varLambda _{km} \end{aligned}$$

(12.1)

$$\begin{aligned}&\psi _{kn} (x):{H}[\omega _k +\omega _n ]=\varLambda _{kn} \end{aligned}$$

(12.2)

$$\begin{aligned}&\psi _{mn} (x):{H}[\omega _n -\omega _m ]=\varLambda _{nm} \end{aligned}$$

(12.3)

$$\begin{aligned}&\psi _{mm} (x):{H}[0]=\varLambda _m \end{aligned}$$

(12.4)

$$\begin{aligned}&\psi _{nn} (x):{H}[0]=\varLambda _n \end{aligned}$$

(12.5)

$$\begin{aligned}&\psi _{kk} (x):{H}[0]=\varLambda _k \end{aligned}$$

(12.6)

$$\begin{aligned}&\psi _{k_2 } (x):{H}[0]=\varLambda _k \end{aligned}$$

(12.7)

where H is defined by

$$\begin{aligned}&{H}[\omega _i ]=H^{iv}-N H^{\prime \prime }-2\alpha _1 w_s ^{\prime \prime }\left( {\mathop {\int }\limits _0^1 w_s ^{\prime }H^{\prime }\hbox {d}x} \right) \nonumber \\&\quad -\frac{2\alpha _2 V_{\mathrm{DCeff}}^2 }{\left( {1-w_s } \right) ^{3}}H-\omega _i ^{2}H \end{aligned}$$

(12.8)

where $\varLambda _{ij}$ and $\varLambda _i$ are defined as

$$\begin{aligned}&\varLambda _{ij} =2\alpha _1 w_s ^{\prime \prime }\varGamma \left( {\phi _j ,\phi _i } \right) \nonumber \\&\quad +\,2\alpha _1 \phi _i ^{\prime \prime }\varGamma \left( {w_s ,\phi _j } \right) +2\alpha _1 \phi _j ^{\prime \prime }\varGamma \left( {w_s ,\phi _i } \right) \nonumber \\&\quad +\,\frac{6\alpha _2 V_{\mathrm{DCEff}} \phi _i \phi _j }{\left( {1-w_s } \right) ^{4}} \end{aligned}$$

(13.1)

$$\begin{aligned}&\varLambda _i =\alpha _1 w_s ^{\prime \prime }\varGamma \left( {\phi _i ,\phi _i } \right) +2\alpha _1 \phi _i ^{\prime \prime }\varGamma \left( {w_s ,\phi _i } \right) \nonumber \\&\quad +\,\frac{3\alpha _2 V_{\mathrm{DCEff}} \phi _i ^{2}}{\left( {1-w_s } \right) ^{4}} \end{aligned}$$

(13.2)

Equations (12.1)–(12.8) are solved using a five-mode Galerkin procedure described in “Appendix B.” Then, the solutions from the first and second orders, Eqs. (9) and (11), are substituted in the third-order Eq. (7) considering the activation conditions and multiplying the result with the adjoint of the modes $\phi _m \left( x \right) \hbox {e}^{\pm i\omega _m T_0 }$, $\phi _n \left( x \right) \hbox {e}^{\pm i\omega _n T_0 }$, and $\phi _k \left( x \right) \hbox {e}^{\pm i\omega _k T_0 }$, which yield the solvability conditions at the third order as

$$\begin{aligned}&2{\mathrm{i}}{\omega _m}{D_2}{A_m} = - 2\mu {D_1}{A_m} - 2{\mathrm{i}}\mu {B_m}{\omega _m} \nonumber \\&\quad - 2{\mathrm{i}}{\omega _m}{D_1}{B_m} - D_1^2{A_m} - {F_{{m_2}}}{{{\bar{A}}}_m}{{\mathrm{e}}^{2{\mathrm{i}}{\sigma _1}{T_1}}} \nonumber \\&\quad - {F_{m{n_1}}}{{{\bar{A}}}_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {2{\sigma _1} - {\sigma _2}} \right) {T_1}}} \nonumber \\&\quad +\,{K_{k{m_1}}}{B_k}{{{\bar{A}}}_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {2{\sigma _2} + {\sigma _3}} \right) {T_1}}} \nonumber \\&\quad +\, {K_{k{m_1}}}{{\bar{B}}_m}{A_k}{{\mathrm{e}}^{{\mathrm{i}}\left( {2{\sigma _2} + {\sigma _3}} \right) {T_1}}} \nonumber \\&\quad +\, {K_{k{n_1}}}{B_k}{{\bar{A}}_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _2} + {\sigma _3}} \right) {T_1}}}\nonumber \\&\quad +\, {K_{k{n_1}}}{A_k}{{{\bar{B}}}_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _2} + {\sigma _3}} \right) {T_1}}} \nonumber \\&\quad +\, {K_{km{k_1}}}{A_k}{A_m}{{\bar{A}}_k} + {K_{kn{k_1}}}{A_k}{A_n}{{\bar{A}}_k}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _2}{T_1}}} \nonumber \\&\quad +\, {K_{mm{m_1}}}A_m^2{{{\bar{A}}}_m}\nonumber \\&\quad +\, {K_{mm{n_1}}}A_m^2{{{\bar{A}}}_n}{{\mathrm{e}}^{ - {\mathrm{i}}{\sigma _2}{T_1}}} + {K_{mn{m_1}}}{A_m}{A_n}{{\bar{A}}_m}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _2}{T_1}}} \nonumber \\&\quad +\, {K_{mn{n_1}}}{A_m}{A_n}{{{\bar{A}}}_n} + {K_{nn{m_1}}}A_n^2{{\bar{A}}_m}{{\mathrm{e}}^{2{\mathrm{i}}{\sigma _2}{T_1}}}\nonumber \\&\quad +\, {K_{nn{n_1}}}A_n^2{{{\bar{A}}}_n}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _2}{T_1}}} - 2{F_{mk}}{A_k}{{\mathrm{e}}^{{\mathrm{i}}\left( { - {\sigma _1} + 2{\sigma _2} + {\sigma _3}} \right) {T_1}}} \end{aligned}$$

(14.1)

$$\begin{aligned}&2{\mathrm{i}}{\omega _n}{D_2}{A_n} = - 2\mu {D_1}{A_n} - 2{\mathrm{i}}\mu {B_n}{\omega _n} \nonumber \\&\quad - 2{\mathrm{i}}{\omega _n}{D_1}{B_n} - D_1^2{A_n} - {F_{m{n_1}}}{{{\bar{A}}}_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {2{\sigma _1} - {\sigma _2}} \right) {T_1}}}\nonumber \\&\quad - {F_{{n_2}}}{{{\bar{A}}}_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {2{\sigma _1} - 2{\sigma _2}} \right) {T_1}}} - 2{F_{nk}}{A_k}{{\mathrm{e}}^{{\mathrm{i}}\left( { - {\sigma _1} + {\sigma _2} + {\sigma _3}} \right) {T_1}}} \nonumber \\&\quad +\, {S_{k{m_1}}}{B_k}{{\bar{A}}_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _2} + {\sigma _3}} \right) {T_1}}}\nonumber \\&\quad +\, {S_{k{m_1}}}{A_k}{{{\bar{B}}}_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _2} + {\sigma _3}} \right) {T_1}}} + {S_{k{n_1}}}{B_k}{{\bar{A}}_n}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _3}{T_1}}} \nonumber \\&\quad +\, {S_{k{n_1}}}{A_k}{{\bar{B}}_n}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _3}{T_1}}}\nonumber \\&\quad +\, {S_{km{k_1}}}{A_k}{A_m}{{{\bar{A}}}_k}{{\mathrm{e}}^{ - {\mathrm{i}}{\sigma _2}{T_1}}} + {S_{kn{k_1}}}{A_k}{A_n}{{{\bar{A}}}_k} \nonumber \\&\quad +\,{S_{mm{m_1}}}A_m^2{{{\bar{A}}}_m}{{\mathrm{e}}^{ - {\mathrm{i}}{\sigma _2}{T_1}}} + {S_{mm{n_1}}}A_m^2{{{\bar{A}}}_n}{{\mathrm{e}}^{ - 2{\mathrm{i}}{\sigma _2}{T_1}}}\nonumber \\&\quad +\, {S_{mn{m_1}}}{A_m}{A_n}{{{\bar{A}}}_m} + {S_{mn{n_1}}}{A_m}{A_n}{{{\bar{A}}}_n}{{\mathrm{e}}^{ - {\mathrm{i}}{\sigma _2}{T_1}}} \nonumber \\&\quad +\, {S_{nn{m_1}}}A_n^2{{\bar{A}}_m}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _2}{T_1}}} + {S_{nn{n_1}}}A_n^2{{{\bar{A}}}_n} \end{aligned}$$

(14.2)

$$\begin{aligned}&2{\mathrm{i}}{\omega _k}{D_2}{A_k} = - 2\mu {D_1}{A_k} - 2{\mathrm{i}}\mu {B_k}{\omega _k} \nonumber \\&\quad - 2{\mathrm{i}}{\omega _k}{D_1}{B_k} - D_1^2{A_k} \nonumber \\&\quad +\,{T_{mm}}{A_m}{B_m}{{\mathrm{e}}^{{\mathrm{i}}\left( { - 2{\sigma _2} - {\sigma _3}} \right) {T_1}}} + {A_n}{B_m}{T_{nm}}{{\mathrm{e}}^{{\mathrm{i}}\left( { - {\sigma _2} - {\sigma _3}} \right) {T_1}}} \nonumber \\&\quad +\, {T_{nm}}{A_m}{B_n}{{\mathrm{e}}^{{\mathrm{i}}\left( { - {\sigma _2} - {\sigma _3}} \right) {T_1}}}\nonumber \\&\quad +\, {T_{nn}}{A_n}{B_n}{{\mathrm{e}}^{ - {\mathrm{i}}{\sigma _3}{T_1}}} + {T_{kkk}}A_k^2{{{\bar{A}}}_k} \nonumber \\&\quad +\, {T_{kmm}}{A_k}{A_m}{{{\bar{A}}}_m} + {T_{kmn}}{A_k}{A_m}{{{\bar{A}}}_n}{{\mathrm{e}}^{ - {\mathrm{i}}{\sigma _2}{T_1}}}\nonumber \\&\quad +\, {T_{knm}}{A_k}{A_n}{{{\bar{A}}}_m}{{\mathrm{e}}^{{\mathrm{i}}{\sigma _2}{T_1}}} \nonumber \\&\quad +\, {T_{knn}}{A_k}{A_n}{{{\bar{A}}}_n} - 2{F_{mk}}{A_m}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _1} - 2{\sigma _2} - {\sigma _3}} \right) {T_1}}} \nonumber \\&\quad - 2{F_{nk}}{A_n}{{\mathrm{e}}^{{\mathrm{i}}\left( {{\sigma _1} - {\sigma _2} - {\sigma _3}} \right) {T_1}}} \end{aligned}$$

(14.3)

where the coefficients $F_{ij}$, $K_{ijl}$, $S_{ijl}$, and $T_{ijl}$ are defined in “Appendix C.” In order to satisfy the Lagrangian formulation, the terms $D_1^2 A_m$, $D_1^2 A_n$ and $D_1^2 A_k$ in Eqs. (14.1)–(14.3) must vanish. Therefore, we impose the following conditions:

$$\begin{aligned}&2\hbox {i}\omega _m D_1 B_m +D_1^2 A_m =0 \end{aligned}$$

(15.1)

$$\begin{aligned}&2\hbox {i}\omega _n D_1 B_n +D_1^2 A_n =0 \end{aligned}$$

(15.2)

$$\begin{aligned}&2\hbox {i}\omega _k D_1 B_k +D_1^2 A_k =0 \end{aligned}$$

(15.3)

Equations (15.1)–(15.3) are integrated while having no explicit dependence on $T_2$ to obtain

$$\begin{aligned} B_m= & {} \frac{\hbox {i}}{2\omega _m }D_1 A_m \end{aligned}$$

(16.1)

$$\begin{aligned} B_n= & {} \frac{\hbox {i}}{2\omega _n }D_1 A_n \end{aligned}$$

(16.2)

$$\begin{aligned} B_k= & {} \frac{\hbox {i}}{2\omega _k }D_1 A_k \end{aligned}$$

(16.3)

To obtain the modulation equations, we use the method of reconstitution [38] to combine the solvability conditions at each order defined by

$$\begin{aligned} \frac{\partial A_i }{\partial t}=\varepsilon D_1 A_i +\varepsilon ^{2}D_2 A_i \end{aligned}$$

(17)

At this stage, the value of $\varepsilon$ is set to unity, and we use the polar transformation

$$\begin{aligned}&A_m \left( t \right) =\frac{1}{2}a_m \hbox {e}^{\mathrm {i(}\beta _m +\sigma _1 t)} \end{aligned}$$

(18.1)

$$\begin{aligned}&A_n \left( t \right) =\frac{1}{2}a_n \hbox {e}^{\mathrm {i}\left( {\beta _n +\left( {\sigma _1 -\sigma _2 } \right) t} \right) } \end{aligned}$$

(18.2)

$$\begin{aligned}&A_k \left( t \right) =\frac{1}{2}a_k \hbox {e}^{\mathrm {i}\left( {\beta _n +\left( {2\sigma _1 -2\sigma _2 -\sigma _3 } \right) t} \right) } \end{aligned}$$

(18.3)

Combining the solvability conditions at each order Eqs. (10.1)–(10.3) and (14.1)–(14.3) into Eq. (17) and using Eqs. (16.1)–(16.3) with the polar transformation Eqs. (18.1)–(18.3) and separating the real and imaginary parts yield

$$\begin{aligned}&\frac{\mathrm{d}a_m }{\mathrm{d}t}=-\mu a_m +\frac{\mu F_{m_1 } }{2\omega _m^2 }\cos \left( {\beta _m } \right) \\&\quad -\frac{F_{m_1 } }{\omega _m }\sin \left( {\beta _m } \right) +\left( \frac{F_{m_1 } K_{km_1 } }{8\omega _m^3 }\right. \\&\quad \left. +\,\frac{F_{n_1 } K_{kn_1 } }{8\omega _m \omega _n^2 }-\frac{F_{mk} }{\omega _m } \right) a_k \sin \left( {\beta _k -\beta _m } \right) \\&\quad +\,\left( {\frac{F_{m_2 } }{2\omega _m }-\frac{F_{k_1 } K_{km_1 } }{8\omega _k^2 \omega _m }} \right) a_m \sin \left( {2\beta _m } \right) \\&\quad +\,\left( {\frac{F_{mn_1 } }{2\omega _m }-\frac{F_{k_1 } K_{kn_1 } }{8\omega _k^2 \omega _m }} \right) a_n \sin \left( {\beta _m +\beta _n } \right) \\&\quad -\frac{R_{m_2 } }{4\omega _m }a_k a_n \sin \left( {\beta _k -\beta _m -\beta _n } \right) \\&\quad +\left( \frac{K_{km_1 } R_{m_2 } }{32\omega _m^3 }+\,\frac{K_{kn_1 } R_{n_2 } }{32\omega _m \omega _n^2 }\right. \\&\quad \left. +\frac{K_{knk_1 } }{8\omega _m } \right) a_k^2 a_n \sin \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\frac{R_{m_1 } }{4\omega _m }a_k a_m \sin \left( {\beta _k -2\beta _m } \right) \\&\quad -\left( {\frac{R_{k_3 } K_{km_1 } }{32\omega _k^2 \omega _m }+\frac{K_{nnm_1 } }{8\omega _m }} \right) a_m a_n^2 \sin ( 2( \beta _m-\beta _n )) \\&\quad -\left( {\frac{R_{k_3 } K_{kn_1 } }{32\omega _k^2 \omega _m }\frac{K_{nnn_1 } }{8\omega _m }} \right) a_n^3 \sin \left( {\beta _m -\beta _n } \right) \\&\quad +\,\left( \frac{R_{k_1 } K_{kn_1 } }{32\omega _k^2 \omega _m }-\frac{R_{k_2 } K_{km_1 } }{32\omega _k^2 \omega _m }\right. \end{aligned}$$

$$\begin{aligned}&\quad \left. +\,\frac{K_{mmn_1 } }{8\omega _m }-\frac{K_{mnm_1 } }{8\omega _m } \right) a_m^2 a_n \sin \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\left( \frac{\mu K_{km_1 } }{8\omega _m^2 }-\frac{\mu K_{km_1 } }{8\omega _k \omega _m }\right. \nonumber \\&\quad \left. +\,\frac{\mu R_{m_1 } }{8\omega _m^2 } \right) a_k a_m \cos \left( {\beta _k -2\beta _m } \right) \nonumber \\&\quad +\,\left( \frac{\mu K_{kn_1 } }{8\omega _m \omega _n }-\frac{\mu K_{kn_1 } }{8\omega _k \omega _m }\right. \nonumber \\&\quad \left. +\,\frac{\mu R_{m_2 } }{8\omega _m^2 } \right) a_k a_n \cos \left( {\beta _k -\beta _m -\beta _n } \right) \\&a_m \frac{\mathrm{d}\beta _m }{\mathrm{d}t}=-\frac{\mu F_{m_1 } }{2\omega _m^2 }\sin \left( {\beta _m } \right) -\frac{F_{m_1 } }{\omega _m }\cos \left( {\beta _m } \right) \nonumber \\&\quad +\,\left( \frac{F_{mk} }{\omega _m }-\frac{F_{n_1 } K_{kn_1 } }{8\omega _m \omega _n^2 }\right. \nonumber \\&\quad \left. -\frac{F_{m_1 } K_{km_1 } }{8\omega _m^3 } \right) a_k \cos \left( {\beta _k -\beta _m } \right) \nonumber \\&\quad -\left( {\frac{\mu ^{2}}{2\omega _m }+\sigma _1 } \right) a_m -\left( \frac{K_{mmm_1 } }{8\omega _m }\right. \nonumber \\&\quad \left. +\,\frac{K_{km_1 } R_{k_1 } }{32\omega _k^2 \omega _m } \right) a_m^3 -\left( \frac{K_{mnn_1 } }{8\omega _m }\right. \nonumber \\&\quad \left. +\,\frac{K_{kn_1 } R_{k_2 } }{32\omega _k^2 \omega _m } \right) a_n^2 a_m \nonumber \\&\quad -\left( \frac{K_{kmk_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{n_1 } }{32\omega _m \omega _n^2 }\right. \nonumber \\&\quad \left. +\,\frac{K_{km_1 } R_{m_1 } }{32\omega _m^3 } \right) a_k^2 a_m \nonumber \\&\quad +\,\left( {\frac{F_{m_2 } }{2\omega _m }-\frac{F_{k_1 } K_{km_1 } }{8\omega _k^2 \omega _m }} \right) a_m \cos \left( {2\beta _m } \right) \nonumber \end{aligned}$$

(19.1)

$$\begin{aligned}&\quad +\,\left( {\frac{F_{mn_1 } }{2\omega _m }-\frac{F_{k_1 } K_{kn_1 } }{8\omega _k^2 \omega _m }} \right) a_n \cos \left( {\beta _m +\beta _n } \right) \nonumber \\&\quad -\frac{R_{m_2 } }{4\omega _m }a_k a_n \cos \left( {\beta _k -\beta _m -\beta _n } \right) \nonumber \\&\quad -\left( \frac{K_{knk_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{n_2 } }{32\omega _m \omega _n^2 }\right. \nonumber \\&\quad \left. +\,\frac{K_{km_1 } R_{m_2 } }{32\omega _m^3 } \right) a_k^2 a_n \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad -\frac{R_{m_1 } }{4\omega _m }a_k a_m \cos \left( {\beta _k -2\beta _m } \right) \nonumber \\&\quad -\left( {\frac{K_{nnm_1 } }{8\omega _m }+\frac{K_{km_1 } R_{k_3 } }{32\omega _k^2 \omega _m }} \right) a_m a_n^2 \cos \left( {2\left( {\beta _m -\beta _n } \right) } \right) \nonumber \\&\quad -\left( {\frac{K_{nnn_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{k_3 } }{32\omega _k^2 \omega _m }} \right) a_n^3 \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad -\left( \frac{K_{mmn_1 } }{8\omega _m }+\frac{K_{mnm_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{k_1 } }{32\omega _k^2 \omega _m }\right. \nonumber \\&\quad \left. +\,\frac{K_{km_1 } R_{k_2 } }{32\omega _k^2 \omega _m } \right) a_m^2 a_n \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\left( \frac{\mu K_{km_1 } }{8\omega _m^2 }-\frac{\mu K_{km_1 } }{8\omega _k \omega _m }\right. \nonumber \\&\quad \left. +\,\frac{\mu R_{m_1 } }{8\omega _m^2 } \right) a_k a_m \sin \left( {\beta _k -2\beta _m } \right) \nonumber \\&\quad +\,\left( \frac{\mu K_{kn_1 } }{8\omega _m \omega _n }-\frac{\mu K_{kn_1 } }{8\omega _k \omega _m }\right. \nonumber \\&\quad \left. +\,\frac{\mu R_{m_2 } }{8\omega _m^2 } \right) a_k a_n \sin \left( {\beta _k -\beta _m -\beta _n } \right) \\&\frac{\mathrm{d}a_n }{\mathrm{d}t}=-\mu a_n +\frac{\mu F_{n_1 } }{2\omega _n^2 }\cos \left( {\beta _n } \right) \nonumber \\&\quad -\frac{F_{n_1 } }{\omega _n }\sin \left( {\beta _n } \right) +\left( \frac{F_{m_1 } S_{km_1 } }{8\omega _m^2 \omega _n }+\frac{F_{n_1 } S_{kn_1 } }{8\omega _n^3 }\right. \nonumber \end{aligned}$$

(19.2)

$$\begin{aligned}&\quad \left. -\frac{F_{nk} }{\omega _n } \right) a_k \sin \left( {\beta _k -\beta _n } \right) \nonumber \\&\quad +\,\left( {\frac{F_{mn_1 } }{2\omega _n }-\frac{F_{k_1 } S_{km_1 } }{8\omega _k^2 \omega _n }} \right) a_m \sin \left( {\beta _m +\beta _n } \right) \nonumber \\&\quad +\,\frac{R_{n_2 } }{4\omega _n }a_k a_n \sin \left( {\beta _k -2\beta _n } \right) +\left( \frac{F_{n_2 } }{2\omega _n }\right. \nonumber \\&\quad \left. -\frac{F_{k_1 } S_{kn_1 } }{8\omega _k^2 \omega _n } \right) a_n \sin \left( {2\beta _n } \right) \nonumber \\&\quad +\,\frac{R_{n_1 } }{4\omega _n }a_k a_m \sin \left( {\beta _k -\beta _m -\beta _n } \right) +\,\left( \frac{\mu S_{km_1 } }{8\omega _m \omega _n }\right. \nonumber \\&\quad \left. -\frac{\mu S_{km_1 } }{8\omega _k \omega _n }+\frac{\mu R_{n_1 } }{8\omega _n^2 } \right) a_k a_m \cos (\beta _k -\beta _m-\beta _n ) \nonumber \\&\quad +\,\left( {\frac{\mu S_{kn_1 } }{8\omega _n^2 }-\frac{\mu S_{kn_1 } }{8\omega _k \omega _n }+\frac{\mu R_{n_2 } }{8\omega _n^2 }} \right) a_k a_n \cos ( \beta _k \nonumber \\&\quad -2\beta _n )+\,\left( {\frac{R_{k_1 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mmm_1 } }{8\omega _n }} \right) a_m^3 \sin \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\left( {\frac{R_{k_1 } S_{kn_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mmn_1 } }{8\omega _n }} \right) a_m^2 a_n \sin \left( {2\left( {\beta _m -\beta _n } \right) } \right) \nonumber \\&\quad +\,\left( {\frac{S_{km_1 } R_{m_1 } }{32\omega _m^2 \omega _n }+\frac{S_{kmk_1 } }{8\omega _n }+\frac{S_{kn_1 } R_{n_1 } }{32\omega _n^3 }} \right) a_k^2 a_m \sin ( \beta _m \nonumber \\&\quad -\,\beta _n )+\,\left( \frac{R_{k_2 } S_{kn_1 } }{32\omega _k^2 \omega _n }-\frac{R_{k_3 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mnn_1 } }{8\omega _n }\right. \nonumber \\&\quad \left. -\frac{S_{nnm_1 } }{8\omega _n } \right) a_m a_n^2 \sin \left( {\beta _m -\beta _n } \right) \\&a_n \frac{\mathrm{d}\beta _n }{\mathrm{d}t}=-\frac{\mu F_{n_1 } }{2\omega _n^2 }\sin \left( {\beta _n } \right) -\frac{F_{n_1 } }{\omega _n }\cos \left( {\beta _n } \right) \nonumber \end{aligned}$$

(19.3)

$$\begin{aligned}&\quad -\left( {\frac{F_{m_1 } S_{km_1 } }{8\omega _m^2 \omega _n }+\frac{F_{n_1 } S_{kn_1 } }{8\omega _n^3 }-\frac{F_{nk} }{\omega _n }} \right) a_k \cos \left( {\beta _k -\beta _n } \right) \nonumber \\&\quad +\,\left( {\frac{F_{mn_1 } }{2\omega _n }-\frac{F_{k_1 } S_{km_1 } }{8\omega _k^2 \omega _n }} \right) a_m \cos \left( {\beta _m +\beta _n } \right) \nonumber \\&\quad -\frac{R_{n_2 } }{4\omega _n }a_k a_n \cos \left( {\beta _k -2\beta _n } \right) +\left( \frac{F_{n_2 } }{2\omega _n }\right. \nonumber \\&\quad \left. -\frac{F_{k_1 } S_{kn_1 } }{8\omega _k^2 \omega _n } \right) a_n \cos \left( {2\beta _n } \right) \nonumber \\&\quad -\frac{R_{n_1 } }{4\omega _n }a_k a_m \cos \left( {\beta _k -\beta _m -\beta _n } \right) +\,\left( \frac{\mu S_{km_1 } }{8\omega _m \omega _n }\right. \nonumber \\&\quad \left. -\,\frac{\mu S_{km_1 } }{8\omega _k \omega _n }+\frac{\mu R_{n_1 } }{8\omega _n^2 } \right) a_k a_m \sin \left( {\beta _k -\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\left( \frac{\mu S_{kn_1 } }{8\omega _n^2 }-\frac{\mu S_{kn_1 } }{8\omega _k \omega _n }\right. \nonumber \\&\quad \left. +\,\frac{\mu R_{n_2 } }{8\omega _n^2 } \right) a_k a_n \sin \left( {\beta _k -2\beta _n } \right) -\left( \frac{R_{k_1 } S_{km_1 } }{32\omega _k^2 \omega _n }\right. \nonumber \\&\quad \left. +\,\frac{S_{mmm_1 } }{8\omega _n } \right) a_m^3 \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad -\left( \frac{R_{k_1 } S_{kn_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mmn_1 } }{8\omega _n } \right) a_m^2 a_n \cos \left( {2\left( {\beta _m -\beta _n } \right) } \right) \nonumber \\&\quad -\left( \frac{R_{m_1 } S_{km_1 } }{32\omega _m^2 \omega _n }+\frac{S_{kmk_1 } }{8\omega _n }\right. \nonumber \\&\quad \left. +\,\frac{R_{n_1 } S_{kn_1 } }{32\omega _n^3 } \right) a_k^2 a_m \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad -\left( \frac{R_{k_3 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mnn_1 } }{8\omega _n }\right. \nonumber \end{aligned}$$

(19.4)

$$\begin{aligned}&\quad \left. +\,\frac{S_{nnm_1 } }{8\omega _n }+\frac{R_{k_2 } S_{kn_1 } }{32\omega _k^2 \omega _n } \right) a_m a_n^2 \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&\quad -\left( {\frac{R_{k_2 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mnm_1 } }{8\omega _n }} \right) a_m^2 a_n \nonumber \\&\quad -\left( {\frac{R_{k_3 } S_{kn_1 } }{32\omega _k^2 \omega _n }+\frac{S_{nnn_1 } }{8\omega _n }} \right) a_n^3 \nonumber \\&\quad -\left( {\frac{R_{m_2 } S_{km_1 } }{32\omega _m^2 \omega _n }+\frac{S_{knk_1 } }{8\omega _n }+\frac{R_{n_2 } S_{kn_1 } }{32\omega _n^3 }} \right) a_k^2 a_n \nonumber \\&\quad +\,a_n \left( {\sigma _2 -\sigma _1 -\frac{\mu ^{2}}{2\omega _n }} \right) \\&\frac{\mathrm{d}a_k }{\mathrm{d}t}=-\mu a_k +\frac{\mu F_{k_1 } }{2\omega _k^2 }\cos \left( {\beta _k } \right) -\frac{F_{k_1 } }{\omega _k }\sin \left( {\beta _k } \right) \nonumber \\&\quad +\,\left( {\frac{F_{mk} }{\omega _k }-\frac{F_{m_1 } T_{mm} }{8\omega _k \omega _m^2 }-\frac{F_{n_1 } T_{nm} }{8\omega _k \omega _n^2 }} \right) a_m \sin ( \beta _k \nonumber \\&\quad -\beta _m ) +\,\left( \frac{F_{nk} }{\omega _k }-\frac{F_{m_1 } T_{nm} }{8\omega _k \omega _m^2 }\right. \nonumber \\&\quad \left. -\frac{F_{n_1 } T_{nn} }{8\omega _k \omega _n^2 } \right) a_n \sin \left( {\beta _k -\beta _n } \right) \nonumber \\&\quad -\frac{R_{k_2 } }{4\omega _k }a_m a_n \sin \left( {\beta _k -\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\left( {\frac{\mu R_{k_1 } }{8\omega _k^2 }-\frac{\mu T_{mm} }{8\omega _k \omega _m }} \right) a_m^2 \cos \left( {\beta _k -2\beta _m } \right) \nonumber \\&\quad +\,\left( {\frac{\mu R_{k_3 } }{8\omega _k^2 }-\frac{\mu T_{nn} }{8\omega _k \omega _n }} \right) a_n^2 \cos \left( {\beta _k -2\beta _n } \right) \nonumber \\&\quad -\frac{R_{k_1 } }{4\omega _k }a_m^2 \sin \left( {\beta _k -2\beta _m } \right) \nonumber \\&\quad -\frac{R_{k_3 } }{4\omega _k }a_n^2 \sin \left( {\beta _k -2\beta _n } \right) +\,\left( \frac{\mu R_{k_2 } }{8\omega _k^2 }-\frac{\mu T_{nm} }{8\omega _k \omega _m }\right. \nonumber \\&\quad \left. -\frac{\mu T_{nm} }{8\omega _k \omega _n } \right) a_m a_n \cos \left( {\beta _k -\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\left( \frac{T_{kmn} }{8\omega _k }-\frac{T_{knm} }{8\omega _k }\right. \nonumber \\&\quad \left. +\,\frac{R_{m_2 } T_{mm} }{32\omega _k \omega _m^2 }-\frac{R_{m_1 } T_{nm} }{32\omega _k \omega _m^2 }+\frac{R_{n_2 } T_{nm} }{32\omega _k \omega _n^2 }\right. \nonumber \end{aligned}$$

(19.5)

$$\begin{aligned}&\quad \left. -\frac{R_{n_1 } T_{nn} }{32\omega _k \omega _n^2 } \right) a_k a_m a_n \sin \left( {\beta _m -\beta _n } \right) \\&a_k \frac{\mathrm{d}\beta _k }{\mathrm{d}t}=-\frac{\mu F_{k_1 } }{2\omega _k^2 }\sin \left( {\beta _k } \right) -\frac{F_{k_1 } }{\omega _k }\cos \left( {\beta _k } \right) \nonumber \\&\quad +\,\left( \frac{F_{mk} }{\omega _k }-\frac{F_{m_1 } T_{mm} }{8\omega _k \omega _m^2 }\right. \nonumber \\&\quad \left. -\frac{F_{n_1 } T_{nm} }{8\omega _k \omega _n^2 } \right) a_m \cos \left( {\beta _k -\beta _m } \right) \nonumber \\&\quad +\,\left( {\frac{F_{nk} }{\omega _k }-\frac{F_{m_1 } T_{nm} }{8\omega _k \omega _m^2 }-\frac{F_{n_1 } T_{nn} }{8\omega _k \omega _n^2 }} \right) a_n \cos \left( {\beta _k -\beta _n } \right) \nonumber \\&\quad -\frac{R_{k_2 } }{4\omega _k }a_m a_n \cos \left( {\beta _k -\beta _m -\beta _n } \right) \nonumber \\&\quad +\,\left( {\frac{\mu T_{mm} }{8\omega _k \omega _m }-\frac{\mu R_{k_1 } }{8\omega _k^2 }} \right) a_m^2 \sin \left( {\beta _k -2\beta _m } \right) \nonumber \\&\quad +\,\left( {\frac{\mu T_{nn} }{8\omega _k \omega _n }-\frac{\mu R_{k_3 } }{8\omega _k^2 }} \right) a_n^2 \sin \left( {\beta _k -2\beta _n } \right) \nonumber \\&\quad -\frac{R_{k_1 } }{4\omega _k }a_m^2 \cos \left( {\beta _k -2\beta _m } \right) \nonumber \\&\quad -\frac{R_{k_3 } }{4\omega _k }a_n^2 \cos \left( {\beta _k -2\beta _n } \right) \nonumber \\&\quad +\,\left( \frac{\mu T_{nm} }{8\omega _k \omega _m }+\frac{\mu T_{nm} }{8\omega _k \omega _n }\right. \nonumber \\&\quad \left. -\frac{\mu R_{k_2 } }{8\omega _k^2 } \right) a_m a_n \sin \left( {\beta _k -\beta _m -\beta _n } \right) \nonumber \\&\quad -\left( \frac{T_{kmn} }{8\omega _k }+\frac{T_{knm} }{8\omega _k }+\frac{R_{m_2 } T_{mm} }{32\omega _k \omega _m^2 }+\,\frac{R_{m_1 } T_{nm} }{32\omega _k \omega _m^2 }\right. \nonumber \\&\quad \left. +\frac{R_{n_2 } T_{nm} }{32\omega _k \omega _n^2 }+\frac{R_{n_1 } T_{nn} }{32\omega _k \omega _n^2 } \right) a_k a_m a_n \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&a_k \left( {\sigma _3 -2\sigma _1 +2\sigma _2 -\frac{\mu ^{2}}{2\omega _k }} \right) \nonumber \\&\quad -\left( \frac{T_{kmm} }{8\omega _k }+\frac{R_{m_1 } T_{mm} }{32\omega _k \omega _m^2 }\right. \nonumber \\&\quad \left. +\,\frac{R_{n_1 } T_{nm} }{32\omega _k \omega _n^2 } \right) a_k a_m^2 -\frac{T_{kkk} }{8\omega _k }a_k^3 \nonumber \\&\quad -\left( \frac{T_{knn} }{8\omega _k }+\frac{R_{m_2 } T_{nm} }{32\omega _k \omega _m^2 }\right. \nonumber \\&\quad \left. +\,\frac{R_{n_2 } T_{nn} }{32\omega _k \omega _n^2 } \right) a_k a_n^2 \end{aligned}$$

(19.6)

Equations (19.1)–(19.6) govern the amplitude and phase modulation of each mode. The fixed points of these equations are obtained by solving the right-hand side using the arc length continuation method [39]. Then, the dynamic solution is expressed using Eqs. (9) and (11) as

$$\begin{aligned} w(x,t)= & {} \phi _m \left( x \right) a_m \cos \left( {\varOmega t+\beta _m } \right) \nonumber \\&+\,\phi _n \left( x \right) a_n \cos \left( {\varOmega t+\beta _n } \right) \nonumber \\&+\,\phi _k \left( x \right) a_k \cos \left( {2\varOmega t+\beta _k } \right) \nonumber \\&+\,\frac{\mu }{2\omega _n }\phi _n \left( x \right) a_n \sin \left( {\varOmega t+\beta _n } \right) \nonumber \\&+\,\frac{\mu }{2\omega _m }\phi _m \left( x \right) a_m \sin \left( {\varOmega t+\beta _m } \right) \nonumber \\&+\,\frac{\mu }{2\omega _k }\phi _k \left( x \right) a_k \sin \left( {2\varOmega t+\beta _k } \right) \nonumber \\&+\,\left( {\frac{R_{n_1 } }{8\omega _n ^{2}}\phi _n \left( x \right) +\frac{R_{m_1 } }{8\omega _m^2 }\phi _m \left( x \right) } \right) \nonumber \\&a_k a_m \cos \left( {\varOmega t+\beta _k -\beta _m } \right) \nonumber \\&+\,\left( \frac{R_{n_2 } }{8\omega _n ^{2}}\phi _n \left( x \right) \right. \nonumber \\&\left. +\,\frac{R_{m_2 } }{8\omega _m^2 }\phi _m \left( x \right) \right) a_k a_n \cos \left( {\varOmega t+\beta _k -\beta _n } \right) \nonumber \\&+\,\frac{R_{k_1 } }{8\omega _k ^{2}}\phi _k \left( x \right) a_m^2 \cos \left( {2\varOmega t+2\beta _m } \right) \nonumber \\&+\,\frac{R_{k_2 } }{8\omega _k ^{2}}\phi _k \left( x \right) a_m a_n \cos \left( {2\varOmega t+\beta _m +\beta _n } \right) \nonumber \\&+\,\frac{R_{k_3 } }{8\omega _k ^{2}}\phi _k \left( x \right) a_n^2 \cos \left( {2\varOmega t+2\beta _n } \right) \nonumber \\&+\,\frac{1}{2}a_k a_m \psi _{km} \left( x \right) \cos \left( {3\varOmega t+\beta _k +\beta _m } \right) \nonumber \\&+\,\frac{1}{2}a_k a_n \psi _{kn} \left( x \right) \cos \left( {3\varOmega t+\beta _n +\beta _k } \right) \nonumber \\&+\,\frac{1}{2}a_k^2 \psi _{k_2 } \left( x \right) \cos \left( {4\varOmega t+2\beta _k } \right) \nonumber \\&+\,\frac{1}{4}a_k^2 \psi _{kk} \left( x \right) \nonumber \\&+\,\frac{1}{4}a_m^2 \psi _{mm} \left( x \right) +\frac{1}{4}a_n^2 \psi _{nn} \left( x \right) \nonumber \\&+\,\frac{1}{2}a_m a_n \psi _{mn} \left( x \right) \cos \left( {\beta _m -\beta _n } \right) \nonumber \\&+\,\frac{F_{k_1 } }{2\omega _k ^{2}}\phi _k \left( x \right) \cos \left( {2\varOmega t} \right) \nonumber \\&+\frac{F_{n_1 } }{2\omega _n ^{2}}\phi _n \left( x \right) \cos \left( {\varOmega t} \right) \nonumber \\&+\,\frac{F_{m_1 } }{2\omega _m^2 }\phi _m \left( x \right) \cos \left( {\varOmega t} \right) \end{aligned}$$

(20)

The stability of each fixed point is determined by first expressing the modulation using the complex Cartesian form detailed in “Appendix D.” Then, the eigenvalues of the system Jacobian are used to assess stability.

3 Results and discussions

One should note that the partial electrode electrostatic actuation breaks the symmetry of forcing causing hybridization of the first symmetric and antisymmetric modes of the arch beam near crossing where the 1:1 and 2:1 internal resonances are observed [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)]. In addition, the quadratic nature of the excitation causes direct excitation of the first and second symmetric modes due to the high values of AC voltages [12, 23]. This makes the dynamic response more complex, especially when combining 1:1 and 2:1 internal resonances.

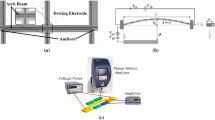
The natural frequencies and the dynamic response of the silicon arch beam under consideration are measured using a stroboscopic video microscopy (a high-speed camera) from Polytec [40]. The fast Fourier transform (FFT) is used to measure the natural frequencies for different $V_{\mathrm{Th}}$ using ring down tests. The dynamic response is measured by sweeping the excitation frequency for various DC and AC electrostatic loads.

As shown in [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)], the first natural frequency, $f_{1}$, increases as increasing the compressive load induced by the applied electrothermal voltage while the first antisymmetric, $f_{2}$, and the second symmetric, $f_{3}$, natural frequencies decrease. Increasing further the electrothermal voltage leads to the crossing of the first symmetric frequency and first antisymmetric frequency, which is necessary condition to activate the 1:1 internal resonance between both modes (Fig. 1a). On the other hand, Fig. 1b shows that the ratio between the second symmetric and first antisymmetric natural frequencies remains equal to two for a wide range of electrothermal voltage, $V_{\mathrm{Th}}$, until crossing while the first symmetric mode has a ratio around two at and slightly after crossing. Hence, this may lead to the possible activation of simultaneous 2:1 and 1:1 internal resonances among different modes.

Fig. 1

Measured natural frequencies. a The variation of the ratio between the first antisymmetric and the first symmetric natural frequencies with the electrothermal voltage, $V_{\mathrm{Th}}$. The inset shows the variation of the first three natural frequencies of the arch beam with $V_{\mathrm{Th}}$. b The variation of the ratio between the second symmetric and first symmetric and antisymmetric natural frequencies with $V_{\mathrm{Th}}$. $f_{1}$ and $f_{3}$ denote the first and second symmetric natural frequencies. $f_{2}$ indicates the first antisymmetric natural frequency

To explore the dynamics of the arch beam around crossing, we experimentally sweep the excitation frequency around the first symmetric and antisymmetric resonance frequencies for different AC excitation voltages. The static DC load is kept constant at $V_{\mathrm{DC}}=15\,\hbox {V}$. The electrothermal voltage is fixed to certain values before, on, and after crossing of the first symmetric and antisymmetric natural frequencies. As sweeping the frequency, we experimentally record the displacement of the arch beam at the midpoint, $x=l/2$, and the quarter, $x=l/4$. One should mention that all the experiments were conducted at atmospheric pressure requiring high AC excitation amplitudes to drive the arch beam nonlinearly.

3.1 At the quarter point: $x=l/4$

Experimentally at high AC voltages, the vibrational amplitude responses near the first antisymmetric frequency at the quarter of the arch beam, before crossing for $V_{\mathrm{Th}}=1.4\hbox { V}$, is split into two branches of two peaks (Fig. 2a). At this level of electrothermal voltage, the two branches of the response represent the direct excitation of the first antisymmetric and symmetric modes with no signs of 1:1 internal resonance interaction. As the AC voltage is increased, we notice the emergence of another response branch near $f=90\,\hbox {kHz}$ suggesting a nonlinear interaction via 2:1 internal resonance between the first antisymmetric mode and the second symmetric mode in addition to the direct excitation of the second symmetric frequency leading to a bistate solution. Numerically, we simulate, for the same $V_{\mathrm{Th}}=1.4\,\hbox {V}$, the dynamic response of the arch beam for different electrostatic excitation forces using the Galerkin method [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)], implementing 4 modes (Fig. 2b) and MTS (Fig. 2c). The Galerkin results in Fig. 2b show good agreement compared to the experimental data in Fig. 2a. Also, the results show that as increasing the excitation force, the range of interaction between both contributed modes in the 2:1 internal resonance broadens. The multiple timescales simulations in Fig. 2c confirm these results and also demonstrate the new branch caused by the 2:1 internal resonance between the second symmetric and first antisymmetric modes without any contribution of the first symmetric mode. This can be further confirmed by examining the contribution of each mode generated using MTS around the first antisymmetric frequency (Fig. 2d). The first symmetric mode $a_{1}$ does not have any 1:1 internal resonance that affects the total response shown in Fig. 2c, while the second symmetric mode $a_{3}$ contributes due to the 2:1 ratio with the first antisymmetric mode $a_{2}$, in addition to the direct excitation of the second symmetric frequency from using high AC voltage. One should mention that this combined effect of the 2:1 internal resonance and the direct excitation was investigated in [23] between the first two symmetric modes of an arch microbeam. It was found that both the nonlinear internal resonance and the direct excitation have considerable impact on the response. Also, at $V_{\mathrm{Th}}=1.4\hbox { V}$, no mode hybridization was shown even for high effective DC bias voltages [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)]; hence, it does not affect the nonlinear coupling among different modes.

The system undergoes a Hopf bifurcation as experiencing 2:1 internal resonance leading to a bistate stable solution. The 2:1 internal resonance interaction disappears through a saddle-node bifurcation. For high AC voltages, the arch beam passes a Hopf bifurcation as shown using the MTS method (Fig. 2c). Drawing the time history and fast Fourier transform (FFT) for the case $V_\mathrm{AC}=80\hbox { V}$ at the upper branch (Fig. 2e), the middle scatters (Fig. 2f), and the lower branch (Fig. 2g) prove the strong contribution of the second symmetric mode into the upper branch. Also, Fig. 2f suggests that the system undergoes quasi-periodic motion as passing from the upper branch to the lower branch dominated by the first antisymmetric mode. Experimentally, the stroboscopic camera was not able to detect any quasi-periodic motion as experiencing 2:1 internal resonance.

Fig. 2

a Experimentally measured frequency response curves at the arch quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=1.4\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. b Simulated frequency response curves at the quarter point, using the Galerkin method, around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=1.4\hbox { V}, V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. The inset shows the linear response at the quarter point for $V_{\mathrm{Th}}=1.4\hbox { V}, V_{\mathrm{DC}}=15\hbox { V}$, and $V_\mathrm{AC}=15\hbox {V}$. c Comparison of the simulated, Galerkin and MTS, and experimental frequency response curves at the quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=1.4\hbox { V}, V_{\mathrm{DC}}=15\hbox { V}$, and $V_\mathrm{AC}=80\hbox { V}$. d Frequency response curves from MTS showing the contribution of the first symmetric and antisymmetric modes as well as the second symmetric mode into the total response shown in (c). The continuous lines denote stable solutions, while the dashed lines indicate unstable solutions. e–g Time history and FFT for the case $V_{\mathrm{Th}}=1.4\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and $V_\mathrm{AC}=80\,\hbox {V}$ at $88\,\hbox {kHz}$, $90\,\hbox {kHz}$, and $91\,\hbox {kHz}$, respectively

Increasing the electrothermal voltage such that the interaction is closer to the crossing zone $V_{\mathrm{Th}}=1.9\,\hbox {V}$, both first symmetric and antisymmetric modes approach each other and start to hybridize [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)]. Experimentally, the response shows a complex dynamic motion as increasing the AC excitation voltages, as shown in Fig. 3a. The softening part of the response combines the influence of each symmetric and antisymmetric modes due to the 1:1 and 2:1 internal resonances. Similarly, the hardening part of the response is a contribution resulted from the second symmetric mode via the 2:1 internal resonance with the first antisymmetric mode. Numerically, we simulated, using Galerkin and MTS, the arch response for different AC excitation voltages (Fig. 3b–d) to confirm the experimental observations. For moderate AC values, the motion of the arch beam near $f=83\;\hbox {kHz}$ merges into one mode solution around the first symmetric mode. The high sensitivity to a small electrostatic excitation and the mode coupling near crossing are extensively studied in the first part of this work [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)]. As increasing more the AC excitation voltages, the motion around the first antisymmetric mode increases and a hardening-type response emerges due to the contribution of the second symmetric mode into the response caused by the 2:1 internal resonance. The high contribution of the second symmetric mode is confirmed in Fig. 3e. Plotting the time history and FFT at different frequencies located in the softening (Fig. 3f) and hardening (Fig. 3g) bands for $V_\mathrm{AC}=120\hbox { V}$ proves the strong contribution of the second symmetric mode via 2:1 internal resonance at the hardening band.

Fig. 3

a Experimentally measured frequency response curves at the arch quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=1.9\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. b, c Simulated frequency response curves at the quarter point, using Galerkin, around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=1.9\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. d Comparison of the simulated, Galerkin and MTS, and experimental frequency response curve at the quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=1.9\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and $V_\mathrm{AC}=100\hbox { V}$. e Frequency response curves from MTS showing the contribution of the first symmetric and antisymmetric modes as well as the second symmetric mode into the total response shown in (d). The continuous lines denote the stable solutions, while the dashed lines denote the unstable solutions. f, g Time history and FFT for the case $V_{\mathrm{Th}}=1.9\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and $V_\mathrm{AC}=120\hbox { V}$ at $80\,\hbox {kHz}$ (located at the softening band) and $87\,\hbox {kHz}$ (located at the hardening band), respectively

Fig. 4

a Experimentally measured frequency response curves at the arch quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=2\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. b, c Simulated frequency response curves at the quarter point, using Galerkin, around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=2\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. d, e Comparison of simulated, Galerkin and MTS, and experimental frequency response curve at the quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=2\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, $V_\mathrm{AC}=90\hbox { V}$, and $V_\mathrm{AC}=110\hbox { V}$, respectively. f, g Frequency response curves from MTS showing the contribution of the first symmetric and antisymmetric modes as well as the second symmetric mode into the total response shown in (d, e), respectively. The continuous lines denote stable solutions, while the dashed lines indicate unstable solutions

At $V_{\mathrm{Th}}=2\,\hbox {V}$, slightly after crossing where the first symmetric and antisymmetric modes interchange places but remain almost having same resonance frequencies, both first symmetric and antisymmetric modes hybridize as exceeding certain threshold of voltage excitation [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)]. Experimentally, the response shows the merging of both modes due to 1:1 internal resonance dominated by the first symmetric mode demonstrating softening behavior for the arch beam, as shown in Fig. 4a. The response indicates the emerging, experimentally and numerically, of a hardening band at high AC excitation voltages demonstrating a simultaneous 2:1 internal resonance with the 1:1 internal resonance among the contributed modes. A good agreement is observed in Fig. 4d, e between the results obtained from MTS and the experimental one. Also, the contribution of each amplitude in Fig. 4f, g demonstrates the strengthening of the hardening behavior due to the increase in the AC voltage. The emergence of the hardening band in the response of the first antisymmetric mode is a result of the 2:1 internal resonance interaction with the second symmetric mode.

After crossing, both first symmetric and antisymmetric modes exchange behaviors. Then, we experimentally show, for $V_{\mathrm{Th}}=2.6\,\hbox {V}$ and low AC voltages, the arch beam experiences hardening as known for the first antisymmetric mode. As increasing the AC voltages, the first antisymmetric mode starts to exhibit softening in addition to mixed behavior due to the interaction with the first symmetric mode as exciting the arch beam (Fig. 5a). Numerically, Fig. 5b–g confirms the phenomena observed experimentally. Figure 5b–d, f demonstrates that the arch beam has a mixed behavior passing from hardening to softening behavior around the first antisymmetric resonance frequency. Figure 5e–g proves that the first and second symmetric mode contribute even far from crossing to the response of the first antisymmetric mode. Good agreement is shown among the experimental, the Galerkin, and MTS results.

Fig. 5

a Experimentally measured frequency response curves at the quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=2.6\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. b, c Simulated frequency response curves at the quarter point, using Galerkin, around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=2.6\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and for different AC voltages. d, e Comparison of simulated, Galerkin and MTS, and experimental frequency response curve at the quarter point around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{Th}}=2.6\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, $V_\mathrm{AC}=60\hbox { V}$, and $V_\mathrm{AC}=80\hbox { V}$, respectively. f, g Frequency response curves from MTS showing the contribution of the first symmetric and antisymmetric modes as well as the second symmetric mode into the total response shown in (d, e), respectively. The continuous lines denote stable solutions, while the dashed lines indicate unstable solutions

3.2 At the midpoint: $x=l/2$

Because the midpoint is known as a nodal point of the first antisymmetric mode, it would be interesting to monitor the arch behavior at that point. The nodal point of the first antisymmetric mode is shifted due to the high effective static electrostatic voltage. Also, we showed in [A. Z. Hajjaj, F. K. Alfosail, N. Jaber, S. Ilyas, and M. I. Younis: Theoretical and Experimental Investigations of the Crossover Phenomenon in Micromachined Arch Resonator: Part I—Linear Problem. Nonlinear Dynamics. Submitted (2019)] that at crossing the mode shapes of the first symmetric and antisymmetric modes hybridize even for low static electrostatic voltage.

For moderate values of AC voltages (Fig. 6a, b), the frequency sweeps, experimentally measured around the first symmetric and antisymmetric resonance frequencies at the midpoint, show that the first antisymmetric frequency starts to be measurable at the midpoint since the mode shapes have been changed due to the break of symmetry. Figure 6a, b also shows that the first antisymmetric frequency has softening behavior after crossing instead of hardening behavior.

Numerically, we simulate using the Galerkin method the frequency response for different electrothermal voltages before, at, and after crossing for different values of AC excitation voltages. Figure 6c, d shows that even away from crossing, the arch beam shows high amplitude of motion at the midpoint around the first antisymmetric frequency due to the 2:1 internal resonance with the second symmetric frequency. Getting closer to the crossing zone, the amplitude of motion at the midpoint seems to be equal to the motion at the quarter point resulted from the mode shapes hybridization (Fig. 6e–h). After crossing, for moderate values of AC voltages, the nonlinear behavior of the first antisymmetric frequency changes from hardening to softening as shown in previous results in Fig. 5b, c.

Fig. 6

a, b Experimentally measured frequency response curves at the arch midpoint around the first symmetric and antisymmetric resonance frequencies for different electrothermal voltages at $V_{\mathrm{DC}}=15\,\hbox {V}$, and $V_\mathrm{AC}=60\,\hbox {V}$$V_{\mathrm{DC}}=80\,\hbox {V}$, respectively. c–j Simulated frequency response curves at the midpoint, using Galerkin, around the first symmetric and antisymmetric resonance frequencies at $V_{\mathrm{DC}}=15\,\hbox {V}$ and for different AC voltages. c, d$V_{\mathrm{Th}}=1.4\hbox { V}$. e, f$V_{\mathrm{Th}}=1.9\hbox { V}$. g, h$V_{\mathrm{Th}}=2\hbox { V}$. i, j$V_{\mathrm{Th}}=2.6\hbox { V}$. The inset in (c) shows the linear response at the midpoint for $V_{\mathrm{Th}}=1.4\hbox { V}$, $V_{\mathrm{DC}}=15\hbox { V}$, and $V_\mathrm{AC}=15\,\hbox {V}$

4 Conclusions

We investigated experimentally and theoretically the 1:1 internal resonance between the first symmetric and antisymmetric modes of an electrothermally tuned and electrostatically actuated arch MEMS resonator. A simultaneous 2:1 internal resonance was also shown with the second symmetric mode as experiencing the 1:1 internal resonance. A complex and rich dynamic behavior was demonstrated. Theoretically, we studied the nonlinear dynamic response of the arch beam using the Galerkin and multiple scales methods. Good agreement among experimental and theoretical results was shown. Other methods can be used in future research to characterize the dynamic response of the system, such as shooting and continuation techniques. Moreover, this work motivates further research to exploit multiple and/or simultaneous types of internal resonances of arch resonators for practical applications, such as sensors, frequency stability, energy dissipation, and mechanical amplifier.

Appendices

Appendix A. Definition of coefficients used in Eqs. (10.1)–(10.3)

To simplify the expressions, we use the following definition to represent the integrals:

$$\begin{aligned}&\left\langle {A,B} \right\rangle =\mathop {\int }_0^1 {A(x)B(x)} \;\mathrm{d}x \end{aligned}$$

(A.1)

$$\begin{aligned}&\mu =\frac{c}{2} \end{aligned}$$

(A.2)

$$\begin{aligned}&F_{m_1 } =\alpha _2 V_\mathrm{AC} V_{\mathrm{DC}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \left( x \right) }{\left( {w_s \left( x \right) -1} \right) ^{2}}\hbox {d}x} \right) \end{aligned}$$

(A.3)

$$\begin{aligned}&F_{n_1 } =\alpha _2 V_\mathrm{AC} V_{\mathrm{DC}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _n \left( x \right) }{\left( {w_s \left( x \right) -1} \right) ^{2}}\hbox {d}x} \right) \end{aligned}$$

(A.4)

$$\begin{aligned}&F_{k_1 } =\frac{1}{4}\alpha _2 V_\mathrm{AC}^2 \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \left( x \right) }{\left( {w_s \left( x \right) -1} \right) ^{2}}\hbox {d}x} \right) \end{aligned}$$

(A.5)

$$\begin{aligned}&R_{m_1 } =2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {\phi _m ,w_s ^{\prime \prime }} \right\rangle \right. \nonumber \\&\qquad \quad \left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _m ,\phi _k ^{\prime \prime }} \right\rangle +\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _m ,\phi _m ^{\prime \prime }} \right\rangle \right) \nonumber \\&\qquad \quad +\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.6)

$$\begin{aligned}&R_{m_2 } =2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {\phi _m ,w_s ^{\prime \prime }} \right\rangle \right. \nonumber \\&\qquad \quad \left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _m ,\phi _k ^{\prime \prime }} \right\rangle +\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _m ,\phi _n ^{\prime \prime }} \right\rangle \right) \nonumber \\&\qquad \quad +\,6V_{\mathrm{DCEff}} \alpha _2 \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \phi _n }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.7)

$$\begin{aligned}&R_{n_1 } =2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {\phi _n ,w_s ^{\prime \prime }} \right\rangle \right. \nonumber \\&\qquad \quad \left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _n ,\phi _k ^{\prime \prime }} \right\rangle +\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _n ,\phi _m ^{\prime \prime }} \right\rangle \right) \nonumber \\&\qquad \quad +\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \phi _n }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.8)

$$\begin{aligned}&R_{n_2 } =2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {\phi _n ,w_s ^{\prime \prime }} \right\rangle \right. \nonumber \\&\qquad \quad \left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _n ,\phi _k ^{\prime \prime }} \right\rangle +\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _n ,\phi _n ^{\prime \prime }} \right\rangle \right) \nonumber \\&\qquad \quad +\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.9)

$$\begin{aligned}&R_{k_1 } =\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _k ,w_s ^{\prime \prime }} \right\rangle \right. \nonumber \\&\qquad \quad \left. +\,2\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _k ,\phi _m ^{\prime \prime }} \right\rangle \right) \nonumber \\&\qquad \quad +\,3\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.10)

$$\begin{aligned}&R_{k_2 } =2\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _k ,w_s ^{\prime \prime }} \right\rangle \right. \nonumber \\&\qquad \quad \left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _k ,\phi _m ^{\prime \prime }} \right\rangle +\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _k ,\phi _n ^{\prime \prime }} \right\rangle \right) \nonumber \\&\qquad \quad +\,\alpha _2 6V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \phi _n }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.11)

$$\begin{aligned}&R_{k_3 } =\alpha _1 \left( \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _k ,w_s ^{\prime \prime }} \right\rangle \right. \nonumber \\&\qquad \quad \left. +\,2\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _k ,\phi _n ^{\prime \prime }} \right\rangle \right) \nonumber \\&\qquad \quad +\,3\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.12)

Appendix B. Galerkin procedure

Here we explain the Galerkin procedure used to find the particular solutions by solving the boundary value problem in Eqs. (12.1)–(12.7) defined by

$$\begin{aligned} H[\omega ]= & {} H^{iv} - N H^{\prime {\prime }} - 2\alpha _{1}{{w}_{s}}^{\prime {\prime }}\left( \mathop \int \limits _{0}^{1}w_{s}^{\prime } H^{\prime } \hbox {d}x\right) \nonumber \\&-\frac{2{\alpha }_{2}V_{\mathrm{DCeff}}^{2}}{(1-w_{s})^{3}} H-\omega _{i}^{2}H \end{aligned}$$

(B.1)

We express the function H as a superposition of five mode shapes $f_{i}(x)$ given by

$$\begin{aligned} H=\sum _{i=1}^{n=5} {q_i f_i (x)} \end{aligned}$$

(B.2)

where $q_{i}$ are coefficients to be solved for in the Galerkin procedure. The $f_{i}(x)$ are the mode shapes of the straight clamped–clamped beam. Then, the equation is reduced via orthogonality of the mode shapes to a set of five algebraic equations that are solved to obtain the value of coefficients.

Appendix C. Definition of coefficient used in Eqs. (14.1)–(14.3)

To simplify the expressions, we use the definition in (C.1) to represent the integrals in (C.2)–(C.34).

$$\begin{aligned} \langle A,B \rangle= & {} \mathop {\int }\limits _{0}^{1} A(x)B(x)\mathrm{d}x \end{aligned}$$

(C.1)

$$\begin{aligned} F_{mk}= & {} -\alpha _2 V_\mathrm{AC} V_{\mathrm{DC}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m }{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) \end{aligned}$$

(C.2)

$$\begin{aligned} F_{m_2 }= & {} -\frac{1}{2}\alpha _2 V_\mathrm{AC}^2 \left( {\mathop {\int }\limits _0^1 \frac{\phi _m ^{2}}{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) \end{aligned}$$

(C.3)

$$\begin{aligned} F_{mn_1 }= & {} -\frac{1}{2}\alpha _2 V_\mathrm{AC}^2 \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n }{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) \end{aligned}$$

(C.4)

$$\begin{aligned} F_{nk}= & {} \alpha _2 V_\mathrm{AC} V_{\mathrm{DC}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n }{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) \end{aligned}$$

(C.5)

$$\begin{aligned} F_{n_2 }= & {} \frac{1}{2}\alpha _2 V_\mathrm{AC}^2 \left( {\mathop {\int }\limits _0^1 \frac{\phi _n ^{2}}{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) \end{aligned}$$

(C.6)

$$\begin{aligned} K_{kmk_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{km} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&+\,\varGamma \left( {\phi _m ,\psi _{kk} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&\left. +\varGamma \left( {w_s ,\psi _{km} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( 2\varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {\phi _k ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&+\,\varGamma \left( {w_s ,\psi _{kk} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&\left. +\varGamma \left( {\phi _k ,\phi _k } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{km} ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{kk} ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \left( x \right) ^{2}\psi _{kk} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \psi _{km} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.7)

$$\begin{aligned} K_{knk_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{kn} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&+\,\varGamma \left( {\phi _n ,\psi _{kk} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&\left. +\varGamma \left( {w_s ,\psi _{kn} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( 2\varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {\phi _k ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&+\,\varGamma \left( {w_s ,\psi _{kk} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&\left. +\varGamma \left( {\phi _k ,\phi _k } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{kk} ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{kn} ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{kk} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \psi _{kn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.8)

$$\begin{aligned} K_{mmm_1 }= & {} 2\alpha _1 \varGamma \left( {\phi _m ,\psi _{mm} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+\,2\alpha _1 \varGamma \left( {w_s ,\psi _{mm} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+\,3\alpha _1 \varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+\,2\alpha _1 \varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{mm} ^{\prime \prime },\phi _m \left( x \right) } \right\rangle \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m ^{2}\psi _{mm} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.9)

$$\begin{aligned} K_{mnm_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\psi _{mm} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\psi _{mm} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{mm} ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,4\alpha _1 \varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+2\alpha _1 \varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{mm} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m ^{2}\psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.10)

$$\begin{aligned} K_{nnm_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _n ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,\alpha _1 \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+2\alpha _1 \varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.11)

$$\begin{aligned} K_{km_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _k ^{\prime \prime }\phi _m } \right\rangle +\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _m ^{\prime \prime }\phi _m } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.12)

$$\begin{aligned} K_{mmn_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,\alpha _1 \varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+2\alpha _1 \varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m ^{2}\psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.13)

$$\begin{aligned} K_{mnn_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\psi _{nn} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{nn} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{nn} ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _m ^{2}\psi _{nn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.14)

$$\begin{aligned} K_{nnn_1 }= & {} 2\alpha _1 \varGamma \left( {\phi _n ,\psi _{nn} } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+2\alpha _1 \varGamma \left( {w_s ,\psi _{nn} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+2\alpha _1 \varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{nn} ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+\,3\alpha _1 \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{nn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.15)

$$\begin{aligned} K_{km_2 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _k ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _m ^{\prime \prime }\phi _m } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.16)

$$\begin{aligned} K_{kn_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {w_s ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _k ^{\prime \prime },\phi _m } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _n ^{\prime \prime },\phi _m } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \phi _n }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.17)

$$\begin{aligned} S_{kmk_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{km} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _m ,\psi _{kk} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{km} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\psi _{kk} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&+\,\varGamma \left( {\phi _k ,\phi _k } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \nonumber \\&\left. +\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{kk} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{km} ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {\phi _k ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{kk} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n \psi _{km} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.18)

$$\begin{aligned} S_{knk_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{kn} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\psi _{kk} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{kn} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\psi _{kk} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _k ,\phi _k } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{kk} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{kn} ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {\phi _k ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _n ^{2}\psi _{kk} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n \psi _{kn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.19)

$$\begin{aligned} S_{mmm_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\psi _{mm} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mm} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{mm} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,3\alpha _1 \varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{mm} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.20)

$$\begin{aligned} S_{mnm_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\psi _{mm} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\psi _{mm} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{mm} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _n ^{2}\psi _{mm} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.21)

$$\begin{aligned} S_{nnm_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _n ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,\alpha _1 \left( 2\varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _n ^{2}\psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.22)

$$\begin{aligned} S_{km_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _k ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \phi _n }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.23)

$$\begin{aligned} S_{mmn_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _n ^{\prime \prime }\phi _n } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.24)

$$\begin{aligned}&S_{mnn_1 } =2\alpha _1 \left( \varGamma \left( {\phi _m ,\psi _{nn} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{nn} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{nn} ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _n ^{2}\psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _m \phi _n \psi _{nn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.25)

$$\begin{aligned} S_{nnn_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _n ,\psi _{nn} } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{nn} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{nn} ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,3\alpha _1 \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _n ^{2}\psi _{nn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.26)

$$\begin{aligned} S_{kn_1 }= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {w_s ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _k ^{\prime \prime },\phi _n } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\phi _n ^{\prime \prime },\phi _n } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.27)

$$\begin{aligned} T_{mm}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _m ^{\prime \prime }\phi _k } \right\rangle \right) \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.28)

$$\begin{aligned} T_{nm}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\phi _n ^{\prime \prime }\phi _k } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \phi _n }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.29)

$$\begin{aligned} T_{nn}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n ^{2}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(C.30)

$$\begin{aligned} T_{kkk}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{kk} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _k ,\psi _{k_2 } } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{kk} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\psi _{k_2 } } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{kk} ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{k_2 } ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,3\alpha _1 \varGamma \left( {\phi _k ,\phi _k } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \nonumber \\&+6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \left( x \right) ^{2}\psi _{kk} \left( x \right) }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k \left( x \right) ^{2}\psi _{k_2 } \left( x \right) }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.31)

$$\begin{aligned} T_{kmm}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{mm} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _m ,\psi _{km} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mm} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _m } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&+\,\varGamma \left( {w_s ,\psi _{km} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _k } \right\rangle \nonumber \\&\left. +\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{mm} ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{km} ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,2\varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {\phi _m ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \psi _{km} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k ^{2}\psi _{mm} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.32)

$$\begin{aligned} T_{knm}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _m ,\psi _{kn} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{kn} } \right) \left\langle {\phi _m ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {\phi _n ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&+\varGamma \left( {w_s ,\phi _m } \right) \left\langle {\psi _{kn} ^{\prime \prime },\phi _k } \right\rangle \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _m \psi _{kn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k ^{2}\psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.33)

$$\begin{aligned} T_{kmn}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{mn} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\psi _{km} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{mn} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _m ,\phi _n } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {\phi _m ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{km} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _k ,\phi _m } \right) \left\langle {\phi _n ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{km} ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{mn} ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n \psi _{km} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k ^{2}\psi _{mn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.34)

$$\begin{aligned} T_{knn}= & {} 2\alpha _1 \left( \varGamma \left( {\phi _k ,\psi _{nn} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {\phi _n ,\psi _{kn} } \right) \left\langle {w_s ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{nn} } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {\phi _n ,\phi _n } \right) \left\langle {\phi _k ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\psi _{kn} } \right) \left\langle {\phi _n ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +\,\varGamma \left( {w_s ,\phi _k } \right) \left\langle {\psi _{nn} ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,2\alpha _1 \left( \varGamma \left( {w_s ,\phi _n } \right) \left\langle {\psi _{kn} ^{\prime \prime },\phi _k } \right\rangle \right. \nonumber \\&\left. +2\varGamma \left( {\phi _k ,\phi _n } \right) \left\langle {\phi _n ^{\prime \prime },\phi _k } \right\rangle \right) \nonumber \\&+\,6\alpha _2 V_{\mathrm{DCEff}} \left( \left( {\mathop {\int }\limits _0^1 \frac{\phi _k \phi _n \psi _{kn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right. \nonumber \\&\left. +\,\left( {\mathop {\int }\limits _0^1 \frac{\phi _k ^{2}\psi _{nn} }{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \right) \end{aligned}$$

(C.35)

Appendix D. Cartesian form of the modulation equations Eqs. (19.1)–(19.6)

To express the modulation equation in complex Cartesian form, we use the complex amplitude definition given by

$$\begin{aligned}&A_m =\frac{1}{2}\left( {p_m -\hbox {i }q_m } \right) e^{\mathrm {i}\lambda _1 t}\end{aligned}$$

(D.1)

$$\begin{aligned}&A_n =\frac{1}{2}\left( {p_n -\hbox {i }q_n } \right) e^{\mathrm {i}\lambda _2 t} \end{aligned}$$

(D.2)

$$\begin{aligned}&A_k =\frac{1}{2}\left( {p_k -\hbox {i }q_k } \right) e^{\mathrm {i}\lambda _3 t} \end{aligned}$$

(D.3)

Equations (D.1)–(D.3) are substituted in Eqs. (10.1)–(10.3) and Eqs. (14.1)–(14.3), and using Eqs. (16.1)–(16.3) with the method of reconstitution defined by Eq. (17) while separating the imaginary and real parts yields

$$\begin{aligned} \frac{\mathrm{d}p_m }{\mathrm{d}t}= & {} -\mu p_m \nonumber \\&+\,\left( {\frac{F_{k_1 } K_{km_1 } }{8\omega _k^2 \omega _m }-\frac{\mu ^{2}}{2\omega _m }-\sigma _1 -\frac{F_{m_2 } }{2\omega _m }} \right) q_m \nonumber \\&+\,\left( {\frac{F_{k_1 } K_{kn_1 } }{8\omega _k^2 \omega _m }-\frac{F_{mn_1 } }{2\omega _m }} \right) q_n +\,\frac{\mu F_{m_1 } }{2\omega _m^2 } \nonumber \\&+\,\left( {\frac{F_{mk} }{\omega _m }-\frac{F_{n_1 } K_{kn_1 } }{8\omega _m \omega _n^2 }-\frac{F_{m_1 } K_{km_1 } }{8\omega _m^3 }} \right) q_k \nonumber \\&-\left( {\frac{K_{mmn_1 } }{4\omega _m }+\frac{K_{kn_1 } R_{k_1 } }{16\omega _k^2 \omega _m }} \right) p_n q_m p_m \nonumber \\&+\,\left( {\frac{\mu K_{km_1 } }{8\omega _m^2 }-\frac{\mu K_{km_1 } }{8\omega _k \omega _m }+\frac{\mu R_{m_1 } }{8\omega _m^2 }} \right) \left( {p_k p_m +q_k q_m } \right) \nonumber \\&+\,\left( {\frac{\mu K_{kn_1 } }{8\omega _m \omega _n }-\frac{\mu K_{kn_1 } }{8\omega _k \omega _m }+\frac{\mu R_{m_2 } }{8\omega _m^2 }} \right) \left( {p_k p_n +q_k q_n } \right) \nonumber \\&-\left( {\frac{K_{mnn_1 } }{8\omega _m }+\frac{K_{nnm_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{k_2 } }{32\omega _k^2 \omega _m }+\frac{K_{km_1 } R_{k_3 } }{32\omega _k^2 \omega _m }} \right) q_m q_n^2 \nonumber \\&-\left( {\frac{K_{nnm_1 } }{4\omega _m }+\frac{K_{km_1 } R_{k_3 } }{16\omega _k^2 \omega _m }} \right) p_n q_n p_m \nonumber \\&+\,\left( {\frac{K_{mmn_1 } }{8\omega _m }-\frac{K_{mnm_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{k_1 } }{32\omega _k^2 \omega _m }-\frac{K_{km_1 } R_{k_2 } }{32\omega _k^2 \omega _m }} \right) \nonumber \\&\left( {q_n p_m^2 -q_m^2 q_n } \right) \nonumber \\&+\,\left( {\frac{K_{nnm_1 } }{8\omega _m }-\frac{K_{mnn_1 } }{8\omega _m }-\frac{K_{kn_1 } R_{k_2 } }{32\omega _k^2 \omega _m }+\frac{K_{km_1 } R_{k_3 } }{32\omega _k^2 \omega _m }} \right) p_n^2 q_m \nonumber \\&+\,\frac{R_{m_1 } }{4\omega _m }\left( {p_k q_m -q_k p_m } \right) \nonumber \\&-\left( {q_m p_k^2 +q_k^2 q_m } \right) \left( {\frac{K_{kmk_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{n_1 } }{32\omega _m \omega _n^2 }+\frac{K_{km_1 } R_{m_1 } }{32\omega _m^3 }} \right) \nonumber \\&-\left( {\frac{K_{mmm_1 } }{8\omega _m }+\frac{K_{km_1 } R_{k_1 } }{32\omega _k^2 \omega _m }} \right) \left( {q_m^3 +p_m^2 q_m } \right) \nonumber \\&-\left( {q_n p_k^2 +q_k^2 q_n } \right) \left( {\frac{K_{knk_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{n_2 } }{32\omega _m \omega _n^2 }+\frac{K_{km_1 } R_{m_2 } }{32\omega _m^3 }} \right) \nonumber \\&+\,\frac{R_{m_2 } }{4\omega _m }\left( {p_k q_n -p_n q_k } \right) \end{aligned}$$

(D.4)

$$\begin{aligned} \frac{\mathrm{d}q_m }{\mathrm{d}t}= & {} -\mu q_m +\left( {\frac{\mu ^{2}}{2\omega _m }+\sigma _1 -\frac{F_{m_2 } }{2\omega _m }+\frac{F_{k_1 } K_{km_1 } }{8\omega _k^2 \omega _m }} \right) p_m \nonumber \\&+\,\left( {\frac{F_{k_1 } K_{kn_1 } }{8\omega _k^2 \omega _m }-\frac{F_{mn_1 } }{2\omega _m }} \right) p_n +\frac{F_{m_1 } }{\omega _m } \nonumber \\&+\,\left( {\frac{F_{n_1 } K_{kn_1 } }{8\omega _m \omega _n^2 }-\frac{F_{mk} }{\omega _m }+\frac{F_{m_1 } K_{km_1 } }{8\omega _m^3 }} \right) p_k \nonumber \\&+\,\frac{R_{m_1 } }{4\omega _m }\left( {p_k p_m +q_k q_m } \right) +\frac{R_{m_2 } }{4\omega _m }\left( {p_k p_n +q_k q_n } \right) \nonumber \\&+\,\left( {\frac{\mu K_{kn_1 } }{8\omega _k \omega _m }-\frac{\mu K_{kn_1 } }{8\omega _m \omega _n }-\frac{\mu R_{m_2 } }{8\omega _m^2 }} \right) \left( {p_k q_n -p_n q_k } \right) \nonumber \\&+\,\left( {\frac{\mu K_{km_1 } }{8\omega _k \omega _m }-\frac{\mu K_{km_1 } }{8\omega _m^2 }-\frac{\mu R_{m_1 } }{8\omega _m^2 }} \right) \left( {p_k q_m -q_k p_m } \right) \nonumber \\&+\,\left( {\frac{K_{nnm_1 } }{4\omega _m }+\frac{K_{km_1 } R_{k_3 } }{16\omega _k^2 \omega _m }} \right) p_n q_m q_n \nonumber \\&+\,\left( {\frac{K_{kn_1 } R_{k_2 } }{32\omega _k^2 \omega _m }+\frac{K_{km_1 } R_{k_3 } }{32\omega _k^2 \omega _m }} \right) \left( {p_n^2 p_m +q_n^2 p_m } \right) \nonumber \\&+\,\left( {\frac{K_{kn_1 } R_{k_1 } }{32\omega _k^2 \omega _m }+\frac{K_{mmn_1 } }{8\omega _m }} \right) \left( {p_n p_m^2 -p_n q_m^2 } \right) \nonumber \\&+\,\left( {\frac{K_{mnn_1 } }{8\omega _m }+\frac{K_{nnm_1 } }{8\omega _m }} \right) \left( {p_n^2 p_m -q_n^2 p_m } \right) \nonumber \\&+\,\left( {\frac{K_{mnm_1 } }{8\omega _m }\frac{K_{km_1 } R_{k_2 } }{32\omega _k^2 \omega _m }} \right) \left( {p_n p_m^2 +p_n q_m^2 } \right) \nonumber \\&+\,\left( {\frac{K_{mmm_1 } }{8\omega _m }+\frac{K_{km_1 } R_{k_1 } }{32\omega _k^2 \omega _m }} \right) \left( {p_m^3 +q_m^2 p_m } \right) \nonumber \\&+\,\left( {\frac{K_{mmn_1 } }{4\omega _m }+\frac{K_{kn_1 } R_{k_1 } }{16\omega _k^2 \omega _m }} \right) q_m q_n p_m \nonumber \\&+\,\left( {\frac{K_{nnn_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{k_3 } }{32\omega _k^2 \omega _m }} \right) \left( {p_n^3 +q_n^2 p_n } \right) \nonumber \\&+\,\left( {\frac{K_{kmk_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{n_1 } }{32\omega _m \omega _n^2 }+\frac{K_{km_1 } R_{m_1 } }{32\omega _m^3 }} \right) \nonumber \\&\left( {p_m p_k^2 +p_m q_k^2 } \right) \nonumber \\&+\,\left( {\frac{K_{knk_1 } }{8\omega _m }+\frac{K_{kn_1 } R_{n_2 } }{32\omega _m \omega _n^2 }+\frac{K_{km_1 } R_{m_2 } }{32\omega _m^3 }} \right) \nonumber \\&\left( {p_n p_k^2 +p_n q_k^2 } \right) \end{aligned}$$

(D.5)

$$\begin{aligned} \frac{\mathrm{d}p_n }{\mathrm{d}t}= & {} -\mu p_n \nonumber \\&+\,q_n \left( {\frac{F_{k_1 } S_{kn_1 } }{8\omega _k^2 \omega _n }-\frac{\mu ^{2}}{2\omega _n }-\sigma _1 +\sigma _2 -\frac{F_{n_2 } }{2\omega _n }} \right) \nonumber \\&+\,\left( {\frac{F_{k_1 } S_{km_1 } }{8\omega _k^2 \omega _n }-\frac{F_{mn_1 } }{2\omega _n }} \right) q_m \nonumber \\&+\,\left( {\frac{F_{nk} }{\omega _n }-\frac{F_{m_1 } S_{km_1 } }{8\omega _m^2 \omega _n }-\frac{F_{n_1 } S_{kn_1 } }{8\omega _n^3 }} \right) q_k \nonumber \\&+\,\left( {\frac{\mu R_{n_2 } }{8\omega _n^2 }-\frac{\mu S_{kn_1 } }{8\omega _k \omega _n }+\frac{\mu S_{kn_1 } }{8\omega _n^2 }} \right) \left( {p_k p_n +q_k q_n } \right) \nonumber \\&+\,\left( {\frac{\mu R_{n_1 } }{8\omega _n^2 }-\frac{\mu S_{km_1 } }{8\omega _k \omega _n }+\frac{\mu S_{km_1 } }{8\omega _m \omega _n }} \right) \left( {p_k p_m +q_k q_m } \right) \nonumber \\&+\,\frac{R_{n_1 } }{4\omega _n }\left( {p_k q_m -q_k p_m } \right) \nonumber \\&+\,\frac{R_{n_2 } }{4\omega _n }\left( {p_k q_n -p_n q_k } \right) \nonumber \\&+\,\left( {\frac{S_{mmn_1 } }{8\omega _n }-\frac{S_{mnm_1 } }{8\omega _n }-\frac{R_{k_2 } S_{km_1 } }{32\omega _k^2 \omega _n }++\frac{R_{k_1 } S_{kn_1 } }{32\omega _k^2 \omega _n }} \right) p_m^2 q_n \nonumber \\&-\left( {\frac{R_{k_1 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mmm_1 } }{8\omega _n }} \right) \left( {q_m^3 +p_m^2 q_m } \right) \nonumber \\&-\left( {\frac{R_{k_1 } S_{kn_1 } }{16\omega _k^2 \omega _n }+\frac{S_{mmn_1 } }{4\omega _n }} \right) p_m p_n q_m \nonumber \\&-\left( {\frac{R_{k_3 } S_{kn_1 } }{32\omega _k^2 \omega _n }+\frac{S_{nnn_1 } }{8\omega _n }} \right) \left( {q_n^3 +p_n^2 q_n } \right) \nonumber \\&-\left( {\frac{R_{k_3 } S_{km_1 } }{16\omega _k^2 \omega _n }+\frac{S_{nnm_1 } }{4\omega _n }} \right) p_n q_n p_m \nonumber \\&+\,\left( {\frac{R_{k_2 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mmn_1 } }{8\omega _n }+\frac{S_{mnm_1 } }{8\omega _n }+\frac{R_{k_1 } S_{kn_1 } }{32\omega _k^2 \omega _n }} \right) q_m^2 q_n \nonumber \\&-\left( {\frac{R_{k_3 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mnn_1 } }{8\omega _n }+\frac{S_{nnm_1 } }{8\omega _n }+\frac{R_{k_2 } S_{kn_1 } }{32\omega _k^2 \omega _n }} \right) q_m q_n^2 \nonumber \\&+\,p_n^2 q_m \left( {\frac{R_{k_3 } S_{km_1 } }{32\omega _k^2 \omega _n }-\frac{S_{mnn_1 } }{8\omega _n }+\frac{S_{nnm_1 } }{8\omega _n }-\frac{R_{k_2 } S_{kn_1 } }{32\omega _k^2 \omega _n }} \right) \nonumber \\&-\left( {\frac{R_{m_1 } S_{km_1 } }{32\omega _m^2 \omega _n }+\frac{S_{kmk_1 } }{8\omega _n }+\frac{R_{n_1 } S_{kn_1 } }{32\omega _n^3 }} \right) \left( {q_m p_k^2 +q_k^2 q_m } \right) \nonumber \\&-\left( {\frac{R_{m_2 } S_{km_1 } }{32\omega _m^2 \omega _n }+\frac{S_{knk_1 } }{8\omega _n }+\frac{R_{n_2 } S_{kn_1 } }{32\omega _n^3 }} \right) \nonumber \\&\left( {q_n p_k^2 +q_k^2 q_n } \right) +\frac{\mu F_{n_1 } }{2\omega _n^2 } \end{aligned}$$

(D.6)

$$\begin{aligned} \frac{\mathrm{d}q_n }{\mathrm{d}t}= & {} -\mu q_n \nonumber \\&+\,p_n \left( {\frac{\mu ^{2}}{2\omega _n }+\sigma _1 -\sigma _2 -\frac{F_{n_2 } }{2\omega _n }+\frac{F_{k_1 } S_{kn_1 } }{8\omega _k^2 \omega _n }} \right) \nonumber \\&+\,\left( {\frac{F_{k_1 } S_{km_1 } }{8\omega _k^2 \omega _n }-\frac{F_{mn_1 } }{2\omega _n }} \right) p_m \nonumber \\&+\,\left( {\frac{F_{m_1 } S_{km_1 } }{8\omega _m^2 \omega _n }-\frac{F_{nk} }{\omega _n }+\frac{F_{n_1 } S_{kn_1 } }{8\omega _n^3 }} \right) p_k \nonumber \\&+\,\left( {\frac{\mu R_{n_2 } }{8\omega _n^2 }-\frac{\mu S_{kn_1 } }{8\omega _k \omega _n }+\frac{\mu S_{kn_1 } }{8\omega _n^2 }} \right) \left( {p_n q_k -p_k q_n } \right) \nonumber \\&+\,\left( {\frac{\mu R_{n_1 } }{8\omega _n^2 }-\frac{\mu S_{km_1 } }{8\omega _k \omega _n }+\frac{\mu S_{km_1 } }{8\omega _m \omega _n }} \right) \left( {q_k p_m -p_k q_m } \right) \nonumber \\&+\,\frac{R_{n_1 } }{4\omega _n }\left( {p_k p_m +q_k q_m } \right) \nonumber \\&+\,\frac{R_{n_2 } }{4\omega _n }\left( {p_k p_n +q_k q_n } \right) \nonumber \\&+\,\left( {\frac{R_{k_2 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mnm_1 } }{8\omega _n }} \right) \left( {p_n p_m^2 +p_n q_m^2 } \right) \nonumber \\&+\,\left( {\frac{S_{mmn_1 } }{8\omega _n }+\frac{R_{k_1 } S_{kn_1 } }{32\omega _k^2 \omega _n }} \right) \left( {p_n p_m^2 -p_n q_m^2 } \right) \nonumber \\&+\,\left( {\frac{S_{mnn_1 } }{8\omega _n }+\frac{R_{k_2 } S_{kn_1 } }{32\omega _k^2 \omega _n }} \right) \left( {p_m p_n^2 +p_m q_n^2 } \right) \nonumber \\&+\,\left( {\frac{R_{k_3 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{nnm_1 } }{8\omega _n }} \right) \left( {p_m p_n^2 -p_m q_n^2 } \right) \nonumber \\&+\,\left( {\frac{R_{k_1 } S_{kn_1 } }{16\omega _k^2 \omega _n }+\frac{S_{mmn_1 } }{4\omega _n }} \right) p_m q_m q_n \nonumber \\&+\,\left( {\frac{R_{k_3 } S_{km_1 } }{16\omega _k^2 \omega _n }+\frac{S_{nnm_1 } }{4\omega _n }} \right) p_n q_m q_n \nonumber \\&+\,\left( {p_m^3 +q_m^2 p_m } \right) \left( {\frac{R_{k_1 } S_{km_1 } }{32\omega _k^2 \omega _n }+\frac{S_{mmm_1 } }{8\omega _n }} \right) \nonumber \\&+\,\left( {\frac{R_{k_3 } S_{kn_1 } }{32\omega _k^2 \omega _n }+\frac{S_{nnn_1 } }{8\omega _n }} \right) \left( {p_n^3 +q_n^2 p_n } \right) \nonumber \\&+\,\left( {\frac{R_{m_1 } S_{km_1 } }{32\omega _m^2 \omega _n }+\frac{S_{kmk_1 } }{8\omega _n }+\frac{R_{n_1 } S_{kn_1 } }{32\omega _n^3 }} \right) \nonumber \\&\left( {p_m p_k^2 +p_m q_k^2 } \right) \nonumber \\&+\,\left( {\frac{R_{m_2 } S_{km_1 } }{32\omega _m^2 \omega _n }+\frac{S_{knk_1 } }{8\omega _n }+\frac{R_{n_2 } S_{kn_1 } }{32\omega _n^3 }} \right) \nonumber \\&\left( {p_n p_k^2 +p_n q_k^2 } \right) +\frac{F_{n_1 } }{\omega _n } \end{aligned}$$

(D.7)

$$\begin{aligned} \frac{\mathrm{d}p_k }{\mathrm{d}t}= & {} -\mu p_k +\left( {2\sigma _2 -2\sigma _1 +\sigma _3 -\frac{\mu ^{2}}{2\omega _k }} \right) q_k \nonumber \\&+\,q_m \left( {\frac{F_{mk} }{\omega _k }-\frac{F_{m_1 } T_{mm} }{8\omega _k \omega _m^2 }-\frac{F_{n_1 } T_{nm} }{8\omega _k \omega _n^2 }} \right) \nonumber \\&+\,q_n \left( {\frac{F_{nk} }{\omega _k }-\frac{F_{m_1 } T_{nm} }{8\omega _k \omega _m^2 }-\frac{F_{n_1 } T_{nn} }{8\omega _k \omega _n^2 }} \right) \nonumber \\&-\left( {\frac{T_{kmm} }{8\omega _k }+\frac{R_{m_1 } T_{mm} }{32\omega _k \omega _m^2 }+\frac{R_{n_1 } T_{nm} }{32\omega _k \omega _n^2 }} \right) \nonumber \\&\left( {q_k p_m^2 +q_k q_m^2 } \right) \nonumber \\&+\,\left( {\frac{\mu R_{k_2 } }{8\omega _k^2 }-\frac{\mu T_{nm} }{8\omega _k \omega _m }-\frac{\mu T_{nm} }{8\omega _k \omega _n }} \right) \left( {p_m p_n -q_m q_n } \right) \nonumber \\&-\frac{R_{k_2 } }{4\omega _k }\left( {p_n q_m +p_m q_n } \right) -\frac{R_{k_1 } }{2\omega _k }p_m q_m \nonumber \\&+\,\left( {\frac{\mu R_{k_1 } }{8\omega _k^2 }-\frac{\mu T_{mm} }{8\omega _k \omega _m }} \right) \left( {p_m^2 -q_m^2 } \right) \nonumber \\&+\,\left( {\frac{\mu R_{k_3 } }{8\omega _k^2 }-\frac{\mu T_{nn} }{8\omega _k \omega _n }} \right) \left( {p_n^2 -q_n^2 } \right) \nonumber \\&-\frac{T_{kkk} }{8\omega _k }\left( {p_k^2 q_k +q_k^3 } \right) \nonumber \\&-\left( \frac{T_{kmn} }{8\omega _k }+\frac{T_{knm} }{8\omega _k }+\frac{R_{m_2 } T_{mm} }{32\omega _k \omega _m^2 }+\frac{R_{m_1 } T_{nm} }{32\omega _k \omega _m^2 }\right. \nonumber \\&\left. +\,\frac{R_{n_2 } T_{nm} }{32\omega _k \omega _n^2 }+\frac{R_{n_1 } T_{nn} }{32\omega _k \omega _n^2 } \right) \left( {q_k p_m p_n +q_k q_m q_n } \right) \nonumber \\&+\,\left( \frac{T_{kmn} }{8\omega _k }-\frac{T_{knm} }{8\omega _k }+\frac{R_{m_2 } T_{mm} }{32\omega _k \omega _m^2 }-\frac{R_{m_1 } T_{nm} }{32\omega _k \omega _m^2 }+\frac{R_{n_2 } T_{nm} }{32\omega _k \omega _n^2 }\right. \nonumber \\&\left. -\frac{R_{n_1 } T_{nn} }{32\omega _k \omega _n^2 } \right) \left( {p_k p_m q_n -p_k p_n q_m } \right) \nonumber \\&-\left( {\frac{T_{knn} }{8\omega _k }+\frac{R_{m_2 } T_{nm} }{32\omega _k \omega _m^2 }+\frac{R_{n_2 } T_{nn} }{32\omega _k \omega _n^2 }} \right) \left( {p_n^2 q_k +q_n^2 q_k } \right) \nonumber \\&-\frac{R_{k_3 } }{2\omega _k }p_n q_n +\frac{\mu F_{k_1 } }{2\omega _k^2 } \\ \frac{\mathrm{d}q_k }{\mathrm{d}t}= & {} -\mu q_k +\left( {\frac{\mu ^{2}}{2\omega _k }+2\sigma _1 -2\sigma _2 -\sigma _3 } \right) p_k \nonumber \\&+\,\left( {\frac{F_{m_1 } T_{mm} }{8\omega _k \omega _m^2 }+\frac{F_{n_1 } T_{nm} }{8\omega _k \omega _n^2 }-\frac{F_{mk} }{\omega _k }} \right) p_m \nonumber \end{aligned}$$

(D.8)

$$\begin{aligned}&+\,\left( {\frac{\mu R_{k_1 } }{4\omega _k^2 }-\frac{\mu T_{mm} }{4\omega _k \omega _m }} \right) p_m q_m \nonumber \\&+\,\left( {\frac{\mu R_{k_3 } }{4\omega _k^2 }-\frac{\mu T_{nn} }{4\omega _k \omega _n }} \right) p_n q_n +\frac{R_{k_2 } }{4\omega _k }\left( {p_m p_n -q_m q_n } \right) \nonumber \\&+\,\frac{R_{k_1 } }{4\omega _k }\left( {p_m^2 -q_m^2 } \right) +\frac{R_{k_3 } }{4\omega _k }\left( {p_n^2 -q_n^2 } \right) \nonumber \\&+\,\left( {\frac{\mu R_{k_2 } }{8\omega _k^2 }-\frac{\mu T_{nm} }{8\omega _k \omega _m }-\frac{\mu T_{nm} }{8\omega _k \omega _n }} \right) \left( {p_n q_m +p_m q_n } \right) \nonumber \\&+\,\left( {\frac{T_{kmm} }{8\omega _k }+\frac{R_{m_1 } T_{mm} }{32\omega _k \omega _m^2 }+\frac{R_{n_1 } T_{nm} }{32\omega _k \omega _n^2 }} \right) \left( {p_k p_m^2 +p_k q_m^2 } \right) \nonumber \\&+\,\left( {\frac{T_{knn} }{8\omega _k }+\frac{R_{m_2 } T_{nm} }{32\omega _k \omega _m^2 }+\frac{R_{n_2 } T_{nn} }{32\omega _k \omega _n^2 }} \right) \left( {p_k p_n^2 +p_k q_n^2 } \right) \nonumber \\&+\,\left( {\frac{T_{kmn} }{8\omega _k }+\frac{R_{m_2 } T_{mm} }{32\omega _k \omega _m^2 }+\frac{R_{n_2 } T_{nm} }{32\omega _k \omega _n^2 }} \right) \nonumber \\&\left( {\left( {p_k p_m p_n +p_k q_m q_n } \right) +\left( {p_m q_k q_n -p_n q_k q_m } \right) } \right) \nonumber \\&+\,\left( {\frac{T_{knm} }{8\omega _k }+\frac{R_{m_1 } T_{nm} }{32\omega _k \omega _m^2 }+\frac{R_{n_1 } T_{nn} }{32\omega _k \omega _n^2 }} \right) \nonumber \\&\left( {\left( {p_k p_m p_n +p_k q_m q_n } \right) -\left( {p_m q_k q_n -p_n q_k q_m } \right) } \right) \nonumber \\&+\,\frac{T_{kkk} }{8\omega _k }\left( {p_k^3 +q_k^2 p_k } \right) +\frac{F_{k_1 } }{\omega _k }\nonumber \\&+\,\left( {\frac{F_{m_1 } T_{nm} }{8\omega _k \omega _m^2 }+\frac{F_{n_1 } T_{nn} }{8\omega _k \omega _n^2 }-\frac{F_{nk} }{\omega _k }} \right) p_n\end{aligned}$$

(D.9)

where the values of $\lambda _1$, $\lambda _2$, and $\lambda _3$ are $\lambda _1 =\sigma _1$, $\lambda _2 =\sigma _1 -\sigma _2$, and $\lambda _3 =2\sigma _1 -2\sigma _2 -\sigma _3$.