1 Introduction

There is an emerging implementation of electrically actuated vibrating beams in several micro-electro-mechanical systems (MEMS) applications including sensing [1,2,3,4], switching [5,6,7,8], signal filtering [9,10,11], and logic operations [12, 13]. These miniature devices have demonstrated numerous advantages when compared to their conventional counterparts. These advantages include low power consumption, easy integration with electronic circuits, and capability to operate in harsh environments. The performance of these microsystems can be assessed at early stages of design by gaining a good understanding of their governing dynamics and exploiting specific physical aspects. The use of computational models with the capability to capture the inherent dynamic features provides guidance to investigate novel designs and operating principles of MEMS devices and enhance their functionality and lifetime. Several research studies have developed mathematical models of electrically actuated microbeams with different levels of fidelity in terms of the capability to embody the associated physical phenomena and to obtain relevant response characteristics and complexity in terms of the numerical implementation and the needed computational resources and simulation time. Indeed, these models have been used to assess the sensitivity and resolution of the MEMS device and predict the level of electrical actuation leading to the failure in the operation due to the undesired collapse of the microstructure resulting from the pull-in instability.

The squeeze-film damping (SQFD) is an inherent dissipation mechanism that takes place due to the interactions between the vibrations of a flexible microstructure and the flow of the surrounding fluid [14]. This is induced by the pressure variations underneath the microstructure. The effect of SQFD on the dynamic behavior depends mainly on the operating pressure, the initial gap distance separating the microstructure and electrode, and the geometry of the microstructure. The operating pressure can be controlled by the way the microsystem is encapsulated. Different modeling approaches and numerical implementations have been reported in the literature to account for the squeeze-film damping effect [5, 15,16,17,18,19]. Among the recent research studies, Ben Sassi et al. [5] formulated a multi-physics model of a capacitive microswitch made of a doubly clamped microbeam by coupling the nonlinear Euler–Bernoulli beam theory with the Reynolds equation to simulate the pressure distribution. They used a combination of the Galerkin discretization approach and the differential quadrature method to integrate the fully coupled fluid–structure equations. The developed model was verified experimentally and then used to examine the impact of different actuation waveforms on the performance of the microswitch. The square waveform was identified as the most efficient and reliable in terms of voltage requirement, switching time, and sensitivity to mechanical and electrical noise. Ouakad et al. [18] developed a coupled fluid–structure system to investigate the influence of the squeeze-film damping on the dynamic behavior of curved microbeams with concave and convex geometries under harmonic excitation. This model is obtained by combining nonlinear Euler–Bernoulli beam equations and Burgdorfer’s model for the surrounding fluid. They found that SQFD has significant effect on the nonlinear dynamic response and snap-through values of the curved down microbeams (convex geometry). On the other hand, its effect was less prominent when using curved up microbeams (concave geometry). Several studies showed that SQFD can be utilized to suppress the shock response and then enhance the reliability of MEMS devices when exposed to shock loading or sudden change in the acceleration. Ahmed et al. [15] conducted an investigation on the dynamic response of electrostatically coupled microcantilever beams under the combined effect of squeeze-film damping and mechanical shock. The squeeze-film damping is incorporated using a nonlinear analytical expression of the microbeams deflection. They found that dual beam microsystems coupled via electric actuation have potential to withstand more to mechanical shock in comparison with the single beam microsystem actuated by a fixed electrode. The SQFD is observed to enable stronger protection of the microsystem in terms of resistance to mechanical shock. This has been also demonstrated by Yagubizade and Younis [16] who investigated the impact of SQFD on the shock response of clamped–clamped microbeams without electric actuation. They solved simultaneously the Reynolds pressure equation and nonlinear Euler–Bernoulli equation using the Galerkin decomposition approach and the finite difference method for the space discretization of the beams displacements and the air pressure, respectively.

Ilyas et al. [20] have recently conducted an experimental study to test the performance of a novel design of a resonator made of electrically coupled cantilever microbeams operating near vacuum conditions. The electric coupling led to expanded bandwidth near primary resonance and higher frequency shift. Therefore, the authors concluded that such design can be more suitable for sensing applications in comparison with the classical systems made of a single beam and fixed electrode. In the present work, we adopt the same conceptual design as Ilyas et al. [20] and follow different modeling approaches to analyze its dynamic response while accounting for the impact of the squeeze-film damping. Such effect is significant when encapsulating the microstructure under high gas pressure. We first formulate a multi-physics model of the device by coupling Euler–Bernoulli beam equations with the nonlinear Reynolds equation to simulate the pressure distribution of the air confined in the gap separating the two microbeams. We consider also another modeling approach, widely used in the literature, which is based on approximating the squeeze-film damping force by a nonlinear function of the variable gap distance. This is referred to as partially coupled model. A comparison of the nonlinear dynamic responses obtained from the models under different operating conditions in terms of electric actuation and applied pressure is presented. The simulation results reveal the limitations of the partial coupled model to capture properly the microsystem dynamics, especially when approaching the onset of the pull-in instability and exciting the harmonic load near resonance. We show that applying a correction factor to the partially coupled model which is much less computationally demanding leads to a good match with the fully coupled model. This correction factor is observed to be dependent mainly on the thickness ratio, the ambient pressure, and the excitation frequency.

2 Microsystem description and model formulation

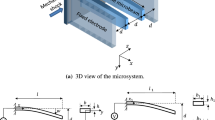
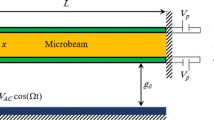
We consider a MEMS device consisting of two microbeams of the same length l and width b, and different thicknesses \(h_1\) and \(h_2\) placed at a gap distance d, as shown in Fig. 1. The dual beam microsystem is electrically coupled by applying a combination of DC and AC voltages among the two movable microbeams. We develop computational models of different fidelity levels to simulate the dynamic behavior of the microbeams while accounting for the fringing field effect and the squeeze-film damping. The latter is a nonlinear dissipation mechanism that results from the air flow between the vibrating microbeams. The damping level can be controlled via the operating pressure. The most common approach to model SQFD is based on Reynolds equation which is derived from Navier–Stokes equations under a number of assumptions [14].

Fig. 1
figure 1

Conceptual design of the electrically actuated microbeams under squeeze-film damping effect

Full size image

Following Euler–Bernoulli beam assumptions, the equations of motion governing the transverse deflections \(w_i\) of the electrically coupled microbeams are given by [15, 21]:

$$\begin{aligned} \rho b h_1&(w_1)_{,tt} + c (w_1)_{,t} + E I_{1} (w_1)_{,xxxx} \nonumber \\ = \,&\frac{k \epsilon _0 b V(t)^2}{2(d-w_1+w_2)^2}\Big (1+\frac{0.65}{b}(d-w_1+w_2)\Big ) \nonumber \\&-\int _0^{b} P{\hbox {d}}y \end{aligned}$$
(1)
$$\begin{aligned} \rho b h_2&(w_2)_{,tt} + c (w_2)_{,t} + E I_{2} (w_2)_{,xxxx} \nonumber \\ =&-\frac{k \epsilon _0 b V(t)^2}{2(d-w_1+w_2)^2}\Big (1+\frac{0.65}{b}(d-w_1+w_2)\Big ) \nonumber \\&+\int _0^{b} P{\hbox {d}}y \end{aligned}$$
(2)

where E denotes the Young’s modulus, c is the damping coefficient, \(I_{i}=\frac{b h_i^{3}}{12}\) is the beam’s cross sectional second moment of area, t is time, and x is the position along the microbeam length. The subscripts \(\{1,2\}\) refer to microbeam 1 and 2. The parameter \(\epsilon _0=8.85\times 10^{-12}\,\hbox {C}^2\,{\hbox {N}}^{-1}\,{\hbox {m}}^{-2}\) is the permittivity of vacuum, and k is the dielectric coefficient of air between the two movable microbeams. V(t) is the time-varying voltage applied between the two microbeams.

The microbeams are subject to fixed and free end boundary conditions expressed as:

At \(x=0,\)

$$\begin{aligned} w_1=w_2=0 \; \text {and} \; (w_1)_{,x}=(w_2)_{,x}=0 \end{aligned}$$
(3)

At \(x=l,\)

$$\begin{aligned} (w_1)_{,xx}=(w_2)_{,xx}=0 \; \text {and} \; (w_1)_{,xxx}=(w_2)_{,xxx}=0 \end{aligned}$$
(4)

The air flow between the two flexible microbeams is governed by the fully nonlinear 2D form of the Reynolds equation given by [5]:

$$\begin{aligned} \Big [&(d-w_1+w_2)^3{\overline{P}}\;{\overline{P}}_{,x}\Big ]_{,x}+ \Big [(d-w_1+w_2)^3{\overline{P}}\;{\overline{P}}_{,y}\Big ]_{,y} \nonumber \\&=12\mu _\mathrm{eff}\Big [(d-w_1+w_2){\overline{P}}_{,t}-{ \overline{P}}((w_1)_{,t}-(w_2)_{,t})\Big ] \end{aligned}$$
(5)

where \({\overline{P}}(x,y,t)=P(x,y,t)+p_\mathrm{a}\) represents the absolute pressure between the two microbeams and \(p_\mathrm{a}\) is the ambient air pressure. \(\mu _\mathrm{eff}\) is the effective viscosity of air. Following Andrews and Harris model based on experimental data fitting [5], the effective viscosity is given by:

$$\begin{aligned} \mu _\mathrm{eff}=\frac{\mu }{1+6.8636K_n^{0.9906}} \end{aligned}$$
(6)

where \(\mu \) is the dynamic viscosity of air at room temperature and atmospheric pressure \(p_\mathrm{o}=101.325\) kPa. The Knudsen number \(K_n\) is expressed in terms of the initial gap distance d and the mean free path \(\lambda _\mathrm{o}\) at the same conditions as:

$$\begin{aligned} K_{n}=\frac{\lambda _\mathrm{o} p_\mathrm{o}}{p_\mathrm{a} d} \end{aligned}$$
(7)

We set \(\lambda _\mathrm{o}\) equal to 65 nm. We assume ambient pressure at the free edges and zero flux at the clamped edges. The pressure field boundary conditions are expressed then as:

$$\begin{aligned}&{\overline{P}}(x,0,t)={\overline{P}}(x,b,t)={\overline{P}}(l,y,t)=p_\mathrm{a} \nonumber \\&{\overline{P}}_{,x}(0,y,t)=0 \end{aligned}$$
(8)

Assuming the microbeams of rectangular cross-sectional geometry, the following parameters are introduced to nondimensionlize equations (1)–(8):

$$\begin{aligned} {\hat{x}}&=\frac{x}{l},\; {\hat{y}}=\frac{y}{b},\; \hat{w_1}=\frac{w_1}{d},\; \hat{w_2}=\frac{w_2}{d}, \nonumber \\ {\hat{t}}&=\frac{t}{\tau },\; {\hat{P}}=\frac{P}{p_\mathrm{a}} \nonumber \\ \tau&= \sqrt{\frac{\rho b h_1 l^4}{E I_1}},\; \alpha _1 = \frac{k \epsilon _0 b l^4}{2 d^3 E I_1}, \nonumber \\ \beta&= \frac{h_1^2}{h_2^2}, \; \mu =\frac{c_1 l^4}{E I_1 \tau } \nonumber \\ \delta&=0.65\frac{d}{b},\; \alpha _2=\frac{12 p_\mathrm{a} l^4}{E h_1^3 d}, \nonumber \\ \alpha _3&=\frac{l^2}{b^2},\; \sigma =\frac{12 \mu _\mathrm{eff}l^2}{p_\mathrm{a} \tau d^2} \end{aligned}$$
(9)

Considering the defined dimensionless form and dropping the hat, the governing equations of motion and their associated boundary conditions can be rewritten as follows:

$$\begin{aligned}&(w_1)_{,tt} + \mu (w_1)_{,t} + (w_1)_{,xxxx} \end{aligned}$$
(10)
$$\begin{aligned}&\quad \!=\alpha _1 V(t)^2 \frac{1+\delta (1-w_1+w_2)}{(1-w_1+w_2)^2} -\alpha _2 \int _0^{1} P{\hbox {d}}y \nonumber \\&(w_2)_{,tt} + \beta \mu (w_2)_{,t} + (w_2)_{,xxxx} \nonumber \\&\quad \!= -\alpha _1 V(t)^2\frac{ 1+\delta (1{-}w_1{+}w_2)}{(1{-}w_1{+}w_2)^2} + \beta ^{3/2} \alpha _2 \int _0^{1} P{\hbox {d}}y \end{aligned}$$
(11)

subject to

$$\begin{aligned}&w_1(0,t)=w_2(0,t)=0 \nonumber \\&(w_1)_{,x}(0,t)=(w_2)_{,x}(0,t)=0 \nonumber \\&(w_1)_{,xx}(1,t)=(w_2)_{,xx}(1,t)=0 \nonumber \\&(w_1)_{,xxx}(1,t)=(w_2)_{,xxx}(1,t)=0 \end{aligned}$$
(12)

Concerning the nondimensional Reynolds equation and associated boundary conditions, it can be expressed as:

$$\begin{aligned}&\Big [(1-w_1+w_2)^3(P+1)\;P_{,x}\Big ]_{,x} \nonumber \\&\quad +\alpha _3\Big [(1-w_1+w_2)^3(P+1)\;P_{,y}\Big ]_{,y}\nonumber \\&\quad =\sigma \Big [(1-w_1+w_2)P_{,t}-(P+1)((w_1)_{,t}-(w_2)_{,t})\Big ] \end{aligned}$$
(13)

subject to

$$\begin{aligned}&{\overline{P}}(x,0,t)={\overline{P}}(x,1,t)={\overline{P}}(1,y,t)=p_\mathrm{a} \nonumber \\&{\overline{P}}_{,x}(0,y,t)=0 \end{aligned}$$
(14)

3 Solution procedure and nonlinear reduced-order Model

To examine the fully coupled dynamics of the electrically coupled microbeams, we derive the reduced-order model (ROM) using a combination of the Galerkin decomposition and the differential quadrature method (DQM). The deflections of the microbeams are expanded as follows [15, 21]:

$$\begin{aligned}&w_1(x,t)=\sum _{i=1}^{m} q_1^i(t)\phi _1^i(x) \end{aligned}$$
(15)
$$\begin{aligned}&w_2(x,t)=\sum _{i=1}^{m} q_2^i(t)\phi _2^i(x) \end{aligned}$$
(16)

where the spatial function \(\phi _{1,2}^i(x)\) is the ith-linear normalized undamped mode shape of a cantilever beam and the time-varying functions \(q_1^i(t)\) and \(q_2^i(t)\) are the corresponding modal coordinates of the microbeams. m denotes the number of the retained modes. The nondimensional form of the mode shapes is given by [22]:

$$\begin{aligned} \phi _j^i(x)=&\sin \beta _i x - \sinh \beta _i x \nonumber \\&- \frac{\sin \beta _i +\sinh \beta _i}{\cos \beta _i + \cosh \beta _i}(\cos \beta _i x -\cosh \beta _i x) \nonumber \\&\qquad j=1,2,\ldots ,m \end{aligned}$$
(17)

where the \(\beta _i\) are solution of the transcendental equation:

$$\begin{aligned} 1+ \cos \beta \cosh \beta =0 \end{aligned}$$
(18)

Next, we substitute Eqs. (15) and (16) into Eqs. (10) and (11), multiply the outcome by the appropriate mode shape \(\phi ^j_{1,2}\), and integrate the resulting equations from 0 to 1 to obtain the following equations:

$$\begin{aligned}&(q_1^j)_{,tt} + \mu (q_1^j)_{,t} + \sum _{i=1}^m q_1^i \int _0^1 \phi _1^j (\phi _1^i)_{,xxxx} {\hbox {d}}x \nonumber \\&\quad -\alpha _1 V(t)^2 \int _0^1 \phi _1^j \nonumber \\&\quad \times \frac{1+\delta \left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i- q_2^i\phi _2^i\right) }{\left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i-q_2^i\phi _2^i\right) ^2}{\hbox {d}}x \nonumber \\&\quad +\alpha _2 \int _0^{1} \int _0^{1} \phi _1^j P(x,y){\hbox {d}}x {\hbox {d}}y =0 \end{aligned}$$
(19)
$$\begin{aligned}&\beta (q_2^j)_{,tt} + \beta \mu (q_2^j)_{,t} + \sum _{i=1}^m q_2^i \int _0^1 \phi _2^j (\phi _2^i)_{,xxxx} {\hbox {d}}x \nonumber \\&\quad + \beta ^{3/2}\alpha _1 V(t)^2 \int _0^1 \phi _2^j \nonumber \\&\quad \times \frac{1+\delta \left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i- q_2^i\phi _2^i\right) }{\left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i- q_2^i\phi _2^i\right) ^2}{\hbox {d}}x \nonumber \\&\quad -\beta ^{3/2}\alpha _2 \int _0^{1} \int _0^{1} \phi _2^j P(x,y){\hbox {d}}x {\hbox {d}}y =0 \nonumber \\&\quad j=1,\ldots ,m \end{aligned}$$
(20)

Substituting Eqs. (15) and (16) into Eq. (13), we obtain:

$$\begin{aligned}&3\left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i- q_2^i\phi _2^i\right) ^2 \left( \sum _{i=1}^{m} q_2^i(\phi _2^i)_{,x}- q_1^i(\phi _1^i)_{,x} \right) \nonumber \\&\quad \times (P+1)P_{,x} +\left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i- q_2^i\phi _2^i\right) ^3 \nonumber \\&\quad \times \Big [P_{,x}^2+(P+1)P_{,xx} \Big ] \nonumber \\&\quad + \alpha _3 \left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i- q_2^i\phi _2^i\right) ^3\Big [P_{,y}^2+(P+1)P_{,yy} \Big ] \nonumber \\&\quad - \sigma \left( 1-\sum _{i=1}^{m} q_1^i\phi _1^i- q_2^i\phi _2^i\right) P_{,t} \nonumber \\&\quad + \sigma (P+1) \left( \sum _{i=1}^{m} (q_1^i)_{,t}\phi _1^i- (q_2^i)_{,t}\phi _2^i\right) =0 \end{aligned}$$
(21)

The Reynolds equation is discretized by applying the DQM in the x and y directions. The basis of DQM is to approximate the spatial derivative of the pressure at each grid point with respect to the position variables x or y by a weighted linear summation of the displacements at all grid points [2, 3, 5]. For example, for the derivative with respect to the axial position, estimated at grid point \((x_i,y_j)\), it is given by:

$$\begin{aligned} \left. {\frac{\partial ^r P(x)}{\partial x^r}}\right| _{x=x_i,y=y_j}=\sum _{k=1}^nA_{ik}^{(r)}P_{kj} \end{aligned}$$
(22)

where \(P_{kj}=P(x_j,y_k)\).

The DQM grid points are defined using the nonuniform Chebyshev–Gauss–Lobatto (CGL) grid distribution scheme as:

$$\begin{aligned} x_i=y_i=\frac{1}{2}\Big [1-\cos \Big (\frac{i-1}{n-1}\pi \Big )\Big ] \qquad i=1, \ldots , n \end{aligned}$$

and \(A_{ij}^{(r)}\) is the coefficient of the rth-order derivative. These coefficients are given, here for the x-direction, by the following recursive formulas:

$$\begin{aligned}&A_{ij}^{(1)} =\frac{ \prod _{v=1;v\ne i}^n (x_i-x_v) }{(x_i-x_j)\prod _{v=1;v\ne j}^n (x_j-x_v)} \nonumber \\&A_{ij}^{(r)} =r\left( A_{ii}^{r-1}A_{ij}^1 - \frac{A_{ij}^{r-1}}{(x_i-x_j)} \right) \nonumber \\&A_{ii}^{(r)} =-\sum _{v=1;v\ne i}^n A_{iv}^{(r)} \nonumber \\&\qquad i,j=1,2,\ldots ,n \end{aligned}$$
(23)

As for the numerical computation of the integrals, we use the Newton–Cotes coefficients [23], given by:

$$\begin{aligned} B_i=\int _0^1 \prod _{j=1;j\ne i}^{n}\frac{x-x_j}{x_i-x_j} {\hbox {d}}x \;\;\;\;\;i=1,2,\ldots ,n \end{aligned}$$
(24)

Applying DQM and Newton–Cotes to approximate the integrals and spatial derivatives at the DQM grid points, taking advantage of the symmetry with respect to the y-axis, we obtain the full nonlinear reduced model describing the motion of the microbeams as follows:

$$\begin{aligned}&(q_1^j)_{,tt} + \mu (q_1^j)_{,t} + \sum _{i=1}^m q_1^i \left( \sum _{r,s=1}^{n} B_r A_{rs}^{(4)} \phi _{1r}^j \phi _{1s}^i \right) \nonumber \\&\quad -\alpha _1 V(t)^2 \sum _{r=1}^n B_r \phi _{1r}^j \nonumber \\&\quad \times \frac{1+\delta \left( 1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i\right) }{\left( 1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i\right) ^2} \nonumber \\&\quad +\alpha _2 \sum _{r,s=1}^n B_r B_s \phi _{1r}^j P_{rs} =0 \end{aligned}$$
(25)
$$\begin{aligned}&\beta (q_2^j)_{,tt} + \beta \mu (q_2^j)_{,t} + \sum _{i=1}^m q_2^i \left( \sum _{r,s=1}^{n} B_r A_{rs}^{(4)} \phi _{2r}^j\phi _{2s}^i\right) \nonumber \\&\quad +\beta ^{3/2}\alpha _1 V(t)^2 \sum _{r=1}^n B_r \phi _{2r}^j \nonumber \\&\quad \times \frac{1+\delta \left( 1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i\right) }{\left( 1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i\right) ^2} \nonumber \\&\quad -\beta ^{3/2}\alpha _2 \sum _{r,s=1}^n B_r B_s \phi _{2r}^j P_{rs} =0 \nonumber \\&\quad j=1,\ldots ,m \end{aligned}$$
(26)

where \(\phi _{1r}^j=\phi _1^i(x_r)\) and \(\phi _{2r}^j=\phi _2^i(x_r)\).

$$\begin{aligned}&3\left( 1 - \sum _{i=1}^{m} q_1^i\phi _{1r}^i - q_2^i \phi _{2r}^i \right) ^2 \Bigg [\left( \sum _{i=1}^{m} q_2^i(\phi _{2r}^i)_{,x}- q_1^i(\phi _{1r}^i)_{,x}\right) \nonumber \\&\quad \times (P_{rs}+1) \sum _{k=1}^n A_{rk}^{(1)} P_{ks}\Bigg ] \nonumber \\&\quad + \left( 1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i - q_2^i \phi _{2r}^i \right) ^3 \Bigg [ \left( \sum _{k=1}^nA_{rk}^{(1)}P_{ks}\right) ^2 \nonumber \\&\quad + (P_{rs}+1) \left( \sum _{k=1}^nA_{rk}^{(2)}P_{ks}\right) \Bigg ] \nonumber \\&\quad + \alpha _3 \left( 1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i - q_2^i \phi _{2r}^i \right) ^3 \nonumber \\&\quad \times \Bigg [ \left( \sum _{k=1}^nA_{rk}^{(1)}P_{rk}\right) ^2 +(P_{rs}+1)\left( \sum _{k=1}^nA_{sk}^{(2)}P_{rk}\right) \Bigg ] \nonumber \\&\quad - \sigma \left( 1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i\right) P_{rs,t}\nonumber \\&\quad + \sigma (P_{rs}+1) \left( \sum _{i=1}^{m} (q_1^i)_{,t}\phi _{1r}^i- (q_2^i)_{,t}\phi _{2r}^i\right) =0 \nonumber \\&\quad \text {for} \;\;r=2,\ldots ,n-1 \text{ and } \quad s=2,\ldots ,\frac{n+1}{2} \end{aligned}$$
(27)

The pressure at the boundaries is determined by using the boundary and symmetry conditions, that is:

$$\begin{aligned}&P(x_r,0)=0, \; P(1,y_s)=0 \nonumber \\&\sum _{k=1}^n A_{1k}^{(1)} P(x_k,y_s)=0 \;\;\; r,s=1,\ldots ,n \nonumber \\&P(x_r,y_{n + 1 - s}) = P(x_r,y_s) \nonumber \\&\qquad r=1,\ldots ,n \text{ and } s=1,\ldots ,\frac{n-1}{2} \end{aligned}$$
(28)

4 Convergence and validation of the proposed solution

4.1 Convergence analysis

To verify the convergence behavior of the numerical solution when varying the number of DQM points and expansion modes, we evaluate the response of the dual microbeam system when applying a DC voltage alone (\(V(t)=V_\mathrm{DC}\)). We note that the DC voltage is set equal to 70 V (near the onset of the pull-in instability). The microsystem material and geometry properties considered in the subsequent numerical simulations are presented in Table 1.

Table 1 Geometric and material properties of the microbeams under investigation
Full size table
Fig. 2
figure 2

Convergence analysis: transient variations of the microbeams displacements when varying the number of DQM points and number of expansion modes

Full size image

We fix the number of DQM points and gradually increase the number of modes. Using a Runge–Kutta fourth-order scheme for the time integration, the transient variations of the microbeams displacements obtained from the fully coupled reduced-order model are depicted in Fig. 2. The simulation results revealed that when selecting improperly the number of DQM points, the numerical solution fails to converge as the number of modes is increased. For instance, when using 9 DQM points, the numerical model does not produce the same steady-state solution when increasing the number of modes up to four. Moreover, an increase in the number of modes in the Galerkin discretization is not accompanied by a convergence in the response, as presented in Fig. 2a. On the other hand, setting the number of DQM points equal to 13 and using only one mode in the Galerkin discretization lead to an acceptable convergence, as shown in Fig. 2c. As such, one needs to first determine the appropriate number of DQM points in order to achieve invariant simulation results when increasing the number of modes. In the subsequent study, the simulation results are obtained using one mode in the Galerkin method and 13 DQM points for space discretization.

One can also conclude from Fig. 2 that adding the squeeze-film effect leads to a dissipation in the motion of the microbeams. For this reason, several authors treating dynamic analysis of MEMS structure in the literature, choose to represent this effect by a simple linear viscous damping term in the equation of motion [6, 8, 24]. In general, a logarithmic decrement formula is applied to the transient response to estimate the corresponding quality factor of the device. This latter represents generally all sources of damping in the system, especially when the transient response is obtained experimentally [5, 25]. In the following sections, it will be shown that this representation is inaccurate. Moreover, even more advanced nonlinear damping models cannot accurately represent the squeeze-film behavior, especially near resonance.

The pressure distribution, when the displacement is at its maximum position, is obtained for the same applied DC voltage and using 13 DQM points, as shown in Fig. 3. The pressure distribution is consistent with those found in the literature for cantilever microbeams [26].

Fig. 3
figure 3

Pressure distribution between the microbeams, obtained for \(V_\mathrm{DC}=70\) V and using 13 DQM points

Full size image

4.2 Comparison with a partially coupled model

Considering microbeams with a length l significantly larger than the width b and assuming small relative displacements of the microbeams \(w_1(x,t)-w_2(x,t)\) compared to the original gap width d, and small relative pressure change along the microbeam P(x, y, t) in comparison with the ambient air pressure \(p_\mathrm{a}\), the squeeze-film damping force can be approximated by [15]:

$$\begin{aligned} F^\mathrm{SQFD}=\frac{\mu _\mathrm{eff}b^3}{(d-w_1+w_2)^3}\Big (\frac{\partial w_1}{\partial t}-\frac{\partial w_2}{\partial t} \Big ) \end{aligned}$$
(29)

Based on the above representation of the SQFD force, the dimensionless governing equations of the electrically coupled microbeams can be expressed as:

$$\begin{aligned} (w_1)_{,tt}&+ \mu (w_1)_{,t} + (w_1)_{,xxxx} \nonumber \\ =&\frac{\alpha _1 V(t)^2}{(1-w_1+w_2)^2}\Big (1+\delta (1-w_1+w_2)\Big )\nonumber \\&-\frac{\kappa }{(1-w_1+w_2)^3} \Big ((w_1)_{,t}-(w_2)_{,t} \Big ) \end{aligned}$$
(30)
$$\begin{aligned} (w_2)_{,tt}&+ \beta \mu (w_2)_{,t} + (w_2)_{,xxxx} \nonumber \\ =&-\frac{\alpha _1 V(t)^2}{(1-w_1+w_2)^2}\Big (1+\delta (1-w_1+w_2)\Big )\nonumber \\&+\frac{\beta ^{3/2}\kappa }{(1-w_1+w_2)^3} \Big ((w_1)_{,t}-(w_2)_{,t} \Big ) \end{aligned}$$
(31)

where \(\kappa =\frac{2\sqrt{3} \mu _\mathrm{eff}b^2l^2}{\sqrt{E}h^2d^3}\).

Expanding the deflections in terms of the mode shapes and following the same numerical approach as described in the previous section, we obtain the following reduced-order model:

$$\begin{aligned}&(q_1^j)_{,tt} + \mu (q_1^j)_{,t} + \sum _{i=1}^m q_1^i \Big ( \sum _{r,s=1}^{n} B_r A_{rs}^{(4)} \phi _{1r}^j\phi _{1s}^i \Big ) \nonumber \\&\quad -\alpha _1 V(t)^2 \nonumber \\&\quad \times \sum _{r=1}^n B_r \phi _{1r}^j \frac{1+\delta (1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i)}{(1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i)^2} \nonumber \\&\quad + \kappa \sum _{r=1}^n B_r \phi _{1r}^j \frac{\sum _{i=1}^{m} (q_1^i)_{,t}\phi _{1r}^i- (q_2^i)_{,t}\phi _{2r}^i}{(1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i)^3}=0 \nonumber \\&\quad j=1,\ldots ,m \end{aligned}$$
(32)
$$\begin{aligned}&\beta (q_2^j)_{,tt} + \beta \mu (q_2^j)_{,t} + \sum _{i=1}^m q_2^i \Big ( \sum _{r,s=1}^{n} B_r A_{rs}^{(4)} \phi _{2r}^j\phi _{2s}^i\Big ) \nonumber \\&\quad +\beta ^{3/2}\alpha _1 V(t)^2 \nonumber \\&\quad \times \,\sum _{r=1}^n B_r \phi _{2r}^j \frac{1+\delta (1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i)}{(1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i)^2} \nonumber \\&\quad -\beta ^{3/2}\kappa \sum _{r=1}^n B_r \phi _{2r}^j \frac{\sum _{i=1}^{m} (q_1^i)_{,t}\phi _{1r}^i- (q_2^i)_{,t}\phi _{2r}^i}{(1-\sum _{i=1}^{m} q_1^i\phi _{1r}^i- q_2^i\phi _{2r}^i)^3}=0 \nonumber \\&\quad j=1,\ldots ,m \end{aligned}$$
(33)

To investigate the predictive capability of the partially coupled model, we simulate the dynamic response of the dual beam system for different operating conditions near the onset of the pull-in instability and compare the results to those obtained using the fully coupled model. We show in Fig. 4 the time response of the dual beam system for different ambient pressures. The thickness ratio \(h_2/h_1\) is set equal to one (identical microbeams). The applied DC voltages are selected in the neighborhood of the pull-in. As expected, increasing the ambient pressure is observed to shift the pull-in voltage to higher values. Both models lead to the same steady-state solution. The discrepancy between the two models is only observed in the transient part. This demonstrates the limitation of the partially coupled model to capture the dynamics of the dual beam system.

Next, we consider dissimilar microbeams in terms of thickness by setting \(h_2/h_1\) equal to 1.5 and show in Fig. 5 a comparison between the time responses obtained from the two models when varying the applied DC voltage while approaching the pull-in instability. The ambient pressure \(p_\mathrm{a}\) is kept constant and equal to \( p_\mathrm{o}=101.325\) kPa. Inspecting the plotted curves in Fig. 5a, b, it is clear that the two models show different transient responses and they both converge to the same steady-state solution. However, when actuating the dual beam system with a DC voltage equal to 92.6 V, the partially coupled model predicts a stable behavior while pull-in instability occurs as per the fully coupled model simulation, as depicted in Fig. 5c. This result shows the possible erroneous predictions of the static pull-in instability when asymmetric beams are considered and hence the limits of applicability of the SQFD partially coupled model.

Fig. 4
figure 4

Time response of the dual beam system for different ambient pressures. Results are obtained from the fully and partially coupled models. The thickness ratio \(h_2/h_1\) is set equal to one (identical microbeams)

Full size image
Fig. 5
figure 5

Time response of the dual beam system for different applied DC voltages. Results are obtained from the fully and partially coupled models. The thickness ratio \(h_2/h_1\) is set equal to 1.5 and \(p_\mathrm{a}= p_\mathrm{o}=101.325\) kPa

Full size image

Next, we examine the impact of the thickness ratio \(h_2/h_1\) on the pull-in voltage, calculated using a transient approach and starting from a rest initial condition [6]. We note that \(h_1\) is maintained fixed at 3 \(\upmu {\hbox {m}}\) and the ambient pressure \(p_\mathrm{a}\) is set equal to \(p_\mathrm{o}=101.325\) kPa. The obtained results from the two models are shown in Fig. 6. As expected, increasing the thickness ratio makes the microsystem stiffer and then results in an increase in the pull-in voltage. This increase saturates when reaching a thickness ratio of 3 and the pull-in voltage of the dual beam system approaches that of the single beam system (of thickness 3 \(\upmu {\hbox {m}}\)). The simulation results show also that the partially coupled model slightly overestimates the pull-in voltages when compared to those obtained from the fully coupled model. This overestimation is more pronounced at higher thickness ratios, as shown in the plotted curves in Fig. 6.

Fig. 6
figure 6

Variations of the pull-in voltage with the thickness ratio \(h_2/h_1\). Results are obtained from the fully and partially coupled models. The dashed line denotes the value of the pull-in voltage of the single beam with a thickness of 3 \(\upmu {\hbox {m}}\). The ambient pressure is set equal to \(p_\mathrm{o}=101.325\) kPa

Full size image
Fig. 7
figure 7

Variations of the pull-in voltage with the operating pressure \(p_\mathrm{a}\) for different thickness ratios \(h_2/h_1\). Results are obtained from the fully coupled model. The thickness \(h_1\) is kept constant and equal to 3 \(\upmu {\hbox {m}}\)

Full size image

We investigate the change in the transient pull-in voltage when varying the operating pressure \(p_\mathrm{a}\) for different thickness ratios \(h_2/h_1\). The results are shown in Fig. 7 in terms of the percentage increase with respect to the pull-in voltage obtained near vacuum conditions. The most significant impact is observed for smaller thickness ratio. The pull-in voltage increases by 8% when operating under atmospheric pressure in comparison with its value obtained near vacuum conditions (pressure is in the order of few Pa).

5 Dynamic response of the system to a DC and AC voltages

Taking advantage of the convergence analysis in Fig. 2, we adopt the same number of mode shapes and DQM grid points in the following dynamic analysis. We propose to plot the frequency-response and force-response curves of the system and investigate the effects of the ambient pressure and thickness ratio between the two microbeams. Also, the proposed fully coupled model is compared to the partially coupled one developed in Sect. 4.

In this analysis, we assume that the applied voltage follows a harmonic signal superimposed to a constant voltage, that is:

$$\begin{aligned} V(t)=V_\mathrm{DC}+V_\mathrm{AC} \cos (\varOmega t) \end{aligned}$$
(34)

where \(\varOmega \) is the nondimensional excitation frequency.

The dynamic solution is obtained by solving Eqs. (25), (26), and (27) for the fully coupled problem, and Eqs. (32) and (33) for the partially coupled problem. A Runge–Kutta discretization technique is used to solve the equations for stable steady-state solutions. In the following, we represent the maximum displacement in the steady-state regime of the difference between the two displacement denoted by \((w_1-w_2)_\mathrm{Max}\).

Fig. 8
figure 8

Frequency-response curves of the dual beam microsystem for different ambient pressures. \(V_\mathrm{DC}=50\) V, \(V_\mathrm{AC}=10\) V, \(d=2\upmu \)m, and \(h_2/h_1=1\). The nondimensional parameter \(\sigma \) is defined as \(\frac{12 \mu _\mathrm{eff}l^2}{p_\mathrm{a} \tau d^2}\)

Full size image

5.1 Influence of the ambient pressure on the frequency- and force-response curves

The operating pressure can be controlled by the way the microstructure is encapsulated, and then it can be considered as a design component. It can be selected based on the MEMS application of interest. For instance, SQFD can be exploited to enable stronger protection of the MEMS device when exposed to mechanical shock or sudden change in the acceleration [15, 16]. In Fig. 8, we present the frequency-response curves of the dual beam system obtained from the fully coupled model at different ambient pressures ranging from 0.1 \(p_\mathrm{o}\) to \(p_\mathrm{o}\). The DC and AC voltages are set equal to 50 V and 10 V, respectively, and the thickness ratio \(h_2/h_1\) is maintained equal to 1. We note that only the stable solutions are shown in this figure. We find that near resonance the ambient pressure can affect significantly the dynamic solution both quantitatively and qualitatively. We observe the occurrence of open regions, where no stable solution can be obtained, when operating under a pressure equal or less than 0.2 \(p_\mathrm{o}\). These are known as the pull-in band in the frequency-response curve [27]. Also, a clear softening effect is observed when the pressure is low enough to let the amplitude of the solution reach relatively high values. As known in the literature, the softening effect is generally attributed to the nonlinearity of the electrostatic force which is of the quadratic type. We note that minor effect of the ambient pressure on the dynamic response is observed when operating away from resonance. Further, an increase in the ambient pressure is accompanied by a decrease in the resonant amplitudes due to the increase in the overall damping in the system. It should be mentioned that pull-in band constitutes an important dynamic aspect to be detected in most MEMS actuators and sensors because it should be avoided when stable periodic solutions are required, such as resonators. On the other hand, dynamic solutions in the neighborhood of the pull-in band have been employed to actuate microswitches [5, 25].

Fig. 9
figure 9

Frequency-response curves of the dual beam microsystem. Comparison between the fully coupled and the partially coupled approaches. \(V_\mathrm{DC}=50\) V, \(V_\mathrm{AC}=10\) V, \(d=2\upmu \)m, and \(h_2/h_1=1\)

Full size image

Next, we compare the frequency-response curves obtained from the two computational models for different operating pressures. Again, the DC and AC voltages are set equal to 50 V and 10 V, respectively, and the thickness ratio \(h_2/h_1\) is maintained equal to 1. The obtained results are shown in Fig. 9. The partially coupled model underestimates the dynamic solution of the dual microbeam system, especially when approaching resonance. Furthermore, the partially coupled model does not capture the pull-in band predicted by the fully coupled model when operating at a pressure of 0.1 \(p_\mathrm{o}\) and shows instead a multi-solution region. This constitutes a major qualitative change in the dynamic response when compared to the fully coupled problem and reveals the limitations of the partially coupled model to properly simulate the dynamics associated with the dual beam system, especially when using it as a microswitch which is intended to operate near resonance. When the ambient pressure is set equal to the atmospheric one, it can be concluded from the plotted curves in Fig. 9 that the partially coupled model underestimates the resonant amplitudes due to inaccurate modeling of the linear and nonlinear coupling terms due to the squeeze-film damping. Indeed, a change in the effective nonlinearity of the system can result in a change in the nonlinear behavior of the system (softening or hardening) and its maximum amplitude.

The force-response curves are generated similarly to the previous case while taking the \(V_\mathrm{AC}\) voltage as control parameters and keeping the excitation frequency fixed and equal to the nondimensional value \(\varOmega =3\). In Fig. 10, the force-response curves are shown for different ambient pressures and a constant thickness ratio \(h_2/h_1=1\). The figure depicts a similar behavior to the frequency-response curves where decreasing the ambient pressure tends to increase the maximum amplitude for a given AC voltage. As expected, the stability of the branches in Fig. 10 is improved as the damping is increased through the ambient pressure adjustments. One can remark that the range of travel of the maximum amplitude can be reduced to 0.4 when operating under an ambient pressure of \(p_\mathrm{a}=0.1p_\mathrm{o}\). These results indicate the possible tuning of the operating pressure to obtain the level microbeam vibrations as per the MEMS application of interest.

Fig. 10
figure 10

Force-response curves of the dual beam microsystem for different ambient pressures. \(V_\mathrm{DC}=50\) V, \(\varOmega =3\), \(d=2\upmu \)m, and \(h_2/h_1=1\)

Full size image

The force-response curves are also used to compare the numerical predictions of the dynamic response obtained from the fully and partially coupled modeling approaches. In Fig. 11, the response of the microbeams confirms that the partially coupled model largely underestimates the maximum amplitude except for very small AC voltages. The discrepancy between the two models is more noticeable as the ambient pressure is increased and when actuating the microsystem at higher AC voltages. In addition, the dynamic solutions obtained from the partially coupled approach lose stability when the fully coupled model is used. This indicates a qualitative difference in the dynamic behavior predicted from the two models and demonstrate the necessity to use the fully coupled approach.

Fig. 11
figure 11

Force-response curves of the microbeams. Comparison between the fully coupled and the partially coupled approaches. \(V_\mathrm{DC}=50\) V, \(\varOmega =3\), \(d=2\upmu \)m, and \(h_2/h_1=1\)

Full size image

5.2 Influence of the thickness ratio on the frequency- and force-response curves

In this section, we investigate the influence of the thickness ratio \(h_2/h_1\) on the dynamic response of the dual beam microsystem. The difference in the thickness of the microbeams can be associated with deficiency in the microfabrication or deliberately used, for sensing applications for example, to create asymmetric behavior of the device. We note that \(h_1\) is kept fixed at 3 \(\upmu {\hbox {m}}\) in the subsequent simulations. Three values of the thickness ratio \(h_2/h_1\) are selected in Fig. 12 along with their associated ambient pressure and applied voltages. The simulation results show that reducing the thickness ratio \(h_2/h_1\) tends to increase the maximum amplitude far from resonance. However, the obtained dynamic solutions lose their stability when approaching resonance as the thickness ratio is reduced. One can deduce that a mismatch in the thickness of the two electrically coupled microbeams can affect significantly their dynamic behavior both quantitatively and qualitatively.

Fig. 12
figure 12

Frequency-response curves of the dual beam microsystem for different thickness ratios

Full size image

The upper beam in Fig. 1 (Beam 1), for which the thickness is fixed to \(3\,\upmu {\hbox {m}}\), should have an unchanged natural frequency if no coupling is taking into account. However, as depicted in Fig. 12, when comparing the frequency-response curves for \(h_2/h_1=1.5\) and \(h_2/h_1=1\), there is a clear mismatch in the natural frequency of the system associated with Beam 1 as manifested by the shift in the peaks. This mismatch is not only associated with the electrostatic force coupling as the same voltages are applied. It is also related to the squeeze film damping coupling. This mismatch indicates again the importance of considering the coupled problem approach because it directly affects not only the nonlinear part of the solution but also its linear part.

Fig. 13
figure 13

Frequency-response curves of the dual beam microsystem for different thickness ratios and ambient pressures. Comparison between the fully coupled and the partially coupled approaches

Full size image

We investigate further the results obtained in the previous section concerning the observed quantitative and qualitative differences between the partially coupled and fully coupled approaches. We plot in Fig. 13 the frequency-response curves obtained from the two models while varying the thickness ratio. The results confirm the finding from the previous section concerning the underestimation of the solution when the partially coupled approach is employed. In addition, one cannot ignore the similitude between the frequency-response curves at \(h_2/h_1=1.5\) in Fig. 13 when \(p_\mathrm{a}=0.2p_\mathrm{o}\). This can serve as a motivation to propose a correction to the partially coupled approach as a coefficient directly applied to the ambient pressure. In Fig. 13, when \(h_2/h_1=1.5\), the ambient pressure has been decreased to \(p_\mathrm{a}=0.06p_\mathrm{o}\) for the partially coupled approach to match the curve corresponding to the response when the fully coupled approach is used while setting the ambient pressure equal to \(p_\mathrm{a}=0.2p_\mathrm{o}\). We deduce that a correction factor of 0.3 can be used in this case. Similarly, for the case \(h_2/h_1=0.5\), a correction factor of 0.53 has been used. We note that the correction factor is identified by gradually varying its value and comparing the dynamic solution of the partially coupled ROM to that of the fully coupled ROM at a fixed excitation frequency. The reported value of the correction factor is found to lead a good match between the two ROMs over an extended frequency range as shown in Fig. 13. Furthermore, the frequency response curves depicted in Fig. 13 indicate the dependency of the correction factor on the thickness ratio of the dual beam system. It turns out that this approach has been previously used by Yagubizade and Younis [16] to calibrate a model, using a partially coupled approach, with finite element results. They claimed that the correction factor depends only on the ambient pressure. However, from Fig. 13, one can conclude that, for the optimal case, this correction factor depends on the excitation frequency as well. Inspecting Fig. 13, a good match between the two models is obtained when applying the correction factor. However, we observe at some excitation frequencies, the dynamic responses are completely different both quantitatively and qualitatively. For instance, this discrepancy is obtained for \(\varOmega =3.25\) when \(h_2/h_1=1.5\) and \(\varOmega =3.22\) when \(h_2/h_1=0.5\). The identification of the correction factor can be obtained by formulating an optimization problem with the objective function to be minimized is the minimum of the difference between the amplitudes of the dynamic solutions of the two ROMs over the full frequency range under investigation. The intent of our study was to inspect the existence of a correction factor that can improve the predictive capability of the partially coupled ROM to some extent as reported in a previously published work based on single beam system without electric actuation [16].

Fig. 14
figure 14

Variations of the dynamic response of the system with the ambient pressure \(p_\mathrm{a}\) (represented as ratio of the atmospheric pressure \(p_\mathrm{o}\)) for different excitation frequencies. \(h_2/h_1=1.5\), \(V_\mathrm{DC}=\)50 V, and \(V_\mathrm{AC}=\)10 V. The horizontal dashed line indicates the same amplitude of motion, and its intersection with the two curves corresponding to the two ROMs enables the identification of the correction factor.

Full size image
Fig. 15
figure 15

Force-response curves of the dual beam microsystem for thickness ratios and ambient pressures

Full size image

Figure 14 shows the dynamic response of the system under different ambient pressures \(p_\mathrm{a}\) (represented as ratio of the atmospheric pressure \(p_\mathrm{o}\) )while fixing the excitation frequency. The correction factor can be determined here by selecting a given amplitude of the response and determine the ratio between the corresponding two ambient pressures, for the fully coupled and partially coupled ROM, when they generate the same amplitude of motion. As depicted in Fig. 14, large variations of the correction factor are observed for different excitation frequencies.

The force-response curves are plotted in Fig. 15 for different thickness ratios and ambient pressures. We note that the force-response curve is obtained by varying the amplitude of the AC voltage while keeping the excitation frequency \(\varOmega \) constant and equal to 3. Considering lower thickness ratio tends to reduce the maximum applied AC voltage for stable solutions. In fact, as this ratio is reduced, the stiffness of the microstructure is also reduced. As such, the balance between the electrostatic force and the restoring force of the device, which controls the occurrence of pull-in, is more vulnerable. If large strokes are needed for a specific MEMS application, only one of the beams’ thicknesses can be increased in order to increase the stiffness of the whole device. As shown in Fig. 15, very large stable amplitude is obtained in the case of \(h_2/h_1=1.5\) with relatively small AC voltage.

6 Conclusions

The nonlinear dynamic response of two coupled cantilever microbeams was investigated in this study. The coupling is maintained by the nonlinear electrostatic force applied between the two microbeams and the nonlinear squeeze-film damping effect due to air motions following the volume variation of the space filling the electrostatic gap. The initial air pressure, in which the device operates, was observed to affect significantly its dynamic response. In addition to the structural modeling of the cantilever microbeams following Euler–Bernoulli theory, we proposed the use of two modeling approaches to analyze the impact of the squeeze-film damping. First, we developed a nonlinear multi-physical model of the device by coupling beam equations with the nonlinear Reynolds equation and employed the Galerkin decomposition and differential quadrature method to discretize the structural and fluidic domains, respectively. We considered also another modeling approach based on approximating the squeeze-film damping force by a nonlinear analytical expression. This approach has been widely used in the literature and referred to as partially coupled model in this study. A comparative study of the nonlinear dynamic responses obtained from the two modeling approaches under different operating conditions in terms of electric actuation and applied pressure was conducted. Quantitative and qualitative discrepancies were observed, especially when operating at high AC voltage or near resonance. Frequency- and force-response curves were generated to show the limitations of the partially coupled model to capture properly the microsystem dynamics, especially when approaching the onset of the pull-in instability and exciting the microsystem with an AC voltage near resonance.

Taking advantage of the developed fully coupled model, the influence of the ambient pressure and the thickness ratio between the two microbeams were investigated in details using the nonlinear dynamic response obtained by time integration of the coupled nonlinear equations. It was found that operating the microsystem at a reduced ambient pressure or when one of the microbeams’ thickness is reduced can lead to a premature instability of the dynamic solution which reduces the maximum amplitude of the device. This feature can be seen as advantage for switching applications of the device, but it constitutes an undesirable effect to resonators.