1 Introduction

Investigating the static and dynamic behaviors of micro/nanoelectromechanical systems MEMS/NEMS resonators has been an intriguing area of research since the advent of these technologies. These resonators, mainly based on microbeams, are simple structures that exhibit interesting static and dynamic characteristics. They are easily fabricated using conventional microfabrication techniques. Thus, microbeam resonators have been implemented in several applications including mass sensing [1, 2], mechanical computing [3,4,5,6,7], and RF communication [8, 9].

Resonators are commonly excited near primary resonance. However, other excitation methods have been explored recently for various applications [10,11,12,13,14,15,16,17,18,19,20,21]. Parametric excitation near twice the structure’s natural frequencies is among the most common. Parametric excitation has been used in various applications including signal amplification [10, 11, 19], thermo-mechanical noise squeezing [12], and RF filtering [13]. Multi- or mixed-frequency excitation has been used as well, in which two or more frequency signals are mixed and applied to the resonator [14]. Mixed-frequency excitation gives birth to interesting behaviors, such as the activation of combination resonances, which has been reported for applications in micro-computing [15]. Multi-frequency parametric excitation has also been investigated, where the influence of one or more external excitation is studied along with simultaneous parametric excitation [16,17,18] or multiple simultaneous parametric excitations [19].

In addition, secondary resonances have drawn significant attention [20,21,22,23,24,25]. The method of multiple scales [20, 21, 26] has been employed to investigate the response of a microbeam resonator for superharmonic [22] and subharmonic resonances [22, 23]. The nonlinear dynamics of these secondary resonances have been extensively studied via reduced order models and shooting techniques to reveal limit cycles, investigate stability, and study the dynamic pull-in phenomenon [24]. The study in [24] also proposes the utilization of these resonances to achieve a sharp roll-off radio frequency (RF) filter. It has been shown that superharmonic excitation of an electrostatically actuated resonator can suppress electrical crosstalk and increase the signal-to-noise ratio compared to primary excitation [25]. Furthermore, secondary resonances have also been proposed for switches triggered by mass sensing utilizing the sudden jumps in amplitude and the dynamic pull-in instability [27]. The nonlinear dynamics of carbon nanotube (CNT)-based resonators have been also investigated under secondary resonances [28]. The study in [28] reveals that subharmonic resonance for such a resonator is uniquely activated over a wide range of frequencies.

In the classic mechanics literature, quenching of primary resonance by the addition of a superharmonic resonance excitation source has been suggested as useful for fatigue problems, where the levels of stress and the number of stress reversals are reduced, thereby increasing the lifetime of the structural elements [29].

When actuating a MEMS resonator using a parallel-plate electrostatic force with a DC component superimposed to an AC harmonic load around its primary resonance, the quadratic form of the electrostatic voltage transforms the actuation into two-source excitation with one frequency around the primary resonance and the other of twice that. However, the contribution from the double-frequency component is usually considered negligible compared to the dominant effect of the primary resonance excitation. This assumption is true in cases where the AC load is very small. However, many applications may require high AC loads, and hence, the contribution from the secondary resonance component cannot be ignored [17, 30,31,32,33,34]. Currently, there is lack of a comprehensive analytical analysis that deals with generic electrostatic loading conditions (small and large AC voltage amplitudes) and gives an accurate response of the resonator irrespective of the amount of DC and AC voltage used.

In this work, we present a comprehensive analytical solution based on MTS for a general loading case, which accounts for most practical excitation conditions. Also, we consider the case of large AC voltages, in which the resonator gets excited from both primary and secondary sources when they are of comparable strength, leading to competing effects from subharmonic and primary resonance excitations. We also present a charge sensor and a resonator-based logic device based on the dynamic characteristics of the proposed system. The rest of the paper is organized as follows. Section 2 presents the problem formulation and background. Section 3 presents the analytical solution using the method of Multiple Time Scales. Finally, Sect. 4 summarizes the findings of the study.

Fig. 1
figure 1

Schematic of a single degree-of-freedom (SDOF) spring mass damper system under parallel-plate electrostatic actuation

Full size image

2 Problem formulation

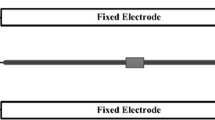
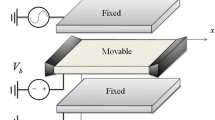
The nondimensional equation of motion for an electrostatically actuated MEMS resonator using a lumped parameter model, Fig. 1, is given by [35].

$$\begin{aligned}&\ddot{x}(t)+2\mu {\dot{x}}(t)+x(t) = \frac{\beta }{(1-x(t))^{2}} \nonumber \\&\quad \left[ \overbrace{\left( {V_\mathrm{DC}^2 +\frac{V_\mathrm{AC}^2 }{2}} \right) }^{V_\mathrm{eff} \hbox { (static)}}+\overbrace{2V_\mathrm{DC} V_\mathrm{AC} \cos (\Omega t)}^{\mathrm {Primary}}\right. \nonumber \\&\quad \left. +\overbrace{\frac{V_\mathrm{AC}^2 }{2}\left( {\cos (2\Omega t)} \right) }^{\mathrm {secondary}} \right] \end{aligned}$$
(1)

where

$$\begin{aligned} \mu =\frac{c}{2\sqrt{mk}}\, ; \beta =\frac{\epsilon A}{2kd^{3}} \end{aligned}$$
(2)

and m is the mass, c is the damping coefficient, k is the spring stiffness coefficient, A is the overlap area, \(\epsilon \) is the permittivity of air, \(V_\mathrm{DC}\) is the DC bias, \(V_\mathrm{AC}\) is the AC harmonic load, and \(\Omega \) is the AC frequency. We notice from Eq. (1) that due to the quadratic nature of the electrostatic forcing, the actuation is transformed into a simultaneous multi-frequency excitation around the primary resonance and twice of that. Furthermore, we notice the contribution of the AC voltage toward the static loading.

The solution of x comprises of a static \(\delta \) and dynamic part u given by

$$\begin{aligned} x(t)=u(t)+\delta \end{aligned}$$
(3)

where

$$\begin{aligned} \delta =\frac{\beta \left( {V_\mathrm{DC}{}^{2}+\frac{V_\mathrm{AC}{}^{2}}{2}} \right) }{(1-\delta )^{2}} \end{aligned}$$
(4)

Equation (4) is cubic in nature and yields three solutions: one is non-physical, one is unstable, and one is stable [35]. We consider here only the stable solution.

Substituting Eq. (3) into (1) yields

$$\begin{aligned}&\ddot{u}(t)+2\mu {\dot{u}}(t)+u(t)+\delta \nonumber \\&\quad =\frac{\beta [V_\mathrm{DC} +V_\mathrm{AC} \cos (\Omega t)]^{2}}{(1-u(t)-\delta )^{2}} \end{aligned}$$
(5)

Expanding the right-hand side of Eq. (5) in Taylor series and dropping the static terms of Eq. (4), we get

$$\begin{aligned}&\ddot{u}(t)+2\mu {\dot{u}}(t)+u(t)+\delta \nonumber \\&=\beta \left[ 2V_\mathrm{DC} V_\mathrm{AC} \cos (\Omega t)\right. \nonumber \\&\left. \quad +\frac{V_\mathrm{AC} {}^{2}}{2}\cos (2\Omega t)\right] \nonumber \\&\quad \times \left( \frac{1}{(1-\delta )^{2}}+\frac{2u}{(1-\delta )^{3}}\right. \nonumber \\&\quad \left. +\frac{3u^{2}}{(1-\delta )^{4}}+\frac{4u^{3}}{(1-\delta )^{5}}+O(u^{4}) \right) \end{aligned}$$
(6)

Using Eq. (6), we perform the multiple scales analysis on three cases derived by considering different higher-order terms and compare them against the long-time integration (LTI) solution of Eq. (1).

2.1 Case 1 (\(V_\mathrm{DC}>>V_\mathrm{AC}\))

This is a common case in MEMS application leading to primary resonance excitation, in which \(V_\mathrm{DC}\) is assumed to be much larger than \(V_\mathrm{AC}\). Here, the effect from the \(\cos (2\Omega t)\) term in Eq. (6) is considered negligible and is dropped out. The governing equation in this case can be simplified to

$$\begin{aligned} \ddot{u}+2\mu {\dot{u}}+\alpha _q u^{2}+\alpha _c u^{3}+\omega ^{2}u=F_p \cos (\Omega t) \end{aligned}$$
(7)

where \(\alpha _q =\frac{-3\beta V_\mathrm{eff} }{(1-\delta )^{4}};\alpha _c =\frac{-4\beta V_\mathrm{eff} }{(1-\delta )^{5}}; \omega ^{2}=1-\frac{2\beta V_\mathrm{eff} }{(1-\delta )^{3}};F_p =\frac{2\beta V_\mathrm{DC} V_\mathrm{AC} }{(1-\delta )^{2}};V_\mathrm{eff} =V_\mathrm{DC}^2\).

Note here that for this case only, the static term comprises of just the \(V_\mathrm{DC}\) part, i.e.,\(V_\mathrm{eff} =V_\mathrm{DC}^2\).

2.2 Case 2 (generic loading)

For the second case, we consider both the \(\cos (\Omega t)\) and \(\cos (2\Omega t)\) direct excitation terms and drop the other parametric terms. The governing equation for this case is given by

$$\begin{aligned}&\ddot{u}+2\mu {\dot{u}}+\alpha _q u^{2}+\alpha _c u^{3}+\omega ^{2}u\nonumber \\&\quad =F_p \cos (\Omega t)+F_s \cos (2\Omega t) \end{aligned}$$
(8)

where \(F_s =\frac{\beta V_\mathrm{AC}^2 }{2(1-\delta )^{2}};V_\mathrm{eff} =V_\mathrm{DC}^2 +\frac{V_\mathrm{AC}^2 }{2}\).

2.3 Case 3 (generic loading)

For the third case, we retain the primary and subharmonic excitation terms as below

$$\begin{aligned}&\ddot{u}+2\mu {\dot{u}}+\alpha _q u^{2}+\alpha _c u^{3}+\omega ^{2}u \nonumber \\&\quad =F_p \cos (\Omega t)+F_s \cos (2\Omega t)+F_\mathrm{spar1} \cos (2\Omega t)u \nonumber \\&\qquad +\,F_\mathrm{spar2} \cos (2\Omega t)u^{2} \end{aligned}$$
(9)

where \(F_\mathrm{spar1} =\frac{\beta V_\mathrm{AC}^2 }{(1-\delta )^{3}};F_\mathrm{spar2} =\frac{3\beta V_\mathrm{AC}^2 }{2(1-\delta )^{4}};V_\mathrm{eff} =V_\mathrm{DC}^2 +\frac{V_\mathrm{AC}^2 }{2}\). Recall here that \(\omega ^{2}=1-\frac{2\beta V_\mathrm{eff} }{(1-\delta )^{3}}\), which shows that both the \(V_\mathrm{DC}\) and \(V_\mathrm{AC}\) have an influence on the natural frequency of the resonator.

Next, we apply the MTS on these cases to determine the frequency response equations.

3 Method of multiple time scales

In order to obtain solutions of the three case studies, MTS analysis is performed on the most generic case, case 3 of Eq. (9). The frequency response equations for the other two cases are then derived from the results of this case.

3.1 Case 3 (generic loading)

We scale Eq. (9) as follows:

$$\begin{aligned}&\ddot{u}+2\varepsilon ^{2}\mu {\dot{u}}+\alpha _q u^{2}+\alpha _c u^{3}+\omega ^{2}u \nonumber \\&\quad =\varepsilon ^{3}F_p \cos (\Omega t)+\varepsilon F_s \cos (2\Omega t)\nonumber \\&\qquad +\varepsilon F_\mathrm{spar1} \cos (2\Omega t)u +\varepsilon F_\mathrm{spar2} \cos (2\Omega t)u^{2} \end{aligned}$$
(10)

where \(\varepsilon \) is a book-keeping parameter. A systematic scaling procedure is followed here according to [20, 21], where the parameter \(\varepsilon \) is introduced with its various orders as a “book-keeping” parameter to label and give importance in the symbolic form for the strength of the various terms in the equation. Using this procedure, we segregate and order the different types of nonlinearities (cubic (\(\varepsilon ^{3}\)) weaker than quadratic (\(\varepsilon ^{2}\))), which is weaker than linear stiffness (\(\varepsilon )\)) as well as the various forces. (The secondary excitation forcing term is scaled with a linear scale \(\varepsilon \) to allow it to influence the response and compete in importance with the strong primary excitation, which is scaled at order \(\varepsilon ^{3}\); again to lower its strength to make it compete with the secondary excitation term.) Once the MTS analysis is completed \(\varepsilon \) is set to one [20, 21].

We seek a three-term expansion of the form

$$\begin{aligned} u(t;\varepsilon )= & {} \varepsilon u_0 (T_0 ,T_1 ,T_2 )+\varepsilon ^{2}u_1 (T_0 ,T_1 ,T_2 )\nonumber \\&+\varepsilon ^{3}u_2 (T_0 ,T_1 ,T_2 ) \end{aligned}$$
(11)

where \(T_n =\varepsilon ^{n}t\).

The temporal derivatives are defined as \(\frac{\mathrm{d}}{\mathrm{d}t}=D_o +\varepsilon D_1 +\varepsilon ^{2}D_2 \), where \(\frac{\delta }{\delta T_n}=D_n \). We substitute Eq. (11) into (10) to obtain

$$\begin{aligned}&O(\varepsilon ^{1}):D_o ^{2}u_0 +\omega ^{2}u_0 =F_s \cos (2\Omega t) \nonumber \\&\quad \Rightarrow u_0 =A\hbox {e}^{i\omega T_o }+\lambda _s \hbox {e}^{2i\Omega T_o }+cc \end{aligned}$$
(12)

where \(\lambda _s =\frac{F_s }{\omega ^{2}-4\Omega ^{2}}\), \(A\Rightarrow A(T_1 ,T_2 )\), and cc stands for complex conjugates.

$$\begin{aligned}&O(\varepsilon ^{2}):D_o ^{2}u_1 +\omega ^{2}u_1 =-2D_o D_1 u_o \nonumber \\&\quad -\,\alpha _q u_o ^{2}+F_\mathrm{spar1} \cos (2\Omega T_o )u_o \end{aligned}$$
(13)
$$\begin{aligned}&O(\varepsilon ^{3}):D_o ^{2}u_2 +\omega ^{2}u_2 =-2D_o D_1 u_1 \nonumber \\&\quad -\,2D_o D_2 u_o -2\mu D_o u_o -D_1 ^{2}u_o \nonumber \\&\quad -\,2\alpha _q u_o u_1 -\alpha _c u_o^3 +F_p \cos \left( {\Omega T_0 } \right) \nonumber \\&\quad +\,F_\mathrm{spar1} \cos \left( {2\Omega T_0 } \right) u_1 +F_\mathrm{spar2} \cos \left( {2\Omega T_0 } \right) u_o^2 \end{aligned}$$
(14)

In order to express the nearness of \(\Omega \) to \(\omega \), we set

$$\begin{aligned} \Omega =\omega +\varepsilon ^{2}\sigma \end{aligned}$$
(15)

Next, we plug Eqs. (12) and (15) into Eq. (13) and eliminate the secular terms, which yield the following solvability condition:

$$\begin{aligned}&-\, 2{\lambda _s}{\alpha _q}\bar{A}{\mathrm{{e}}^{2\mathrm{{i}}\sigma {T_2}}} - 2\mathrm{{i}}\omega {D_1}A \nonumber \\&+\, \frac{1}{2}{F_\mathrm{spar1}}\bar{A}{\mathrm{{e}}^{2\mathrm{{i}}\sigma {T_2}}} + cc = 0 \end{aligned}$$
(16)

where A is a complex-valued quantity and \({\bar{A}}\) is its complex conjugate. From Eq. (16), we get

$$\begin{aligned} \begin{array}{l} {D_1}A = \frac{{\mathrm{{i}}{\lambda _s}{\alpha _q}\bar{A}{\mathrm{{e}}^{2\mathrm{{i}}\sigma {T_2}}}}}{\omega } - \frac{{\mathrm{{i}}{F_\mathrm{spar1}}\bar{A}{\mathrm{{e}}^{2\mathrm{{i}}\sigma {T_2}}}}}{{4\omega }}\mathrm{{ }}\\ {D_1}\bar{A} = - \frac{{\mathrm{{i}}{\lambda _s}{\alpha _q}A{\mathrm{{e}}^{ - 2\mathrm{{i}}\sigma {T_2}}}}}{\omega } + \frac{{\mathrm{{i}}{F_\mathrm{spar1}}A{\mathrm{{e}}^{ - 2\mathrm{{i}}\sigma {T_2}}}}}{{4\omega }}\\ D_1^2A = - \frac{{{\lambda _s}{F_\mathrm{spar1}}{\alpha _q}A}}{{2{\omega ^2}}} + \frac{{F_\mathrm{spar1}^2A}}{{16{\omega ^2}}} + \frac{{\lambda _s^2\alpha _q^2A}}{{{\omega ^2}}} \end{array} \end{aligned}$$
(17)

Next, we solve Eq. (13), exclude the secular terms of Eq. (16) and get the particular solution \(u_1 \)

$$\begin{aligned} {u_1}= & {} - \frac{{({F_\mathrm{spar1}} - 4{\lambda _s}{\alpha _q})\bar{A}{\mathrm{{e}}^{ - \mathrm{{i}}(\omega + 2\Omega ){T_0}}}}}{{8\Omega (\omega + \Omega )}}\nonumber \\&- \frac{{2{\alpha _q}A\bar{A}}}{{{\omega ^2}}} + \frac{{{\alpha _q}{{\bar{A}}^2}{\mathrm{{e}}^{ - 2\mathrm{{i}}\omega {T_0}}}}}{{3{\omega ^2}}}\nonumber \\&- \frac{{({F_\mathrm{spar1}} - 4{\lambda _s}{\alpha _q})A{\mathrm{{e}}^{\mathrm{{i}}(\omega + 2\Omega ){T_0}}}}}{{8\Omega (\omega + \Omega )}}\nonumber \\&+ \frac{{{\alpha _q}{A^2}{\mathrm{{e}}^{2\mathrm{{i}}\omega {T_0}}}}}{{3{\omega ^2}}} + \frac{{{\lambda _s}({F_\mathrm{spar1}} - 2{\lambda _s}{\alpha _q})}}{{{\omega ^2}}}\nonumber \\&+ \frac{{{\lambda _s}({F_\mathrm{spar1}} - 2{\lambda _s}{\alpha _q}){\mathrm{{e}}^{ - 4\mathrm{{i}}\Omega {T_0}}}}}{{2({\omega ^2} - 16{\Omega ^2})}}\nonumber \\&+ \frac{{{\lambda _s}({F_\mathrm{spar1}} - 2{\lambda _s}{\alpha _q}){\mathrm{{e}}^{4\mathrm{{i}}\Omega {T_0}}}}}{{2({\omega ^2} - 16{\Omega ^2})}} \end{aligned}$$
(18)

Next, we substitute Eqs. (12) and (18) into Eq. (14), obtain the secular terms and set them equal to zero

$$\begin{aligned}&\left( \begin{array}{l} - 6\lambda _s^2{\alpha _c} - \frac{{2{\lambda _s}{F_\mathrm{spar1}}{\alpha _q}}}{{{\omega ^2}}} + \frac{{{\lambda _s}{F_\mathrm{spar1}}{\alpha _q}}}{{2\Omega (\omega + \Omega )}} - \frac{{F_\mathrm{spar1}^2}}{{16\Omega (\omega + \Omega )}} + 2{\lambda _s}{F_\mathrm{spar2}}\\ - 2\mathrm{{i}}\mu \omega + \frac{{4\lambda _s^2\alpha _q^2}}{{{\omega ^2}}} - \frac{{2\lambda _s^2\alpha _q^2}}{{2\omega \Omega + 2{\Omega ^2}}} \end{array} \right) A\nonumber \\&\qquad + \left( {\frac{{10\alpha _q^2}}{{3{\omega ^2}}} - 3{\alpha _c}} \right) {A^2}\bar{A} - 2\mathrm{{i}}\omega {D_2}A \nonumber \\&\qquad - \,D_1^2A + \frac{1}{2}{F_p}{\mathrm{{e}}^{\mathrm{{i}}\sigma {T_2}}} + cc = 0 \end{aligned}$$
(19)

From Eq. (19), we get

$$\begin{aligned} {D_2}A= & {} \left( \begin{array}{l} \frac{{3\mathrm{{i}}\lambda _s^2{\alpha _c}}}{\omega } + \frac{{\mathrm{{i}}{\lambda _s}{F_\mathrm{spar1}}{\alpha _q}}}{{{\omega ^3}}} - \frac{{\mathrm{{i}}{\lambda _s}{F_\mathrm{spar1}}{\alpha _q}}}{{4\omega \Omega (\omega + \Omega )}} + \frac{{\mathrm{{i}}F_\mathrm{spar1}^2}}{{32\omega \Omega (\omega + \Omega )}} - \frac{{\mathrm{{i}}{\lambda _s}{F_\mathrm{spar2}}}}{\omega }\\ - \mu - \frac{{2\mathrm{{i}}\lambda _s^2\alpha _q^2}}{{{\omega ^3}}} + \frac{{\mathrm{{i}}\lambda _s^2\alpha _q^2}}{{2\omega \Omega (\omega + \Omega )}} \end{array} \right) A\nonumber \\&+\,\left( {\frac{{3\mathrm{{i}}{\alpha _c}}}{{2\omega }} - \frac{{5\mathrm{{i}}\alpha _q^2}}{{3{\omega ^3}}}} \right) {A^2}\bar{A} + \frac{{\mathrm{{i}}D_1^2A}}{{2\omega }} - \frac{{\mathrm{{i}}{F_p}{\mathrm{{e}}^{\mathrm{{i}}\sigma {T_2}}}}}{{4\omega }} \end{aligned}$$
(20)

Next, we use the method of reconstitution

$$\begin{aligned} \frac{\mathrm{d}A}{\mathrm{d}t}=D_1 A+D_2 A \end{aligned}$$
(21)

and set \(\varepsilon \) to unity

where

$$\begin{aligned} A\left( {T_1 ,T_2 } \right) =\frac{1}{2}a\left( t \right) e^{i\beta (t)} \end{aligned}$$
(22)

Using the definitions from Eqs. (17) and (20) in (21), and then using the resulting equation and Eq. (22) into (19), we obtain

$$\begin{aligned} \frac{{a'}}{2} + \frac{1}{2}\mathrm{{i}}a\beta '= & {} \frac{{3\mathrm{{i}}{a^3}{\alpha _c}}}{{16\omega }} - \frac{{5\mathrm{{i}}{a^3}\alpha _q^2}}{{24{\omega ^3}}} + \frac{{3\mathrm{{i}}a\lambda _s^2{\alpha _c}}}{{2\omega }}\nonumber \\&+\, \frac{{3\mathrm{{i}}a{\lambda _s}{F_\mathrm{spar1}}{\alpha _q}}}{{8{\omega ^3}}} - \frac{{\mathrm{{i}}a{\lambda _s}{F_\mathrm{spar1}}{\alpha _q}}}{{8\omega \Omega (\omega + \Omega )}}\nonumber \\&+\, \frac{{\mathrm{{i}}aF_\mathrm{spar1}^2}}{{64{\omega ^3}}} + \frac{{\mathrm{{i}}aF_\mathrm{spar1}^2}}{{64\omega \Omega (\omega + \Omega )}}\nonumber \\&-\, \frac{{\mathrm{{i}}a{F_\mathrm{spar1}}{\mathrm{{e}}^{2\mathrm{{i}}\sigma {T_2} - 2\mathrm{{i}}\beta }}}}{{8\omega }} - \frac{{\mathrm{{i}}a{\lambda _s}{F_\mathrm{spar2}}}}{{2\omega }} \nonumber \\&-\, \frac{{a\mu }}{2} - \frac{{3\mathrm{{i}}a\lambda _s^2\alpha _q^2}}{{4{\omega ^3}}} + \frac{{\mathrm{{i}}a\lambda _s^2\alpha _q^2}}{{4\omega \Omega (\omega + \Omega )}}\nonumber \\&+\, \frac{{\mathrm{{i}}a{\lambda _s}{\alpha _q}{\mathrm{{e}}^{2\mathrm{{i}}\sigma {T_2} - 2\mathrm{{i}}\beta }}}}{{2\omega }} - \frac{{\mathrm{{i}}{F_p}{\mathrm{{e}}^{\mathrm{{i}}\sigma {T_2} - \mathrm{{i}}\beta }}}}{{4\omega }}\nonumber \\ \end{aligned}$$
(23)

where \(\left( \right) ^{\prime }\) is the derivative with respect to t. Next, we set \(\beta -\sigma T_2 =\gamma \) and separate the real and imaginary parts to get the modulation equations

$$\begin{aligned}&Re:\frac{{a}'}{2}=-\frac{a\mu }{2}-\frac{F_p }{4\omega }\sin (\gamma )\nonumber \\&\qquad +\left( {\frac{a\lambda _s \alpha _q )}{2\omega }-\frac{aF_\mathrm{spar1} }{8\omega }} \right) \sin (2\gamma ) \end{aligned}$$
(24)
$$\begin{aligned}&Im:\frac{a\gamma ^{\prime }}{2}=\frac{F_p \cos (\gamma )}{4\omega }+a^{3}\left( {\frac{5\alpha _q^2 }{24\omega ^{3}}-\frac{3\alpha _c }{16\omega }} \right) \nonumber \\&\qquad +a\cos (2\gamma )\left( {\frac{F_\mathrm{spar1} }{8\omega }-\frac{\lambda _s \alpha _q }{2\omega }} \right) \nonumber \\&\qquad +\,a\left( {\begin{array}{l} \frac{\sigma }{2}-\frac{F_\mathrm{spar1}^2 }{64\omega ^{3}}-\frac{F_\mathrm{spar1}^2 }{64\omega \Omega (\omega +\Omega )}+\frac{a\lambda _s F_\mathrm{spar2} }{2\omega }-\frac{3\lambda _s \alpha _q F_\mathrm{spar1} }{8\omega ^{3}} \\ +\frac{\lambda _s \alpha _q F_\mathrm{spar1} }{8\omega \Omega (\omega +\Omega )}-\frac{3\lambda _s^2 \alpha _c }{2\omega }+\frac{3\lambda _s^2 \alpha _q^2 }{4\omega ^{3}}-\frac{\lambda _s^2 \alpha _q^2 }{4\omega \Omega (\omega +\Omega )} \\ \end{array}} \right) \nonumber \\ \end{aligned}$$
(25)

where a and \(\gamma \) are the nondimensional amplitude and phase, \(\sigma \) is the frequency detuning parameter, and \(\Omega \) is defined in Eq. (15) for \(\varepsilon =1\). The steady-state (equilibrium) solution is then obtained by setting \({a}'=0\), \({\gamma }'=0\) in Eqs. (24) and (25), and algebraically solving the resulting equations. The stability of the solution is determined by solving for the eigenvalues of the Jacobian of the modulation equations, Eqs. (24) and (25) [20, 21, 35].

Finally, the solution is given by

$$\begin{aligned} u(t)= & {} \left( {\frac{\lambda _s F_\mathrm{spar1} }{\omega ^{2}}-\frac{2\lambda _s^2 \alpha _q }{\omega ^{2}}} \right) \nonumber \\&+\,a\cos \left( {\Omega t+\gamma } \right) -\frac{\alpha _q }{2\omega ^{2}}a^{2} \nonumber \\&+\frac{\alpha _q }{6\omega ^{2}}a^{2}\cos \left( {2\Omega t+2\gamma } \right) \nonumber \\&+\frac{2F_s }{(\omega ^{2}-4\Omega ^{2})}\cos \left( {2\Omega t} \right) \nonumber \\&+\left( {\frac{4\lambda _s \alpha _q -F_\mathrm{spar1} }{8\Omega \left( {\omega +\Omega } \right) }} \right) a\cos \left( {3\Omega t+\gamma } \right) \nonumber \\&+\left( {\frac{\lambda _s F_\mathrm{spar1} -2\lambda _s^2 \alpha _q }{\omega ^{2}-16\Omega ^{2}}} \right) \cos \left( {4\Omega t} \right) \end{aligned}$$
(26)

3.2 Case 2 (generic loading)

For a scaling scheme similar to that of Eq. (10), the solution to Eq. (8) can be obtained by setting \(F_\mathrm{spar1}\) and \(F_\mathrm{spar2}\) equal to zero in Eqs. (24) and (25). The steady-state equations for this case are given by

$$\begin{aligned} Re:0= & {} -\frac{a\mu }{2}+\frac{a\lambda _s \alpha _q \sin (2\gamma )}{2\omega }-\frac{F_p \sin (\gamma )}{4\omega } \end{aligned}$$
(27)
$$\begin{aligned} Im:0= & {} a^{3}\left( {\frac{5\alpha _q^2 }{24\omega ^{3}}-\frac{3\alpha _c }{16\omega }} \right) \nonumber \\&+a\left( {\frac{\sigma }{2}-\frac{3\lambda _s^2 \alpha _c }{2\omega }+\frac{3\lambda _s^2 \alpha _q^2 }{4\omega ^{3}}-\frac{\lambda _s^2 \alpha _q^2 }{4\omega \Omega (\omega +\Omega )}} \right) \nonumber \\&-\frac{a\alpha _q \lambda _s \cos (2\gamma )}{2\omega }+\frac{F_p \cos (\gamma )}{4\omega } \end{aligned}$$
(28)

Equations (27) and (28) can be solved algebraically to get the frequency response plots.

3.3 Case 1 (\(V_\mathrm{DC}>>V_\mathrm{AC}\))

Finally, the solution to Eq. (7) is obtained by setting \(F_s ,F_\mathrm{spar1} ,\) and \(F_\mathrm{spar2}\) equal to zero in Eqs. (24) and (25). The solution can be transformed into the following classical algebraic equation [20, 21]:

$$\begin{aligned} \left( {a\mu } \right) ^{2}+\left( {a\sigma -\frac{3a^{3}\alpha _c }{8\omega }+\frac{5a^{3}\alpha _q^2 }{12\omega ^{3}}} \right) ^{2}=\left( {\frac{F_p }{2\omega }} \right) ^{2} \end{aligned}$$
(29)

Equation (29) represents the typical frequency response equation of a SDOF oscillator with cubic and quadratic nonlinearity under primary excitation [21].

4 Results

4.1 Results from the three cases

In this section, the frequency responses of the resonator for the three cases of Sect. 3 are compared along with the long- time integration (LTI) of Eq. (1). As a case study, we assume a structure with \(\beta =7.14 \times 10^{-5}\,\hbox {V}^{-2}\). Note that the rest of parameters in the equations of Eq. (9) will be calculated based on the assumed voltage loads. Figure 2 shows the results.

It can be noticed that for the loads of \(V_\mathrm{DC}\approx \hbox {V}_\mathrm{AC}\) and \(V_\mathrm{DC}>>V_\mathrm{AC}\), case 1 accurately predicts the response of the microresonator, Fig. 2a, b. This shows that for these cases, the contribution from \(F_s \cos (2\Omega t\)) is very small compared to \(F_p \cos (\Omega t)\) and hence can be safely ignored. However, as \(V_\mathrm{AC}\) becomes large, the contribution from \(F_s \cos (2\Omega t)\) becomes not negligible and the frequency response given by case 1 becomes erroneous, Fig. 2c, d. It is interesting to note that even case 2 fails to predict the accurate response. This shows that including only the direct excitation term of twice the excitation frequency is not enough. However, case 3 is able to closely predict the behavior of the resonator with respect to the LTI solution of Eq. (1), Fig. 2c, d. This is attributed to the missing higher-order parametric terms that have significant contribution to the resonator’s response. Hence, in order to predict the response of the resonator at any values of \(V_\mathrm{DC}\) and \(V_\mathrm{AC}\), a more comprehensive form given by case 3 is required, which includes the higher-order parametric terms. A slight deviation from the response of LTI of Eq. (1) is noticed due to the truncation of the higher-order forcing terms in the Taylor series expansion. This effect is more evident in Fig. 2b, d, where the resonator vibrates with larger amplitudes. As the forcing amplitude is increased, the effect of the truncated higher-order terms of the electrostatic force term in Eq. (6) starts to become significant and hence causes the deviation. As mentioned in [35, 36], at least 20 terms need to be used in the Taylor series expansion to represent accurately the electrostatic force term. It is important to note here that even though the excitation voltages of Fig. 2c, d are almost the same, the damping conditions are different. A much lower damping is used for the case of Fig. 2d. Hence, there is larger deviation in Fig. 2d compared to Fig. 2c. In order to confirm the influence of the truncated terms, LTI is performed on Eq. (9) for Fig. 2d only. It can be observed that LTI of the truncated response matches that of the MTS response of case 3.

Fig. 2
figure 2

Analytical and numerical frequency response curves of the resonator against the frequency detuning parameter \(\sigma \) for a\(V_\mathrm{DC}=5\,\hbox {V}\), \(V_\mathrm{AC}=5\,\hbox {V}\) and \(\mu =0.01\), b\(V_\mathrm{DC}=27\,\hbox {V}\), \(V_\mathrm{AC}=2\,\hbox {V}\), and \(\mu =0.01\), c\(V_\mathrm{DC}=1\,\hbox {V}\), \(V_\mathrm{AC}=15\,\hbox {V}\), and \(\mu =0.01\), and d\(V_\mathrm{DC}=0.1\,\hbox {V}\), \(V_\mathrm{AC}=16.5\,\hbox {V}\), and \(\mu =0.005\). Here, the frequency response equations obtained after solving through MTS give only the dynamic solution “a,” and hence the static solution calculated from (4) is superimposed afterward to compare to the LTI solution. The y-axis label “Amplitude” refers to the amplitude of the resonator including both the static and dynamics solutions, “\(\delta \)+a”

Full size image

Note that all the parametric terms that survive the scaling are included in Eq. (9) to maintain consistency. However, one of these terms may have a stronger influence on the overall response of the resonator compared to the other. In order to investigate this, the response of the resonator using Eqs. (24) and (25) with different contributions from parametric terms is simulated and shown in Fig. 3. The figure shows that the contribution of the parametric term associated with \(u^{2}\) is negligible compared to the parametric term associated with u toward the response predicted by case 3, Fig. 3. Hence, the parametric term associated with \(u^{2}\) may be dropped and the resulting equations of motion for case 3 given by Eqs. (24) and (25) can be also used with \(F_\mathrm{spar2} =0\).

Fig. 3
figure 3

Analytical frequency response of the resonator against the frequency detuning parameter \(\sigma \) for \(V_\mathrm{DC}=0.1\,\hbox {V}\), \(V_\mathrm{AC}=16.5\,\hbox {V}\) and \(\mu =0.005\). Different parametric terms of Eq. (9) are set to zero to determine the contribution of each one on the total response. The y-axis label “Amplitude” refers to the amplitude of the resonator including both the static and dynamics solutions, “\(\delta \)+a”

Full size image

4.2 Other scaling methods

Other scaling approaches for the MTS have been explored. The findings of some of those cases are given below.

4.2.1 Case 4 (generic loading)

For this case, the scaling of Eq. (9) is chosen such that damping is scaled as \(\varepsilon \mu {\dot{u}}\). The equation of motion in this case with the appropriate scaling is given by

$$\begin{aligned}&\ddot{u}+2\varepsilon \mu {\dot{u}}+\alpha _q u^{2}+\alpha _c u^{3}+\omega ^{2}u \nonumber \\&\quad =\varepsilon ^{3}F_p \cos (\Omega t)+\varepsilon F_s \cos (2\Omega t)+\varepsilon F_\mathrm{spar1} \cos (2\Omega t)u \nonumber \\&\qquad +\,\varepsilon F_\mathrm{spar2} \cos (2\Omega t)u^{2} \end{aligned}$$
(30)

The resulting frequency response equations after carrying out the analysis are given by

$$\begin{aligned}&Re : 0=-\frac{a\mu }{2}+\sin (2\gamma )\left( {\frac{a\lambda _s \alpha _q }{2\omega }-\frac{aF_\mathrm{spar1} }{8\omega }} \right) \nonumber \\&\quad -\,\frac{\sin (\gamma )F_p }{4\omega } \nonumber \\&\quad +\,a\cos (2\gamma )\left( {-\frac{\mu F_\mathrm{spar1} }{8\omega ^{2}}+\frac{2\lambda _s \mu \Omega \alpha _q }{\omega (\omega ^{2}-4\Omega ^{2})}+\frac{\lambda _s \mu \alpha _q }{2\omega ^{2}}} \right) \nonumber \\\end{aligned}$$
(31)
$$\begin{aligned}&Im:0=a^{3}\left( {\frac{5\alpha _q^2 }{24\omega ^{3}}-\frac{3\alpha _c }{16\omega }} \right) \nonumber \\&\quad +\,a\left( {\begin{array}{l} \frac{\sigma }{2}-\frac{3\lambda _s^2 \alpha _c }{2\omega }-\frac{3\lambda _s F_\mathrm{spar1} \alpha _q }{8\omega ^{3}}+\frac{\lambda _s F_\mathrm{spar1} \alpha _q }{8\omega \Omega (\omega +\Omega )} \\ -\frac{F_\mathrm{spar1}^2 }{64\omega ^{3}}-\frac{\mu ^{2}}{4\omega }-\frac{F_\mathrm{spar1}^2 }{64\omega \Omega (\omega +\Omega )}+\frac{\lambda _s F_\mathrm{spar2} }{2\omega } \\ +\frac{3\lambda _s^2 \alpha _q^2 }{4\omega ^{3}}-\frac{\lambda _s^2 \alpha _q^2 }{4\omega \Omega (\omega +\Omega )} \\ \end{array}} \right) \nonumber \\&\quad +\,a\sin (2\gamma )\left( {-\frac{\mu F_\mathrm{spar1} }{8\omega ^{2}}+\frac{2\lambda _s \mu \Omega \alpha _q }{\omega (\omega ^{2}-4\Omega ^{2})}+\frac{\lambda _s \mu \alpha _q }{2\omega ^{2}}} \right) \nonumber \\&\quad +\,a\cos (2\gamma )\left( {\frac{F_\mathrm{spar1} }{8\omega }-\frac{\lambda _s \alpha _q }{2\omega }} \right) +\frac{\cos (\gamma )F_p }{4\omega } \end{aligned}$$
(32)

The new terms added due to the damping can be observed in Eqs. (31) and (32).

4.3 Case 5 (generic loading)

For this case, damping is scaled as \(\varepsilon \mu {\dot{u}}\) and the primary force appears at the quadratic order. This allows for the parametric term associated with the primary excitation to be included as well. The equation of motion in this case with the appropriate scaling is written as

$$\begin{aligned}&\ddot{u}+2\varepsilon \mu {\dot{u}}+\alpha _q u^{2}+\alpha _c u^{3}+\omega ^{2}u \nonumber \\&\quad =\varepsilon ^{2}F_p \cos (\Omega t)+\varepsilon F_s \cos (2\Omega t)+\varepsilon ^{2}F_{ppar} \cos (\Omega t)u \nonumber \\&\qquad +\,\varepsilon F_\mathrm{spar1} \cos (2\Omega t)u+\varepsilon F_\mathrm{spar2} \cos (2\Omega t)u^{2} \end{aligned}$$
(33)

where, \(F_{ppar} =\frac{4\beta V_\mathrm{DC} V_\mathrm{AC} }{(1-\delta )^{3}}\). Subsequently, the resulting frequency response equations are given by

$$\begin{aligned}&Re:0=-\frac{a\mu }{2}-\frac{\mu F_p Cos\left( \gamma \right) }{8\omega ^{2}}\nonumber \\&\quad +\,aSin(2\gamma )\left( {-\frac{F_\mathrm{spar1} }{8\omega }+\frac{\alpha _q \lambda _s }{2\omega }} \right) \nonumber \\&\quad +\,Sin(\gamma )\left( {-\frac{F_p }{4\omega }+\frac{F_p F_\mathrm{spar1} }{32\omega ^{3}}-\frac{F_{ppar} \lambda _s }{4\omega }-\frac{F_p \alpha _q \lambda _s }{8\omega ^{3}}} \right) \nonumber \\&\quad +\,aCos\left( {2\gamma } \right) \left( {-\frac{\mu F_\mathrm{spar1} }{8\omega ^{2}}+\frac{\mu \alpha _q \lambda _s }{2\omega ^{2}}+\frac{2\mu \Omega \alpha _q \lambda _s }{\omega (\omega ^{2}-4\Omega ^{2})}} \right) \end{aligned}$$
(34)
$$\begin{aligned}&Im:0=-\frac{\mu F_p Sin\left( \gamma \right) }{8\omega ^{2}}+a^{3}\left( {-\frac{3\alpha _c }{16\omega }+\frac{5\alpha _q^2 }{24\omega ^{3}}} \right) \nonumber \\&\quad +\,aCos\left( {2\gamma } \right) \left( {\frac{F_\mathrm{spar1} }{8\omega }-\frac{\alpha _q \lambda _s }{2\omega }} \right) \nonumber \\&\quad +\,aSin\left( {2\gamma } \right) \left( {-\frac{\mu F_\mathrm{spar1} }{8\omega ^{2}}+\frac{\mu \alpha _q \lambda _s }{2\omega ^{2}}+\frac{2\mu \Omega \alpha _q \lambda _s }{\omega (\omega ^{2}-4\Omega ^{2})}} \right) \nonumber \\&\quad +\,Cos\left( \gamma \right) \left( {\frac{F_p }{4\omega }-\frac{F_p F_\mathrm{spar1} }{32\omega ^{3}}+\frac{F_{ppar} \lambda _s }{4\omega }+\frac{F_p \alpha _q \lambda _s }{8\omega ^{3}}} \right) \nonumber \\&\quad +\,a\left( {\begin{array}{l} \frac{\sigma }{2}-\frac{\mu ^{2}}{4\omega }-\frac{F_\mathrm{spar1}^2 }{64\omega ^{3}}-\frac{F_\mathrm{spar1}^2 }{64\omega \Omega (\omega +\Omega )}+\frac{F_\mathrm{spar1} \lambda _s }{2\omega }-\frac{3F_\mathrm{spar1} \alpha _q \lambda _s }{8\omega ^{3}} \\ +\frac{F_\mathrm{spar1} \alpha _q \lambda _s }{8\omega \Omega (\omega +\Omega )}-\frac{3\alpha _c \lambda _s^2 }{2\omega }+\frac{3\alpha _q^2 \lambda _s^2 }{4\omega ^{3}}-\frac{\alpha _q^2 \lambda _s^2 }{4\omega \Omega (\omega +\Omega )} \\ \end{array}} \right) \nonumber \\ \end{aligned}$$
(35)

Figure 4 shows a comparison among these cases and case 3 when \(V_\mathrm{AC}>>V_\mathrm{DC}\). We notice that these new cases show good agreement with case 3. However, it is easier to use case 3 considering the complexity of the frequency response equations obtained from the other cases.

Fig. 4
figure 4

Analytical frequency response curves of the resonator against the frequency detuning parameter \(\sigma \) for \(V_\mathrm{DC}=0.1\,\hbox {V}\), \(V_\mathrm{AC}=16.5\,\hbox {V}\), and \(\mu =0.005\). The plot compares the response obtained using the frequency response equations of cases 3, 4, and 5. The y-axis label “Amplitude” refers to the amplitude of the resonator including both the static and dynamics solutions, “\(\delta \)+a”

Full size image

5 Subharmonic excitation (case 3)

In order to investigate the dynamic behavior of the resonator, first, the response of the resonator of case 3 is simulated under AC only (subharmonic, \(V_\mathrm{DC}=0\)) excitation. Subharmonic resonance is activated, and its response is given by Fig. 5. A shift in the natural frequency is observed, which is believed to be from the static term associated with \(V_\mathrm{AC}\). The frequency shift due to only AC excitation can be potentially used for applications in MEMS resonator-based logic devices [3,4,5, 15], where it is desired to unify the input and output signal waveforms, i.e., AC signal, which is helpful for cascading.

Fig. 5
figure 5

Analytical frequency response curves of the resonator given by case 3 against the frequency detuning parameter \(\sigma \) for a\(V_\mathrm{DC}=0\), \(V_\mathrm{AC}=\hbox {variable}\) and \(\mu =0.005\). The y-axis label “Amplitude” refers to the amplitude of the resonator including both the static and dynamics solutions, “\(\delta \)+a”. The trivial solution is not shown here

Full size image
Fig. 6
figure 6

Analytical frequency response curves of the resonator given by case 3 against the frequency detuning parameter \(\sigma \) for \(V_\mathrm{DC}=\hbox {variable}\), \(V_\mathrm{AC}=17\,\hbox {V}\), and \(\mu =0.005\). The y-axis label “Amplitude” refers to the amplitude of the resonator including both the static and dynamics solutions, “\(\delta \)+a”

Full size image

5.1 Combined primary and subharmonic excitation (case 3)

Next, the response of the resonator under a simultaneous primary and subharmonic excitation is investigated. The \(V_\mathrm{DC}\) value is set at zero at first to get a pure subharmonic response, Fig. 6(black). The fixed \(V_\mathrm{AC}\) value defines a fixed strength of the subharmonic excitation (\(\sim V_\mathrm{AC}^2 \cos (2\Omega t)\)). Afterward, the \(V_\mathrm{DC}\) voltage is applied that adds the primary excitation onto the resonator (\(\sim 2V_\mathrm{DC} V_\mathrm{AC} \cos (\Omega t)\)). This \(V_\mathrm{DC}\) is then increased in small increments to examine the effect of increasing the strength of the primary excitation over the subharmonic excitation on the overall response of the resonator. Figure 6 shows this comparison. It can be noticed that there is a competition between the primary and subharmonic excitations, and the response of the resonator is a result of the dominant component among the two. Figure 6 shows that as \(V_\mathrm{DC}\) is increased, the abrupt onset of the resonance (subharmonic feature) diminishes and one can see then more gradual increase in amplitude (primary feature and also due to the perturbed pitchfork bifurcation). It is also observed that the monostable regime starts to widen. It can be observed from Fig. 6 that adding a small amount of \(V_\mathrm{DC}\) causes a shift in the frequency jump-up point. This is due to the breaking of symmetry of the two perfect pitchfork bifurcations (the super and subcritical) [20, 21, 35]. As a result, perturbed pitchfork bifurcations are observed, which result in the smoothening of the curve. This is in fact a very distinctive sign of the presence of the DC bias. This can be potentially used for applications where the detection of a very small increase in the DC bias is desired. One such application can be in charge sensing or MEMS electrometers [37,38,39,40].

6 Conclusions

An electrostatically actuated MEMS resonator modeled as a SDOF spring mass system under generic electorate loading and then including the simultaneous primary and subharmonic excitation is investigated theoretically. A comprehensive solution using the perturbation technique MTS is obtained and is validated for a general electrostatic loading case. It was established that in order to predict the response of a resonator under larger AC voltages, the secondary excitation component must be considered. Case 3 in the manuscript, which takes into account the direct primary and secondary excitation as well as the principal parametric excitation associated with the secondary forcing term, must be used to predict the response of the resonator accurately under a generic electrostatic loading. Different scaling schemes were also examined, which produced accurate results; however, case 3 was found to yield the simplest solutions. The competing effect of the simultaneous primary and subharmonic excitations is explored by varying the associated AC and DC voltages. It is observed that even a small addition of primary excitation significantly affects the subharmonic resonance, and the beam shows qualitatively more primary-like response behavior, due to the perturbed pitchfork bifurcations, Fig. 6. The second part of this work verifies the theoretical finding against experimental results [41]. Furthermore, the potential applications in MEMS resonator-based logic devices and MEMS electrometer are explored experimentally.