On the response of MEMS resonators under generic electrostatic loadings: experiments and applications

Abstract

We present an investigation of the dynamic behavior of an electrostatically actuated clamped–clamped microbeam, under the simultaneous excitation of primary and subharmonic resonance. The simultaneous excitation of primary and subharmonic resonances of similar strength is experimentally investigated by using different combinations of AC and DC voltages. It is observed that the response of the resonator is governed by a mixed effect of both excitations. Subharmonic-dominated response shows sharp amplitude transitions and smaller monostable regime, while primary-dominated response shows gradual amplitude transition and larger monostable regime. Two potential applications are experimentally demonstrated. The first is a resonator-based MEMS AND logic gate based on AC only subharmonic excitation. The second is a charge sensor based on the transition from subharmonic-dominated response to primary-dominated response, which is potentially capable of detecting a small amount of electric charges.

1 Introduction

Nonlinear dynamics of electrostatically actuated micro/nanoelectromechanical (MEMS/NEMS) beam resonators are being studied extensively and used in various applications [1]. These applications span various areas, such as mass sensing [2, 3], mechanical computing [4,5,6,7,8], and radio frequency (RF) communication [9, 10].

A theoretical and experimental study analyzing the performance parameters of resonant sensors as they are scaled down to nanoregimes is presented in [11]. The study in [11] examined the nonlinear and fringing field effects, which are significant for thin beam resonators. Enhancing the dynamic range of NEMS cantilevers for gas sensing applications is discussed in [12]. Furthermore, the actuation of higher harmonics in arrays of MEMS cantilevers is investigated to achieve distinct resonance peak separation for a variety of resonance-based sensing applications [13]. Resonance-based mass sensing is recently demonstrated to be capable of sensing traumatic brain injury protein biomarkers [3]. Intermodal interaction due to nonlinear modal coupling between the flexural vibration modes of a clamped–clamped beam have been also investigated [14]. The study in [14] demonstrates that an arbitrary flexural mode can be used as a self-detector for amplitude of another mode, which allows measuring the energy stored in a specific resonance mode. Moreover, strong and tunable mode coupling in carbon nanotube resonators has also been demonstrated [15]. Recently, experimental efforts are made to tailor the nonlinear response of the resonator for targeted applications, through shape optimization of the resonator [16]. Currently, the nonlinear dynamics of 2-D materials, such as single-layer MoS$_{2 }$ resonators [17], are increasingly explored.

MEMS resonators can be electrostatically actuated using various techniques, such as direct excitation in the neighborhood of primary resonance [5, 10], parametric excitation at twice the resonance frequency [18,19,20,21], multi or mixed-frequency excitation [4, 22, 23], and secondary resonances, i.e., subharmonic and superharmonic excitations [24,25,26,27,28,29,30,31,32,33,34]. The response of the resonators to these secondary resonances has been investigated extensively, both theoretically [24,25,26,27,28,29,30,31,32,33] and experimentally [34,35,36]. These studies involve revealing limit cycles, understanding the nonlinear behavior, investigating the stability, and exploring the dynamic pull-in phenomenon. Several applications were also proposed including sharp roll-off RF filters [29], using superharmonic resonance to increase the signal-to-noise ratio [34], switch triggered by mass sensing [31], and quenching of primary resonance by adding a super harmonic excitation source [33] for reduction in the stress levels in the structural fatigue problems.

MEMS resonator-based logic devices are gaining significant attention recently as ultra-low power alternate computing technology [4,5,6,7,8, 37,38,39]. An AC only gate input for such MEMS computing devices can be an attractive approach due to the fact that it unifies the input and output wave forms, i.e., the logic unit receives an AC signal and produces also an AC signal from the detected motional current. This presents a path for cascadability of these devices, which has been a major problem hindering the spread use of such electromechanical logic gates.

Furthermore, an AC excitation-based device that can detect small amount of charge is also desired for applications in MEMS electrometers [40,41,42,43]. Different dynamics phenomenon that respond to an input charge in terms of frequency shift via stiffness perturbation [40,41,42], and amplitude shift through principles like mode localization [43] have been used to demonstrate these electrometers.

Typically, a parallel-plate load is comprised of a DC voltage source $V_\mathrm{DC}$ superimposed to an AC voltage source of amplitude $V_\mathrm{AC}$ and frequency $\Omega$. The quadratic nature of the electrostatic force transforms a single source excitation into a two source simultaneous excitations, i.e., $\left[ {V_\mathrm{DC} +V_\mathrm{AC} \cos (\Omega t)} \right] ^{2}=\left[ {V_\mathrm{DC}^2 +2 V_\mathrm{DC} V_\mathrm{AC} \cos (\Omega t)+\frac{V_\mathrm{AC}^2 }{2}\left( {1+\cos (2\Omega t)} \right) } \right]$.

Commonly, the contribution from the secondary source associated with $V_\mathrm{AC}^2$ is neglected, which is acceptable for small values of $V_\mathrm{AC}$. However, for large values of $V_\mathrm{AC}$, as several applications may require, this can lead to erroneous simulation results. Hence, it is important to investigate the influence of these excitations onto the overall resonator response both theoretically and experimentally, and possibly use it for potential applications. In a complementary work to this paper [Ilyas, S., Alfosail, F., Younis, M. I.: On the Response of MEMS Resonators under Generic Electrostatic Loadings: Theoretical Analysis. Nonlinear Dynamics. Submitted (2018)], we present analytical solutions, based on the method of Multiple Time Scales (MTS), for the problem of an electrostatic resonator subjected to small and large $V_\mathrm{AC}$. We also discuss the case of simultaneous subharmonic and primary resonance excitations. In this work, we build on the theoretical analysis of [Ilyas, S., Alfosail, F., Younis, M. I.: On the Response of MEMS Resonators under Generic Electrostatic Loadings: Theoretical Analysis. Nonlinear Dynamics. Submitted (2018)] and experimentally demonstrate the simultaneous subharmonic and primary resonance excitations on a doubly-clamped MEMS microbeam, and investigate the competing effects of the two excitation sources. Furthermore, based on the outcomes of this investigation, we demonstrate potential applications of using such electrostatic excitation in MEMS resonator-based logic devices, and MEMS electrometers.

The rest of the paper is organized as follows. Section 2 presents the problem formulation and mathematical model. Section 3 presents the experimental results. Section 4 demonstrates experimentally potential applications. Finally, Sect. 5 summarizes the outcomes of the study.

2 Problem formulation

2.1 Mathematical model

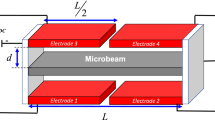
The nondimensional equation of motion that governs that transverse deflection w(x, t) for a MEMS clamped–clamped microbeam, which is electrostatically actuated by $V_\mathrm{DC}$, and $V_\mathrm{AC,}$ using a distributed parameter model, Fig. 1, is given by [44]

Fig. 1

Schematic of an electrostatically actuated clamped–clamped microbeam

$$\begin{aligned}&\frac{\partial ^{4}w}{\partial x^{4}}+\frac{\partial ^{2}w}{\partial t^{2}}+2\mu \frac{\partial w}{\partial t}-N\frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\qquad -\alpha _1 \left( {\mathop \int \nolimits _0^1 \left( {\frac{\partial w}{\partial x}} \right) ^{2}\hbox {d}x} \right) \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\quad =\frac{\beta \left[ {V_\mathrm{AC} \cos \left( {\Omega t} \right) +V_\mathrm{DC} } \right] ^{2}}{\left( {1-w} \right) ^{2}} \end{aligned}$$

(1)

where the coefficients in Eq. (1) are defined as

$$\begin{aligned}&w=\frac{\hat{w}}{d}; \quad x=\frac{\hat{x}}{L}; \nonumber \\&t={\hat{t}}{\sqrt{\frac{EI}{{{L}^{4}}{m}}}};\quad 2\mu =c{\sqrt{\frac{EI}{{{L}^{4}}{m}}}} \nonumber \\&N=\frac{{\bar{N}L}^{2}}{EI};\quad \alpha _1={\frac{d}{h}}^{2} ; \beta =\frac{{bL}^{4}\varepsilon }{{2d}^{3}{EI}} \end{aligned}$$

(2)

where $\hat{{t}}$ is time, $\hat{{x}}$ is the position along the beam length, E is the elastic modulus, I is the moment of inertia defined as $I=\frac{1}{12}bh^{3}$, b is the beam width, h is the beam thickness, c is the viscous damping coefficient, $\bar{N}$ is the axial load, A is the cross-sectional area of the beam, L is the beam length, d is the gap between the beam and lower electrode, and $\varepsilon$ is the dielectric constant.

The beam is subjected to the following boundary conditions:

$$\begin{aligned} w=0;\quad \frac{\partial w}{\partial {x}}=0 \;\hbox {at } x=0;\quad x=1 \end{aligned}$$

(3)

In order to solve for the static deflection $w_s (x)$ of the beam, we drop the time-dependent terms in Eq. (1), and solve for $w_s (x)$ using the iteration scheme [45]. Then, we perturb the dynamic solution $w_d$ around the equilibrium position to study the linear and nonlinear dynamics of the system. Hence, the total dynamic solution is assumed of the form

$$\begin{aligned} w\left( {x,t} \right) =w_s \left( x \right) +w_d \left( {x,t} \right) \end{aligned}$$

(4)

Substituting Eqs. (4) into (1), dropping the terms pertaining to the static part, and expanding the electrostatic term around the static configuration yields

$$\begin{aligned}&\frac{\partial ^{2}w_d }{\partial t^{2}}+\frac{\partial ^{4}w_d }{\partial x^{4}}+2\mu \frac{\partial w_d }{\partial t}\nonumber \\&\quad =\alpha _1 \frac{\partial ^{2}w_d }{\partial x^{2}}\left( N+\mathop \int \limits _0^1 \left( {w_s ^{\prime }} \right) ^{2}\hbox {d}x\right. \nonumber \\&\qquad \left. +\,2\mathop \int \limits _0^1 w_s ^{\prime }\frac{\partial w_d }{\partial x}\hbox {d}x+\mathop \int \limits _0^1 \left( {\frac{\partial w_d }{\partial x}} \right) ^{2}\hbox {d}x \right) \nonumber \\&\qquad +\,\alpha _1 w_s{\prime {\prime }}\left( {\mathop \int \limits _0^1 \left( {\frac{\partial w_d }{\partial x}} \right) ^{2}\hbox {d}x+2\mathop \int \limits _0^1 w_s ^{\prime }\frac{\partial w_d }{\partial x}\hbox {d}x} \right) \nonumber \\&\qquad +\,\beta \frac{V(t)}{2\left( {1-w_s } \right) ^{2}} \nonumber \\&\qquad +\,\beta \frac{\left( {V(t)+2 V_\mathrm{eff} } \right) }{\left( {1-w_s } \right) ^{3}}w_d +3\beta \frac{\left( {V(t)+2 V_{\mathrm{eff}} } \right) }{2\left( {1-w_s } \right) ^{4}}w_d ^{2} \nonumber \\&\qquad +\,2\beta \frac{\left( {V(t)+2 V_{\mathrm{eff}} } \right) }{\left( {1-w_s } \right) ^{5}}w_d ^{3}+ \cdots \end{aligned}$$

(5)

where $V(t)=\left( {4 V_\mathrm{AC} V_\mathrm{DC} \cos \left( {t\Omega } \right) +V_\mathrm{AC}^2 \cos \left( {2t\Omega } \right) } \right)$ and $V_{\mathrm{eff}} =V_\mathrm{DC}^2 +\frac{V_\mathrm{AC}^2 }{2}$. The superscript “prime” indicates the spatial derivative.

The linear problem of Eq. (5) is solved using the Galerkin method [44] using 4 unforced straight beam (zero voltage) modeshapes. Next, we assume no interaction from the other not-directly excited modes or internal resonance. Accordingly, we express the forced vibration part using a single-mode Galerkin approximation as

$$\begin{aligned} w_d (x,t)=\phi _j \left( x \right) u_j (t) \end{aligned}$$

(6)

where $\phi _j \left( x \right)$ is the modeshape under the influence of V$_\mathrm{DC}$, and $u_j$ is the modal coordinate for the microbeam. Substituting Eqs. (6) into (5) and using the orthogonality condition yield

$$\begin{aligned}&{\ddot{u}}_j +\omega _j^2 u_j +2\mu \dot{u}_j +\alpha _q u_j ^{2}+\alpha _c u_j ^{3}\nonumber \\&\quad =F_p \cos \left( {\Omega t} \right) +F_s \cos \left( {2\Omega t} \right) \nonumber \\&\qquad +\left( {F_\mathrm{ppar1} \cos \left( {\Omega t} \right) +F_{\mathrm{spar}1} \cos \left( {2\Omega t} \right) } \right) u_j \nonumber \\&\qquad +\left( {F_{\mathrm{ppar}2} \cos \left( {\Omega t} \right) +F_{\mathrm{spar}2} \cos \left( {2\Omega t} \right) } \right) u_j ^{2} \nonumber \\&\qquad +\left( {F_{\mathrm{ppar}3} \cos \left( {\Omega t} \right) +F_{\mathrm{spar}3} \cos \left( {2\Omega t} \right) } \right) u_j ^{3} \end{aligned}$$

(7)

The superscript “dot” indicates the temporal derivative. The coefficients $\alpha _q ,\alpha _c ,F_p ,F_s ,F_{\mathrm{ppar}1} ,F_{\mathrm{spar}1}, F_{\mathrm{ppar}2}, F_{\mathrm{spar}2} ,F_{\mathrm{ppar}3} ,$and $F_{\mathrm{spar}3}$ are defined in “Appendix”. Based on the results from [Ilyas, S., Alfosail, F., Younis, M. I.: On the Response of MEMS Resonators under Generic Electrostatic Loadings: Theoretical Analysis. Nonlinear Dynamics. Submitted (2018)], the term $F_{\mathrm{spar}1}$ is the only parametric term that has significant contribution on the resonator’s response, and hence the rest of the parametric terms in Eq. (7) can be ignored.

This approach of a single-mode discretization and then applying a perturbation analysis is known to yield less accurate results compared to directly attacking the partial differential equation with the multiple scales method [46]. However, we opted to use this method so that the resulting equation can be related to the equation of a lumped parameter model for generic-shaped resonators. In this case for j = 1, the resulting Eq. (7) is identical to the single degree of freedom model for a generic shape resonator analyzed using MTS in [Ilyas, S., Alfosail, F., Younis, M. I.: On the Response of MEMS Resonators under Generic Electrostatic Loadings: Theoretical Analysis. Nonlinear Dynamics. Submitted (2018)].

Based on the results from [Ilyas, S., Alfosail, F., Younis, M. I.: On the Response of MEMS Resonators under Generic Electrostatic Loadings: Theoretical Analysis. Nonlinear Dynamics. Submitted (2018)], the modulation equations can be written as

$$\begin{aligned}&\mathrm{Re}:\hbox { }\frac{\dot{a}}{2}=-\frac{a\mu }{2}+\frac{a\lambda _2 \alpha _q \sin (2\gamma )}{2\omega }\nonumber \\&\qquad -\frac{F_p \sin (\gamma )}{4\omega }-\frac{aF_{\mathrm{spar}1} \sin (2\gamma )}{8\omega } \end{aligned}$$

(8.1)

$$\begin{aligned}&\mathrm{Im}:\hbox { }\frac{a\dot{\gamma }}{2}=\frac{a\sigma }{2}-\frac{3a^{3}\alpha _c }{16\omega }+\frac{5a^{3}\alpha _q^2 }{24\omega ^{3}}\nonumber \\&\qquad -\frac{3a\lambda _2^2 \alpha _c }{2\omega }-\frac{a\lambda _2 \alpha _q \cos (2\gamma )}{2\omega }-\frac{3a\lambda _2 \alpha _q F_{\mathrm{spar}1} }{8\omega ^{3}} \nonumber \\&\qquad \hbox { }+\frac{a\lambda _2 \alpha _q F_{\mathrm{spar}1} }{8\omega \Omega (\omega +\Omega )}+\frac{F_{\mathrm{spar}1} a\cos (2\gamma )}{8\omega }\nonumber \\&\qquad -\frac{aF_{\mathrm{spar}1}^2 }{64\omega ^{3}}-\frac{aF_{\mathrm{spar}1}^2 }{64\omega \Omega (\omega +\Omega )} \nonumber \\&\qquad \hbox { }+\frac{3a\lambda _2^2 \alpha _q^2 }{4\omega ^{3}}-\frac{a\lambda _2^2 \alpha _q^2 }{4\omega \Omega (\omega +\Omega )}+\frac{F_p \cos (\gamma )}{4\omega } \end{aligned}$$

(8.2)

where a and $\gamma$ are the nondimensional amplitude and phase, $\sigma$ is the frequency detuning parameter, and $\Omega =\omega +\sigma$ is the excitation frequency. The steady-state dynamic response is then obtained by setting the right-hand side of the modulation equations, Eqs. (8.1) and (8.2), equal to zero and solve the resulting algebraic equations. Since algebraic equations are solved to get the desired frequency response, where the influence of quadratic and cubic nonlinearities is captured, the MTS solution is computationally faster. The stability of the solution is determined by solving for the eigenvalues of the Jacobin of the modulation equations [44], Eqs. (8.1) and (8.2).

Fig. 2

Analytical frequency response curves of the resonator versus the nondimensional excitation frequency.a$V_\mathrm{DC}$ = 0, $V_\mathrm{AC}$ = variable, and $\upmu$ = 0.01. The response for activated subharmonic resonance is shown only. The inset shows the enlarged view to highlight the frequency shift. b$V_\mathrm{DC}$ = variable, $V_\mathrm{AC}$ = 4 V, and $\upmu$ = 0.01. (Color figure online)

2.2 Numerical results

The results will be demonstrated for a clamped–clamped microbeam that is 500 $\upmu$m long, 50 $\upmu$m wide, 1.25 $\upmu$m thick, and has an air gap $d=2.5$$\upmu$m. More details on the beam are presented in Sect. 3.

First, we investigate the dynamic response of the microbeam under an AC only excitation (pure subharmonic, $V_\mathrm{DC}$ = 0) using Eqs. (8.1) and (8.2), Fig. 2a. The figure indicates a shift in the natural frequency similar to the one caused by the DC bias in a typical electrostatic loading of a microbeam. This shift is due to the static term associated with the $V_\mathrm{AC}$.

Next, the response of the resonator under a simultaneous primary and subharmonic excitation is simulated to investigate the competing effects from both excitations. We start from a pure subharmonic response at zero $V_\mathrm{DC}$ and then $V_\mathrm{DC}$ is increased in small increments to see the effect of primary excitation on the response. Figure 2b shows the competing effects from the two excitations. It is observed that at zero $V_\mathrm{DC}$ the resonator’s response exhibits typical subharmonic characteristics i.e., abrupt onset of resonance and small monostable regime. However, as $V_\mathrm{DC }$ is increased, the response starts to deviate from the typical subharmonic response and becomes more primary-like, characterized by a gradual increase in amplitude and a wider monostable regime. It is concluded that even very small amount of $V_\mathrm{DC}$ is enough to generate a considerable primary resonance influence on the overall response.

3 Experimental results

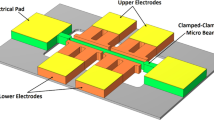
A clamped–clamped microbeam, of same geometric specifications in Sect. 2, is fabricated and characterized to study the dynamic behavior. The microbeam is made of SiN$_{3}$ and is fabricated using conventional surface micromachining processes [47]. Figure 3 shows the microscopic image of the fabricated microbeam along with the used experimental setup. The fundamental resonance frequency of the microbeam is $\sim$ 96.5 kHz.

A laser Doppler vibrometer (LDV), Micro System Analyzer 500 from Ploytec, is used to measure the amplitude of vibration of the resonator. The measurements are recorded using a displacement decoder (DD900), which has a resolution of 0.6 nm. A data acquisition card (DAQ) NI6251 from National Instruments is used to excite the resonator and record the output from the LDV. The excitation signal is generated using a Labview program. The data collected from the LDV is then post-processed and presented in the form of frequency response plots. All the experiments are performed at ambient temperature and at a pressure of $\sim$ 5 mTorr.

Figure 4a, b shows the frequency response of the resonator for the case of large $V_\mathrm{DC}$ near primary and subharmonic resonances, respectively. In this case, the term $F_p \cos \left( {\Omega t} \right)$ in Eq. (7) is the main dominant excitation term. Figure 4c shows the subharmonic excitation using an AC only excitation. In this case, the dominant excitation term is $F_s \cos \left( {2\Omega t} \right)$; $F_p$ = 0. Hence, the beam effectively experiences twice the values of frequency on the x-axis of the figure. Thus, although Fig. 4c may indicate primary resonance around 96.5 kHz; it actually shows subharmonic resonance due to this quadratic effect of the electrostatic force and $F_s \cos \left( {2\Omega t} \right)$.

Fig. 3

a Experimental setup along with the microscopic image of the fabricated device. b Image of the LDV and vacuum chamber containing the device. All the experimental results are performed in vacuum conditions $\sim$3–6 mTorr. A laser Doppler vibrometer (LDV) is used to optically detect the motion of the resonator. A data acquisition card (DAQ) is used to generate the desired signal and measure the output from the LDV

Fig. 4

Experimental forward sweep frequency response plots of the microresonator (a) at the primary resonance for an electrostatic loading of $V_\mathrm{DC}$ =1 V; $V_\mathrm{AC}$ = 1 V around the natural frequency ($\sim$96.5 kHz), b at the subharmonic resonance at $V_\mathrm{DC}$ =2 V, $V_\mathrm{AC}$ = 2 V, around twice the natural frequency, and c showing the subharmonic resonance for an electrostatic loading of $V_\mathrm{DC}$ =0 V, $V_\mathrm{AC}$ = 4 V around the natural frequency

Next, the behavior of the resonator under an AC only excitation is further explored under various loading conditions. Figure 5 shows the response of the resonator under a backward frequency sweep, which captures the monostable regime for a hardening behavior. A forward frequency sweep, for most of the loading cases considered here, results in dynamic pull-in of the device. Hence, in order to protect the device from stiction issues, only backward frequency sweeps were performed. Moreover, in order to realize the applications presented in this work, the device must operate in a monostable regime, which is achieved through a backward frequency sweep for hardening nonlinearity.

Fig. 5

Experimental backward sweep frequency response curves of the microresonator showing the subharmonic resonance when $V_\mathrm{DC}$ = 0 V. Note that because of the quadratic form of the electrostatic force, the beam will experience twice the values of the frequencies shown on the x-axis. (Color figure online)

It is observed that by increasing the AC voltage, the monostable regimes shift toward the left while the overall amplitude and the span of the monostable regimes are increased. This behavior qualitatively matches the analytical prediction in Fig. 2a.

Next, the effect of the simultaneous excitation of subharmonic and primary resonance, where both resonances are of similar strength, is experimentally investigated. Figure 6 shows the experimental frequency response of the microbeam for a reverse frequency sweep, which aims to capture the monostable regime. First, the resonator is excited with AC only ($V_\mathrm{DC} =0)$ to get a pure subharmonic excitation. We observe that the response of the resonator in this case is characterized by a sudden onset of resonance and a narrow monostable regime. Then, the DC bias voltages are slowly increased to investigate the influence of the primary excitation term over the subharmonic resonance as the strength of the primary excitation is increased. We notice that as the strength of primary resonance is increased, the subharmonic-like response starts to fade away and a more primary-like response appears. The new response exhibits a gradual onset of resonance and a wider monostable regime. Qualitative agreement with the analytical results of Fig. 2b is observed.

One can observe from Fig. 6, and as shown also theoretically in Fig. 2b, that adding a small DC voltage breaks the symmetric of the two perfect pitchfork bifurcations (the super- and subcritical). Hence, the outcome is perturbed pitchfork bifurcations; and hence they result in the smoothening of the curve, which gives a very distinctive sign of the presence of the DC bias. This can be used in applications, as will be shown in Sect. 4.2, for charge sensors.

Fig. 6

Experimental backward frequency sweep response plots of the microresonator at $V_\mathrm{AC}$ = 13.7 V and variable $V_\mathrm{AC }$values. (Color figure online)

4 Potential applications

4.1 MEMS logic

The response of the resonator under an AC only excitation can be useful in applications, such as MEMS vibration-based logic devices [4,5,6,7,8, 37,38,39]. Dynamic-based resonant structures have been recently under increasing interest for logic applications, where their on-resonance large response is considered a “High” state and their off-resonance response is taken as “Low” state. The fact these are non-contact devices make them especially attractive compared to MEMS and NEMS switch-based logic devices

One major obstacle in this field is the difficulty in cascading such logic devices, i.e., the output of one logic unit should be usable as direct input for another logic unit. This requires unifying the input and output signal waveforms. Because most resonant-based logic devices produce AC current and AC voltage as output, for example due to capacitive motional current, this requirement calls for these mechanical logic devices to be operated based on AC input commands.

Another essential and challenging requirement for cascadability is that the input and output frequency of the resonator remains same.

Here, we propose to resolve these problems by making use of an AC only excitation of the beam at subharmonic resonance. In this case, an AC only excitation signal is applied at the frequency $\Omega$ in the neighborhoods of natural frequency $\omega _n$, while the microbeam experiences an excitation at $2\Omega$ due to the squaring of the electrostatic forcing term, hence exciting the subharmonic resonance at $2\omega _n$. As it is well-known, at subharmonic resonance, the microbeam actually responds with the main dynamical component at the main natural frequency $\omega _n$. In this case, the input and output frequency for the potential logic device stays the same. Figure 7a shows a schematic illustrating the concept.

Fig. 7

a Schematic illustrating that the input and output frequency stays the same for an AC only excitation of the resonator-based logic unit. b Experimental frequency response of the microresonator showing the subharmonic resonance for an electrostatic loading of $V_{AC}$ = 0 V (black) $V_\mathrm{AC}$ = 6.4 V (red) and $V_\mathrm{AC}$ = 12.8 V (blue) through a backward frequency sweep. Logic input state “0” and “1” are characterized by “0 V” and “6.4 V” of AC signal at 94.225 kHz, respectively. These inputs are added together and applied to the resonator. c Time history for various logic input conditions showing an AND/NAND demonstration. (Color figure online)

Figure 7b shows an AND logic gate that can be achieved using the subharmonic excitation. A high amplitude at resonance is characterized as “1” logic output and a non-resonant state with negligible amplitude is characterized as “0” logic output. The shift in the onset frequencies of the subharmonic resonance due to different AC excitation voltages is used as the basic principle of the logic operation. The logic inputs in this case are the two AC signals each of 6.4 V and at a frequency of 94.225 kHz. The logic inputs are added together using a mixer and provided to the resonator. One should note here that the use of a mixer can be avoided if the resonator was designed with independent input electrodes, where each one can be used to input one AC load at a time to the beam. For a (0,0) logic input, the resonator does not experience any electrostatic excitation and hence the response remains buried in the noise defining the “0” output state. Next, for the operating frequency of 94.225 kHz, a high output signal is experienced only for the logic input condition of (1,1). For any of the (1,0) or (0,1) scenario, the resonance signal (red) is shifted off the operating point and still gives a “0” output signal. Hence, at this operating point the device is configured to operate as an AND logic gate. It is worth to mention here that even though the resonator operates in the nonlinear regime, the operating point is chosen in the monostable regime. This avoids problems associated with the hysteresis region where unwanted jumps between the “1” and “0” vibration states of the resonator may occur. Figure 7c shows a time history plot for the AND logic operation. A similar principle can be extended to multi-bit AND logic operation upon careful selection of the input voltage sources and operating frequency points. The same logic gate can also be operated as a NAND gate upon reversing the assignment of high “1” and low “0” logic output states [6]. NAND being a universal gate can potentially allow such a logic gate to act as a basic building block to achieve various other logic operations via cascading of multiple devices.

The proposed device here is presented as a proof of concept and hence does not compete well with the state of the art in performance parameters, such as speed, power consumption, and area integration density [4,5,6,7,8, 37,38,39]. Using AC only provides advantages in terms of cascadability but may consume more energy to activate the subharmonic resonance and hence execute the logic operations. Further, it is important to note that low damping is necessary to activate the subharmonic resonance, and hence a vacuum encapsulation is required for practical applications. We believe that having a dedicated design to optimize the energy consumption, area integration density, and speed of operation will improve these performance parameters of the device.

Fig. 8

Experimental shift in the frequency value $\Omega _j$(kHz) for accumulated charge on the fixed drive electrode. A quadratic polynomial fit is used to estimate the responsivity of the electrometer $\sim 10^{-5 }$Hz fC$^{-2 }$.The frequency shift data are acquired from Fig. 6

4.2 MEMS electrometer

It is observed from Figs. 2b and  6 that for a backward frequency sweep the frequency jump up point “$\Omega _j$” shifts toward the right with a very small increase in the DC bias voltage. It is important to note here that this effect is caused due to transformation of the overall response of the resonator from subharmonic-like to primary-like, which is a direct consequence of the two source simultaneous excitations. This effect can be used for applications where the detection of a very small increase in the DC bias is desired. One such application can be in charge sensing or MEMS electrometer [40,41,42,43]. Shift in $\Omega _j$ can be used to monitor the charge detected by the microbeam. Figure 8 shows the shift in $\Omega _j$ against the added charge ($q=CV$, where $C=\frac{\varepsilon A}{d}=88.5 \mathrm{fF})$ for the results of Fig. 6. The quadratic responsivity of the electrometer is found out to be $\sim 10^{-5}$ Hz fC$^{-2}$ after polynomial fitting of the measured data. The responsivity reported here is one of the lowest reported in MEMS-based electrometers [40,41,42,43]. This shows that such a technique is potentially capable of detecting very small charges. Furthermore, a minimum detectable frequency shift of the resonator needs to be determined, which can be calculated by measuring the frequency fluctuation at the point of interest using Alan deviation technique [38]. It usually lies within a few Hz range for the MEMS beam resonators [40, 41, 43, 48]. It is important to note here that for demonstration purpose the bifurcation point is used for monitoring the input charge; however, frequency fluctuations due to noise near the bifurcation point maybe large. This, however, can be avoided by choosing a point closer to the bifurcation point.

The major advantage of adapting such technology for charge sensing comes from the simplicity of the device design and operation, and the sensitivity to very small value of charge. Many of MEMS electrometer devices require a separate port for the DC bias applied to the beam from the DC bias or charge to be detected. This can add design, fabrication, and circuit implementation complexities, which can be avoided using such a system for this application. However, due to the excitation of subharmonic resonance it is important to operate in low damping conditions and hence a vacuum encapsulation is required. It is important to note that this application is shown here as a proof of concept and a dedicated design is expected to improve upon the performance, sensitivity, and resolution of the proposed charge sensor.

5 Conclusions

A theoretical and experimental investigation of the simultaneous primary and subharmonic resonance excitation of a clamped–clamped microbeam has been presented. A one-mode reduced order model has been derived and the results from the MTS analysis in [Ilyas, S., Alfosail, F., Younis, M. I.: On the Response of MEMS Resonators under Generic Electrostatic Loadings: Theoretical Analysis. Nonlinear Dynamics. Submitted (2018)] have been employed to predict the resonator’s behavior. This behavior has been then verified experimentally under varying electrostatic loading conditions. The behavior of the resonator under an AC only excitation has been used to demonstrate experimentally a resonance-based AND logic gate. The device is shown to be potentially cascadable. Furthermore, the competing effect from the primary and subharmonic resonance has been proposed for a potential small charge sensor.

Appendix

$$\begin{aligned}&\alpha _q =-3\beta V_{\mathrm{eff}} \left( {\mathop \int \limits _0^1 \frac{\phi _j ^{3}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \nonumber \\&\quad -\,\alpha _1 \left( {\mathop \int \limits _0^1 \phi _j w_s ^{\prime \prime }\left( {\mathop \int \limits _0^1 \left( {\phi _j ^{\prime }} \right) ^{2}\hbox {d}x} \right) \hbox {d}x} \right) \end{aligned}$$

(A.1)

$$\begin{aligned}&\quad -\,2\alpha _1 \left( {\mathop \int \limits _0^1 \phi _j \phi _j ^{\prime \prime }\left( {\mathop \int \limits _0^1 \phi _j ^{\prime }w_s ^{\prime }\hbox {d}x} \right) \hbox {d}x} \right) \end{aligned}$$

(A.2)

$$\begin{aligned}&\alpha _c =-4\beta V_{\mathrm{eff}} \left( {\mathop \int \limits _0^1 \frac{\phi _j ^{4}}{\left( {1-w_s } \right) ^{5}}\hbox {d}x} \right) \nonumber \\&\quad -\,\alpha _1 \left( {\mathop \int \limits _0^1 \phi _j \phi _j ^{\prime \prime }\left( {\mathop \int \limits _0^1 \left( {\phi _j ^{\prime }} \right) ^{2}\hbox {d}x} \right) \hbox {d}x} \right) \end{aligned}$$

(A.3)

$$\begin{aligned}&F_p =2\beta V_\mathrm{AC} V_\mathrm{DC} \left( {\mathop \int \limits _0^1 \frac{\phi _j }{\left( {1-w_s } \right) ^{2}}\hbox {d}x} \right) ;\nonumber \\&\quad F_s =\beta \frac{V_\mathrm{AC}^2 }{2}\left( {\mathop \int \limits _0^1 \frac{\phi _j }{\left( {1-w_s } \right) ^{2}}\hbox {d}x} \right) \end{aligned}$$

(A.4)

$$\begin{aligned}&F_{\mathrm{ppar}1} =4\beta V_\mathrm{AC} V_\mathrm{DC} \left( {\mathop \int \limits _0^1 \frac{\phi _j ^{2}}{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) ;\nonumber \\&\quad F_{\mathrm{spar}1} =\beta V_\mathrm{AC}^2 \left( {\mathop \int \limits _0^1 \frac{\phi _j ^{2}}{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) \end{aligned}$$

(A.5)

$$\begin{aligned}&F_{\mathrm{ppar}2} =6\beta V_\mathrm{AC} V_\mathrm{DC} \left( {\mathop \int \limits _0^1 \frac{\phi _j ^{3}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) ;\nonumber \\&\quad F_{\mathrm{spar}2} =\beta \frac{3 V_\mathrm{AC}^2 }{2}\left( {\mathop \int \limits _0^1 \frac{\phi _j ^{3}}{\left( {1-w_s } \right) ^{4}}\hbox {d}x} \right) \end{aligned}$$

(A.6)

$$\begin{aligned}&F_{\mathrm{ppar}3} =8\beta V_\mathrm{AC} V_\mathrm{DC} \left( {\mathop \int \limits _0^1 \frac{\phi _j ^{4}}{\left( {1-w_s } \right) ^{5}}\hbox {d}x} \right) ;\nonumber \\&\quad F_{\mathrm{spar}3} =2\beta V_\mathrm{AC}^2 \left( {\mathop \int \limits _0^1 \frac{\phi _j ^{4}}{\left( {1-w_s } \right) ^{5}}\hbox {d}x} \right) \end{aligned}$$

(A.7)