An electrically actuated imperfect microbeam: Dynamical integrity for interpreting and predicting the device response

Abstract

In this study we deal with a microelectromechanical system (MEMS) and develop a dynamical integrity analysis to interpret and predict the experimental response. The device consists of a clamped-clamped polysilicon microbeam, which is electrostatically and electrodynamically actuated. It has non-negligible imperfections, which are a typical consequence of the microfabrication process. A single-mode reduced-order model is derived and extensive numerical simulations are performed in a neighborhood of the first symmetric natural frequency, via frequency response diagrams and behavior chart. The typical softening behavior is observed and the overall scenario is explored, when both the frequency and the electrodynamic voltage are varied. We show that simulations based on direct numerical integration of the equation of motion in time yield satisfactory agreement with the experimental data. Nevertheless, these theoretical predictions are not completely fulfilled in some aspects. In particular, the range of existence of each attractor is smaller in practice than in the simulations. This is because these theoretical curves represent the ideal limit case where disturbances are absent, which never occurs under realistic conditions. A reliable prediction of the actual (and not only theoretical) range of existence of each attractor is essential in applications. To overcome this discrepancy and extend the results to the practical case where disturbances exist, a dynamical integrity analysis is developed. After introducing dynamical integrity concepts, integrity profiles and integrity charts are drawn. They are able to describe if each attractor is robust enough to tolerate the disturbances. Moreover, they detect the parameter range where each branch can be reliably observed in practice and where, instead, becomes vulnerable, i.e. they provide valuable information to operate the device in safe conditions according to the desired outcome and depending on the expected disturbances.

1 Introduction

Microelectromechanical systems (MEMS) are a growing area of research. They are a very attractive technology, with application covering various functions, including sensing and actuation, which may be applied in a large variety of fields, such as industrial, communications and bioengineering [1]. Numerous studies emphasize the importance of accurately predicting their dynamic behavior. This issue is faced with various challenges, since the problem is inherently multiphysical [2]. Difficulties are due, for instance, to the intrinsically nonlinear electric excitation, the geometrical nonlinearities, the uncertainties in the damping estimation, and the imperfections coming from the microfabrication process.

Several nonlinear phenomena may arise in MEMS. The possibility to exploit them in practice is widely emphasized in the literature [3–16]. Towfighian et al. [3] explore the effects of a controller applied in an electrostatic resonator. A deep parametric analysis detects frequency and magnitude of the electrodynamic voltage required to develop chaotic oscillations. In slender shallow arched microbeams [4], Krylov et al. highlight that this configuration may exhibit a rich complex behavior, which may include bistable static deflections and snap-through motion. A careful theoretical and experimental investigation is performed and a satisfactory concurrence of theory and experiments is observed. In a clamped-clamped microbeam resonator, Mestrom et al. [5] experimentally acquire the behavior chart reporting the electrodynamic voltage and the electrodynamic frequency where the cyclic fold bifurcations occur. The hysteresis interval is analyzed, which is observed to first increase and then decrease. Rhoads et al. [6] explore a particular class of MEMS, which exhibits a wide array of interesting nonlinear features. The dynamic response is shown to display not only typical hardening or softening nonlinear characteristics, but also mixed nonlinear ones. The frequency-dynamic voltage behavior chart underlines the complexity of the response, which includes Arnold tongues and saddle-node bifurcations and shows a strong correlation with the experimental data. Gottlieb and Champneys [7] focus on the nonlinear dynamics arising in thermoelastic electrically actuated microbeams. They develop a careful analysis to alert the escape threshold and shed light on possible existence of global bifurcations and chaotic transients. In a MEMS sensor, Alsaleem et al. [8] experimentally observe jumps, hysteresis, dynamic pull-in, primary and secondary resonances. The theoretical investigation provides a satisfactory matching with the experimentation. Moreover, after performing a basin of attraction analysis, the safety of the device is discussed by resorting to integrity profiles. Interesting nonlinear features are observed also in many other micro and nanostructures, e.g. in atomic force microscopy [9], in micro-oscillators [10–13], in microresonators arrays [14], and in nanosystems [15, 16].

The present paper is motivated by the increasing attention toward describing and predicting the nonlinear phenomena in MEMS. We deal with an electrostatically and electrodynamically actuated microbeam, with some imperfections due to microfabrication. A schematic is illustrated in Fig. 1. Frequency response diagrams and behavior chart are performed. They provide a good matching with the experiments. However, they are not able to forewarn the practical range of existence of each attractor. A similar discrepancy between the actual and the theoretical response is observed in many different systems [17]. Its interpretation calls for additional investigations, where not only the local but also the global dynamics are examined. In fact, as observed in Thompson [18], the aforementioned theoretical investigations do not take into account the presence of disturbances, which, instead, are unavoidable in experiments and practice. Disturbances give uncertainties to the operating initial conditions. If the safe basin is not sufficiently “robust” to tolerate them, the actual response may be completely different from what theoretically expected. This idea is extensively developed through a series of papers, where dynamical integrity concepts are investigated in depth, as the issue of a reliable integrity measure [19–21] and the definition of safe basin [22–24]. We refer to Rega and Lenci [25] for a deep overview on this topic.

Fig. 1

A schematic of the MEMS device

Theoretical simulations based on dynamical integrity concepts are performed in many different fields. Soliman and Thompson [26] apply these tools to investigate the capsize of a ship. They observe that the safe basin is eroded quite suddenly, which implies that the wave height corresponding to the capsizes is really smaller than that one where the final steady state motions lose their stability. This kind of analysis offered a new approach to the quantification of ship stability in waves. Infeld et al. [27] analyze the effect of dam breaking on a symmetric downstream floating body. They investigate the basin erosion, as caused by a water surface soliton. The results provide a relevant guide to design the distance that a marina should keep from a large dam. In a suspension bridge, De Freitas et al. [28] focus on the initial conditions in the phase space where the bridge does not collapse. They highlight the erosion of this region, which is enhanced by the appearance of incursive fingers. In a 2-degrees-of-freedom oscillator, De Souza and Rodrigues [29] analyze the evolution of the safe basin and depict the parameter regions where there are rapid or slow losses. Gonçalves et al. [30] investigate the parametric instability and escape boundaries in an excited cylindrical shell. They examine the changes of the basins of attraction in the four-dimensional phase space and develop integrity profiles to measure the magnitude of the safe basin of the various solutions. Analyzing the dynamical response of a carbon nanotube, Ruzziconi et al. [31] perform a dynamical integrity analysis via the combined use of different dynamical integrity tools, in order to investigate the structural safety of the device from different perspectives. A good concurrence between dynamical integrity predictions and experimental data is noticed in Lenci and Rega [32] in a pendulum parametrically excited by wave motion, where rotating solutions appear exactly where the dynamical integrity is large enough to sustain the experimental imperfections.

Dynamical integrity concepts are applied also in MEMS devices. Ruzziconi et al. [33], investigating a MEMS capacitive accelerometer, use this analysis to interpret and predict the experimental data coming from a frequency sweeping process. They observe that the experimental pull-in bands do not overlap to the classical curves of appearance and/or disappearance of the attractors, but are anticipated from them. They exactly “follow” the integrity curves, i.e. these curves are able to alert where the capacitive sensor can be operated in safe conditions, and where, instead, may practically fail. Alsaleem et al. [34] further develop these results, by examining not only a neighborhood of the primary resonance, but also a neighborhood of the subharmonic one. They highlight that also in this case, the dynamical integrity analysis is able to accurately predict the experimental pull-in bands. Settimi and Rega [35] explore the nonlinear response of a noncontact atomic force microscope via integrity profiles to ensure acceptable safety targets. Ruzziconi et al. [24], analyzing a MEMS device with bistable static configuration, underline that the dynamical integrity analysis may be used not only to detect the classical problem of the disappearance of an attractor, but also to predict the practical jump and the practical escape (pull-in). Lenci and Rega [36] develop erosion profiles to design a controller which is able to shift the pull-in threshold toward higher excitation amplitudes.

In the present study, we perform a dynamical integrity analysis with the aim of detecting the parameter ranges where the device may be effectively operated in practice in safe conditions according to the desired behavior, and forewarning where, instead, a different outcome may arise.

The paper is organized as follows. After introducing the mechanical model (Sect. 2), we analyze the theoretical multistability (Sect. 3) and the practical multistability via integrity profiles and integrity charts (Sect. 4). The main conclusions are summarized (Sect. 5).

2 Mechanical model

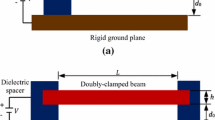
The considered MEMS device consists of a polysilicon microbeam actuated by an electrode, placed directly underneath it on a substrate (Fig. 1). The electrode provides both an electrostatic and an electrodynamic load, where V _DC is the electrostatic voltage and $V_{AC}\cos(\hat {\varOmega} \hat{t})$ is the electrodynamic excitation, with voltage V _AC and frequency $\hat{\varOmega}$. The microbeam is not straight, but curled up few microns, which is a typical imperfection due to the microfabrication process. This microstructure was previously analyzed in [37, 38]. In this section we briefly recall the major results, since they are the starting point of the present paper.

In [37], a deep experimental investigation is developed. The first symmetric natural frequency is shown to occur at $\hat{\varOmega} \cong 148.32\mbox{ kHz}$. In this neighborhood, several experimental frequency sweeps are performed, where the electrodynamic voltage is kept constant and the frequency is increased (forward sweep) or decreased (backward sweep) slowly, i.e. quasi-statically. They are attained at V _DC =0.7 V and V _AC =[0;5] V. Two examples are reported in Fig. 2. All these sweeps are acquired at about a small constant pressure, by using a frequency step that is small enough to guarantee the steady-state condition at the end of each step, where the maximum frequency amplitude of oscillations is recorded.

Fig. 2

Frequency response diagram (in dimensional form) at (a) V _AC =2.5 V and (b) V _AC =3.5 V. The theoretical results achieved by Eq. (9) are in black solid line. The experimental sweeps acquired in [37] are in grey stars (forward sweep) and circles (backward sweep)

Starting from these experimental data, in [38] a model of the MEMS device is introduced. The microstructure is simulated as a fixed-fixed microbeam, with length L and constant rectangular cross-section of width b and thickness h. The shape imperfections are expressed by a shallow arched initial shape, delineated as $y_{0}(\hat{z}) = (1/2)y_{0}(1 - \cos(2\pi\hat{z}/L))$, where y ₀ is the maximum initial rise. Residual stresses are represented by a constant axial load P, which produces the axial displacement w _B at the right end B. The nondimensional governing equation of the transverse deflection can be written as

$$ \ddot{v} + \xi\dot{v} + v'''' + \alpha\bigl(v'' + y_{0}'' \bigr) = - \gamma F_{e} $$

(1)

where

(2)

and

(3)

and the boundary conditions are

(4)

In Eqs. (1)–(4) we use the nondimensional variables, which are related to the dimensional parameters with hats as

(5)

and we express in microns the remaining variables of length. The other parameters are

(6)

where EA is the axial stiffness, EJ is the bending stiffness, A and J are the area and the moment of inertia of the cross section, E is the effective Young’s modulus, ρ is the material density, d is the gap width between the stationary electrode and the ideal straight configuration, A _c =bL is the overlapped area between the microbeam and the stationary electrode, ε ₀ is the dielectric constant in the free space, ε _r is the relative permittivity of the gap space medium with respect to the free space, and c is the viscous damping coefficient.

According to [37, 38], the device parameters are E=1.66⋅10¹¹ N/m² and ρ=2332 kg/m³ (polysilicon material), ε _r =1 (air), length L=440 μm and width b=55.8 μm, h=1.873 μm, y ₀=1.323 μm, n=64.274, d=0.7 μm, and ξ=0.085. Assuming the electrostatic contribution negligible, which is the case here since we deal with small V _DC , both the static nonlinear equation and the eigenvalue problem associated to the linear unforced undamped dynamics can be solved in closed form. Consequently, the static deflection is

(7)

and the first symmetric mode is

(8)

These results are collected to generate a reduced-order model. After approximating the microbeam deflection as $v(z,t) \cong v_{s}(z) + \sum_{i = 1}^{M} \phi_{i} (z)Y_{i}(t)$, where v _s (z) is the static configuration and ϕ _i (z) are the corresponding mode shapes, the single first symmetric mode dynamics (M=1) are considered, the Galerkin technique is applied. Since the resulting integral term in the electric contribution is not very practical to be computed at each time step, we approximate it by curve fitting. This yields

(9)

where Y(t) is the modal coordinate amplitude. It is worth underlining that this model has many approximations, since, despite the experimental tests, no information is available about the actual dimensions of several parameters, e.g. a constant thickness is assumed, but it could be varying. However, the identification process used in [38] to extrapolate the unknowns is very careful in providing a reliable matching with the experiments.

Equation (9) is the reduced-order model that we use for the forthcoming simulations. All of them are mainly performed via self-developed codes implemented in Mathematica and Matlab. Attractor-basins phase portraits are obtained by the software package Dynamics [39].

3 Theoretical and experimental multistability

We consider the device response in a neighborhood of the first symmetric natural frequency and develop a theoretical investigation, based on frequency response curves, behavior charts and attractor-basins phase portraits, in order to examine the theoretical disappearance of each attractor. This analysis is indispensable for understanding the dynamics of the device, but is not enough to predict the experimental range of existence of each branch.

3.1 The frequency response

To analyze the dynamics, we investigate the frequency response diagrams, which represent the maximum amplitude of the oscillations, i.e. the maximum minus the minimum of ϕ(z)Y(t) at each Ω. Two examples are reported in Fig. 2, which illustrate the response at V _AC =2.5 V and V _AC =3.5 V, expressed in dimensional form. We can observe the non-resonant branch (left frequency curve) and the resonant one (right frequency curve). They exhibit the characteristic bending toward lower frequencies, which is typical of a softening oscillator. This feature provides an interval where both the attractors coexist, i.e. two different kinds of oscillations with different characteristics may take place at the same values of (Ω,V _AC ). This is a noteworthy aspect of the dynamics, since equips the device of a certain versatility of behavior, which is valuable in a variety of applications.

The theoretical frequency response curves are overlapped with the experimental data. They show that the model is able to achieve a very good matching, since theoretical predictions and experimental response nearly coincide. All the main features are adequately represented, as the value where the first symmetric natural frequency appears, the bending toward lower frequencies that arises in its neighbourhood and the separation width between the two branches. This occurs not only at low electrodynamic voltages (Fig. 2a) but also at higher ones (Fig. 2b). Of course, the simulations are not able to catch the 1/3 second symmetric superharmonic, which occurs at $\hat{\varOmega} \cong 149.5\mbox{ kHz}$, and the 1/3 second antisymmetric one, which occurs at $\hat{\varOmega} \cong145.3\mbox{ kHz}$, since Eq. (9) includes only the single first symmetric mode dynamics. However, the concurrence of results in all the main relevant nonlinear phenomena confirms our confidence in the reduced-order model, which is essential to develop any further investigation.

The comparison between experiments and simulations highlights that the range of existence of each attractor, and consequently the multistability, is smaller in practice. In the theoretical curves, both the non-resonant branch and the resonant one loose stability (in classical sense) by saddle-node (SN) bifurcation, after which they vanish. In the experiments, the response directly jumps from a branch to the other one at different points from the bifurcation points predicted in the theoretical curves.

In all the analyzed cases, when an attractor vanishes, there is a safe jump to the other branch, and not dynamic pull-in. Thanks to the large difference between the maximum amplitude of the two attractors, the jump is paralleled with a large stroke, which enhances the signal-to-noise ratio, i.e. the quality of the signal. Multistability combined with jumps (with large stroke) provides an interesting scenario from a practical point of view, since there is the opportunity to activate a hysteretic loop between the non-resonant and the resonant oscillations. This feature may be desirable for instance in filters, where we are looking for an interval with large oscillations bounded by ranges with small ones, and in detection, where the device is expected to exhibit a certain motion and to switch into a different kind of oscillation upon detection of a physical parameter. Also, the frequency curves achieved in the present case-study refer to moderately low values of electrodynamic excitation, i.e. these phenomena may be triggered at low power consumption, which is even more desirable. The valuable relevance of all these nonlinear dynamic features in applications underlines the importance of detecting where the disappearance of each attractor effectively occurs in practice, and not only in theory, i.e. where we can count on an effective multistability of attractors and where we should expect the safe jump between them.

On one hand, the theoretical length of each branch corroborates the reliability of the model, since it underlines that the simulations are able to catch all the experimental extent of both the attractors, and not only a part of it. On the other hand, this discrepancy emphasizes the need of additional investigations to be interpreted.

3.2 The overall scenario

We focus on the theoretical predictions and develop a behavior chart to illustrate the overall scenario of the main dynamical events, when both the electrodynamic voltage and the frequency are varying. This is reported in Fig. 3 along with the measured experimental data [37]. Operatively, the chart is obtained by performing many frequency response diagrams, like those in Fig. 2, by detecting the frequency Ω and the voltage V _AC where each attractor theoretically disappears, and by reporting these coordinates in the (Ω,V _AC ) space.

Fig. 3

Behavior chart showing the nondimensional frequency versus the dynamic voltage. The experimental disappearance of the non-resonant and resonant branch is represented, respectively, in diamonds and circles

In the neighbourhood of the resonance, at (Ω,V _AC ) approximately equal to (39.6,0.14), we can observe the degenerate cusp bifurcation point where the non-resonant and the resonant attractor separate. At this point, the theoretical appearance and/or disappearance of the non-resonant and the resonant branch coincides. Beneath this voltage threshold, the response of the system presents only one branch, whereas, beyond it, it splits into the non-resonant and the resonant one, and both of them need to be examined. The curves denote their theoretical bounds of existence. The region where the non-resonant attractor exists is located at the left hand side of the chart, from the unforced dynamics to its SN bifurcation (SN non-res). The resonant one, instead, appears at its SN (SN res) and extends its range of existence beyond this line, throughout all the right hand side of the chart, up to exceed the analyzed parameter range.

The two curves of SN bifurcation delimitate the range of parameters where both the non-resonant and the resonant oscillations coexist, i.e. where the theoretical simulations predict multistability of behavior in the device response. The chart clearly illustrates the considerable enlargement of the range of multistability, which gradually characterizes wider and wider frequency values, when increasing V _AC . This phenomenon is deeply influenced by the resonant branch, since a slight increment of V _AC provides a large shift of its SN bifurcation toward lower frequency values, which significantly broadens the range of existence of the attractor. The non-resonant branch, instead, reduces its extent when V _AC increases, but this decrement is not substantial.

In addition to the theoretical results, in the chart we show the (Ω,V _AC ) values where the non-resonant and the resonant attractor experimentally disappear, which are denoted, respectively, with diamonds and circles. They are extracted from the experimental data in [37] by repeating the same procedure used to provide the theoretical curves. The experimental bands of disappearance of each branch do not coincide with the theoretical ones, but are slightly shifted from them and occur in the region where each attractor is theoretically expected to exist. This is because, as previously observed, the peaks in the experimental frequency sweeps do not coincide with the peaks in the theoretical frequency responses.

3.3 Attractor-basins scenario

To understand the previous discrepancy between theoretical predictions and experimental data, it is essential to analyze the device response not only locally, by studying each single attractor, but also globally, by focusing on the attractor-basin scenario. For this reason, we systematically perform attractor-basins phase portraits to achieve detailed information about the global dynamics. In Fig. 4 we show some examples at V _AC =3.5 V. The basins are orange and green, respectively, for the non-resonant and the resonant branch. The white color denotes a third scenario, the escape, where the system experiences dynamic pull-in.

Fig. 4

Attractor-basins phase portrait at V _AC =3.5 V and (a) Ω=38; (b) Ω=38.8; (c) Ω=39; (d) Ω=39.22

Approaching the resonance, the resonant branch appears. At Ω=38 (Fig. 4a), its basin is still rather narrow, whereas the other basin is particularly wide. Increasing Ω, this outline rapidly changes. At Ω=38.8 (Fig. 4b), the two basins are comparable. Each one of them presents a compact area, which is appreciably large and mainly develops around the attractor, and a non-compact one, which is even wider and consists of thin tongues spiraling around the compact part. A wide compact part is very important to reliably operate the device. In fact, disturbances inevitably give uncertainties to the operating initial conditions. The wide compact area is essential to tolerate them since all the initial conditions in this area reach the same attractor at steady dynamics. Conversely, the non-compact region is sensitive to disturbances, because a small shift in the initial conditions may lead to a different outcome. Further increasing Ω, the basin and the compact part of the resonant branch significantly enlarges at the expense of the basin of the non-resonant one, which considerably shrinks. At Ω=39 (Fig. 4c) the magnitude of this last basin is still wide. At Ω=39.22 (Fig. 4d), instead, it becomes nearly residual. The experimental disappearance of the non-resonant branch exactly occurs at Ω=39.08 ($\hat{\varOmega} = 146.55\mbox{ kHz}$), i.e. between these two last scenarios, where the compact area of its basin becomes too small and vulnerable to disturbances. Similarly, the resonant branch experimentally disappears at Ω=38.59 ($\hat{\varOmega} = 144.71\mbox{ kHz}$), which is in the interval between Fig. 4a and Fig. 4b.

For the sake of completeness, it is worth observing that, at the experimental disappearance, each attractor and the compact part of its basin are located far from the escape. They are immersed and surrounded by the other basin. This guarantees the safe jump between the two branches, as observed in the experimental data. However, further amplifying the electric excitation beyond the analyzed range, the resonant attractor and its basin turn closer and closer to the escape (not shown in the figures). When an attractor disappears, this outline may prevent the safe jump and may directly lead to the unsafe dynamic pull-in, i.e. the failure of the device.

4 Practical multistability

In Sect. 3, we can observe that the extent of each branch is longer in the numerical simulations than in the experimental data. This is because numerical simulations are theoretical limits. They do not consider the inevitable presence of disturbances, which are unavoidable in experiments and applications. To take them into account and explore their effects, we develop a dynamical integrity analysis, based on integrity profiles and integrity charts, in order to predict the range of existence of each attractor in practice.

4.1 Disturbances

Many sources of disturbances are inevitably encountered in microstructures in experiments and applications. Before performing the dynamical integrity analysis, it is worth providing some examples to highlight them.

Disturbances may arise in the initial conditions. For instance, the following of the attractor in the frequency response is experimentally achieved via a sweeping process, which is based on varying the frequency through discontinuous steps. This procedure inevitably induces perturbations in the initial conditions. In all the sweeps in [37], much attention is devoted in decreasing this kind of disturbances, e.g. by choosing a small frequency step and by applying a large settling time to ensure steady state, in order that the experimental data are as much reliable as possible. Despite the efforts to reduce disturbances, they cannot be completely cancelled. If the considered attractor is not provided of a large “safe” basin, the attractor may not be able to tolerate perturbations. This shrinks the actual range of existence of the considered attractor. The response may switch to another final behavior, and the resulting outcome may differ from the theoretical predictions. The theoretical analysis conducted in Sect. 3 is not able to catch this aspect, since it predicts the disappearance of an attractor at the same values of (Ω,V _AC ), both in case of a large and a small frequency step.

In addition to disturbances in the initial conditions, we have to mention also at least another source of uncertainty. This is represented by the slight imperfections of the device with respect to the considered theoretical model, e.g. the approximations in estimating the damping, in deriving the model, in identifying the unknown parameters, etc. These disturbances are conceptually different from the previous case, since refer to small perturbations in the structure. Nevertheless, they are unavoidable as well. They coexist and mix with the previous ones. For this reason, the dynamical integrity is called to take all of them into account.

4.2 Integrity profiles

In this section we perform the dynamical integrity analysis. In particular, after introducing the dynamical integrity tools of safe basin and dynamical integrity measure, we develop integrity profiles to investigate the loss of structural safety.

It is worth underlining that our aim is to detect the parameter ranges where each branch may practically (and not theoretically) vanish because of the presence of disturbances. Therefore, we use the dynamical integrity analysis to investigate the phenomenon of disappearance of each attractor (and not other phenomena, as the jump or the dynamic pull-in). To this purpose, we consider both the non-resonant branch and the resonant one, and investigate each one of them, one by one, separately.

The safe basin is the set, in the phase space, of all the initial conditions sharing a certain property. Many different definitions of safe basin have been considered in the literature [22–24], according to which safe condition is desired to be investigated. In the present case-study, since we focus on the existence and/or disappearance of each single attractor, the safe condition is represented by having, at the steady-state dynamics, the motion under consideration, whereas the unsafe condition is represented by other motions (the other bounded oscillation or the escape). Hence, for each attractor, we assume as safe basin its own basin of attraction.

We measure the dynamical integrity by using the Local Integrity Measure (LIM) introduced by Soliman and Thompson [19]. The LIM is the normalized minimum distance from the attractor to the boundary of the safe basin, i.e. the radius of the largest circle entirely belonging to the safe basin and centered at the attractor. Examples of circles used in the definition of LIM are reported in Fig. 5. We normalize each radius with the analogous radius drawn for the non-resonant branch at (Ω;V _AC ) equal to (44;0.01), i.e. next to the unforced dynamics and far from resonance.

Fig. 5

Attractor-basins phase portrait at (Ω;V _AC ) equal to (38.85;5) with examples of circles for the evaluation of LIM

The LIM is an appropriate measure for our case. It takes into account the steady-state dynamics, considers only the compact ‘core’ of the safe basin and rules out the non-compact regions, which are dangerous in practice. Thus, it is suitable for the analysis of these experimental data, since they are coming from a sweeping process, where at the end of each step the system is in steady-state conditions. Nevertheless, other measurements could be accurate; for instance the Integrity Factor proposed by Lenci and Rega in [20].

To analyze the structural safety of the device, we build integrity profiles, where we report the LIM as a function of the frequency, at a certain fixed V _AC value. Operatively, once fixed V _AC , each integrity profile is obtained by performing many attractor-basins phase portraits, which are sampled using a grid in the frequency of ΔΩ=0.1 (or less), by computing the LIM (normalized radius) for both the non-resonant and the resonant branch, and by plotting LIM versus frequency. The obtained profiles are reported in Fig. 6.

Fig. 6

Integrity profiles for (a) the resonant branch and (b) the non-resonant one, at different V _AC values

We focus on the resonant branch and analyze the range Ω=[37.8;39.3], Fig. 6a. As an example, we consider the profile at V _AC =3.5 V. At Ω=39.1, there is LIM ≅15 %, which is not particularly wide, but is still large enough to guarantee the attractor to be experimentally visible. Decreasing Ω, the LIM slides down to smaller values. This fall is gradual but inexorable. It produces a significant deterioration in the reliability of the attractor, because it now has a narrow safe basin. The smaller integrity enhances the sensitivity of the system to unexpected excitations, and eventually makes the attractor vulnerable to the experimental disturbances. The experimental disappearance of the resonant branch exactly occurs in this range, at Ω=38.59, with LIM ≅6.64 %. The last part of the integrity profile is characterized by a tiny dynamical integrity. The LIM keeps decreasing, but slowlier, up to the disappearance of the attractor (not shown in the figure). Since the dynamical integrity is only residual, this remaining theoretical range of existence of the attractor cannot be caught in practice by the sweeping process.

Comparing the frequency response (Fig. 2b) to the integrity profile (Fig. 6a) when Ω decreases, the amplitude of the resonant oscillations gradually increases while the dynamical integrity drops. Moderately large motions can still be experimentally observed, since they are equipped with an acceptable integrity. However, considerably larger vibrations do not exist from a practical point of view, since they are not robust enough to tolerate disturbances.

Varying the electrodynamic voltage, the scenario in Fig. 6a practically remains unchanged, except for some minor differences. At V _AC =2.5 V, the range with negligible LIM is nearly imperceptible, then, it progressively enlarges. When increasing V _AC , the values of LIM corresponding to the experimental disappearance slightly increase, but remain confined in a precise and very narrow interval, LIM = 6.2–6.8 %. This is in agreement with the experimental data, since these frequency sweeps are acquired under very similar experimental conditions (e.g. with the same frequency step, at about same pressure, etc.), and therefore, the attractor is expected to disappear in the experiment at about the same level of integrity. Only exceptions occur at higher V _AC , in particular at V _AC =4.5 V, where the resonant branch disappears at LIM ≅7.5 %, and at V _AC =5 V, where it disappears at LIM ≅8.9 %. These values are slightly higher, but not excessively. This fact may be due to the model. As explained in Sect. 2 and underlined in [38], we are aware that the present model has many approximations, since many physical parameters are unknown. Raising V _AC , the effects of the nonlinearities increase and the effects of the approximations of the model amplify, which affects the reliability of the results. Nevertheless, it may be related also to deterioration of the device, which is due to the multiplicity of the performed experiments. Note that the experimental backward sweep at V _AC =5 V was the last sweep that we were able to achieve, after which the microstructure broke.

A similar dynamical integrity analysis is developed for the non-resonant branch. According to the remarks in the attractor-basins phase portraits (Figs. 4), the compact part of its basin strongly reduces very close to the curve of disappearance, which may make the attractor vanish in practice in this neighborhood. On the contrary, slightly far from this curve, this attractor has a basin with a large compact part, since the resonant branch either does not exist or has a small basin. Consequently, in this range the attractor is expected to have a broad dynamical integrity, i.e. to be robust and not vulnerable to disturbances. For this reason, in the non-resonant case, we can investigate the dynamical integrity in a smaller interval than in the resonant one. In particular, we consider Ω=[38.3;39.35], since this is the most critical range where the attractor needs to be analyzed from a dynamical integrity perspective (Fig. 6b).

The integrity profiles are slightly different from those of the resonant attractor. Considering V _AC =3.5 V at increasing Ω, the integrity curve initially declines slowly, then descends more rapidly, and finally drops abruptly within a narrow range, which directly ends with the theoretical SN bifurcation. The experimental disappearance occurs at LIM ≅17.7 %. This general outline does not substantially change by varying V _AC . Similarly to the resonant branch, when V _AC increases, the experimental disappearance occurs at a slightly higher LIM. Nevertheless, we can identify a precise range where the attractor experimentally vanishes in all the analyzed frequency sweeps, LIM = 16–19 %. Even if this interval is slightly larger than that one observed for the resonant branch, it corresponds to a small band of frequency, where the attractor may practically vanish.

Note that there is a very relevant difference in the dynamical integrity scenario between the two branches. The loss of robustness is very rapid in the non-resonant case. In the resonant one, instead, the fall is considerably slow, and, consequently, a small interval of LIM denotes a broad band of frequency. Hence, accuracy in detecting the LIM is particularly valuable in the resonant branch, more than in the non-resonant one.

4.3 Integrity charts

To have a detailed description of the loss of structural safety when both the frequency and the electrodynamic voltage are varying, we make the integrity charts in Fig. 7. They are obtained by performing several integrity profiles at different values of V _AC , with step ΔV _AC =0.5 V, and by plotting the curves of constant percentage of LIM. They summarize the overall scenario.

Fig. 7

Frequency-dynamic voltage integrity charts for the practical disappearance of the attractors: (a) resonant branch; (b) non-resonant branch

We can observe that the experimental data “follow” exactly these curves. In the resonant branch, Fig. 7a, safe conditions are ensured at LIM > 8 % (except at V _AC =5 V). Below this percentage, the attractor becomes practically vulnerable, since the safe basin is not sufficiently robust to tolerate the disturbances. It is at about LIM = 6–8 % that, in practice, the final motion may become different from the theoretical predictions, leading to a jump to the other branch. The last range with LIM < 6 % actually does not exist under realistic conditions, with these expected disturbances. Similarly, the non-resonant attractor, Fig. 7b, can safely operate the device up to LIM > 20 %. Then, the LIM drops faster (the lines of constant percentage of LIM are closer and closer) up to the disappearance of the attractor (at SN non-res). At about LIM = 15–20 %, which corresponds to a tiny frequency range, the response jumps to the other branch. The final range of existence of the attractor is only theoretical.

These results highlight that, despite numerous uncertainties in the model, dynamical integrity is able to detect a precise range of LIM, which corresponds to a certain range of frequency, where we can expect to observe the experimental disappearance of the analyzed attractor. Beneath this interval, the branch practically does not exist, although it appears in the theoretical predictions. Therefore, this analysis is able to provide a satisfactory interpretation of the disturbances inevitably encountered in the experimentation. Of course, the more accurate is the model, the more precise will be the dynamical integrity analysis in predicting the threshold of practical disappearance.

Hence, Eq. (9) is able not only to predict the general outline of the frequency sweeps, but also to provide reliable (and not rough) predictions of the experimental extent of each branch. Note that, up to V _AC =4.5 V, the practical disappearance occurs within a very small range of LIM. After this V _AC value, the range gradually enlarges, both in the non-resonant and in the resonant branch. Thus, the dynamical integrity analysis may be used also as a valuable tool to denote the threshold of applicability of the model, since is able to detect the voltage boundary after that the model slowly starts to decrease its accuracy. In the present case, this threshold practically covers all the range with available experimental data.

We can observe that each integrity chart sketches not only the curves detecting the range of experimental disappearance of each attractor, but also many other curves at different values of constant percentage of LIM. Accordingly, each chart is able to abstract from the particular case-study and examine a more general scenario, where different disturbances are assumed. It illustrates that the wideness of the range where each attractor practically exists may be enlarged (reduced) by decreasing (increasing) the disturbances. It predicts the expected boundaries of disappearance of each attractor. Therefore, each chart may serve as a guideline for the design, since, depending on the magnitude of the expected disturbances, it can be used to establish safety factors in order to operate the device in safe conditions with the desired behavior.

The final scenario is schematically summarized in Fig. 8, where we report the major results. For each attractor, the integrity curves divide the region of its theoretical existence into two different areas: the area of practical existence and the area of practical disappearance. In the range of practical existence, the attractor can be reliably observed under realistic conditions, because it is robust enough to tolerate the inevitable disturbances. In the range of practical disappearance, the attractor exists in the theoretical predictions but cannot be used in practice, because is practically vulnerable. To operate the device in safe conditions with a certain final motion, this last region has to be avoided. This area may be quite narrow, as for the non-resonant attractor, or wide, as for the resonant one, where the range where we can rely on the attractor is considerably reduced. Thus, these curves detect the practical bounds of existence of each attractor, identify where only the non-resonant branch can be experimentally observed, where only the resonant one, and where, instead, they actually coexist, and underline that, because of disturbances, the range of practical existence is inevitably a subset of the range of theoretical one.

Fig. 8

Schematic integrity chart. The white region represents the parameter range where only one branch (non-resonant or resonant) exists both in theory and in practice. The light grey region represents the range where only one branch exists in practice, whereas the other one (expressed in brackets) practically disappears. The region where both the branches practically coexist is dark grey

5 Conclusions

A MEMS device based on an imperfect microbeam electrically actuated has been investigated in a neighborhood of its first symmetric natural frequency. The experimental data of a frequency sweeping process have been interpreted and predicted via a dynamical integrity analysis.

After introducing a reduced-order model, we have developed an extensive investigation of the theoretical response. Frequency response curves and behavior charts have been performed. This analysis is essential to understand the dynamics arising in the device and to confirm the reliability of the reduced-order model. It provides a very detailed description of the overall scenario when both the frequency and the electrodynamic voltage are varying. Nevertheless, despite the very good matching between theoretical results and experimental data, we have observed that the attractors in the experiments have a smaller range of existence than in the theoretical predictions. This is because all these results do not consider the presence of disturbances. They may come from many different areas, ranging from the discontinuous frequency steps in the sweeping process, to the approximations in the modeling, uncertainties in the shape, material properties, damping estimation, etc. Their presence is unavoidable in experiments and practice.

To take them into account, we have introduced a dynamical integrity analysis, which is able to investigate the practical response under realistic conditions. We have focused on the practical disappearance of each attractor. The definition of the safe basin and the choice of the integrity measure have been selected in order to establish a continuous parallelism between dynamical integrity tools and experimental frequency sweeps. Many integrity profiles have been performed. We have highlighted that they provide quantitative information about the practical loss of structural safety. Moreover, they are able to describe and forewarn the experimental disappearance of each attractor.

All these results have been collected in the integrity charts. They are able to predict, properly and accurately, the final behavior of the MEMS device. They detect the range of LIM where each attractor practically vanishes, i.e. they tell in advance at what percentage of LIM the jumps will happen. They identify the threshold which separates the area of practical existence, where the attractor can safely operate the device, from the area of practical disappearance, where the attractor becomes vulnerable to disturbances. We have observed that the practical range of existence of each branch (and, consequently, the practical range of multistability) is smaller, and sometimes remarkably smaller than the theoretical one.

We have highlighted the valuable information provided by these charts for the engineering design. In fact, they may be used to predict the experimental response under different experimental conditions, i.e. to establish factors of safety to operate the device reliably in safe conditions, depending on the expected disturbances.

We have stressed that this study cannot prescind from a good classical modeling, since the more accurate is the mechanical modeling, and the more precise is the dynamical integrity analysis in predicting the experimental response.

Therefore, the integrity charts are able both to interpret the experimental data, and to predict the expected behavior when varying the experimental disturbances, and to detect the range of applicability of the model, after which the theoretical results slowly start to decrease their accuracy.

Summarizing, in this paper, by investigating the response of a particular MEMS device, the issue of exploring the dynamical integrity in a system has been addressed and its efficiency in the design to operate the structure according to the desired outcome has been highlighted. We have underlined the large applicability of this analysis both in MEMS and, more in general, in systems.