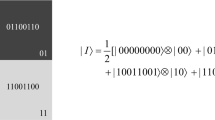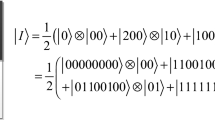Quantum watermarking scheme through Arnold scrambling and LSB steganography

Abstract

Based on the NEQR of quantum images, a new quantum gray-scale image watermarking scheme is proposed through Arnold scrambling and least significant bit (LSB) steganography. The sizes of the carrier image and the watermark image are assumed to be $2n\times 2n$ and $n\times n$, respectively. Firstly, a classical $n\times n$ sized watermark image with 8-bit gray scale is expanded to a $2n\times 2n$ sized image with 2-bit gray scale. Secondly, through the module of PA-MOD N, the expanded watermark image is scrambled to a meaningless image by the Arnold transform. Then, the expanded scrambled image is embedded into the carrier image by the steganography method of LSB. Finally, the time complexity analysis is given. The simulation experiment results show that our quantum circuit has lower time complexity, and the proposed watermarking scheme is superior to others.

1 Introduction

Images are an important medium in visual information transmission. Image processing becomes more popular because of the need to extract visual information from the natural world. Due to the rapid development of quantum computation and quantum information in the past several decades, quantum computer has demonstrated a bright prospect over classic computer, particularly in Feynman’s computation model [1], Deutsch’s quantum parallelism assertion [2], Shor’s integer factoring algorithm [3], and Grover’s database searching algorithm [4].

Quantum image processing (QIMP), a new emerging sub-discipline of information and image processing, is devoted to utilizing the quantum computing technologies to capture, manipulate, and recover quantum image in different formats for different purposes. The investigation of QIMP is beginning with how to store and retrieve a quantum image in quantum computers. Venegas-Andraca and Bose proposed the quantum image representation of qubit lattice [5] in 2003 using one qubit to hold one pixel. Then, Latorre’s Real Ket presented a way to store image information using quantum superposition state [6]. More recently, in 2010, Le et al. [7] proposed a flexible representation of quantum image (FRQI), which integrates the information of colors and the corresponding positions in an image into an entanglement state and captures the positions information into a normalized superposition quantum state. It encodes the color information of an image into angle $\theta$ using 1 qubit and uses the two-dimensional position information (Y-axis and X-axis). Further, in 2013, more quantum image representations were proposed. A novel enhanced quantum image representation (NEQR) of digital images [8] improves the color information representation of FRQI from 1 qubit to q qubits encoding the pixel value from 0 to $2^{q}-1$, which makes the complex and elaborates color operations perform easier than FRQI does. QUALPI [9] stores images sampled in log-polar coordinates. Color image representation utilizes two sets of quantum states for M colors and N coordinates, respectively (QSMC and QSNC) [10]. Multi-dimensional image representation uses a normal arbitrary quantum superposition state (NAQSS) [11] and simple quantum representation of infrared images (SQR) [12]. A novel quantum representation of color digital images was proposed [13] in 2016.

In the literature [14, 15], the QIMP is broadly classified into two groups: quantum-inspired image processing and classical-inspired image processing [16, 17]. The quantum-inspired image processing aims to exploit some of the properties responsible for the potency of quantum computing to improve some well-known classical or digital (i.e., conventional or non-quantum) image processing. The classical-inspired image processing derives inspiration from the expectation that quantum computing hardware will soon be physically realized. Hence, such research focuses on extending classical image processing to the quantum computing framework. Some of the available literatures that fall under this direction include geometric transformations [18,19,20], color transformation [21], quantum image translation [22,23,24], quantum image scaling [25,26,27], image scrambling [28,29,30,31,32], image segmentation [33], feature extraction [34], edge detection [35], and image matching [36].

Quantum image protection devotes to protecting images from unauthorized use, copying, and manipulation when images are used for commercial purpose. It has been a very important theme for experts and researchers and mainly divided into two categories: quantum image cryptography and quantum image watermarking. The image cryptography is to transform a meaningful image into a meaningless (or disorder) form, while the image watermarking is to hide image information by embedding it into some other images. The quantum image scrambling realizes image cryptography in [29,30,31,32]. The quantum Arnold and Fibonacci image scrambling algorithms [28] and quantum Hilbert image scrambling algorithm [30] were proposed by Jiang et al; Several quantum watermarking schemes have been proposed in [37,38,39,40,41] using complex quantum circuits such as QFT [37], QWT [38], and Hadamard transform [39], and some other schemes were proposed, for example, a quantum watermarking scheme using simple and small-scale quantum circuits [40] and a novel LSB-based quantum watermarking [41].

This paper is organized as follows. Section 2 briefly introduces the quantum representation of NEQR, classical LSB steganography, Arnold transformation, the parallel adder, subtractor modulo N, and quantum equal. Section 3 presents the quantum watermarking scheme. Section 4 analyzes the time complexity of circuits and the experimental results. The conclusions are drawn in Sect. 5.

2 Preliminaries

2.1 Novel enhanced quantum image representation (NEQR) of digital image

Comparing to FRQI, the NEQR has improved the gray-scale value representation from 1 qubit to q qubits, which makes more image operations can be performed conveniently [8]. A gray-scale image f(Y, X) with $\hbox {2}^{n}\times 2^{n}$ pixels is expressed in Eq. (1) based on NEQR. Figure 1 shows an example of an image of $2\times 2$, and the corresponding NEQR is on the right of the image.

$$\begin{aligned} \left| \hbox {I} \right\rangle =\frac{\hbox {1}}{\hbox {2}^{\hbox {n}}}\sum _{i=0}^{2^{2n}-1} {\left| {C_i } \right\rangle \otimes \left| i \right\rangle =\frac{\hbox {1}}{\hbox {2}^{\hbox {n}}}} \sum _{Y=0}^{2^{n}-1} {\sum _{X=0}^{2^{n}-1} {\mathop \otimes \limits _{k=0}^{q-1} } } \left| {C_{YX}^k } \right\rangle \otimes \left| Y \right\rangle \left| X \right\rangle \end{aligned}$$

(1)

where

$$\begin{aligned} \left| {C_i } \right\rangle =\left| {C_i^{q-1} \ldots C_i^1 C_i^0 } \right\rangle \end{aligned}$$

Fig. 1

An example of $2 \times 2$ image and its NEQR

2.2 The classic LSB scheme

Steganography is a branch of information hiding which hides a message into a cover. It is a kind of subliminal channel that provides secret communication so that the intended hacker or attacker is unable to detect the presence of the message. The LSB steganography, first proposed by Tirkel [42] in 1993, is a fundamental and simple data hiding method. The principle is using message bits to substitute the least significant bits of the cover. In general, the cover is a 24-bit or 8-bit image. Taking the latter, for example, it has $2^{8}=256$ colors (or gray scales). The least significant bit of one of the pixels is shown in Fig. 2. The message bit is “1”; then, we only need to change the least significant bit from “0” to“1,” i.e., color 90 should be changed to color 91. The receiver can get the message by simply reading the least significant bit.

Fig. 2

Least significant bit

2.3 Arnold scramble method

The Arnold transform or Arnold’s cat map was set up during the research of ergodic theory by Arnold [43]. Dyson et al. quoted the Arnold transform as an image scrambling method in 1992 [44]. Since then, it has been widely used in image processing.

2.3.1 The principle of Arnold scramble

Supposing that I(x, y) is an original image with size $2^{n}\times 2^{n}$, (X, Y) and $(X_A ,Y_A )$ are the pixel coordinates of the original image and the scrambled image, respectively. Two-dimensional Arnold scrambling proceed is written by Eq. (2), and its inverse operation is shown in Eq. (3).

$$\begin{aligned} \left[ {{\begin{array}{ll} {X_A } \\ {Y_A } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} 1&{} 1 \\ 1&{} 2 \\ \end{array} }} \right] \;\left[ {{\begin{array}{l} X \\ Y \\ \end{array} }} \right] \;\bmod 2^{n} \end{aligned}$$

(2)

where

$$\begin{aligned} X_A =(X+Y)\bmod 2^{n}\;,Y_A =(X+2Y)\bmod 2^{n} \end{aligned}$$

The inverse Arnold transformation is

$$\begin{aligned} \left[ {{\begin{array}{ll} X \\ Y \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} 1&{} 1 \\ 1&{} 2 \\ \end{array} }} \right] ^{-1}\;\left[ {{\begin{array}{ll} {X_A } \\ {Y_A } \\ \end{array} }} \right] \bmod 2^{n}=\;\left[ {{\begin{array}{ll} {2}&{} {-1} \\ {-1}&{} {1} \\ \end{array} }} \right] \;\left[ {{\begin{array}{ll} {X_A } \\ {Y_A } \\ \end{array} }} \right] \;\bmod 2^{n}, \end{aligned}$$

(3)

i.e.,

$$\begin{aligned} X=(2X_A -Y_A )\;\bmod \;2^{n}\;,Y=(Y_A -X_A )\;\bmod \;2^{n} \end{aligned}$$

2.3.2 The safety analysis of Arnold scrambling in quantum watermarking

Arnold transform is not a “pure” two-dimensional affine transformation because it has a “mod” operator. It can be seen as a process of cutting and splicing. Using Arnold scrambling, an original quantum image transforms into a disordered or meaningless quantum image. Besides, as an image preprocessing technology, it can reduce the distribution of scattered error bits of a quantum watermarked image to improve the robustness.

The Arnold scrambling algorithm is simple and cyclical, i.e., if repeating Arnold transform in certain iteration steps, it will surely resume the image. Based on Eq. (2), the iteration equation of Arnold transform is shown in Eq. (4). In [44], Dyson researched the period. Generally speaking, the explicit value of the period cannot be calculated. He gave the upper bound and the lower bound of the period and gave explicit values for particular cases as shown in Table 1. We can see that the period is connected with the image size N from Table 1.

$$\begin{aligned} \left\{ {\begin{array}{l} I^{1}=\left[ {{\begin{array}{ll} {X_A } \\ {Y_A } \\ \end{array} }} \right] ,\;A=\left[ {{\begin{array}{ll} 1&{} 1 \\ 1&{} 2 \\ \end{array} }} \right] ,I^{0}=\left[ {{\begin{array}{l} X \\ Y \\ \end{array} }} \right] \\ I^{1}=AI^{0}\bmod 2^{n} \\ I^{n}=AI^{n-1}\bmod 2^{n}\;,n=0,1,2,\ldots \\ \end{array}} \right. \end{aligned}$$

(4)

Table 1 Period of Arnold transform

Figure 3 shows the scrambling results and corresponding period of a real image. The size of the original image named “cameraman” is $256\times 256$. (b)–(d) is the Arnold transformation, the sub-captions of which are the iteration times. For more comprehensive and state-of-the-art surveys of this topic, refer to paper [43, 44].

Fig. 3

Result of Arnold transformation after the specific iteration times. a Original image, b 12 times, c 48 times, d 192 times

2.4 Parallel adder and subtractor modulo N

Islam M S et al. proposed the reversible full adder based on Peres gate (PG) in [45]. Here, the introductions about the design of half adder, full adder, and parallel adder are given. Then, the module of parallel adder modulo N (PA-MOD) and parallel subtractor modulo N (PS-MOD) are designed.

2.4.1 Reversible half adder (RHA)

Figure 4a shows the Peres Gate working as a half adder and its quantum circuit, where $Q=A\oplus B$ represents the sum of $A+B$ and $R=AB$ represents the carry of $A+B$. Figure 4b, c are the quantum circuit realization of RHA and corresponding diagram of RHA, respectively.

Fig. 4

Reversible half adder (RHA). a PG gate working as half adder, b quantum circuit implement of half adder, c simplified diagram of RHA

Where Vis a square root of NOT gate defined by

$$\begin{aligned} \hbox {V}=\frac{i+1}{2}\left( {{\begin{array}{ll} 1&{} {-i} \\ {-i}&{} 1 \\ \end{array} }} \right) \end{aligned}$$

$V^{+}$ is the Hermitian matrix of V. V and $V^{+}$ have the following properties:

$$\begin{aligned} \begin{array}{l} V\times V=V^{+}\times V^{+}=NOT \\ V\times V^{+}=V^{+}\times V=I \\ \end{array} \end{aligned}$$

2.4.2 Reversible full adder (RFA)

Based on the PG gates, we design the full adder as shown in Fig. 5, where $R=A\oplus B\oplus C$ represents the sum of $(A+\hbox {B}+\hbox {C})$ and $S=(A\oplus B)C\oplus AB$ represents the carry, respectively. The quantum circuit realization of RFA is shown in Fig. 5a, and its simplified graph is shown in Fig. 5b.

Fig. 5

Reversible full adder (RFA). a quantum implement of the reverse full adder, b simplified diagram of RFA

2.4.3 Reversible parallel adder (PA)

The reversible parallel adder adds an n qubits Y from an n qubits X designed by one reversible half adder (RHA) and ($n-1$) reversible full adders (RFA) as shown in Fig. 6a. Here, $S_n S_{n-1} \ldots S_1 S_0$ represents the sum of $X+Y$. Other unremarked qubits are the garbage output, and the constant input qubit 0 is the ancillary qubit. For convenience, the block diagram of PA omits the ancillary inputs and the garbage outputs as shown in Fig. 6b.

Fig. 6

Reversible parallel adder. a Reverse parallel adder (PA), b block diagram of PA

2.4.4 Parallel adder modulo N (PA-MOD)

As shown in Fig. 7, X and Y are two n-bit binary numbers. Assuming that $N=2^{n}$, it is easy to find that $X+Y$ is a ($n+1$)-bit binary numbers $S_nS_{n-1}{\ldots }S_1S_0$ as shown in Fig. 6a. According to the mathematical proof of theorem 1 in [29], the result of $(X+Y)\;\text {mod}\;N$ is $S_{n-1}{\ldots }S_1S_0,$ which just omits the highest-order bit of $S_n$. Figure 7a, b give the quantum circuit realization of PA-MOD and corresponding diagram of PA-MOD, respectively.

Fig. 7

Parallel adder modulo N. a Parallel adder modulo N (PA-MOD), b diagram of PA-MOD N

2.4.5 Parallel subtractor modulo N (PS-MOD)

The subtraction operation can be converted into complement addition to achieve addition and subtraction operations of the binary bit. Supposing that we need to calculate the difference between the two binary numbers X and Y, where $Y=y_{n-1}y_{n-2}\ldots y_0$ and $X=x_{n-1}x_{n-2}\ldots x_0$, then we can derive

$$\begin{aligned}&(Y-X)\mod 2^n\nonumber \\&\quad = [Y + (-X)] \mod 2^n\nonumber \\&\quad =[Y+(\bar{X}+1)]\mod 2^n\nonumber \\&\quad =(y_{n-1}y_{n-2}\ldots y_0+\bar{x}_{n-1}\bar{x}_{n-2}\ldots \bar{x}_{0}+1)\mod 2^n \end{aligned}$$

(5)

According to Eq. (5), the construction of PS-MOD is shown in Fig. 8a. The module diagram of PS-MOD is shown in Fig. 8b where the ancillary inputs and the garbage outputs are omitted.

Fig. 8

Parallel subtractor modulo N. a Parallel subtract modulo N (PA-MOD), and b diagram of PS-MOD N

2.5 Quantum equal (QE)

The quantum equal compares two numbers $\left| {YX} \right\rangle =\left| Y \right\rangle \left| X \right\rangle$ and $\left| {AB} \right\rangle =\left| A \right\rangle \left| B \right\rangle$ to find out whether they are equal or not, where $\left| Y \right\rangle =\left| {y_{n-1} \ldots y_1 y_0 } \right\rangle ,\left| X \right\rangle =\left| {X_{n-1} \ldots X_1 X_0 } \right\rangle ,\left| A \right\rangle =\left| {a_{n-1} \ldots a_1 a_0 } \right\rangle ,\left| B \right\rangle =\left| {b_{n-1} \ldots b_1 b_0 } \right\rangle$ .Therein, $x_i ,y_i ,a_i ,b_i \in \{0,\;1\},\;i=n-1,\ldots 1$. The output qubit$\left| c \right\rangle$ represents the comparative result. If $\left| c \right\rangle =\left| 1 \right\rangle ,\left| {YX} \right\rangle =\left| {AB} \right\rangle$; otherwise, $\left| {YX} \right\rangle \ne \left| {AB} \right\rangle$. The quantum circuit of QE and its diagram are shown in Fig. 9.

Fig. 9

Quantum equal (QE) circuit realization and its diagram. a Circuit of quantum equal (QE), b diagram of QE

3 The proposed quantum watermarking scheme

In this section, a quantum watermarking scheme was proposed based on NEQR, which hides a secret gray-scale image (watermark) into a gray-scale image (carrier). Assume that the size of the carrier image and the watermark image is $2^{n}\times 2^{n}$ and $2^{n-1}\times 2^{n-1}$, respectively.

In order to explain the scheme, we take a small watermark (secret) image with $1\times 1$ pixels and a small carrier image with $2\times 2$ pixel as the example shown in Fig. 10.

Fig. 10

Watermark image and carrier image. a $1\times 1$ watermark image, b $2\times 2$ carrier image

3.1 Embedding procedure

Proposed embedding procedure of quantum watermarking shown in Fig. 11(a) is as follows.

• 1. Transform a classical carrier image with $2^{n}\times 2^{n}$ size and 8-bit gray scale into a quantum image by the NEQR $\left| C \right\rangle$.

• 2. Expand a classical watermark image with $2^{n-1}\times 2^{n-1}$ size and 8-bit gray scale to an image with $2^{n}\times 2^{n}$size and 2-bit gray scale. An example is shown in Fig. 12 (where n = 1), as we can see, the 8-bit string is divided into four 2-bit strings.

• 3. Transform the expanded watermark image into a quantum image by the NEQR $\left| W \right\rangle$.

• 4. Scramble the expanded watermark image to a meaningless image $\left| {{W}'} \right\rangle$ through Arnold scrambling.

• 5. Embed the watermark image into the carrier image according to the embedding procedure shown in Fig. 11a to obtain watermarked image $\left| {C{W}'} \right\rangle$ and generate the extracting key image $K_1 ,K_0$.

• 6. Transform$\left| {C{W}'} \right\rangle$ into a classical digital watermarked image through quantum measurement.

Fig. 11

Procedures of proposed quantum watermarking scheme. a Embedding procedure of quantum watermarking and b extracting procedure of quantum watermarking

Fig. 12

An example of expanding a watermark image from $1\times 1$ size into $2 \times 2$ size

3.1.1 Quantum image preparing works

The watermark image with $2^{n-1}\times 2^{n-1}$ size and 8-bit gray scale is firstly expanded to an image with $2^{n}\times 2^{n}$ size and 2-bit gray scale; thus, a 8-bit string is divided into four 2-bit strings. Then, the expanded image is transformed into the quantum image $\left| W \right\rangle$ by the NEQR as shown in Eq. (6).

$$\begin{aligned} \left| W \right\rangle =\frac{1}{2^{n}}\sum _{YX=0}^{2^{2n}-1} {\left| {W}_{YX} \right\rangle } \otimes \left| {YX} \right\rangle =\frac{1}{2^{n}}\sum _{Y=0}^{2^{n}-1} {\sum _{X=0}^{2^{n}-1} {\mathop \otimes \limits _{k=0}^1 } } \left| {W_{YX}^k } \right\rangle \otimes \left| {YX} \right\rangle \end{aligned}$$

(6)

For example, the watermark image with $1\times 1$ image size and 8-bit gray scale is expanded to the image with $2\times 2$ image size as shown in Fig. 12. Since the value of gray scale 183 is expressed as $(10110111)_2$ by 8 bits, the expanded image consists of four pixels: $(10)_2 ,(11)_2 ,(01)_2$ and $(11)_2$, respectively. Then, we can obtain the NEQR as follows.

$$\begin{aligned} \left| W \right\rangle =\frac{1}{2}\left( {\left| {10} \right\rangle \left| {00} \right\rangle +\left| {11} \right\rangle \left| {01} \right\rangle +\left| {01} \right\rangle \left| {10} \right\rangle +\left| {11} \right\rangle \left| {11} \right\rangle } \right) \; \end{aligned}$$

Transform the carrier image into the NEQR as shown in Eq. (7).

$$\begin{aligned} \left| \hbox {C} \right\rangle =\frac{\hbox {1}}{\hbox {2}^{\hbox {n}}}\sum _{i=0}^{2^{2n}-1} {\left| {C_i } \right\rangle } \otimes \left| i \right\rangle =\frac{\hbox {1}}{\hbox {2}^{\hbox {n}}}\sum _{YX=0}^{2^{2n}-1} {\mathop \otimes \limits _{k=0}^{q-1} \left| {C_{YX}^k } \right\rangle } \otimes \left| {YX} \right\rangle \end{aligned}$$

(7)

where

$$\begin{aligned} C_{YX}=C_{YX}^{q-1} C_{YX}^{q-2} \ldots C_{YX}^0. \end{aligned}$$

The prepared quantum key image ${K}_{0}$ and ${K}_{1}$ are expressed by Eq. (8)

$$\begin{aligned} \left| {K_1 } \right\rangle= & {} I\otimes H^{\otimes n}\left| 0 \right\rangle ^{\otimes (n+1)}=\frac{1}{2^{n}}\sum _{i=0}^{2^{2n}-1} {\left| {C_i^{k1} } \right\rangle } \otimes \left| i \right\rangle ,\left| {C_i^{k1} } \right\rangle =\left| 0 \right\rangle \nonumber \\ \left| {K_0 } \right\rangle= & {} I\otimes H^{\otimes n}\left| 0 \right\rangle ^{\otimes (n+1)}=\frac{1}{2^{n}}\sum _{i=0}^{2^{2n}-1} {\left| {C_i^{k0} } \right\rangle } \otimes \left| i \right\rangle ,\;\left| {C_i^{k0} } \right\rangle =\left| 0 \right\rangle \end{aligned}$$

(8)

3.1.2 Arnold scrambling

In order to enhance the confidentiality, we adopt two-step process. In the first step, a watermark with $2^{n-1}\times 2^{n-1}$ image size and 8-bit gray scale is expanded to an image with $2^{n}\times 2^{n}$ image size and 2-bit gray scale as shown in Fig. 12. In the second step, the watermark image $\left| W \right\rangle$ is scrambled into a disorder image $\left| {{W}'} \right\rangle$ through Arnold scrambling as shown in Fig. 13.

Fig. 13

Arnold scrambling of watermark image

Fig. 14

Quantum watermarking embedding procedure

Fig. 15

Embedding circuit

3.1.3 Implement embedding

A scrambled watermark image $\left| {{W}'} \right\rangle$ is embedded into a carrier image $\left| C \right\rangle$ through the LSB method as shown in Fig. 14. Therein, the output qubits $|{c_0}\rangle$, $|{c_1}\rangle$ and $|{c_2}\rangle$ are acted as the control qubits of Embedding Circuit. As shown in Fig. 15, under the control qubits, $|{W_{YX}^{'0}}\rangle$ and $|{W_{YX}^{'1}}\rangle$ of $|{W_{YX}^{'}}\rangle$ are used to substitute the least significant qubit $|{C_{YX}^{0}}\rangle$ of $|{C_{YX}}\rangle$ twice. The QE module is a quantum circuit as shown in Fig. 9a. Firstly, the three QE modules are used to compare the coordinates of the carrier image $\left| C \right\rangle$, the scrambled expanded watermark image $\left| {{W}'} \right\rangle$, the two prepared key images $\left| {K_1 } \right\rangle$, and $\left| {K_0 } \right\rangle$.

The pixel embedding steps are as follows:

If the coordinates of all the input images are equal, the outputs $\left| {c_0 } \right\rangle$, $\left| {c_1 } \right\rangle$, and $\left| {c_2 } \right\rangle$ of each QE module would be state $\left| 1 \right\rangle$. The qubits$\left| {c_0 } \right\rangle$, $\left| {c_1 } \right\rangle$, and $\left| {c_2 } \right\rangle$ are acted as the control qubits in Fig. 15, which is implemented by the following steps:

If $\left| {{w}_i^{'0} } \right\rangle =\left| {c_i^0 } \right\rangle \oplus \left| {{w}_i^{'0} } \right\rangle$, then $\left| {c_i^0 } \right\rangle =\left| {{w}_i^{'0} } \right\rangle \oplus \left| {c_i^0 } \right\rangle , \left| {C_i^{k0} } \right\rangle =\left| {{w}_i^{'0} } \right\rangle \oplus \left| 0 \right\rangle$. Otherwise, no change will be made.

If $\left| {{w}_i^{'1} } \right\rangle =\left| {c_i^0 } \right\rangle \oplus \left| {{w}_i^{'1} } \right\rangle$, then $\left| {c_i^0 } \right\rangle =\left| {{w}_i^{'1} } \right\rangle \oplus \left| {c_i^0 } \right\rangle ,\left| {C_i^{k1} } \right\rangle =\left| {{w}_i^{'1} } \right\rangle \oplus \left| 0 \right\rangle$. Otherwise, no changes will be made.

By doing these, the watermark image is embedded into the carrier image, and it will generate two key images $\left| {K_1 } \right\rangle$ and $\left| {K_0 } \right\rangle$ at the same time.

Fig. 16

Quantum watermarking extracting procedure

3.2 Extracting procedure

Extracting procedure shown in Fig. 11b is as follows.

• 1. Extract the scrambled expanded watermark image $\left| {{W}'} \right\rangle$ according to the extracting circuit, and the two extracting key images $K_1 ,K_0$ and the watermarked image$\left| {C{W}'} \right\rangle$ are needed.

• 2. Implement the inverse Arnold scrambling $\left| {{W}'} \right\rangle$ to get the expanded watermark image $\left| W \right\rangle$.

• 3. Measure the expanded watermark quantum image$\left| W \right\rangle$to get the corresponding classic image, and further implement the inverse expanded transformation to get the watermark image.

3.2.1 Implement extracting

A scrambled watermark image $\left| {{W}'} \right\rangle$ is extracted from the carrier image $\left| C \right\rangle$ through the LSB method as shown in Fig. 16. Therein, the output qubits $|{c_{0}}\rangle$ and $|{c_{1}}\rangle$ are acted as the control qubits of Extracting Circuit. As shown in Fig. 17, under the control qubits, $\left| {C_i^{k0} } \right\rangle$ and $\left| {C_i^{k1} } \right\rangle$ of $\left| {c_i^0 } \right\rangle$ are used to retrieve the pixel qubits $\left| {{W}_{YX}^{'1} } \right\rangle$ and $\left| {{W}_{YX}^{'0} } \right\rangle$. The two QE modules are used to compare the coordinates of the watermarked image $\left| {C{W}'} \right\rangle$, and the two key images $\left| {K_1 } \right\rangle$, $\left| {K_0 } \right\rangle$.

The pixel extracting steps are as follows:

If the coordinates of all the input images are equal, the outputs $\left| {c_0 } \right\rangle$ and $\left| {c_1 } \right\rangle$ of each QE module would be state $\left| 1 \right\rangle$. Then qubits $\left| {c_0 } \right\rangle$ and $\left| {c_1 } \right\rangle$ are acted as the control qubits in Fig. 17, which is implemented by the following steps:

$$\begin{aligned}\left| {{w}_i^{'1} } \right\rangle =\left| {c_i^0 } \right\rangle \oplus \left| 0 \right\rangle , \left| {c_i^0 } \right\rangle =\left| {C_i^{k1} } \right\rangle \oplus \left| {c_i^0 } \right\rangle , \left| {{w}_i^{'0} } \right\rangle =\left| {c_i^0 } \right\rangle \oplus \left| 0 \right\rangle and \left| {c_i^0 } \right\rangle =\left| {C_i^{k0} } \right\rangle \oplus \left| {c_i^0 } \right\rangle .\end{aligned}$$

By doing these, the scrambled expanded watermark image $\left| {{W}'} \right\rangle$ is extracted from the carrier image, and the carrier image $\left| C \right\rangle$ is retrieved at the same time.

Fig. 17

Extracting circuit

3.2.2 Inverse Arnold scrambling

As shown in Fig. 11b, the extracting watermark image is a scrambled image; thus, we need do the inverse Arnold image scrambling to obtain the expanded watermark image $\left| W \right\rangle$. According to Eq. (3), the concrete circuit realizes inverse Arnold scrambling as shown in Fig. 18 where the constant input qubits $\left| 0 \right\rangle$ act as the ancillary qubit.

Fig. 18

Inverse Arnold scrambling

After we obtain the expanded watermark image, we need do the inverse expand operation and quantum measurement to obtain the classic watermark image.

3.3 Measurement

Obviously, the quantum watermark image is quantum superposition state as a composite quantum system composed by $2n+q$ qubits. In order to obtain the classical watermark image, we need do measurements on these states. For a $2^{n}\times 2^{n}$ NEQR watermark image with gray range $[0,\;2^{q-1}]$, the measurement results are some collection of basis states$\left\{ {S_1 ,S_2 ,\ldots ,S_{2(n+m)} } \right\}$dimension Hilbert space. In [36], based on Grover’s algorithm, the probability of pixels could be modified to measure the target pixel with higher probability. It points that we can measure with probability $t_{\mathop {i}\limits ^\wedge }^{2}$ to get the result after certain iterations $\mathop {i}\limits ^\wedge$, where

$$\begin{aligned}&\mathop {i}\limits ^\wedge \approx 0.7962a-0.6057, t_{\mathop {i}\limits ^\wedge }^2 \ge (0.9194+0.0567a^{-1}+0.2302a^{-2}-0.0336a^{-3})^{2},\\&\qquad a=2^{n+\frac{q}{2}} . \end{aligned}$$

In practice, however, the quantum state cannot be practically observed in quantum system because a measurement will destroy the superposition. And what is worse, it is not allowed to make copies of the state and measure each one due to the non-cloning theorem. Hence, it is necessary to repeat the construction of the quantum watermarked image state n times ($n>1$) and measure each one to summarize the measurement results, from which we can estimate the watermark image. For more details, refer to the literature [36].

4 Circuit complexity and simulation experiments

4.1 Circuit complexity

The time complexity of the circuit depends on the number of the basic quantum gate. Literatures [46, 47] pointed out that any reversible gate can be realized using $1\times 1$ NOT gate and $2\times 2$ reversible gates such as Controlled-V, Controlled-V$^{+}$, and Controlled-NOT gate (CNOT). Thus, we take any one-qubit or two-qubit gate as the basic quantum gate, the time complexity of which is 1.

4.1.1 The time complexity of embedding procedure

The watermarking embedding procedure is shown in Fig. 11a. The quantum Arnold scrambling circuit (shown in Fig.13) needs 2 PA-MOD modules and n constant qubits $\left| 0 \right\rangle$. The PA-MOD module contains 1 RHA and ($n-1$) RFA. The circuit realization of RHA is shown in Fig. 4b, the complexity of which is 4. The circuit realization of RFA is shown in Fig. 5a and the complexity is 8. Thus, the complexity of the single PA-MOD is $8n-4$. Therefore, the circuit complexity of Arnold scrambling is ${\hbox {O}}(n)$ and n constant qubits are needed. In realizing embedding procedure steps as shown in Fig. 14, it includes three QE modules and the embedding circuit is shown in Fig. 15. The literatures [48] pointed out that only ($4~k-8$) 2-Control-Not gates were needed to construct a k-Control-Not gate, as well as some assistant qubits. The QE module (see Fig. 9a) contains 4n Controlled-Not gates and one 2n-Controlled-Not gate (it means 2n qubits act as the controlled qubits). Thus, the complexity of single QE is $\mathrm{O}(n)$. Besides, the embedding circuit as shown in Fig. 15 can be regarded as containing six 4-Controlled-Not gates, and the complexity of which is $\mathrm{O}(1)$. Therefore, the circuit complexity of embedding the scrambling expanded watermark image into the carrier image is ${\hbox {O}}(n)$.

4.1.2 The time complexity of extracting procedure

The watermarking extracting procedure is shown in Fig. 11b. In realizing extracting procedure steps as shown in Fig. 16, it includes two QE modules and the extracting circuit is shown in Fig. 17, which can be regarded as containing four 3-Controlled-Not gates, the time complexity of which is around O(1). The quantum inverse Arnold scrambling operation circuit shown in Fig. 17 includes two PS-MOD modules and $n+1$ constant input qubits $\left| 0 \right\rangle$. The single PS-MOD contains a PA module and a PA-MOD module, the time complexity of which is around ${\hbox {O}}(n)$. Thus, the circuit complexity of realizing extracting the scrambling expanded watermark image from the watermarked image is ${\hbox {O}}(n)$.

Therefore, according to the above analysis, the time complexity of watermarking embedding and extracting procedures of the proposed scheme is around ${\hbox {O}}(n)$. Compared to classical image processing, the complexity of the Arnold scrambling and Arnold reverse scrambling is ${\hbox {O}}(2^{2n})$ for a $2^{n}\times 2^{n}$ sized image. The complexity of the watermark embedding and extracting algorithm based on the least significant bit is also $\mathrm{O}(2^{2n})$ for a $2^{n}\times 2^{n}$sized image. Thus, the complexity of the scheme in classic image processing is $\mathrm{O}(2^{2n})$ for a $2^{n}\times 2^{n}$ sized image. However, in quantum image processing, if we omit the quantum image processing and measurement procedure, the quantum circuit cost is around $\mathrm{O}(n)$, which is very low for quantum image processing compared to classical image processing.

4.2 Simulation experiments analysis

This section gives the simulation experiment results of the proposed watermarking scheme. All experiments are simulated on the MATLAB R2014b. Three images named “baboon,” “cameraman,” and “Lena” are used. The sizes of carrier image and watermark image are $256\times 256$ and $128\times 128$, respectively.

The peak signal-to-noise ratio (PSNR) is one of the most used quantities to compare the fidelity of a stego image with its original version. PSNR is defined as follows:

$$\begin{aligned} PSNR=10\;\log _{10} \frac{MAX_I^2 }{MSE}=20\;\log \;\frac{MAX_I }{\sqrt{MSE}} \end{aligned}$$

(9)

Therein, MAX$_{I}$ is the maximum gray-level value of the image. MSE is the mean squared error for two $m\times n$ gray-scale images: a carrier image I and its watermarked image version O, as defined in Eq. (10).

$$\begin{aligned} MSE=\frac{1}{mn}\;\sum _{i=0}^{m-1} {\sum _{j=0}^{n-1} {\left[ {I(i,j)-O(i,j)} \right] ^{2}} } \end{aligned}$$

(10)

The experimental results are shown in Fig. 19. The size of the watermark image is $128\times 128$, and the size of the carrier image is $256\times 256$.

Fig. 19

Result of quantum watermarking experiments. a Carrier image, b watermark image, c watermarked image, d watermark image, e watermarked image, f carrier image, g watermark image, h watermarked image, i watermark image, j watermarked image

Comparing to the carrier image of the experimental shown in Fig. 19, Table 2 shows the visual quality of the watermarked images. The visual quality PSNR is all around 54 dB. Therefore, we can conclude that the PSNR by our scheme is obviously higher than previous studies in [39] (around 30 dB) and [40] (around 44 dB).

In a noiseless environment, our proposed scheme can extract an error-free watermark image. However, considering the complexity and difficulty to describe the noise environment in the quantum system, it is unreasonable to take it for granted that the noise types in classical image (macroscopic world) exist in quantum image (microscopic world). Thus, the robustness analysis of the watermark scheme in the noise environment is not discussed in this paper.

Table 2 Similarity of watermarked images of our proposed scheme (PSNR [dB])

5 Conclusions

In this paper, a quantum gray-scale watermarking scheme using Arnold scrambling and LSB method based on NEQR is proposed. We assume that the size of carrier image and watermark image is $2n\times 2n$ and $n\times n$, respectively.

Watermark embedding and extracting procedures consist of two processes: comparing coordinates and replacing pixel bit. Before realizing the watermarking scheme, a series of quantum modules are designed to realize special functions, which mainly include QE, PA-MOD, and PS-MOD. The QE is used to compare the coordinates of all input images whether they are equal or not. The PA-MOD and PS-MOD are used to scramble and recover the watermark image, respectively. Besides, comparing with the other watermarking schemes, the experiment results show that our proposed scheme is superior to other schemes whether or not in noisy environment.