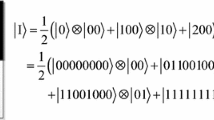Quantum realization of the nearest-neighbor interpolation method for FRQI and NEQR

Abstract

This paper is concerned with the feasibility of the classical nearest-neighbor interpolation based on flexible representation of quantum images (FRQI) and novel enhanced quantum representation (NEQR). Firstly, the feasibility of the classical image nearest-neighbor interpolation for quantum images of FRQI and NEQR is proven. Then, by defining the halving operation and by making use of quantum rotation gates, the concrete quantum circuit of the nearest-neighbor interpolation for FRQI is designed for the first time. Furthermore, quantum circuit of the nearest-neighbor interpolation for NEQR is given. The merit of the proposed NEQR circuit lies in their low complexity, which is achieved by utilizing the halving operation and the quantum oracle operator. Finally, in order to further improve the performance of the former circuits, new interpolation circuits for FRQI and NEQR are presented by using Control-NOT gates instead of a halving operation. Simulation results show the effectiveness of the proposed circuits.

1 Introduction

Along with the bright prospect of quantum computers [1, 2], quantum image processing has inspired interest by researchers in recent years. Until the arrival of practical quantum computers, the first task in this direction was the construction of a pattern for capturing and storing the images on quantum computers. A great number of research results concerning quantum image representation exist in the literature, i.e., qubit lattice [3], entangled image [4], real ket [5], a flexible representation for quantum images (FRQI) [6], multi-channel representation of quantum image (MCRQI) [7], quantum representation for log-polar images [8] and a novel enhanced quantum representation (NEQR) [9].

Among numerous quantum image models, FRQI and NEQR, which capture information about colors and their corresponding positions in an image into a normalized quantum state, are the two most important and convenient models in considering the way in which a gray image is encoded under rectangular coordinate system.

The FRQI method contains the color information and corresponding position information of every pixel in an image into the entangled quantum state [6]. Many quantum image processing algorithms have been proposed based on FRQI, such as quantum image watermarking [10–12], quantum image encryption [13–16], quantum image scrambling [17–19] and the geometric transformations on quantum images (GTQI) [20]. For the convenience of frequency domain research, quantum Fourier transform [21], quantum wavelet transform [22] and quantum discrete cosine transform [23, 24] were given.

In 2013, Zhang improved the storage mode for color information in FRQI and named the new representation as NEQR [9]. The major difference between the two is that in NEQR the color encoding is a binary form of $\left| {c_{yx} } \right\rangle = \left| {c_{yx}^{q - 1} c_{yx}^{q - 2} \cdots c_{yx}^0 } \right\rangle$, while in FRQI it is in the shape of $\left( {\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle } \right)$ corresponding to a classical image sized $2^n \times 2^n$ and with a gray range of $\left[ {0,2^q - 1} \right]$. Because of the difference, the number of qubits needed for encoding FRQI and NEQR is also distinct and is $2n + 1$ and $2n + q$, respectively. Also, the preparation process for FRQI and NEQR is different. Taking these characteristics of the NEQR binary color encoding information into consideration, selections of the algorithms have been examined, such as quantum image translation algorithm [25], scaling transform [26] and local feature point extraction algorithm [27].

Image geometric transformations mainly contain translation, transposition, mirroring and scaling, in which the first three transformations have been thoroughly researched based on FRQI [20]. For the first three transformations, each pixel of the output quantum image has a specific pixel corresponding to the input quantum image. But for a scaling operation, such as expanding the quantum image, the relationship between the pixels of the output quantum image and the pixels of the input quantum image is not bijective. Unfortunately, none of these studies has been done concerning FRQI. The first aim of this paper is to test the reliability of the scaling transformation regarding FRQI.

Recently, based on the improved novel enhanced quantum representation (INEQR), Jiang et al. [26] started the research of the quantum image nearest-neighbor interpolation method. However, the complexity regarding the quantum image scaling down circuit is $O\left( {q \cdot 2^n \cdot \left( {2n + m} \right) } \right)$, with n and m representing an image that is scaled down from $2^{n + m}$ to $2^{n}$. Further work regarding the nearest-neighbor interpolation method for NEQR should be researched. This paper plans to provide two NEQR circuits with lower complexity to improve the previous quantum circuit in [26].

The following advantages of NEQR and FRQI are suggested to make them suitable for quantum image scaling algorithms:

• (1) FRQI and NEQR acquire color information and their corresponding positions in an image into a normalized quantum state. Thus, quantum Control-NOT gate and other simple quantum gates are used to flexibly link color and location information, providing an easy to process image for the user.

• (2) FRQI and NEQR both use a binary qubit basis to encode position information. It is easy to design unitary operators to change the number of positions for binary qubits, which achieves the aim of changing the size of an image.

• (3) For FRQI, colors are encoded in the form of $\left( {\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle } \right)$ which makes it easier to use quantum rotation gates to prepare pixels values.

• (4) For NEQR, colors are stored in binary quantum sequence which is similar to the representations of classical digital images. This makes it relatively easy to apply image interpolation algorithms from classical computers to quantum computers.

In this paper, a substantially different method for the quantum realization is proposed for nearest-neighbor interpolation of NEQR and FRQI. In the proposed method, the reliance on using multi-control-qubit-NOT gate to copy color information is no longer necessary. The key idea is how to assign a color value for the interpolation mapping relationship between the position of the original and the interpolated image if the size of an empty interpolated image and the color, and the position of original image are known. A method of designing unitary operators to prepare pixel values of original image is resorted to, which is the equivalent to the pixel of resulting image. Specifically, the FRQI interpolation problem is solved by utilizing a quantum control rotation gate to regenerate color values. The NEQR problem is figured out using a quantum oracle operator to prepare color. From a circuit’s complexity perspective, the method proposed in this paper is simpler than previous NEQR results in [26].

The contributions of this paper are listed as follows: First, by using a halving operation or Control-NOT gate, the relationship between original image’s position and interpolated image’s position is established. Second, the halving operation and control rotation gates are utilized to construct FRQI interpolation circuit. Third, the halving operation and the quantum oracle operation are introduced to design the circuit of NEQR interpolation method, with the benefit of improving the complexity of the previous circuit. Forth, Control-NOT gate is utilized to improve the performance of the former designed FRQI and NEQR circuits.

This paper is organized as follows: Sect. 2 briefly introduces related works, Sect. 3 explains the feasibility of the nearest-neighbor interpolation method for NEQR and FRQI, and in Sect. 4, the proposed quantum circuits are detailed. The further improvements of the quantum circuits are then given in Sect. 5. The simulation experiment and its discussion are shown in Sect. 6. The conclusion and future directions are finally drawn in Sect. 7.

2 Preliminaries

2.1 FRQI

Inspired by the pixel representation for images in classical computers, FRQI on quantum computers was proposed in [6], in which the quantum image corresponding to a classical image sized $2^n\times 2^n$ is defined by a quantum encoding state about the image color and position.

FRQI was proposed by Le et al. in the form of a normalized state which captures information about colors and their corresponding positions in the images. The quantum representation for an $2^n\times 2^n$ image is described as follows:

$$\begin{aligned} \left| {I\left( \theta \right) } \right\rangle= & {} \frac{1}{{2^n }}\sum \limits _{i = 0}^{2^{2n} - 1} {\left( {\cos \theta _i \left| 0 \right\rangle + \sin \theta _i \left| 1 \right\rangle } \right) \otimes \left| i \right\rangle } \nonumber \\= & {} \frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left( {\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle } \right) \otimes \left| {yx} \right\rangle } } \end{aligned}$$

(1)

where $\theta _i \in \left[ {0,\frac{\pi }{2}} \right]$, $i = 0,1, \ldots 2^{2n} - 1$, $\cos \theta _i \left| 0 \right\rangle + \sin \theta _i \left| 1 \right\rangle$ encodes the color information, and $\left| i \right\rangle$ encodes the corresponding position of the quantum image. The position information includes two parts: the vertical and horizontal coordinates. Considering a quantum image in the 2n-qubit system,

$$\begin{aligned}&\left| i \right\rangle = \left| y \right\rangle \left| x \right\rangle = \left| {y_{n - 1} y_{n - 2} \cdots y_0 } \right\rangle \left| {x_{n - 1} x_{n - 2} \cdots x_0 } \right\rangle \nonumber \\&\quad x,y \in \left\{ {0,1, \ldots 2^n - 1} \right\} ,\left| {x_j } \right\rangle ,\left| {y_j } \right\rangle \in \left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} ,\quad j = 0,1, \ldots n - 1 \end{aligned}$$

(2)

where $\left| y \right\rangle = \left| {y_{n - 1} y_{n - 2} \cdots y_0 } \right\rangle$ encodes the first n-qubits along the vertical location and $\left| x \right\rangle = \left| {x_{n - 1} x_{n - 2} \cdots x_0 } \right\rangle$ encodes the second n-qubits along the horizontal axis. In addition, [6] provided a polynomial preparation theorem that proves the existence of a unitary preparation process which can use a polynomial number of simple operators to transform quantum computers from the initial state to the FRQI state. The FRQI state is a normalized state, i.e, $\left\| {\left| {I\left( \theta \right) } \right\rangle } \right\| = 1$ as given by $\left\| {\left| {I\left( \theta \right) } \right\rangle } \right\| = \frac{1}{{2^n }}\sqrt{\sum \limits _{i = 0}^{2^{2n} - 1} {\left| {\cos ^2 \theta _i + \sin ^2 \theta _i } \right| } } = 1$.

An example of a $2 \times 2$ FRQI image is shown in Fig. 1.

Fig. 1

A simple $2 \times 2$ FRQI image and its FRQI state

2.2 NEQR

Based on the analysis of existing FRQI quantum image representation, a novel enhanced quantum representation (NEQR) for digital images is proposed [9]. NEQR uses the basis state of a qubit sequence to store the grayscale value of each pixel in the image for the first time, instead of the probability amplitude of a qubit, as in FRQI. Also NEQR employs two entangled qubit sequences to store the grayscale and position information and stores the whole image in the superposition of the two qubit sequences. Suppose that the gray range of an image is $\left[ {0,2^q - 1} \right]$, binary sequence $C_{yx}^{q - 1} C_{yx}^{q - 2} \cdots C_{yx}^1 C_{yx}^0$ encodes the grayscale value $f\left( {y,x} \right)$ of the corresponding pixel $\left( {y,x} \right)$ as in Eq. (3):

$$\begin{aligned} f\left( {y,x} \right) = C_{yx}^{q - 1} C_{yx}^{q - 2} \cdots C_{yx}^1 C_{yx}^0 ,C_{yx}^k \in \left[ {0,1} \right] ,f\left( {y,x} \right) \in \left[ {0,2^q - 1} \right] \end{aligned}$$

(3)

The representative expression of a quantum image for a $2^n \times 2^n$ image is described as follows [9]:

$$\begin{aligned} \left| I \right\rangle = \frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left| {f\left( {y,x} \right) } \right\rangle \left| y \right\rangle \left| x \right\rangle } } \end{aligned}$$

(4)

And the same is for FRQI, where the position information includes both the vertical y and the horizontal x coordinates. NEQR uses the basis qubit sequence to store the grayscale information for each pixel in an image. Some digital image processing operations, for example, certain complex color operations, partial color operations and statistical color operations, can be conveniently performed in light of NEQR [27].

A $4 \times 4$ NEQR quantum image is shown in Fig. 2. $f\left( {y,x} \right)$ denotes the grayscale value of pixel $\left( {y,x} \right)$, which is stored as the basis state $\left| {f\left( {y,x} \right) } \right\rangle$ of a qubit sequence. Compared with the example of FRQI in Fig. 1, the obvious difference is that NEQR utilizes the basis state of qubit sequence to represent the gray scale of pixels instead of probability amplitude of a single qubit in FRQI.

Fig. 2

A $4 \times 4$ NEQR quantum image

Figure 3 illustrates a $2 \times 2$ grayscale image and its representative expression in NEQR. In this figure, because the gray scale ranges between 0 and 255, eight qubits are needed in NEQR to store the grayscale information for the pixels. Hence, NEQR needs $q + 2n$ qubits to represent a $2^n \times 2^n$ image with gray range $2^q$.

Fig. 3

A $2 \times 2$ example image and its representative expression in NEQR

The major difference between FRQI and NEQR is mainly in the color encoding stage. For FRQI, color encoding is in the form of $\left( {\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle } \right)$ and obviously 1 qubit to encode is needed. NEQR color encoding is in the shape of $\left| {c_{yx} } \right\rangle = \left| {c_{yx}^{q - 1} c_{yx}^{q - 2} \cdots c_{yx}^0 } \right\rangle$ and it requires q qubit. So the number of qubits required for encoding FRQI and NEQR is $2n + 1$ and $2n + q$, respectively. Due to the different pattern of color encoding state, the preparation process for NEQR and FRQI is also distinct [6, 9].

2.3 Classical nearest-neighbor interpolation method

Nearest-neighbor interpolation makes a unique contribution to classical image scaling transformation, which is a basic image scaling method and the basis of the bilinear interpolation method. Now, the principle of classical nearest-neighbor interpolation method is reviewed.

Suppose that there is an image, with a size that is $M \times N$. M is the width of the image, and N is the height of the image. The interpolated image with a size that is $M' \times N'$. The principle can be described in the following way: Pixel value in position $\left( {x',y'} \right)$ of the interpolated image equals to the pixel value of the original image in $\left( {x,y} \right)$. The coordinates restored from the original image can be calculated according to the following formula:

$$\begin{aligned} x = \left\lfloor {x' \times \left( {\frac{M}{{M'}}} \right) } \right\rfloor ,\quad y = \left\lfloor {y' \times \left( {\frac{N}{{N'}}} \right) } \right\rfloor \end{aligned}$$

(5)

Nearest-neighbor interpolation has the advantage of fewer calculations. The algorithm is also simple, which leads to a faster operation. Expanding the classical image operation to the quantum image processing is meaningful [17]. The quantum realization of nearest-neighbor interpolation method is concentrated in this paper.

2.4 Halving operation

Recently, Zhang et al. [27] have designed a quantum circuit for the halving operation $U_H$ based on NEQR. This operation makes the gray scale of all pixels reduced by half, and all the qubits in the color sequence cycle shift downwards. Consider the following NEQR image with a color encoding: $\left| I \right\rangle _\mathrm{NEQR} = \frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left| {f\left( {y,x} \right) } \right\rangle \otimes \left| {yx} \right\rangle } }$.

The concrete transformations of the quantum operation $U_H$ on NEQR are shown in Eq. (6), where $\left| {f\left( {y,x} \right) } \right\rangle = \left| {C_{yx}^{q - 1} \cdots C_{yx}^i \cdots C_{yx}^0 } \right\rangle = \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle$.

$$\begin{aligned} \begin{array}{l} {\quad }U_H \left( {\left| {I_\mathrm{NEQR} } \right\rangle } \right) \\ = U_H \left( {\frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left| {f\left( {y,x} \right) } \right\rangle \left| y \right\rangle \left| x \right\rangle } } } \right) \\ = U_H \left( {\frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle \left| y \right\rangle \left| x \right\rangle } } } \right) \\ = \frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {U_H \left( {\mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle } \right) \left| y \right\rangle \left| x \right\rangle } } \\ = \frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left( {\left| {C_{yx}^0 } \right\rangle \mathop \otimes \limits _{i = 0}^{q - 2} \left| {C_{yx}^{i + 1} } \right\rangle \left| y \right\rangle \left| x \right\rangle } \right) } } \\ \mathrm{{ = }}\frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left( {\left| {C_{yx}^0 } \right\rangle \left| {f\left( {y,x} \right) / 2} \right\rangle \left| y \right\rangle \left| x \right\rangle } \right) } } \\ \end{array} \end{aligned}$$

(6)

In Eq. (6), because NEQR has the form of $\frac{1}{{2^n }}\sum \nolimits _{y = 0}^{2^{n} - 1} {\sum \nolimits _{x = 0}^{2^{n} - 1} {\left| {f\left( {y,x} \right) } \right\rangle \left| y \right\rangle \left| x \right\rangle } }$, the first equal sign sets up. The second equal sign holds because the color information of the NEQR has the form of $\mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle$. The third equal sign can be verified because halving operation $U_H$ only acts on the color qubits sequence. Again, the halving operation $U_H$ implements the function of shifting $q - 1$ qubits to the right. That is $U_H \left( {\mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle } \right) = \left| {C_{yx}^0 } \right\rangle \mathop \otimes \limits _{i = 0}^{q - 2} \left| {C_{yx}^{i + 1} } \right\rangle$. So the fourth sign establishes. The fifth sign holds since $\mathop \otimes \limits _{i = 0}^{q - 2} \left| {C_{yx}^{i + 1} } \right\rangle = \left| {f\left( {y,x} \right) /2} \right\rangle$. That is to say, the final $q - 1$ color encoding qubits carry the halving color information $\left| {f\left( {y,x} \right) / 2} \right\rangle$. For a quantum image in the model NEQR, this operation will make all the qubits in the color sequence cycle shift down.

Fig. 4

Quantum circuit of the halving operation [27]

The specific quantum circuit concerning the halving operation $U_H$ is shown in Fig. 4. The left side of Fig. 4 is the input quantum state $\left| {C_{q - 1} C_{q - 2} \cdots C_1 C_0 } \right\rangle$. The concrete procedure of Fig. 4 can be explained by Eq. (7).

$$\begin{aligned} \begin{array}{l} \left| {C_{q - 1} C_{q - 2} \cdots C_2 C_1 C_0 } \right\rangle \rightarrow \left| {C_{q - 1} C_{q - 2} \cdots C_2 C_0 C_1 } \right\rangle \rightarrow \left| {C_{q - 1} C_{q - 2} \cdots C_0 C_2 C_1 } \right\rangle \\ \rightarrow \cdots \rightarrow \left| {C_{q - 1} C_0 C_{q - 2} \cdots C_3 C_2 C_1 } \right\rangle \rightarrow \left| {C_0 C_{q - 1} C_{q - 2} \cdots C_3 C_2 C_1 } \right\rangle \\ \end{array} \end{aligned}$$

(7)

From Fig. 4 and Eq. (7), the first swap gate exchanging $\left| {C_1 } \right\rangle$ with $\left| {C_0 } \right\rangle$ can be realized. The second quantum swap gate exchanging $\left| {C_2 } \right\rangle$ with $\left| {C_0 } \right\rangle$ and the final $q - 1$th quantum swap gate exchanging $\left| {C_q-1 } \right\rangle$ with $\left| {C_0 } \right\rangle$ are fulfilled. Finally, the circuit outputs $\left| {C_0 C_{q - 1} C_{q - 2} \cdots C_3 C_2 C_1 } \right\rangle$ are implemented under the action of the halving operation $U_H$.

There is $\left| {C_0 C_{q - 1} C_{q - 2} \cdots C_3 C_2 C_1 } \right\rangle = \left| {C_0 } \right\rangle \left| C/2 \right\rangle$, since $\left| {C_{q - 1} C_{q - 2} \cdots C_3 C_2 C_1 } \right\rangle = \left| C/2 \right\rangle$. It signifies that the halving operation $U_H$ implements the function of shifting $q - 1$ qubits to the right. Just like a classical binary bit shift operation, the binary bit shift to the left (or right) means expanding (or reducing) twice the number, and the quantum halving operation can be seen as a qubit shift operation.

We should note that the circuit of halving operation in Fig. 4 is composed of $q-1$ number of quantum swap gates. Obviously, many quantum swap gates are used to construct halving operation, and it is the disadvantage of halving operation.

Now correspondingly, the halving operation about x coordinate and y coordinate which are shown in Eqs. (8) and (9) is given.

$$\begin{aligned} U_{H_x } \left( {\left| {x'} \right\rangle } \right)= & {} U_{H_x } \left( {\mathop \otimes \limits _{i = 0}^{n + m - 1} \left| {x'_i } \right\rangle } \right) = \left| {x'_0 } \right\rangle \mathop \otimes \limits _{i = 0}^{n + m - 2} \left| {x'_{i + 1} } \right\rangle \mathrm{{ = }}\left| {x'_0 } \right\rangle \left| {x'}/2 \right\rangle \end{aligned}$$

(8)

$$\begin{aligned} U_{H_y } \left( {\left| {y'} \right\rangle } \right)= & {} U_{H_y } \left( {\mathop \otimes \limits _{i = 0}^{n + m - 1} \left| {y'_i } \right\rangle } \right) = \left| {y'_0 } \right\rangle \mathop \otimes \limits _{i =0 }^{n + m - 2} \left| {y'_{i + 1} } \right\rangle \mathrm{{ = }}\left| {y'_0 } \right\rangle \left| {y'}/2 \right\rangle \end{aligned}$$

(9)

Taking $x'$ as an input to the circuit shown in Fig. 5, the circuit realizes the aim of the halving operation about the x coordinate.

Fig. 5

Quantum circuit of the halving operation about x coordinates

With respect to the halving operation about the y coordinate, it is identical to the halving operation about the x coordinate so the details about it are not needed to be addressed here.

The halving operation circuit about the x coordinate is composed of $n+m-1$ quantum swap gates. Under the conditions of choosing the Control-NOT gate to be the basic unit, one quantum swap gate can be constructed by 3 Control-NOT gates. Hence, the complexity of the circuit in Fig. 5 is $O\left( {3(n + m - 1)} \right)$.

3 Feasibility and rationality of quantum image nearest-neighbor interpolation

In this paper, we aim to construct the quantum circuits of the nearest-neighbor interpolation method for FRQI and NEQR. Therefore, the first problem is how to prove its practicality for FRQI and NEQR.

There are only few works on the nearest-neighbor interpolation method for NEQR and FRQI. Jiang et al. [26] proposed the first nearest-neighbor interpolation method for INEQR. INEQR is a new quantum image representation, but actually, it is the generalization of NEQR, which describes non-square NEQR image. In their scheme, according to the scale ratio, color information of the interpolated image is set as the same value with the color information of the original image. Their studies maybe have been more reasonable if they had integrated a theoretical derivation corresponding to the classical image’s nearest-neighbor interpolation considering this situation.

Before elaborating more on the quantum realization of the nearest-neighbor interpolation for FRQI and NEQR, the key idea of the proposed circuits mathematically in Eq. (10) is explained.

$$\begin{aligned} \begin{array}{l} x = \frac{{x'}}{{2^m }},y = \frac{{y'}}{{2^m }} \\ \left| {C_{y'x'} } \right\rangle = \left| {C_{yx} } \right\rangle \\ \underbrace{\left| {x'} \right\rangle \left| {y'} \right\rangle \left| 0 \right\rangle }_\mathrm{empty\ image} \rightarrow \underbrace{\left| {x'} \right\rangle \left| {y'} \right\rangle \left| {C_{y'x'} } \right\rangle }_\mathrm{resulting\ image} \\ \end{array} \end{aligned}$$

(10)

From Eq. (10), it should be observed that in order to prepare the color information $\left| {C_{y'x'} } \right\rangle$ for all the pixels in the resulting image, what actually is prepared is the pixel value in position $\left( {x,y} \right)$ of the original image. One reason for this approach is that the two different positions share the same pixel value. That is, once a position $\left( {x,y} \right)$ has been allocated to a color value $\left| {C_{yx} } \right\rangle$, the value would be used again and assigned to pixel $\left( {x',y'} \right)$ in the resulting image. Other reason for this is that for a given original image, its dimension is known and all the pixels would have fixed color values. At the same time, the dimension of the resulting image is known. Therefore, $x'$ and $y'$ can be considered as the input state when designing quantum circuits. Under the guidance of this key idea, the qualification process has been built.

Using the halving operation described by Zhang et al. [27], the reasonability of the nearest-neighbor interpolation method for quantum image can be proven.

Theorem 1

Nearest-neighbor interpolation method generated by Eq. (10) is rational for quantum images $\mathrm{FRQI}$ and $\mathrm{NEQR}$.

Proof

Assume that the original two quantum images $\left| {I_\mathrm{FRQI} } \right\rangle$ and $\left| {I_\mathrm{NEQR} } \right\rangle$ are both of size $2^n \times 2^n$ and have a gray range $\left[ {0, 2^q - 1} \right]$. The two image expressions are shown in Eq. (11).

$$\begin{aligned} \left| {I_\mathrm{FRQI} } \right\rangle= & {} \frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left( {\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle } \right) \otimes \left| {yx} \right\rangle } } \nonumber \\ \left| {I_\mathrm{NEQR} } \right\rangle= & {} \frac{1}{{2^n }}\sum \limits _{y = 0}^{2^n - 1} {\sum \limits _{x = 0}^{2^n - 1} {\left| {C_{yx} } \right\rangle } \otimes \left| {yx} \right\rangle } \end{aligned}$$

(11)

Also suppose the dimension of the resulting quantum image $\left| {I_{\mathrm{int}}} \right\rangle$ is $2^{n + m} \times 2^{n + m}$. In the following analysis, the concrete feasibility of nearest-neighbor interpolation for FRQI and NEQR is proven.

Case 1 Nearest-neighbor interpolation is reasonable for FRQI in (11) with the above assumption.

• (1) Problem 1: the interpolation mapping relationship between the pixel of resulting image and original image.

According to Eq. (5), we derive Eq. (12).

$$\begin{aligned} x = x' \times \left( {\frac{{2^n }}{{2^{n + m} }}} \right) = \frac{{x'}}{{2^m }}, y = y' \times \left( {\frac{{2^n }}{{2^{n + m} }}} \right) = \frac{{y'}}{{2^m }} \end{aligned}$$

(12)

where $x'=x'_{n + m - 1} \cdots x'_1 x'_0$ and $y'=y'_{n + m - 1} \cdots y'_1 y'_0$.

To get the result of x and y described by Eq. (12), the halving operations $U_{H_x }$ and $U_{H_y }$ are chosen as the unitary operators. The functions of $U_{H_x }$ and $U_{H_y }$ are to reduce the position information by half. Then repeating m times the halving operation about x coordinate $U_{H_x }$ and m times the halving operation about y coordinate $U_{H_y }$, the interpolation mapping relationship between the position of original image and the position of interpolated image has established.

• (2) Problem 2: the color value of the resulting image pixels.

For every pixel $\left( {x',y'} \right)$ in the resulting image, $C_{y'x'}$ is the gray value to be determined, which is equal to the pixel value of the original quantum image in coordinates $\left( {x,y} \right)$. The control rotation gates will be used to prepare the color information, and the detailed structure is described as follows.

Suppose the corresponding color encoding information about the original quantum image is $\theta _{yx} , yx = 0, \ldots 2^{2n} - 1$. Then the concrete function of the rotation gates $R_y \left( {2\theta _{yx} } \right)$ can be described as Eq. (13).

$$\begin{aligned} R_y \left( {2\theta _{yx} } \right) \left| 0 \right\rangle = \left( \begin{array}{cc} \cos \theta _{yx}&{}\quad {\mathrm{- sin}}\theta _{yx} \\ {\mathrm{sin}}\theta _{yx} &{}\quad {\mathrm{cos}}\theta _{yx} \\ \end{array} \right) \left( \begin{array}{l} 1 \\ 0 \\ \end{array} \right) = \left( \begin{array}{l} \cos \theta _{yx} \\ \sin \theta _{yx} \\ \end{array} \right) = \cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle \nonumber \\ \end{aligned}$$

(13)

The quantum control rotation gates $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right)$, $yx = 0, \ldots 2^{2n} - 1$ achieve the aim of preparing the color information $\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle$ in position $\left( {x,y} \right)$ of the original image. Again, the color information $\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle$ equals to the pixel value of the resulting image in $\left( {x',y'} \right)$.

Therefore, for two quantum images $\left| {I_\mathrm{FRQI} } \right\rangle$ and an empty resulting image $\left| {I_{{\mathrm{empty}} } } \right\rangle$, the quantum image nearest-neighbor interpolation can be done via m numbers of the $U_{H_x }$ operation and m numbers of $U_{H_y }$ operation on the two-position qubit sequences $\left| {x'_{n + m - 1} \cdots x'_0 } \right\rangle$ and $\left| {y'_{n + m - 1} \cdots y'_0 } \right\rangle$ and the quantum control rotation gates on the $2n+1$ qubit sequence $\left| 0 \right\rangle ^{ \otimes 2n+1}$. As can be seen in the circuits given later, these ideas render that the nearest-neighbor interpolation for FRQI is feasible.

Case 2 Nearest-neighbor interpolation is reasonable for NEQR in (11) with above assumption.

• (1) Problem 1: the interpolation mapping relationship between the pixel of the resulting image and the original image.

By following similar lines as in the proof of problem (1) in the FRQI case, the problem is solved.

• (2) Problem 2: the color value of the resulting image pixels.

For every pixel $\left( {x',y'} \right)$ in the resulting image, the gray scale $\left| {C_{y'x'} } \right\rangle$ is equal to the pixel value of the original quantum image in coordinates $\left( {x,y} \right)$. Because $C_{yx} \in \left[ {0,2^q - 1} \right]$, it is known that $C_{y'x'} \in \left[ {0,2^q - 1} \right]$, and therefore, q qubits are needed to store the result, which is to say, $\left| {C_{y'x'} } \right\rangle = \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{y'x'}^i } \right\rangle$.

Then, a quantum oracle operator $\varOmega _{yx}$ is designed to compute the result $\left| {C_{y'x'} } \right\rangle = \left| {C_{yx} } \right\rangle$. A quantum oracle operator $\varOmega _{yx}$ can realize the aim of assigning color information $\left| {C_{yx} } \right\rangle$ to the ancillary qubits $\left| 0 \right\rangle ^{ \otimes q}$. The detailed equation can be expressed as Eq. (14).

$$\begin{aligned} \varOmega _{yx} \left| 0 \right\rangle ^{ \otimes q} = \mathop \otimes \limits _{i = 0}^{q - 1} \left( {\varOmega _{yx}^i \left| 0 \right\rangle } \right) = \mathop \otimes \limits _{i = 0}^{q - 1} \left( {\left| {0 \oplus C_{yx}^i } \right\rangle } \right) = \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle = \left| {C_{yx} } \right\rangle \end{aligned}$$

(14)

q oracle operations $\varOmega _{YX}^i ,i = 0, \ldots q - 1$ have the following definition. If $C_{YX}^i = 1$, $\varOmega _{YX}^i$ is a 2n-Control-NOT qubit gate. Otherwise, it is a quantum identity gate. That is to say, every oracle operation $\varOmega _{YX}^i ,i = 0, \ldots q - 1$ is at most a 2n-Control-NOT qubit gate.

Therefore, for two quantum images $\left| {I_\mathrm{NEQR} } \right\rangle$ and the empty resulting NEQR image $\left| {I_{{\mathrm{empty}} } } \right\rangle$, the nearest-neighbor interpolation can be accomplished via m numbers of the $U_{H_x }$ operation and m numbers of $U_{H_y }$ operation on the two-position qubit sequences $\left| {x'_{n + m - 1} \cdots x'_0 } \right\rangle$and $\left| {y'_{n + m - 1} \cdots y'_0 } \right\rangle$ and a quantum oracle operator on the q qubit sequence $\left| 0 \right\rangle ^{ \otimes q}$ to obtain the resulting NEQR image $\left| {I_{{\mathrm{int}} } } \right\rangle$.

From cases (1) and (2), we verified theorem 1.

Note It should be noted that Eq. (12) is not the same as Eq. (5), which needs floor operation. But the halving operation acted on the position qubit sequence of resulting image ensures that (12) has the functionality of the floor operation.

4 Quantum realization of nearest-neighbor interpolation method

In the previous section, using the halving operation, the theoretical feasibility of the nearest-neighbor interpolation method in the model of FRQI and NEQR is discussed. Under the support of theoretical analysis, the quantum circuits of the nearest-neighbor interpolation method for FRQI and NEQR are proposed in this section.

4.1 Quantum realization of nearest-neighbor interpolation method for FRQI

In this subsection, the concrete interpolation circuit in the model of FRQI and the time complexity of the proposed circuit will be discussed.

4.1.1 Concrete FRQI circuit

On the basis of control rotation gates $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right)$, $yx = 0, \ldots 2^{2n} - 1$ and the halving operations $U_{H_x }$ and $U_{H_y }$, the task of constructing the relationship between the coordinates $\left( {x,y} \right)$ of the original quantum image and the coordinates $\left( {x',y'} \right)$ of the resulting image is accomplished. The interpolation circuit for FRQI is designed and shown in Fig. 6. The corresponding modules are displayed in Fig. 7.

Fig. 6

Quantum circuit of nearest-neighbor interpolation method for FRQI

Fig. 7

Quantum circuit of $U_{H_x }$, $U_{H_y }$, $U_{H_x }^{ - 1}$ and $U_{H_y }^{ - 1}$ modules

Next, the concrete flow of quantum circuit in Fig. 6 is considered.

• Step 1. Obtain $x = \frac{{x'}}{{2^m }}$ via m times halving operation $U_{H_x }$ on the $x'$ coordinates. Correspondingly, obtain $y = \frac{{y'}}{{2^m }}$ through m times halving operation $U_{H_y }$ on the $y'$ coordinates.

• Step 2. Choose the method of using the quantum swap gate m times which acts on the x coordinates and the first n qubits $\left| 0 \right\rangle$ to make the first n qubits $\left| 0 \right\rangle$ carry the x coordinates’ information. Meanwhile, execute m times the quantum swap gate between the y coordinates and the second n qubits $\left| 0 \right\rangle$ so the second n qubits $\left| 0 \right\rangle$ brings the y coordinate information.

• Step 3. Employ $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right) , yx = 0, \ldots 2^{2n} - 1$ to produce the color information being carried on the final qubits $\left| 0 \right\rangle$.

• Step 4. Perform the n times quantum swap gate between $y_{n - 1} , \ldots y_0$ coordinates and the second n qubits $\left| 0 \right\rangle$ to make the second n qubits $\left| 0 \right\rangle$ carry its original information. Performing n times quantum swap gate between $x_{n - 1} , \ldots x_0$ coordinates and the second n qubits $\left| 0 \right\rangle$ to make the first n qubits $\left| 0 \right\rangle$ also take its own information in an approximate form.

• Step 5. Execute the m times inverse halving operation $U_{H_x }^{ - 1}$ operated on the x coordinates to recover the $x'$ coordinates information of the interpolated image. Then, perform the m times inverse halving operation $U_{H_y }^{ - 1}$ operated on the y coordinates to recover the $y'$ coordinates information of the resulting image.

• Step 6. Carry out the quantum swap gates between the first ancillary qubit $\left| 0 \right\rangle$ and the final ancillary qubit $\left| 0 \right\rangle$ to make the first qubit $\left| 0 \right\rangle$ carry color information.

Furthermore, the above steps can be summarized as in the following Eq. (15).

$$\begin{aligned} \begin{array}{l} {\mathrm{{ }} \underbrace{\left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \left| 0 \right\rangle }_\mathrm{the \ empty \ FRQI \ image} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle } \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} y'_{n + m - 1} \cdots y'_m } \right\rangle \left| 0 \right\rangle \\ {\quad } \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} 0 \cdots 0} \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} 0 \cdots 0} \right\rangle \left| 0 \right\rangle \\ {\quad } \left| {x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_{n + m - 1} \cdots y'_m } \right\rangle \left| 0 \right\rangle \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} 0 \cdots 0} \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} 0 \cdots 0} \right\rangle \left| 0 \right\rangle \\ {\quad } \left| {x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_{n + m - 1} \cdots y'_m } \right\rangle \left| {f(y,x)} \right\rangle \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} y'_{n + m - 1} \cdots y'_m } \right\rangle \left| 0 \right\rangle \\ {\quad } \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| {f(y,x)} \right\rangle \\ \rightarrow \left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \left| 0 \right\rangle \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| {f(y,x)} \right\rangle \\ \rightarrow \underbrace{\left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \left| {f(y,x)} \right\rangle }_\mathrm{the \ interpolated \ FRQI \ image} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \\ \end{array} \end{aligned}$$

(15)

In summary, Fig. 6 outputs the interpolated FRQI quantum image on the corresponding qubits.

Note 1 There are some quantum control rotation gates that are omitted. The total number of quantum control rotation gates in Fig. 6 is $2^{2n}$.

4.1.2 Circuit complexity

In quantum image processing, the network complexity depends on what is considered to be an elementary gate. Following the discussion in Sect. 2.4, the Control-NOT gate is chosen to be the basic unit. Now the complexity of Fig. 6 will be analyzed.

To each m halving operation, it contains

$$\begin{aligned} \left( {n + m - 1} \right) + \left( {n + m - 2} \right) + \cdots n = \frac{{m\left( {2n + m - 1} \right) }}{2} \end{aligned}$$

(16)

quantum swap gates.

Barenco et al. [28] have pointed out that one quantum swap gate can be constructed by three Control-NOT gates and $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right)$ can be broken down into $2^{2n} - 1$ simple operations $R_y \left( {\frac{{2\theta _{yx} }}{{2^{2n} - 1}}} \right)$, $R_y \left( { - \frac{{2\theta _{yx} }}{{2^{2n} - 1}}} \right)$ and $2^{2n} - 2$ Control-NOT operations. Hence, the network complexity of m times $U_{H_x }$, $U_{H_y }$, $U_{H_x }^{ - 1}$ and $U_{H_y }^{ - 1}$ is $\frac{{3m\left( {2n + m - 1} \right) }}{2}$.

There are $4n + 1$ quantum swap gates, m halving operation $U_{H_x }$, m halving operation $U_{H_y }$, m quantum inverse halving operation $U_{H_x }^{ - 1}$, m quantum inverse halving operation $U_{H_y }^{ - 1}$ and $2^{2n}$ quantum control rotation operations $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right)$.

Hence, the complexity of Fig. 6 is

$$\begin{aligned} \begin{array}{l} O\left( {\frac{{3m\left( {2n + m - 1} \right) }}{2} \times 4 + {\left( {4n+1} \right) } \times 3 + \left( {2^{2n} - 1 + 2^{2n} - 2} \right) \times 2^{2n}} \right) \\ = O\left( {2^{4n + 1} - 3 \cdot 2^{2n} + 12mn + 6m^2 - 6m + 12n + 3} \right) \\ \end{array} \end{aligned}$$

(17)

Obviously, it is an approximate to $O\left( {2 \cdot \left( {2^{2n} } \right) ^2 + 12mn + 6m^2 + 12n} \right)$. This number is quadratic to the total $2^{2n}$ angle values, $\theta _{yx} ,y = 0,1, \ldots 2^{n} - 1, x=0,1, \ldots 2^{n} - 1$ and indicates the efficiency of the circuits.

In order to better understand Fig. 6, the interpolation case in Fig. 8 is used as an example to describe quantum interpolation circuits in more detail. The case describes the expanding quantum image from $2 \times 2$ to $2^2 \times 2^2$.

Fig. 8

Example quantum circuit of nearest-neighbor interpolation method for FRQI

4.2 Quantum realization of nearest-neighbor interpolation method for NEQR

In this subsection, attention is focused on the process of the quantum circuit of nearest-neighbor interpolation in the model of NEQR.

4.2.1 Concrete NEQR circuit

First, an introduction of how to obtain the concrete circuit is given.

Since the only distinguishing feature between NEQR and FRQI is the color encoding information, the interpolation circuits for NEQR and FRQI are therefore distinct regarding calculating pixel values at positions $\left( {x,y} \right)$.

Quantum operator $\varOmega _{yx}$ is used to assign color value for the resulting NEQR image. The detailed equation about the quantum operator $\varOmega _{yx}$ is described in the following way:

$$\begin{aligned}&\varOmega _{yx} \left| 0 \right\rangle ^{ \otimes q} = \mathop \otimes \limits _{i = 0}^{q - 1} \left( {\varOmega _{yx}^i \left| 0 \right\rangle } \right) = \mathop \otimes \limits _{i = 0}^{q - 1} \left( {\left| {0 \oplus C_{yx}^i } \right\rangle } \right) = \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle = \left| {f\left( {y,x} \right) } \right\rangle \end{aligned}$$

(18)

$$\begin{aligned}&\varOmega _{YX}^i :\left| 0 \right\rangle \rightarrow \left| {0 \oplus C_{YX}^i } \right\rangle \end{aligned}$$

(19)

where $\left| {f\left( {y,x} \right) } \right\rangle = \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle$ is the color information of the original image. q oracle operations $\varOmega _{YX}^i ,i = 0, \ldots q - 1$ have been given in Sect. 3, and every oracle operation $\varOmega _{YX}^i ,i = 0, \ldots q - 1$ is at most a 2n-Control-NOT qubit gate. For more information about the black-box operation $\varOmega _{yx}$, refer to [9].

Fig. 9

Quantum circuit of nearest-neighbor interpolation method for NEQR

The whole quantum circuit of the nearest-neighbor interpolation method for NEQR is shown in Fig. 9. The modules appeared in Fig. 9 are already given in Fig. 7. Because the size of the resulting image is known, namely $x'$ and $y'$ are known. Moreover, the color and coordinates of the original quantum image are also known. So, $\left| {x'} \right\rangle ,\left| {y'} \right\rangle$, $\left| x \right\rangle$ ,$\left| y \right\rangle$ and $f\left( {y,x} \right)$ are considered to be the input information of the quantum circuit. In addition, when designing the quantum circuit, introducing ancillary qubits $\left| 0 \right\rangle$ is a commonly used method.

In order to better analyze the circuit, the concrete framework of Fig. 9 is elaborated as the following algorithm.

• Step 1. Obtain the result of $x = \frac{{x'}}{{2^m }}$ by executing the m times halving operation $U_{H_x }$ which operates on the x coordinates. Then, get the result of $y = \frac{{y'}}{{2^m }}$ through the m times halving operation $U_{H_y }$ which operates on the y coordinates.

• Step 2. By performing the n times quantum swap gates on the x coordinates $\left| {x_{n - 1} } \right\rangle \cdots \left| {x_0 } \right\rangle$ and the first n qubits $\left| 0 \right\rangle ^{ \otimes n}$ to make the first n qubits $\left| 0 \right\rangle ^{ \otimes n}$ carry the x coordinates information. At same time, executing the n times quantum swap gates between the y coordinates $\left| {y_{n - 1} } \right\rangle \cdots \left| {y_0 } \right\rangle$ and the second n qubits $\left| 0 \right\rangle ^{ \otimes n}$. Then the second n qubits $\left| 0 \right\rangle ^{ \otimes n}$ carries the y coordinates information.

• Step 3. Choose the method for computing the gradient of the pixels. To obtain the color information, the quantum oracle operator $\varOmega _{yx}$ is used on the first q qubits $\left| 0 \right\rangle ^{ \otimes q}$, middle 2n qubits $\left| 0 \right\rangle ^{ \otimes 2n}$ and f(y, x).

• Step 4. Perform the m times quantum swap gates between the $y_{n - 1} , \ldots y_0$ coordinates and the second n qubits $\left| 0 \right\rangle ^{ \otimes n}$. Then the y coordinates restores the original information $\left| {y_{n - 1} } \right\rangle \cdots \left| {y_0 } \right\rangle$. Similarly, executing the m times quantum swap operations between the $x_{n - 1} , \ldots x_0$ coordinates and the first n qubits $\left| 0 \right\rangle ^{ \otimes n}$, which renders the x coordinates carry its original information $\left| {x_{n - 1} } \right\rangle \cdots \left| {x_0 } \right\rangle$.

• Step 5. Execute the m times inverse halving operation $U_{H_x }^{ - 1}$ operated on the x coordinates to realize the aim of recovering the $x'$ coordinates information of the resulting image. Meanwhile, carry out the m times inverse halving operation $U_{H_y }^{ - 1}$ operated on the y coordinates, which can recover the $y'$ coordinates information of the interpolated quantum image.

The above steps can be summarized as the following Eq. (20):

$$\begin{aligned} \begin{array}{l} \underbrace{\left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \left| 0 \right\rangle ^{ \otimes q}}_\mathrm{the \ empty \ NEQR \ image} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \left| {f(y,x)} \right\rangle \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} y'_{n + m - 1} \cdots y'_m } \right\rangle \left| 0 \right\rangle ^{ \otimes q} \\ {\quad } \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \left| {f(y,x)} \right\rangle \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} 0 \cdots 0} \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} 0 \cdots 0} \right\rangle \left| 0 \right\rangle ^{ \otimes q} \\ {\quad } \left| {x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_{n + m - 1} \cdots y'_m } \right\rangle \left| 0 \right\rangle \left| {f(y,x)} \right\rangle \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} 0 \cdots 0} \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} 0 \cdots 0} \right\rangle \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle \\ {\quad } \left| {x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_{n + m - 1} \cdots y'_m } \right\rangle \left| 0 \right\rangle \left| {f(y,x)} \right\rangle \\ \rightarrow \left| {x'_0 x'_1 \cdots x'_{m - 1} x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_0 y'_1 \cdots y'_{m - 1} y'_{n + m - 1} \cdots y'_m } \right\rangle \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle \\ {\quad } \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \\ \rightarrow \underbrace{\left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \mathop \otimes \limits _{i = 0}^{q - 1} \left| {C_{yx}^i } \right\rangle }_\mathrm{the \ interpolated \ NEQR \ image}\left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \\ \end{array} \end{aligned}$$

(20)

As shown in Fig. 9, the corresponding resulting quantum image $\left| I \right\rangle _{{\mathrm{int}} }$ is prepared. Simply stated, the aim of the expanding quantum image using the nearest-neighbor interpolation method is realized for NEQR.

4.2.2 Circuit Complexity and comparison with other methods

In Fig. 9, the circuit has 4n quantum swap gate, m halving operation $U_{H_x }$, m halving operation $U_{H_y }$, m inverse halving operation $U_{H_x }^{ - 1}$, m inverse halving operation $U_{H_y }^{ - 1}$ and one quantum oracle operation $\varOmega _{yx}$.

Just as Sect. 4.1.2 has pointed out, the complexity of the m times halving operation $U_{H_x }$,$U_{H_y }$, $U_{H_x }^{ - 1}$, and $U_{H_y }^{ - 1}$ is not more than $\frac{{3m\left( {2n + m - 1} \right) }}{2}$.

Also, [9] has indicated that the complexity of the quantum oracle operation is $O\left( {q \cdot 2n} \right)$.

Therefore, the network complexity of Fig. 9 is

$$\begin{aligned} \begin{array}{l} O\left( {\frac{{3m\left( {2n + m - 1} \right) }}{2} \times 4 + 4n \times 3 + q \cdot 2n} \right) \\ = O\left( {2n(6m + q + 6) + 6m(m - 1)} \right) \\ \end{array} \end{aligned}$$

(21)

It is not more than $O\left( {2n(6m + q + 6) + 6m^2 } \right)$, which means that the complexity is in the polynomial level.

Compared with the complexity $O\left( {2^{n + 1} \cdot q \cdot \left( {24n + 12m} \right) } \right)$ for INEQR in [26], the complexity of constructing the nearest-neighbor interpolation has experienced an approximately exponential decrease. In order to fully display the advantage of the circuit, the detailed comparison with the quantum circuit in [26] will be provided. Before the discussion about comparing these two methods, a note regarding the background assumption of the interpolation problem which is the quantum image being scaled down from $2^{n + m} \times 2^{n + m}$ to $2^n \times 2^n$ is necessary.

The key of the proposed quantum circuit in [26] lies in using the $2n + m + 1$-control-qubit-NOT gate to copy color value $\left| {C_{yx} } \right\rangle$ of the original image to the interpolated image. However, since $\left| {C_{yx} } \right\rangle$ is encoded in the form of $\left| {C_{yx}^{q - 1} \cdots C_{yx}^0 } \right\rangle$, in order to copy pixel value $\left| {C_{yx} } \right\rangle$, it needs to execute q times the $2n + m + 1$-control-qubit-NOT gate to copy every qubit $\left| {C_{yx}^i } \right\rangle ,i = 0,1 \cdots q - 1$ of $\left| {C_{yx} } \right\rangle$. For the horizontal axis and vertical axis, both of them have $2^n$ pixels and every pixel has gray value $\left| {C_{yx} } \right\rangle$ which corresponds to q number of $2n + m + 1$-control-qubit-NOT gate. At the condition of choosing the Control-NOT gate as the elementary unit, [21] pointed out that a t-control-qubit-NOT gate is equivalent to $\left( {12t - 11} \right)$ Control-NOT gates. Consequently, the complexity of the $2n + m + 1$-control-qubit-Not gate is $24n + 12m + 1$. Hence, the complexity of the circuit in [26] is at least $O\left( {2^{n + n} \cdot q \cdot \left( {24n + 12m} \right) } \right)$.

The key of our designed NEQR interpolation method exists in using the quantum halving operation, quantum swap gates and quantum oracle operator to prepare the color information instead of using the $2n + m + 1$-control-qubit-NOT gate to copy the color information. As analyzed above, the complexity is in the level of polynomial and the proposed method has been proven simpler than the complexity in [26].

Obviously, our designed circuit uses simple quantum gates, such as halving operation, quantum swap gates and oracle operator instead of multi-control-NOT gates to prepare color information. It is the major reason that our designed circuit is simpler than circuit in [26].

In addition, the relationship between the methods of our paper and the reference [26] can be elaborated from the following aspects.

First aspect is from the angle of quantum image model. In reference [26], the nearest-neighbor interpolation algorithm is based on INEQR (the improved NEQR) model. INEQR deals with quantum images having $2^{n_1 } \times 2^{n_2 }$ pixels, and the size of interpolated image is $2^{m_1 } \times 2^{m_2 }$. Our methods are based on FRQI and NEQR which are dealing with square images. These three quantum image models have the following relationship described by Fig. 10.

Fig. 10

The relationship between FRQI, NEQR and INEQR

Obviously, when $n_1 = n_2 = n$ and $m_1 = m_2 = m$, INEQR model becomes NEQR model. Hence, method in [26] is suitable for NEQR.

Jiang et al. [26] start the research of quantum image interpolation method for INEQR. We will explore the interpolation method for FRQI and NEQR in this paper. Our work is a continuation and improvement of the previous work. Jiang et al. [26] proposed an opening scaling method which designs circuit from the angle of copying color information. Our NEQR interpolation method is an improved method which considers preparing color information. The improvement mainly embodies in the complexity of the circuit. Jiang et al. [26] and our method have one thing in common. That is the way of introducing additional qubit to complete the circuit.

Finally, the original NEQR expanding case from $2 \times 2$ to $2^2 \times 2^2$ is used as an example to describe the quantum nearest-neighbor interpolation in details, which is shown in Fig. 11.

Fig. 11

Example quantum circuit of nearest-neighbor interpolation method for NEQR

5 Improved circuits of nearest-neighbor interpolation for FRQI and NEQR

The feasibility and reasonability of nearest-neighbor interpolation for FRQI and NEQR have been proven in Sect. 3. Quantum circuits of nearest-neighbor interpolation for FRQI and NEQR have been designed in Sect. 4. However, the m times repeated halving operations are used in the circuits to make scaling. To some extent, it is a naive algorithm because there are many redundant quantum swap operations which will lead to a bad performance.

In the discussion that follows, we present more new interpolation circuits for FRQI and NEQR. Such circuits can be obtained quite simply by employing the Control-NOT gate instead of the halving operation. Such circuits are of interest because they are relatively low in complexity and therefore provide a useful starting point for introducing nearest-neighbor interpolation for FRQI and NEQR.

5.1 New FRQI interpolation circuit

The aim is to improve the quantum circuit of Fig. 6 concerning the structure and content of a FRQI image.

5.1.1 New FRQI circuit

Consider an array of 2n qubits which are proposed to be used as the original image’s position storage. Each qubit in the array may be associated with two parameters, x and y, which together represent coordinates information of the original quantum image. Prior to putting the information into the array, a suggestion that each qubit is initialized to state $\left| 0 \right\rangle$ is put forth. The initial state is therefore given by the following expression

$$\begin{aligned} \left| {x'_{n + m - 1} \cdots x'_0 } \right\rangle \left| {y'_{n + m - 1} \cdots y'_0 } \right\rangle \left| 0 \right\rangle \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \end{aligned}$$

(22)

The objective is to store color information about the resulting image in the first $\left| 0 \right\rangle$ qubit. Extending color information of the original image to the first qubit $\left| 0 \right\rangle$, we associate the relationship between the color information of the original image and the interpolated image using swap gate. However, certain recovery of the interpolated image’s position information is necessary to fully output a complete interpolated image.

For a given original quantum image $\left| {I_\mathrm{NEQR} } \right\rangle$ sized $2^n \times 2^n$, a typical resulting image created by nearest-neighbor interpolation is shown in Fig. 12.

Fig. 12

New quantum circuit of nearest-neighbor interpolation method for FRQI

In the following, the process is analyzed and a description of the state of the quantum image interpolation circuit at each step of the computation as marked in Fig. 12 is given.

• Step 1. Obtain $x = \frac{{x'}}{{2^m }}$ using the n times Control-NOT gates on $\left| {x'_{n + m - 1} \cdots x'_m }\right\rangle$ coordinates. Correspondingly, obtain $y = \frac{{y'}}{{2^m }}$ through the n times Control-NOT gates on $\left| {y'_{n + m - 1} \cdots y'_m }\right\rangle$ coordinates.

• Step 2. Employ $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right) , yx = 0, \ldots 2^{2n} - 1$ to produce the color information being carried on the final $\left| 0 \right\rangle$ qubit.

• Step 3. Carry out the quantum swap gates between the first ancillary qubit $\left| 0 \right\rangle$ and the final ancillary qubit $\left| 0 \right\rangle$ to make the first qubit $\left| 0 \right\rangle$ carry color information.

The concrete procedure about Fig. 12 can be described as (23).

$$\begin{aligned} \begin{array}{l} \underbrace{\left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_{n + m - 1} \cdots y'_0 } \right\rangle \left| 0 \right\rangle }_\mathrm{the \ empty \ FRQI \ image} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle \\ \rightarrow \left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \left| 0 \right\rangle \\ {\quad } \underbrace{\left| {x'_{n + m - 1} \cdots x'_m } \right\rangle }_{x ={x'/ 2^m }} \cdots \underbrace{\left| {y'_{n + m - 1} \cdots y'_m } \right\rangle }_{y ={y'/ 2^m }}\left| 0 \right\rangle \\ \rightarrow \left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \left| 0 \right\rangle \\ {\quad } \left| {x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_{n + m - 1} \cdots y'_m } \right\rangle \left| {f\left( {y,x} \right) } \right\rangle \\ \rightarrow \underbrace{\left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_{n + m - 1} \cdots y'_0 } \right\rangle \left| {f\left( {y,x} \right) } \right\rangle }_\mathrm{the \ interpolated \ FRQI \ image} \\ {\quad } \left| {x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_{n + m - 1} \cdots y'_m } \right\rangle \left| 0 \right\rangle \\ \end{array} \end{aligned}$$

(23)

5.1.2 Circuit complexity

It is clear that Fig. 12 contains 2n Control-NOT gates, $2^{2n}$ control rotation gates $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right) ,yx = 0,1, \ldots 2^{2n} - 1$ and one quantum swap gate. Barenco et al. [28] have pointed out that quantum operation $C^{2n} \left( {R_y \left( {2\theta _{yx} } \right) } \right)$ can be broken down into $2^{2n} - 1$ simple operations $R_y \left( {\frac{{2\theta _{yx} }}{{2^{2n} - 1}}} \right)$, $R_y \left( { - \frac{{2\theta _{yx} }}{{2^{2n} - 1}}} \right)$ and $2^{2n} - 2$ Control-NOT operations.

Hence, the complexity of Fig. 12 is:

$$\begin{aligned} \begin{array}{l} \mathrm{{ }}O\left( {2n + 2^{2n} \times \left( {2^{2n} - 1 + 2^{2n} - 2} \right) + 3 \times 1} \right) \\ \simeq O\left( {2\left( {2^{2n} } \right) ^2 + 2n} \right) \\ \end{array} \end{aligned}$$

(24)

The number is quadratic to the total $2^{2n}$ angle values, $\theta _i ,i = 0,1, \ldots 2^{2n} - 1$, which indicates the efficiency of the circuit.

Here the Control-NOT gates are used instead of the halving operation to produce position information $x = \frac{{x'}}{{2^m }}$ and $y = \frac{{y'}}{{2^m }}$ in qubits $\left| 0 \right\rangle ^{ \otimes n}$ and $\left| 0 \right\rangle ^{ \otimes n}$. So the complexity of Fig. 12 is lower than that of Fig. 6.

The circuit’s complexity for FRQI method is shown in Table 1.

Table 1 The circuit’s complexity for FRQI interpolation methods

5.2 New NEQR interpolation circuit

The objective is to improve the quantum circuit in Fig. 9 concerning the structure and content of a NEQR image.

5.2.1 New NEQR circuit

The proposed approach for designing the interpolation circuit for NEQR will use Control-NOT gates. It also relies on the oracle operator to prepare color information $\left| {C_{q - 1} \cdots C_0 } \right\rangle$.

Figure 13 provides the quantum circuit that implements the nearest-neighbor interpolation method for NEQR, while Eq. (25) presents the proposed quantum procedure for constructing the circuit of NEQR.

Fig. 13

New quantum circuit of nearest-neighbor interpolation method for NEQR

And the concrete steps about Fig. 13 can be described as follows.

• Step 1. Obtain $x = \frac{{x'}}{{2^m }}$ using the n times Control-NOT gates on the $\left| {x'_{n + m - 1} \cdots x'_m }\right\rangle$ coordinates. Correspondingly, obtain $y = \frac{{y'}}{{2^m }}$ through the n times Control-NOT gates on the $\left| {y'_{n + m - 1} \cdots y'_m }\right\rangle$ coordinates.

• Step 2. Employ oracle operator $\varOmega _{yx}$ to produce the color information being carried on the final q qubits $\left| 0 \right\rangle$.

In order to clearly display the proposed circuit, the steps about Fig. 13 are shown in Eq. (25) .

$$\begin{aligned} \begin{array}{l} \underbrace{\left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_{n + m - 1} \cdots y'_0 } \right\rangle \left| 0 \right\rangle ^{ \otimes q}}_\mathrm{the \ empty \ NEQR \ image} \left| 0 \right\rangle ^{ \otimes n} \left| 0 \right\rangle ^{ \otimes n} \left| {f\left( {y,x} \right) } \right\rangle \\ \rightarrow \left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_{n + m - 1} \cdots y'_0 } \right\rangle \left| 0 \right\rangle ^{ \otimes q} \\ {\quad } \underbrace{\left| {x'_{n + m - 1} \cdots x'_m } \right\rangle }_{x ={x'/ 2^m }} \cdots \underbrace{\left| {y'_{n + m - 1} \cdots y'_m } \right\rangle }_{y ={y'/ 2^m }}\left| 0 \right\rangle \\ \underbrace{\rightarrow \left| {x'_{n + m - 1} \cdots x'_m \cdots x'_0 } \right\rangle \cdots \left| {y'_{n + m - 1} \cdots y'_m \cdots y'_0 } \right\rangle \left| {C_{q - 1} \cdots C_0 } \right\rangle }_\mathrm{the \ interpolated \ NEQR \ image} \\ {\quad } \left| {x'_{n + m - 1} \cdots x'_m } \right\rangle \left| {y'_{n + m - 1} \cdots y'_m } \right\rangle \left| {f\left( {y,x} \right) } \right\rangle \\ \end{array} \end{aligned}$$

(25)

5.2.2 Circuit complexity

Now, the complexity of the proposed interpolation circuit is analyzed. It has 2n Control-NOT gates and one oracle operator $\varOmega _{yx}$. It is indicated that the complexity of quantum oracle operator is $O\left( {q \cdot 2n} \right)$ [9] .

Consequently, the network complexity is

$$\begin{aligned} O\left( {q \cdot 2n + 2n} \right) \end{aligned}$$

(26)

Evidently, this number is simpler than the network complexity in [26] and the previous network of Fig. 9. However, in contrast, Control-NOT gate is used to produce coordinates information instead of utilizing multi-control Toffoli gates in [26] or the halving operation in the previous work. The smaller number of basic Control-NOT gates guarantees the better performance of new NEQR circuits.

The circuit’s complexity for NEQR method in [26] and our NEQR methods is shown in Table 2.

Table 2 Comparison of the circuit’s complexity for NEQR interpolation methods

6 Simulation-based experiments and analysis

In this section, the simulation experiment is performed to show the FRQI and NEQR interpolated results. Also, the comparative simulations between NEQR method in [26] and our NEQR method are carried out based on the previous network. All experiments are simulated on the MATLAB 7.12.

6.1 FRQI and NEQR interpolation simulation results

Figure 14 gives some examples to show the results of the proposed interpolation scheme. (a) and (b) utilize “Lena” and “Cameraman” as original images of size $64 \times 64$. ($a_1$) and ($b_1$) are the correspondingly interpolated FRQI images of size $128 \times 128$. ($a_2$) and ($b_2$) are the correspondingly interpolated NEQR images of size $128\times 128$.

Fig. 14

Examples using 256 gray scale for $64 \times 64$ image interpolation. a, b are the original $64 \times 64$ images, $a_1$ and $b_1$ are the interpolated $128 \times 128$ FRQI images, and $a_2$ and $b_2$ are the interpolated $128 \times 128$ NEQR images

Figure 14 depicts the interpolated FRQI and NEQR images, from which we can see that the designed nearest-neighbor interpolation scheme produces acceptable interpolated results. FRQI and NEQR are two different quantum image representation models; when we execute simulation experiments, there will be the quantum measurement operation, which leads to quantum images shown in the form of classical images and that yields the interpolated FRQI and NEQR results.

6.2 Comparative simulations for NEQR interpolation methods

Figure 15 gives some examples to show the comparison of the proposed NEQR interpolation scheme and existed method in [26]. (a) utilizes “Lena” of size $32 \times 32$ as an original image. (b) and (c) are the interpolated “Lena” images of size $64 \times 64$ and of size $128 \times 128$ corresponding to method in [26]. (d) and (e) are the interpolated “Lena” images of size $64 \times 64$ and of size $128 \times 128$ corresponding to our method.

Fig. 15

Examples using 256 gray scale for $32 \times 32$ image interpolation. a is the original $32 \times 32$ image, b to c are the interpolated $64 \times 64$ and $128 \times 128$ images of method in [26], d, e are the interpolated $64 \times 64$ and $128 \times 128$ images of our proposed NEQR method

Because these two methods are designed to realize the nearest-neighbor interpolation for NEQR, the final interpolated results are the same. The only difference between method in [26] and our method exists in the complexity of circuit, which has been described in Sect. 4.2.2.

6.3 Analysis of quantum measurement on the interpolated images

The concrete interpolated FRQI image can be described as in the following form.

$$\begin{aligned} \left| {I\left( \theta \right) } \right\rangle _{{\mathrm{int}} } = \frac{1}{{2^{n + m} }}\sum \limits _{y = 0}^{2^{n + m} - 1} {\sum \limits _{x = 0}^{2^{n + m} - 1} {\left( {\cos \theta _{yx} \left| 0 \right\rangle + \sin \theta _{yx} \left| 1 \right\rangle } \right) \otimes \left| {yx} \right\rangle }} \end{aligned}$$

(27)

Again, the interpolated NEQR image can be expressed as in the following form.

$$\begin{aligned} \left| I \right\rangle _{{\mathrm{int}} } = \frac{1}{{2^{n + m} }}\sum \limits _{y = 0}^{2^{n + m} - 1} {\sum \limits _{x = 0}^{2^{n + m} - 1} {\left| {c_{yx}^{q - 1} \cdots c_{yx}^1 c_{yx}^0 } \right\rangle \left| y \right\rangle \left| x \right\rangle } } \end{aligned}$$

(28)

Obviously, interpolated FRQI and NEQR images are quantum superposition state and can be seen as a composite quantum system composed by $2n + 1$ qubits and $2n + q$ qubits, respectively.

In practice, the quantum state cannot be practically observed in quantum system because a measurement will destroy the superposition. And what is worse, it is not allowed to make copies of the state and measure each one due to the non-cloning theorem. Hence, it is necessary to repeat the construction of the interpolated image state n $\left( {n > 1} \right)$ times and measure each one to summarize the measurement results from which we can estimate the interpolated image. We execute probability measurement on the interpolated image. Probability measurement converts the quantum information into classical information in form of probability distributions, i.e., it converts a single qubit state $\left| \Psi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle$ into a probability classical bit M (distinguished from a qubit by drawing it as a double-line wire), which is 0 with probability $\left| \alpha \right| ^2$, or 1 with probability $\left| \beta \right| ^2$ as shown in Fig. 16.

Fig. 16

Quantum circuit symbol for measurement

Fig. 17

Block diagram of measurement procedure on quantum computers

In the following, we analyze the impact of quantum measurements on the interpolated images. The measurement results on the interpolated FRQI image of size $2^{n + m} \times 2^{n + m}$ are some collection of basis states $\left\{ {s_1 ,s_2 , \ldots s_{2^{2(n + m) + 1} } } \right\}$ in $2^{2(n + m) + 1}$ dimension Hilbert space. The measurement results on the interpolated NEQR image sized $2^{n + m} \times 2^{n + m}$ and gray ranged $\left[ {0,2^q - 1} \right]$ are some collection of basis states $\left\{ {s_1 ,s_2 , \ldots s_{2^{2(n + m) + q} } } \right\}$ in $2^{2(n + m) + q}$ dimension Hilbert space. After multiple measurements, these basis states follow a probability distribution. The measurement will be continued until the probability of every basis state is stabilized at a fixed value. According to law of large numbers, there is a limit for these basis states which can be used to estimate the color information of the interpolated image. The block diagram of measurement procedure on quantum computers is shown in Fig. 17.

7 Conclusion

In this paper, new methods of nearest-neighbor interpolation for FRQI and NEQR are proposed. The proposed methods construct an interpolated image and mainly consist of two steps: (1) position mapping and (2) preparation of color. In the position mapping stage, the halving operation or Control-NOT gates are used to build the relationship between result image’s position $\left( {x',y'} \right)$ and original image’s position $\left( {x,y} \right)$. Through position mapping, the resulting image’s pixel which needs a color value assignment is equivalent to the original image’s corresponding pixel in position $\left( {x,y} \right)$. The preparation color step exploits the control rotation gates and the oracle operator to prepare the color of the original image in position $\left( {x,y} \right)$. The empty resulting image and original image are encoded, such that the proposed circuit is stable. Different from existing methods, the method suggested in this paper does not rely on copy color information, which is typically complex for using multi-control-NOT gates. Complexity results and simulation results show that the proposed methods have good performance. However, quantum realization of the interpolation method has just begun and further efforts should be made to improve the existed circuits. Applying an enlarged quantum image which is expanded by the nearest-neighbor interpolation to the area of quantum image information hiding will require more investigation. Other future work will entail, analyzing the quantum realization of other classical interpolation methods such as bilinear and bicubic because nearest-neighbor interpolation method appears visible aliasing.