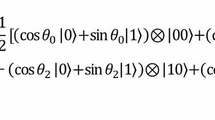Quantum image translation

Abstract

Image translation, which maps the position of each picture element into a new position, is a basic image transformation. Although it has been deeply researched and widely used in classical image processing, its quantum version is a vacancy. This paper studies the quantum image translation (QIT) for the first time to promote the development of quantum image processing. Two types of QIT: entire translation and cyclic translation are proposed by giving the quantum translation circuits. The translation in $X$-direction and $Y$-direction is separable, and the circuits for translating right or left are different.

1 Introduction

With reference to the importance of digital image processing in classical computers, quantum image processing (QIP) will meet and has met its substantial development along with the bright prospect of quantum computers.

We think that the research about QIP has three main directions: (1) representing quantum images; (2) transplanting basic classical image transformation into quantum computers; and (3) senior QIP algorithms. We describe them briefly in the following.

• (1) Representation of quantum images.

Research in the field of QIP started with proposals on quantum image representations such as qubit lattice [1], real ket [2], FRQI [3], novel enhanced quantum representation (NEQR) [4] and etc. The quantum images are two-dimensional arrays of qubits in [1] and a quantum state in [2].

In 2011, Le et al. [3] proposed the flexible representation of quantum images (FRQI), which captures information about colors and their corresponding positions in an image into quantum states. FRQI fully uses the physical characteristics of quanta and provides a flexible method to link color and location information, which makes users to process any part of the image.

In 2013, Zhang et al. [4] improved the storage mode of color information in FRQI and named the new representation as NEQR, which puts not only positions but also colors in binary qubits. The improvement makes NEQR more similar to the representation of digital images in classical computers and easy to transplant classical image processing algorithms to quantum computers. (We will introduce NEQR in Sect. 2.1)

• (2) Basic QIP algorithms

Basic QIP algorithms are a set of processing modules, which are the foundations of QIP. At present, there are four types of basic QIP algorithms: geometric transformation, color processing, image scrambling and frequency domain transformation.

• Geometric transformation: In 2010, the geometric transformations on quantum images (GTQI) [5] was proposed which can realize flip, transposition and orthogonal rotation ($90^{\circ }$, $180^{\circ }$ and $270^{\circ }$). Jiang and Wang [6] realized a quantum image scaling algorithm using nearest neighbor interpolation. It is the first time to give a QIP method that changes the size of an image.

• Color processing: While it proposed the NEQR, Ref. [4] gave methods for color inverse and image binaryzation to prove one of the advantages of NEQR: more quantum image operations related to gray-scale information in the image can be performed conveniently.

• Image scrambling: Arnold, Fibonacci and Hilbert image scrambling methods and their improvements are given in Refs. [7–9]. Arnold and Fibonacci methods are based on quantum adder. Hilbert method is decomposed into a alternate processing about odd and even.

• Frequency domain transformation: Quantum Fourier transform [10], quantum wavelet transform [11] and quantum discrete cosine transform [12, 13] are proposed to satisfy the requirement about frequency domain transformation.

Compared with huge amounts of classical image processing algorithms, the number of the existing basic QIP algorithms is very small. Many algorithms such as rotation, spatial warping, morphologic processing have never been studied.

• (3) Senior QIP algorithms

Under the restrictions on the lack of basic QIP algorithms, senior QIP algorithms, such as edge detection, image segmentation, image enhancement are still vacancies.

In this paper, we focus on image translation that belongs to basic QIP algorithms. We discuss two kinds of image translations:

• (1) Entire translation (ET): Translate the whole image. Fill the vacated position with black (or other specified colors) and abandon the pixels over the image boundary.

• (2) Cyclic translation (CT): Translate the whole image cyclically. Wrap the pixels over the image boundary to fill the vacated position.

ET is widely used. Almost all of the image processing softwares have the function of ET. Users can select all of an image and then move it. Figure 1 provides two examples.

Fig. 1

Entire translation. a An animation. b A montage

Figure 1a gives a dolphin jumping animation by implementing ET twice. Although the animation is simple and not exquisite, it is an interesting application of ET and maybe it will be the beginning of quantum animation or quantum video (because we will offer its quantum circuit in Sect. 4).

Figure 1b shows a common scene of image processing software: moving the shapes in two or more pictures to appropriate positions and combining them into one picture.

CT is often used as an intermediate step of image processing algorithms. For example, in general, after the Fourier transform of an image, the zero-frequency component should be shifted to the center of the spectrum image. The shifting process (we call it “fftshift”) is a kind of CT. Figure 2a, b gives the amplitude of the Fourier spectrum of an image before and after fftshift. In these two figures, the brighter a pixel, the greater the amplitude value of the pixel. Figure 2c is the schematic drawing that illustrates the processing steps of fftshift.

Fig. 2

Cyclic translation. a The original amplitude image, b the amplitude image after fftshift, c the schematic drawing of fftshift

This paper proposes quantum image translation (QIT) algorithms by giving quantum circuits to realize ET and CT respectively. As we know, this work has not been studied yet.

The rest of the paper is organized as follows. A brief background on the NEQR representation, image translation, quantum adder networks and quantum comparator is presented in Sect. 2. The quantum circuit architecture of image translation is discussed in Sect. 3. This is followed in Sect. 4 by some examples to explain the circuit further. Finally, a conclusion is given in Sect. 5.

2 Preliminaries

2.1 Quantum image representation

In this paper, the NEQR is used to store quantum images as the form shown below.

$$\begin{aligned} |I\rangle&= \frac{1}{2^{n}}\sum \limits _{i=0}^{2^{2n}-1}|c_{i} \rangle \otimes |i\rangle \nonumber \\ |c_{i}\rangle&= |c_{i}^{q-1}\ldots c_{i}^{1}c_{i}^{0}\rangle , c_{i}^{k}\in \{0,1\}, k=q-1,\ldots ,1,0, i=0,1,\ldots ,2^{2n}-1\nonumber \\ |i\rangle&= |y\rangle |x\rangle =|y_{n-1}y_{n-2}\ldots y_{0}\rangle |x_{n-1}x_{n-2}\ldots x_{0}\rangle , |y_{j}\rangle |x_{j}\rangle \in \{0,1\} \end{aligned}$$

(1)

where the binary sequence $c_{i}^{q-1}\ldots c_{i}^{1}c_{i}^{0}$ encodes the color value (or gray value), and the color range is $2^{q}$; $|i\rangle$, for $i=0,1,\ldots ,2^{2n}-1$, encodes pixels’ positions in the image; $y_{n-1},y_{n-2},\ldots ,y_{0}$ along the vertical location and $x_{n-1},x_{n-2},\ldots ,x_{0}$ along the horizontal axis; and $\otimes$ denote the Kronecker product. The size of the quantum image is $2^{n}\times 2^{n}$.

2.2 Image translation

Image translation is a geometric transformation that maps the position of each picture element in an input (or original) image into a new position in an output (or translated) image.

Assume $I(x,y)$ is the original image, where $(x,y)$ is the pixel coordinates, $x,y=0,1,\ldots ,2^{n}-1$. The image translation is defined as follows.

$$\begin{aligned} x_{t}&= x\pm t_{x}\nonumber \\ y_{t}&= y\pm t_{y} \end{aligned}$$

(2)

where $(x_{t},y_{t})$ is the pixel coordinates in the translated image, $(t_{x},t_{y})$ is the translation parameter which specify the desired horizontal and vertical pixel displacements, $0\le t_{x},t_{y}\le 2^{n}-1$. If $+$ is used, the image is translated right and/or down; if $-$ is used, the image is translated left and/or up.

Note 1 Equation (2) gives only the main features of image translation and does not reflect the nuances between ET and CT. This problem will be solved in Sect. 3.

2.3 Quantum adder

Assume that $|a\rangle =|a_{n-1}a_{n-2}\ldots a_{0}\rangle$ and $|b\rangle =|b_{n-1}b_{n-2}\ldots b_{0}\rangle$ are two $n$-qubit binary numbers, $a_{i},b_{i}\in \{0,1\}$, $i=n-1,n-2,\ldots ,0$. Reference [14] gives the quantum network ADDER that can add $|a\rangle$ and $|b\rangle$.

$$\begin{aligned} |d\rangle =|a\rangle +|b\rangle \end{aligned}$$

where the output $|d\rangle =|d_{n}d_{n-1}d_{n-2}\ldots d_{0}\rangle$ is a $(n+1)$-qubit number and $d_{n}$ is the carry. If $a+b<2^{n}$, $d_{n}=0$; otherwise, $d_{n}=1$.

Reference [9] defines a quantum circuit module ADDER-MOD$2^{n}$ which can realize $(a+b)\mathrm{mod } 2^{n}$ simply by ignoring the carry bit from ADDER module.

Figure 3 shows the two quantum modules.

Fig. 3

ADDER and ADDER-MOD$2^{n}$

Note 2 There is a thick black bar on the right-hand side of ADDER. In the following, readers will see another case that the black bar is on the left-hand side. A network with a bar on the left side represents the reversed sequence of elementary gates embedded in the same network with the bar on the right side, i.e. they achieve opposite functions according to the unitarity of quantum circuits. If we reverse the action of ADDER with the input $(a,b)$, the output will produce $(a,a-b)$ when $a\ge b$. When $a<b$, the output is $(a,2^{n}+(a-b))$.

2.4 Quantum comparator

Wang et al. [15] give a quantum comparator circuit shown in Fig. 4 which compares $a$ and $b$. Its useful outputs are two qubits $|e_{0}\rangle$ and $|e_{1}\rangle$. In this paper, we only use $|e_{0}\rangle$: $e_{0}=0$ indicates that $a\ge b$; $e_{0}=1$ indicates that $a<b$.

Fig. 4

Quantum comparator

3 Quantum image translation

In Eq. (2), $x/x_{t}$ and $y/y_{t}$ appear in two formulas. There is no crossover between them which indicates that the image translation processing can be decomposed into two separable parts (or steps): $X$-direction translation and $Y$-direction translation. In this section, we take $X$-direction for instance to give the quantum image translation circuits.

We define the quantum circuits that realize entire translation and cyclic translation as ET($\pm t_{x}$) and CT($\pm t_{x}$) respectively, where $t_{x}$ is the translation parameter, $0\le t_{x}\le 2^{n}-1$.

3.1 Entire translation

Figure 5 gives a schematic drawing about entire translation.

Fig. 5

The schematic drawing about ET. a Translating right. b Translating left

• (1) Translating right: $x_{t}=x+t_{x}$

According to Fig. 5a, ET can be described as below.

$$\begin{aligned} c_{x_{t}y}=\left\{ \begin{array}{cl} 0 &{}\quad \text { if }0\le x_{t}\le t_{x}-1\\ c_{xy} &{}\quad \text { if }t_{x}\le x_{t}\le 2^{n}-1 \end{array} \right. \end{aligned}$$

(3)

In order to realize the entire translation in quantum computers, Eq. (3) is changed into another form. Because $0\le x\le 2^{n}-1$, $t_{x}\le x_{t}=x+t_{x}\le 2^{n}-1+t_{x}$. We separate the interval $[t_{x},2^{n}-1+t_{x}]$ into two subintervals: $[t_{x},2^{n}-1]$ and $[2^{n},2^{n}-1+t_{x}]$.

The subinterval $[t_{x},2^{n}-1]$ is the range of $x_{t}$ in the second line of Eq. (3). In this case, the carry bit $x_{tn}$ of $x+t_{x}$ is 0 and we set $c_{x_{t}y_{t}}=c_{xy}$ directly.

To the subinterval $[2^{n},2^{n}-1+t_{x}]$, the carry bit $x_{tn}$ of $x+t_{x}$ is 1. $[2^{n},2^{n}-1+t_{x}]-2^{n}=[0,t_{x}-1]$ is the range of $x_{t}$ in the first line of Eq. (3).

Hence, the quantum ADDER is used firstly to get $x_{t}$. Then, the carry bit $x_{tn}$ can be used as the control bit: if $x_{tn}=0$, set $c_{x_{t}y_{t}}=c_{xy}$; otherwise, set $c_{x_{t}y_{t}}=0$. The quantum circuit is shown in Fig. 6a.

• (2) Translating left: $x_{t}=x-t_{x}$

According to Fig. 5b, ET can be described as below.

$$\begin{aligned} c_{x_{t}y}=\left\{ \begin{array}{cl} 0 &{}\quad \text { if } 2^{n}-t_{x}\le x_{t}\le 2^{n}-1 \\ c_{xy} &{}\quad \text { if }0\le x_{t}\le 2^{n}-1-t_{x} \end{array} \right. \end{aligned}$$

(4)

Plug $x_{t}=x-t_{x}$ into Eq. (4),

$$\begin{aligned} c_{x_{t}y}=\left\{ \begin{array}{cl} 0 &{}\quad \text { if } 2^{n}\le x\le 2^{n}-1+t_{x} \\ c_{xy} &{}\quad \text { if } t_{x}\le x\le 2^{n}-1 \end{array} \right. \end{aligned}$$

However, $2^{n}\le x\le 2^{n}-1+t_{x}$ conflicts with $0\le x\le 2^{n}-1$. The reason for this phenomenon is that the abandoned pixels are on the left side of the reserved pixels, but the vacated pixels are on the right side of the reserved pixels. The distance between them is just $2^{n}$. Hence, $2^{n}\le x\le 2^{n}-1+t_{x}$ should be rewrote as $0\le x\le t_{x}-1$.

Fig. 6

Entire translation circuits. a $x+t_{x}$, b $x-t_{x}$

Therefore, the quantum comparator is used firstly to compare $x$ and $t_{x}$. Then, the reversed ADDER is used to get $x-t_{x}$. Finally, the output qubit $e_{0}$ of the comparator is used as the control bit: if $e_{0}=0$ ($x\ge t_{x}$), set $c_{x_{t}y_{t}}=c_{xy}$; otherwise, set $c_{x_{t}y_{t}}=0$. The quantum circuit is shown in Fig. 6b.

3.2 Cyclic translation

• (1) Translating right: $x_{t}=x+t_{x}$

Cyclic translation can be described as below.

$$\begin{aligned} c_{x_{t}y_{t}}=c_{xy},\quad \mathrm{where }\, x_{t}=(x+t_{x})\mathrm{mod }2^{n} \end{aligned}$$

(5)

It can be realized by the ADDER-MOD$2^{n}$ module easily.

• (2) Translating left: $x_{t}=x-t_{x}$

Cyclic translation can be described as below.

$$\begin{aligned} c_{x_{t}y_{t}}=c_{xy},\quad \mathrm{where }\, x_{t}=(x-t_{x})\mathrm{mod }2^{n} \end{aligned}$$

(6)

In order to give the quantum cyclic translation circuit, we propose Theorem 1.

Theorem 1

If the inputs of the reversed ADDER are two $n$-qubit numbers $a$ and $b$, the output of it is equivalent to $(a-b)\mathrm{mod }2^{n}$.

Proof

As stated in Note 2, when $a\ge b$, the output of the reversed ADDER is $a-b$; when $a<b$, the output is $2^{n}+(a-b)$. Therefore, to prove Theorem 1 is correct, we only need to prove that when $a\ge b$, $(a-b)\mathrm{mod }2^{n}=a-b$; when $a<b$, $(a-b)\mathrm{mod }2^{n}=2^{n}+(a-b)$.

• A. When $a\ge b$

Because $a,b$ are two $n$-qubit numbers, $0\le a,b\le 2^{n}-1$. Hence, $0\le a-b\le 2^{n}-1$ under the hypothesis that $a\ge b$. Then

$$\begin{aligned} (a-b)\mathrm{mod }2^{n}=a-b. \end{aligned}$$

• B. When $a<b$

Because $a,b$ are two $n$-qubit numbers,

$$\begin{aligned} a<b\Rightarrow 1-2^{n}\le a-b\le -1\Rightarrow 1\le 2^{n}+(a-b)\le 2^{n}-1 \end{aligned}$$

Hence,

$$\begin{aligned} (a-b)\mathrm{mod }2^{n}=2^{n}+(a-b). \end{aligned}$$

Theorem 1 is proved according to A and B.

Based on Theorem 1, the quantum image cyclic translation circuits are shown in Fig. 7.

Fig. 7

Cyclic translation circuits. a $x+t_{x}$, b $x-t_{x}$

3.3 Network complexity

The network complexity depends very much on what is considered to be an elementary gate. In this section, we choose the Control-NOT to be our basic unit. References [7] and [9] have pointed out that the network complexities of ADDER and ADDER-MOD$2^{n}$ are all $28n$, where $n$ indicates that the size of the quantum image is $2^{n}\times 2^{n}$.

Now, we analyze the complexity of quantum comparator. It has $n$ groups of quantum gates $\alpha _{0},\alpha _{1},\ldots ,\alpha _{n-1}$ as shown in Fig. 8. The two layers belonging to one group have the same complexity because they have the same number of $\circ$ and $\bullet$ control qubits. For $\alpha _{i}$, the number of $\circ$ and $\bullet$ of one layer are $2i+1$ and 1 respectively, $i=0,1,\ldots ,n-1$.

Fig. 8

The quantum comparator

Because the results shown in Fig. 9 and one Toffoli gate can be simulated by six Control-NOT gates [10], for $\alpha _{i}$, the complexity of one layer is $24i+15$. Hence, the complexity of quantum comparator is

$$\begin{aligned} 2\sum _{i=0}^{n-1}(24i+15)=24n^{2}+6n. \end{aligned}$$

Consequently, the network complexity is shown below:

• ET right (Fig. 6a): $(28n-12)+12n=40n-12$.

• ET left (Fig. 6b): $(24n^{2}+6n)+(28n-12)+12n=24n^{2}+46n-12$.

• CT right (Fig. 7a): $28n-12$.

• CT left (Fig. 7b): $28n-12$.

Fig. 9

Equivalence relation between logic gates [10]

4 Examples

• (1) Example 1

Let us take the $128\times 128$ 256-grayscale image Lena as an example, where $n=7$ and $q=8$, and entire translate it left with $t_{x}=20$ and cyclic translate it down with $t_{y}=40$. The translation circuit is shown in Fig. 10. Figure 11 is the input image and the output image of this circuit.

Fig. 10

The translation circuit for the $128\times 128$ Lena image (Example 1)

Fig. 11

The effect of the circuit shown in Fig. 7. a The input image, b the output image

Although the practical value of Example 1 is not large, it combines $X$-direction and $Y$-direction translation together and helps readers to understand the translation circuits more clearly.

• (2) Examples 2–4

We take the three examples proposed in Figs. 1 and 2 as Examples 2–4 and give their quantum realization in this section.

Example 2 is the dolphin jumping animation. Assume that the translation parameters of the two entire translations are $(t_{x1},-t_{y1})$ and $(t_{x2},t_{y2})$, the quantum circuit is shown in Fig. 12a where the “Display to screen” module is responsible for displaying the picture to the screen.

Fig. 12

The translation circuit for Example 2–4. a The dolphin jumping animation (Example 2), b the montage (Example 3), c fftshift (Example 4)

Example 3 assumes the translation parameter is $(t_{x},-t_{y})$. The role of the module “Combine the two image” (see Fig. 12b) is to merge the two images into one. We do not intend to describe this module in detail because it is not the key issue to be addressed in this article.

Figure 12c gives the quantum circuit of fftshift which uses two CT($2^{n-1}$) to translate the amplitude of the Fourier spectrum on two directions. The translation parameter is $2^{n-1}$ because the image size is $2^{n}\times 2^{n}$ and the zero-frequency component should be shifted to the center of the spectrum image.

5 Conclusion

Image translation, which maps the position of each picture element into a new position, is a basic image transformation. This paper studies the QIT for the first time to promote the development of QIP. Two types of QIT: entire translation and cyclic translation are proposed by giving the quantum translation circuits. The translation in $X$-direction and $Y$-direction is separable and the circuits for translating right or left are different. Examples help to explain the circuits more clearly and put image translation into a number of applications.

The future works may include:

• (1) Sometimes users may want to translate part of an image. For example, as shown in Fig. 13, after a user combined the two images, he wants to move the flower to the lower left corner because he feels the flower and the text are too close. We call this kind of operation as partial translation (PT). Maybe PT is more common than ET and CT. However, because the position relation between the original image and the subimage that to be translated is complex, we will study it later.

  Fig. 13

  

  The partial translation

• (2) The network complexity of ET left is high. How to reduce network complexity is another issue to be studied.