1 Introduction

In recent decades, the propagation of laser beams through the turbulent environment has attracted more and more attention due to its important applications, such as laser communications, remote sensing, laser radar, laser weapons, and tracking. Many studies have been conducted to investigate the various properties of laser beams in turbulent medium, including beam wander (Wu et al. 2016), beam spreading (Chang et al. 2020), scintillation index (Korotkova et al. 2012; Boufalah et al. 2022), intensity distribution (Boufalah et al. 2018; Chib et al. 2020; Hricha et al. 2021; Nossir et al. 2021), field correlations of lasers, and more. At the same time, the field of ultrashort pulse technology has made significant progress in recent years, attracting attention from numerous researchers and leading to a growing body of literature (Pan 2013; Zou and Hu 2016; Wang 2018; Duan et al. 2020; Li et al. 2020; Zhu et al. 2021; Benzehoua et al. 2021a, b; Liu and Lü 2004; Kandpal and Vaishy 2002). The investigation into how laser beams change spectrally, as they move through different media and optical systems, has gained significant attention. These advancements have opened up new possibilities in areas like optical communication, information encoding and transmission, and lattice spectroscopy (Yadav et al. 2007, 2008; Han 2009), with the potential for significant impact in the near future. Two types of spectral changes are observed: spectral shift and spectral switches. The first one refers to when the frequency of the spectrum shifts to either lower (red shift) or higher (blue shift) frequencies during the beam's propagation. Spectral switches is also a topic of interest in optical imaging systems and has been both theoretically predicted (Liu and Lü 2004) and experimentally verified (Kandpal and Vaishy 2002). Over the years, various studies have been conducted to explore the spectral changes of laser beams as they propagate through different media and optical systems. In 2016, Zou et al. investigated the spectral anomalies of a diffracted chirped pulsed super-Gaussian beam (Zou and Hu 2016). Duan et al. studied the impact of biological tissue and spatial correlation on the spectral changes of a Gaussian-Schell model vortex beam (Duan et al. 2020).

On the other hand, the propagation of laser beams in oceanic turbulence and the impact of factors such as salinity and temperature fluctuations on them has become a topics of increased interest. In recent times, the investigation of random beam propagation properties in oceanic turbulence has received considerable attention from researchers due to its practical applications in optical underwater communication, imaging, and sensing (Johnson et al. 2014). A number of studies have been conducted to investigate the evolution of various properties of stationary beams, such as intensity, coherence, polarization, beam quality, beam wander, beam scintillation, and spectral changes (Xu and Zhao 2014). Liu et al. studied the effect of oceanic turbulence on the spectral properties of a chirped Gaussian pulsed beam (Liu et al. 2016). Recently, Jo et al. studied the impact of oceanic turbulence on the spectral changes of a diffracted chirped Gaussian pulsed beam (Jo et al. 2022). This study aims to understand how oceanic turbulence affects the spectral characteristics of the beam as it diffracts, which can cause distortions in the beam's intensity and shape.

This paper focuses on examining the spectral characteristics of a pulsed LHChG beam when it travels through a turbulent oceanic environment. The pulsed LHChG beam is a versatile form of laser beam, which can also include pulsed Laguerre-Gaussian (LG) and Gaussian beams as special cases. Its intensity in the central region can be manipulated by changing the beam parameters, making it a useful tool for various applications. The cosh function used in the pulsed LHChG beam is a combination of Gaussian functions, additionally, the Laguerre-Gaussian beam, which is a Laguerre polynomial modulated by a Gaussian envelope, has already been demonstrated and has practical uses as a vortex beam. This work aims to analyze the spectral properties of pulsed LHChG beam propagation in turbulent oceanic environments. To the best of the authors' knowledge, this topic has not been previously studied. The structure of the current manuscript is as follows: In Sect. 2, we outline the electric field distribution of pulsed LHChG beam in cylindrical coordinates at the source plane and explain the theory model regarding the spectral characteristics of the considered pulsed beam during oceanic turbulence.

The influence of turbulent oceanic parameters and the beam on the evolution behavior of pulsed LHChG beam is presented in Sect. 3. In the end, the brief summary of the main results obtained is given in Sect. 4.

2 Propagation of pulsed LHChG through the oceanic turbulence

In order to analyze the propagation of pulsed LHChG beam in a turbulent oceanic environment, we first examine the propagation of its Fourier monochromatic component and then perform the inverse Fourier transform to determine the propagation equation in the space–time domain. The electric field distribution of the pulsed LHChG beam at source plane (z = 0) is defined in cylindrical coordinates

$$E_{l,m}^{n} \left( {\rho ,\phi ,z = 0,t} \right) = A_{0} \left( {\frac{\sqrt 2 }{{w_{0} }}\rho } \right)^{l} L_{m}^{l} \left( {\frac{{2\rho^{2} }}{{w_{0}^{2} }}} \right)cosh^{n} \left( {\Omega \rho^{2} } \right)\exp \left( { - \frac{{\rho^{2} }}{{w_{0}^{2} }}} \right){\text{e}}^{il\phi } f\left( t \right),$$
(1)

where \(\rho\) and \(\varphi\) are radial and azimuthal coordinates, \(A_{0}\) is a constant (to simplify, we will take it equal to 1), \(L_{m}^{l} (.)\) denotes the Laguerre polynomial with m and l are the radial and angular mode orders, n is the order of the beam,\(w_{0}\) is the waist width of the Gaussian part, \(e^{il\phi }\) is the phase term for the beam, \(\Omega\) is the displacement parameter associated with the cosh-part, and \(f(t)\) is the temporal envelop of the initial pulsed beam with t is the time.

By using of the following relation between LG and Hermite-Gaussian modes (Abramowitz and Stegun 1970)

$$e^{il\phi } \rho^{l} L_{m}^{l} \left( {\rho^{2} } \right) = \frac{{\left( { - 1} \right)^{m} }}{{2^{2m + l} m!}}\sum\limits_{p = 0}^{m} {\sum\limits_{q = 0}^{l} {i^{q} \left( {\begin{array}{*{20}c} m \\ p \\ \end{array} } \right)\left( {\begin{array}{*{20}c} l \\ q \\ \end{array} } \right)\,H_{2p + l - q} \left( x \right)} } H_{2m - 2p + q} \left( y \right),$$
(2)

where \(H_{j} \left( . \right)\) is the jth order Hermite polynomial and \(\left( {\begin{array}{*{20}c} m \\ p \\ \end{array} } \right)\) denotes the binomial coefficient, and applying the following expression formula (Abramowitz and Stegun 1970)

$$\cosh^{n} \left( {\rho^{2} } \right) = \frac{1}{{2^{n} }}\sum\limits_{s = 0}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}e^{{a_{sn} \rho^{2} }} } ,\,{\text{with}}\,a_{sn} = 2s - n$$
(3)

Equation (1) can be expressed in the following alternative form in Cartesian coordinates

$$\begin{gathered} E_{l,m}^{n} \left( {x,y,z = 0,t} \right) = \exp \left( { - \frac{{x^{2} }}{{w_{0x}^{2} }} - \frac{{y^{2} }}{{w_{0y}^{2} }}} \right)\,\sum\limits_{p = 0}^{m} {\sum\limits_{q = 0}^{l} {\,\frac{{\left( { - 1} \right)^{m} }}{{2^{2m + l + 1} m!}}i^{q} \left( {\begin{array}{*{20}c} m \\ p \\ \end{array} } \right)\,\left( {\begin{array}{*{20}c} l \\ q \\ \end{array} } \right)H_{2p + l - q} \left( {\frac{\sqrt 2 x}{{w_{0x} }}} \right)} H_{2m - 2p + q} \left( {\frac{\sqrt 2 y}{{w_{0y} }}} \right)} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \frac{1}{{2^{n} }}\sum\limits_{s = 0}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}\exp \left( {\Omega a_{sn} x^{2} } \right)\exp \left( {\Omega a_{sn} y^{2} } \right)f\left( t \right)} . \hfill \\ \end{gathered}$$
(4)

The last equation represents the input field for the pulsed LHChG beam, which is represented as a finite sum of Hermite–Gaussian modes in the x and y Cartesian coordinates with \(r^{2} = x^{2} + y^{2} .\)

Assume that the incident pulsed beam has a Gaussian form (Agrawal 1999)

$$f\left( t \right) = e^{{ - t^{2} /T^{2} }} e^{{ - i\omega_{0} t}}$$
(5)

where \(T\) is the pulse duration and \(\omega_{0}\) is the central frequency.

Performing the Fourier transform on Eq. (4), we can obtain the following result, i.e., the field expressed in the space-frequency domain as

$$E(x,y,z = 0,\omega ) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {E(x,y,z = 0,t)e^{ - i\omega t} } dt\, = E(x,y,z = 0)f(\omega )$$
(6)

where \(f(\omega )\) is the original Fourier spectrum of the pulsed beam and is given by

$$f(\omega ) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {f(t){\text{e}}^{i\omega t} } dt$$
(7)

On substituting from Eqs. (5) into (7), the integral calculation yields

$$S^{\left( 0 \right)} \left( \omega \right) = \left| {f\left( \omega \right)} \right|^{2} = \left| {\frac{T}{\sqrt 2 }\exp \left( {\frac{{ - T^{2} \left( {\omega - \omega_{0} } \right)^{2} }}{4}} \right)} \right|^{2}$$
(8)

where \(S^{\left( 0 \right)} \left( \omega \right)\) is the original power spectrum of the incident beam.

The cross-spectral density function of pulsed LHChG beam at the input plane is given by

$$W_{0} \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{\mathbf{r}}_{{\mathbf{2}}} ,0,\omega } \right) = \left\langle {E\left( {x_{1} ,y_{1} ,0,\omega } \right)\,E^{*} \left( {x_{2} ,y_{2} ,0,\omega } \right)} \right\rangle ,\,\,$$
(9)

where \({\mathbf{r}}_{1} = \left( {x_{1} ,y_{1} } \right)\) and \({\mathbf{r}}_{{\mathbf{2}}} = \left( {x_{2} ,y_{2} } \right)\) are two arbitrary position vectors in the source plane.

Being based on the extended Huygens-Fresnel principle (Andrews and Phillips 2005), the cross-spectral density function of pulsed LHChG beam propagating through the oceanic turbulence is expressed as

$$\begin{aligned} W_{l,m}^{n} \left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} ,z,\omega } \right) = & \left( {\frac{k}{2\pi z}} \right)^{2} S^{\left( 0 \right)} \left( \omega \right)\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {W_{0} \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{\mathbf{r}}_{{\mathbf{2}}} ,0} \right)\exp \left[ { - \frac{ik}{{2z}}\left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} - {\mathbf{r}}_{{\mathbf{1}}} } \right)^{2} + \frac{ik}{{2z}}\left( {{{\varvec{\uprho}}}_{{\mathbf{2}}} - {\mathbf{r}}_{{\mathbf{2}}} } \right)^{2} } \right]} } \\ & \times \left\langle {\exp \left[ {\psi^{ * } \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{1}}} } \right) + \psi \left( {{\mathbf{r}}_{{\mathbf{2}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)} \right]} \right\rangle_{m} d^{2} {\mathbf{r}}_{{\mathbf{1}}} d^{2} {\mathbf{r}}_{{\mathbf{2}}} , \\ \end{aligned}$$
(10)

where \({{\varvec{\uprho}}}_{{\mathbf{1}}}\) and \({{\varvec{\uprho}}}_{{\mathbf{2}}}\) are two position vectors at the receiver plane. \(k = \frac{\omega }{c}\) is the wave number with c is the speed of the source radiation in vacuum, \(\left\langle . \right\rangle_{m}\) is the ensemble average over the statistics of the medium covering the fluctuation of log-amplitude and phase due to turbulent, \(\psi \left( {{\mathbf{r}},{{\varvec{\uprho}}}} \right)\) denotes the random part of the complex phase, and the asterisk denotes complex conjugate. The expression for the ensemble average is obtained from the quadratic approximation of Rytov, given by (Andrews and Phillips 2005)

$$\left\langle {\exp \left[ {{\uppsi }^{ * } \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{1}}} } \right) + {\uppsi }\left( {{\mathbf{r}}_{{\mathbf{2}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)} \right]} \right\rangle_{m} \approx \exp \left\{ { - \frac{1}{{\rho_{0}^{2} }}\left[ {\left( {{\mathbf{r}}_{{\mathbf{1}}} - {\mathbf{r}}_{{\mathbf{2}}} } \right)^{2} + \left( {{\mathbf{r}}_{{\mathbf{1}}} - {\mathbf{r}}_{{\mathbf{2}}} } \right)\left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} - {{\varvec{\uprho}}}_{{\mathbf{2}}} } \right) + \left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} - {{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)^{2} } \right]} \right\}.$$
(11)

Thus, the spatial coherence radius of a spherical wave in oceanic turbulence is read as (Belafhal et al. 2021)

$$\rho_{0} = \left[ {\frac{{\pi^{2} }}{3}k^{2} z\int\limits_{0}^{ + \infty } {\kappa^{3} \Phi_{n} \left( \kappa \right)d\kappa } } \right]^{ - 1/2} .$$
(12)

In this paper, considering the finite outer scale of oceanic turbulence and eddy diffusivity ratio effects, the spatial power spectrum model of oceanic turbulence is expressed as (Li et al. 2019)

$$\Phi_{n} \left( \kappa \right) = \beta A^{2} \varepsilon^{{ - \frac{1}{3}}} \chi_{t} \frac{{\left[ {1 + C_{1} \left( {\kappa \eta } \right)^{\frac{2}{3}} } \right]}}{{4\pi \varpi^{2} \left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{\frac{11}{6}} }}\left\{ {\varpi^{2} \exp \left[ { - \frac{{(\kappa \eta )^{2} }}{{R_{T}^{2} }}} \right]} \right.\left. { + \frac{1}{{d_{r} }}\exp \left[ { - \frac{{(\kappa \eta )^{2} }}{{R_{S}^{2} }}} \right] - \frac{{1 + d_{r} }}{{d_{r} }}\varpi \exp \left[ { - \frac{{(\kappa \eta )^{2} }}{{R_{TS}^{2} }}} \right]} \right\},\,$$
(13)

where \(\beta\) is the Obukhov–Corrsin constant, \(A = 2.6 \times 10^{ - 4} \,{\text{liter}}/\deg ,\) \(\varepsilon\) is the rate of dissipation of kinetic energy per unit mass of fluid ranging from \(10^{ - 10} \,{\text{m}}^{2} /{\text{s}}^{3}\) to \(10^{ - 1} \,{\text{m}}^{2} /{\text{s}}^{3}\), \(\chi_{t}\) is the dissipation rate of temperature variance and has the range \(10^{ - 10} \,{\text{K}}^{2} /{\text{s}}\) to \(10^{ - 2} \,{\text{K}}^{2} /{\text{s}}\), \(\eta\) is the inner scale of turbulence, \(\kappa\) is the spatial frequency of turbulent fluctuations \((0 < \kappa < \infty )\), \(\kappa_{0} = 1/L_{0}\), \(L_{0}\) is outer scale of turbulence, \(C_{1}\) is a free parameter, \(\varpi\) is the ratio of temperature and salinity contributions to the refractive index spectrum, \(R_{i} = \sqrt 3 {\kern 1pt} \left[ {W_{i} - 1/3 + 1/(9W_{i} )} \right]^{3/2} /Q^{3/2} ,\,\,(i = T; S; TS)\) with \(Q = 2.5\) is the non-dimensional constant, \(W_{i} = \left\{ {\left[ {\Pr_{i}^{2} /\left( {6\beta Q^{ - 2} } \right)^{2} - \Pr_{i}^{{}} /\left( {81\beta Q^{ - 2} } \right)} \right]^{1/2} - \left[ {1/27 - \Pr_{i}^{{}} /\left( {6\beta Q^{ - 2} } \right)} \right]} \right\}^{1/3} ,\)\(\Pr_{T} = 7\) and \(\Pr_{T} = 700\) represent the Prandtl numbers of the temperature and salinity, respectively,\(\Pr_{TS} = 2\Pr_{T} \Pr_{S} /(\Pr_{T} + \Pr_{S} ),\)and \(d_{r}\) defines the eddy diffusivity ratio and can be expressed (Li et al. 2019)

$$d_{r} = \frac{\left| \varpi \right|}{{R_{F} }} \approx \left\{ {\begin{array}{*{20}l} {1/(1 - \sqrt {(|\varpi | - 1)/|\varpi |} } & {|\varpi |\, \ge 1} \\ {1.85|\varpi | - 0.85} & {0.5 \le \,|\varpi |\, \le 1} \\ {0.15|\varpi |} & {|\varpi |\, \le 0.5} \\ \end{array} } \right.$$
(14)

where \(R_{F}\) is the eddy flux ratio.

By invoking the integral formula (Belafhal et al. 2021).

$$\int\limits_{0}^{ + \infty } {\frac{{t^{2\mu - 1} e^{{ - \varepsilon t^{2} }} }}{{\left( {1 + ct^{2} } \right)^{\nu } }}} dt = \frac{\Gamma \left( \mu \right)}{{2c^{\mu } }}U\left( {\mu ;\mu + 1 - \nu ;\frac{\varepsilon }{c}} \right),\,{\text{with}}\,\mu > 0\,\mu > 0$$
(15)

where \(U\left( {a;b;z} \right)\) denoting the Tricomi function, and after tedious but straightforward integral calculations, the expression of the spatial coherence length can be arranged as

$$\rho _{0} = \left( {\frac{1}{{24}}\pi k^{2} z\beta A^{2} \varepsilon ^{{ - \frac{1}{3}}} \chi _{t} } \right)^{{ - 1/2}} \left\{ \begin{gathered} \kappa _{0}^{{1/3}} \left[ \begin{aligned} U\left( {2;\frac{7}{6};\frac{{\kappa _{0}^{2} \eta ^{2} }}{{R_{T}^{2} }}} \right) & + \frac{1}{{\varpi ^{2} d_{r} }}U\left( {2;\frac{7}{6};\frac{{\kappa _{0}^{2} \eta ^{2} }}{{R_{S}^{2} }}} \right) \\ - \frac{{1 + d_{r} }}{{\varpi d_{r} }}U\left( {2;\frac{7}{6};\frac{{\kappa _{0}^{2} \eta ^{2} }}{{R_{{TS}}^{2} }}} \right) \\ \end{aligned} \right] \hfill \\ + 1.191C_{1} \eta ^{{\frac{2}{3}}} \kappa _{0} \times \left[ \begin{gathered} U\left( {\frac{7}{3};\frac{3}{2};\frac{{\kappa _{0}^{2} \eta ^{2} }}{{R_{T}^{2} }}} \right) + \frac{1}{{\varpi ^{2} d_{r} }}U\left( {\frac{7}{3};\frac{3}{2};\frac{{\kappa _{0}^{2} \eta ^{2} }}{{R_{S}^{2} }}} \right) \hfill \\ - \frac{{1 + d_{r} }}{{\varpi d_{r} }}U\left( {\frac{7}{3};\frac{3}{2};\frac{{\kappa _{0}^{2} \eta ^{2} }}{{R_{{TS}}^{2} }}} \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right\}^{{ - 1/2}}$$
(16)

In the next step, we will investigate the propagation properties of a pulsed LHChG beam through oceanic turbulence. By letting \({{\varvec{\uprho}}}_{{\mathbf{1}}} = {{\varvec{\uprho}}}_{2} = {{\varvec{\uprho}}}\) and inserting Eqs. (11) and (16) into Eq. (10), the following result is obtained

$$\begin{aligned} W_{l,m}^{n} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) = & S^{\left( 0 \right)} \left( \omega \right)\left( {\frac{k\,}{{2\pi \,z}}} \right)^{2} \frac{1}{{2^{4m + 2l + 2n} \left( {m!} \right)^{2} }}\sum\limits_{p = 0}^{m} {\sum\limits_{q = 0}^{l} {\sum\limits_{{r_{1} = 0}}^{m} {\sum\limits_{{r_{2} = 0}}^{l} {\sum\limits_{{s_{1} = 0}}^{n} {\sum\limits_{{s_{2} = 0}}^{n} {\left( {\begin{array}{*{20}c} m \\ p \\ \end{array} } \right)} } \,\left( {\begin{array}{*{20}c} l \\ q \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ {r_{1} } \\ \end{array} } \right)\,\left( {\begin{array}{*{20}c} l \\ {r_{2} } \\ \end{array} } \right)} } \,\left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ {s_{2} } \\ \end{array} } \right)\,i^{q} \left( { - i} \right)^{{r_{2} }} } } \\ & \times \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {H_{2p + l - q} \left( {{{\sqrt 2 x_{1} } \mathord{\left/ {\vphantom {{\sqrt 2 x_{1} } {w_{0x} }}} \right. \kern-0pt} {w_{0x} }}} \right)\exp \left[ { - \beta_{1x} x_{1}^{2} + 2\left( {v_{x} + \frac{{x_{2} }}{{\rho_{0}^{2} }}} \right)x_{1} } \right]H_{2m - 2p + q} \left( {{{\sqrt 2 y_{1} } \mathord{\left/ {\vphantom {{\sqrt 2 y_{1} } {w_{0y} }}} \right. \kern-0pt} {w_{0y} }}} \right)\exp \left[ { - \beta_{1y} y_{1}^{2} + 2\left( {v_{y} + \frac{{y_{2} }}{{\rho_{0}^{2} }}} \right)y_{1} } \right]} } dx_{1} dy_{1} \\ & \times \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {H_{{2r_{1} + l - r_{2} }} \left( {{{\sqrt 2 x_{2} } \mathord{\left/ {\vphantom {{\sqrt 2 x_{2} } {w_{0x} }}} \right. \kern-0pt} {w_{0x} }}} \right)\exp \left[ { - \beta_{2x}^{{}} x_{2}^{2} - \frac{ik}{z}\rho_{x} x_{2} } \right]H_{{2m - 2r_{1} + r_{2} }} \left( {{{\sqrt 2 y_{2} } \mathord{\left/ {\vphantom {{\sqrt 2 y_{2} } {w_{0y} }}} \right. \kern-0pt} {w_{0y} }}} \right)\exp \left[ { - \beta_{2y}^{{}} y_{2}^{2} - \frac{ik}{z}\rho_{y} y_{2} } \right]dx_{2} dy_{2} } } , \\ \end{aligned}$$
(17)

where

$$\beta_{1j} = \frac{1}{{w_{0j}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{ik}{{2z}} - \Omega a_{{s_{1} n}} ,$$
(18)
$$\beta_{2j} = \frac{1}{{w_{0j}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}} - \Omega a_{{s_{2} n}} ,$$
(19)

and

$$v_{j} = \frac{{ik\rho_{j} }}{z},$$
(20)

with (j = x or y).

Furthermore, by using the expansion formulae (Abramowitz and Stegun 1970; Belafhal et al. 2020)

$$H_{n} \left( x \right) = \sum\limits_{k = 0}^{{\left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right]}} {\left( { - 1} \right)^{k} \frac{n!}{{k!\left( {n - 2k} \right)!}}\left( {2x} \right)^{n - 2k} } ,$$
(21)
$$H_{n} \left( {x + y} \right) = \frac{1}{{2^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}}} }}\sum\limits_{k = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ k \\ \end{array} } \right)H_{k} \left( {\sqrt 2 x} \right)} H_{n - k} \left( {\sqrt 2 y} \right),$$
(22)

and the following integrals

$$\int\limits_{ - \infty }^{ + \infty } {\exp \left( { - px^{2} + 2qx} \right)H_{m} \left( {\alpha x} \right)\,dx} = \sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\left[ {1 - \frac{{\alpha^{2} }}{p}} \right]^{{{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}}} H_{m} \left[ {\frac{\alpha q}{{p\sqrt {1 - \left( {{{\alpha^{2} } \mathord{\left/ {\vphantom {{\alpha^{2} } p}} \right. \kern-0pt} p}} \right)} }}} \right],$$
(23)

and

$$\int\limits_{ - \infty }^{ + \infty } {x^{l} \exp \left( { - px^{2} + 2qx} \right)H_{m} \left( {\alpha x} \right)\,dx} = \sqrt {\frac{\pi }{p}} \frac{{\exp \left( {{{q^{2} } \mathord{\left/ {\vphantom {{q^{2} } p}} \right. \kern-0pt} p}} \right)}}{{2^{l} }}\sum\limits_{k = 0}^{{\left[ {{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0pt} 2}} \right]}} {\frac{{\left( { - 1} \right)^{k} m!}}{{k!\left( {m - 2k} \right)!}}} H_{m + l - 2k} \left( {\frac{iq}{{\sqrt p }}} \right)\left( {\frac{\alpha }{i\sqrt p }} \right)^{m + l - 2k} ,$$
(24)

with \(\Re e\,p > 0\),and after extensive algebraic calculations, the spectral intensity of a pulsed LHChG beam in oceanic turbulence is given by

$$S_{l,m}^{n} \left( {\rho_{x} ,\rho_{y} ,z,\omega } \right) = W_{l,m}^{n} \left( {{{\varvec{\uprho}}},{{\varvec{\uprho}}},z,\omega } \right) = S^{\left( 0 \right)} \left( \omega \right)M_{l,m}^{n} \left( {\rho_{x} ,\rho_{y} ,z,\omega } \right)$$
(25)

where

$$M_{l,m}^{n} \left( {\rho_{x} ,\rho_{y} ,z,\omega } \right) = \left( {\frac{k\,}{{2\pi \,z}}} \right)^{2} \frac{1}{{2^{5(m + 0.5l) + 2n} \left( {m!} \right)^{2} }}\sum\limits_{p = 0}^{m} {\sum\limits_{q = 0}^{l} {\sum\limits_{{r_{1} = 0}}^{m} {\sum\limits_{{r_{2} = 0}}^{l} {\sum\limits_{{s_{1} = 0}}^{n} {\sum\limits_{{s_{2} = 0}}^{n} {\left( {\begin{array}{*{20}c} m \\ p \\ \end{array} } \right)} } \,\left( {\begin{array}{*{20}c} l \\ q \\ \end{array} } \right)\left( {\begin{array}{*{20}c} m \\ {r_{1} } \\ \end{array} } \right)\,\left( {\begin{array}{*{20}c} l \\ {r_{2} } \\ \end{array} } \right)} } \,} } \left( {\begin{array}{*{20}c} n \\ {s_{1} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ {s_{2} } \\ \end{array} } \right)\,i^{q} \left( { - i} \right)^{{r_{2} }} S_{x} S_{y} ,$$
(26)

with

$$\begin{aligned} {\text{S}}_{x} = & \frac{1}{{\sqrt {\beta_{1x} b_{x} } }}\exp \left( {\frac{{v_{x}^{2} }}{{\beta_{1x} }} + \frac{{{\upgamma }_{x}^{2} }}{{b_{x} }}} \right)\left( {1 - \frac{2}{{w_{0x}^{2} \beta_{1x} }}} \right)^{{\frac{2p + l - q}{2}}} \sum\limits_{\mu = 0}^{2p + l - q} {\sum\limits_{{f_{1} = 0}}^{{\left[ {{\mu \mathord{\left/ {\vphantom {\mu 2}} \right. \kern-0pt} 2}} \right]}} {\sum\limits_{{h_{1} = 0}}^{{\left[ {{{(2r_{1} + l - r_{2} )} \mathord{\left/ {\vphantom {{(2r_{1} + l - r_{2} )} 2}} \right. \kern-0pt} 2}} \right]}} {\left( {\begin{array}{*{20}c} {2p + l - q} \\ \mu \\ \end{array} } \right)} } } \\ & \times \frac{{\left( { - 1} \right)^{{f_{1} + h_{1} }} }}{{2^{{\mu - 2f_{1} }} }}\frac{\mu !}{{f_{1} !\left( {\mu - 2f_{1} } \right)!}}\frac{{\left( {2q + l - r_{1} } \right)!}}{{h_{1} !\left( {2r_{1} + l - r_{2} - 2h_{1} } \right)!}}\left( {\frac{{2\sqrt 2 \alpha_{x} }}{{\rho_{0}^{2} }}} \right)^{{\mu - 2f_{1} }} \\ & \times \left( {\frac{\sqrt 2 }{{iw_{0x} \sqrt {b_{x} } }}} \right)^{{2r_{1} + l - r_{2} + \mu - 2f_{1} - 2h_{1} }} H_{2p + l - q - \mu } \left( {\sqrt 2 \alpha_{x} v_{x} } \right)H_{{2r_{1} + l - r_{2} + \mu - 2f_{1} - 2h_{1} }} \left( {\frac{{i\gamma_{x} }}{{\sqrt {b_{x} } }}} \right), \\ \end{aligned}$$
(27)
$$\begin{aligned} S_{y} = & \frac{1}{{\sqrt {\beta_{1y} b_{y} } }}\exp \left( {\frac{{v_{y}^{2} }}{{\beta_{1y} }} + \frac{{\gamma_{y}^{2} }}{{b_{y} }}} \right)\left( {1 - \frac{2}{{w_{0y}^{2} \beta_{1y} }}} \right)^{{\frac{2m - 2p + q}{2}}} \sum\limits_{\sigma = 0}^{2p + l - q} {\sum\limits_{{f_{2} = 0}}^{{\left[ {{\sigma \mathord{\left/ {\vphantom {\sigma 2}} \right. \kern-0pt} 2}} \right]}} {\sum\limits_{{h_{2} = 0}}^{{\left[ {{{(2m - 2r_{1} + r_{2} )} \mathord{\left/ {\vphantom {{(2m - 2r_{1} + r_{2} )} 2}} \right. \kern-0pt} 2}} \right]}} {\left( {\begin{array}{*{20}c} {2p + l - q} \\ \sigma \\ \end{array} } \right)} } } \\ & \times \frac{{\left( { - 1} \right)^{{f_{2} + h_{2} }} }}{{2^{{\sigma - 2f_{2} }} }}\frac{\sigma !}{{f_{2} !\left( {\sigma - 2f_{2} } \right)!}}\frac{{\left( {2m - 2r_{1} + r_{2} } \right)!}}{{h_{2} !\left( {2m - 2r_{1} + r_{2} - 2h_{2} } \right)!}}\left( {\frac{{2\sqrt 2 \alpha_{y} }}{{\rho_{0}^{2} }}} \right)^{{\sigma - 2f_{2} }} \\ & \times \left( {\frac{\sqrt 2 }{{iw_{0y} \sqrt {b_{y} } }}} \right)^{{2m - 2r_{1} + r_{2} + \sigma - 2f_{2} - 2h_{2} }} H_{2m - 2p + q - \sigma } \left( {\sqrt 2 \alpha_{y} v_{y} } \right)H_{{2m - 2p + q + \sigma - 2f_{2} - 2h_{2} }} \left( {\frac{{i\gamma_{y} }}{{\sqrt {b_{y} } }}} \right), \\ \end{aligned}$$
(28)
$$b_{j} = \beta_{2j} - \frac{1}{{\beta_{j} \rho_{0}^{4} }},$$
(29)
$$\gamma_{j} = v_{j} \left( {\frac{1}{{\beta_{1j} \rho_{0}^{2} }} - 1} \right),$$
(30)

and

$$\alpha_{j} = \frac{\sqrt 2 }{{w_{0j} \beta_{j} \sqrt {1 - \left( {{2 \mathord{\left/ {\vphantom {2 {w_{0j}^{2} \beta_{j} }}} \right. \kern-0pt} {w_{0j}^{2} \beta_{j} }}} \right)} }},\,\left( {j\, = \,x\,{\text{or}}\,y} \right).$$
(31)

In Eq. (25), \(M_{l,m}^{n} \left( {\rho_{x} ,\rho_{y} ,z,\omega } \right)\) is referred to as a spectral modifier. They state that the spectral intensity of this beam is determined by a combination of two factors: the original spectrum of the beam \(S^{(0)} \left( \omega \right)\) and a spectral modifier \(M_{l,m}^{n} \left( {\rho_{x} ,\rho_{y} ,z,\omega } \right)\). The original spectrum depends on the pulse duration T and the central frequency \(\omega_{0}\), while the spectral modifier depends on the observation point, propagation distance z, initial beam parameters and oceanic parameters.

Based on the findings from this Section, we will examine numerically the change in behavior of a pulsed LHChG beam as it travels through the turbulence in oceanic environment.

3 Simulation results and discussion

In this Section, the influence of oceanic turbulence on the spectral intensity of pulsed LHChG beam is demonstrated through numerical calculations using Eq. (25). The normalized on-axis and off-axis spectral intensities of the resulting beam after propagation through oceanic turbulence are discussed by using the relative spectral shift. This later is given by \({{\delta \omega } \mathord{\left/ {\vphantom {{\delta \omega } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} = {{\left( {\omega_{\max } - \omega_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {\omega_{\max } - \omega_{0} } \right)} {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}\), where \(\omega_{\max }\) is the frequency related to the maximum spectral intensity. For \({{\delta \omega } \mathord{\left/ {\vphantom {{\delta \omega } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} > 0\), the spectral intensity is blue-shifted and for \({{\delta \omega } \mathord{\left/ {\vphantom {{\delta \omega } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }} < 0\), the spectral intensity is red-shifted. For the sake of simplicity, the normalized original spectrum is taken as \(S^{00} (\omega ) = S^{\left( 0 \right)} \left( \omega \right)/S^{\left( 0 \right)} \left( {\omega_{0} } \right)\), the normalized spectral intensity is \(S_{l,m}^{n} (\omega ) = S_{l,m}^{n} (\rho_{x} ,\rho_{y} ,z,\omega )/S_{l,m}^{n} (\rho_{x} ,\rho_{y} ,z,\omega_{\max } )\) and the normalized spectral modifier is given by \(M_{l,m}^{n} (\omega_{0} ) = M_{l,m}^{n} (\rho_{x} ,\rho_{y} ,z,\omega_{0} )/M_{(l,m)\max }^{n} (\rho_{x} ,\rho_{y} ,z,\omega_{0} )\) where \(M_{(l,m)\max }^{n} (\rho_{x} ,\rho_{y} ,z,\omega_{0} )\) is the maximum value of \(M_{l,m}^{n} (\rho_{x} ,\rho_{y} ,z,\omega_{0} )\) at the observation point \((\rho_{x} ,\rho_{y} ,z)\).

The study focuses on investigating the effects of oceanic turbulence on the spectral modifier of a pulsed LHChG beam during propagation. The calculation parameters are \(\Omega = 0.1\,m^{ - 1}\), \(\varepsilon = 10^{ - 7} {\text{m}}^{2} /{\text{s}}^{3}\), \(\chi_{t} = 10^{ - 5} {\text{K}}^{2} /s,\)\(\varpi = - 3\), \(\lambda = 532\,{\text{nm}}\), \(w_{0x} = w_{0y} = 1{\text{mm}}\), \(\omega_{0} = 2\pi c/\lambda\), \({\text{m}} = l = 1\) and n = 3.

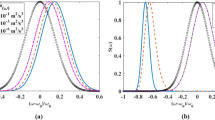
To begin this study, we depict in Fig. 1 the cross line \((\rho_{y} = 0)\) and corresponding contour graphs of the normalized spectral modifier of a pulsed LHChG beam at the plane \(z = 200\,{\text{m}}\) for several dissipation rates of temperature variance \(\chi_{t} .\) As shown in Fig. 1, we observe that the pulsed LHChG beam will transform into a profile that resembles a Gaussian beam more quickly as the \(\chi_{t}\) increases. This behavior can be attributed to the fact that the strength of oceanic turbulence intensifies with an increase in \(\chi_{t}\).¨

Fig. 1
figure 1

Evolution of the normalized spectral modifier of a pulsed LHChG beam in turbulence oceanic with several dissipation rates of temperature variance \(\chi_{t}\) at a propagation distance \(z = 200\,{\text{m}}\)

Full size image

Figure 2 illustrates the cross line and contour graphs of the normalized spectral modifier of a pulsed LHChG beam for various rates of dissipation of kinetic energy per unit mass of fluid ε, using the calculation parameters outlined in Fig. 1.

Fig. 2
figure 2

Evolution of the normalized spectral modifier of a pulsed LHChG beam in turbulence oceanic with several rate of dissipation of kinetic energy per unit mass of fluid at a propagation distance \(z = 200\,m\)

Full size image

The results indicate that as ε decreases, the pulsed LHChG beam transforms into a profile resembling a Gaussian beam more rapidly. This trend can be attributed to the fact that the strength of oceanic turbulence increases as ε decreases.

Here, we present the impact of initial beam parameters, oceanic turbulence, and transverse positions on the spectral intensity and relative spectral shifts of the pulsed LHChG beam. The calculation parameters used for this analysis are \(\Omega = 0.1\,{\text{m}}^{ - 1}\), \(\varepsilon = 10^{ - 7}\, {\text{m}}^{2} /{\text{s}}^{3}\), \(\chi_{t} = 10^{ - 3} \,{\text{K}}^{2} /{\text{s}}\), \(\varpi = - 3\), \(\lambda = 532\,{\text{nm}}\), \(w_{0x} = w_{0y} = 1\,{\text{mm}}\), \(z = 900\,{\text{m}}\), \(\omega_{0} = 2\pi c/\lambda\), \(T = 3fs,\)\(\rho_{y} = 0,\) \({\text{m}} = {\text{l}} = 1\) and n = 3.

We depict in Fig. 3, the normalized on-axis and off-axis spectral intensities of the pulsed LHChG beam for different values of the pulse duration. The original spectral intensity is indicated by circles. As depicted in Fig. 3a, it's clear that the on-axis spectral intensity of the pulsed LHChG beam shows a blue-shift, which decreases as the pulse duration increases. However, Fig. 3b displays the normalized off-axis \((\rho_{x} = 0.2286{\kern 1pt} {\kern 1pt} {\text{m}})\) spectral intensity of the pulsed LHChG beam. The results show that the spectral intensity has a blue-shift and is divided into two peaks with different heights. At T = 3 fs, the initially blue-shifted spectrum splits into two peaks with unequal heights. As the pulse duration increases, the blue shift decreases, and the two peaks become equal in height at T = 5 fs. Beyond T = 7 fs, the secondary peak becomes higher than the first.

Fig. 3
figure 3

Normalized spectral intensity of pulsed LHChG beam in oceanic turbulence with varying pulse duration, for both a on-axis and b off-axis \((\rho_{x} = 0.2286\;{\text{m}})\)

Full size image

Figure 4 displays the normalized on-axis and off-axis spectral intensity of the pulsed LHChG beam for various values of the rate of dissipation of kinetic energy per unit mass of fluid. The original spectral intensity is depicted as circles. In Fig. 4a, it is evident that the on-axis spectral intensity of the pulsed LHChG beam has a blue shift. Moreover, the magnitude of this blue shift increases as ε increases. In contrast, Fig. 4b illustrates that the off-axis spectral intensity of the pulsed LHChG beam has a blue shift and is split into two peaks with different heights. As ε decreases, the second peak increases gradually in height. At \(\varepsilon = 10^{ - 8} {\text{m}}^{2} /{\text{s}}^{3}\) the spectrum is split into two peaks with equal heights. This phenomenon is called the spectral switch. Further decreasing ε to \(\varepsilon = 10^{ - 9} {\text{m}}^{2} /{\text{s}}^{3}\) leads to the second peak becoming the maximum peak, i.e., the spectrum is red-shifted.

Fig. 4
figure 4

Normalized spectral intensity of pulsed LHChG beam in oceanic turbulence with varying the rate of dissipation of kinetic energy per unit mass of fluid, for both a on-axis and b off-axis \((\rho_{x} = 0.24\;{\text{m}})\)

Full size image

The normalized on-axis and off-axis spectral intensities of the pulsed LHChG beam for different values of the dissipation rate of temperature variance \(\chi_{t}\) are depicted in Fig. 5, respectively, where the circles denote the normalized original spectrum. Figure 5a shows that the normalized on-axis spectrum is blue-shifted, and the blue shift increases with increasing \(\chi_{t} .\) For example, for \(\chi_{t} = 10^{ - 6}\, {\text{K}}^{2} /{\text{s}}\), \(\chi_{t} = 10^{ - 5}\, {\text{K}}^{2} /{\text{s}}\), and \(\chi_{t} = 10^{ - 3}\, {\text{K}}^{2} /{\text{s}}\), we have \(\delta \omega /\omega_{0} = 0.0334,\) 0.0522 and 0.0602, respectively. However, as illustrated in Fig. 5b, the off-axis \((\rho_{x} = 0.12{\kern 1pt} {\text{m}})\) spectral intensity exhibits a red shift, which becomes a blue shift with an increase in the dissipation rate of temperature variance \(\chi_{t}\). For instance, for values of \(\chi_{t} =\): \(10^{ - 6}\, {\text{K}}^{2} /{\text{s}}\), \(10^{ - 5} \,{\text{K}}^{2} /{\text{s}}\) and \(10^{ - 3}\, {\text{K}}^{2} /{\text{s}}\), the corresponding spectral shifts are \(\delta \omega /\omega_{0}\) = − 0.0147, 0.0067, and 0.0682, respectively.

Fig. 5
figure 5

Normalized spectral intensity of pulsed LHChG beam in oceanic turbulence for three values of the dissipation rate of temperature variance with a on-axis and b off axis \((\rho_{x} = 0.12\;{\text{m}})\)

Full size image

Figure 6 shows the normalized on-axis and off-axis spectral intensities of the pulsed LHChG beam for different values of the ratio of the temperature and salinity contributions to the refractive index spectrum, indicated by \(\varpi\). The original normalized spectrum is represented by circles. In Fig. 6a, it is evident that the spectral intensity along the axis of the pulsed LHChG beam is blue-shifted, and that its magnitude of this blue shift decreases as \(\varpi\) increases.

Fig. 6
figure 6

Normalized spectral intensity of pulsed LHChG beam in oceanic turbulence for three values of the ratio of temperature and salinity contributions to the refractive index spectrum with a on-axis and b off axis \((\rho_{x} = 0.35\;{\text{m}})\)

Full size image

Conversely, the off-axis spectral intensity is red-shifted for all values of \(\varpi\) (from the results in Fig. 6b), and the red shift increases as \(\varpi\) decreases. These observations suggest that the on-axis and off-axis spectra tend to approach the original spectrum when is close to \(\varpi = - 1\).

Figure 7 depicts the off-axis relative spectral shift of a pulsed LHChG beam in oceanic turbulence as a function of transverse coordinate \(\rho_{x}\) for various pulse durations and different values of the ratio of temperature and salinity contributions to the refractive index spectrum \(\varpi\). Within the range of 0 to 0.5 m, the spectrum shows a slight blue shift at the starting point of \(\rho_{x}\) = 0, and this blue shift becomes more pronounced as both the pulse duration decreases and increases. As the transverse coordinate continues to increase, the spectrum exhibits a red shift, and the magnitude of this red shift gradually increases, accompanied by a spectral switch.

Fig. 7
figure 7

Relative spectral shift versus \(\rho_{x}\) for the different a pulse duration and b the ratio of temperature and salinity contributions to the refractive index spectrum

Full size image

Additionally, it can be observed that the third spectral switch disappears as T decreases (see Fig. 7a) and \(\varpi\) increases (see Fig. 7b).

In Fig. 8, the off-axis relative spectral shift is shown as a function of the transverse coordinate \(\rho_{x}\) for different values of the rate of dissipation of kinetic energy per unit mass of fluid ε and the dissipation rate of temperature variance \(\chi_{t}\). This figure shows that the spectral shift exhibits a slight blue shift at \(\rho_{x}\) = 0, and the blue shift becomes larger as ε and \(\chi_{t}\) increase. As the position parameter continues to increase, the spectrum is red-shifted, and the amount of red shift increases gradually, accompanied by a spectral switch.

Fig. 8
figure 8

Relative spectral shift versus \(\rho_{x}\) and for the different a the rate of dissipation of kinetic energy per unit mass of fluid and b the dissipation rate of temperature variance

Full size image

Figure 8a demonstrates that with the decrease of the energy dissipation rate per unit mass ε, the third spectral switches disappears for the case of \(\varepsilon = 10^{ - 10}\, {\text{m}}^{2} /{\text{s}}^{3}\). On the other hand, Fig. 8b shows that with decreasing the dissipation rate of temperature variance \(\chi_{t}\) and as the position parameter increases, the third spectral switch disappears for the case of \(\chi_{t} = 10^{ - 4}\, {\text{K}}^{2} /{\text{s}}\). In addition, the second and third spectral switches disappear for the case of \(\chi_{t} = 10^{ - 6}\, {\text{K}}^{2} /{\text{s}}.\)

In Fig. 9, the normalized off-axis spectral intensity of a pulsed LHChG beam propagating through the oceanic turbulence for different values of the transverse coordinate is depicted.

Fig. 9
figure 9

The variation of normalized off-axis spectral intensity of pulsed LHChG beam in oceanic turbulence

Full size image

It is shown that the off-axis spectrum is split into two peaks, i.e., one maximum peak with the second peak. Figures 9a and b show that as \(\rho_{x}\) increases from 0.205 to 0.22 m, the red shift increases and the second peak of the spectrum becomes large. Figure 9c shows that the two peaks reach the same height at \(\rho_{x} =\) 0.2273 m. Figures 9d and e show that as d continues to increase, blue shift occurs and the blue shift decreases gradually. This means that the spectral shift changes abruptly from red to blue when \(\rho_{x}\) reaches a critical value.

4 Conclusion

In summary, the changes in spectral intensity of a pulsed LHChG beam as it propagates through oceanic turbulence are investigated in the present work. To achieve that, a formula based on the Huygens-Fresnel principle and Fourier Transform method is presented, and numerical simulations are conducted to validate the results. The paper analyzes the impact of oceanic turbulence parameters and pulse duration on the spectral behavior of the beam and provides a physical explanation for the spectral transition observed. The findings have significant implications for information coding and transmission.