Scintillation index analysis of generalized Bessel-Laguerre-Gaussian beam

Abstract

In this paper, we present a detailed investigation of the Generalized Bessel-Laguerre-Gaussian (GBLG) beam propagating in a maritime turbulent atmosphere. Based on the born approximation and the Rytov theory with the use of the Von Karman spectrum, the scintillation index of the GBLG beam is evaluated and examined numerically. The obtained results indicate that the comportment of the GBLG beam is influenced by the turbulent strength, the inner scale of the maritime turbulent atmosphere, and the input beam parameters. The scintillation indexes of Laguerre-Bessel-Gaussian, Laguerre-Gaussian, Bessel-Gaussian and Gaussian beams through the considered medium are deduced as particular cases from our study.

1 Introduction

In recent years, several studies have been conducted to study the impact of the maritime turbulent atmosphere on the propagation properties of laser beams due to their practical applications in free-space optical communications, remote detection, optical imaging and laser radar (Andrews and Phillips 1998; Andrews et al. 2001; Majumdar 2014). Different aspects of optical turbulence in a turbulent medium are examined such as the average intensity, the beam spread, the beam wander and the scintillation index and others (Andreas 1988; Al-Habash et al. 2001; Andrews 1992; Andrews and Philips 2005; Arimoto 2010; Barry 1994; Bird and Riordan 1986). However, during the propagation of a laser beam in a turbulent atmosphere with small variations in the temperature causing random changes in the atmospheric refractive index; which leads to scintillation. This later is one of the most important effects of the atmospheric turbulence which can limit the performance of the propagation beam.

Using the scintillation index, the propagation properties of laser beams propagating in maritime atmospheric turbulence have been widely investigated, including those of Gaussian beams (Ata and Baykal 2019), flat-topped Gaussian beams (Khannous and Belafhal 2016a, b) and (Baykal and Eyyuboglu 2006), Li’s flattened Gaussian and hollow Gaussian beams (Khannous et al. 2014; Khannous and Belafhal 2016a, b), lowest order Bessel-Gaussian beams (Eyyuboglu et al. 2008), Laguerre-Gaussian beams (Eyyuboglu et al. 2010) and Flattened-Gaussian beams (Cowan 2006). More recently, the scintillation index of focused Gaussian, sinusoidal Gaussian and Mathieu-Gaussian beams has been examined (Abbas et al. 2021; Gerçekcioğlu and Baykal 2021; Bayraktar 2021; Du et al. 2021).

In this study, we will interest to the scintillation index of the GBLG beam propagating in the marine atmospheric turbulence by using the born approximation, Rytov theory, and Von Karman spectrum. In Sect. 2, we evaluate the analytical expression of the scintillation index of the GBLG beam based on the normalized perturbation with the born approximation and the statistical moments in the Rytov approximation. In Sect. 3 we deduce from our main result the scintillation index of several beams as: Laguerre-Bessel-Gaussian, Laguerre-Gaussian, Bessel-Gaussian and fundamental Gaussian beams. To illustrate the obtained results, we will present some numerical examples and discussion in Sect. 4. Finally, the main results are underlined in conclusion.

2 The scintillation index of GBLG beam

The field distribution of the GBLG beam at the source plane is defined by (Boufalah et al. 2019) as the following form

$$ V(r,\theta ,0) = \left( {\frac{\sqrt 2 r}{{\omega_{0} }}} \right)^{\ell } L_{q}^{\ell } \left( {\frac{{2r^{2} }}{{\omega_{0}^{2} }}} \right)\sum\limits_{n = 0}^{N} {\exp \left( {i\left( {\ell + n} \right)\theta } \right)b_{n} J_{n} \left( {\frac{\alpha r}{{\omega_{0} }}} \right)\sum\limits_{m = 1}^{M} {g_{mM} \exp \left( { - \frac{{m\varpi r^{2} }}{{\omega_{0}^{2} }}} \right)} } , $$

(1)

where

$$ g_{mM} = \left( { - 1} \right)^{m + 1} \frac{{M\left( {M - 1} \right)...\left( {M - m + 1} \right)}}{m!}, $$

(1.a)

and

$$ \varpi = \sum\limits_{m = 1}^{M} \frac{1}{m} . $$

(1.b)

In Eq. (1), $\omega_{0}$ is the spot size of the fundamental Gaussian mode, M the order of flat-topped, N the order of generalized Bessel, $b_{n}$ is an arbitrary constant, $(r,\theta )$ are the polar coordinates, $J_{n} \left( . \right)$ is the nth-order Bessel function of the first kind, $\alpha$ represents the transverse component of the wave factor and $L_{q}^{\ell } \left( . \right)$ indicates the associated Laguerre polynomial with $\ell$ and $q$ corresponding to radial mode numbers.

The scintillation index of laser beam propagating in maritime turbulent atmosphere is expressed as (Andrews and Philips 2005; Cowan 2006)

$$ \sigma_{I}^{2} \left( L \right) = 2{\text{Re}} \,\left[ {E_{2} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) + E_{3} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right)} \right], $$

(2)

where $E_{2} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right)$ and $E_{3} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right)$ are the statistical moments defined as

$$ E_{2} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) = < \Phi_{1} \left( {\vec{r}_{1} } \right)\Phi_{1}^{*} \left( {\vec{r}_{2} } \right) > , $$

(3)

_and

$$ E_{3} \left( {\vec{r}_{1} ,\vec{r}_{2} } \right) = < \Phi_{1} \left( {\vec{r}_{1} } \right)\Phi_{1} \left( {\vec{r}_{2} } \right) > , $$

(4)

with $\left\langle . \right\rangle$ represents the overall average of two quantities, * denotes the conjugate complex and $\Phi_{1} \left( {\vec{r}} \right)$ is the normalized first order perturbation.

The scintillation index of the GBLG beam is evaluated by using the field distribution of this beam propagating through free space at z plane, expressed in Ref. (Boufalah et al. 2019) as

$$ \begin{aligned} V_{0} (r,\theta ,z) & = A_{\ell } \left( z \right)r^{\ell } \exp \left( {\frac{{ikr^{2} }}{{2z}}} \right)\sum\limits_{{m = 1}}^{M} {\frac{{g_{{mM}} }}{{\beta _{m}^{{\ell + 1}} \left( z \right)}}\exp \left( { - \frac{{k^{2} r^{2} }}{{4z^{2} \beta _{m} \left( z \right)}}} \right)} \\ & \times \,\sum\limits_{{n = 0}}^{N} {b_{n} D_{n} \left( z \right)r^{n} \exp \left( {i\left( {\ell + n} \right)\theta } \right)\,} \sum\limits_{{p = 0}}^{q} {B_{p} \left( z \right)} \sum\limits_{{j = 0}}^{\infty } {C_{j} \left( z \right)L_{{p + j}}^{{\ell + n}} \left( {\frac{{k^{2} r^{2} }}{{4z^{2} \beta _{m} \left( z \right)}}} \right)} , \\ \end{aligned}$$

(5)

where

$$ \beta_{m} \left( z \right) = m\gamma \varpi - \frac{ik}{{2z}}, $$

(5.a)

$$ A_{\ell } \left( z \right) = \frac{ - ik}{{2z}}\,\left( {\frac{i\sqrt 2 k}{{2\omega_{0} z}}} \right)^{\ell } \exp \left( {ikz} \right), $$

(5.b)

$$ B_{p} \left( z \right) = \frac{{\left( { - 1} \right)^{p} \left( {q + \ell } \right)!}}{{p!\left( {\ell + p} \right)!\left( {q - p} \right)!}}\left( {\frac{2\gamma }{{\beta_{m} \left( z \right)}}} \right)^{p} , $$

(5.c)

$$ C_{j} \left( z \right) = \frac{{\left( { - 1} \right)^{j} \Gamma \left( {p + j + 1} \right)}}{{\Gamma \left( {n + j + 1} \right)j!}}\left( {\frac{{\alpha^{2} \gamma }}{{4\beta_{m} \left( z \right)}}} \right)^{j} , $$

(5.d)

and

$$ D_{n} \left( z \right) = \left( {\frac{i\alpha k}{{4\omega_{0} z\beta_{m} \left( z \right)}}} \right)^{n} . $$

(5.e)

$k = \frac{2\pi }{\lambda }$ is the wavenumber with $\lambda$ represents the wavelength and $\gamma = \frac{1}{{\omega_{0}^{2} }}$.

We will start to evaluate the normalized first order perturbation in the Born approximation $\Phi_{1} \left( {\vec{r},L} \right)$ defined as (Andrews and Philips 2005; Cowan 2006)

$$ \Phi_{1} \left( {\vec{r},L} \right) = \frac{{V_{1} (\vec{r},L)}}{{V_{0} (\vec{r},L)}}, $$

(6)

where the first order perturbation $V_{1} (\vec{r},L)$ at the propagation distance $z = L$ is given by

$$ V_{1} (\vec{r},L) = \frac{{k^{2} }}{2\pi }\int_{0}^{L} {dz\int_{0}^{2\pi } {\int_{0}^{ + \infty } {d^{2} } s} } \exp \left[ {ik\left( {L - z} \right) + \frac{ik}{{2\left( {L - z} \right)}}\left| {\vec{r} - \vec{s}} \right|^{2} } \right]V_{0} (s,\varphi ,z)\frac{{n_{1} \left( {\vec{s},z} \right)}}{L - z}, $$

(7)

where the refraction index flux $n_{1} (\vec{s},z)$ can be written in the form of two-dimensional Riemann-Stieltjes integral as (Andrews and Philips 2005; Cowan 2006)

$$ n_{1} (\vec{s},z) = \iint {\exp \left( {i\vec{K}.\vec{s}} \right)d\nu (\vec{K},z),} $$

(8)

with $d\nu (\vec{K},z)$ is the random amplitude of the refractive index flux, and $\vec{K} = \left( {\kappa_{x} ,\kappa_{y} ,0} \right)$ represents the three dimensional wave vector with $\kappa_{z} = 0$.

By replacing Eqs. (5) and (8) into Eq. (7), we find

$$ \begin{gathered} V_{1} (\vec{r},L) = \frac{{k^{2} }}{2\pi }\exp \left( {ikL} \right)\,\sum\limits_{m = 1}^{M} {g_{mM} } \sum\limits_{n = 0}^{N} {b_{n} } \sum\limits_{p = 0}^{q} {\sum\limits_{j = 0}^{\infty } {\int_{0}^{L} {\frac{{A_{\ell } \left( z \right)B_{p} \left( z \right)C_{j} \left( z \right)D_{n} \left( z \right)}}{{\left( {L - z} \right)\beta_{m}^{\ell + 1} \left( z \right)}}} } } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - ikz} \right)\iint {\exp \left( {i\vec{K}.\vec{s}} \right)}\int_{0}^{2\pi } {\int_{0}^{ + \infty } {s^{\ell + n + 1} } \exp \left( {i\left( {\ell + n} \right)\varphi } \right)\exp \left( {\frac{{iks^{2} }}{2z}} \right)} \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\exp \left[ {\frac{{ik\left| {\vec{r} - \vec{s}} \right|^{2} }}{{2\left( {L - z} \right)}}} \right]L_{p + j}^{\ell + n} \left( {\frac{{k^{2} s^{2} }}{{4z^{2} \beta_{m} \left( z \right)}}} \right)d\nu \left( {\vec{K},z} \right)dzdsd\varphi . \hfill \\ \end{gathered} $$

(9)

By substituting $V_{1} (\vec{r},L)$ in Eq. (6), one obtains

$$ \begin{gathered} \Phi_{1} (\vec{r},L) = \frac{{k^{2} }}{{2\pi \,V_{0} (\vec{r},L)}}\exp \left( {ikL} \right)\sum\limits_{m = 1}^{M} {g_{mM} } \sum\limits_{n = 0}^{N} {b_{n} } \sum\limits_{p = 0}^{q} {\sum\limits_{j = 0}^{\infty } {\int_{0}^{L} {dz\frac{{A_{\ell } \left( z \right)C_{j} \left( z \right)B_{p} \left( z \right)D_{n} \left( z \right)}}{{\left( {L - z} \right)\beta_{m}^{\ell + 1} \left( z \right)}}} } } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - ikz} \right)\iint {d\nu (\vec{K},z)}\int_{0}^{2\pi } {\int_{0}^{ + \infty } {s^{\ell + n + 1} } \exp \left( {i\left( {\ell + n} \right)\phi } \right)\exp \left( {i\vec{K}.\vec{s}} \right)\exp \left( {\frac{{iks^{2} }}{2z}} \right)} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - \frac{{k^{2} s^{2} }}{{4\beta_{m} \left( z \right)z^{2} }}} \right)\exp \left[ {\frac{ik}{{2\left( {L - z} \right)}}\left| {\vec{r} - \vec{s}} \right|^{2} } \right]\,L_{p + j}^{\ell + n} \left( {\frac{{k^{2} s^{2} }}{{4\beta_{m} \left( z \right)z^{2} }}} \right)dsd\phi , \hfill \\ \end{gathered} $$

(10)

where

$$ \begin{gathered} V_{0} (\vec{r},\theta ,\,\,L) = A_{\ell } \left( L \right)r^{\ell } \exp \left( {\frac{{ikr^{2} }}{2L}} \right)\sum\limits_{t = 1}^{M} {\frac{{g_{tM} }}{{\beta_{t}^{{^{\ell + 1} }} \left( L \right)}}\exp \left( { - \frac{{k^{2} r^{2} }}{{4\beta_{t} \left( L \right)L^{2} }}} \right)} \sum\limits_{\tau = 0}^{N} {b_{\tau } D_{\tau } \left( L \right)} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\exp \left( {i\left( {\ell + \tau } \right)\theta } \right)r^{\tau } \sum\limits_{\mu = 0}^{q} {B_{\mu } \left( L \right)} \sum\limits_{\chi = 0}^{\infty } {C_{j} \left( L \right)L_{\mu + \chi }^{\ell + \tau } \left( {\frac{{k^{2} r^{2} }}{{4\beta_{t} \left( L \right)L^{2} }}} \right)} , \hfill \\ \end{gathered} $$

(10.a)

and $\beta_{t}$, $A_{\ell }$, $B_{\mu }$, $C_{\chi }$, and $D_{\tau }$ are given Eqs. (5a) (5b) (5c) (5d) and (5e) with $z = L$.

By using the following identities (Gradshteyn and Ryzhik 1994)

$$ \,\int_{0}^{2\pi } {\exp \left[ { - i\frac{kr}{L}s\cos (\theta_{1} - \theta_{2} )} \right]} \exp \left( {in\phi } \right)d\theta_{1} = 2\pi \,i^{n} \exp \left( {in\theta_{2} } \right)J_{n} \left( {\frac{kr}{L}s} \right), $$

(11)

and

$$ \int_{0}^{ + \infty } {s^{n + \ell + 1} } \exp \left( { - \varepsilon s^{2} } \right)L_{p + j}^{n + \ell } \left( {\sigma s^{2} } \right)J_{n + \ell } \left( {\delta s} \right)\,ds = \frac{{\left( {\varepsilon - \sigma } \right)^{p + j} \delta^{n + \ell } }}{{2^{n + \ell + 1} \varepsilon^{{\left( {p + j + n + \ell + 1} \right)}} }}\exp \left( { - \frac{{\delta^{2} }}{4\varepsilon }} \right)\;L_{p + j}^{n + \ell } \left( {\frac{{\sigma \delta^{2} }}{{4\varepsilon \left( {\sigma - \varepsilon } \right)}}} \right), $$

(12)

and after some algebraic calculations and simplifications, Eq. (10) is written as

$$ \begin{gathered} \Phi_{1} (\vec{r},L) = \left( \frac{i}{2} \right)^{\ell } \frac{{k^{2} }}{{2V_{0} (\vec{r},L)}}\exp \left( {ikL} \right)\sum\limits_{m = 1}^{M} {g_{mM} } \sum\limits_{n = 0}^{N} {\left( \frac{i}{2} \right)^{n} } b_{n} \,\exp \left( {i\left( {n + \ell } \right)\theta } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \sum\limits_{p = 0}^{q} {\sum\limits_{j = 0}^{\infty } {\int_{0}^{L} {dz\,} \;\frac{{\left( {\varepsilon - \sigma } \right)^{p + j} A_{\ell } \left( z \right)D_{n} \left( z \right)C_{j} \left( z \right)B_{p} \left( z \right)}}{{\varepsilon^{{\left( {p + j + n + \ell + 1} \right)}} (L - z)\beta_{m}^{\ell + 1} \left( z \right)}}} } \exp \left( { - ikz} \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\,\exp \left( { - \frac{{\delta^{2} }}{4\varepsilon }} \right)\exp \left( {\frac{{ikr^{2} }}{{2\left( {L - z} \right)}}} \right)\iint {\delta^{n + \ell } L_{p + j}^{n + \ell } \left( {\frac{{\sigma \delta^{2} }}{{4\varepsilon \left( {\sigma - \varepsilon } \right)}}} \right)d\nu (\vec{K},z)}, \hfill \\ \end{gathered} $$

(13)

where

$$ \varepsilon = \frac{{k^{2} }}{{4z^{2} \beta_{m} \left( z \right)}} - \frac{ikL}{{2z\left( {L - z} \right)}}, $$

(13.a)

$$ \delta = \left\| {\vec{K} - \frac{{k\vec{r}}}{{\left( {L - z} \right)}}} \right\|, $$

(13.b)

and

$$ \sigma = \frac{{k^{2} }}{{4z^{2} \beta_{m} \left( z \right)}}. $$

(13.c)

Now, we will calculate the on-axis scintillation index of the GBLG beam propagating in a maritime turbulent atmosphere, with weak fluctuations by using the Von Karman spectrum, defined by Eq. (2), with $E_{2} \left( {0,0} \right)$ and $E_{3} \left( {0,0} \right)$ are the second-order and third statistical moments at $r_{1} = r_{2} = 0$.

The second-order statistical moments $E_{2} \left( {0,0} \right)$ of the GBLG beam is given in the Rytov approximation by

$$ \begin{gathered} E_{2} \left( {0,0} \right) = E_{02} \sum\limits_{{m_{1} = 1}}^{M} {\frac{{g_{{m_{1} M}} }}{{\left( {2L\gamma_{{m_{1} }} - ik} \right)}}} \sum\limits_{{n_{1} = 0}}^{N} {E_{{n_{1} }} } \sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }} \sum\limits_{{d_{1} = 0}}^{{p_{1} + j_{1} }} {E_{{d_{1} }} } \sum\limits_{{m_{2} = 1}}^{M} {\frac{{g_{{m_{2} M}} }}{{\left( {2L\gamma_{{m_{2} }} + ik} \right)}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \sum\limits_{{n_{2} = 0}}^{N} {E_{{n_{i} }}^{{}} } \sum\limits_{{j_{2} = 0}}^{\infty } \; E_{{j_{i} }}^{{}} \sum\limits_{{d_{2} = 0}}^{{p_{2} + j_{2} }} {E_{{d_{i} }}^{{}} } \int\limits_{0}^{1} {d\zeta } \left( {1 - \zeta } \right)^{{n_{1} + n_{2} + 2d_{1} + 2d_{2} }} \int\limits_{ - \infty }^{ + \infty } {\kappa^{{n_{1} + n_{2} + 2d_{1} + 2d_{2} + 1}} } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times {\text{ex}} \left( {\frac{{ - L^{2} \left( {\gamma_{{m_{1} }} + \gamma_{{m_{2} }} } \right)\left( {1 - \zeta } \right)^{2} }}{{\left( {2L\gamma_{{m_{2} }} + ik} \right)\left( {2L\gamma_{{m_{1} }} - ik} \right)}}\kappa^{2} } \right)\Phi_{n} \left( \kappa \right)d\kappa , \hfill \\ \end{gathered} $$

(14)

where

$$ \xi = \frac{z}{L}, $$

(14.a)

$$ E_{02} = \frac{{4\pi^{2} k^{4} L}}{{A_{0} \left( L \right)\sum\limits_{{t_{1} = 1}}^{M} {\frac{{g_{{t_{1} M}} }}{{\beta_{{t_{1} }} \left( L \right)}}} \sum\limits_{{\mu_{1} = 0}}^{q} {B_{{\mu_{1} }} \left( L \right)\sum\limits_{{\chi_{1} = 0}}^{\infty } {C_{{\chi_{1} }} \left( L \right)A_{0}^{ * } \left( L \right)\sum\limits_{{t_{2} = 1}}^{M} {\frac{{g_{{t_{2} M}} }}{{\beta_{{t_{2} }}^{ * } \left( L \right)}}} \sum\limits_{{\mu_{2} = 0}}^{q} {B_{{\mu_{2} }}^{ * } \left( L \right)\sum\limits_{{\chi_{2} = 0}}^{\infty } {C_{{\chi_{2} }}^{ * } \left( L \right)} } } } }}, $$

(14.b)

$$ \,E_{{n_{i} }} = b_{{n_{i} }} \left( {\frac{ - i\alpha L}{{2\omega_{0} \left( {2L\gamma_{{m_{i} }} - ik} \right)}}} \right)^{{n_{i} }} \exp \left( {in_{i} \theta } \right)\sum\limits_{{p_{i} = 0}}^{q} {\frac{q!}{{p_{i} !p_{i} !\left( {q - p_{i} } \right)!}}\left( {\frac{ - 4L}{{\omega_{0}^{2} \left( {2L\gamma_{{m_{i} }} - ik} \right)}}} \right)^{{p_{i} }} } , $$

(14.c)

$$ E_{{j_{i} }} = \frac{{\Gamma \left( {p_{i} + j_{i} + 1} \right)}}{{\left( {2L\gamma_{{m_{i} }} - ik} \right)^{{j_{i} }} \Gamma \left( {n_{i} + j_{i} + 1} \right)j_{i} !}}\left( {\frac{{ - \alpha^{2} L\gamma }}{2}} \right)^{{j_{i} }} , $$

(14.d)

$$ E_{{d_{i} }} = \frac{{\left( {p_{i} + j_{i} + n_{i} } \right)\,!}}{{\left( {n_{i} + d_{i} } \right)\,!\left( {p_{i} + j_{i} - d_{i} } \right)\,!d_{i} \,!}}\left( {\frac{ - L}{{2\left( {2L\gamma_{{m_{i} }} - ik} \right)}}} \right)^{{d_{i} }} , $$

(14.e)

with $i = 2,3.$

and

$$ E_{{n_{2} }}^{{}} = E_{{n_{1} }}^{ * } ,\,E_{{j_{2} }}^{{}} = E_{{j_{1} }}^{ * } ,\,E_{{d_{2} }}^{{}} = E_{{d_{1} }}^{ * } . $$

(14.f)

The third statistical moment $E_{3} \left( {0,0} \right)$ is expressed as

$$ \begin{gathered} E_{3} \left( {0,0} \right) = E_{03} \sum\limits_{{m_{1} = 1}}^{M} {\frac{{g_{{m_{1} M}} }}{{\left( {2L\gamma_{{m_{1} }} - ik} \right)}}} \sum\limits_{{n_{1} = 0}}^{N} {E_{{n_{1} }} } \sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }} \sum\limits_{{d_{1} = 0}}^{{p_{1} + j_{1} }} {E_{{d_{1} }} } \sum\limits_{{m_{3} = 1}}^{M} {\frac{{g_{{m_{3} M}} }}{{\left( {2L\gamma_{{m_{3} }} - ik} \right)}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \sum\limits_{{n_{3} = 0}}^{N} {E_{{n_{i} }} } \sum\limits_{{j_{3} = 0}}^{\infty } {E_{{j_{i} }} } \sum\limits_{{d_{3} = 0}}^{{p_{3} + j_{3} }} {E_{{d_{i} }} } \int\limits_{0}^{L} {\left( {1 - \zeta } \right)^{{n_{1} + n_{3} + 2d_{1} + 2d_{3} }} d\zeta } \int\limits_{ - \infty }^{ + \infty } {\kappa^{{n_{1} + n_{3} + 2d_{1} + 2d_{3} + 1}} } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( {\frac{iL}{{2k}}\left( {1 - \zeta } \right)\left( {G_{{m_{1} .m_{3} }} + 1} \right)\left( {1 - \frac{{\left( {G_{{m_{1} .m_{3} }} - 1} \right)}}{{\left( {G_{{m_{1} .m_{3} }} + 1} \right)}}\zeta } \right)\kappa^{2} } \right)\Phi_{n} \left( \kappa \right)d\kappa , \hfill \\ \end{gathered} $$

(15)

where

$$ E_{03} = \frac{{16\pi^{2} Lk^{4} }}{{A_{0} \left( L \right)\sum\limits_{{t_{1} = 1}}^{M} {\frac{{g_{{t_{1} M}} }}{{\beta_{{t_{1} }} \left( L \right)}}} \sum\limits_{{\mu_{1} = 0}}^{q} {b_{{\mu_{1} }} \left( L \right)\sum\limits_{{\chi_{1} = 0}}^{\infty } {C_{{\chi_{1} }} \left( L \right)A_{0} \left( L \right)\sum\limits_{{t_{3} = 1}}^{M} {\frac{{g_{{t_{3} M}} }}{{\beta_{{t_{3} }} \left( L \right)}}} \sum\limits_{{\mu_{3} = 0}}^{q} {b_{{\mu_{3} }} \left( L \right)\sum\limits_{{\chi_{3} = 0}}^{\infty } {C_{{\chi_{3} }} \left( L \right)} } } } }}, $$

(15.a)

and

$$ G_{{m_{1} .m_{3} }} = \frac{{ - \left( {k^{2} + 4L^{2} \gamma_{{m_{1} }} \gamma_{{m_{3} }} } \right)}}{{\left( {2L\gamma_{{m_{1} }} - ik} \right)\left( {2L\gamma_{{m_{3} }} - ik} \right)}}. $$

(15.b)

In Eqs. (14) and (15), $\Phi_{n} \left( \kappa \right)$ represents the Von Karman spectrum given by (Andrews and Philips 2005)

$$ \Phi_{n} \left( \kappa \right) = \frac{{0.033C_{n}^{2} }}{{\left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{\frac{11}{6}} }}\exp \left( { - \frac{{\kappa^{2} }}{{\kappa_{H}^{2} }}} \right), $$

(16)

where $\kappa_{0} = \frac{2\pi }{{L_{0} }},$$L_{0}$ represents the outer scale of turbulence, $\kappa_{H} = \frac{5.92}{{l_{0} }}$, $l_{0}$ specifies the inner scale of turbulence, and $C_{n}^{2}$ is the constant structure of the turbulence.

By substituting Eq. (16) into Eq. (14), and using the following identities (Belafhal et al. 2021)

$$ \int\limits_{0}^{ + \infty } {\frac{{\kappa^{2\mu } }}{{\left( {\kappa^{2} + \kappa_{0}^{2} } \right)^{\frac{11}{6}} }}\exp \left( { - \frac{{\kappa^{2} }}{{\kappa_{m}^{2} }}} \right)} d\kappa = \frac{1}{2}\kappa_{0}^{{2\mu - \frac{8}{3}}} \Gamma \left( {\mu + \frac{1}{2}} \right)U\left( {\mu + \frac{1}{2};\mu - \frac{1}{3};\frac{{\kappa_{0}^{2} }}{{\kappa_{m}^{2} }}} \right), $$

(17)

with $U$ is the confluent hypergeometric function of the second kind.

and (Gradshteyn and Ryzhik 1994)

$$ \int\limits_{0}^{x} {\frac{{t^{\mu - 1} }}{{\left( {1 + \beta t} \right)^{\nu } }}} dt = \frac{{x^{\mu } }}{\mu }{}_{2}F_{1} \left( {\nu ,\mu ;1 + \mu ; - \beta x} \right),\,\mu > 0, $$

(18)

and after some tedious calculations, the expression of $E_{2} \left( {0,0} \right)$ can be expressed as

$$ \begin{gathered} E_{2} \left( {0,0} \right) = 0,0165C_{n}^{2} E_{02} \sum\limits_{{m_{1} = 1}}^{M} {\frac{{g_{{m_{1} M}} }}{{\left( {2L\gamma_{{m_{1} }} - ik} \right)}}} \sum\limits_{{n_{1} = 0}}^{N} {E_{{n_{1} }} } \sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }} \sum\limits_{{d_{1} = 0}}^{{p_{1} + j_{1} }} {E_{{d_{1} }} } \sum\limits_{{m_{2} = 1}}^{M} {\frac{{g_{{m_{2} M}} }}{{\left( {2L\gamma_{{m_{2} }} + ik} \right)}}} \sum\limits_{{n_{2} = 0}}^{N} {E_{{n_{1} }}^{ * } } \sum\limits_{{j_{2} = 0}}^{\infty } \; E_{{j_{1} }}^{ * } \sum\limits_{{d_{2} = 0}}^{{p_{2} + j_{2} }} {E_{{d_{1} }}^{ * } } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\left( \begin{gathered} \frac{{\kappa_{0}^{{ - \frac{5}{3} + n_{1,2} d_{1,2} }} }}{{(1 + n_{1,2} d_{1,2} )}}\frac{1}{{\Gamma \left( \frac{11}{6} \right)}}\Gamma \left( {1 + \frac{{n_{1,2} d_{1,2} }}{2}} \right)\Gamma \left( {\frac{5}{6} - \frac{{n_{1,2} d_{1,2} }}{2}} \right) \hfill \\ + \frac{{\kappa_{H}^{{ - \frac{5}{3} + n_{1,2} d_{1,2} }} }}{{(1 + n_{1,2} d_{1,2} )}}\Gamma \left( { - \frac{5}{6} + \frac{{n_{1,2} d_{1,2} }}{2}} \right){}_{2}F_{1} \left( { - \frac{5}{6} + \frac{{n_{1,2} d_{1,2} }}{2},\frac{1}{2} + \frac{{n_{1,2} d_{1,2} }}{2};\frac{3}{2} + \frac{{n_{1,2} d_{1,2} }}{2}; - G_{{m_{1} .m_{2} }} \kappa_{H}^{2} } \right) \hfill \\ \end{gathered} \right), \hfill \\ \end{gathered} $$

(19)

where

$$ n_{1,2} d_{1,2} = n_{1} + n_{2} + 2d_{1} + 2d_{2} , $$

(19.a)

and

$$ G_{{m_{1} .m_{2} }} = \frac{{L^{2} \left( {\gamma_{{m_{1} }} + \gamma_{{m_{2} }} } \right)}}{{\left( {2L\gamma_{{m_{2} }} + ik} \right)\left( {2L\gamma_{{m_{1} }} - ik} \right)}}. $$

(19.b)

The substitution of Eq. (16) into Eq. (15) and the use of Eqs. (17) and (18) yield

$$ \begin{gathered} E_{3} \left( {0,0} \right) = 4.10^{ - 3} C_{n}^{2} E_{03} \sum\limits_{{m_{1} = 1}}^{M} {\frac{{g_{{m_{1} M}} }}{{\left( {2L\gamma_{{m_{1} }} - ik} \right)}}} \sum\limits_{{n_{1} = 0}}^{N} {E_{{n_{1} }} } \sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }} \sum\limits_{{d_{1} = 0}}^{{p_{1} + j_{1} }} {E_{{d_{1} }} } \sum\limits_{{m_{3} = 1}}^{M} {\frac{{g_{{m_{3} M}} }}{{\left( {2L\gamma_{{m_{3} }} - ik} \right)}}} \sum\limits_{{n_{3} = 0}}^{N} {E_{{n_{3} }} } \sum\limits_{{j_{3} = 0}}^{\infty } {E_{{j_{3} }} } \sum\limits_{{d_{3} = 0}}^{{p_{3} + j_{3} }} {E_{{d_{3} }} } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\left( \begin{gathered} \frac{{\Gamma \left( {\frac{5}{6} - \frac{{n_{1,3} d_{1,3} }}{2}} \right)\Gamma \left( {1 + \frac{{n_{1,3} d_{1,3} }}{2}} \right)}}{{\Gamma \left( \frac{11}{6} \right)}}\kappa_{0}^{{ - \frac{5}{3} + n_{1,3} d_{1,3} }} \int\limits_{0}^{1} {\left( {1 - \zeta } \right)^{{n_{1,3} d_{1,3} }} d\zeta } \hfill \\ + \frac{{\Gamma \left( { - \frac{5}{6} + \frac{{n_{1,3} d_{1,3} }}{2}} \right)}}{{\Gamma \left( {1 + \frac{{n_{1,3} d_{1,3} }}{2}} \right)}}\kappa_{H}^{{ - \frac{5}{3} + n_{1,3} d_{1,3} }} \int\limits_{0}^{1} {\left( {1 - \zeta } \right)^{{n_{1,3} d_{1,3} }} } \left( {1 + \eta \kappa_{H}^{2} } \right)^{{\frac{5}{6} - \frac{{n_{1,3} d_{1,3} }}{2}}} d\zeta \hfill \\ \end{gathered} \right),\,\, \hfill \\ \end{gathered} $$

(20)

where

$$ n_{1,3} d_{1,3} = n_{1} + n_{3} + 2d_{1} + 2d_{3} , $$

(20.a)

and

$$ \eta = \frac{{iL\left( {1 - \zeta } \right)}}{2k}\left( {G_{{m_{1} .m_{3} }} + 1} \right)\left( {1 - \frac{{\left( {G_{{m_{1} .m_{3} }} - 1} \right)}}{{\left( {G_{{m_{1} .m_{3} }} + 1} \right)}}\zeta } \right), $$

(20.b)

with $G_{{m_{1} .m_{3} }}$ is defined by Eq. (15.e).

After some algebraic calculations, the expression of $E_{3} \left( {0,0} \right)$ can be rewritten as

$$ \begin{gathered} E_{3} \left( {0,0} \right) = 4,125.10^{ - 3} C_{n}^{2} E_{03} \sum\limits_{{m_{1} = 1}}^{M} {\frac{{g_{{m_{1} M}} }}{{\left( {2L\gamma_{{m_{1} }} - ik} \right)}}} \sum\limits_{{n_{1} = 0}}^{N} {E_{{n_{1} }} } \sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }} \sum\limits_{{d_{1} = 0}}^{{p_{1} + j_{1} }} {E_{{d_{1} }} } \sum\limits_{{m_{3} = 1}}^{M} {\frac{{g_{{m_{3} M}} }}{{\left( {2L\gamma_{{m_{3} }} - ik} \right)}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \sum\limits_{{n_{3} = 0}}^{N} {E_{{n_{3} }} } \sum\limits_{{j_{3} = 0}}^{\infty } {E_{{j_{3} }} } \,\sum\limits_{{d_{3} = 0}}^{{p_{3} + j_{3} }} {E_{{d_{3} }} } \,\left( \begin{gathered} \frac{{\Gamma \left( {\frac{5}{6} - \frac{{n_{1,3} d_{1,3} }}{2}} \right)\Gamma \left( {1 + \frac{{n_{1,3} d_{1,3} }}{2}} \right)}}{{\Gamma \left( \frac{11}{6} \right)}}\frac{{\kappa_{0}^{{ - \frac{5}{3} + n_{1,3} d_{1,3} }} }}{{\left( {1 + n_{1,3} d_{1,3} } \right)}} \hfill \\ + \Gamma \left( { - \frac{5}{6} + \frac{{n_{1,3} d_{1,3} }}{2}} \right)\frac{{\kappa_{H}^{{ - \frac{5}{3} + n_{1,3} d_{1,3} }} }}{{\left( {1 + n_{1,3} d_{1,3} } \right)}}{}_{2}F_{1} \left( {\frac{{n_{1,3} d_{1,3} }}{2} - \frac{5}{6},n_{1,3} d_{1,3} + 1;n_{1,3} d_{1,3} + 2; - \vartheta \kappa_{H}^{2} } \right) \hfill \\ \end{gathered} \right),\,\, \hfill \\ \end{gathered} $$

(21)

where

$$ \vartheta = \frac{iL}{k}\left( {1 + \frac{{\left( {2 + n_{1,3} d_{1,3} } \right)\,\left( {G_{{m_{1} .m_{3} }} - 1} \right)}}{{2\left( {3 + n_{1,3} d_{1,3} } \right)}}} \right). $$

(21.a)

By substituting Eqs. (19) and (21) into Eq. (2), and after some algebraic simplifications, we obtain the analytical expression of the scintillation index $\sigma_{I}^{2} \left( L \right)$ for the GBLG beam propagating in the maritime atmospheric turbulence as

$$ \sigma_{I}^{2} \left( L \right) = 8,25.10^{ - 3} C_{n}^{2} {\text{Re}} \left[ \begin{gathered} \sum\limits_{{m_{1} = 1}}^{M} {\frac{{g_{{m_{1} ,M}} }}{{\left( {2L\gamma_{{m_{1} }} - ik} \right)}}} \sum\limits_{{n_{1} = 0}}^{N} {E_{{n_{1} }} } \sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }} \sum\limits_{{d_{1} = 0}}^{{p_{1} + j_{1} }} {E_{{d_{1} }} } \hfill \\ \left( \begin{gathered} 4E_{02} \sum\limits_{{m_{2} = 1}}^{M} {\frac{{g_{{m_{2} M}} }}{{\left( {2L\gamma_{{m_{2} }} + ik} \right)}}} \sum\limits_{{n_{2} = 0}}^{N} {E_{{n_{1} }}^{ * } } \sum\limits_{{j_{2} = 0}}^{\infty } \; E_{{j_{1} }}^{ * } \sum\limits_{{d_{2} = 0}}^{{p_{2} + j_{2} }} {E_{{d_{1} }}^{ * } } \frac{{F_{1.2}^{GBLG} }}{{\left( {n_{1,2} d_{1,2} + 1} \right)}} \hfill \\ + E_{03} \sum\limits_{{m_{3} = 1}}^{M} {\frac{{g_{{m_{3} M}} }}{{\left( {2L\gamma_{{m_{3} }} - ik} \right)}}} \sum\limits_{{n_{3} = 0}}^{N} {E_{{n_{3} }} } \sum\limits_{{j_{3} = 0}}^{\infty } {E_{{j_{3} }} } \sum\limits_{{d_{3} = 0}}^{{p_{3} + j_{3} }} {E_{{d_{3} }} } \frac{{F_{1,3}^{GBLG} }}{{\left( {n_{1,3} d_{1,3} + 1} \right)}} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right], $$

(22)

where

$$ \begin{aligned} F_{1,2}^{GBLG} & = \kappa_{0}^{{ - \frac{5}{3} + n_{1,2} d_{1,2} }} \frac{{\Gamma \left( {\frac{5}{6} - \frac{{n_{1,2} d_{1,2} }}{2}} \right)\Gamma \left( {1 + \frac{{n_{1,2} d_{1,2} }}{2}} \right)}}{{\Gamma \left( \frac{11}{6} \right)}} \\ & + \kappa_{H}^{{ - \frac{5}{3} + n_{1,2} d_{1,2} }} \Gamma \left( { - \frac{5}{6} + \frac{{n_{1,2} d_{1,2} }}{2}} \right){}_{2}F_{1} \left( {\frac{{n_{1,2} d_{1,2} }}{2} - \frac{5}{6},\frac{{n_{1,2} d_{1,2} }}{2} + \frac{1}{2};\frac{{n_{1,2} d_{1,2} }}{2} + \frac{3}{2}; - G_{{m_{1} \cdot m_{2} }} \kappa_{H}^{2} } \right), \\ \end{aligned} $$

(22.a)

_and

$$ \begin{gathered} F_{1,3}^{GBLG} = \kappa_{0}^{{ - \frac{5}{3} + n_{1,3} d_{1,3} }} \frac{{\Gamma \left( {\frac{5}{6} - \frac{{n_{1,3} d_{1,3} }}{2}} \right)\Gamma \left( {1 + \frac{{n_{1,3} d_{1,3} }}{2}} \right)}}{{\Gamma \left( \frac{11}{6} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, + \kappa_{H}^{{ - \frac{5}{3} + n_{1,3} d_{1,3} }} \Gamma \left( { - \frac{5}{6} + \frac{{n_{1,3} d_{1,3} }}{2}} \right){}_{2}F_{1} \left( {\frac{{n_{1,3} d_{1,3} }}{2} - \frac{5}{6},n_{1,3} d_{1,3} + 1;n_{1,3} d_{1,3} + 2; - \vartheta \kappa_{H}^{2} } \right). \hfill \\ \end{gathered} $$

(22.b)

The analytical expression given by Eq. (22) represents the scintillation index of the GBLG beam propagating through maritime atmospheric turbulence with weak fluctuations. It's our first mains result elaborated in the present work.

3 Special cases

By considering the main result as the general case, we can deduce the scintillation indexes of some laser beams in maritime atmospheric turbulence.

3.1 Case of Bessel-Laguerre-Gaussian (BLG) beam

The scintillation index of the BLG beam is obtained from our main result established by Eq. (22) when $n_{1} = n_{2} = n_{3} = N$ and $M = m = 1$.

So, in this case, one finds the following expression

$$ \sigma_{I}^{2} \left( L \right)_{BLG} = 0.008C_{n}^{2} {\text{Re}} \left[ \begin{gathered} \sum\limits_{{p_{1} = 0}}^{q} {E_{{p_{1} }} } \sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }}^{BLG} \sum\limits_{{d_{1} = 0}}^{{p_{1} + j_{1} }} {E_{{d_{1} }}^{BLG} } \hfill \\ \times \left( \begin{gathered} 4E_{02}^{BLG} \sum\limits_{{p_{2} = 0}}^{q} {E_{{p_{2} }} } \sum\limits_{{j_{2} = 0}}^{\infty } \; E_{{j_{2} }}^{BLG} \sum\limits_{{d_{2} = 0}}^{{p_{2} + j_{2} }} {E_{{d_{2} }}^{BLG} } \frac{{F_{1.2}^{BLG} }}{{1 + 2d_{1,2} }} \hfill \\ + E_{03}^{BLG} \sum\limits_{{p_{3} = 0}}^{q} {E_{{p_{3} }} } \sum\limits_{{j_{3} = 0}}^{\infty } {E_{{j_{3} }}^{BLG} } \sum\limits_{{d_{3} = 0}}^{{p_{3} + j_{3} }} {E_{{d_{3} }}^{BLG} } \frac{{F_{1,3}^{BLG} }}{{1 + d_{1,3} }} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right], $$

(23)

where

$$ E_{02}^{BLG} = \frac{{4\pi^{2} k^{2} L}}{{\sum\limits_{{\mu_{1} = 0}}^{q} {B_{{\mu_{1} }} \left( L \right)\sum\limits_{{\chi_{1} = 0}}^{\infty } {C_{{\chi_{1} }} \left( L \right)\sum\limits_{{\mu_{2} = 0}}^{q} {B_{{\mu_{2} }}^{ * } \left( L \right)\sum\limits_{{\chi_{2} = 0}}^{\infty } {C_{{\chi_{2} }}^{ * } \left( L \right)} } } } }}, $$

(23a)

$$ \,E_{{p_{1} }} = \frac{q!}{{p_{1} !p_{1} !\left( {q - p_{1} } \right)!}}\left( {\frac{ - 4L\gamma }{{\left( {2L\gamma - ik} \right)}}} \right)^{{p_{1} }} , $$

(23b)

$$ E_{{j_{1} }}^{BLG} = \frac{{\Gamma \left( {p_{1} + j_{1} + 1} \right)}}{{\left( {2L\gamma - ik} \right)^{{j_{1} }} \Gamma \left( {j_{1} + 1} \right)j_{1} !}}\left( {\frac{{ - \alpha^{2} \gamma L}}{2}} \right)^{{j_{1} }} , $$

(23c)

$$ E_{{d_{1} }}^{BLG} = \frac{{\left( {p_{1} + j_{1} } \right)\,!}}{{d_{1} !d_{1} !\left( {p_{1} + j_{1} - d_{1} } \right)\,!}}\left( {\frac{ - L}{{2\left( {2L\gamma - ik} \right)}}} \right)^{{d_{1} }} , $$

(23d)

$$ E_{{p_{2} }}^{{}} = E_{{p_{1} }}^{ * } ,\,E_{{j_{2} }}^{BLG} = E_{{j_{1} }}^{BLG * } ,\,E_{{d_{2} }}^{BLG} = E_{{d_{1} }}^{BLG * } , $$

(23e)

$$ E_{03}^{BLG} = \frac{{ - 16\pi^{2} Lk^{2} }}{{\sum\limits_{{\mu_{1} = 0}}^{q} {b_{{\mu_{1} }} \left( L \right)\sum\limits_{{\chi_{1} = 0}}^{\infty } {C_{{\chi_{1} }} \left( L \right)\sum\limits_{{\mu_{3} = 0}}^{q} {b_{{\mu_{3} }} \left( L \right)\sum\limits_{{\chi_{3} = 0}}^{\infty } {C_{{\chi_{3} }} \left( L \right)} } } } }}, $$

(23f)

$$ E_{{p_{3} }} = \,\sum\limits_{{p_{3} = 0}}^{q} {\frac{q!}{{p_{3} !p_{3} !\left( {q - p_{3} } \right)!}}\left( {\frac{ - 4L}{{\omega_{0}^{2} \left( {2L\gamma - ik} \right)}}} \right)^{{p_{3} }} } , $$

(23g)

$$ E_{{j_{3} }}^{BLG} = \frac{{\Gamma \left( {p_{3} + j_{3} + 1} \right)}}{{\left( {2L\gamma - ik} \right)^{{j_{3} }} \Gamma \left( {j_{3} + 1} \right)j_{3} !}}\left( {\frac{{ - \alpha^{2} L}}{{2\omega_{0}^{2} }}} \right)^{{j_{3} }} , $$

(23h)

$$ E_{{d_{3} }}^{BLG} = \frac{{\left( {p_{3} + j_{3} } \right)\,!}}{{d_{3} !d_{3} !\,\left( {p_{3} + j_{3} - d_{3} } \right)\,!}}\left( {\frac{ - L}{{2\left( {2L - ik} \right)}}} \right)^{{d_{3} }} , $$

(23i)

$$ \beta \left( L \right) = \gamma - \frac{ik}{{2L}}, $$

(23j)

$$ F_{1,2}^{BLG} = \kappa_{0}^{{ - \frac{5}{3} + d_{1.2} }} \frac{{\Gamma \left( {\frac{5}{6} - \frac{{d_{1.2} }}{2}} \right)\Gamma \left( {1 + \frac{{d_{1.2} }}{2}} \right)}}{{\Gamma \left( \frac{11}{6} \right)}} + \kappa_{H}^{{ - \frac{5}{3} + d_{1.2} }} \Gamma \left( { - \frac{5}{6} + \frac{{d_{1.2} }}{2}} \right){}_{2}F_{1} \left( {\frac{{d_{1.2} }}{2} - \frac{5}{6},\frac{{d_{1.2} }}{2} + \frac{1}{2};\frac{{d_{1.2} }}{2} + \frac{3}{2}; - G\kappa_{H}^{2} } \right), $$

(23k)

and

$$ F_{1,3}^{BLG} = \kappa_{0}^{{ - \frac{5}{3} + d_{1.3} }} \frac{{\Gamma \left( {\frac{5}{6} - \frac{{d_{1.3} }}{2}} \right)\Gamma \left( {1 + \frac{{d_{1.3} }}{2}} \right)}}{{\Gamma \left( \frac{11}{6} \right)}} + \kappa_{H}^{{ - \frac{5}{3} + d_{1.3} }} \Gamma \left( {\frac{{d_{1.3} }}{2} - \frac{5}{6}} \right){}_{2}F_{1} \left( {\frac{{d_{1.3} }}{2} - \frac{5}{6},d_{1.3} + 1;d_{1.3} + 2; - \vartheta^{\prime}\kappa_{H}^{2} } \right), $$

(23l)

with

$$ G = \frac{{2L^{2} \gamma }}{{\left( {k^{2} + 4L^{2} \gamma^{2} } \right)}}, $$

(23m)

$$ \vartheta^{\prime} = \frac{2}{3} - \frac{{k^{2} + 4L^{2} \gamma^{2} }}{{\left( {2L\gamma - ik} \right)^{2} }}, $$

(23n)

$$ d_{1.2} = 2d_{1} + 2d_{2} , $$

(23o)

and

$$ d_{1.3} = 2d_{1} + 2d_{3} . $$

(23p)

The analytical expression of the BLG beam scintillation index, with the use of the Von Karman spectrum, is found for the first time in this work.

3.2 Case of Laguerre-Gaussian (LG) beam

In the analytical expression of the scintillation index of a GBLG beam established by Eq. (22), when the parameters $\alpha = n_{1} = n_{2} = n_{3} = N = 0$ and $M = 1,$ the scintillation index of the a LG beam is expressed as

$$ \sigma_{I}^{2} \left( L \right)_{LG} = 8,25.10^{ - 3} C_{n}^{2} {\text{Re}} \left[ {\sum\limits_{{p_{1} = 0}}^{q} {E_{{p_{1} }}^{LG} } \sum\limits_{{d_{1} = 0}}^{{p_{1} }} {E_{{d_{1} }}^{LG} } \left( \begin{gathered} 4E_{02}^{LG} \sum\limits_{{p_{2} = 0}}^{q} {E_{{p_{2} }}^{LG} } \sum\limits_{{d_{2} = 0}}^{{p_{2} }} {E_{{d_{2} }}^{LG} } \frac{{F_{1.2}^{LG} }}{{1 + 2d_{1,2} }} \hfill \\ + E_{03}^{LG} \sum\limits_{{p_{3} = 0}}^{q} {E_{{p_{3} }}^{LG} } \sum\limits_{{d_{3} = 0}}^{{p_{3} }} {E_{{d_{3} }}^{LG} } \frac{{F_{1,3}^{LG} }}{{1 + d_{1,3} }} \hfill \\ \end{gathered} \right)} \right], $$

(24)

where

$$ E_{02}^{LG} = \frac{{4\pi^{2} k^{2} L}}{{\sum\limits_{{\mu_{1} = 0}}^{q} {\frac{\left( q \right)!}{{\mu_{1} !\left( {q - \mu_{1} } \right)!}}\left( {\frac{ - 2\gamma }{{\beta \left( L \right)}}} \right)^{{\mu_{1} }} \sum\limits_{{\mu_{2} = 0}}^{q} {\frac{\left( q \right)!}{{\mu_{2} !\left( {q - \mu_{2} } \right)!}}\left( {\frac{ - 2\gamma }{{\beta^{ * } \left( L \right)}}} \right)^{{\mu_{2} }} } } }}, $$

(24a)

$$ \,E_{{p_{1} }}^{LG} = \frac{q!}{{\left( {q - p_{1} } \right)!}}\left( {\frac{ - 4L\gamma }{{\left( {2L\gamma - ik} \right)}}} \right)^{{p_{1} }} , $$

(24b)

$$ E_{{d_{1} }}^{LG} = \frac{1}{{d_{1} !d_{1} !\left( {p_{1} - d_{1} } \right)\,!}}\left( {\frac{ - L}{{2\left( {2L\gamma - ik} \right)}}} \right)^{{d_{1} }} , $$

(24c)

$$ E_{{p_{2} }}^{LG} = E_{{p_{1} }}^{LG * } ,\,E_{{d_{2} }}^{LG} = E_{{d_{1} }}^{LG * } , $$

(24d)

$$ E_{03}^{LG} = \frac{{ - 16\pi^{2} k^{2} L}}{{\sum\limits_{{\mu_{1} = 0}}^{q} {\frac{\left( q \right)!}{{\mu_{1} !\left( {q - \mu_{1} } \right)!}}\left( {\frac{ - 2\gamma }{{\beta \left( L \right)}}} \right)^{{\mu_{1} }} \sum\limits_{{\mu_{3} = 0}}^{q} {\frac{\left( q \right)!}{{\mu_{3} !\left( {q - \mu_{3} } \right)!}}\left( {\frac{ - 2\gamma }{{\beta \left( L \right)}}} \right)^{{\mu_{3} }} } } }}, $$

(24e)

$$ E_{{p_{3} }}^{LG} = \,\sum\limits_{{p_{3} = 0}}^{q} {\frac{q!}{{\left( {q - p_{3} } \right)!}}\left( {\frac{ - 4L\gamma }{{\left( {2L\gamma - ik} \right)}}} \right)^{{p_{3} }} } , $$

(24f)

$$ E_{{d_{3} }}^{LG} = \frac{1}{{d_{3} !d_{3} !\,\left( {p_{3} - d_{3} } \right)\,!}}\left( {\frac{ - L}{{2\left( {2L\gamma - ik} \right)}}} \right)^{{d_{3} }} , $$

(24g)

$$ F_{1,2}^{LG} = F_{1,2}^{BLG} , $$

(24h)

and

$$ F_{1,3}^{LG} = F_{1,3}^{BLG} . $$

(24i)

Equation (24) is the result of the propagation of the LG beam through a maritime atmospheric turbulence that is elaborated numerically by Ref. (Eyyuboglu et al. 2010).

3.3 Case of Bessel-Gaussian (BG) beam

The scintillation index of the BG beam is obtained from our main result that is established in Eq. (22) when$q = 0$, $M = 1$ and$n_{1} = n_{2} = n_{3} = N.$ The corresponding scintillation index is given by

$$ \sigma_{I}^{2} \left( L \right)_{LG} = 8,25.10^{ - 3} C_{n}^{2} {\text{Re}} \left[ {\sum\limits_{{j_{1} = 0}}^{\infty } \; E_{{j_{1} }}^{BG} \sum\limits_{{d_{1} = 0}}^{{j_{1} }} {E_{{d_{1} }}^{BG} } \left( \begin{gathered} 4E_{02}^{BG} \sum\limits_{{j_{2} = 0}}^{\infty } \; E_{{j_{2} }}^{BG} \sum\limits_{{d_{2} = 0}}^{{j_{2} }} {E_{{d_{2} }}^{BG} } \frac{{F_{1.2}^{BG} }}{{1 + 2d_{1,2} }} \hfill \\ + E_{03}^{BG} \sum\limits_{{j_{3} = 0}}^{\infty } {E_{{j_{3} }}^{BG} } \sum\limits_{{d_{3} = 0}}^{{j_{3} }} {E_{{d_{3} }}^{BG} } \frac{{F_{1,3}^{BG} }}{{1 + d_{1,3} }} \hfill \\ \end{gathered} \right)} \right], $$

(25)

where

$$ E_{02}^{BG} = \frac{{4\pi^{2} Lk^{2} }}{{\sum\limits_{{\chi_{1} = 0}}^{\infty } {\frac{1}{{\chi_{1} !}}\left( {\frac{{ - \alpha^{2} \gamma }}{4\beta \left( L \right)}} \right)^{{\chi_{1} }} \sum\limits_{{\chi_{2} = 0}}^{\infty } {\frac{1}{{\chi_{2} !}}\left( {\frac{{ - \alpha^{2} \gamma }}{{4\beta^{ * } \left( L \right)}}} \right)^{{\chi_{2} }} } } }}, $$

(25a)

$$ E_{{j_{1} }}^{BG} = \frac{1}{{\left( {2L\gamma - ik} \right)^{{j_{1} }} }}\left( {\frac{{ - \alpha^{2} L\gamma }}{2}} \right)^{{j_{1} }} , $$

(25b)

$$ E_{{d_{1} }}^{BG} = \frac{1}{{d_{1} !d_{1} !\left( {j_{1} - d_{1} } \right)\,!}}\left( {\frac{ - L}{{2\left( {2L\gamma - ik} \right)}}} \right)^{{d_{1} }} , $$

(25c)

$$ E_{{j_{2} }}^{BG} = E_{{j_{1} }}^{BG * } ,\,E_{{d_{2} }}^{BG} = E_{{d_{1} }}^{BG * } , $$

(25d)

$$ E_{03}^{BG} = \frac{{ - 16\pi^{2} Lk^{2} }}{{\sum\limits_{{\chi_{1} = 0}}^{\infty } {\frac{1}{{\chi_{1} !}}\left( {\frac{{ - \alpha^{2} \gamma }}{4\beta \left( L \right)}} \right)^{{\chi_{1} }} \sum\limits_{{\chi_{3} = 0}}^{\infty } {\frac{1}{{\chi_{3} !}}\left( {\frac{{ - \alpha^{2} \gamma }}{4\beta \left( L \right)}} \right)^{{\chi_{3} }} } } }}, $$

(25e)

$$ E_{{j_{3} }}^{BG} = \left( {\frac{{ - \alpha^{2} L\gamma }}{{2\left( {2L\gamma - ik} \right)}}} \right)^{{j_{3} }} , $$

(25f)

$$ E_{{d_{3} }}^{BG} = \frac{1}{{d_{3} !d_{3} !\left( {j_{3} - d_{3} } \right)\,!}}\left( {\frac{ - L}{{2\left( {2L - ik} \right)}}} \right)^{{d_{3} }} , $$

(25g)

$$ F_{1,2}^{BG} = F_{1,2}^{BLG} , $$

(25h)

and

$$ F_{1,3}^{BG} = F_{1,3}^{BLG} . $$

(25i)

Equation (25) corresponds to the result established numerically by Ref. (Eyyuboglu et al. 2008) for the propagation of the Bessel-Gaussian beam through a maritime turbulent atmosphere.

3.4 Case of the Gaussian beam

The scintillation index of the Gaussian beam traveling in a marine turbulent atmosphere is obtained from the main result (Eq. 22), where $q = n_{1} = n_{2} = n_{3} = \alpha = 0$ and$M = 1$. The formula describing this scintillation index is given by

$$ \sigma_{I}^{2} \left( L \right)_{G} = 1.302\,\Gamma \left( { - \frac{5}{6}} \right)L\,k^{2} C_{n}^{2} \kappa_{H}^{{ - \frac{5}{3}}} {\text{Re}} \left[ \begin{gathered} {}_{2}F_{1} \left( { - \frac{5}{6},\frac{1}{2};\frac{3}{2}; - G\kappa_{H}^{2} } \right) \hfill \\ - {}_{2}F_{1} \left( { - \frac{5}{6},1;2; - \left( {\frac{2}{3} - \frac{{k^{2} + 4L^{2} \gamma^{2} }}{{\left( {2L\gamma - ik} \right)^{2} }}} \right)\kappa_{H}^{2} } \right) \hfill \\ \end{gathered} \right]. $$

(26)

Equation (26) represents theoretical formula of the Gaussian beam scintillation index utilizing the Von Karman spectrum is also found for the first time in in this finding.

4 Numerical simulations and discussion

In this part, we examine the scintillation index of the GBLG beam through a maritime turbulent atmosphere with weak fluctuations by using the analytical expression given by Eq. (22). The scintillation index for the GBLG beam is illustrated versus the propagation distance $L$ by varying the source beam parameters, the inner scale and the turbulence strength of the medium.

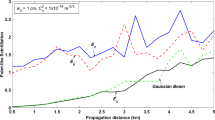
The scintillation index of the GBLG beam is plotted in Fig. 1 as a function of the propagation distance $L$ for different values of the waist size of beam. It can observe from the plots that the scintillation index of the GBLG beam increases during the propagation in a turbulent maritime atmosphere. The evolution of the scintillation index with the beam waist size presents two comportments as it is seen from this figure. For short propagation distance, the scintillation index increases when the beam waist size tends to small value while it becomes large as the beam waist size increases for higher values of the propagation distance. We can deduce that the diffracted beam with beam small waist size is less affected by the maritime atmospheric turbulence.

Fig. 1

Scintillation index of the GBLG beam versus the propagation distance $L$ for different values of the waist beam $\omega_{0}$. The other parameters are:$\lambda = 1060\,{\text{nm}},$ $l_{0} = 7\,{\text{mm}}$, $C_{n}^{2} = 10^{ - 15} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}$, $q = 1$,$N = 1$, $M = 5$ and $\alpha = 1.$

Figure 2 shows the variation of the scintillation index of the GBLG beam upon propagation under the influence of the wavelength radiation source. From the curves, we can note that the effect of the wavelength on the scintillation index is more observed when the propagation distance is greater than or equal to 3 km. After this value, as large the wavelength as lower the impact of the turbulent maritime atmosphere on the propagation of GBLG beam.

Fig. 2

Scintillation index of the GBLG beam as function of the propagation distance $L$ with different wavelength values of $\lambda$, for $l_{0} = 7\,{\text{mm}}$, $\omega_{0} = 20\,{\text{mm}}$, $C_{n}^{2} = 10^{ - 15} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}$, $q = 1$, $N = 1$, $M = 5$ and $\alpha = 1.$

Figure 3 displays the scintillation index of the GBLG beam against the propagation distance for various values of the atmospheric turbulent structure parameter. As it is seen from this figure, the scintillation index increases when the maritime atmospheric is more turbulent and tends to be large for higher propagation distances, which means that the scintillations are very pronounced whenever the turbulence of the maritime atmosphere is strong.

Fig. 3

Scintillation index of the GBLG beam as a function of the propagation distance $L$ for different values of structure constant $C_{n}^{2}$, with $l_{0} = 7\,{\text{mm}}$, $\omega_{0} = 20\,{\text{mm}}$, $\lambda = 1550\,{\text{nm}}$, $q = 1$, $N = 1$, $M = 5$ and $\alpha = 1.$

Figure 4 depicts the effects of the beam order $q$ on the scintillation index of GBLG beam illustrated as a function of the propagation distance $L$. From the figure, it is noted that when $q = 0$ the scintillation index corresponds to that of the generalized Bessel-Gaussian (GBG) beam. From the plots, we can also observe that the GBLG beam has less scintillation index compared to GBG beam. Therefore, the GBLG beam has better performance than GBG beam and can advantageous in optical wireless communications systems.

Fig. 4

Scintillation index of the GBLG beam as a function of the propagation distance $L$ for $l_{0} = 7\,{\text{mm}}$,$\omega_{0} = 20\,{\text{mm}}$, $C_{n}^{2} = 10^{ - 15} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}$, $\lambda = 1060\,{\text{nm}}$, $N = 1$, $M = 5$ and $\alpha = 1.$

Figure 5 presents the scintillation index as a function of the inner scale for different values of propagation distance (see Fig. 5a), and as a function of the propagation distance for several values of the inner scale (see Fig. 5b).

Fig. 5

Scintillation index of the GBLG beam with $\omega_{0} = 200\,{\text{mm}}$, $\lambda = 1060\,{\text{mm}}$, $q = 1$, $N = 1$, $M = 5$, $C_{n}^{2} = 10^{ - 14} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}$ and $\alpha = 1.$ a as a function of inner scale $l_{0}$ for different propagation distance $L$ and b as a function of the propagation distance $L$ for different inner scale $l_{0}$

In Fig. 5a), the scintillation index is lightly decreased with the increase of the inner scale, the degree of this decrease is almost the same for different values of L. And from Fig. 5b, we note that the GBLG beam has smaller scintillation index at large inner scale, although the phenomenon is not obvious. We can conclude that the effect of the inner scale on the scintillation index is weak compared to the impact of the other studied parameters.

5 Numerical simulations of some particular cases

By using Eq. (22), we have developed some numerical simulations of the Laguerre Gaussian beam, Bessel Gaussian beam and Gaussian beam.

5.1 Laguerre Gaussian beam

We plot in Fig. 6 the variation of the scintillation index of LG beam versus the Gaussian source size at several values of the parameter $q$. We can see from the plots that the scintillation index of Laguerre Gaussian beam has the same behavior as that of the fundamental Gaussian beam when q = 0, while it starts to decrease by keeping the same comportment for all values of q greater than zero. This result coincides with the work of Eyyuboglu et al. (2010) (see Fig. 7 of this reference).

Fig. 6

On-axis scintillation index variation as a function of the source size at several values of the parameter $q$ with $l_{0} = 1\,{\text{mm}}$,$\lambda = 1550\,{\text{nm}}$, $L = 1\,{\text{km}}$, and $C_{n}^{2} = 10^{{ - 15}} {\text{m}}^{{{\raise0.5ex\hbox{$\scriptstyle { - 2}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}$

Fig. 7

On-axis scintillation index variation as a function of the propagation distance at several values of the parameter $q$ with $l_{0} = 1\,{\text{mm}}$, $\omega_{0} = 10\,{\text{mm}}$, $\lambda = 1550\,{\text{nm}}$ and $C_{n}^{2} = 10^{{ - 15}} {\text{m}}^{{{\raise0.5ex\hbox{$\scriptstyle { - 2}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}$

Figure 7 displays the variation of the scintillation index of LG beam with the propagation distance $L$ at various values of the parameter $q$. We can note from the Figure that by comparing the evolution of the scintillation index of the fundamental Gaussian beam and the LG beam, it reveals that Laguerre Gaussian beam has less scintillation index than that of the fundamental Gaussian beam. Moreover, our result is in good agreement with the work of Eyyuboglu et al. (2010) (see Fig. 3 of this reference).

5.2 Bessel Gaussian beam

In this particular case, we will give the evolution of the scintillation index of BG beam during the propagation, with weakly turbulent atmosphere, based on the work of Eyuboglu et al. (2008) and by using the results of our study. In Fig. 8, the scintillation index of BG beam versus the propagation distance $L$ is illustrated for different values of the width parameter$\left( {{\text{a}}_{B} = \frac{\alpha }{{\omega_{0} }}} \right)$. It is shown from the Figure that the scintillation index of the BG beam decreases with increasing${\text{a}}_{B}$. Furthermore, we can note that the BG beam presents a scintillation index weaker compared to the Gaussian beam$\left( {{\text{a}}_{B} = 0} \right)$. However, this characteristic tends to vanish when ${\text{a}}_{B}$ achieves the value 100 m⁻¹.

Fig. 8

Scintillation index of BG beam with propagation distance $L$ at several values of the parameter ${\text{a}}_{B}$ with $l_{0} = 1\,{\text{mm}}$, $\omega_{0} = 50\,{\text{mm}}$, $\lambda = 1550\,{\text{nm}}$ and $C_{n}^{2} = 10^{{ - 15}} {\text{m}}^{{{\raise0.5ex\hbox{$\scriptstyle { - 2}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}$

5.3 Gaussian beam

Figure 9 presents a comparative study of the scintillation index for the Gaussian beam and GBLG, BLG, BG and LG beams. We can see from the Figure that the scintillation index of the Gaussian beam is in good agreement with the result given by Eyyuboglu and Baykal (2007) (see Fig. 2 of this reference). Furthermore, we can note that the scintillation index of the GBLG beam is lower than the scintillation index of the BLG beam especially at shorter propagation ranges, but after that, it becomes larger than that of the other presented beams. We can also deduce that the use of the BG beam can be more suitable in practical application compared to the other studied beams.

Fig. 9

Scintillation index of GBLG, BLG, BG, LG and Gaussian beams versus the propagation distance $L$, with $\lambda = 1550\,{\text{nm}},$ $l_{0} = 20\,{\text{mm}}$, $C_{n}^{2} = 10^{ - 15} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}$ and $\omega_{0} = 10\,{\text{mm}}$

6 Conclusion

The scintillation index of the GBLG beam propagating in a marine atmospheric turbulence with weak fluctuations is studied based on the Born approximation, the Rytov theory, and the Von Karman spectrum by calculating the second and the third-order statistical moments. From the numerical results, it is concluded that the scintillation index of GBLG beam increases with the enhancement of the beam waist size and the atmospheric turbulent structure constant. While the diffracted beam is less affected by the turbulence of the maritime atmosphere for small values of the wavelength, the inner scale and the beam order. Some special cases of the scintillation index of GBLG beam as Laguerre-Bessel-Gaussian beam, Laguerre-Gaussian beam, Bessel-Gaussian beam, and Gaussian beam are deduced from this study and they are illustrated numerically. Our main result derived here can be beneficial in the design of an optical wireless communication link in the marine environment.