Introduction of generalized Bessel–Laguerre–Gaussian beams and its central intensity travelling a turbulent atmosphere

Abstract

The so-called Generalized Bessel–Laguerre–Gaussian (GBLG) beam is introduced, in this paper, and an approximate formula of the average axial intensity of its propagation through a turbulent atmosphere is investigated using the extended Huygens–Fresnel diffraction integral in the paraxial approximation and on the Rytov theory. The analytical expression elaborated is regarded as the main result of this work. Several above studies are derived here as special cases from our research. The impact of some parameters, including incident beam parameters and turbulence strength, on the distribution of the axial intensity of the GBLG beam and on the profiles of some particular beams through a turbulent atmosphere are carried out numerically in the paper. From our numerical results-, the propagation of Gaussian beams, Laguerre–Gaussian beams and Bessel–Gaussian beams through the considered medium are deduced as particular cases.

1 Introduction

It is known that the evolution of laser beams through atmospheric turbulence is of great importance and receive the attention of several people. This interest is due to its attractive applications in various domains such as remote sensing, tracking, long-distance optical communication, imaging system and so on (Andrews et al. 2001; Noriega-Manez and Gutiérrez-Vega 2007; Korotkova and Gbur 2007; Cang and Zhang 2010). So, the propagation of optical laser beams in turbulent atmosphere is widely studied by the laser community. For instance, we cite those about the propagation of Laguerre–Gaussian beams (Wang et al. 2010; Zhu et al. 2015), Bessel–Gaussian and modified Bessel–Gaussian beams (Zhu et al. 2012; Xiu-bo and En-bang 2009; Eyyuboglu and Hardalaç 2008), Flattened Gaussian beams (Kinani et al. 2011; Khannous et al. 2014; Khannous and Belafhal 2016; Ata and Baykal 2017) and others (Wang and Zheng 2009; Wen et al. 2015; Ez-zariy et al. 2016; Zhou et al. 2009; Liu et al. 2013; Ya-Qing et al. 2014; Belafhal et al. 2011; Boufalah et al. 2016).

On other hand, in 2000, by means of a linear combination of the well-known Hermite-Gaussian that have a rectangular symmetry, Tovar (2000) have derived the so-called Laguerre–Bessel–Gaussian (LBG) beams as novel solutions to the wave equation expressed in rotational coordinates. So, this research well be considered as a crucial and general investigation, because by changing the parameters, these beams can be reduced to: ideal Bessel, to Bessel-Gaussian, to pure Laguerre, to Laguerre–Gaussian and to fundamental Gaussian beams. Later, the LBG beam has been the subject of other studies. For example, based on the Rayleigh–Sommerfeld theory, Mei and Zhao (2007) have examined the properties of the non-paraxial of the vectorial LBG beams. Using the vector diffraction theory, Nie et al. (2015) have examined analytically and numerically the intensity characteristics, near the focus, of the radially polarized LBG beams focused by a high numerical objective immersed in a liquid. More recently, Saad et al. (2017) members of our research group have contributed in the study of this beam by the analysis of its propagation through a helical axicon using the Fresnel integral formula.

Based on the works of Li et al. (2004) and Tovar (2000) concerning the generalized Bessel–Gaussian and the LBG beams respectively, in this paper we will introduce for the first time the so-named Generalized Bessel–Laguerre–Gaussian (GBLG) beams as novel solutions of the paraxial wave equation in cylindrical coordinates. Yet, by means of the extended Huygens- Fresnel integral formula (Andrews and Philips 1998), an approximate analytical expression of the on-axis intensity of GBLG beam through a turbulent atmosphere is derived. The paper is organized as follows. In the coming Section, we introduce the analytical expression of the electrical field of the GBLG beams in the emitter plane. An approximate expression of the on-axis intensity of the GBLG beam travelling a turbulent atmosphere is elaborated in Sect. 3 using the extended Huygens-Fresnel integral formula. In the Sect. 4, by the change of some parameters, we deduce the formulae of the central intensities of the generalized Bessel–Gaussian, Flattened Bessel–Gaussian, Bessel–Gaussian, generalized Laguerre–Gaussian, Laguerre–Gaussian, and fundamental Gaussian beams through a turbulent atmosphere as special cases of the general GBLG beam developed in the above Section which regarded the main study. Numerical simulations and results discussions are outlined in the Sect. 5. And a simple conclusion is outlined in the end of the paper.

2 Input electrical field distribution of GBLG beams

In the cylindrical coordinates system, we introduce the electrical field distribution of the GBLG beam as a product of the so-called generalized Laguerre function, $L_{s}^{\left| \ell \right|} \left( . \right)$, of order $\left| \ell \right|$, generalized Bessel function which expressed as a finite sum of Bessel functions, $J_{n} (.)$, of successive orders $n$ and a Li’s Flat-topped Gaussian profile of order $M$. At the waist plane $\left( {z = 0} \right)$ the distribution of the GBLG beam proposed is given by

$$v_{N,M} (r,\theta ,0) = L_{\left| \ell \right|} (r)B_{N} (r,\theta ,0)G_{M} (r,\theta ,0) ,$$

(1)

where

$$B_{N} (r,\theta ,0) = \sum\limits_{n}^{N} {b_{n} } J_{n} (\frac{\alpha }{{\omega_{0} }}r)\exp (in\theta ) ,$$

(2)

where $b_{n}$ is an arbitrary constant,

$$L_{\left| \ell \right|} (r) = (\frac{\sqrt 2 r}{{\omega_{0} }})^{\left| \ell \right|} L_{s}^{\left| \ell \right|} \left( {\frac{{2r^{2} }}{{\omega_{0}^{2} }}} \right)\exp ( - i\left| \ell \right|\theta ) ,$$

(3)

and

$$G_{\text{M}} \left( {r,0} \right) = \sum\limits_{m = 1}^{M} {g_{m,M} } \exp \left( { - m\gamma \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right) ,$$

(4a)

with

$$g_{m,M} = \left( { - 1} \right)^{m + 1} \frac{{M\left( {M - 1} \right) \cdots \left( {M - m + 1} \right)}}{m!} ,$$

(4b)

$$\gamma = \sum\limits_{m = 1}^{M} {\frac{1}{m}} ,$$

(4c)

where $J_{n} \left( . \right)$ is the nth-order Bessel function, $(r,\theta )$ are polar coordinates and $\alpha$ is the transverse component of the wave factor. $L_{s}^{\left| \ell \right|} \left( . \right)$ denotes the Laguerre polynomial with $s$ and $\left| \ell \right|$ are the radial and angular mode orders, respectively. $\exp (in\theta )$ and $\exp ( - i\left| \ell \right|\theta )$ are the phase terms for the beams. Finally, the analytical expression of the field distribution of the GBLG beams in the cylindrical coordinates $(r,\theta ,z)$ at the plane $z = 0$ can be written as

$$V_{N,M}^{\ell ,s} (r,\theta ,0) = \sum\limits_{n}^{N} {\sum\limits_{m = 1}^{M} {b_{n} g_{m,M} \left( {\frac{\sqrt 2 r}{{\omega_{0} }}} \right)^{\left| \ell \right|} L_{s}^{\left| \ell \right|} \left( {\frac{{2r^{2} }}{{\omega_{0}^{2} }}} \right)J_{n} \left( {\frac{\alpha r}{{\omega_{0} }}} \right)\exp \left( { - \frac{{m\gamma r^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - i\left( {\left| \ell \right| - n} \right)\theta } \right)} } .$$

(5)

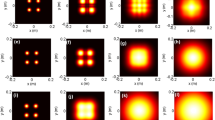
Figure 1 presents the incident 3D-transverse intensity of the GBLG beams with its contour at the source plane $\left( {z = 0} \right)$ for different values of the coefficient $\alpha$. From the plots of this figure, it can be seen that, when $\alpha \ne 0,$ there are two central lobes surrounded by side-lobes. Also, it observed that the intensity of secondary lobes decrease with the increase of $\alpha$ and the depth of the center dark region becomes more greater with large values of the coefficient $\alpha$.

Fig. 1

Incident transverse intensity of the GBLG beams with $\left| \ell \right| = 3$, $s = 4$, $\omega_{0} = 1\,{\text{mm}}$, $M = 20$,$\gamma = 3.6$ and $N = 4$ for various values of the coefficient $\alpha$ at the input plane ($z = 0$): a $\alpha = 0\,{\text{mm}}^{ - 1}$, b $\alpha = 1.5\,{\text{mm}}^{ - 1}$ and c $\alpha = 3.5\,{\text{mm}}^{ - 1}$

3 On-axis intensity of GBLG beams in turbulent atmosphere

Within the framework of the paraxial approximation and the Rytov theory, the propagation of the electric field of GBLG beams in a turbulent atmosphere can be treated as the following extended Huygens-Fresnel integral formula as (Andrews and Philips 1998)

$$V_{N,M}^{\ell ,s} (\overrightarrow {\rho } ,z,t) = - \frac{ik}{2\pi z}\exp \left( {ikz} \right)\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {V_{N,M}^{\ell ,s} (\overrightarrow {r}_{1} ,0)\exp \left[ {\frac{ik}{2z}\left( {\overrightarrow {{r_{1} }} - \overrightarrow {\rho } } \right)^{2} + \psi \left( {\overrightarrow {{r_{1} }} - \overrightarrow {\rho } } \right) - 2i\pi ft} \right]} } d\overrightarrow {{r_{1} }} ,$$

(6)

where $k = 2\pi /\lambda$ is the wave number of the incident GLBG beams and $\lambda$ being the wavelength, $a$ is the emitting aperture radius, $z$ is the propagation distance. $\psi (\vec{r}_{1} ,\rho )$ represents the random part due to the turbulent atmosphere of the complex phase of a spherical wave propagating from the source plane to the output one. $\vec{r}_{1} (r_{1} ,\theta_{1} )$ and $\vec{\rho }(\rho ,\phi )$ are the position vectors in the source plane and the receiver one, respectively, $f$ and $t$ denote the frequency and the time, respectively. In Fig. 2, we illustrate a schematic propagation of the GBLG beams in a turbulent atmosphere optical system.

Fig. 2

A schematic propagation of the GBLG beams in a turbulent atmosphere optical system

The average intensity of GBLG beams in turbulent atmosphere is defined as

$$\begin{aligned} \left\langle {I_{s} \left( {\overrightarrow {\rho } ,z} \right)} \right\rangle & = \left\langle {V_{N,M}^{\ell ,s} (\overrightarrow {\rho } ,z,t){V_{N,M}^{\ell ,s}}^{ * } (\overrightarrow {\rho } ,z,t)} \right\rangle = \left( {\frac{k}{2z\pi }} \right)^{2} \int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\left\langle {V_{N,M}^{\ell ,s} (\overrightarrow {{r_{1} }} ,0){V_{N,M}^{\ell ,s}}^{ * } (\overrightarrow {{r_{2} }} ,0)} \right\rangle } } } } \\ & \quad \times \exp \left[ {\frac{ik}{2z}\left( {\left( {\overrightarrow {{r_{1} }} - \overrightarrow {\rho } } \right)^{2} - \left( {\overrightarrow {{r_{2} }} - \overrightarrow {\rho } } \right)^{2} } \right)} \right]\exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {\overrightarrow {{r_{1} }} - \vec{r}_{2} } \right)^{2} } \right]d\overrightarrow {{r_{1} }} d\overrightarrow {{r_{2} }} , \\ \end{aligned}$$

(7)

where $*$ and 〈〉 denote the complex conjugate and ensemble average over the turbulent media, respectively.

Equation (7) is obtained by using the following identity (Andrews and Philips 1998)

$$\left\langle {\exp \left[ {\psi \left( {r_{1} ,\rho } \right) + \psi^{ * } \left( {r_{2} ,\rho } \right)} \right]\,} \right\rangle = \exp \left[ { - \frac{1}{2}D_{\psi } \left( {r_{1} ,r_{2} ,\rho } \right)} \right] \cong \exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {r_{1} - r_{2} } \right)^{2} } \right] ,$$

(8)

where $D_{\psi }$ is the wave structure function of the random complex phase in the Rytov’s representation, and $\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}}$ is the coherence length of a spherical wave propagating in the turbulent medium, with $C_{n}^{2}$ is the refractive index structure constant indicating the turbulent strength. By submitting Eq. (5) into Eq. (7), the expression of the average intensity of the output beam can be written as

$$\begin{aligned} \left\langle {I_{s} \left( {\overrightarrow {\rho } ,z} \right)} \right\rangle = \left( {\frac{1}{z\lambda }} \right)^{2} \sum\limits_{{n_{1} }}^{N} {b_{{n_{1} }} \sum\limits_{{m_{1} = 1}}^{M} {g_{{m_{1} ,M}} \sum\limits_{{n_{2} }}^{N} {b_{{n_{2} }} \sum\limits_{{m_{2} = 1}}^{M} {g_{{m_{2} ,M}} } } } } \int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\left( {\frac{{\sqrt 2 r_{1} }}{{\omega_{0} }}} \right)^{\left| \ell \right|} \left( {\frac{{\sqrt 2 r_{2} }}{{\omega_{0} }}} \right)^{\left| \ell \right|} \exp \,\frac{ik}{z}\left[ {r_{2} \rho \cos \,\left( {\theta_{2} - \phi } \right) - r_{1} \rho \cos \,\left( {\theta_{1} - \phi } \right)} \right]} } } } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \,\left[ {\left( {\frac{ik}{2z} - \frac{{m_{1} \gamma }}{{\omega_{0}^{2} }} - \frac{1}{{\rho_{0}^{2} }}} \right)r_{1}^{2} - \left( {\frac{ik}{2z} + \frac{1}{{\rho_{0}^{2} }} + \frac{{m_{2} \gamma }}{{\omega_{0}^{2} }}} \right)r_{2}^{2} } \right]\exp \,\left[ {\frac{1}{{\rho_{0}^{2} }}\left( {2r_{1} r_{2} \cos \,\left( {\theta_{1} - \theta_{2} } \right)} \right)} \right]\,\,\exp \,\left( { - i\left( {\left| \ell \right| - n_{1} } \right)\theta_{1} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\exp \left( {i\,\left( {\left| \ell \right| - n_{2} } \right)\theta_{2} } \right)L_{s}^{\left| \ell \right|} \,\left( {\frac{{2r_{1}^{2} }}{{\omega_{0}^{2} }}} \right)L_{s}^{\left| \ell \right|} \left( {\frac{{2r_{2}^{2} }}{{\omega_{0}^{2} }}} \right)J_{{n_{1} }} \left( {\frac{{\alpha r_{1} }}{{\omega_{0} }}} \right)J_{{n_{2} }} \left( {\frac{{\alpha r_{2} }}{{\omega_{0} }}} \right)d\overrightarrow {{r_{1} }} d\overrightarrow {{r_{2} }} , \hfill \\ \end{aligned}$$

(9)

The on-axis average intensity of GBLG beams propagating in atmospheric turbulence is evaluated by transforming the finite integral of Eq. (9) into an infinite one by using the famous hard aperture function $H\left( r \right)$ which is defined as

$$H\left( r \right) = \left\{ \begin{aligned} 1,\,\,\,\,\,\,\,\left| r \right| \le a \hfill \\ 0,\,\,\,\,\,\,\,\left| r \right| > a \hfill \\ \end{aligned} \right. ,$$

(10a)

with $a$ is the half-width of the rectangular function.

The function $H\left( r \right)$ can be expanded into a finite sum of complex Gaussian functions with finite numbers, in the circular coordinates system, as (Wen and Breazeale 1988)

$$H\left( r \right) = \sum\limits_{g = 1}^{K} {A_{g} \exp \left( {\frac{{ - B_{g} }}{{a^{2} }}r^{2} } \right)} ,$$

(10b)

where $A_{g}$ and $B_{g}$ denote the expansion and Gaussian coefficients, respectively (Wen and Breazeale 1988), and $k$ represents the number of the expansion terms. Generally, the number $k$ is a equal to ten (Wen and Breazeale 1988).

By putting $\vec{\rho } = \overrightarrow {0}$ into Eq. (9), one obtains

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle = \left( {\frac{1}{z\lambda }} \right)^{2} \sum\limits_{g = 1}^{K} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{K} {A_{{g^{\prime}}} } \sum\limits_{{n_{1} }}^{N} {b_{{n_{1} }} \sum\limits_{{m_{1} = 1}}^{M} {g_{{m_{1} ,M}} \sum\limits_{{n_{2} }}^{N} {b_{{n_{2} }} \sum\limits_{{m_{2} = 1}}^{M} {g_{{m_{2} ,M}} } } } } \int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\exp \left[ { - \left( { - \frac{ik}{2z} + \frac{{m_{1} \gamma }}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{B_{g} }}{{a^{2} }}} \right)r_{1}^{2} } \right]} } } } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\exp \left[ { - \left( {\frac{ik}{2z} + \frac{1}{{\rho_{0}^{2} }} + \frac{{m_{2} \gamma }}{{\omega_{0}^{2} }} + \frac{{B_{{g^{\prime}}} }}{{a^{2} }}} \right)r_{2}^{2} } \right]\left( {\frac{{\sqrt 2 r_{1} }}{{\omega_{0} }}} \right)^{\left| \ell \right|} \left( {\frac{{\sqrt 2 r_{2} }}{{\omega_{0} }}} \right)^{\left| \ell \right|} \exp \left[ {\frac{1}{{\rho_{0}^{2} }}\left( {2r_{1} r_{2} \cos \left( {\theta_{1} - \theta_{2} } \right)} \right)} \right]\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\exp \left( { - i\left( {\left| \ell \right| - n_{1} } \right)\theta_{1} } \right)\exp \left( {i\left( {\left| \ell \right| - n_{2} } \right)\theta_{2} } \right)L_{s}^{\left| \ell \right|} \left( {\frac{{2r_{1}^{2} }}{{\omega_{0}^{2} }}} \right)L_{s}^{\left| \ell \right|} \left( {\frac{{2r_{2}^{2} }}{{\omega_{0}^{2} }}} \right)J_{{n_{1} }} \left( {\frac{{\alpha r_{1} }}{{\omega_{0} }}} \right)J_{{n_{2} }} \left( {\frac{{\alpha r_{2} }}{{\omega_{0} }}} \right)r_{1} dr_{1} d\theta_{1} r_{2} dr_{2} d\theta_{2} . \hfill \\ \end{aligned}$$

(11)

Recalling the following integrals (Gradshteyn and Ryzhik 1994)

$$I_{m} \left( z \right) = \left( { - i} \right)^{m} J_{m} \left( {iz} \right),$$

(12a)

$$\int\limits_{0}^{\infty } {\exp \left[ { - im\theta_{1} + x\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} = 2\pi \exp \,\left( { - im\theta_{2} } \right)I_{m} \left( x \right),$$

(12b)

and

$$\int\limits_{0}^{\infty } {\left( x \right)^{t} \exp \left[ { - cx^{2} } \right]} J_{f} \left( {dx} \right)dx = \frac{{d^{f} \varGamma \left( {\frac{\upsilon + f + 1}{2}} \right)}}{{2^{f + 1} c^{{\frac{t + f + 1}{2}}} \varGamma \left( {f + 1} \right)}}{}_{1}F_{1} \left( {\frac{t + f + 1}{2};\,f + 1; - \frac{{d^{2} }}{4c}} \right),{\text{with}}\,\left[ {\text{Re} c > 0,\,\text{Re} \left( {t + f} \right) > 0} \right].$$

(12c)

with $\Gamma \left( . \right)$ and ${}_{1}F_{1} \left( {.,.;.} \right)$ are the Gamma and the hypergeometric functions, respectively, and after some algebraic manipulations, the analytical expression of the on-axis average intensity distribution of GBLG beams propagating into a turbulent atmosphere received at the output plane is written as

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle = \left( {\frac{\pi }{z\lambda }} \right)^{2} \left( {\frac{2}{{\rho_{0}^{2} \omega_{0}^{2} }}} \right)^{\left| \ell \right|} \sum\limits_{g = 1}^{K} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{K} {A_{{g^{\prime}}} } \sum\limits_{n}^{N} {b_{n} \frac{{\alpha^{2n} }}{{\omega_{0}^{2n} \left( {\varGamma \left( {n + 1} \right)} \right)^{2} }}\left( {\frac{{\rho_{0}^{2} }}{4}} \right)}^{n} \sum\limits_{j = 0}^{\infty } {\frac{1}{{\rho_{0}^{4j} \varGamma \left( {\left| \ell \right| + j - n + 1} \right)j!}}} \hfill \\ \,\,\,\,\,\, \times \,\sum\limits_{p = 0}^{s} {\frac{{\left( {s + \left| \ell \right|} \right)\,!\left( {{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} {\omega_{1}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{1}^{2} }$}}} \right)^{p} }}{{\left( {\left| \ell \right| + p} \right)\,!\left( {s - p} \right)\,!p\,!}}} \sum\limits_{{m_{1} = 1}}^{M} {g_{{m_{1} ,M}} \frac{1}{{\beta_{1}^{\left| \ell \right| + j + p + 1} }}} \sum\limits_{q = 0}^{s} {\frac{{\left( {s + \left| \ell \right|} \right)\,!\left( {{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} {\omega_{1}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{1}^{2} }$}}} \right)^{q} }}{{\left( {\left| \ell \right| + q} \right)\,!\left( {s - q} \right)\,!q\,!}}} \sum\limits_{{m_{2} = 1}}^{M} {g_{{m_{2} ,M}} \frac{1}{{\beta_{2}^{\left| \ell \right| + j + q + 1} }}} \hfill \\ \,\,\,\,\,\,\, \times \varGamma \left( {\left| \ell \right| + p + j + 1} \right)\,\varGamma \left( {\left| \ell \right| + q + j + 1} \right)\,\,{}_{1}F_{1} \left( {\left| \ell \right| + p + j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta_{1} }}} \right)\,{}_{1}F_{1} \left( {\left| \ell \right| + q + j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta_{2} }}} \right). \hfill \\ \end{aligned}$$

(13a)

where

$$\beta_{1} = \left( { - \frac{ik}{2z} + \frac{{m_{1} \gamma }}{{\omega_{1}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{B_{g} }}{{a^{2} }}} \right) ,$$

(13b)

and

$$\beta_{2} = \left( {\frac{ik}{2z} + \frac{1}{{\rho_{0}^{2} }} + \frac{{m_{2} \gamma }}{{\omega_{1}^{2} }} + \frac{{B_{{g^{\prime}}} }}{{a^{2} }}} \right) .$$

(13c)

The analytical expression of the axial average intensity given by Eqs. (13) is the main result of the present work. In the following, we study numerically the influence of the beam parameters, and the turbulent strength of atmosphere on the propagation of the GLBG beams in turbulent atmosphere.

4 Special cases

4.1 Generalized Bessel–Gaussian beam

4.1.1 Input beam

In the analytical expression of the GBLG beam established by Eq. (5), when the parameters s and $\left| \ell \right|$ are equals to zero, the terms of Laguerre and Hollow functions vanish and the incident beam becomes a Generalized Bessel Gaussian beam expressed by the equation

$$V_{N,M}^{0,0} (r,\theta ,0) = \sum\limits_{n}^{N} {\sum\limits_{m = 1}^{M} {b_{n} g_{m,M} J_{n} \left( {\frac{\alpha r}{{\omega_{0} }}} \right)\exp \left( { - \frac{{m\gamma r^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { + in\theta } \right)} } .$$

(14a)

This is a finite sum of Bessel beams with successive orders modulated by a Li’s flattened Gaussian envelope.

4.2 Axial intensity in the output plane

So, in the conditions specified in the latest sub-section, i.e. when $\left| \ell \right| = s = 0$, Eqs. (13) reduce to

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle = \left( {\frac{\pi }{z\lambda }} \right)^{2} \sum\limits_{g = 1}^{K} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{K} {A_{{g^{\prime}}} } \sum\limits_{n}^{N} {b_{n} \frac{{\alpha^{2n} }}{{\omega_{0}^{2n} \left( {\varGamma \left( {n + 1} \right)} \right)^{2} }}\left( {\frac{{\rho_{0}^{2} }}{4}} \right)}^{n} \sum\limits_{j = 0}^{\infty } {\frac{1}{{\rho_{0}^{4j} \varGamma \left( {j - n + 1} \right)}}} \sum\limits_{{m_{1} = 1}}^{M} {g_{{m_{1} ,M}} \frac{1}{{\beta_{1}^{j + 1} }}} \hfill \\ \quad \times \sum\limits_{{m_{2} = 1}}^{M} {g_{{m_{2} ,M}} \frac{1}{{\beta_{2}^{j + 1} }}} \times \varGamma \left( {j + 1} \right){}_{1}F_{1} \left( {j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta_{1} }}} \right){}_{1}F_{1} \left( {j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta_{2} }}} \right), \hfill \\ \end{aligned}$$

(14b)

where $\beta_{1}$ and $\beta_{2}$ are as given in Eqs. (13b) and (13c). Equation (14b) is the expression of the on-axis intensity of the generalized Bessel Gaussian beam through a turbulent atmosphere.

4.3 Flattened Bessel-Gaussian beam

4.3.1 Input beam

When $\left| \ell \right| = s = 0$ and $N = n$, the initial GBLG beam reduces to an ideal nondiffracting Bessel beam of order n modulated by Li’s Flattened Gaussian beam given by

$$V_{n,M}^{0,0} (r,\theta ,0) = \sum\limits_{m = 1}^{M} {b_{n} g_{m,M} J_{n} \left( {\frac{\alpha r}{{\omega_{0} }}} \right)\exp \left( { - \frac{{m\gamma r^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( {in\theta } \right)} .$$

(15a)

This is a simple nth order Bessel beam truncated by a Li’s flattened Gaussian module.

4.4 Axial intensity in the output plane

The axial intensity of the Li’s Flattened Bessel–Gaussian beam through a turbulent atmosphere could be derived from Eqs. (13) by considering the parameters fixed in the above sub-section. In such conditions we obtain

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle = \left( {\frac{\pi }{z\lambda }} \right)^{2} \sum\limits_{g = 1}^{P} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{P} {A_{{g^{\prime}}} } b_{n} \frac{{\alpha^{2n} }}{{\omega_{0}^{2n} \left( {\varGamma \left( {n + 1} \right)} \right)^{2} }}\left( {\frac{{\rho_{0}^{2} }}{4}} \right)^{n} \sum\limits_{j = 0}^{\infty } {\frac{1}{{\rho_{0}^{4j} \varGamma \left( {j - n + 1} \right)}}} \times \varGamma \left( {j + 1} \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\sum\limits_{{m_{1} = 1}}^{M} {\frac{{g_{{m_{1} ,M}} }}{{\beta_{1}^{j + 1} }}} \sum\limits_{{m_{2} = 1}}^{M} {\frac{{g_{{m_{2} ,M}} }}{{\beta_{2}^{j + r + 1} }}} \,\,{}_{1}F_{1} \left( {j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta_{1} }}} \right)\,{}_{1}F_{1} \left( {j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta_{2} }}} \right). \hfill \\ \,\,\,\,\,\,\, \hfill \\ \end{aligned}$$

(15b)

This is an approximate formula of the on-axis intensity of the flattened Bessel Gaussian beam traveling a turbulent atmosphere.

4.5 Bessel–Gaussian beam

4.5.1 Input beam

When $\left| \ell \right| = s = 0$ and $N = n$ and $M = 1$, the initial GBLG beam reduces to a Bessel–Gaussian beam of order $n$ given by

$$V_{N,1}^{0,0} (r,\theta ,0) = b_{n} J_{n} \left( {\frac{\alpha r}{{\omega_{0} }}} \right)\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( {in\theta } \right).$$

(16a)

4.5.2 Axial intensity in the output plane

The axial intensity of the Bessel–Gaussian beam is obtained from our main result established in Eqs. (13) if when $\left| \ell \right| = s = 0$ and $N = n$ and $M = 1$.

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle & = \left( {\frac{\pi }{z\lambda }} \right)^{2} \frac{{b_{n} \alpha^{2n} }}{{\omega_{0}^{2n} \left( {\varGamma \left( {n + 1} \right)} \right)^{2} }}\left( {\frac{{\rho_{0}^{2} }}{4}} \right)^{n} \sum\limits_{g = 1}^{K} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{K} {A_{{g^{\prime}}} } \sum\limits_{j = 0}^{\infty } {\frac{1}{{\rho_{0}^{4j} \varGamma \left( {j - n + 1} \right)j!}}} \times \,\frac{1}{{{\beta^{\prime}_{1}}^{j + 1} }}\frac{1}{{{\beta^{\prime}_{2}}^{j + 1} }} \\ & \quad \times \varGamma \left( {j + 1} \right)\,\varGamma \left( {j + 1} \right)\,\,{}_{1}F_{1} \left( {j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta^{\prime}_{1} }}} \right)\,{}_{1}F_{1} \left( {j + 1;n + 1; - \frac{{\alpha^{2} }}{{4\omega_{0}^{2} \beta^{\prime}_{2} }}} \right), \\ \end{aligned}$$

(16b)

where

$$\beta^{\prime}_{1} = \left( { - \frac{ik}{2z} + \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{{B_{g} }}{{a^{2} }}} \right) ,$$

(16c)

and

$$\beta^{\prime}_{2} = \left( {\frac{ik}{2z} + \frac{1}{{\rho_{0}^{2} }} + \frac{1}{{\omega_{0}^{2} }} + \frac{{B_{{g^{\prime}}} }}{{a^{2} }}} \right) .$$

(16d)

Equation (16b) is identical to the main result established by Eq. (20) of Ref. (Cang and Zhang 2010) about the on-axis intensity of the Bessel–Gaussian beam passing through a turbulent atmosphere.

4.6 Generalized Laguerre–Gaussian beams

4.6.1 Input beam

If $N = n = \alpha = 0$ and $M = 1$, the Bessel term, in Eq. (5) vanishes and the flattened Gaussian term to a fundamental Gaussian module. For such parameters, the incident beam at the emitter plane stands to a generalized Laguerre Gaussian beam as elaborated by

$$V_{0,1}^{\ell ,s} (r,\theta ,z = 0) = \left( {\frac{\sqrt 2 r}{{\omega_{0} }}} \right)^{\left| \ell \right|} L_{s}^{\left| \ell \right|} \left( {\frac{{2r^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - i\left| \ell \right|\theta } \right).$$

(17a)

4.6.2 Axial intensity at the output plane

The axial intensity of the Generalized Laguerre–Gaussian beam is derived from the main result of this work for the parameters $N = n = \alpha = 0$ and $M = 1$.

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle & = \left( {\frac{\pi }{z\lambda }} \right)^{2} \left( {\frac{2}{{\rho_{0}^{2} \omega_{0}^{2} }}} \right)^{\left| \ell \right|} \sum\limits_{g = 1}^{K} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{K} {A_{{g^{\prime}}} } \sum\limits_{j = 0}^{\infty } {\frac{1}{{\rho_{0}^{4j} \varGamma \left( {\left| \ell \right| + j + 1} \right)j!}}} \times \sum\limits_{p = 0}^{s} {\frac{{\varGamma \left( {\left| \ell \right| + p + j + 1} \right)\left( {s + \left| \ell \right|} \right)!\left( { - 2/\omega_{1}^{2} } \right)^{p} }}{{\left( {\left| \ell \right| + p} \right)\,!\left( {s - p} \right)!p!}}} \frac{1}{{{\beta '_{1}}^{\left| \ell \right| + j + p + 1} }} \\ & \quad \times \sum\limits_{q = 0}^{s} {\frac{{\varGamma \left( {\left| \ell \right| + q + j + 1} \right)\,\left( {s + \left| \ell \right|} \right)\,!\left( { - 2/\omega_{1}^{2} } \right)^{q} }}{{\left( {\left| \ell \right| + q} \right)\,!\left( {s - q} \right)\,!q\,!}}} \frac{1}{{{\beta '_{2}}^{\left| \ell \right| + j + q + 1} }}, \\ \end{aligned}$$

(17b)

where $\beta_{1}^{'}$ and $\beta_{2}^{'}$ are as given in Eqs. (16c) and (16d).

4.7 Laguerre–Gaussian beam

4.7.1 Input beam

When $N = n = \alpha = \left| \ell \right| = 0$ and $M = 1$ the generalized Laguerre–Gaussian beam given in Eq. (17a) reduces to a Laguerre Gaussian beam as established as

$$V_{0,1}^{0,s} (r,\theta ,0) = L_{s}^{{}} \left( {\frac{{2r^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right).$$

(18a)

4.7.2 Axial intensity in the output plane

The axial intensity of the Laguerre Gaussian beam travelling a turbulent atmosphere is obtained from the main result (Eq. 13), when $N = n = \alpha = \left| \ell \right| = 0$ and $M = 1$. The formula describes this intensity is

$$\begin{aligned} \left\langle {I_{s} \left( {0,z} \right)} \right\rangle & = \left( {\frac{\pi }{z\lambda }} \right)^{2} \sum\limits_{g = 1}^{K} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{K} {A_{{g^{\prime}}} } \frac{1}{{\beta^{\prime}_{1} \beta^{\prime}_{2} }}\sum\limits_{j = 0}^{\infty } {\frac{1}{{\rho_{0}^{4j} \varGamma \left( {j + 1} \right)j!}}} \frac{1}{{\left( {\beta^{\prime}_{1} \beta^{\prime}_{2} } \right)^{j} }}\sum\limits_{p = 0}^{s} {\frac{{\varGamma \left( {p + j + 1} \right)s!\left( {{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} {\omega_{0}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{0}^{2} }$}}} \right)^{p} }}{{\left( p \right)!\left( {s - p} \right)!p!}}} \frac{1}{{{\beta^{\prime}_{1}}^{p} }} \\ & \quad \times \sum\limits_{q = 0}^{s} {\frac{{\varGamma \left( {q + j + 1} \right)\left( s \right)\,!\left( {{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} {\omega_{0}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{0}^{2} }$}}} \right)^{q} }}{{\left( q \right)\,!\left( {s - q} \right)\,!q\,!}}} \frac{1}{{{\beta^{\prime}_{2}}^{q} }}, \\ \end{aligned}$$

(18b)

where $\beta_{1}^{'}$ and $\beta_{2}^{'}$ are as established in Eqs. (16c) and (16d), respectively.

4.8 Flattened Gaussian beam

4.8.1 Input beam

If $N = n = \alpha = \left| \ell \right| = s = 0$, the initial beam at the emitter plane reduces to a Li’s Flattened Gaussian beam expressed by

$$V_{0,M}^{0,0} (r,\theta ,0) = \sum\limits_{m = 1}^{M} {g_{m,M} \exp \left( { - \frac{{m\gamma r^{2} }}{{\omega_{0}^{2} }}} \right)} .$$

(19a)

This is a finite sum of Gaussian beams with successive orders and different waists.

4.8.2 Axial intensity in the output plane

The central intensity of the Li’s flattened Gaussian beam in the turbulent atmosphere is obtiened from the main result if $N = n = \alpha = \left| \ell \right| = s = 0$. The irradiance in the receiver plane is given by

$$\left\langle {I_{s} \left( {0,z} \right)} \right\rangle = \left( {\frac{\pi }{z\lambda }} \right)^{2} \sum\limits_{g = 1}^{K} {A_{g} } \sum\limits_{{g^{\prime} = 1}}^{K} {A_{{g^{\prime}}} } \sum\limits_{{m_{1} = 1}}^{M} {g_{{m_{1} ,M}} } \sum\limits_{{m_{2} = 1}}^{M} {g_{{m_{2} ,M}} } \sum\limits_{j = 0}^{\infty } {\frac{1}{{\rho_{0}^{4j} }}} \,\,\,\frac{1}{{\beta_{1}^{j + 1} }}\,\frac{1}{{\beta_{2}^{j + 1} }}\,\,.$$

(19b)

where $\beta_{1}$ and $\beta_{2}$ are as given in Eqs. (13b) and (13c)

This expression is a double sum of that concerning the fundamental Gaussian beam described in the below in the Eq. (20b).

4.9 Fundamental Gaussian beam

4.9.1 Input beam

This beam is obtained from the GBLG beams, if we have $N = n = \alpha = \left| \ell \right| = s = 0$ and $M = 1$. So, for such parameters, Eq. (5) stands to

$$V_{0,1}^{0,0} (r,\theta ,0) = \exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right).$$

(20a)

4.9.2 Axial intensity at the output plane

By setting $N = n = \alpha = \left| \ell \right| = s = 0$ and $M = 1$ in Eq. (13), this equation reduces to a

formula describing the average intensity of the propagation of a fundamental Gaussian beam in turbulent atmosphere

$$\left\langle {I\left( {0,z} \right)} \right\rangle = \left( {\frac{\pi }{z\lambda }} \right)^{2} \sum\limits_{g = 1}^{P} {A_{g} \sum\limits_{{g^{\prime} = 1}}^{P} {A_{{g^{\prime}}} } } \frac{1}{{\beta^{\prime}_{2} \beta^{\prime}_{3} }}.$$

(20b)

where $\beta_{1}^{'}$ and $\beta_{2}^{'}$ are as established in Eqs. (16c) and (16d), respectively.

This last Equation is in good agreement with Eq. (20a) of the Ref. (Cang and Zhang 2010) concerning the central intensity of the propagation of a fundamental Gaussian beam through a turbulent atmosphere.

In absence of the turbulence $(\rho_{0} \to \infty )$, the above equations reduce to the propagation average on-axis intensity for the cited beams in free space. Our results are in good agreement with those of the literature.

5 Numerical results and discussion

5.1 Average axial intensity of the GBLG beams through a turbulent atmosphere

Numerical simulations were performed by using the analytical expression of the average intensity given by Eq. (13a). In Fig. 3 the on-axis average intensity of GBLG beams versus the propagation distance z is illustrated for three values of turbulent strength $C_{n}^{2}$, with two values of the width beam $\omega_{0}$, and with $\lambda = 1060\,{\text{nm}}$, $a = 0.15m$, $\alpha = 2m^{ - 1}$ and $\left| \ell \right| = 1$. It’s shown that the axial intensity decreases with the increase of $C_{n}^{2}$ and $\omega_{0}$. Also from this figure, it can be observed that when the width beam $\omega_{0}$ increases the position of the maximum tends to large values of the propagation distance. Furthermore, we can note that the axial intensity disappears rapidly and the propagation is shorter when the atmosphere is very turbulent. Figure 4 displays the on-axis average intensity distribution of GLBG beams through a turbulent atmosphere for two values of the turbulent strength $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}$ and $C_{n}^{2} = 1 \times 10^{ - 15} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}$, and for which several curves were plotted for different values of the wavelength. The parameters are chosen as $\left| \ell \right| = 2$, $\alpha = 1m^{ - 1}$, $\omega_{0} = 0.05\,{\text{m}}$ and $a = 0.15m$. From this figure, it’s shown that the intensity is equal to zero within the first several hundred meters of the near field. We can see that the axial intensity decreases with increasing the wavelength $\lambda$ but it increases when the turbulent strength $C_{n}^{2}$ increases, while the position of the maximum decreases when $\lambda$ and $C_{n}^{2}$ increase. It’s also observed from the plots that the propagation of beams is very faster when the wavelength is larger.

Fig. 3

The on-axis average intensity of GLBG beams versus the propagation distance $z$: a $\omega_{0} = 0.05m$ and b $\omega_{0} = 0.07m$, with three values of the turbulent strengths and for $\lambda = 1060\,{\text{nm}}$, $a = 0.15m$, $M = 2$, $\alpha = 2m^{ - 1}$ and $\left| \ell \right| = 1$

Fig. 4

The on-axis average intensity of GLBG beams versus the propagation distance $z$: a $C_{n}^{2} = 1 \times 10^{ - 15} {\text{m}}^{ - 2/3}$ and b $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}$, with three values of $\lambda$ and for $\left| \ell \right| = 2$, $a = 0.15m$, $M = 2$, $\alpha = 1m^{ - 1}$ and $\omega_{0} = 0.05m$

In Fig. 5, we illustrate the on-axis average intensity of GBLG beams versus the propagation distance z for $\lambda \, = 1060\,\,\,{\text{nm}}$, $a = 0.15m$, $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}$ and $\alpha = 2m^{ - 1}$ with two values of the order of the beams $\left| \ell \right| = 1$ and $\left| \ell \right| = 2$. We can see from Fig. 5 that the on-axis average intensity decreases with increasing the waist beam $\omega_{0}$ and by decreasing the order of the beam $\left| \ell \right|$ and the position of the maximum is larger when $\omega_{0}$ and $\left| \ell \right|$ increase. It’s shown that the propagation of beams becomes shorter when the waist beam and the order of beam are smaller.

Fig. 5

The on-axis average intensity of GLBG beams versus the propagation distance $z$ with three values of $\omega_{0}$ and for $a = 0.15m$, $\lambda = 1060\,{\text{nm}}$, $M = 2$, $\alpha = 2m^{ - 1}$ and $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}$ with: a $\left| \ell \right| = 1$, b $\left| \ell \right| = 2$

5.2 Numerical simulations of some particular cases

5.2.1 Bessel-Gaussian beam

By using Eq. (16a), we have developed some numerical simulations. The effect of the turbulent strength on the on-axis average intensity is given in Fig. 6a–d for different beam topological charges.

Fig. 6

The on-axis average intensity of Bessel–Gaussian beams for several different topological charges $m$ with different turbulent strength. The other parameters are chosen as : $a = 0.05m$, $\alpha = 50m^{ - 1}$, $\omega_{0} = 0.05m$, $\lambda = 1060\,{\text{nm}}$ and a $m = 0$, b $m = 1$, c $m = 2$ and d $m = 5$

It’s shown from Fig. 6a that when the topological charge m is equal to zero, the intensity oscillates strongly in the near field ($z < 1000m$) and decreases with the increase of propagation distance beyond the near field. When the turbulent strength is larger, the average intensity becomes smaller and decreases faster. From Fig. 6b–d, we can see that the profile of intensity remains unchanged and is equal to zero for the first hundred meters of the near field. The oscillation of intensity increases with increasing the turbulent strength and disappears for larger topological charge $m$. The intensity decreases when $m$ becomes larger and increases with increasing the turbulent strength. The intensity is always equal to zero in free space. It’s shown that the propagation of beams is shorter when the turbulent strength is larger.

The on-axis average intensity versus the propagation distance is illustrated in Fig. 7a–d for different beam topological charges by varying the beam wavelength. From Fig. 7a, we can note that when the topological charge $m$ is equal to zero, the intensity presents intense oscillations in the near field ($z < 1000m$) and decreases with the increase of propagation distance beyond the near field. The decrease of the intensity is faster when wavelength is longer. From Fig. 7b–d, it can be seen that the intensity is equal to zero for the first hundred meters of the near field. We can also observe that the propagation becomes faster with smaller value of wavelength. The oscillation of intensity disappears when topological charge $m = 5$ and the axial intensity reach zero for beams with larger wavelength, while the axial intensity is zero first, then increases with the increase of the propagation distance for smaller wavelength beams. From the plots, it’s shown that the propagation is shorter with large wavelength when $m = 0$ while it becomes faster with small wavelength when $m \ne 1$.

Fig. 7

The on-axis average intensity of Bessel-Gaussian beams for several different topological charges $m$ with different wavelength. The other parameters are chosen as : $a = 0.05m$, $\alpha = 50m^{ - 1}$, $\omega_{0} = 0.05m$, $C_{n}^{2} = 1 \times 10^{ - 15} {\text{m}}^{ - 2/3}$ and a $m = 0$, b $m = 1$, c $m = 2$ and d $m = 5$

Figure 8a–d shows the on-axis average intensity with different beam topological charges, for each of which several curves were plotted for different values of beam waist. From Fig. 8a, we can see that when the topological charge m is equal to zero, the intensity oscillates in the near field ($z < 1000m$) and decreases with the increase of propagation distance beyond the near field. The smaller beam waist the decrease of intensity is faster. From Fig. 8b, it‘s shown that the intensity is zero for the first hundred meters of the near field. Beyond the near field, the intensity increases first and then decreases with the increase of propagation distance. In Fig. 8c, the intensity follows the same rule of variation compared to Fig. 8b except the oscillations of intensity becomes weak. In Fig. 8d, the axial intensity is zero for a long propagation distance and then increases with the increase of the propagation distance. From the plots, we can conclude that the propagation is shorter with small waist beam when $m = 0$ while it becomes faster with large waist beam when $m \ne 1$. We note that ours numerical results are similar to those of Ref. (Cang and Zhang 2010).

Fig. 8

The on-axis average intensity of Bessel–Gaussian beams for several different topological charges $m$ with different waist beam. The other parameters are chosen as : $a = 0.05m$, $\alpha = 50m^{ - 1}$, $C_{n}^{2} = 1 \times 10^{ - 15} {\text{m}}^{ - 2/3}$, $\lambda = 1060\,{\text{nm}}$ and a $m = 0$, b $m = 1$, c $m = 2$ and d $m = 5$

5.2.2 Laguerre–Gaussian beams

The on-axis average intensity versus the propagation distance z of Laguerre–Gaussian beams is given in Fig. 9 with several values of $C_{n}^{2}$ and in free space.

Fig. 9

The on-axis average intensity of Laguerre–Gaussian beams versus the propagation distance $z$ with three values of $C_{n}^{2}$ and for $\lambda = 1060\,{\text{nm}}$, $a = 0.08m$ and $\omega_{0} = 0.05m$

We can see from the curves that the intensity presents oscillations in the near field ($z < 1000m$). We note that when the turbulent strength is larger, the intensity decreases i.e. the propagation becomes shorter.

The variation of the on-axis average intensity versus the propagation distance $z$ of Laguerre-Gaussian beams with three values of wavelength is illustrated in Fig. 10. It’s shown that the intensity oscillates in the near field ($z < 1000m$). The phenomenon of propagation becomes shorter when the wavelength is larger.

Fig. 10

The on-axis average intensity of Laguerre-Gaussian beams versus the propagation distance $z$ with three values of $\lambda$ and for $C_{n}^{2} = 1 \times 10^{ - 14} m^{ - 2/3}$, $a = 0.05m$ and $\omega_{0} = 0.05m$

Figure 11 shows the on-axis average intensity versus the propagation distance $z$ of Laguerre-Gaussian beams with three values of waist beams. We can see from the plots that the intensity presents oscillations in the near field ($z < 1000m$) and the propagation is faster when the waist beams is smaller.

Fig. 11

The on-axis average intensity of Laguerre-Gaussian beams versus the propagation distance $z$ with three values of $\omega_{0}$ and for $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}$, $a = 0.05m$, and $\lambda = 1060\,{\text{nm}}$

5.2.3 Fundamental Gaussian beam

By using the analytical Eq. (20b), some numerical simulations are performed. Figure 12 shows the on-axis average intensity versus the propagation distance $z$ of the fundamental Gaussian beams with three values of $C_{n}^{2}$ and in free space. From the curves, we can see that the propagation becomes shorter when the turbulent strength is larger i.e. the atmosphere is very turbulent.

Fig. 12

The on-axis average intensity of Gaussian beams versus the propagation distance $z$ with three values of $C_{n}^{2}$ and for $\lambda = 1060\,{\text{nm}}$, $a = 0.09m$ and $\omega_{0} = 0.02m$

In Fig. 13, the on-axis average intensity versus the propagation distance $z$ of Gaussian beams with three values of the wavelength is represented. It’s shown that the propagation of the beams is faster for larger values of the wavelength in a turbulent atmosphere.

Fig. 13

The on-axis average intensity of Gaussian beams versus the propagation distance $z$ with three values of $\lambda$ and for $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}$, $a = 0.09m$ and $\omega_{0} = 0.02m$

Now, we will examine the effect of the waist beams on the on-axis average intensity distribution of Gaussian beams. Figure 14 shows the on-axis average intensity versus the propagation distance $z$ of this beams family with three values of the waist beams. From the plots, it’s shown that the propagation in a turbulent atmosphere is shorter when the waist beam is smaller.

Fig. 14

The on-axis average intensity of Gaussian beams versus the propagation distance $z$ with three values of $\omega_{0}$ and for $C_{n}^{2} = 1 \times 10^{ - 14} {\text{m}}^{ - 2/3}$, $a = 0.09\,{\text{m}}$ and $\lambda = 1060\,{\text{nm}}$

6 Conclusion

In this paper, we have studied the propagation properties of a new family of beams called GBLG beams through a turbulent atmosphere. Based on the extended Huygens–Fresnel integral formula in the paraxial approximation and the Rytov theory, the analytical expression of the on-axis average intensity of GBLG beams has been obtained. The average on-axis intensity of the propagation of the Generalized Bessel–Gaussian, Flattened–Bessel–Gaussian, Bessel–Gaussian, Generalized Laguerre–Gaussian, Laguerre–Gaussian, Li’s Flattened Gaussian and fundamental Gaussian beams travelling a turbulent atmosphere are derived from our main analytical and numerical results as particular cases. It is pointed out that our results are in good agreement with those given in the literature. It’s shown that the axial average intensity of GBLG beams is affected by the change of the wavelength, the waist beam, the beam order and the turbulent strengths. We conclude that the propagation of GBLG beams with small waist beam, small beam order and large wavelength is very shorter when the atmosphere is very turbulent. Finally, our results will be useful for the applications of GBLG beams in remote sensing and free space optical communications.