Evolution of the partially coherent Generalized Flattened Hermite-Cosh-Gaussian beam through a turbulent atmosphere

Abstract

The current paper investigates the impact of a turbulent atmosphere on the propagation of a partially coherent Generalized Flattened Hermite Cosh-Gaussian (GFHChG) beam. The evaluation of a theoretical expression of the average intensity distribution for the partially coherent GFHChG beam is based on the extended Huygens-Fresnel diffraction integral and the Rytov’s quadratic approximation. The results of some laser beams are deduced as special cases from the present work. The behavior of the studied beam which is propagating through a turbulent atmosphere is analyzed through numerical illustrations. Results indicate that the partially coherent GFHChG beam successively changes shape from a doughnut to a flattened then to a Gaussian profile during its propagation in a turbulent atmosphere.

1 Introduction

Over the past decades, a great deal of research has been directed to study the propagation characteristics of laser beams in a turbulent atmosphere (Eyyuboğlu and Baykal 2005; Cai and He 2006; Chu et al. 2007; Bao-Suan and Ji-Xiong 2009; Zhou 2011; Belafhal et al. 2011; Hennani et al. 2013; Ez-zariy et al. 2016; Boufalah et al. 2016, 2018; Saad et al. 2017; Yaalou et al. 2019), with some paying a particular attention to the propagation of spatially partially coherent laser beams through a turbulent atmosphere (Shirai et al. 2003; Eyyuboğlu 2008; Wang 2008; Lin and Pu 2009; Eyyuboğlu and Sermutlu 2013; Gbur 2014) for its significance in some fields like optical information processing (Zhuang and Yu 1982), remote detection (Wu and Cai 2011), optical scattering (van Dijk et al. 2010) and free-space optical communication (Korotkova 2004). Moreover, it has been reported that partially coherent laser beams are less affected by the turbulent atmosphere than fully coherent beams (Jian 1990). This has also experimentally demonstrated by Dogariu and Amarande (2003). Recently, the propagation properties of Hermite-cosh-Gaussian beams traveling through an atmospheric turbulence are studied in details by Eyyuboğlu (2005). It has been observed that by choosing suitable parameters, the average intensity distribution of these beams presents a cosh distribution shape, then a sine or cosine distribution and finally takes a Gaussian distribution. After, Yang et al. have analyzed the evolution of partially coherent Hermite-cosh-Gaussian beams in a turbulent atmosphere (Yang et al. 2009). It was shown that the considered beams are influenced by the atmospheric turbulence and the beam parameters.

Henceforth, taking into consideration that low temperature variations occur during the propagation of light in a turbulent atmosphere, which results from a change in the refraction index. This subsequently induces intensity fluctuations of light. Hence, our interest to study the propagation characteristics of the partially coherent GFHChG beam propagating in a turbulent atmosphere.

The remainder of the paper is organized as follows: Sect. 2 introduces an analytical expression of the average intensity distribution of the partially coherent GFHChG beam propagating through a turbulent atmosphere; Section 3 lists the special cases of the obtained results, while numerical illustrations are performed and discussed in Sect. 4; and finally, Sect. 5 concludes with a summary.

2 Average intensity of partially coherent GFHChG beam in a turbulent atmosphere

Based on the works of Belafhal and Ibnchaikh (Belafhal and Ibnchaikh 2000) and Zhu et al. (Zhu et al. 2002) concerning the flattened light beams and the Hermite-cosh-Gaussian laser beams, respectively, we have introduced a novel beam family called Generalized Flattened Hermite Cosh-Gaussian (GFHChG) beam. The electric field of the considered beam at the plane z = 0 in the Cartesian coordinates system can be defined as (Chib et al. 2020)

$$ E_{mnp}^{N} \left( {{{\varvec{\uprho}}},z = 0} \right) = A_{0} H_{m} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{x} } \right)H_{n} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{y} } \right)\exp \left( { - \frac{{\rho_{x}^{2} + \rho_{y}^{2} }}{{\omega_{0}^{2} }}} \right)\sum\limits_{l = L}^{N} {\chi_{l} } \cosh^{p} \left( {\Omega_{l} \rho_{x} + \Omega_{l} \rho_{y} } \right), $$

(1)

where $H_{j} \left( . \right)$ represents the jth order Hermite polynomial $\left( {j = m,n} \right)$, $\omega_{0}$ is the waist width of the Gaussian part, $\Omega_{l} = l\Omega$ with $\Omega$ is the parameter associated to cosh part, $N$ and $L$ are two constant integers, $\chi_{l} = \left( {1 - \frac{{\delta_{l0} }}{2}} \right)\exp \left( { - l^{2} } \right)$ with $\delta_{l0}$ is the Kronecker symbol and $\left( {m,n,p} \right)$ are the orders of the beams family.

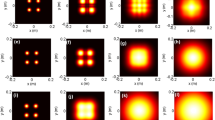
The intensity distribution representation of the partially coherent GFHChG beam field in 3-D and its corresponding contour graph are depicted in Figs. (1, 2) at the input plane, for different values of $\Omega$, $\omega_{0}$ and $p$. The other parameters are taken as: $N = 5$,$L = 10$ and $m = n = 1$. From the plots of these figures, it is noted that the profile of the partially coherent GFHChG beam is characterized by two main lobes surrounded by two side lobes whose intensity increases gradually for higher values of the waist width $\omega_{0}$, the cosh parameter $\Omega$ and the beam order $p$. It’s also observed that the side lobes disappear while the central dark region widens when $\Omega$, $\omega_{0}$ and $p$ increase.

Fig. 1

Intensity distribution of the GFHChG beam at the source plane $z = 0$ in 3-D and 2-D for different values of $\Omega$ and $\omega_{0}$, with $p = 1$

Fig. 2

Intensity distribution of the GFHChG beam at the source plane $z = 0$ in 3-D and 2-D for different values of $\Omega$ and $\omega_{0}$, with $p = 2$

By inserting the vector ${{\varvec{\uprho}}} \equiv \left( {\rho_{x} ,\rho_{y} } \right)$ in Eq. (1), where $\rho_{x}$ and $\rho_{y}$ denote the two-dimensional position vector at the source plane $z = 0$, the cross-spectral density function of the partially coherent GFHChG beam at the input plane is given as

$$ \begin{gathered} W\left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} ,z = 0} \right) = A_{0}^{2} H_{m} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{1x} } \right)H_{n} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{1y} } \right)\exp \left( { - \frac{{\rho_{1x}^{2} + \rho_{1y}^{2} }}{{\omega_{0}^{2} }}} \right)\sum\limits_{l = L}^{N} {\chi_{l} } \cosh^{p} \left( {\Omega_{l} \rho_{1x} + \Omega_{l} \rho_{1y} } \right)\exp \left( { - \frac{{(\rho_{1x} - \rho_{2x} )^{2} }}{{2\sigma_{0}^{2} }}} \right) \hfill \\ \quad \times \, H_{m} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{2x} } \right)H_{n} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{2y} } \right)\exp \left( { - \frac{{\rho_{2x}^{2} + \rho_{2y}^{2} }}{{\omega_{0}^{2} }}} \right)\sum\limits_{{l^{\prime} = L}}^{N} {\chi_{{l^{\prime}}} } \cosh^{p} \left( {\Omega_{{l^{\prime}}} \rho_{2x} + \Omega_{{l^{\prime}}} \rho_{2y} } \right)\exp \left( { - \frac{{(\rho_{1y} - \rho_{2y} )^{2} }}{{2\sigma_{0}^{2} }}} \right),\,\, \hfill \\ \end{gathered} $$

(2)

where $\sigma_{0}$ is the spatial correlation length of the partially coherent GFHChG beam at $z = 0$.

By using the following identity

$$ \cosh^{p} \left( t \right) = \frac{1}{{2^{p} }}\sum\limits_{s = 0}^{p} {\frac{p!}{{\left( {p - s} \right)!s!}}} \exp \left( {a_{sp} t} \right), $$

(3)

where

$$ a_{sp} = 2s - p, $$

(3a)

Equation (2) yields

$$ \begin{gathered} W\left( {\rho_{1} ,\rho_{2} ,z = 0} \right) = \frac{{A_{0}^{2} }}{{2^{2p} }}H_{m} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{1x} } \right)H_{n} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{1y} } \right)\exp \left( { - \frac{{\rho_{1x}^{2} + \rho_{1y}^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - \frac{{(\rho_{1x} - \rho_{2x} )^{2} }}{{2\sigma_{0}^{2} }}} \right)\sum\limits_{l = L}^{N} {\chi_{l} } \sum\limits_{{s_{1} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{1} } \\ \end{array} } \right)\exp \left[ {a_{{s_{1p} }} \Omega_{l} \left( {\rho_{1x} + \rho_{1y} } \right)} \right]} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times H_{m} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{2x} } \right)H_{n} \left( {\frac{\sqrt 2 }{{\omega_{0} }}\rho_{2y} } \right)\exp \left( { - \frac{{\rho_{2x}^{2} + \rho_{2y}^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - \frac{{(\rho_{1y} - \rho_{2y} )^{2} }}{{2\sigma_{0}^{2} }}} \right)\sum\limits_{{l^{\prime} = L}}^{N} {\chi_{{l^{\prime}}} } \sum\limits_{{s_{2} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{2} } \\ \end{array} } \right)\exp \left[ {a_{{s_{2p} }} \Omega_{{l^{\prime}}} \left( {\rho_{2x} + \rho_{2y} } \right)} \right]} . \hfill \\ \end{gathered} $$

(4)

The cross-spectral density function of the partially coherent GFHChG beam propagating through a turbulent atmosphere is expressed by the extended Huygens-Fresnel diffraction integral (Andrews and Phillips 2005) as

$$ \begin{aligned} W\left( {{\mathbf{\rho^{\prime}}}_{{\mathbf{1}}} ,{\mathbf{\rho^{\prime}}}_{{\mathbf{2}}} ,z} \right) &= \left( {\frac{k}{2\pi z}} \right)^{2} \iint {d^{2} \rho_{1} }\iint {d^{2} \rho_{2} }W\left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} ,{{\varvec{\uprho}}}_{{\mathbf{2}}} ,z = 0} \right)\exp \left\{ {\frac{ik}{{2z}}\left[ {\left( {{\mathbf{\rho^{\prime}}}_{{\mathbf{1}}} - {{\varvec{\uprho}}}_{{\mathbf{1}}} } \right)^{2} - \left( {{\mathbf{\rho^{\prime}}}_{{\mathbf{2}}} - {{\varvec{\uprho}}}_{{\mathbf{2}}} } \right)^{2} } \right]} \right\} \hfill \\ &\quad \times \, \left\langle {\exp \left[ {\psi \left( {{{\varvec{\uprho}}}_{{\mathbf{1}}} ,{\mathbf{\rho^{\prime}}}_{{\mathbf{1}}} } \right) + \psi^{ * } \left( {{{\varvec{\uprho}}}_{{\mathbf{2}}} ,{\mathbf{\rho^{\prime}}}_{{\mathbf{2}}} } \right)} \right]} \right\rangle_{m} , \hfill \\ \end{aligned} $$

(5)

where ${\mathbf{\rho^{\prime}}} \equiv \left( {\rho^{\prime}_{x} ,\rho^{\prime}_{y} } \right)$ is the two-dimensional position vector at the z plane, $z$ is the propagation distance, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }$ represents the wave number with $\lambda$ is the wavelength, $\left\langle . \right\rangle_{m}$ is the ensemble average over the medium statistics covering the log-amplitude and the phase fluctuation due to the turbulent atmosphere, $\psi \left( {{{\varvec{\uprho}}},{\mathbf{\rho^{\prime}}}} \right)$ denotes the random part of the complex phase, and the asterisk signifies the complex conjugate. Based on the Rytov’s quadratic approximation (Yura 1972), the expression of the ensemble average is given as

$$ \left\langle {\exp \left[ {\psi \left( {\rho_{1} ,\rho_{1}^{\prime } } \right) + \psi^{ * } \left( {\rho_{2} ,\rho_{2}^{\prime } } \right)} \right]} \right\rangle_{m} \approx \exp \left\{ { - \frac{1}{{\rho_{0}^{2} }}\left[ {\left( {\rho_{1} - \rho_{2} } \right)^{2} + \left( {\rho_{1} - \rho_{2} } \right)\left( {\rho_{1}^{\prime } - \rho_{2}^{\prime } } \right) + \left( {\rho_{1}^{\prime } - \rho_{2}^{\prime } } \right)^{2} } \right]} \right\}, $$

(6)

where $\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - \frac{3}{5}}}$ is the spatial coherence radius of a spherical wave propagating through the atmospheric turbulence and $C_{n}^{2}$ represents the refraction index structure constant.

In the following, we will change the variables of the integration by making the next transformation

$$ {\mathbf{u}} = \frac{{{{\varvec{\uprho}}}_{{\mathbf{2}}} + {{\varvec{\uprho}}}_{{\mathbf{1}}} }}{2}, $$

(7.a)

and

$$ {\mathbf{v}} = {{\varvec{\uprho}}}_{{\mathbf{2}}} - {{\varvec{\uprho}}}_{{\mathbf{1}}} . $$

(7.b)

Setting ${\mathbf{\rho^{\prime}}}_{{\mathbf{1}}} = {\mathbf{\rho^{\prime}}}_{{\mathbf{2}}} = {\mathbf{\rho^{\prime}}}$ into Eqs. (5) and (6) and substituting Eqs. (4), (6) and (7) into Eq. (5), the average intensity of the partially coherent GFHChG beam at the output plane can be written as

$$ \begin{gathered} I\left( {\rho^{\prime},z} \right) = W\left( {\rho^{\prime},\rho^{\prime},z} \right) \hfill \\ \quad = \frac{{A_{0}^{2} }}{{2^{2p} }}\left( {\frac{k}{2\pi z}} \right)^{2} \sum\limits_{l = L}^{N} {\chi_{l} \sum\limits_{{s_{1} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{1} } \\ \end{array} } \right)} } \sum\limits_{{l^{\prime} = L}}^{N} {\chi_{{l^{\prime}}} \sum\limits_{{s_{2} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{2} } \\ \end{array} } \right)} } \iint {d^{2} u\iint {d^{2} v\exp \left( { - \frac{{2u^{2} }}{{\omega_{0}^{2} }}} \right)}} \hfill \\ \quad \times \,\exp \left( { - \frac{{v^{2} }}{{\gamma^{2} }}} \right)\exp \left( { - \frac{ik}{z}u.v} \right)\exp \left( {\frac{ik}{z}\rho^{\prime}.v} \right)H_{m} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{x} - \frac{{v_{x} }}{2}} \right)} \right]H_{n} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{y} - \frac{{v_{y} }}{2}} \right)} \right] \hfill \\ \quad \times \, H_{m} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{x} + \frac{{v_{x} }}{2}} \right)} \right]H_{n} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{y} + \frac{{v_{y} }}{2}} \right)} \right]\exp \left[ {a_{{s_{1p} }} \Omega_{l} \left( {u_{x} - \frac{{v_{x} }}{2}} \right) + a_{{s_{2p} }} \Omega_{{l^{\prime}}} \left( {u_{x} + \frac{{v_{x} }}{2}} \right)} \right] \hfill \\ \quad \times \, \exp \left[ {a_{{s_{1p} }} \Omega_{l} \left( {u_{y} - \frac{{v_{y} }}{2}} \right) + a_{{s_{2p} }} \Omega_{{l^{\prime}}} \left( {u_{y} + \frac{{v_{y} }}{2}} \right)} \right], \hfill \\ \end{gathered} $$

(8)

where

$$ \frac{1}{{\gamma^{2} }} = \frac{1}{{2\omega_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }}. $$

(9)

Equation (8) can be expressed in the form

$$ I\left( {{\mathbf{\rho^{\prime}}},z} \right) = \frac{{A_{0}^{2} }}{{2^{2p} }}\left( {\frac{k}{2\pi z}} \right)^{2} \sum\limits_{l = L}^{N} {\chi_{l} \sum\limits_{{s_{1} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{1} } \\ \end{array} } \right)} } \sum\limits_{{l^{\prime} = L}}^{N} {\chi_{{l^{\prime}}} \sum\limits_{{s_{2} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{2} } \\ \end{array} } \right)} } I_{x}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{x} ,z} \right)I_{y}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{y} ,z} \right), $$

(10)

where

$$ \begin{gathered} I_{x}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{x} ,z} \right) = \iint {du_{x} dv_{x} }H_{m} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{x} - \frac{{v_{x} }}{2}} \right)} \right]H_{m} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{x} + \frac{{v_{x} }}{2}} \right)} \right]\exp \left( { - \frac{{2u_{x} }}{{\omega_{0}^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - \frac{{v_{x}^{2} }}{{\gamma^{2} }}} \right)\exp \left( { - \frac{ik}{z}u_{x} .v_{x} } \right)\exp \left( {\frac{ik}{z}\rho^{\prime}_{x} .v_{x} } \right)\exp \left( {hu_{x} + h^{\prime}v_{x} } \right), \hfill \\ \end{gathered} $$

(11)

$$ \begin{gathered} I_{y}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{y} ,z} \right) = \iint {du_{y} dv_{y} }H_{n} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{y} - \frac{{v_{y} }}{2}} \right)} \right]H_{n} \left[ {\frac{\sqrt 2 }{{\omega_{0} }}\left( {u_{y} + \frac{{v_{y} }}{2}} \right)} \right]\exp \left( { - \frac{{2u_{y} }}{{\omega_{0}^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - \frac{{v_{y}^{2} }}{{\gamma^{2} }}} \right)\exp \left( { - \frac{ik}{z}u_{y} .v_{y} } \right)\exp \left( {\frac{ik}{z}\rho^{\prime}_{y} .v_{y} } \right)\exp \left( {hu_{y} + h^{\prime}v_{y} } \right), \hfill \\ \end{gathered} $$

(12)

with

$$ h = a_{{s_{1p} }} \Omega_{l} + a_{{s_{2p} }} \Omega_{{l^{\prime}}} , $$

(13)

and

$$ h^{\prime} = \frac{{\left( {a_{{s_{2p} }} \Omega_{{l^{\prime}}} - a_{{s_{1p} }} \Omega_{l} } \right)}}{2}. $$

(14)

Let us, evaluate the integral $I_{x}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{x} ,z} \right)$ by using the following integral formula (Gradshteyn et al. 2007)

$$ \int\limits_{ - \infty }^{ + \infty } {\exp ( - x^{2} )H_{m} \left( {x + t} \right)} H_{n} \left( {x + u} \right)ds = 2^{n} \sqrt \pi m!t^{n - m} u^{n - m} L_{n}^{n - m} ( - 2tu). $$

(15)

Thus, Eq. (11) becomes

$$ \begin{gathered} I_{x}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{x} ,z} \right) = 2^{m} \sqrt \pi m!\frac{{\omega_{0} }}{\sqrt 2 }\int {dv_{x} \exp \left[ {\frac{{\omega_{0}^{2} }}{8}\left( {h - \frac{{ikv_{x} }}{z}} \right)^{2} } \right]} \exp \left( { - \frac{{v_{x}^{2} }}{{\gamma^{2} }}} \right)\exp \left( {\frac{{ik\rho^{\prime}_{x} }}{z}v_{x} } \right) \hfill \\ \quad \times \, \exp \left( {h^{\prime}v_{x} } \right)L_{m}^{0} \left[ { - \frac{{\omega_{0}^{2} }}{4}\left( {h - \frac{ik}{z}v_{x} } \right)^{2} + \frac{{v_{x}^{2} }}{{\omega_{0}^{2} }}} \right]. \hfill \\ \end{gathered} $$

(16)

By employing the identities of the generalized Laguerre polynomial (Gradshteyn et al. 2007) and the integral formula (Belafhal et al. 2019)

$$ L_{m}^{\mu + \nu + 1} \left( {a + b} \right) = \sum\limits_{n}^{m} {L_{n}^{\mu } } \left( a \right)L_{m - n}^{\nu } \left( b \right), $$

(17)

$$ L_{n}^{0} (a) = \sum\limits_{m = 0}^{n} {\left( { - 1} \right)^{m} } \left( {\begin{array}{*{20}c} n \\ {n - m} \\ \end{array} } \right)\frac{{a^{m} }}{m!}, $$

(18)

$$ \int\limits_{ - \infty }^{ + \infty } {x^{l} \exp \left( { - px^{2} + 2qx} \right)} dx = \sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\left( {\frac{1}{2i\sqrt p }} \right)^{l} H_{l} \left( \frac{iq}{p} \right), $$

(19)

one obtains the expression of the integral $I_{x}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{x} ,z} \right)$ as follows

$$ \begin{gathered} I_{x}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{x} ,z} \right) = 2^{m} m!\frac{{\omega_{0} }}{{\sqrt {2a} }}\exp \left( { - \frac{{ika_{x} \omega_{0}^{2} h}}{2cz}} \right)\exp \left( {\frac{{k^{2} \alpha \omega_{0}^{4} h^{2} }}{{16c^{2} z^{2} }}} \right)\exp \left( {\frac{{\omega_{0}^{2} h^{2} }}{8}} \right)\exp \left( {\frac{{\beta_{x}^{2} }}{\alpha }} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \sum\limits_{q = 0}^{m} {L_{m - q}^{ - 1} } \left( {\frac{{k^{2} \omega_{0}^{4} h^{2} }}{{16cz^{2} }} - \frac{{\omega_{0}^{2} h^{2} }}{4}} \right)\sum\limits_{r = 0}^{q} {\left( { - 1} \right)^{r} } \left( {\begin{array}{*{20}c} q \\ {q - r} \\ \end{array} } \right)\,\frac{{c^{r} }}{r!}\left( {\frac{1}{2i\sqrt \alpha }} \right)^{2r} H_{2r} \left( {\frac{{i\beta_{x} }}{\sqrt \alpha }} \right), \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$

(20)

where

$$ \alpha = \frac{1}{{\gamma^{2} }} + \frac{{\omega_{0}^{2} k^{2} }}{{8z^{2} }}, $$

(20a)

$$ c = \frac{1}{{\omega_{0}^{2} }} + \frac{{k^{2} \omega_{0}^{2} }}{{4z^{2} }}, $$

(20b)

$$ a_{x} = \frac{1}{2}\left[ {\frac{ik}{z}\rho^{\prime}_{x} - \frac{{ik\omega_{0}^{2} h}}{4z} + h^{\prime}} \right], $$

(20c)

and

$$ \beta_{x} = a_{x} + \frac{{ik\omega_{0}^{2} \alpha h}}{4cz}. $$

(20d)

$I_{y}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{y} ,z} \right)$ is evaluated in the same way as $I_{x}^{{s_{1} s_{2} }} \left( {\rho^{\prime}_{x} ,z} \right)$ by replacing the beam order $m$ and the dimensional position $\,\rho^{\prime}_{x}$ of $I_{x}^{{s_{1} s_{2} }}$ with $n$ and $\rho^{\prime}_{y}$, respectively.

After tedious manipulations of calculation, the average intensity of the partially coherent GFHChG beam can be rewritten as

$$ I\left( {{\mathbf{\rho^{\prime}}},z} \right) = \frac{{A_{0}^{2} \omega_{0}^{2} }}{{2^{2p + 1} \alpha }}\left( \frac{k}{2z} \right)^{2} \sum\limits_{l = L}^{N} {\chi_{l} \sum\limits_{{s_{1} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{1} } \\ \end{array} } \right)} } \sum\limits_{{l^{\prime} = L}}^{N} {\chi_{{l^{\prime}}} \sum\limits_{{s_{2} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{2} } \\ \end{array} } \right)} } \left[ {\exp \left( {\frac{{\omega_{0}^{2} h^{2} }}{4}} \right)\exp \left( {\frac{{\alpha k^{2} \omega_{0}^{4} h^{2} }}{{8c^{2} z^{2} }}} \right)B_{x}^{m} \left( {s_{1} ,s_{2} } \right)B_{y}^{n} \left( {s_{1} ,s_{2} } \right)} \right], $$

(21)

where

$$ B_{i}^{\mu } \left( {s_{1} ,s_{2} } \right) = 2^{\mu } \mu !\exp \left( { - \frac{{ika_{i} \omega_{0}^{2} h}}{2cz}} \right)\exp \left( {\frac{{\beta_{i}^{2} }}{\alpha }} \right)\sum\limits_{q = 0}^{\mu } {L_{\mu - q}^{ - 1} } \left( {\frac{{k^{2} \omega_{0}^{4} h^{2} }}{{16cz^{2} }} - \frac{{\omega_{0}^{2} h^{2} }}{4}} \right)\sum\limits_{r = 0}^{q} {\left( { - 1} \right)^{r} } \left( {\begin{array}{*{20}c} q \\ {q - r} \\ \end{array} } \right)\,\frac{{c^{r} }}{r!}\left( {\frac{1}{2i\sqrt \alpha }} \right)^{2r} H_{2r} \left( {\frac{{i\beta_{i} }}{\sqrt \alpha }} \right), $$

(22)

with $i = x,y$ and $\mu = m,n$.

The closed form of the partially coherent GFHChG beam passing through the atmospheric turbulence given by Eq. (21) represents our main result. In the following section, we will deduce the results of some laser beams treated in the previous works as special cases from our study.

3 Special cases

3.1 Partially coherent GFHChG beam propagating in free space

In order to obtain the average intensity of the partially coherent GFHChG beam propagating in free space, we take $C_{n}^{2} = 0$. Then, the expression of the average intensity remains the same as that of Eq. (21), whereas Eq. (9) yields

$$ \frac{1}{{\gamma^{2} }} = \frac{1}{{2\omega_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}. $$

(23)

3.2 Partially coherent Generalized Flattened Hermite Gaussian (GFHG) beam

In this case, we put $\Omega = 0$. Therefore, Eq. (21) becomes

$$ I\left( {{\mathbf{\rho^{\prime}}},z} \right) = \frac{{A_{0}^{2} \omega_{0}^{2} }}{{2^{2p + 1} \alpha }}\left( \frac{k}{2z} \right)^{2} \sum\limits_{l = L}^{N} {\chi_{l} \sum\limits_{{s_{1} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{1} } \\ \end{array} } \right)} } \sum\limits_{{l^{\prime} = L}}^{N} {\chi_{{l^{\prime}}} \sum\limits_{{s_{2} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{2} } \\ \end{array} } \right)} } \left[ {B_{x}^{m} \left( {s_{1} ,s_{2} } \right)B_{y}^{n} \left( {s_{1} ,s_{2} } \right)} \right], $$

(24)

where

$$ B_{i}^{\mu } (s_{1} ,s_{2} ) = 2^{\mu } \mu !\exp \left( {\frac{{ - k^{2} }}{{4\alpha z^{2} }}\rho_{i}^{\prime 2} } \right)\sum\limits_{q = 0}^{\mu } {\left( { - 1} \right)^{q} } \left( {\begin{array}{*{20}c} \mu \\ {\mu - q} \\ \end{array} } \right)\frac{{c^{q} }}{q!}\left( {\frac{1}{2i\sqrt \alpha }} \right)^{2q} H_{2q} \left( {\frac{ - k}{{2z\sqrt \alpha }}\rho_{x}^{\prime } } \right), $$

(25)

with $i = x,y$ and $\mu = m,n.$

The above equation defines the average intensity of the GFHG beam in a turbulent atmosphere.

3.3 Partially coherent Generalized Flattened Cosh-Gaussian (GFChG) beam

By taking $m = n = 0$ into Eq. (21), we can readily obtain the expression of the average intensity for the GFChG beam propagating through a turbulence atmosphere

$$ I\left( {{\mathbf{\rho^{\prime}}},z} \right) = \frac{{A_{0}^{2} \omega_{0}^{2} }}{{2^{2p + 1} \alpha }}\left( \frac{k}{2z} \right)^{2} \sum\limits_{l = L}^{N} {\chi_{l} \sum\limits_{{s_{1} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{1} } \\ \end{array} } \right)} } \sum\limits_{{l^{\prime} = L}}^{N} {\chi_{{l^{\prime}}} \sum\limits_{{s_{2} = 0}}^{p} {\left( {\begin{array}{*{20}c} p \\ {s_{2} } \\ \end{array} } \right)} } \left[ {\exp \left( {\frac{{\omega_{0}^{2} h^{2} }}{4}} \right)\exp \left( {\frac{{\alpha k^{2} \omega_{0}^{4} h^{2} }}{{8c^{2} z^{2} }}} \right)B_{x}^{0} \left( {s_{1} ,s_{2} } \right)B_{y}^{0} \left( {s_{1} ,s_{2} } \right)} \right], $$

(26)

where.

$$ B_{i}^{0} \left( {s_{1} ,s_{2} } \right) = \exp \left( { - \frac{{ik\omega_{0}^{2} a_{i} h}}{2cz}} \right)\exp \left( {\frac{{\beta_{i}^{2} }}{\alpha }} \right), \,{\text{ with}}\;i = x,y. $$

(27)

3.4 Partially coherent Hermite-Cosh-Gaussian (HChG) beam

By letting $l = l^{\prime} = 1$ and $p = 1$, Eq. (21) becomes identical to the expression of the average intensity for the partially coherent HChG beam through an atmospheric turbulence investigated by Yang et al. (Yang et al. 2009) (see Eq. (8) of this reference).

3.5 Partially coherent Cosh-Gaussian (ChG) beam

The partially coherent ChG beam can be regarded as a special case of our general result when $l = l^{\prime} = 1$, $p = 1$ and $m = n = 0$. Consequently, Eq. (21) reduces to Eq. (16) of Ref. (Yang et al. 2009).

3.6 Partially coherent Hermite Gaussian (HG) beam

By using the combination of the parameters $l = l^{\prime} = 1$, $p = 1$ and $\Omega = 0$, another case can be added in our list and it is referred to the propagation of the partially coherent HG beam in a turbulent atmosphere established by Yang et al. (Yang et al. 2009) (see Eq. (17) of this reference).

3.7 Gaussian Schell model (GSM) beam

For $l = l^{\prime} = 1$, $p = 1$, $\Omega = 0$ and $m = n = 0$, Eq. (21) simplifies to the average intensity of GSM beams (see Eq. (19) of Ref. (Yang et al. 2009)).

4 Numerical results and discussions

As previously mentioned, Eq. (21) represents the analytical expression of the average intensity distribution for the partially coherent GFHChG beam propagating in the atmospheric turbulence. In the present section, graphical representations are performed to analyze the behavior of the considered beam through a turbulence atmosphere, by varying the characteristic parameters of the incident laser beam and the propagation medium, respectively.

Fig. (3) depicts the normalized average intensity of the partially coherent GFHChG beam versus the slanted axis for diverse values of the structure constant $C_{n}^{2}$. The other parameters are taken as follows: $z = 5km$, $N = 5$, $L = 10$, $p = 2$, $m = n = 1$, $\sigma_{0} = 4cm$, $\lambda = 1060nm$, $\omega_{0} = 3cm$ and $\Omega = 10m^{ - 1}$. From Fig. 3, it can be seen that for $C_{n}^{2} = 0$ (i.e. free space), the average intensity of the peaks takes its maximum, and then it begins to decrease when $C_{n}^{2}$ increases. Furthermore, from $C_{n}^{2} = 0$ to $5 \times 10^{ - 15} m^{{{\raise0.5ex\hbox{$\scriptstyle { - 2}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}$ the lateral lobes have the same value of the normalized average intensity at $\rho^{\prime} = \pm 0.13m$. In addition, for the large value of the structure constant $C_{n}^{2} \left( { = 10^{ - 14} m^{{ - {\raise0.5ex\hbox{$\scriptstyle 2$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}} } \right)$, the partially coherent GFHChG beam changes into a flattened beam.

Fig. 3

Normalized average intensity distributions of the partially coherent GFHChG beam propagating in a turbulence atmosphere at $z = 5\,km$ and for different values of $C_{n}^{2}$

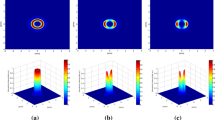
In order to show the influence of the spatial correlation length $\sigma_{0}$ on the propagation properties of the partially coherent GFHChG beam passing through a turbulent atmosphere, numerical illustrations are plotted in Fig. 4 for several values of the spatial correlation length $\sigma_{0}$: (a) $\sigma_{0} \to \infty$, (b) $\sigma_{0} = 1.5\,cm$ and (c) $\sigma_{0} = 0.5\,cm$, with $C_{n}^{2} = 5 \times 10^{ - 15} m^{{{\raise0.5ex\hbox{$\scriptstyle { - 2}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}$. The other parameters are similar to those of Fig. 3. As shown from Fig. 4(a)–(c), under specific conditions of the propagation distance $z$ and the beam parameters, the average intensity profile of the partially coherent GFHChG beam changes upon propagation for all values of spatial correlation length $\sigma_{0}$.

Fig. 4

Normalized average intensity distributions of the partially coherent GFHChG beam propagating in a turbulence atmosphere at a different propagation distance $z$, with a $\sigma_{0} = \infty$, b $\sigma_{0} = 1.5\,cm$ and c $\sigma_{0} = 0.5\,cm$, for $C_{n}^{2} = 5 \times 10^{ - 15} m^{{{\raise0.5ex\hbox{$\scriptstyle { - 2}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}$

We note that the beam has a hollow beam shape, which becomes to disappear during the propagation in the turbulent atmosphere by taking a flattened profile and tends eventually to a Gaussian profile while the maximum intensity of the peaks decreases. It is can also mentioned that, when the spatial correlation length $\sigma_{0}$ is small, the profile of the considered beam changes rapidly (i.e., during a small propagation distance $z$).

The effect of the wavelength $\lambda$ on the evolution of the normalized average intensity of the partially coherent GFHChG beam through an atmospheric turbulence is illustrated in Fig. 5 for $C_{n}^{2} = 5 \times 10^{ - 15} m^{{{\raise0.5ex\hbox{$\scriptstyle { - 2}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}}}$ and the other calculation parameters are fixed as those of Fig. 3. From Fig. 5, it’s seen that when the wavelength $\lambda$ gradually decreases, the maximum average intensity increases. Furthermore, the partially coherent GFHChG beam propagating in a turbulence atmosphere takes a profile of flattened beam for the larger value of the wavelength $\lambda$.

Fig. 5

Normalized average intensity distributions of the partially coherent GFHChG beam propagating in a turbulence atmosphere at the reference plane of $z = 5\,km$ and for different values of $\lambda$

The variation of the normalized average intensity for the partially coherent GFHChG beam versus $\rho^{\prime}$ is given in Fig. 6(a)–(d) for different values of the cosh parameter $\Omega$ (Fig. 6(a), (b)), and different values of the beam order $p$ (Fig. 6(c), (d)). The other parameters are chosen as $z = 5km$, $N = 5$,$L = 10$, $m = n = 1$, $\sigma_{0} = 4cm$, $\lambda = 1060nm$, and $\omega_{0} = 3cm$. From Fig. 6(a), it is observed that for the small value of the cosh parameter $\Omega$, the average intensity profile of the partially coherent GFHChG beam is similar to a Gaussian distribution and takes the shape of flattened and doughnut distribution with the increase of $\Omega$. Figure 6(b) plots the transition from the Gaussian profile to the doughnut one, by varying slowly $\Omega$ from $12\,\,m^{ - 1}$ to $20\,\,m^{ - 1}$. It is noted from Fig. 6(c) that when the beam order $p$ is equal to $1$, the average intensity of the partially coherent GFHChG beam has a bright spot in the center. Moreover, the main peak divides into two peaks and the maximum average intensity increases with increasing $p$. In addition, the higher the beam order $p$ is, the larger the dark core is (see Fig. 6(d)).

Fig. 6

Normalized average intensity distributions of the partially coherent GFHChG beam propagating in a turbulent atmosphere for: a, b different values of $\Omega$ with $p = 1$, c different values of $p$ with $\Omega = 10m^{ - 1}$ and d $p = 5$ and $\Omega = 10m^{ - 1}$

In Fig. 7(a)–(c), we investigate the characteristic properties of the partially coherent GFHChG beam propagating in a turbulent atmosphere for several values of the waist width $\omega_{0}$, by varying the propagation distance $z$ and the cosh parameter $\Omega$. From Fig. 7(a), (b), it is seen that the average intensity profile takes a shape of doughnut beam and the maximum average intensity increases when the waist width $\omega_{0}$ increases. We can also observe that the peaks move towards the large value of $\rho^{\prime}$ and the dark central part becomes widens when $\omega_{0}$ and $\Omega$ increase. Figure 7(c) shows that the shape of the considered beam becomes Gaussian when the propagation distance $z$ increases. We also note that the intensity begins to divide into two lobes when $\omega_{0}$ takes a large value.

Fig. 7

Normalized average intensity distributions of the partially coherent GFHChG beam propagating in a turbulent atmosphere for four values of the waist width $\omega_{0}$, with a $z = 2$ km and $\Omega = 10\,{\textbf{m}}^{ - 1}$, b $z = 2$ km and $\Omega = 20\,{\textbf{m}}^{ - 1}$ and c $z = 3$ km and $\Omega = 10\,{\textbf{m}}^{ - 1}$

5 Conclusion

In this paper, based on the extended Huygens-Fresnel principle and the Rytov’s quadratic approximation, the analytical expression of the average intensity distribution of the partially coherent GFHChG beam travelling through a turbulent atmosphere is derived. From the numerical results, it can be noted that the profile of the partially coherent GFHChG beam changes rapidly for the small values of the spatial correlation $\sigma_{0}$ and the dark core of the beams becomes larger for the higher values of the cosh parameter $\Omega$ and the beam order $p$. It is also shown that the profile of the partially coherent GFHChG beam changes into a flattened and doughnut profile with increasing the wavelength $\lambda$ and the waist width $\omega_{0}$, respectively. The main result of the present work can be regarded as a generalized closed-form of some partially coherent beams propagating in a turbulent atmosphere such as, GFHG, GFChG, HChG, ChG, HG and GSM beams. Finally, these findings can be useful for optical information processing and optical scattering in a turbulent atmosphere.