1 Introduction

In the last years, the propagation of light beams has attracted much attention due to potential applications in wireless optical communication (Eyyuboğlu et al. 2006; Wang et al. 2015; Ata and Baykal 2015; Tang and Zhao 2015; Baykal 2016a, 2016b). In particular, underwater optical transmission has been a hotspot research spot due to the high demand for data transmission for underwater sensors, submarines, and underwater vehicles (Johnson et al. 2014). It is established that the spatial structure of a light beam is generally altered by turbulence when the beam propagates through the oceanic medium resulting in the degradation of the transmission performance. So, extensive studies were conducted on the evolution properties of different spatially partially coherent laser beams under oceanic turbulence to get the desirable candidates for underwater optical communications. Up to now, many types of partially coherent laser beams have been investigated for their propagation in the oceanic atmosphere, e.g., the stochastic beam (Korotkova and Farwell. 2011), radially polarized beam (Tang and Zhao 2013], stochastic electromagnetic vortex beam (Xu and Zhao 2014), stigmatic stochastic electromagnetic beam (Zhou et al. 2014), partially coherent radially polarized doughnut beam (Fu and Zhang 2013), Gaussian Schell-model vortex beam (Huang et al. 2014), flat-topped vortex hollow beam (Liu et al. 2015; 2016), random electromagnetic multi-Gaussian Schell-model vortex beam (Liu and Wang 2018), partially coherent Hermite–Gaussian linear array beam (Huang et al. 2015), Lorentz beam (Liu and Wang 2017), partially coherent Lorentz–Gauss vortex beam (Liu et al. 2017a), partially coherent four-petal Gaussian vortex beam (Liu et al. 2017b), partially coherent four-petal Gaussian beam (Liu et al. 2017c), and partially coherent anomalous hollow vortex beam (Liu et al. 2019).

More recently, a new laser beam called the partially coherent vortex cosine-hyperbolic-Gaussian beams (PCvChGB) has been introduced and its propagation features in free space. The PCvChGB is a vortex field with more control parameters, i.e.; more degree of freedom, compared to the partially coherent Gaussian vortex beam (Lazrek et al. 2021). The beam intensity exhibits a flexible-shaped profile; the intensity distribution can be controlled by the decentered parameter b and vortex charge number M. By choosing appropriate values of b and M, the beam intensity distribution in the initial plane can be a hollow vortex Gaussian-like or a four-petal vortex Gaussian-like. The PCvChGB’s profile is preserved upon propagation in the near-field, and its stability can be controlled by adjusting the initial spatial coherence, and the parameters b and M. In the far-field, the PCvChGB evolves into a multi-lobe structure. The beam propagation properties can used in many practical applications, such as optical trapping, micromanipulation, beam splitting, and optical communications. The propagation characteristics of the PCvChGB through a paraxial focusing system, and in a turbulent atmosphere have also been investigated in detail (Lazrek et al. 2021; Hricha et al. 2022a, 2022b; Lazrek et al. 2022]. However, to the best of our knowledge, the evolution properties of PCvChGB in oceanic turbulence have not been reported yet. The present work aims to study the propagation characteristics of a PCvChGB in weak oceanic turbulence. Based on the coherence theory and Rytov method, the average intensity distribution of the beam is derived analytically. The influence of oceanic turbulence on the propagation properties of the PCvChGB under different beam conditions is illustrated by numerical examples. The remainder of the manuscript is structured as follows: in the forthcoming Section, we expose the theoretical model and derive the propagation formula of the PCvChGB in oceanic turbulence. In Sect. 3, the influences of different beam parameters and the oceanic turbulence on the evolution of the average intensity distribution are discussed with illustrative numerical examples. Finally, the main results are highlighted in the conclusion part.

2 Theoretical model of a PCvChGB propagating through oceanic turbulence

In the Cartesian coordinate system, the electric field of a vortex cosine-hyperbolic-Gaussian beam propagating along the z-axis in the source plane z = 0 can be expressed as Hricha et al. (2021)

$$ E\left( {\vec{r}_{0} ,z = 0} \right) = \cosh \left( {b\frac{{x_{0} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{0} }}{{\omega_{0} }}} \right)\exp \left( { - \frac{{x_{0}^{2} + y_{0}^{2} }}{{\omega_{0}^{2} }}} \right)\left( {x_{0} + iy_{0} } \right)^{M} , $$
(1)

where \(\vec{r}_{0} = \left( {x_{0} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} y_{0} {\kern 1pt} {\kern 1pt} } \right)\) is the position vector in the Cartesian coordinate system at plane z = 0, and \(\omega_{0}\) is the waist width of the Gaussian part, b is the decentered parameter associated with the cosh part, and M is a positive integer which denotes the topological charge of the beam.

In the Schell model theory, the cross-spectral density of a PCvChGB in the initial plane z = 0 can be expressed as follows (Mandel and Wolf 1995)

$$ W\left( {\vec{r}_{01} ,\vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right) = E\left( {\vec{r}_{01} ,{\kern 1pt} {\kern 1pt} 0} \right)\,E*\left( {\vec{r}_{02} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 0} \right)\,g\left( {\vec{r}_{01} - \vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right), $$
(2)

where \(g\left( {{\kern 1pt} .{\kern 1pt} {\kern 1pt} } \right)\) is the degree of coherence of the source given by

$$ g\left( {\vec{r}_{01} - \vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right) = \exp \left( { - \frac{{\left( {\vec{r}_{01} - \vec{r}_{02} } \right)^{2} }}{{2\sigma_{0}^{2} }}} \right), $$
(3)

with \(\sigma_{0}\) is the spatial coherence length, and \(\vec{r}_{0i} = (x_{0i} ,y_{0i} )\) with i = 1 or 2 are the transverse coordinates in the source plane.

Equation (2) represents a general form of a partially vortex Gaussian beam; i.e., a beam with controllable dark region and adjustable spatial coherence.

Based on the extended Huygens–Fresnel principle, the average intensity of a PCvChGB propagating through oceanic turbulence at the receiver z plane can be written (Andrews and Philips 1998)

$$ \begin{aligned} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = & \frac{{k^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {W\left( {\vec{r}_{01} ,\vec{r}_{02} {\kern 1pt} ,{\kern 1pt} z = 0} \right)} } } } \\ & \times \exp \left[ { - \frac{ik}{{2z}}\left\{ {\left( {x_{01} - x} \right)^{2} + \left( {y_{01} - y} \right)^{2} - \left( {x_{02} - x} \right)^{2} - \left( {y_{02} - y} \right)^{2} } \right\}} \right]\left\langle {\exp \left[ {\psi \left( {\vec{r}_{01} ,\vec{r}} \right) + \psi *\left( {\vec{r}_{02} ,\vec{r}} \right)} \right]} \right\rangle d\vec{r}_{01} d\vec{r}_{02} . \\ \end{aligned} $$
(4)

where \(\vec{r} = (x,y)\) is the position vector in the receiver plane, \(\psi \left( {\vec{r}_{0i} ,\vec{r},z} \right)\) represents the random part for the complex phase of a spherical wave spreading from the source plane to the output plane, \(k = \frac{2\pi }{\lambda }\) is the wave number, and \(\lambda\) is the wavelength. The * and \(\langle {} \rangle\) denote the complex conjugation and ensemble average over the medium statistics, respectively.

In the Rytov method, the ensemble average term in Eq. (4) can be expressed as Andrews and Philips (1998); Wang et al. (2015)

$$ \left\langle {\exp \left[ {\psi \left( {\overrightarrow {r}_{01} ,\overrightarrow {r} } \right) + \psi *\left( {\overrightarrow {r}_{02} ,\overrightarrow {r} } \right)} \right]} \right\rangle {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {\vec{r}_{01} - \vec{r}_{02} } \right)^{2} } \right], $$
(5)

where \(\rho_{0}\) is the coherence length of a spherical wave propagating in oceanic turbulence, \(\rho_{0} = \left[ {\frac{{\pi^{2} k^{2} z}}{3}\int_{0}^{ + \infty } {d\kappa \kappa^{3} \Phi \left( \kappa \right)} } \right]^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}}\) with \(\kappa\) is spatial frequency, and \(\Phi \left( \kappa \right)\) is the one-dimensional spatial power spectrum of oceanic turbulence, which can be expressed as Nikishov and Nikishov (2000)

$$ \Phi \left( \kappa \right) = 0.388 \times 10^{ - 8} \varepsilon^{{ - {{11} \mathord{\left/ {\vphantom {{11} 3}} \right. \kern-0pt} 3}}} \left[ {1 + 2.35\,\left( {\kappa \eta } \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} } \right]\,f\left( {\kappa ,\varsigma ,\chi_{T} } \right), $$
(6)

where \(\varepsilon\) is the rate of dissipation of turbulent kinetic energy per unit mass, which may vary in the range [10–10,10–1] m2s−3, \(\eta = 10^{ - 3}\) is the Kolmogorov inner scale, and

$$ f\left( {\kappa ,\varsigma ,\chi_{T} } \right) = \frac{{\chi_{T} }}{{\varsigma^{2} }}\left[ {\varsigma^{2} \exp \left( { - A_{T} \delta } \right) + \exp \left( { - A_{S} \delta } \right) - 2\varsigma \exp \left( { - A_{TS} \delta } \right)} \right], $$
(7)

with \(\chi_{T}\) is the rate of dissipation of mean square temperature varying in the range [10−10,10−4] K2s−1, \(\delta = 8.284\left( {\kappa \eta } \right)^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}}} + 12.978\left( {\kappa \eta } \right)^{2}\) \(A_{T} = 1.863 \times 10^{ - 2}\) \(A_{S} = 1.9 \times 10^{ - 4}\) \(A_{TS} = 9.41 \times 10^{ - 3}\) and \(\varsigma\) stands for the relative strength of temperature and salinity fluctuations, which varies in the range from − 5 to 0. The limit conditions \(\varsigma {\kern 1pt} {\kern 1pt} = 0\)\(\varsigma {\kern 1pt} {\kern 1pt} = - 5\) describe the cases when salinity-driven turbulence dominates, and when temperature-driven turbulence prevails, respectively.

Substituting from Eqs. (2), (3), and (5) into Eq. (4), and recalling the binomial formula (Abramowitz and Stegun 1964)

$$ \left( {u{\kern 1pt} + {\kern 1pt} v{\kern 1pt} } \right)^{m} {\kern 1pt} = {\kern 1pt} \sum\limits_{l = 0}^{m} {C_{l}^{m} } u^{l} v^{{_{m - l} }} , $$
(8a)

where

$$ C_{l}^{m} = {\kern 1pt} \frac{m!}{{l!\left( {m - l} \right)!}}, $$
(8b)

leads to

$$ \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( {\frac{k}{2\pi z}} \right)^{2} \sum\limits_{l = 0}^{M} {C_{l}^{M} \left( i \right)^{M - l} } \sum\limits_{n = 0}^{M} {C_{n}^{M} \left( { - i} \right)^{M - n} } \int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {F_{xy} \left( {x_{01} ,y_{01} } \right)\,G_{xy} \left( {x_{01} ,y_{01} } \right)} } dx_{01} \,dy_{01} {\kern 1pt} , $$
(9a)

where

$$ \begin{aligned} F_{xy} \left( {x_{01} ,y_{01} } \right) = & x_{01}^{l} \,\left( {y_{01}^{{_{{}} }} } \right)^{M - l} \cosh \left( {b\frac{{x_{01} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{01} }}{{\omega_{0} }}} \right) \\ & \times \exp \left( { - \delta *x_{01}^{2} - \frac{ikx}{z}x_{01} } \right)\exp \left( { - \delta *y_{01}^{2} - \frac{iky}{z}y_{01} } \right), \\ \end{aligned} $$
(9b)

and

$$ G_{xy} \left( {x_{01} ,y_{01} } \right) = \int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\left\{ \begin{gathered} x_{02}^{n} \,\cosh \left( {b\frac{{x_{02} }}{{\omega_{0} }}} \right)\exp \left[ { - \delta x_{02}^{2} + \left( {\frac{ikx}{z} + \frac{{2x_{01} }}{{\rho_{0}^{2} }}} \right)x_{02} } \right] \hfill \\ \times \left( {y_{02}^{{_{{}} }} } \right)^{M - n} \cosh \left( {b\frac{{y_{02} }}{{\omega_{0} }}} \right)\exp \left[ { - \delta y_{02}^{2} + \left( {\frac{iky}{z} + \frac{{2y_{01} }}{{\rho_{0}^{2} }}} \right)y_{02} } \right] \hfill \\ \end{gathered} \right\}dx_{02} \,dy_{02} } } , $$
(9c)

with δ is the auxiliary parameter defined by

$$ \delta = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }} + \frac{ik}{{2z}}. $$
(9d)

By using the explicit form of the cosh function and the separation of the variable method to perform the double integral in Eq. (9c), we obtain

$$ G_{xy} \left( {x_{01} ,y_{01} } \right) = G_{n} \left( {x_{01} ,x} \right)G_{M - n} \left( {y_{01} ,y} \right), $$
(10a)

where

$$ G_{n} \left( {s_{01} ,s} \right) = \frac{1}{2}\left( {G_{n}^{ + } \left( {s_{01} ,s} \right) + G_{n}^{ - } \left( {s_{01} ,s} \right)} \right), $$
(10b)

in which s represents either x or y,

$$ G_{p}^{ \pm } \left( {s_{01} ,s} \right) = \int\limits_{ - \infty }^{ + \infty } {u^{p} \,\exp \left( { - \delta \,u^{2} } \right)\exp \left[ {\left( {\frac{iks}{z} + \frac{{2s_{01} }}{{\rho_{0}^{2} }} \pm \frac{b}{{\omega_{0} }}} \right)u} \right]} \,du. $$
(10c)

Now, recalling the following formulas (Belafhal et al. 2020, see also Eq. (2), 3.462 of Gradshteyn and Ryzhik (1994))

$$ \int\limits_{ - \infty }^{ + \infty } {x^{n} e^{{ - px^{2} + 2qx}} } dx = e^{{\frac{{q^{2} }}{p}}} \sqrt {\frac{\pi }{p}} \left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right),Re\left( p \right) > 0, $$
(11)
$$ H_{m} \left( x \right) = \sum\limits_{j = 0}^{{\left[ {{\raise0.7ex\hbox{$m$} \!\mathord{\left/ {\vphantom {m 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right]}} {\frac{{( - 1)^{j} m!}}{{j!\left( {m - 2j} \right)!}}\left( {2x} \right)^{m - 2j} } , $$
(12)

where \(H_{n} \left( {.{\kern 1pt} {\kern 1pt} } \right)\) is the Hermite polynomial of nth-order, and after carrying out the tedious algebraic calculations, one can obtain

$$ \begin{aligned} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = & \frac{1}{16}\frac{\pi }{\delta \eta }\left( \frac{k}{2z} \right)^{2} \left( {\frac{1}{2i\sqrt \delta }} \right)^{M} \,\sum\limits_{l = 0}^{M} {C_{l}^{M} \left( i \right)^{M - l} \sum\limits_{n = 0}^{M} {C_{n}^{M} } } \left( { - i} \right)^{M - n} \\ & \times \left[ {Q_{l,n}^{ + } \left( x \right) + Q_{l,n}^{ - } \left( x \right)} \right]\,\left[ {Q_{M - l,n - l}^{ + } \left( y \right) + Q_{M - l,M - n}^{ - } \left( y \right)} \right], \\ \end{aligned} $$
(13)

where

$$ \begin{aligned} Q_{l,n}^{ \pm } \left( x \right) = & \exp \left\{ {\frac{1}{\delta }\left( { - \frac{ikx}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\sum\limits_{s = 0}^{n} {C_{s}^{n} } \left( {\frac{i}{\sqrt \delta }\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)} \right)^{s} H_{n - s} \left( {\frac{i}{\sqrt \delta }\left( { - \frac{ikx}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right)} \right)\left( {\frac{1}{2i\sqrt \eta }} \right)^{l + s} \\ & \times \left\{ {\exp \left\{ {\frac{{\left( {q_{1}^{ \pm } \left( x \right)} \right)^{2} }}{\eta }} \right\}H_{l + s} \left( {\frac{{iq_{1}^{ \pm } \left( x \right)}}{\sqrt \eta }} \right) + \exp \left\{ {\frac{{\left( {q_{2}^{ \pm } \left( x \right)} \right)^{2} }}{\eta }} \right\}H_{l + s} \left( {\frac{{iq_{2}^{ \pm } \left( x \right)}}{\sqrt \eta }} \right)\,} \right\}, \\ \end{aligned} $$
(14a)

and

$$ \begin{aligned} Q_{M - l,M - n}^{ \pm } \left( y \right) = & \exp \left\{ {\frac{1}{\delta }\left( {\frac{iky}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\sum\limits_{j = 0}^{M - n} {C_{j}^{M - n} } \left( {\frac{i}{\sqrt \delta }\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)} \right)^{j} H_{M - n - j} \left( {\frac{i}{\sqrt \delta }\left( { - \frac{iky}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right)} \right) \\ & \times \left( {\frac{1}{2i\sqrt \eta }} \right)^{M - l + j} \left\{ {\exp \left\{ {\frac{{\left( {q_{1}^{ \pm } \left( y \right)} \right)^{2} }}{\eta }} \right\}H_{M - l + j} \left( {\frac{{iq_{1}^{ \pm } \left( y \right)}}{\sqrt \eta }} \right)\, + \exp \left\{ {\frac{{\left( {q_{2}^{ \pm } \left( y \right)} \right)^{2} }}{\eta }} \right\}H_{M - l + j} \left( {\frac{{iq_{2}^{ \pm } \left( y \right)}}{\sqrt \eta }} \right)} \right\}, \\ \end{aligned} $$
(14b)

with

$$ \eta = \delta * - \frac{1}{\delta }\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)^{2} , $$
(14c)
$$ q_{1}^{ \pm } \left( s \right) = \frac{1}{\delta }\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)\left( { - \frac{iks}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right) + \left( {\frac{iks}{{2z}} + \frac{b}{{2\omega_{0} }}} \right) $$
(14d)

and

$$ q_{2}^{ \pm } \left( s \right) = \frac{1}{\delta }\left( {\frac{1}{{\rho_{0}^{2} }} + \frac{1}{{2\sigma_{0}^{2} }}} \right)\left( { - \frac{iks}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right) + \left( {\frac{iks}{{2z}} - \frac{b}{{2\omega_{0} }}} \right). $$
(14f)

Equation (13) is the analytical formula for the average intensity of a PCvChGB propagating through oceanic turbulence at the output plane z.

In the limiting case when \(\sigma_{0}\) tends to be infinite (i.e., in the full coherence case), Eq. (13) will give the intensity expression of a fully coherent vChGB in oceanic turbulence; and the obtained formula is identical to Eq. (21) in Lazrek et al. (2022).

By setting b = 0 and \(\sigma_{0}\) tends to be infinite in Eq. (13), one may obtain the propagation equation for a hollow vortex Gaussian beam through oceanic turbulence. In this case, the average intensity reduces to

$$ \left\langle {I_{0} \left( {\vec{r},z} \right)} \right\rangle = \left( \frac{k}{2z} \right)^{2} \frac{1}{\alpha \,\chi }\left( {\frac{1}{2i\sqrt \alpha }} \right)^{M} \sum\limits_{l = 0}^{M} {C_{l}^{M} \sum\limits_{n = 0}^{M} {C_{n}^{M} } } \,R_{l,n} \left( {x,z} \right)\,R_{M - l,M - n} \left( {y,z} \right), $$
(15)

where

$$ \alpha = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}}, $$
(15a)
$$ R_{l,n} \left( {v,z} \right) = \exp \left( {Bv^{2} } \right)\sum\limits_{s = 0}^{{\left[ \frac{n}{2} \right]}} {\frac{{\left( { - 1} \right)^{s\,} \,n\,!}}{{s!\,\left( {n - 2s} \right)\,!}}} \,\left( {\frac{2i}{{\sqrt \alpha }}} \right)^{n - 2s} \sum\limits_{j = 0}^{n - 2s} {C_{j}^{n - 2s} \,\left( {\frac{1}{2i\sqrt \chi }} \right)^{l + j} \left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{j} \,} H_{l + j} \left( {\frac{iA}{{\sqrt \chi }}v} \right), $$
(15b)

in which \(v\) represents either x or y, with

$$ A = \frac{ik}{{2z}}\left( {1 - \frac{1}{{\alpha \rho_{0}^{2} }}} \right), $$
(15c)

and

$$ B = \frac{{A^{2} }}{\chi } - \frac{{k^{2} }}{{4\,\alpha \,z^{2} }}. $$
(15d)

We note that we have numerically checked that Eq. (15) is equivalent to Eq. (16) of (Li et al. (2019)) even if they are different in form.

3 Numerical simulations and analysis

In this Section, based on the propagation formula derived above, we have performed numerical calculations to analyze the evolution of the average intensity distribution of PCvChGB propagating in oceanic turbulence. In the following numerical examples, unless it is specified in the figure captions, the parameters are set to be \(\lambda = 417\,{\text{nm}}\), \(\omega_{0} = 2\,{\text{cm}}\), σ0 = 2 mm, \(\varepsilon = 10^{ - 7}\), \(\chi_{T} = 10^{ - 9}\), M = 1, and \(\varsigma = - 2.5\). In our simulations, the choice of some used parameters values is based on their values given in some references as (Baykal et al. 2009). As it is previously mentioned, the incident PCvChGB has two types of intensity profiles depending on the value of the parameter b (Liu and Wang 2017), so in the numerical analysis, both of the beam configurations (i.e., the small and large b cases) are examined separately.

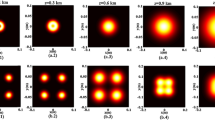
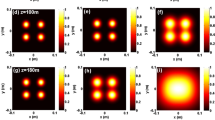
Figure 1 shows the (1D) and (3D) normalized average intensity of a PCvChGB in oceanic turbulence at some propagation distances (z = 0.05 km, 0.15 km, 0.4 km, and 0.8 km). From the plots, it can be seen that the PCvChGB propagating through oceanic turbulence can keep almost its original intensity pattern at the short propagation distances (z = 0.05 km and 0.15 km). Then, as the propagation distance increases, the PCvChGB with a small b configuration will lose its initial dark hollow center and transform into a Gaussian-like beam in the far-field. Whereas for the beam with large b configuration, the four petal lobes get closer and bond gradually during the transmission process, and the beam intensity evolves into a flat­topped profile-like in the far-field (see column d2).

Fig. 1
figure 1

1D and 3D normalized intensity of a PCvChGB with M = 1 in oceanic turbulence for z = 0.05 km, 0.15 km, 0.4 km, and 0,8 km. The first and second rows for b = 0.1, and the third and fourth rows for b = 4. a.1, b.1, c.1, d.1 z = 0.05 km, a.2, b.2, c.2, d.2 z = 0.15 km, a.3, b.3, c.3, d.3 z = 0.4 km, a.4, b.4, c.4, d.4 z = 0.8 km

Full size image

The influence of the initial coherence length σ0 on the average intensity distribution for a PCvChGB in oceanic turbulence is illustrated in Figs. 2 and 3. It can be seen from the plots that a PCvChGB with smaller σ0 spreads fast during propagation and loses its original dark hollow center more rapidly (see the first column) compared to the one with large σ0. One can also observe from Fig. 3 that for a beam with a large b configuration, the lobes will be slightly narrower and their lobes interspace smaller when σ0 decreases. It is worth noting that the PCvChGB propagation behavior in the oceanic medium is similar to that observed for the turbulent atmosphere.

Fig. 2
figure 2

1D and 3D normalized intensity of a PCvChGB with M = 1 in oceanic turbulence for different values of σ0. with \(\omega_{0} = 0.02\,\,{\text{m}}\), \(\lambda = 417\,\,{\text{nm}}\), \(\varepsilon = 10^{ - 7}\),\(\chi_{T} = 10^{ - 9}\), \(\varsigma = - 2.5\) and b = 0.1. a.1, b.1, c.1 z = 0.05 km, a.2, b.2, c.2 z = 0.15 km, a.3, b.3, c.3 z = 0.4 km, a.4, b.4, c.4 z = 0.8 km

Full size image
Fig. 3
figure 3

The same as Fig. 2 except b = 4

Full size image

The effect of the topological charge M on the output beam is illustrated in Figs. 4 and 5 for the small b and large b configurations, respectively. It can be seen that for both beam configurations the rise speed of the central peak intensity is slower as the topological charge M is larger, this means that a beam with larger M can keep its dark center (or four-petal profile) better than the one with smaller M.

Fig. 4
figure 4

The average intensity of a PCvChGB in the oceanic turbulence for different values of the topological charge M with \(\omega_{0} = 0.02\,\,{\text{m}}\), σ0 = 2 mm, \(\lambda = 417\,\,{\text{nm}}\) \(\varepsilon = 10^{ - 7}\),\(\chi_{T} = 10^{ - 9}\), \(\varsigma = - 2.5\) and b = 0.1, for a z = 0.05 km, b z = 0.15 km, c z = 0.4 km, and d z = 0.8 km

Full size image
Fig. 5
figure 5

The same as Fig. 4 except b = 4

Full size image

To analyze the influences of oceanic turbulence on the propagation properties of PCvChGB, we have displayed in Figs. 6, 7, 8 the normalized on-axis intensity as a function of the propagation distance z for different σ0 in oceanic turbulence under different rates of dissipation of temperature \(\chi_{T}\), relative strengths of temperature and salinity fluctuations \(\varsigma\), and rate of dissipation of turbulent kinetic energy per unit mass of fluid \(\varepsilon\), respectively. As can be seen from the plots, the increase of parameters (\(\chi_{T}\) and \(\varsigma\)) or the decrease of the parameter \(\varepsilon\) leads to the increase of the rising speed of the central peak. The central intensity increases gradually until reaching the maximum value and after that, with further propagation distance, the central intensity declines because of diffraction.

Fig. 6
figure 6

Normalized on-axis average intensity of a PCvChGB in oceanic turbulence versus the propagation z, for different values of the rate of dissipation of mean-square temperature \(\chi_{T}\). with M = 1, \(\omega_{0} = 0.02\,\,{\text{m}}\), \(\lambda = 417\,\,{\text{nm}}\) \(\varepsilon = 10^{ - 7}\), and \(\varsigma = - 2.5\), rows a–d for σ0 = 2 mm, b–e for σ0 = 3 mm and c–f for \(\sigma_{0} = + \infty\)

Full size image
Fig. 7
figure 7

Normalized on-axis average intensity of the perturbed PCvChGB versus propagation distance z for different values of the ratio of temperature to salinity \(\varsigma\), with M = 1, \(\omega_{0} = 0.02\,\,{\text{m}}\), \(\lambda = 417\,\,{\text{nm}}\) \(\varepsilon = 10^{ - 7}\), and \(\chi_{T} = 10^{ - 9}\), rows a–d for σ0 = 2 mm, b–e for σ0 = 3 mm and c–f for \(\sigma_{0} = + \infty\)

Full size image
Fig. 8
figure 8

On-axis average intensity of the perturbed vChGB versus the propagation distance z for different values of \(\varepsilon\), with M = 1, \(\omega_{0} = 0.02\,\,{\text{m}}\), \(\lambda = 417\,\,{\text{nm}}\), \(\varsigma = - 2.5\), and \(\chi_{T} = 10^{ - 9}\), rows a–d for σ0 = 2 mm, b–e for σ0 = 3 mm and c–f for \(\sigma_{0} = + \infty\)

Full size image

4 Conclusion

Based on the Huygens–Fresnel integral and Rytov method, the analytical expression of the average intensity of a PCvChGB propagating in oceanic turbulence is derived. From the obtained formula, the evolution properties of a PCvChGB in oceanic turbulence are illustrated numerically and discussed as a function of the initial beam parameters and oceanic turbulence conditions. The results show that a PCvChGB propagating in oceanic turbulence can keep its initial hollow profile with a dark centre at short propagation distances, and then evolves into a Gaussian-like beam (i.e., with a bright centre) or flat-topped as the propagation distance is larger. Furthermore, It is found that as the oceanic turbulence strength increases (i.e., when parameters \(\chi_{T}\) or \(\varsigma\) increase or \(\varepsilon\) decreases) or the initial beam parameters (b, M, and σ0) decrease, the rising speed of the central peak becomes faster. The obtained results could help for understanding the transmission properties of PCvChGB in the oceanic media, which are useful for practical application of optical wireless communication, imaging, etc.