Evaluation of integral transforms using special functions with applications to biological tissues

Abstract

In this paper, we aim to establish several new closed-form evaluations of certain integral transforms involving the rational and exponential functions, which are expressed in terms of confluent hypergeometric function and related functions. Also, we consider some special cases. The presented integral formulas are useful in many fields of mathematical physics, particularly in the propagation of some waves through random turbulent media. The main result is applied to investigate the closed-form of unusual scattering parameters used in the biological tissues. It is found that there is a good agreement between the numerical and theoretical evaluations.

1 Introduction

In this investigation, we evaluate some integral transforms using special functions. The results obtained are then applied to some integrals occurring in continuous random media applications such biological tissues. In recent years, many works are investigated on the relationship between optical and biological properties of tissues (see Ghosh et al. 2001; Kong et al. 2016; Li et al. 2019; Yin et al. 2017; Duan et al. 2020; Gökçe et al. 2020; Liu et al. 2020; Chen et al. 2020; Saad and Belafhal 2017; Ebrahim and Belafhal 2021). The methodologies presented in previous papers are used to study the scattering parameters which play a major role in the description of the distribution of refractive index (Radosevich et al. 2012) through:

$\bullet$ the following statistical autocorrelation function:

$$\begin{aligned} \mathcal {B}_n = \frac{{4\pi }}{r}\int \limits _0^\infty {\kappa .{\Phi _s}\left( \kappa \right) } \sin \left( {r\kappa } \right) \mathrm{d}\kappa , \end{aligned}$$

(1.1)

$\bullet$ the spatial coherence radius of spherical waves (see Wu et al. 2016)

$$\begin{aligned} \rho _{s}^{-2}=\frac{1}{3}{{\pi }^{2}}{{k}^{2}}zT, \end{aligned}$$

(1.2)

with T is the tissue turbulence intensity and it given by $T=\int \limits _{0}^{\infty }{{{\kappa }^{3}}{{\Phi }_{s}}\left( \kappa \right) \mathrm{d}\kappa }$, $\kappa$ is the spatial frequency of turbulent fluctuations, z is the propagation distance, $k = \frac{{2\pi }}{\lambda }$ is the wave number of light with $\lambda$ is the wavelength and ${{\Phi _\mathrm{s}}}$ is the one-dimensional power spectrum of the biological tissue turbulent fluctuations,

$\bullet$  the differential scattering cross section per unit volume

$$\begin{aligned} \sigma \left( \theta \right) = 2\pi {k^4} \left( {1 + {{\cos }^2}\theta } \right) {\Phi _\mathrm{s}}\left( \kappa \right) , \end{aligned}$$

(1.3)

$\bullet$ the scattering coefficient or the total scattered power per unit volume

$$\begin{aligned} {\mu _\mathrm{s}} = 2\pi \int \limits _{ - 1}^1 {\sigma \left( {\cos \theta } \right) d\cos \theta }, \end{aligned}$$

(1.4)

$\bullet$ the backscattering coefficient or the power scattered in the backward direction per unit volume

$$\begin{aligned} {\mu _\mathrm{b}} = 4\pi \cdot \sigma \left( {\theta = \pi } \right) , \end{aligned}$$

(1.5)

$\bullet$ the anisotropy factor g which describes how forward directed the scattering

$$\begin{aligned} g=\frac{{2\pi }}{{{\mu _s}}}\int \limits _{ - 1}^1 {\cos \theta \cdot \sigma \left( {\cos \theta } \right) d\cos \theta }, \end{aligned}$$

(1.6)

$\bullet$ the reduced scattering coefficient

$$\begin{aligned} \mu _\mathrm{s}^ * = {\mu _\mathrm{s}}\cdot \left( {1 - g} \right) , \end{aligned}$$

(1.7)

$\bullet$ and the wave structure function associated with a plane wave which is given by

$$\begin{aligned} {D_\mathrm{pl}}\left( {\rho ,L} \right) = 8{\pi ^2}{k^2}L\int \limits _0^\infty {\kappa {\Phi _s}\left( \kappa \right) \left[ {1 - {J_0}\left( {\rho \kappa } \right) } \right] \mathrm{d}\kappa }, \end{aligned}$$

(1.8)

where L is the propagation distance along the positive z-axis and, $\rho$ is the vector in the receiver plane transverse to the propagation axis.

Note that the above scattering quantities have no closed-form solutions and are evaluated only numerically (see Chen and Korotkova 2018; Liang et al. 2019; Radosevich et al. 2012; Yu and Zhang 2018). On the other hand, many errors are propagated in some papers using some usual equations.

Now, we recall some definitions which are essential for the present work. With a view to introducing special functions, we begin by some identities involving the Gamma function $\Gamma (z)$ given by (see Rainville 1971; Srivastava and Karlsson 1985; Srivastava and Manocha 1984)

$$\begin{aligned} {\Gamma (z)=\left\{ \begin{array}{*{35}{l}} \int \limits _{0}^{\infty }{{{t}^{z-1}}{{e}^{-t}}\mathrm{d}t} &{} \left( \mathfrak {R}(z)>0 \right) , \\ \frac{\Gamma \left( z+n \right) }{z\left( z+1 \right) \ldots \left( z+n-1 \right) } &{} \left( \mathfrak {R}(z)>-n,\,\,n\in \mathbb {N},\,\,z\in \mathbb {C}\backslash \mathbb {Z}_{0}^{-} \right) . \\ \end{array} \right. } \end{aligned}$$

(1.9)

and the Pochhammer’s symbol $(\lambda )_\nu$ defined by Shilin et al. (2020)

$$\begin{aligned} \begin{aligned}&{{\left( \lambda \right) }_{\nu }}:=\frac{\Gamma \left( \lambda +\nu \right) }{\Gamma \left( \lambda \right) }\,\,\,\,\left( \lambda +\nu \in \mathbb {C}\backslash \mathbb {Z}_{0}^{-} \right) \\&\,\,\,\,\,\,\,\,\,\,\,=\Bigg \{\begin{matrix} 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \lambda \left( \lambda +1 \right) \ldots \left( \lambda +n-1 \right) \\ \end{matrix}\,\,\,\begin{matrix} \left( \nu =0 \right) \\ \,\,\,\,\left( \nu =n\in \mathbb {N} \right) \\ \end{matrix} \\ \end{aligned} \end{aligned}$$

(1.10)

and yields the following identity (Srivastava and Karlsson 1985)

$$\begin{aligned} (\lambda )_{m+n}=(\lambda )_{m}(\lambda +m)_n. \end{aligned}$$

(1.11)

The Gauss or hypergeometric function (see Rainville 1971; Srivastava and Manocha 1984) is defined by

$$\begin{aligned} \begin{array}{l} {}_{2}{{F}_{1}}\left( a,b;c;z \right) =\displaystyle \sum \limits _{n=0}^{\infty }{\frac{{{\left( a \right) }_{n}}{{\left( b \right) }_{n}}}{{{\left( c \right) }_{n}}}}\frac{{{z}^{n}}}{n!}, \end{array} \end{aligned}$$

(1.12)

and the Kummer confluent hypergeometric function have the form

$$\begin{aligned} \begin{array}{l} {}_1F_{1}(a;b;z)=\displaystyle \sum _{k=0}^{\infty } \frac{(a)_{k}}{(b)_{k}}\frac{z^{k}}{k!}. \end{array} \end{aligned}$$

(1.13)

We recall the confluent hypergeometric of the second kind, which is a linear combination of functions of the first kind that can be expressed as (see Rainville 1971; Srivastava and Manocha 1984)

$$\begin{aligned} U\left( a;b;z \right) =\frac{\Gamma \left( 1-b \right) }{\Gamma \left( 1+a-b \right) }{}_{1}{{F}_{1}}\left( a;b;z \right) +\frac{\Gamma \left( b-1 \right) }{\Gamma \left( a \right) }{{z}^{1-b}}{}_{1}{{F}_{1}}\left( 1+a-b;2-b;z \right) .\nonumber \\ \end{aligned}$$

(1.14)

For $\mathfrak {R}(a)>0$ and $\mathfrak {R}(z)>0$, the integral representation of this function has the form

$$\begin{aligned} U\left( a;b;z \right) =\frac{1}{\Gamma \left( a \right) }\int \limits _{0}^{\infty }{{{e}^{-zt}}{{t}^{a-1}}{{\left( 1+t \right) }^{b-a-1}}\mathrm{d}t}. \end{aligned}$$

(1.15)

Also, we mention the following functions of two variables which are called Humbert functions (see Gradshteyn and Ryzhik 1994; Rainville 1971; Srivastava and Manocha 1984) defined by

$$\begin{aligned} \Psi _{1}\left[ \alpha ,\beta ;\gamma , \gamma ^{\prime } ; x, y\right] =\sum _{m=0}^{\infty } \sum _{n=0}^{\infty } \frac{(\alpha )_{m+n}(\beta )_{m}}{\left( \gamma )_{m} (\gamma ^{\prime }\right) _{n}} \frac{x^{m}}{m!}\frac{y^{n}}{n!}, \end{aligned}$$

(1.16)

and

$$\begin{aligned} \Phi {}_{1}\left[ \alpha ,\beta ;\gamma ;x,y \right] =\sum \limits _{m=0}^{\infty }{\sum \limits _{n=0}^{\infty }{\frac{{{\left( \alpha \right) }_{m+n}}{{\left( \beta \right) }_{m}}}{{{\left( \gamma \right) }_{m+n}}}}}\frac{{{x}^{m}}}{m!}\frac{{{y}^{n}}}{n!}, \end{aligned}$$

(1.17)

with $|x|<1$ and $|y|<\infty$.

The one-index Bessel function of the first kind (see Rainville 1971; Srivastava and Manocha 1984) is defined by

$$\begin{aligned} {{J}_{\nu }}\left( z \right) =\sum \limits _{r=0}^{\infty }{\frac{{{\left( -1 \right) }^{r}}}{\left( \nu +r \right) !\left( r \right) !}}{{\left( \frac{z}{2} \right) }^{\nu +2r}},\quad \forall \,z\in \mathbb {C}\setminus (-\infty ,0), \end{aligned}$$

(1.18)

where $\nu$ is the order of the Bessel function.We also introduce the Humbert function (see Pasricha 1942; Varma 1941) defined as

$$\begin{aligned} \begin{aligned}&{{J}_{m,n}}\left( z \right) =\sum \limits _{s=-\infty }^{+\infty }{{{J}_{n-s}}\left( z \right) }{{J}_{m-s}}\left( z \right) {{J}_{s}}\left( z \right) , \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{{{\left( {z}/{3}\; \right) }^{m+n}}}{m!n!}\,~{}_{0}{{F}_{2}}\left( -,m+1,n+1;-\frac{{{z}^{3}}}{27} \right) , \\ \end{aligned} \end{aligned}$$

(1.19)

Table 1 Relationships between the Whittaker function and some functions and polynomials

where

$$\begin{aligned} {}_{0}{{F}_{2}}\left( -;b,c;z \right) =\sum \limits _{l=0}^{\infty }{\frac{1}{{{\left( b \right) }_{l}}{{\left( c \right) }_{l}}}}\frac{{{z}^{l}}}{l!}. \end{aligned}$$

It is obvious to remark here that the Kummer confluent hypergeometric function given by (1.13) can be replaced, by taking special values to the parameters a and b, by the Whittaker functions $M_{{\xi },{\eta }}$ and $W_{{\xi },{\eta }}$, the generalized Laguerre polynomial $L^{(\alpha )}_{n}$, the Hermite polynomial $H_{n}$, the modified Bessel function $I_{\nu }(z)$, the error function erf(z) and the incomplete gamma functions (or generalized exponential integrals) $\gamma (2\eta ,z)$ and $\Gamma (2\eta ,z)$ and so on. We summarize in Table 1 the relationships between theses functions and the Whittaker functions by giving their special values of $\xi$ and $\eta$ (see Buchholz 1969; Gradshteyn and Ryzhik 1994; Prudnikov et al. 1986).

In the next sections, our main objective is to evaluate the following integrals:

$$\begin{aligned} {{I}_{1}}= & {} \int \limits _{0}^{\infty }{\frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( 1+c{{t}^{2}} \right) }^{v}}}}\mathrm{d}t, {{I}_{2}}=\int \limits _{0}^{x }{\frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( 1+c{{t}^{2}} \right) }^{v}}}}\mathrm{d}t, {{I}_{3}}=\int \limits _{0}^{x }{\frac{{{e}^{-{\varepsilon }{{t}}}}{{t}^{2\mu -1}}}{{{\left( 1+c{{t}} \right) }^{v}}}}\mathrm{d}t\\ {{I}_{4}}= & {} \int \limits _{0}^{\infty }{\frac{{{J}_{\nu }}\left( \beta t \right) {{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t, {{I}_{5}}=\int \limits _{0}^{\infty }{\frac{{{J}_{\nu }}\left( \beta t \right) {{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t\\ {{I}_{6}}= & {} \int \limits _{0}^{\infty }{{{M}_{\xi ,\eta }}}\left( 2\delta {{t}^{2}} \right) \frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t~~\text {and}~~{{I}_{7}}=\int \limits _{0}^{\infty }{{{M}_{\xi ,\eta }}}\left( 2\delta {{t}^{2}} \right) \frac{{{J}_{\nu }}\left( \beta t \right) {{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t, \end{aligned}$$

involving the rational and exponential functions. The evaluations are expressed in terms of confluent hypergeometric function and other special functions. In the subsequent sections, some particular cases are evaluated, and the main results are applied to investigate the unusual scattering parameters used in the biological tissues. Further, some graphical simulations are shown to compare the theoretical and numerical results.

2 Main results

2.1 Evaluation of $I_{1}$, $I_{2}$ and $I_{3}$

In this section, we evaluate some integral transforms involving the product of exponential function and a rational function of the form $\frac{{{t}^{2\mu -1}}}{{{\left( 1+c{{t}^{n}} \right) }^{v }}}$ with $n=1$ or 2, $\mathfrak {R}(\mu )>0$ and $c>0$.

Theorem 1

If $\mu >0$ and $c>0$, the following transformations hold true:

$$\begin{aligned} {{I}_{1}}= & {} \int \limits _{0}^{\infty }{\frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( 1+c{{t}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{\Gamma \left( \mu \right) }{2{{c}^{\mu }}}\,U\left( \mu ;\mu +1-v;\frac{{\varepsilon }}{c} \right) ,\end{aligned}$$

(2.1)

$$\begin{aligned} {{I}_{2}}= & {} \int \limits _{0}^{x }{\frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( 1+c{{t}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{{{\left( {}^{x}/{}_{c} \right) }^{\mu }}}{2\mu }\,{{\Phi }_{1}}\left[ \mu ,v;\mu +1;-x,-\frac{{\varepsilon }}{c}x \right] , \end{aligned}$$

(2.2)

and

$$\begin{aligned} {{I}_{3}}=\int \limits _{0}^{x }{\frac{{{e}^{-{\varepsilon }{{t}}}}{{t}^{2\mu -1}}}{{{\left( 1+c{{t}} \right) }^{v}}}}\mathrm{d}t=\frac{{{ {x}}^{2\mu }}}{2\mu }\,{{\Phi }_{1}}\left[ 2\mu ,v;2\mu +1;{-{c}{x}},-{{\varepsilon }}x \right] , \end{aligned}$$

(2.3)

with $\mathfrak {R}(\mu )>0$.

Proof

To derive (2.1), we use the following change of variable $z=ct^{2}$, and the integral $I_1$ can be written as

$$\begin{aligned} {{I}_{1}}=\frac{1}{2{{c}^{\mu }}}\int \limits _{0}^{\infty }{\frac{{{e}^{-\frac{{\varepsilon }}{c}z}}{{z}^{\mu -1}}}{{{\left( 1+z \right) }^{v}}}\mathrm{d}z.} \end{aligned}$$

(2.4)

With the help of the following integral representation of the confluent hypergeometric of the second kind

$$\begin{aligned} U\left( a;b;s \right) =\frac{1}{\Gamma \left( a \right) }\int \limits _{0}^{\infty }{{{e}^{-sz}}{{z}^{a-1}}{{\left( 1+z \right) }^{b-a-1}}\mathrm{d}z,} \end{aligned}$$

(2.5)

with $\mathfrak {R}(a)>0$ and $\mathfrak {R}(s)>0$, and by putting $s=\frac{{\varepsilon }}{c}$, $a=\mu$ and $b=\mu +1-v$, we easily obtain (2.1).

To prove (2.2), we take the same change of variable as above $z=ct^{2}$ and use the expansion of the exponential function. So, $I_2$ can be rearranged as

$$\begin{aligned} \begin{aligned}&{{I}_{2}}=\frac{1}{2{{c}^{\mu }}}\int \limits _{0}^{x}{\frac{{{e}^{-\frac{{\varepsilon }}{c}z}}{{z}^{\mu -1}}}{{{\left( 1+z \right) }^{v}}}\mathrm{d}z} \\&\,\,\,\,\,=\frac{1}{2{{c}^{\mu }}}\sum \limits _{m=0}^{\infty }{\frac{{{\left( -{\varepsilon }/{c}\; \right) }^{m}}}{m!}}\int \limits _{0}^{x}{\frac{{{z}^{m+\mu -1}}}{{{\left( 1+z \right) }^{v}}}}\mathrm{d}z. \end{aligned} \end{aligned}$$

(2.6)

Starting from the following equation (see Gradshteyn and Ryzhik 1994)

$$\begin{aligned} \int \limits _{0}^{x}{\frac{{{t}^{\alpha -1}}}{{{\left( 1+\beta t \right) }^{v}}}\mathrm{d}t=\frac{{{x}^{\alpha }}}{\alpha }}~{}_{2}{{F}_{1}}\left( v,\alpha ;\alpha +1;-\beta x \right) , \end{aligned}$$

(2.7)

(2.6) becomes with the use of (1.11) and (1.12)

$$\begin{aligned} \begin{aligned}&{{I}_{2}}=\frac{{{x}^{\mu }}}{2{{c}^{\mu }}}\sum \limits _{m,n=0}^{\infty }{\frac{{{\left( -{{\varepsilon }x}/{c}\; \right) }^{m}}}{m!\left( m+\mu \right) }}\frac{{{\left( v \right) }_{n}}{{\left( m+\mu \right) }_{n}}}{{{\left( m+\mu +1 \right) }_{n}}}\frac{{{\left( -x \right) }^{n}}}{n!}, \\&\,\,\,\,\,=\frac{{{\left( {x}/{c}\; \right) }^{\mu }}}{2\mu }\sum \limits _{m,n=0}^{\infty }{\frac{{{\left( \mu \right) }_{m+n}}{{\left( v \right) }_{n}}}{{{\left( \mu +1 \right) }_{m+n}}}}\frac{{{\left( -{{\varepsilon }x}/{c}\; \right) }^{m}}}{m!}\frac{{{\left( -x \right) }^{n}}}{n!}, \\&\,\,\,\,=\frac{{{\left( {x}/{c}\; \right) }^{\mu }}}{2\mu }\sum \limits _{m,n=0}^{\infty }{\frac{{{\left( \mu \right) }_{m+n}}{{\left( v \right) }_{m}}}{{{\left( \mu +1 \right) }_{m+n}}}}\frac{{{\left( -x \right) }^{m}}}{m!}\frac{{{\left( -{{\varepsilon }x}/{c}\; \right) }^{n}}}{n!}. \\ \end{aligned} \end{aligned}$$

(2.8)

Finally, this completes the proof by employing (1.17).

To determine (2.3), we making use the integral formula given by (2.7) and $I_{3}$ becomes

$$\begin{aligned} \begin{aligned}&{{I}_{3}}=\sum \limits _{m=0}^{\infty }{\frac{{{\left( -{\varepsilon }\right) }^{m}}}{m!}}\int \limits _{0}^{x}{\frac{{{t}^{2\mu -1}}}{{{\left( 1+{c } t \right) }^{v}}}}\mathrm{d}t \\&\,\,\,\,\,=\sum \limits _{m=0}^{\infty }{\frac{{{\left( -{\varepsilon } \right) }^{m}}}{m!}}\frac{{{x}^{2\mu +m}}}{\left( 2\mu +m \right) }~{}_{2}{{F}_{1}}\left( v,2\mu +m,2\mu +m;-{c } x \right) \\&\,\,\,\,\,=\sum \limits _{m,n=0}^{\infty }{\frac{{{\left( -{\varepsilon }\right) }^{m}}}{m!}\frac{{{x}^{2\mu +m}}}{\left( 2\mu +m \right) }}\frac{{{\left( v \right) }_{n}}{{\left( 2\mu +m \right) }_{n}}}{{{\left( 2\mu +1+m \right) }_{n}}}\frac{{{\left( -{c }x \right) }^{n}}}{n!} \\&\,\,\,\,\,=\frac{{{x}^{2\mu }}}{2\mu }\sum \limits _{m,n=0}^{\infty }{\frac{{{\left( 2\mu \right) }_{m+n}}{{\left( v \right) }_{n}}}{{{\left( 2\mu +1 \right) }_{m+n}}}\frac{{{\left( -{\varepsilon }x \right) }^{m}}}{m!}\frac{{{\left( -{c } x \right) }^{n}}}{n!}}. \\ \end{aligned} \end{aligned}$$

(2.9)

This completes the proof using (1.17). $\square$

Remark 1

Using (2.1), we prove the following identity (see Andrews and Philips 2005)

$$\begin{aligned} \int \limits _{0}^{\infty }{\frac{{{\kappa }^{2\alpha }}{{e}^{{-{{\kappa }^{2}}}/{\kappa _{m}^{2}}\;}}}{{{\left( \kappa _{0}^{2}+{{\kappa }^{2}} \right) }^{{}^{D}/{}_{2}}}}}\mathrm{d}\kappa =\frac{\kappa _{0}^{2\alpha +1-D}}{2}~\Gamma \left( \alpha +\frac{1}{2} \right) U\left( \alpha +\frac{1}{2};\alpha +\frac{3}{2}-\frac{D}{2};\frac{\kappa _{0}^{2}}{\kappa _{m}^{2}} \right) , \end{aligned}$$

(2.10)

which becomes for $D=\frac{11}{3}$

$$\begin{aligned} \int \limits _{0}^{\infty }{\frac{{{\kappa }^{2\alpha }}{{e}^{{-{{\kappa }^{2}}}/{\kappa _{m}^{2}}\;}}}{{{\left( \kappa _{0}^{2}+{{\kappa }^{2}} \right) }^{{}^{11}/{}_{6}}}}}\mathrm{d}\kappa =\frac{\kappa _{0}^{\left( 2\alpha -{}^{8}/{}_{3} \right) }}{2}~\Gamma \left( \alpha +\frac{1}{2} \right) U\left( \alpha +\frac{1}{2};\alpha -\frac{1}{3};\frac{\kappa _{0}^{2}}{\kappa _{m}^{2}} \right) . \end{aligned}$$

(2.11)

2.2 Evaluation of $I_4$ and $I_5$

Theorem 2

The undermentioned integral transforms hold true:

$$\begin{aligned} \begin{aligned}&{{I}_{4}}=\int \limits _{0}^{\infty }{\frac{{{J}_{\nu }}\left( \beta t \right) {{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t \\&\,\,\,\,\,=\frac{\left( v-1 \right) !{{\left( {a\beta }/{2}\; \right) }^{\nu }}}{2\nu !{{a}^{2\left( v-\mu \right) }}\Gamma \left( \mu +\frac{\nu }{2} \right) }\,~{}_{0}{{F}_{2}}\left( -;\mu +\frac{\nu }{2},\nu +1;-\frac{{{a}^{2}}{{\beta }^{2}}}{4} \right) , \end{aligned} \end{aligned}$$

(2.12)

and

$$\begin{aligned} \begin{aligned}&{{I}_{5}}=\int \limits _{0}^{\infty }{\frac{{{J}_{\nu }}\left( \beta t \right) {{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t \\&\,\,\,\,\,=\frac{\Gamma \left( \mu +{}^{\nu }/{}_{2} \right) {{\left( {\beta }/{2\sqrt{{\varepsilon }}}\; \right) }^{\nu }}}{2\nu !{{{\varepsilon }}^{\mu }}{{a}^{2v}}}\,{{\Psi }_{1}}\left[ \mu +\frac{\nu }{2},v;-,\nu +1;-\frac{1}{{\varepsilon }{{a}^{2}}},-\frac{{{\beta }^{2}}}{4{\varepsilon }} \right] , \end{aligned} \end{aligned}$$

(2.13)

with

$$\begin{aligned} \mathfrak {R}\left( \mu +\frac{\nu }{2}\right)>0, \mathfrak {R}(v)>-1, \beta>0\, \text {and}\, a>0. \end{aligned}$$

Proof

To prove (2.12), starting with the expansion of $J_{\nu }$ given by (1.18), the integral $I_4$ becomes

$$\begin{aligned} {{I}_{4}}=\sum \limits _{m=0}^{\infty }{\frac{{{\left( -1 \right) }^{m}}{{\left( {\beta }/{2}\; \right) }^{\nu +2m}}}{m!\left( \nu +m \right) !}}{{I}_{m}}, \end{aligned}$$

(2.14)

where

$$\begin{aligned} {{I}_{m}}=\int \limits _{0}^{\infty }{\frac{{{t}^{2s+1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t, \end{aligned}$$

(2.15)

with $s=m+\mu +\frac{\nu }{2}-1$.

Using the known identity (see Prudnikov et al. 1986)

$$\begin{aligned} \int \limits _{0}^{\infty }{\frac{{{t}^{2s+1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{1}{2{{a}^{2\left( v-s-1 \right) }}}\displaystyle \sum \limits _{k=0}^{s}{{{\left( -1 \right) }^{k}}\left( \begin{matrix} s \\ k \\ \end{matrix} \right) }\frac{1}{\left( v-s+k-1 \right) }, \end{aligned}$$

(2.16)

with $\left( \begin{matrix} s \\ k \\ \end{matrix} \right)$ is the binomial coefficient and the formula

$$\begin{aligned} \displaystyle \sum \limits _{k=0}^{s}{{{\left( -1 \right) }^{k}} \left( \begin{matrix} s \\ k \\ \end{matrix} \right) }\frac{1}{\left( k+b \right) }= \frac{s!}{b\left( b+1 \right) \cdots \left( b+s \right) }=\frac{\left( b+s \right) !}{\left( b-1 \right) !}\,={{\left( s+1 \right) }_{b}}, \end{aligned}$$

(2.17)

(2.14) can be written as

$$\begin{aligned} {{I}_{4}}=\frac{\left( v-1 \right) !}{2{{a}^{2\left( v-\mu \right) }}}\sum \limits _{m=0}^{\infty }{\frac{{{\left( -1 \right) }^{m}}{{\left( {\beta }/{2}\; \right) }^{\nu +2m}}{{a}^{2m+\nu }}}{m!\left( \nu +m \right) !\left( m+\mu +\frac{\nu }{2}-1 \right) !}}. \end{aligned}$$

(2.18)

Finally, with the help of the following expressions

$$\begin{aligned} \left( \nu +m \right) !=\Gamma \left( m \right) {{\left( m \right) }_{\nu +1}}, \end{aligned}$$

(2.19)

and

$$\begin{aligned} \left( m+\mu +\frac{\nu }{2}-1 \right) !=\Gamma \left( \mu +\frac{\nu }{2} \right) {{\left( \mu +\frac{\nu }{2} \right) }_{m}}, \end{aligned}$$

(2.20)

we obtain

$$\begin{aligned} {{I}_{4}}=\frac{\left( v-1 \right) !}{2\nu !{{a}^{2\left( v-\mu \right) }}}\frac{{{\left( {a\beta }/{2}\; \right) }^{\nu }}}{\Gamma \left( \mu +{}^{\nu }/{}_{2} \right) }\sum \limits _{m=0}^{\infty }{\frac{{{\left( {-{{a}^{2}}{{\beta }^{2}}}/{4}\; \right) }^{m}}}{m!}}\frac{1}{{{\left( \mu +{}^{\nu }/{}_{2} \right) }_{m}}{{\left( \nu +1 \right) }_{m}}}, \end{aligned}$$

(2.21)

which can be rearranged as

$$\begin{aligned} {{I}_{4}}=\frac{\left( v-1 \right) !{{\left( {a\beta }/{2}\; \right) }^{\nu }}}{2{{a}^{2\left( v-\mu \right) }}}~\frac{{}_{0}{{F}_{2}}\left( -;\mu +\frac{\nu }{2},\nu +1;-\frac{{{a}^{2}}{{\beta }^{2}}}{4} \right) }{\Gamma \left( \mu +\frac{\nu }{2} \right) \Gamma \left( \nu +1 \right) }. \end{aligned}$$

(2.22)

This completes the proof of (2.12).

For the proof of (2.13), we use the expansion of $J_{\nu }$ and the result given by (2.1), which yields

$$\begin{aligned} \begin{aligned}&{{I}_{5}}=\frac{{{a}^{2\left( \mu -v \right) }}}{2\nu !}{{\left( \frac{a\beta }{2} \right) }^{\nu }}\Gamma \left( \mu +\frac{\nu }{2} \right) \displaystyle \sum \limits _{m=0}^{\infty }{\frac{{{\left( -{{{a}^{2}}{{\beta }^{2}}}/{4}\; \right) }^{m}}}{m!}}\frac{{{\left( \mu +\frac{\nu }{2} \right) }_{m}}}{{{\left( \nu +1 \right) }_{m}}} \\&\,\,\,\,\,\,\times U\left( m+\mu +\frac{\nu }{2},m+\mu +\frac{\nu }{2}+1-v;{\varepsilon }{{a}^{2}} \right) . \end{aligned} \end{aligned}$$

(2.23)

Applying the known relation (see Prudnikov et al. 1986)

$$\begin{aligned} U\left( \alpha ;\alpha -\beta +1;z \right) =\frac{1}{{{z}^{\alpha }}}\,{}_{2}{{F}_{0}}\left( \alpha ,\beta ;-\frac{1}{z} \right) , \end{aligned}$$

(2.24)

and the expansion of ${}_{2}{{F}_{0}}$ , we obtain for the confluent hypergeometric function

$$\begin{aligned} U\left( m+\mu +\frac{\nu }{2};v;{\varepsilon }{{a}^{2}} \right) =\frac{1}{{{\left( {\varepsilon }{{a}^{2}} \right) }^{m+\mu +{}^{\nu }/{}_{2}}}}\sum \limits _{n=0}^{\infty }{{{\left( m+\mu +\frac{\nu }{2} \right) }_{n}}{{\left( v \right) }_{n}}}\frac{{{\left( -{}^{1}/{}_{{\varepsilon }{{a}^{2}}} \right) }^{n}}}{n!}. \end{aligned}$$

(2.25)

So, (2.23) can be written as

$$\begin{aligned} {{I}_{5}}=\frac{\Gamma \left( \mu +\frac{\nu }{2} \right) {{\left( \frac{\beta }{2\sqrt{{\varepsilon }}} \right) }^{\nu }}}{2\nu !{{{\varepsilon }}^{\mu }}{{a}^{2v}}}\sum \limits _{m,n=0}^{\infty }{\frac{{{\left( -\frac{{{\beta }^{2}}}{4{\varepsilon } } \right) }^{n}}}{n!}\frac{{{\left( -\frac{1}{{\varepsilon }{{a}^{2}}} \right) }^{m}}}{m!}\frac{{{\left( \mu +{}^{\nu }/{}_{2} \right) }_{m+n}}{{\left( v \right) }_{m}}}{{{\left( \nu +1 \right) }_{n}}}}. \end{aligned}$$

(2.26)

This completes the proof by the use of the definition of $\psi _{1}$ given by (1.16). $\square$

Remark 2

Note that the Bessel function of the third kind or the Humbert function (see Pasricha 1942; Varma 1941) is given by

$$\begin{aligned} {{J}_{m,n}}\left( x \right) =\frac{{{\left( {x}/{3}\; \right) }^{m+n}}}{m!n!}\,{}_{0}{{F}_{2}}\left( -;m+1,n+1;-\frac{{{x}^{3}}}{27} \right) . \end{aligned}$$

(2.27)

So, we can express (2.22) in terms of the above functions as

$$\begin{aligned} {{I}_{4}}=\frac{\left( v-1 \right) !}{2}\frac{{{\left( {}^{a\beta }/{}_{2} \right) }^{\nu }}}{{{a}^{2\left( v-\mu \right) }}}\frac{{{J}_{\mu +\frac{\nu }{2}-1,\nu }}\left( x \right) }{{{\left( {}^{x}/{}_{3} \right) }^{_{\mu +\frac{3\nu }{2}-1 }}}}, \end{aligned}$$

(2.28)

with $x=3{{\left( \frac{{{a}^{2}}{{\beta }^{2}}}{4} \right) }^{\frac{1}{3}}},$ and give the integral representation of the Humbert function

$$\begin{aligned} {{J}_{\mu +\frac{\nu }{2}-1,\nu }}\left[ 3{{\left( \frac{{{a}^{2}}{{\beta }^{2}}}{4} \right) }^{{}^{1}/{}_{3}}} \right] =\frac{2}{\Gamma \left( v \right) }\frac{{{\left( {{{\beta }^{2}}}/{4}\; \right) }^{\frac{\mu -1}{3}}}}{{{\left( {{a}^{2}} \right) }^{\left( \frac{2\mu +1}{3}-v \right) }}}\int \limits _{0}^{\infty }{{{J}_{\nu }}\left( \beta t \right) \frac{{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t}. \end{aligned}$$

(2.29)

2.3 Evaluation of $I_6$ and $I_7$

Theorem 3

For $\mathfrak {R}(\xi +\mu )>-\frac{1}{2}$ ,$\mathfrak {R}(v)>0$, $a>0$, $\mathfrak {R}(\xi )>-\frac{1}{2}$, $\mathfrak {R}({\varepsilon })>0$, $\delta >0$ and $\mathfrak {R}(\mu )>0$, the undermentioned formulae holds true:

$$\begin{aligned} \begin{aligned}&{{I}_{6}}=\int \limits _{0}^{\infty }{{{M}_{\xi ,\eta }}}\left( 2\delta {{t}^{2}} \right) \frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \eta +\mu +\frac{1}{2} \right) }{2{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{2\delta }{{\varepsilon }+\delta } \right) }^{\eta +\frac{1}{2}}} \\&\,\,\,\,\,\times {{F}_{2}}\left[ \eta +\mu +\frac{1}{2},\eta +\frac{1}{2}-\xi ,v;2\eta +1,-;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] , \end{aligned} \end{aligned}$$

(2.30)

and for $\delta >0$ ,$\beta >0$, $\mathfrak {R}({\varepsilon })>0$, $a>0$, $\mathfrak {R}(\mu )>0$, $\mathfrak {R}(\nu )>0$, $\mathfrak {R}(\eta +\mu +\frac{\nu }{2})>\frac{1}{2}$, $\mathfrak {R}(\eta )>-\frac{1}{2}$ and $\mathfrak {R}(\xi )<\mathfrak {R}(\eta +\frac{1}{2})$, we have

$$\begin{aligned} \begin{aligned}&{{I}_{7}}=\int \limits _{0}^{\infty }{{{M}_{\xi ,\eta }}}\left( 2\delta {{t}^{2}} \right) \frac{{{J}_{\nu }}\left( \beta t \right) {{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \eta +\mu +\frac{\nu +1}{2} \right) }{2\nu !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }} \\&\times {{\left( \frac{2\delta }{{\varepsilon }+\delta } \right) }^{\eta +\frac{1}{2}}} F_{A}^{(3)}\left[ \eta +\mu +\frac{\nu +1}{2},\eta +\frac{1}{2}-\xi ,v,-;2\eta +1,-,\nu +1;\right. \\&\left. \frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] , \end{aligned} \end{aligned}$$

(2.31)

where $F_{2}$ is the double hypergeometric series (Srivastava and Karlsson 1985) (known as Appel series) given by

$$\begin{aligned} F_{2}\left[ a,b,b^{\prime };c,c^{\prime }; x,y\right] =\displaystyle \sum _{m,n=0}^{\infty } \frac{(a)_{m+n}(b)_{m}(b^{\prime })_{n}}{(c)_{m}(c^{\prime })_{n}} \frac{x^{m}}{m!}\frac{y^{n}}{n!}, \end{aligned}$$

(2.32)

with $|x|+|y|<1$, and $F_{A}^{(3)}$ is the triple hypergeometric series (known as Lauricella series) defined by (see Srivastava and Karlsson 1985)

$$\begin{aligned} F_{A}^{(3)}\left[ a,{{b}_{1}},{{b}_{2}},{{b}_{3}};{{c}_{1}},{{c}_{2}},{{c}_{3}};x,y,z \right] =\sum \limits _{p,m,n=0}^{\infty }{\frac{{{\left( a \right) }_{p+m+n}}{{\left( {{b}_{1}} \right) }_{p}}{{\left( {{b}_{2}} \right) }_{m}}{{\left( {{b}_{3}} \right) }_{n}}}{{{\left( {{c}_{1}} \right) }_{p}}{{\left( {{c}_{2}} \right) }_{m}}{{\left( {{c}_{3}} \right) }_{n}}}}\frac{{{x}^{p}}}{p!}\frac{{{y}^{m}}}{m!}\frac{{{z}^{n}}}{n!},\nonumber \\ \end{aligned}$$

(2.33)

with ${|x|}+{|y|}+{|z|}<1$.

Proof

To prove (2.30), we use the following expansion of the Whittaker function (see Buchholz 1969)

$$\begin{aligned} {{M}_{\xi ,\eta }}\left( 2\delta {{t}^{2}} \right) ={{\left( 2\delta \right) }^{\eta +{}^{1}/{}_{2}}}{{t}^{2\eta +1}}{{e}^{-\delta {{t}^{2}}}}\sum \limits _{m=0}^{\infty }{\frac{{{\left( {}^{1}/{}_{2}+\eta -\xi \right) }_{m}}}{{{\left( 2\eta +1 \right) }_{m}}}}\frac{{{\left( 2\delta {{t}^{2}} \right) }^{m}}}{m!}, \end{aligned}$$

(2.34)

and with the help of (2.1), we obtain

$$\begin{aligned} \begin{aligned}&{{I}_{6}}=\frac{{{\left( 2\delta \right) }^{\eta +{}^{1}/{}_{2}}}{{a}^{2\eta +2\mu +1}}}{2{{a}^{2v}}}\Gamma \left( \eta +\mu +\frac{1}{2} \right) \sum \limits _{m=0}^{\infty }{\frac{{{\left( {}^{1}/{}_{2}+\eta -\xi \right) }_{m}}}{{{\left( 2\eta +1 \right) }_{m}}}}\frac{{{\left( 2\delta {{a}^{2}} \right) }^{m}}}{m!} \\&\times {\left( \eta +\mu +\frac{1}{2} \right) }_{m} U\left( m+\eta +\mu +\frac{1}{2};m+\eta +\mu +\frac{3}{2}-v;\left( {\varepsilon }+\delta \right) {{a}^{2}} \right) . \end{aligned} \end{aligned}$$

(2.35)

This last equation can be rearranged, using (2.24), as

$$\begin{aligned} \begin{aligned}&{{I}_{6}}=\frac{\Gamma \left( \eta +\mu +{}^{1}/{}_{2} \right) }{2{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{2\delta }{{\varepsilon }+\delta } \right) }^{\eta +\frac{1}{2}}} \\&\,\,\,\,\,\times \sum \limits _{m,n=0}^{\infty }{\frac{{{\left( \eta +\mu +{}^{1}/{}_{2} \right) }_{m+n}}{{\left( \eta +{}^{1}/{}_{2}-\xi \right) }_{m}}{{\left( v \right) }_{n}}}{{{\left( 2\eta +1 \right) }_{m}}}}\frac{{{\left[ {}^{2\delta }/{}_{\left( {\varepsilon }+\delta \right) } \right] }^{m}}}{m!}\frac{{{\left[ -{}^{1}/{}_{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] }^{n}}}{n!}, \\ \end{aligned} \end{aligned}$$

(2.36)

which is equivalent to (2.30) if we use the expression of $F_{2}$ given by (2.32).

To prove (2.31), we use two methods: For the first one, we use the expansion of the Bessel function $J_{\nu }$, and for the second one, we use the expansion of the Whittaker function.

First method: Using the expansion of $J_{\nu }$ (1.18) and the result given by (2.30), the integral $I_{7}$ can be written as

$$\begin{aligned}&{{I}_{7}}=\frac{\Gamma \left( \eta +\mu +\frac{\nu +1}{2} \right) }{2{{a}^{2v}}\nu !{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }}{{\left( \frac{2\delta }{{\varepsilon }+\delta } \right) }^{\eta +\frac{1}{2}}}\sum \limits _{p=0}^{\infty }{\frac{{{\left[ -{}^{{{\beta }^{2}}}/{}_{4\left( {\varepsilon }+\delta \right) } \right] }^{p}}}{p!{{\left( \nu +1 \right) }_{p}}}}{{\left( \eta +\mu +\frac{\nu +1}{2} \right) }_{p}} \nonumber \\&\,\,\,\,\,\times {{F}_{2}}\left[ \eta +\mu +p+\frac{\nu +1}{2},\eta +\frac{1}{2}-\xi ,v;2\eta +1,-;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] , \end{aligned}$$

(2.37)

which, with the help of the identity

$$\begin{aligned} {{\left( p+\eta +\mu +\frac{\nu +1}{2} \right) }_{m+n}}=\frac{{{\left( \eta +\mu +\frac{\nu +1}{2} \right) }_{p+m+n}}}{{{\left( \eta +\mu +\frac{\nu +1}{2} \right) }_{p}}}, \end{aligned}$$

(2.38)

(2.37) can be rewritten as

$$\begin{aligned} \begin{aligned}&{{I}_{7}}=\frac{\Gamma \left( \eta +\mu +\frac{\nu +1}{2} \right) }{2{{a}^{2v}}\nu !{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }}{{\left( \frac{2\delta }{{\varepsilon }+\delta } \right) }^{\eta +\frac{1}{2}}} \\&\,\,\,\,\,\,\times \sum \limits _{p,m,n=0}^{\infty }{\frac{{{\left( \eta +\mu +\frac{\nu +1}{2} \right) }_{p+m+n}}{{\left( \eta +\frac{1}{2}-\xi \right) }_{m}}{{\left( v \right) }_{n}}}{{{\left( \nu +1 \right) }_{p}}{{\left( 2\eta +1 \right) }_{m}}}\frac{{{x}^{p}}}{p!}}\frac{{{y}^{m}}}{m!}\frac{{{z}^{n}}}{n!}, \\ \end{aligned} \end{aligned}$$

(2.39)

where $x=-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) }$, $y=\frac{2\delta }{{\varepsilon }+\delta }$ and $z=-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) }$.

Finally, the proof of (2.31) quickly follows using the first method.

Second method: To evaluate $I_{7}$, we use (2.34) and the result given by (2.13). Consequently, $I_{6}$ becomes

$$\begin{aligned}&{{I}_{7}}=\frac{{{\left( 2\delta \right) }^{\eta +\frac{1}{2}}}}{2\nu !{{a}^{2v}}}\frac{{{\left( {\beta }/{2\sqrt{{\varepsilon }+\delta }}\; \right) }^{\nu }}}{{{\left( {\varepsilon }+\delta \right) }^{\eta +\mu +\frac{1}{2}}}}\sum \limits _{m=0}^{\infty }{\frac{{{\left( \eta +{}^{1}/{}_{2}-\xi \right) }_{m}}}{{{\left( 2\eta +1 \right) }_{m}}}\frac{{{\left[ {}^{2\delta }/{}_{\left( {\varepsilon }+\delta \right) } \right] }^{m}}}{m!}}\Gamma \left( m+\eta +\mu +\frac{\nu +1}{2} \right) \nonumber \\&\,\,\,\,\,\,\times {{\Psi }_{1}}\left[ m+\eta +\mu +\frac{\nu +1}{2},v;-,\nu +1;-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] , \end{aligned}$$

(2.40)

which, by the use of the identity

$$\begin{aligned} \Gamma \left( m+\eta +\mu +\frac{\nu +1}{2} \right) ={{\left( \eta +\mu +\frac{\nu +1}{2} \right) }_{m}}\Gamma \left( \eta +\mu +\frac{\nu +1}{2} \right) , \end{aligned}$$

(2.41)

can be written as

$$\begin{aligned} \begin{aligned}&{{I}_{7}}=\frac{\Gamma \left( \eta +\mu +\frac{\nu +1}{2} \right) }{2\nu !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }}{{\left( \frac{2\delta }{{\varepsilon }+\delta } \right) }^{\eta +\frac{1}{2}}} \\&\times F_{A}^{(3)}\left[ \eta +\mu +\frac{\nu +1}{2},\eta +\frac{1}{2}-\xi ,v,-;2\eta +1,-,\nu +1;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}({\varepsilon }+\delta )},-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] . \\ \end{aligned}\nonumber \\ \end{aligned}$$

(2.42)

$\square$

Lemma 1

The undermentioned property holds true:

$$\begin{aligned} F_{A}^{(3)}\left[ a,{{b}_{1}},{{b}_{2}},-;{{c}_{1}},-,{{c}_{3}};x,y,z \right] =F_{A}^{(3)}\left[ a,-,{{b}_{1}},{{b}_{2}};{{c}_{3}},{{c}_{1}},-;z,x,y \right] . \end{aligned}$$

(2.43)

It is easy to prove this last equation using the following equality

$$\begin{aligned} \displaystyle \sum \limits _{m,p,r=0}^{\infty }{\frac{{{\left( a \right) }_{m+p+r}}{{\left( {{b}_{1}} \right) }_{m}}{{\left( {{b}_{2}} \right) }_{p}}}{{{\left( {{c}_{1}} \right) }_{m}}{{\left( {{c}_{3}} \right) }_{r}}}}\frac{{{x}^{m}}}{m!}\frac{{{y}^{p}}}{p!}\frac{{{z}^{r}}}{r!}=\displaystyle \sum \limits _{m,p,r=0}^{\infty }{\frac{{{\left( a \right) }_{m+p+r}}{{\left( {{b}_{1}} \right) }_{p}}{{\left( {{b}_{2}} \right) }_{r}}}{{{\left( {{c}_{3}} \right) }_{m}}{{\left( {{c}_{1}} \right) }_{p}}}}\frac{{{z}^{m}}}{m!}\frac{{{x}^{p}}}{p!}\frac{{{y}^{r}}}{r!},\nonumber \\ \end{aligned}$$

(2.44)

and consequently, we obtain (2.43).

Therefore, with the help of the Lemma 1, we refind that (2.42) is the same as (2.39).

Remark 3

Setting $\nu =\beta =0$ and using the Lemma 1, we can easily find $I_{6}$ from $I_{7}$.

3 Particular cases

Corollary 1

The undermentioned transformations hold true:

$$\begin{aligned} \begin{aligned} \int \limits _{0}^{\infty }{\frac{{{e}^{-\left( {\varepsilon }-\delta \right) {{t}^{2}}}}{{t}^{2\mu -2\xi -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{\Gamma \left( \mu -\xi \right) }{2{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu -\xi }}}&~{{F}_{2}}\left[ \mu -\xi ,-2\xi ,v;-2\xi ,-;\right. \\&\left. \frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] , \end{aligned} \end{aligned}$$

(3.1)

and

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty }{\frac{{{J}_{\nu }}\left( \beta t \right) {{e}^{-\left( {\varepsilon }-\delta \right) {{t}^{2}}}}{{t}^{2\mu -2\xi -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{\Gamma \left( \mu -\xi +{}^{\nu }/{}_{2} \right) }{2\nu !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu -\xi }}}{{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }} \\&\times F_{A}^{(3)}\left[ \mu -\xi +\frac{\nu }{2},-2\xi ,v,-;-2\xi ,-,\nu +1;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] . \\ \end{aligned} \end{aligned}$$

(3.2)

(3.1) and (3.2) can be established by taking in Theorem 3: $\eta =-\xi -\frac{1}{2}$ and ${{M}_{\xi ,-\xi -\frac{1}{2}}}\left( z \right) ={{e}^{{}^{z}/{}_{2}}}{{z}^{-\xi }}$.

Corollary 2

The undermentioned transformations hold true:

$$\begin{aligned} \begin{aligned} \int \limits _{0}^{\infty }&{{{I}_{\eta }}\left( \delta {{t}^{2}} \right) \frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu }}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{\Gamma \left( \eta +\mu +{}^{1}/{}_{2} \right) }{\sqrt{2\delta }{{a}^{2v}}\eta !{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{\delta }{2\left( {\varepsilon }+\delta \right) } \right) }^{\eta +\frac{1}{2}}} \\&\times {{F}_{2}}\left[ \eta +\mu +\frac{1}{2},\eta +\frac{1}{2},v;2\eta +1,-;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] , \\\end{aligned} \end{aligned}$$

(3.3)

and

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty }{{{J}_{\nu }}}\left( \beta t \right) {{I}_{\eta }}\left( \delta {{t}^{2}} \right) \frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu }}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \eta +\mu +\frac{\nu +1}{2} \right) }{\sqrt{2\delta }\nu !\eta !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }} \\&\times {{\left( \frac{\delta }{2\left( {\varepsilon }+\delta \right) } \right) }^{\eta +\frac{1}{2}}} F_{A}^{(3)}\left[ \eta +\mu +\frac{\nu +1}{2},\eta +\frac{1}{2},v,-;2\eta +1,-,\nu +1;\right. \\&\left. \frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] . \\ \end{aligned} \end{aligned}$$

(3.4)

This corollary is established by taking $\xi =0$ and $\eta =\frac{1}{2}$ and using Theorem 3.

Corollary 3

The undermentioned transformations hold true:

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty }{\sinh \left( \delta {{t}^{2}} \right) }\frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\mu !}{4{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu }}}\left( \frac{2\delta }{{\varepsilon }+\delta } \right) \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\times {{F}_{2}}\left[ \mu +1,1,v,2,-;\frac{2\delta }{\left( {\varepsilon }+\delta \right) },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] ,\\ \end{aligned} \end{aligned}$$

(3.5)

and

$$\begin{aligned} \begin{aligned} \int \limits _{0}^{\infty }\sinh&\left( \delta {{t}^{2}} \right) {{J}_{\nu }}\left( \beta t \right) \frac{{{e}^{-{\varepsilon }{{t}^{2}}}}{{t}^{2\mu -1}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \mu +{}^{\nu }/{}_{2}+1 \right) }{4\nu !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu }}}{{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }} \\&\times \left( \frac{2\delta }{{\varepsilon }+\delta } \right) F_{A}^{(3)}\left[ \mu +\frac{\nu }{2}+1,1,v,-;2,-,\nu +1;\right. \\&\left. \frac{2\delta }{\left( {\varepsilon }+\delta \right) },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] . \\ \end{aligned} \end{aligned}$$

(3.6)

Proof

The above corollary can be proved by taking $\xi =0$ and $\eta =\frac{1}{2}$ and using Theorem 3. In this case (see Table 1), the Whittaker function is given in terms of sinh as

$$\begin{aligned} {{M}_{0,\frac{1}{2}}}\left( 2z \right) =2\sinh \left( z \right) . \end{aligned}$$

(3.7)

$\square$

Corollary 4

The undermentioned transformations hold true:

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty }{L_{q}^{p}\left( 2\delta {{t}^{2}} \right) \frac{{{e}^{-\left( {\varepsilon }+\delta \right) {{t}^{2}}}}{{t}^{2\mu +p}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{{{\left( p+1 \right) }_{q}}\Gamma \left( \mu +\frac{p+1}{2} \right) }{2p!{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu +\frac{p+1}{2}}}}} \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\times {{F}_{2}}\left[ \mu +\frac{p+1}{2},-q,v;p+1,-;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] , \\ \end{aligned} \end{aligned}$$

(3.8)

and

$$\begin{aligned} \begin{aligned} \int \limits _{0}^{\infty }{{J}_{\nu }}&\left( \beta t \right) L_{q}^{p}\left( 2\delta {{t}^{2}} \right) \frac{{{e}^{-\left( {\varepsilon }+\delta \right) {{t}^{2}}}}{{t}^{2\mu +p}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{{{\left( p+1 \right) }_{q}}\Gamma \left( \mu +\frac{p+\nu +1}{2} \right) }{2p!\nu !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu +\frac{p+1}{2}}}} \\&\times {{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }} F_{A}^{(3)}\left[ \mu +\frac{p+\nu +1}{2},-q,v,-;p+1,-,\nu +1;\right. \\&\left. \frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] . \\ \end{aligned} \end{aligned}$$

(3.9)

This corollary can be established by setting $\xi =\frac{p}{2}+q+\frac{1}{2}$ and $\eta =\frac{p}{2}$ and using Theorem 3. In this case, the Whittaker function is given in terms of the Generalized Laguerre polynomial as (see Table 1)

$$\begin{aligned} {{M}_{\frac{p}{2}+q+\frac{1}{2},\frac{p}{2}}}\left( z \right) =\frac{p!}{{{\left( p+1 \right) }_{q}}}{{e}^{-{}^{z}/{}_{2}}}{{\left( z \right) }^{\frac{p+1}{2}}}L_{q}^{p}\left( z \right) . \end{aligned}$$

(3.10)

Corollary 5

The undermentioned transformations hold true:

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty }{{{H}_{2p}}\left( \sqrt{2\delta }t \right) \frac{{{e}^{-\left( {\varepsilon }+\delta \right) {{t}^{2}}}}{{t}^{2\mu -{}^{1}/{}_{2}}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{{{\left( -1 \right) }^{p}}\left( 2p \right) !\Gamma \left( \mu +\frac{1}{4} \right) }{2p!{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu +{}^{1}/{}_{4}}}} \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\times {{F}_{2}}\left[ \mu +\frac{1}{4},-p,v;\frac{1}{2},-;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] , \\ \end{aligned} \end{aligned}$$

(3.11)

and

$$\begin{aligned} \begin{aligned} \int \limits _{0}^{\infty }{H}_{2p}&\left( \sqrt{2\delta }t \right) {{J}_{\nu }}\left( \beta t \right) \frac{{{e}^{-\left( {\varepsilon }+\delta \right) {{t}^{2}}}}{{t}^{2\mu -{}^{1}/{}_{2}}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{{{\left( -1 \right) }^{p}}\left( 2p \right) !\Gamma \left( \mu +\frac{\nu }{2}+\frac{1}{4} \right) }{2p!\nu !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu +{}^{1}/{}_{4}}}} \\&\times {{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }} F_{A}^{(3)}\left[ \mu +\frac{\nu }{2}+\frac{1}{4},-p,v,-;\frac{1}{2},-,\nu +1;\right. \\&\left. \frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] . \\ \end{aligned} \end{aligned}$$

(3.12)

By setting $\xi =p+\frac{1}{4}$ and $\eta =-\frac{1}{4}$, the Whittaker function is linked to the Hermite Polynomial by (see Table 1)

$$\begin{aligned} {{M}_{p+\frac{1}{4},-\frac{1}{4}}}\left( {{z}^{2}} \right) ={{\left( -1 \right) }^{p}}\frac{p!}{\left( 2p \right) !}{{e}^{-{}^{{{z}^{2}}}/{}_{2}}}\sqrt{z}{{H}_{2p}}\left( z \right) . \end{aligned}$$

(3.13)

Theorem 3 yields easily (3.11) and (3.12).

Corollary 6

The undermentioned transformations hold true:

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty }{{{H}_{2p+1}}\left( \sqrt{2\delta }t \right) \frac{{{e}^{-\left( {\varepsilon }+\delta \right) {{t}^{2}}}}{{t}^{2\mu -{}^{1}/{}_{2}}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{{{\left( -1 \right) }^{p}}\left( 2p+1 \right) !\Gamma \left( \mu +\frac{3}{4} \right) \sqrt{2\delta }}{p!{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu +{}^{3}/{}_{4}}}} \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\times {{F}_{2}}\left[ \mu +\frac{3}{4},-p,v;\frac{3}{2},-;\frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) } \right] , \\ \end{aligned} \end{aligned}$$

(3.14)

and

$$\begin{aligned} \begin{aligned}&\int \limits _{0}^{\infty }{{{H}_{2p+1}}\left( \sqrt{2\delta }t \right) {{J}_{\nu }}\left( \beta t \right) \frac{{{e}^{-\left( {\varepsilon }+\delta \right) {{t}^{2}}}}{{t}^{2\mu -{}^{1}/{}_{2}}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}}\mathrm{d}t=\frac{{{\left( -1 \right) }^{p}}\left( 2p+1 \right) !\Gamma \left( \mu +\frac{\nu }{2}+\frac{3}{4} \right) \sqrt{2\delta }}{p!\nu !{{a}^{2v}}{{\left( {\varepsilon }+\delta \right) }^{\mu +{}^{3}/{}_{4}}}}\\&\times {\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu } F_{A}^{(3)}\left[ \mu +\frac{\nu }{2}+\frac{3}{4},-p,v,-;\frac{3}{2},-,\nu +1;\right. \\&\left. \frac{2\delta }{{\varepsilon }+\delta },-\frac{1}{{{a}^{2}}\left( {\varepsilon }+\delta \right) },-\frac{{{\beta }^{2}}}{4\left( {\varepsilon }+\delta \right) } \right] . \\ \end{aligned} \end{aligned}$$

(3.15)

This corollary can be established by taking $\xi =p+\frac{3}{4}$ and $\eta =\frac{1}{4}$. In this case, we have

$$\begin{aligned} {{M}_{p+\frac{3}{4},\frac{1}{4}}}\left( {{z}^{2}} \right) =\frac{{{\left( -1 \right) }^{p}}}{2}\frac{p!}{\left( 2p+1 \right) !}{{e}^{-{}^{{{z}^{2}}}/{}_{2}}}\sqrt{z}{{H}_{2p+1}}\left( z \right) . \end{aligned}$$

(3.16)

Corollary 7

The undermentioned transformations hold true:

$$\begin{aligned} \begin{aligned}&\int _{0}^{\infty }{\gamma \left( 2\eta ,2\delta {{t}^{2}} \right) \frac{{{e}^{-\left( {\varepsilon }-\delta \right) {{t}^{2}}}}{{t}^{2\mu -2\eta }}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \eta +\mu +\frac{1}{2} \right) }{4\eta {{({\varepsilon }+\delta )}^{\mu +\eta +\frac{1}{2}}}}}{{\left( 2\delta \right) }^{2\eta }} \\&\times {{F}_{2}}\left[ \eta +\mu +\frac{1}{2},1,v;2\eta +1,-;x,y \right] ,\\ \end{aligned} \end{aligned}$$

(3.17)

and

$$\begin{aligned} \begin{aligned}&\int _{0}^{\infty }{\gamma \left( 2\eta ,2\delta {{t}^{2}} \right) {{J}_{\nu }}\left( \beta t \right) \frac{{{e}^{-\left( {\varepsilon }-\delta \right) {{t}^{2}}}}{{t}^{2\mu -2\eta }}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \eta +\mu +\frac{\nu +1}{2} \right) }{4\eta \nu !{{a}^{2v}}{({{\varepsilon }+\delta })^{\mu +\eta +\frac{1}{2}}}}} \\&\times {{\left( \frac{\beta }{2\sqrt{{\varepsilon }+\delta }} \right) }^{\nu }} {\left( 2\delta \right) }^{2\eta }\, F_{A}^{\left[ 3 \right) }\left[ \eta +\mu +\frac{\nu +1}{2},1,v,-;2\eta +1,-,\nu +1;x,y,z \right] . \\ \end{aligned} \end{aligned}$$

(3.18)

where $x=\frac{2\delta }{{\varepsilon }+\delta }$, $y=-\frac{1}{{{a}^{2}}({\varepsilon }+\delta )}$ and $z=-\frac{{{\beta }^{2}}}{4({\varepsilon }+\delta )}$.

In this case, we set $\xi =\eta -\frac{1}{2}$. So, we have (see Table 1)

$$\begin{aligned} {{M}_{\eta -\frac{1}{2},\eta }}\left( z \right) =2\eta {{e}^{\frac{z}{2}}}{{z}^{\frac{1}{2}-\eta }}\gamma \left( 2\eta ,z \right) . \end{aligned}$$

(3.19)

and the corollary is established.

Corollary 8

The undermentioned transformations hold true:

$$\begin{aligned} \int _{0}^{\infty }{erf\left( \sqrt{2\delta }t \right) \frac{{{e}^{-\left( {\varepsilon }-\delta \right) {{t}^{2}}}}{{t}^{2\mu -\frac{1}{2}}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \mu +\frac{3}{4} \right) }{{{a}^{2v}}{({{\varepsilon }+\delta })^{\mu +\frac{3}{4}}}}}\sqrt{\frac{2\delta }{\pi }}{{F}_{2}}\left[ \mu +\frac{3}{4},1,v;\frac{3}{2},-;x,y \right] ,\nonumber \\ \end{aligned}$$

(3.20)

and

$$\begin{aligned} \begin{aligned}&\int _{0}^{\infty }{erf\left( \sqrt{2\delta }t \right) {{J}_{\nu }}\left( \beta t \right) \frac{{{e}^{-\left( {\varepsilon }-\delta \right) {{t}^{2}}}}{{t}^{2\mu -\frac{1}{2}}}}{{{\left( {{t}^{2}}+{{a}^{2}} \right) }^{v}}}\mathrm{d}t=\frac{\Gamma \left( \mu +\frac{\nu }{2}+\frac{3}{4} \right) }{\nu !{{a}^{2v}}{({{\varepsilon }+\delta })^{\mu +\frac{\nu }{2}+\frac{3}{4}}}}{{\left( \frac{\beta }{2} \right) }^{\nu }}} \\&\times \sqrt{\frac{2\delta }{\pi }} \,F_{A}^{\left( 3 \right) }\left[ \mu +\frac{\nu }{2}+\frac{3}{4},1,v,-;\frac{3}{2},-,\nu +1;x,y,z \right] , \\ \end{aligned} \end{aligned}$$

(3.21)

where $x=\frac{2\delta }{({\varepsilon }+\delta )}$, $y=-\frac{1}{{{a}^{2}}({\varepsilon }+\delta )}$ and $z=-\frac{{{\beta }^{2}}}{4({\varepsilon }+\delta )}$.

The corollary can be established by setting $\xi =-\eta =-\frac{1}{4}$ and the Whittaker function is given by (see Table 1)

$$\begin{aligned} {{M}_{-\frac{1}{4},\frac{1}{4}}}\left( {{z}^{2}} \right) =\frac{{{e}^{{}^{{{z}^{2}}}/{}_{2}}}}{2}\sqrt{\pi z}erf\left( z \right) \end{aligned}$$

(3.22)

4 Biological tissue application

In this section, we examine an important application of the present investigation in the biological tissues field. Setting in this investigation that the spatial power is given by (see Andrews and Philips 2005)

$$\begin{aligned} {{\Phi }_{s}}\left( \kappa \right) =S\frac{e{}^\frac{-{{\kappa }^{2}}}{\kappa _{l}^{2}}}{{{\left( {{\kappa }^{2}}+\kappa _{0}^{2} \right) }^{{}^{11}/{}_{6}}}}f\left( \kappa \right) , \end{aligned}$$

(4.1)

with $S=0.033C_{n}^{2}$, $f\left( \kappa \right) =1+1.802\left( {}^{\kappa }/{}_{{{\kappa }_{l}}} \right) -0.254{{\left( {}^{\kappa }/{}_{{{\kappa }_{l}}} \right) }^{{}^{7}/{}_{6}}}$, ${{\kappa }_{l}}={}^{3.3}/{}_{{{l}_{0}}}$, $C_{n}^{2}$ is the index of refraction structure constant (in ${{m}^{-{}^{2}/{}_{3}}}$) and ${{l}_{0}}$ is the inner scale. For the simplicity, setting that $f\left( \kappa \right) \sim 1$ for certain ranges for $\kappa$.

Following up, we now evaluate the scattering parameters for this particular spatial power by noting that the generalization of each expression of ${{\Phi }_{s}}$ still easy.

4.1 Evaluation of ${\mathcal {B}_n}$

Using Maclaurin series representation

$$\begin{aligned} \frac{\sin \left( r\kappa \right) }{r\kappa }=1+\sum \limits _{n=1}^{\infty }{\frac{{{\left( -1 \right) }^{n}}}{\left( 2n+1 \right) !}{{\left( {{r}^{2}}{{\kappa }^{2}} \right) }^{n}}}, \end{aligned}$$

(4.2)

(1.1) becomes

$$\begin{aligned} {\mathcal {B}_n}=4\pi S\left( {{I}_{0}}-\sum \limits _{n=1}^{\infty }{\frac{{{\left( -1 \right) }^{n-1}}{{r}^{2n}}}{\left( 2n+1 \right) !}{{I}_{n}}} \right) , \end{aligned}$$

(4.3)

where

$$\begin{aligned} {{I}_{0}}=\frac{1}{\kappa _{0}^{{}^{11}/{}_{3}}}\int _{0}^{\infty }{\frac{{{\kappa }^{2}}{{e}^{-{}^{{{\kappa }^{2}}}/{}_{\kappa _{l}^{2}}}}}{{{\left( 1+c{{\kappa }^{2}} \right) }^{{}^{11}/{}_{6}}}}\mathrm{d}\kappa }, \end{aligned}$$

(4.4)

and

$$\begin{aligned} {{I}_{n}}=\int _{0}^{\infty }{\frac{{{\kappa }^{2n+2}}{{e}^{-{}^{{{\kappa }^{2}}}/{}_{\kappa _{l}^{2}}}}}{{{\left( {{\kappa }^{2}}+\kappa _{0}^{2} \right) }^{{}^{11}/{}_{6}}}}\mathrm{d}\kappa }, \end{aligned}$$

(4.5)

with $c=\frac{1}{\kappa _{0}^{2}}$.

With the help of (2.1), we find that ${{I}_{0}}$ and ${{I}_{n}}$ can be expressed as

$$\begin{aligned} {{I}_{0}}=\frac{\Gamma \left( {}^{3}/{}_{2} \right) }{2\kappa _{0}^\frac{2}{3}}U\left( \frac{3}{2};\frac{2}{3};\frac{\kappa _{0}^{2}}{\kappa _{l}^{2}} \right) , \end{aligned}$$

(4.6)

and

$$\begin{aligned} {{I}_{n}}=\frac{\Gamma \left( n+{}^{3}/{}_{2} \right) }{2\kappa _{0}^\frac{2}{3}}{{\left( {{\kappa }_{0}} \right) }^{2n}}U\left( n+\frac{3}{2};n+\frac{2}{3};\frac{\kappa _{0}^{2}}{\kappa _{l}^{2}} \right) . \end{aligned}$$

(4.7)

Consequently, (4.3) can be written as

$$\begin{aligned} {\mathcal {B}_n}=\frac{2\pi S}{\kappa _{0}^\frac{2}{3}}\left( \frac{\sqrt{\pi }}{2}U\left( \frac{3}{2};\frac{2}{3};\frac{\kappa _{0}^{2}}{\kappa _{l}^{2}} \right) +\mathcal {S} \right) , \end{aligned}$$

(4.8)

where

$$\begin{aligned} \mathcal {S} =\sum \limits _{n=1}^{\infty }{\frac{{{\left( -{{r}^{2}}\kappa _{0}^{2} \right) }^{n}}}{\left( 2n+1 \right) !}\Gamma \left( n+\frac{3}{2} \right) U\left( n+\frac{3}{2};n+\frac{2}{3};\frac{\kappa _{0}^{2}}{\kappa _{l}^{2}} \right) }. \end{aligned}$$

(4.9)

The identities

$$\begin{aligned} \Gamma \left( n+\frac{3}{2} \right) =\frac{\sqrt{\pi }}{2}{{\left( \frac{3}{2} \right) }_{n}}, \end{aligned}$$

(4.10)

and

$$\begin{aligned} \left( 2n+1 \right) !={{4}^{n}}n!{{\left( \frac{3}{2} \right) }_{n}}, \end{aligned}$$

(4.11)

yield the expression of ${\mathcal {B}_n}$

$$\begin{aligned} {\mathcal {B}_n}=\frac{{{\pi }^{{}^{3}/{}_{2}}}}{\kappa _{0}^{{}^{2}/{}_{3}}}S\sum _{n=0}^{\infty }{\frac{{{\left( -\kappa _{0}^{2}{{{r}^{2}}}{}/{}_{4} \right) }^{n}}}{n!}U\left( n+\frac{3}{2};n+\frac{2}{3};\frac{\kappa _{0}^{2}}{\kappa _{l}^{2}} \right) }, \end{aligned}$$

(4.12)

which, with the help of (2.25), can be rewritten as

$$\begin{aligned} {\mathcal {B}_n}=0.033{{\pi }^{{}^{3}/{}_{2}}}C_{n}^{2}\frac{\kappa _{l}^{3}}{\kappa _{0}^{{}^{11}/{}_{3}}}{{\Psi }_{1}}\left[ \frac{3}{2},\frac{11}{6};-,\frac{3}{2};-\frac{\kappa _{l}^{2}{{r}^{2}}}{4},-\frac{\kappa _{l}^{2}}{\kappa _{0}^{2}} \right] . \end{aligned}$$

(4.13)

Using the Laguerre–Gauss quadrature method, the integral in (1.1) can be expressed

$$\begin{aligned} {\mathcal {B}_n=\frac{4\pi }{r}\sum \limits _{i=1}^{15}{{{w}_{i}}}\exp \left( {{\kappa }_{i}} \right) g\left( {{\kappa }_{i}} \right) ,} \end{aligned}$$

(4.14)

with ${{\kappa }_{i}}$, ${{w}_{i}}\exp \left( {{\kappa }_{i}} \right)$ are given in Table 2 and $g\left( {{\kappa }_{i}} \right) ={{\kappa }_{i}}{{\Phi }_{s}} \left( {{\kappa }_{i}} \right) \sin \left( r{{\kappa }_{i}} \right)$.

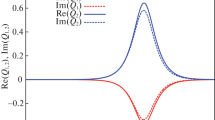
To show the equivalence between a closed-form in (4.13) and a numerical (4.14) solutions, we present in Fig. 1, the statistical autocorrelation function ${\mathcal {B}_n}$ for both equations. The calculation parameters are set to be ${{L}_{0}}=10$ mm, ${{l}_{0}}={{10}^{2}}$ mm and ${{K}_{0}}=\frac{1}{{{L}_{0}}}={{10}^{-1}}\,\,\mathrm{m}{\mathrm{m}^{-1}}.$ From this figure, we can conclude that there is an excellent agreement between our numerical and theoretical evaluations.

Fig. 1

Illustration of ${\mathcal {B}_n}$ as a function of $r.\kappa _{0}^{-1}$ evaluated from (4.13) and (4.14)

4.2 Evaluation of ${{\rho }_\mathrm{s}^{-2}}$ and T

Starting from (1.2) and (2.1), one finds easily

$$\begin{aligned} {{\rho }_{s}^{-2}}=0.0055{{\pi }^{2}}{{k}^{2}}zC_{n}^{2}\kappa _{0}^{{}^{1}/{}_{3}}U\left( 2;\frac{7}{6};\frac{\kappa _{0}^{2}}{\kappa _{l}^{2}} \right) , \end{aligned}$$

(4.15)

and

$$\begin{aligned} T=0.0165C_{n}^{2}\kappa _{0}^{{}^{1}/{}_{3}}U\left( 2;\frac{7}{6};\frac{\kappa _{0}^{2}}{\kappa _{l}^{2}} \right) . \end{aligned}$$

(4.16)

4.3 Evaluation of ${{\mu }_\mathrm{s}}$

With the help of (1.3) and (1.4), we can evaluate the following scattering coefficient

$$\begin{aligned} {{\mu }_{s}}=\frac{{4{{\pi }^{2}}{{k}^{4}}S}}{\kappa _{0}^{{}^{11}/{}_{3}}}\int _{-1}^{1}{\frac{\left( 1+{{x}^{2}} \right) {{e}^{-2{\varepsilon }\,{{k}^{2}}\left( 1-x \right) }}}{{{\left[ 1+2c{{k}^{2}}\left( 1-x \right) \right] }^{{}^{11}/{}_{6}}}}\mathrm{d}x}, \end{aligned}$$

(4.17)

which can be written as

$$\begin{aligned} \frac{{{\mu }_{s}\kappa _{0}^{{}^{11}/{}_{3}}}}{4{{\pi }^{2}}{{k}^{4}}S}=2{{I}_{1}}-2{{I}_{2}}+{{I}_{3}}, \end{aligned}$$

(4.18)

where

$$\begin{aligned} {{I}_{1}}= & {} \int _{0}^{2}{\frac{{{e}^{-2{\varepsilon }\,{{k}^{2}}t}}}{{{\left( 1+2c{{k}^{2}}t \right) }^{{}^{11}/{}_{6}}}}\mathrm{d}t}, \end{aligned}$$

(4.19)

$$\begin{aligned} {{I}_{2}}= & {} \int _{0}^{2}{\frac{t{{e}^{-2{\varepsilon } \,{{k}^{2}}t}}}{{{\left( 1+2c{{k}^{2}}t \right) }^{{}^{11}/{}_{6}}}}\mathrm{d}t}, \end{aligned}$$

(4.20)

and

$$\begin{aligned} {{I}_{3}}=\int _{0}^{2}{\frac{{{t}^{2}}{{e}^{-2{\varepsilon }\,{{k}^{2}}t}}}{{{\left( 1+2c{{k}^{2}}t \right) }^{{}^{11}/{}_{6}}}}\mathrm{d}t}. \end{aligned}$$

(4.21)

Using (2.3), one finds the final expression of the scattering coefficient

$$\begin{aligned} \begin{aligned} {{\mu }_{s}}=\frac{4{{\pi }^{2}}{{k}^{4}}S}{\kappa _{0}^\frac{11}{3}}&\left\{ 4{{\Phi }_{1}}\left[ 1,\frac{11}{6};2;-4{{k}^{2}}c,-4{{k}^{2}}{\varepsilon }\right] -4{{\Phi }_{1}}\left[ 2,\frac{11}{6};3;-4{{k}^{2}}c,-4{{k}^{2}}{\varepsilon }\right] \right. \\&\left. +\frac{8}{3}{{\Phi }_{1}}\left[ 3,\frac{11}{6};4;-4{{k}^{2}}c,-4{{k}^{2}}{\varepsilon }\right] \right\} . \\ \end{aligned} \end{aligned}$$

(4.22)

4.4 Evaluation of ${{\mu }_\mathrm{b}}$, g and $\mu _\mathrm{s}^{*}$

In this subsection, we derive closed-form expressions of the total scattered power per unit volume, the coefficient g and the reduced scattering coefficient. For the total scattered power, it is easy to find it, using (1.3) and (1.5). Its expression is as follows

$$\begin{aligned} {{\mu }_\mathrm{b}}=16{{\pi }^{2}}k^{4}\Phi \left( 2k \right) , \end{aligned}$$

(4.23)

which is evaluated for $\theta =\pi$.

The anisotropy factor g can by written as

$$\begin{aligned} g=\frac{N}{{{\mu }_\mathrm{s}}}, \end{aligned}$$

(4.24)

where

$$\begin{aligned} N=\frac{{4{{\pi }^{2}}{{k}^{4}}S}}{\kappa _{0}^{{}^{11}/{}_{3}}}({{\mu }_\mathrm{S}}-J), \end{aligned}$$

(4.25)

with

$$\begin{aligned} J=2{{I}_{2}}-2{{I}_{3}}+{{I}_{4}}, \end{aligned}$$

(4.26)

and

$$\begin{aligned} {{I}_{4}}=\int _{0}^{2}{\frac{{{t}^{3}}{{e}^{-2{\varepsilon }\,{{k}^{2}}t}}}{{{\left( 1+2c{{k}^{2}}t \right) }^{{}^{11}/{}_{6}}}}\mathrm{d}t}, \end{aligned}$$

(4.27)

and ${{I}_{2}}$ and ${{I}_{3}}$ are given by (4.20) and (4.21).

By the use of (2.3), the numerator of the coefficient g is expressed as

$$\begin{aligned}&N=\frac{4{{\pi }^{2}}{{k}^{4}}S}{\kappa _{0}^\frac{11}{3}}\left\{ {{\mu }_{s}}-4{{\Phi }_{1}}\left[ 2,\frac{11}{6};3;-4{{k}^{2}}c,-4{{k}^{2}}{\varepsilon }\right] +\frac{16}{3}{{\Phi }_{1}}\left[ 3,\frac{11}{6};4;-4{{k}^{2}}c,-4{{k}^{2}}{\varepsilon }\right] \right. \nonumber \\&\qquad \left. -4{{\Phi }_{1}}\left[ 4,\frac{11}{6};5;-4{{k}^{2}}c,-4{{k}^{2}}{\varepsilon }\right] \right\} . \end{aligned}$$

(4.28)

and with the help of (4.22) and (4.28), the reduced scattering coefficient can be derived from the following identity

$$\begin{aligned} \mu _\mathrm{s}^{*}={{\mu }_\mathrm{s}}-N. \end{aligned}$$

(4.29)

With the help of the Legendre–Gauss quadrature formula, the reduced scattering coefficient is written as follows

$$\begin{aligned} {\mu _{s}^{*}=\frac{4{{\pi }^{2}}{{k}^{4}}S}{\kappa _{0}^{{}^{11}/{}_{3}}}\sum \limits _{i=1}^{4}{{{w}_{i}}g\left( {{\kappa }_{i}} \right) },} \end{aligned}$$

(4.30)

with ${{\kappa }_{i}}$, ${{w}_{i}}$ are presented in Table 3 and $g\left( {{\kappa }_{i}} \right) =\left( 1-{{\kappa }_{i}} \right) \frac{{{e}^{-2{{k}^{2}}{\varepsilon }\left( 1-{{\kappa }_{i}} \right) }}}{{{\left[ 1+2{{k}^{2}}c\left( 1-{{\kappa }_{i}} \right) \right] }^{{}^{11}/{}_{3}}}}$.

Figure 2 gives the reduced scattering coefficient of the spatial power $\Phi _{s}(\kappa )$ vs. the wavelength $\lambda$ plotted by numerical and theoretical methods. The calculation parameters are the same of these taken in Fig. 1. Figure 2 shows good compatibility of the numerical solution obtained using Legendre–Gauss quadrature and the closed-form solution.

Fig. 2

Illustration of $\mu _\mathrm{s}^{*}$ as a function of $\lambda$ evaluated from (4.29) and (4.30)

4.5 Evaluation of ${{D}_\mathrm{pl}}$

The wave structure function can be written from (1.8) as

$$\begin{aligned} {{D}_\mathrm{pl}}\left( \rho ,L \right) =8{{\pi }^{2}}{{k}^{2}}L({{A}_{1}}-{{A}_{2}}), \end{aligned}$$

(4.31)

where

$$\begin{aligned} {{A}_{1}}=\int \limits _{0}^{\infty }{\kappa {{\Phi }_{s}}\left( \kappa \right) \mathrm{d}\kappa }, \end{aligned}$$

(4.32)

and

$$\begin{aligned} {{A}_{2}}=\int \limits _{0}^{\infty }{\kappa {{\Phi }_{s}}\left( \kappa \right) {{J}_{0}}\left( \rho \kappa \right) \mathrm{d}\kappa }. \end{aligned}$$

(4.33)

Using (2.10) and (2.13), (4.32) and (4.33) become

$$\begin{aligned} {{A}_{1}}=\frac{S}{2\kappa _{0}^{{}^{5}/{}_{3}} }U\left( 1;\frac{1}{6};\frac{{\varepsilon }}{c} \right) , \end{aligned}$$

(4.34)

and

$$\begin{aligned} {{A}_{2}}=\frac{S}{2{\varepsilon }\kappa _{0}^{{}^{11}/{}_{3}} }{{\psi }_{1}}\left[ 1,\frac{11}{6};-,1;-\frac{c}{{\varepsilon }},-\frac{{{\rho }^{2}}}{4{\varepsilon }} \right] . \end{aligned}$$

(4.35)

Finally, ${{D}_\mathrm{pl}}$ can be rewritten as

$$\begin{aligned} {{D}_\mathrm{pl}}\left( \rho ,L \right) =4{{\pi }^{2}}{{k}^{2}}LS\left\{ \frac{1}{\kappa _{0}^{{}^{5}/{}_{3}}}U\left( 1;\frac{11}{6};\frac{{\varepsilon }}{c} \right) -\frac{1}{{\varepsilon }\kappa _{0}^{{}^{11}/{}_{3}}}{{\psi }_{1}}\left[ 1,\frac{11}{6};-,1;-\frac{c}{{\varepsilon }},-\frac{{{\rho }^{2}}}{4{\varepsilon }} \right] \right\} .\nonumber \\ \end{aligned}$$

(4.36)

Based on the Laguerre–Gauss quadrature, the integral in (1.8) is written in the following form

$$\begin{aligned} {{{D}_\mathrm{pl}}\left( \rho ,L \right) =8{{\pi }^{2}}{{k}^{2}}L\sum \limits _{i=1}^{15}{{{w}_{i}}{{e}^{{{\kappa }_{i}}}}f\left( {{\kappa }_{i}} \right) },} \end{aligned}$$

(4.37)

with ${{w}_{i}}{{e}^{{{\kappa }_{i}}}}$, ${{\kappa }_{i}}$ are introduced in Table 2 and $f\left( {{\kappa }_{i}} \right) =\left( 1-{{J}_{0}}\left( \rho {{\kappa }_{i}} \right) \right) {{\kappa }_{i}}{{\Phi }_{s}}\left( {{\kappa }_{i}} \right)$.

The variation of the wave structure function as a function of $\rho$ is given in Fig. 3 for the following parameters $\lambda =0.6\,{\upmu }\mathrm{m}$, $C_{n}^{2}={{10}^{-6}}{{\left( \mu m \right) }^{-{}^{2}/{}_{3}}}$, $L=9{\upmu }\mathrm{m}$ and the other calculation parameters are the same of these taken in Fig. 2 see ( Saad and Belafhal 2017). From this figure, we observe clearly that our result obtained theoretically is identical with this obtained numerically.

Fig. 3

Illustration of $D_\mathrm{pl}$ as a function of $\rho$ evaluated from (4.36) and (4.37) with $\lambda =0.6 {\mu }\mathrm{m}$, $C_{n}^{2}={{10}^{-6}}{{\left( \upmu \mathrm{m} \right) }^{-{}^{2}/{}_{3}}}$ and $L=9{\upmu }\mathrm{m}$

Note that, in the above numerical simulations, the number of terms used in the sum of each special function is equal to one hundred iterations.

5 Conclusion

Several theorems, corollaries and new closed-form expressions are derived in this paper that is useful for evaluating infinite and definite integrals representations involving some special functions. These results are interesting for the characterization of the turbulent medium in general and of the biological tissue in particular. As applications, the developed transformations give an adequate tool to derive the scattering quantities as the autocorrelation function ${\mathcal {B}_\mathrm{n}}$, scattering coefficient ${{\mu }_\mathrm{s}}$, backscattering coefficient ${{\mu }_\mathrm{b}}$, anisotropy factor g, reduced scattering coefficient $\mu _\mathrm{s}^{*}$ and wave structure function ${{D}_\mathrm{pl}}$. The closed-form of these parameters has not yet been fully studied. To compare our theoretical and numerical results for these scattering quantities, some numerical simulations have been done. The obtained results show that there is an excellent agreement between the numerical solution obtained using Laguerre–Gauss quadrature, Legendre–Gauss quadrature and our theoretical results.

Appendix

In this appendix, we present the abscissas and weight factors for Laguerre and Legendre–Gauss quadrature (Ebrahim and Belafhal 2021).

Table 2 Table of abscissas and weight factors for Laguerre integration

Table 3 Table of abscissas and weight factors for Gaussian quadratures of high order