1 Introduction

Finding explicit solutions to nonlinear equations is one of the main pillars of understanding the dynamics of many physical applications and complex processes in chemistry, biology, geophysics, fluids, and nonlinear optical fibers. Over the past years, many effective schemes were used to solve nonlinear equations such as the tanh-method, sine-cosine function method (Wazwaz 2007; Alquran and Al-Khaled 2011; Alquran 2012), exp-function method (He and Wu 2006; Jaradat and Alquran 2022; Inan et al. 2022), mapping method El-Wakil and Abdou (2006), direct method Ma and Chen (2009), polynomial method (Huang 2006; Alquran et al. 2021, 2022), Kudryashov-expansion (Jaradat et al. 2021; Jaradat and Alquran 2020; Alquran 2021), Riccati-expansion Conte and Musette (1992), modified rational sine-cosine and sinh-cosh method (Ali et al. 2022; Alquran and Alhami 2022; Alquran 2021; Alquran and Alqawaqneh 2022), and many others (Akinyemi et al. 2022, 2022; Arnous et al. 2022; Sulaiman 2020; Baskonus et al. 2017; Alquran 2022).

Recently, W.X. Ma and other scholars implemented the Hirota bilinear form and Cole-Hopf transformation of the form \(u=\alpha (\ln {\phi })_x\) and \(u=\beta (\ln {\phi })_{xx}\) to extract new types of singular solutions known as lumps and breather waves (Ma 2015, 2013; Ma et al. 2016; Ma 2013; Ma et al. 2009). For example, if the test function \(\phi \) is a quadratic polynomial, the resulting solution is of type lump-soliton. While as, a linear combination of quadratic polynomial with the sine or cosine function will produce lump-periodic. Moreover, linear combinations of the sine or cosine with exponential function, trigonometric with hyperbolic functions, and combined exponential-trigonometric-hyperbolic functions, will produce different types of breather waves (Sulaiman et al. 2021, 2021; Alquran and Alhami 2022a, b; Feng and Bilige 2021; Sulaiman et al. 2021; Kumar et al. 2022).

In this work, we present for the first time a modified version of the potential-KdV under the name stochastic potential-KdV (spKdV) which takes the following form:

$$\begin{aligned} \psi _t +\alpha \psi _x +\beta \left( \psi _x\right) ^2 +\gamma \psi _{xxx}=0, \end{aligned}$$
(1.1)

where \(\alpha \) is the stochastic parameter, \(\beta \) is the nonlinearity coefficient, and \(\gamma \) refers to the dispersion coefficient. In the absence of the stochastic term, \(\alpha =0\), the above equation is known as the potential-KdV and generally seen during the study of water waves. The spKdV serves as an approximate model for the description of week dispersive effects on the propagation of nonlinear optical-soliton and photons, and appears in the applications of electric-circuits and multi-component plasmas.

The contribution of the current paper is threefold. First, we derive the Hirota bilinear form of the new proposed model. Then, we construct multi-waves, lump-type. and breather-type solutions upon different selections of the Cole-Hopf test-function. Finally, we study the impact of the model’s coefficients acting on the propagation of the obtained solutions.

2 Cole-Hopf transformation

To find a suitable Cole-Hopf transformation to (1.1), we apply the bilinear method which requires that the function

$$\begin{aligned} g(x,t)=e^{a x-b t}, \end{aligned}$$
(2.1)

satisfies the linear terms of (1.1). As a result, we get the dispersion relation:

$$\begin{aligned} b=a \alpha + a^3 \gamma . \end{aligned}$$
(2.2)

Then, we assume the solution of (1.1) in the following form

$$\begin{aligned} G(x,t)=R \left( \ln (1+A\ e^{a x-(a \alpha + a^3 \gamma ) t})\right) _{x}. \end{aligned}$$
(2.3)

Substitute (2.3) in (1.1) to obtain

$$\begin{aligned} R=\frac{6\gamma }{\beta }. \end{aligned}$$
(2.4)

Finally, we assign the following Cole-Hopf transformation

$$\begin{aligned} \psi (x,t)=\frac{6\gamma }{\beta } \left( \ln (f(x,t))\right) _x, \end{aligned}$$
(2.5)

where f(x, t) is known as the test function.

3 One-soliton and two-soliton solutions

To extract one-soliton and two-soliton solutions to (1.1), we consider the following steps:

  • Generalize the dispersion relation (2.2) into

    $$\begin{aligned} b_i= a_i \alpha + a_i^3 \gamma . \end{aligned}$$
    (3.1)

  • Choose the function f(x, t) as

    $$\begin{aligned} f(x,t)=1+e^{a_1 x-\left( a_1 \alpha + a_1^3 \gamma \right) t}. \end{aligned}$$
    (3.2)

  • Substitute (2.5) and (3.2) in (1.1) to get the one-soliton solution labeled as \(\psi _1\)

    $$\begin{aligned} \psi _1(x,t)=\frac{6\gamma a_1 e^{a_1 x}}{\beta (e^{a_1\left( \alpha + a_1^2 \gamma \right) t}+e^{a_1 x})}. \end{aligned}$$
    (3.3)

  • Consider the following two dispersion relations:

    $$\begin{aligned} b_1= & {} a_1 \alpha +c a_1^3 \gamma , \nonumber \\ b_2= & {} a_2 \alpha +c a_2^3 \gamma . \end{aligned}$$
    (3.4)

  • Consider the new form of f(x, t),

    $$\begin{aligned} f(x,t)=1+e^{a_1 x-b_1 t}+e^{a_2 x-b_2 t}+\frac{(a_1-a_2)^2}{(a_1+a_2)^2}\ e^{(a_1 x-b_1 t)+(a_2 x-b_2 t)}. \end{aligned}$$
    (3.5)

  • Substitute (2.5) and (3.5) in (1.1) to get the two-soliton solution labeled as \(\psi _2\)

    $$\begin{aligned} \psi _2(x,t)=\frac{6\gamma \left( a_1 e^{a_1 \delta _1}+a_2 e^{a_2 \delta _2}+\frac{(a_1-a_2)^2}{a_1+a_2}\ e^{(a_1+a_2)\theta }\right) }{\beta \left( 1+e^{a_1 \delta _1}+e^{a_2 \delta _2}+\frac{(a_1-a_2)^2}{(a_1+a_2)^2}\ e^{(a_1+a_2)\theta }\right) }, \end{aligned}$$
    (3.6)

    where \(\delta _i=-\alpha t+x-\gamma a_i^2 t\) and \(\theta =\delta _1+\gamma a_1 a_2 t-\gamma a_2^2 t\).

4 Hirota bilinear equation

In this section, we construct the Hirota bilinear form to the proposed spKdV (1.1). First, we recall the definition of the Hirota operator D

$$\begin{aligned} D_x^{i}D_t^{j}p.q=\left(\frac{\partial }{\partial x}-\frac{\partial }{\partial x^{*}}\right)^i \left(\frac{\partial }{\partial t}-\frac{\partial }{\partial t^{*}}\right)^j p(x,t)q(x^{*},t^{*})|_{x^{*}=x,t^{*}=t}, \end{aligned}$$
(4.1)

where \(p,\ q \in {\textbf {C}}^{\infty }({\mathbb {R}}^{2})\). Next, we consider the following assumption

$$\begin{aligned} \psi (x,t)=v_x(x,t). \end{aligned}$$
(4.2)

Insert (4.2) in (1.1) to get

$$\begin{aligned} v_{xt}+\alpha v_{xx}+\beta v_{xx}^2+\gamma v_{xxxx}=0. \end{aligned}$$
(4.3)

Then, the function v(x, t) is to be assumed as

$$\begin{aligned} v(x,t)= \frac{6\gamma }{\beta } \ln (\phi (x,t)). \end{aligned}$$
(4.4)

Substitution of (4.4) in (4.3), produces the Hirota’s form to spKdV as

$$\begin{aligned} -\phi _t \phi _x+\phi \phi _{xt}- \alpha \phi _x^2+ \alpha \phi \phi _{xx}+3\gamma \phi _{xx}^2-4\gamma \phi _x \phi _{xxx}+\gamma \phi \phi _{xxxx}=0, \end{aligned}$$
(4.5)

which is equivalent to

$$\begin{aligned} \left( D_x D_t+\alpha D_x ^2+\gamma D_x ^4\right) \phi \cdot \phi =0. \end{aligned}$$
(4.6)

5 Lump solutions

The aim of this section is to derive two types of lump solutions to the spKdV.

5.1 Lump-soliton

To obtain lump-soliton, we choose the test-function \(\phi (x,t)\) to be a quadratic polynomial as:

$$\begin{aligned} \phi (x,t)=\phi _1(x,t)=X^T A X+\sigma , \end{aligned}$$
(5.1)

where

$$\begin{aligned} A= \begin{bmatrix} a_{1,1} &{} a_{1,2} &{} a_{1,3} \\ a_{2,1} &{} a_{2,2} &{} a_{2,3} \\ a_{3,1} &{} a_{3,2} &{} a_{3,3} \\ \end{bmatrix}, \quad X=\begin{bmatrix} 1 \\ x \\ t \\ \end{bmatrix}. \end{aligned}$$
(5.2)

The parameters \(a_{i,j},\ (i,j=1,2,3)\) and \(\sigma \) are real constants to be determined. Substitute (5.1) in (4.5), equate the coefficients of different polynomials of x, t to zero, then solve the resulting system to get two solution’s sets:

Set I:

$$\begin{aligned} a_{2,2}= & {} 0,\\ a_{3,3}= & {} -\alpha \left( a_{2,3}+a_{3,2}\right) ,\\ \sigma= & {} \frac{\alpha a_{1,2}^2+a_{1,2} \left( 2 \alpha a_{2,1}+a_{1,3}+a_{3,1}\right) +\alpha a_{2,1}^2+a_{1,3} a_{2,1}-a_{1,1} a_{2,3}+a_{2,1} a_{3,1}-a_{1,1} a_{3,2}}{a_{2,3}+a_{3,2}}. \end{aligned}$$

Thus,

$$\begin{aligned} \phi _1(x,t)=\frac{\left( t \left( a_{2,3}+a_{3,2}\right) +a_{1,2}+a_{2,1}\right) \left( \alpha a_{1,2}+\alpha a_{2,1}-\alpha t a_{2,3}-\alpha t a_{3,2}+x a_{2,3}+x a_{3,2}+a_{1,3}+a_{3,1}\right) }{a_{2,3}+a_{3,2}}. \end{aligned}$$
(5.3)

Accordingly, the first lump-soliton solution labeled as \(\psi _{L_1}\) is

$$\begin{aligned} \psi _{L_1}(x,t)=\frac{6 \gamma \left( a_{2,3}+a_{3,2}\right) }{\beta \left( \alpha a_{1,2}+\alpha a_{2,1}-\alpha t a_{2,3}-\alpha t a_{3,2}+x a_{2,3}+x a_{3,2}+a_{1,3}+a_{3,1}\right) }. \end{aligned}$$
(5.4)

Set II:

$$\begin{aligned} a_{2,1}= & {} -\alpha (a_{1,2}+a_{2,1})-a_{1,3},\\ a_{3,2}= & {} -a_{2,3},\\ a_{2,2}= & {} a_{3,3}=0. \end{aligned}$$

Therefore,

$$\begin{aligned} \phi _1(x,t)=\sigma +a_{1,1}+(x-\alpha t)(a_{1,2}+a_{2,1}), \end{aligned}$$
(5.5)

and the second lump-soliton solution labeled as \(\psi _{L_2}\) is

$$\begin{aligned} \psi _{L_2}(x,t)=\frac{6 \gamma (a_{1,2}+a_{2,1})}{\beta (\sigma +a_{1,1}+(x-\alpha t)(a_{1,2}+a_{2,1}))}. \end{aligned}$$
(5.6)

5.2 Lump-periodic

Linear combination of quadratic and trigonometric functions produces lump-periodic solution. Therefore, the test function is to be chosen as:

$$\begin{aligned} \phi (x,t)=\phi _2(x,t)=\omega \sin (x p_1+t p_2+p_3)+Y^T A X+\sigma , \end{aligned}$$
(5.7)

where \(\quad Y=\begin{bmatrix} 1 \\ t \\ x \\ \end{bmatrix}\). Now, insert (5.7) in (4.5) leads to:

Set I:

$$\begin{aligned} a_{1,3}= & {} -\alpha a_{1,2}+3\gamma p_1^2 a_{1,2}-a_{2,1}-\alpha a_{3,1}+3\gamma p_1^2 a_{3,1},\nonumber \\ \omega= & {} \mp \frac{a_{1,2}+a_{3,1}}{p_1},\nonumber \\ p_2= & {} -\alpha p_1+\gamma p_1^3,\nonumber \\ a_{3,3}= & {} -a_{2,2},\nonumber \\ a_{2,3}= & {} a_{3,2}=0. \end{aligned}$$
(5.8)

Let \(\triangle =p_1(x-\alpha t )+\gamma p_1^3 t+p_3\), then

$$\begin{aligned} \phi _2(x,t)=\sigma +a_{1,1} \mp \frac{(\sin (\triangle ) \pm p_1(\alpha t -x) \mp 3\gamma p_1^3 t)(a_{1,2}+a_{3,1})}{p_1}, \end{aligned}$$
(5.9)

and the first lump-periodic solution labeled as \(\psi _{L_3}\) is

$$\begin{aligned} \psi _{L_3}(x,t)=-\frac{6\gamma (\pm 1+\cos (\triangle ))p_1 (a_{1,2}+a_{3,1})}{\beta (\sin (\triangle )(a_{1,2}+a_{3,1}) \mp p_1(\sigma +a_{1,1}-(\alpha t -x-3\gamma t p_1^2)(a_{1,2}+a_{3,1})))}. \end{aligned}$$
(5.10)

Set II:

$$\begin{aligned} p_2= & {} -\alpha p_1+4\gamma p_1^3,\\ a_{1,2}= & {} -a_{3,1},\\ a_{1,3}= & {} -a_{2,1},\\ a_{3,3}= & {} -a_{2,2},\\ \sigma= & {} -a_{1,1},\\ a_{2,3}= & {} a_{3,2}=0. \end{aligned}$$

Accordingly, the test function \(\phi _2\) is of the form

$$\begin{aligned} \phi _2(x,t)=\omega \sin ((x-\alpha t)p_1+4\gamma p_1^3 t+p_3). \end{aligned}$$
(5.11)

Thus, the second lump-periodic solution labeled as \(\psi _{L_4}\) is

$$\begin{aligned} \psi _{L_4}(x,t)=-\frac{6\gamma p_1 \cot ((x-\alpha t)p_1+4\gamma p_1^3 t+p_3)}{\beta }. \end{aligned}$$
(5.12)

6 Breather wave solutions

Different types of breather wave solutions can be constructed based on the selection of the test function \(\phi (x,t)\). Here, we derive three types of breather solutions.

6.1 Type-1

This type is constructed by a linear combination of cosine and exponential functions defined as:

$$\begin{aligned} \phi (x,t)=\phi _3(x,t)=\mu _1 \cos {(k_2(b_2 t+x))}+\mu _2 e^{k_1(b_1 t+x)}+ e^{-k_1(b_1 t+x)}. \end{aligned}$$
(6.1)

Substitute (6.1) in (4.5) to get

$$\begin{aligned} b_1= & {} -\alpha -\gamma k_1^2+3\gamma k_2^2,\nonumber \\ b_2= & {} -\alpha -3\gamma k_1^2+\gamma k_2^2,\nonumber \\ \mu _2= & {} -\frac{k_2^2 \mu _1^2}{4 k_1^2}. \end{aligned}$$
(6.2)

As a result, the breather type-1 solution is

$$\begin{aligned} \psi (x,t)=\psi _{B_1}(x,t)=-\frac{6\gamma k_1(4k_1^2+4k_1 k_2 \mu _1 e^{T}\sin (P)+k_2^2 \mu _1^2 e^{2T})}{\beta (-k_2^2 \mu _1^2 e^{2T}+4k_1^2(1+\mu _1 e^{T}\cos {(P)}))}, \end{aligned}$$
(6.3)

where \(T=k_1(x-(\alpha +\gamma k_1^2-3\gamma k_2^2)t)\) and \(P=k_2(x-(\alpha +3\gamma k_1^2-\gamma k_2^2)t)\).

6.2 Type-2

This type is a linear combination of trigonometric and hyperbolic functions, i.e.,

$$\begin{aligned} \phi (x,t)=\phi _4(x,t)=\cosh {(k_1 x+k_2 t+k_3)}+\mu _1 \cos {(l_1 x+l_2 t+l_3)}+\mu _2 \sinh {(k_1 x+k_2 t+k_3)}. \end{aligned}$$
(6.4)

Substitution of (6.4) in (4.5) produces the following outputs:

$$\begin{aligned} k_2= & {} -\alpha k_1-\gamma k_1^3+3\gamma k_1 l_1^2,\nonumber \\ l_2= & {} -\alpha l_1-3\gamma k_1^2 l_1+\gamma l_1^3,\nonumber \\ \mu _2= & {} \mp \frac{\sqrt{k_1^2+l_1^2 \mu _1^2}}{k_1}. \end{aligned}$$
(6.5)

Thus, the breather type-2 solution is

$$\begin{aligned} \psi (x,t)=\psi _{B_2}(x,t)=\frac{6\gamma k_1(\pm k_1 \sinh {(Y)} \mp l_1 \mu _1 \sin {(Z)} +\sqrt{k_1^2+l_1^2 \mu _1^2} \cosh {(Y)})}{\pm b k_1(\cosh {(Y)}+\mu _1 \cos {(Z)})+b \sqrt{k_1^2+l_1^2 \mu _1^2} \sinh {(Y)}}, \end{aligned}$$
(6.6)

where \(Y= k_1 x+k_3-(\alpha k_1+\gamma k_1^3-3\gamma k_1 l_1^2)t\) and \(Z= l_1 x+l_3-(\alpha l_1+3\gamma k_1^2 l_1-\gamma l_1^3)t\).

6.3 Type-3

This type is a linear combination of three functions; exponential, trigonometric and hyperbolic, i.e.,

$$\begin{aligned} \phi (x,t)=\phi _5(x,t)=\kappa _1 e^{\varrho t+x}+\kappa _2 e^{-(\varrho t+x)}+\kappa _3 \sin {(\alpha _1 t+x)}+\kappa _4 \sinh {(\alpha _2 t+x)}. \end{aligned}$$
(6.7)

Substitution of (6.7) in (4.5) gives three cases.

Case I: \(\kappa _3=0\) and \(\varrho =\alpha _2=-(\alpha +4\gamma )\). Then,

$$\begin{aligned} \psi (x,t)=\psi _{B_3}=\frac{-6\gamma (2\kappa _2-\kappa _4)e^{2(\alpha +4\gamma )t}+6\gamma (2\kappa _1+\kappa _4)e^{2x}}{\beta (2\kappa _2-\kappa _4)e^{2(\alpha +4\gamma )t}+\beta (2\kappa _1+\kappa _4)e^{2x}} \end{aligned}$$
(6.8)

Case II: \(\kappa _2=-\frac{\kappa _4^2}{4\kappa _1},\kappa _3=0,\alpha _2=-2\alpha -8\gamma -\varrho \). Then,

$$\begin{aligned} \psi (x,t)=\psi _{B_4}(x,t)=\frac{6\gamma }{\beta }\left( \frac{4\kappa _1}{2\kappa _1-\kappa _4 e^{2(\alpha +4\gamma ) t-2x}}-1\right) \end{aligned}$$
(6.9)

Case III: \(\kappa _2=-\frac{\kappa _3^2}{4\kappa _1},\kappa _4=0,\varrho =-(\alpha -2\gamma )\) and \(\alpha _1=-(\alpha +2\gamma )\). Then,

$$\begin{aligned} \psi (x,t)=\psi _{B_5}(x,t)=\frac{6\gamma (4\kappa _1^2 e^{4\gamma t+2x}+4\kappa _1 \kappa _3 e^{\alpha t+2\gamma t+x}\cos {((\alpha +2\gamma )t-x)}+\kappa _3^2 e^{2\alpha t})}{\beta (4\kappa _1^2 e^{4\gamma t+2x}+4\kappa _1 \kappa _3 e^{\alpha t+2\gamma t+x}\sin {(x-(\alpha +2\gamma )t)}-\kappa _3^2 e^{2\alpha t})}. \end{aligned}$$
(6.10)

7 Graphical analysis

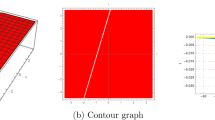
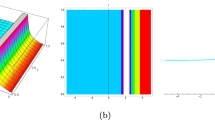
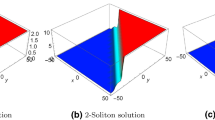
The aim of this section is twofold. First, we plot the obtained solutions to recognize the physical structures of (1.1). Second, we study the impact of the stochastic, nonlinearity, and dispersion parameters, \(\alpha \), \(\beta \), \(\gamma \), being acting on the propagation of the stochastic potential-KdV. Figure 1, shows the one- and the two-soliton solutions. Figure 2, shows the lump-soliton and the lump-periodic. Figure 3, shows three different types of breather waves.

To investigate the impact of the aforementioned parameters on the propagation of (1.1), we study the solution-function \(\psi _{B_5}(x,t)\), see Fig. 4, where we observe the following physical properties:

  • The propagation is transitive when \(\alpha \) changes its sign.

  • The propagation has a reflexive relation when \(\beta \) changes its sign.

  • The propagation is symmetric due to the sign of \(\gamma \).

Fig. 1
figure 1

One-soliton solution as depicted in \(\psi _1(x,t)\), and two-soliton solution as depicted in \(\psi _2(x,t)\)

Full size image
Fig. 2
figure 2

Different types of lumps as depicted in \(\psi _{L_2}(x,t)\), \(\psi _{L_3}(x,t)\), and \(\psi _{L_4}(x,t)\)

Full size image
Fig. 3
figure 3

Different types of breather waves as depicted in \(\psi _{B_1}(x,t)\), \(\psi _{B_2}(x,t)\), \(\psi _{B_3}(x,t)\), and \(\psi _{B_4}(x,t)\)

Full size image
Fig. 4
figure 4

Propagations of \(\psi _{B_5}(x,t)\) for different values of: a The stochastic parameter \(\alpha \). b The nonlinearity parameter \(\beta \). c The dispersion parameter \(\gamma \)

Full size image

8 Conclusion

This work included the study of a new extension of the potential KdV model by adding a new stochastic term \(\alpha \psi _x(x,t)\). The new model describes the propagation of nonlinear optical solitons and photons and appears in the applications of electric-circuits and multi-component plasmas. Several solutions of types multi-waves, lumps, and breathers are generated to the proposed model by means of Cole-Hopf transformation and Hirota bilinear method. Also, we performed a graphical analysis to study the impacts of the model’s parameters acting on the propagations of the recovery solutions.

For future work, we aim to extract lumps, breathers, and rogue-wave solutions to nonlinear models involving complex-valued field-functions. Moreover, we may study systems of nonlinear equations and investigate the possibility of having such types of solutions similar to those reported in this work.