1 Introduction

Nonlinear phenomena play a significant role in applied mathematics and physics. Exact and numerical solutions of nonlinear equations in mathematical physics, especially the computation of traveling wave solutions, have an important role in soliton theory. Recently, it has become more motivating to provide exact solutions for nonlinear partial differential equations using symbolic computer programs such as Maple, Matlab, Mathematica, which facilitate complex algebraic calculations. Finding exact solutions of nonlinear partial differential equations is of crucial importance. These equations are mathematical models of complex physical phenomena that occur in several disciplines such as engineering, chemistry, biology, mechanics, and physics. A number of effective methods have been developed to understand the mechanisms of these physical models to assist medical practitioners and engineers, and to have knowledge about physical problems and their applications.

Traveling wave solutions is a special category of analytical solutions for nonlinear evolution equations (NLEEs). Solitary waves, are localized traveling waves. In 1965, Zabusky and Kruskal invented the soliton. It seems to be a specific form of the solitary wave which proliferates at the constant shape, speed, and intensity and arises in the solution of a variety of nonlinear evolution equations. It has some intriguing characteristics, and it describes a slew of significant applied phenomena that we are already familiar with (Cariello and Tabor 1989; Fan 2000a; Clarkson 1989). As a consequence, studying exact traveling wave solutions for NLFPDEs is important.

Several analytical methods have been found in literature (Shang 2007; Bock and Kruskal 1979; Matveev and Salle 1991; Abourabia and Horbaty 2006; Malfliet 1992; Chuntao 1996; Cariello and Tabor 1989; Fan 2000a; Clarkson 1989). Besides these methods, there are many methods which reach to solution by using an auxiliary equation. These methods are given in Malfliet (1992); Fan 2000b; Elwakil et al. 2002; Chen and Zhang 2004; Fu et al. 2001; Shen and Pan 2003; Chen and Hong-Qing 2004; Chen et al. 2004; Chen and Yan 2006; Wang et al. 2008; Guo and Zhou 2010; Lü et al. 2010; Li et al. 2010; Manafian 2016; Khater 2015). Many researchers have applied such methods to various equations (Khater and Zahran 2016a, 2016b; Wazwaz and Mehanna 2021; Wu and Li 2020; Kumar et al. 2020, in press; Hendi et al. 2021; Ouahid et al. 2021; Kumar and Mohan 2021; Kumar and Rani 2021).

We used the extended \(exp\left(-\varphi \left(\upxi \right)\right)\)-expansion method for finding some exact solutions of (3 + 1)-dimensional and coupled NLSEs. This method is developed by Khater and Zahran (2016b).

2 Analysis of method

Before the application, a brief information about the method to be used is necessary. Let’s express a nonlinear partial differential equation with two variables as follows:

$$ Q\left( {u,u_{x} ,u_{t} ,u_{xx} \ldots } \right) = 0, $$
(1)

When we apply the transformation \(u\left(x,t\right)=u\left(\upxi \right),\upxi =x-kt\) this equation, Eq. (1) turns into the following ordinary differential equation:

$$ Q^{\prime}\left( {u^{\prime},\;u^{\prime\prime},\;u^{\prime\prime\prime}, \ldots } \right) = 0, $$
(2)

Here \(k\) is a constant. Let’s consider the solution function of Eq. (2) as:

$$ u\left( {\upxi } \right) = \mathop \sum \limits_{i = - m}^{m} a_{i} \left( {exp\left( { - \varphi { }\left( {\upxi } \right)} \right)} \right)^{i} $$
(3)

In the solution function, \(m\) is a positive integer. It is calculated by balancing the highest order linear term with the highest order nonlinear term in Eq. (2).

In addition, \({a}_{i},s\) are constants.If the solution function given in (3) is substituted in Eq. (2), an algebraic system of equations is obtained for \({a}_{i}\) s and \(k\). Then, when the system is solved by equating the coefficients of \(exp\left(\pm \varphi \left(\upxi \right)\right)\) having the same power values in this system to zero, the constants \(k\) and \({a}_{i}\) are calculated. \(\varphi =\varphi \left(\upxi \right)\) in the solution function (3) provides the following first-order ordinary differential equation (ODE):

$$ \varphi^{\prime}\left( {\upxi } \right) = exp\left( { - \varphi { }\left( {\upxi } \right)} \right) + \mu exp\left( {\varphi { }\left( {\upxi } \right)} \right) + {\lambda } $$
(4)

The solutions of this ODE are as follows:

When \({\uplambda }^{2}-4\mu >0, \mu \ne 0,\)

$$ \varphi \left( {\upxi } \right) = ln\left( {\frac{{ - \sqrt {\lambda^{2} - 4\mu } tanh\left( {\frac{{\sqrt {\lambda^{2} - 4\mu } }}{2}\left( {{\upxi } + C_{1} } \right)} \right) - \lambda }}{2\mu }} \right). $$

and

$$ \varphi \left( {\upxi } \right) = ln\left( {\frac{{ - \sqrt {\lambda^{2} - 4\mu } coth\left( {\frac{{\sqrt {\lambda^{2} - 4\mu } }}{2}\left( {{\upxi } + C_{1} } \right)} \right) - \lambda }}{2\mu }} \right). $$

When \({\uplambda }^{2}-4\mu >0, \quad \mu =0,\)

$$ \varphi \left( {\upxi } \right) = - ln\left( {\frac{\lambda }{{exp\left( {\lambda \left( {{\upxi } + C_{1} } \right)} \right) - 1}}} \right). $$

When \({\uplambda }^{2}-4\mu =0, \; \mu \ne 0,\lambda \ne 0,\)

$$ \varphi \left( {\upxi } \right) = ln\left( { - \frac{{2\left( {\lambda \left( {{\upxi } + C_{1} } \right) + 2} \right)}}{{\lambda^{2} \left( {{\upxi } + C_{1} } \right)}}} \right). $$

When \({\uplambda }^{2}-4\mu =0, \; \mu =0, \; \lambda =0,\)

$$ \varphi \left( {\upxi } \right) = ln\left( {{\upxi } + C_{1} } \right). $$

When \({\uplambda }^{2}-4\mu <0,\)

$$ \varphi \left( {\upxi } \right) = ln\left( {\frac{{\sqrt {4\mu - \lambda^{2} } tan\left( {\frac{{\sqrt {4\mu - \lambda^{2} } }}{2}\left( {{\upxi } + C_{1} } \right)} \right) - \lambda }}{2\mu }} \right). $$

and

$$ \varphi \left( {\upxi } \right) = ln\left( {\frac{{\sqrt {4\mu - \lambda^{2} } cot\left( {\frac{{\sqrt {4\mu - \lambda^{2} } }}{2}\left( {{\upxi } + C_{1} } \right)} \right) - \lambda }}{2\mu }} \right). $$

Example 1.

Let’s consider the (3 + 1)-dimensional NLSE (Wazwaz and Mehanna 2021),

$$ iu_{t} - u_{xx} - u_{yy} - u_{zz} + su\left| u \right|^{2} + d_{1} u_{xy} + d_{2} u_{yz} + d_{3} u_{zx} + i\left( {d_{4} u_{x} + d_{5} u_{y} + d_{6} u_{z} } \right) = 0,\quad \left( {i = \sqrt { - 1} } \right) $$
(5)

when the following transformation is applied to this equation, in which \(\upxi =\left(x+y+z+{h}_{5}t\right), \theta =\left({h}_{1}x+{h}_{2}y+{h}_{3}z+{h}_{4}t\right)\)

$$ u\left( {x,y,t} \right) = e^{i\left( \theta \right)} U\left( {\upxi } \right) $$
(6)

where the first term is the temporal evolution of the pulses, while t, x,y and z represent temporal and spatial variables respectively, and \({d}_{r},{h}_{k}, \; r=1,\dots ,6, \; k=1,\dots ,5\), \(s\) are constant parameters. \(U\left(\zeta \right)\) is a real function. We obtain the following ODE

$$ T_{1} U + sU^{3} + T_{2} U^{\prime\prime} = 0. $$
(7)

Here \({T}_{1}=\left(-{d}_{4}{h}_{1}+{h}_{1}^{2}-{d}_{5}{h}_{2}-{d}_{1}{h}_{1}{h}_{2}+{h}_{2}^{2}-{d}_{6}{h}_{3}-{d}_{3}{h}_{1}{h}_{3}-{d}_{2}{h}_{2}{h}_{3}+{h}_{3}^{2}-{h}_{4}, \right), \;{T}_{2}=\left({d}_{1}+{d}_{2}+{d}_{3}-3\right)\) and \({h}_{5}=\left(-{d}_{4}-{d}_{5}-{d}_{6}+2{h}_{1}-{d}_{1}{h}_{1}-{d}_{3}{h}_{1}+2{h}_{2}-{d}_{1}{h}_{2}-{d}_{2}{h}_{2}+2{h}_{3}-{d}_{2}{h}_{3}-{d}_{3}{h}_{3}\right)\). If \({U}^{^{\prime}{\prime}}\) and \({U}^{3}\) are balanced in Eq. (7), \(m=1\) is obtained. In this case, the solution function is as follows:

$$ U\left( {\upxi } \right) = a_{ - 1} exp\left( {{{\varphi }}\left( {\upxi } \right)} \right) + a_{0} + a_{1} exp\left( { - {{\varphi }}\left( {\upxi } \right)} \right) $$
(8)

In the solution expressed by (8) \({a}_{-1},\;{a}_{0},\;{a}_{1},\) are constants to be found and \({\alpha }_{-1}\) or \({a}_{1}\) are nonzero.

If Eq. (8) is substituted in Eq. (7), the following algebraic equation system is obtained:

$$ sa_{0}^{3} + 6sa_{ - 1} a_{0} a_{1} + a_{0} T_{1} + \lambda a_{ - 1} T_{2} + \lambda \mu a_{1} T_{2} = 0, $$
$$ 3sa_{ - 1} a_{0}^{2} + 3sa_{ - 1}^{2} a_{1} + a_{ - 1} T_{1} + \lambda^{2} a_{ - 1} T_{2} + 2\mu a_{ - 1} T_{2} = 0, $$
$$ 3sa_{ - 1}^{2} a_{0} + 3\lambda \mu a_{ - 1} T_{2} = 0, $$
$$ sa_{ - 1}^{3} + 2\mu^{2} a_{ - 1} T_{2} = 0, $$
$$ sa_{1}^{3} + 2a_{1} T_{2} = 0, $$
$$ 3sa_{0} a_{1}^{2} + 3\lambda a_{1} T_{2} = 0, $$
$$ 3sa_{0}^{2} a_{1} + 3sa_{ - 1} a_{1}^{2} + a_{1} T_{1} + \lambda^{2} a_{1} T_{2} + 2\mu a_{1} T_{2} = 0. $$

If this algebraic equations system is solved, we obtain the following coefficients.

Case 1:

$$ T_{2} \ne 0,\lambda = \pm \frac{{\sqrt 2 \sqrt {T_{1} + 2\mu T_{2} } }}{{\sqrt {T_{2} } }},a_{ - 1} = 0,s \ne 0,a_{0} = \pm \frac{{\sqrt { - T_{1} - 2\mu T_{2} } }}{\sqrt s },a_{0} \ne 0,a_{1} = - \frac{{\lambda T_{2} }}{{sa_{0} }} $$
(9)

Case 2:

$$ \mu T_{2} \ne 0,\lambda = \pm \frac{{\sqrt 2 \sqrt {T_{1} + 2\mu T_{2} } }}{{\sqrt {T_{2} } }},s \ne 0,a_{ - 1} = \pm \frac{{{\text{i}}\sqrt 2 \mu \sqrt {T_{2} } }}{\sqrt s },a_{ - 1} \ne 0,a_{0} = - \frac{{\lambda \mu T_{2} }}{{sa_{ - 1} }},a_{1} = 0 $$
(10)

Case 3:

$$ \mu = 0,T_{2} \ne 0,\lambda = \pm \frac{{\sqrt 2 \sqrt {T_{1} } }}{{\sqrt {T_{2} } }},a_{ - 1} = 0,s \ne 0,a_{0} = \pm \frac{{{\text{i}}\sqrt {T_{1} } }}{\sqrt s },\lambda \ne 0,a_{1} = \frac{{2a_{0} }}{\lambda } $$
(11)

Case 4:

$$ T_{2} \ne 0,\mu = \pm \frac{{T_{1} }}{{4T_{2} }},\lambda = 0,s \ne 0,a_{ - 1} = \pm \frac{{{\text{i}}\sqrt 2 \mu \sqrt {T_{2} } }}{\sqrt s },a_{0} = 0,a_{ - 1} \ne 0,a_{1} = \frac{{ - T_{1} - 2\mu T_{2} }}{{3sa_{ - 1} }} $$
(12)

Here, the coefficients found in (9)–(12) are also substituted in the solution of (8), then if the acquired solution (8) is also substituted in (6), the solutions of Eq. (5) will be as follows:

For Case 1

When \({\uplambda }^{2}-4\mu >0, \quad \mu \ne 0,\)

$$ u_{1} \left( {x,y,z,t} \right) = \left( {\frac{{ - T_{1} + 2\mu T_{2} \left( { - 1 + \frac{{\sqrt {T_{1} + 2\mu T_{2} } }}{{\sqrt {T_{1} + 2\mu T_{2} } + \sqrt {\frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } {\text{Tanh}}\left( {\frac{{\left( {\left( {x + y + z + h_{5} t} \right) + C_{1} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)}}} \right)}}{{\sqrt { - sT_{1} - 2s\mu T_{2} } }}} \right)e^{i\theta } $$
(13)
$$ u_{2} \left( {x,y,z,t} \right) = \left( {\frac{{2\mu T_{2} \left( { - 1 + \frac{{\sqrt {T_{1} + 2\mu T_{2} } }}{{{\text{Coth}}\left( {\frac{{\left( {\left( {x + y + z + h_{5} t} \right) + C_{1} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } + \sqrt {T_{1} + 2\mu T_{2} } }}} \right) - T_{1} }}{{\sqrt { - sT_{1} - 2s\mu T_{2} } }}} \right)e^{i\theta } $$
(14)

When \({\uplambda }^{2}-4\mu <0,\)

$$ u_{3} \left( {x,y,z,t} \right) = \left( {\frac{{ - T_{1} + 2\mu T_{2} \left( { - 1 + \frac{{\sqrt {T_{1} + 2\mu T_{2} } }}{{\sqrt {T_{1} + 2\mu T_{2} } - \sqrt { - \frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } {\text{Tan}}\left( {\frac{{\left( {\left( {x + y + z + h_{5} t} \right) + C_{1} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)}}} \right)}}{{\sqrt { - sT_{1} - 2s\mu T_{2} } }}} \right)e^{i\theta } $$
(15)
$$ u_{4} \left( {x,y,z,t} \right) = \left( {\frac{{2\mu T_{2} \left( { - 1 + \frac{{\sqrt {T_{1} + 2\mu T_{2} } }}{{ - {\text{Cot}}\left( {\frac{{\left( {\left( {x + y + z + h_{5} t} \right) + C_{1} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } + \sqrt {T_{1} + 2\mu T_{2} } }}} \right) - T_{1} }}{{\sqrt { - sT_{1} - 2s\mu T_{2} } }}} \right)e^{i\theta } $$
(16)

For Case 2

When \({\uplambda }^{2}-4\mu >0, \quad \mu \ne 0,\)

$$ u_{5} \left( {x,y,z,t} \right) = \left( {\frac{{{\text{i}}\sqrt {\frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } {\text{Tanh}}\left( {\frac{{\left( {\left( {x + y + z + h_{5} t} \right) + C_{1} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)}}{\sqrt s }} \right)e^{i\theta } $$
(17)
$$ u_{6} \left( {x,y,z,t} \right) = \left( {\frac{{{\text{iCoth}}\left( {\frac{{\left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } }}{\sqrt s }} \right)e^{i\theta } $$
(18)

When \({\uplambda }^{2}-4\mu <0,\)

$$ u_{7} \left( {x,y,z,t} \right) = \left( {\frac{{{\text{i}}\sqrt { - \frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } {\text{Tan}}\left( {\frac{{\left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)}}{\sqrt s }} \right)e^{i\theta } $$
(19)
$$ u_{8} \left( {x,y,z,t} \right) = \left( {\frac{{{\text{iCot}}\left( {\frac{{\left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} }}{\sqrt 2 }} \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } }}{\sqrt s }} \right)e^{i\theta } $$
(20)

For Case 3

When \({\uplambda }^{2}-4\mu >0, \quad \mu =0,\)

$$ u_{9} \left( {x,y,z,t} \right) = \left( {\frac{{{\text{i}}\left( {1 + \frac{2}{{ - 1 + {\text{e}}^{{\frac{{\sqrt 2 \left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt {T_{1} } }}{{\sqrt {T_{2} } }}}} }}} \right)\sqrt {T_{1} } }}{\sqrt s }} \right)e^{i\theta } $$
(21)

For Case 4

When \({\uplambda }^{2}-4\mu >0, \quad \mu \ne 0,\)

$$ u_{10} \left( {x,y,z,t} \right) = \left( {\frac{{{\text{i}}\sqrt 2 {\text{Csch}}\left( {\left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } }}{\sqrt s }} \right)e^{i\theta } $$
(22)
$$ u_{11} \left( {x,y,z,t} \right) = \left( { - \frac{{{\text{i}}\sqrt 2 {\text{Csch}}\left( {\left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} } \right)\sqrt { - \frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } }}{\sqrt s }} \right)e^{i\theta } $$
(23)

When \({\uplambda }^{2}-4\mu <0,\)

$$ u_{12} \left( {x,y,z,t} \right) = \left( {\frac{{{\text{i}}\sqrt 2 {\text{Csc}}\left( {\left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } }}{\sqrt s }} \right)e^{i\theta } $$
(24)
$$ u_{13} \left( {x,y,z,t} \right) = \left( { - \frac{{{\text{i}}\sqrt 2 {\text{Csc}}\left( {\left( {x + y + z + h_{5} t + C_{1} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} } \right)\sqrt {\frac{{T_{1} }}{{T_{2} }}} \sqrt {T_{2} } }}{\sqrt s }} \right)e^{i\theta } $$
(25)

In the above solutions, \(\theta =\left({h}_{1}x+{h}_{2}y+{h}_{3}z+{h}_{4}t\right), {T}_{1}=\left(-{d}_{4}{h}_{1}+{h}_{1}^{2}-{d}_{5}{h}_{2}-{d}_{1}{h}_{1}{h}_{2}+{h}_{2}^{2}-{d}_{6}{h}_{3}-{d}_{3}{h}_{1}{h}_{3}-{d}_{2}{h}_{2}{h}_{3}+{h}_{3}^{2}-{h}_{4}\right), \; {T}_{2}=\left({d}_{1}+{d}_{2}+{d}_{3}-3\right)\) and \({h}_{5}=\left(-{d}_{4}-{d}_{5}-{d}_{6}+2{h}_{1}-{d}_{1}{h}_{1}-{d}_{3}{h}_{1}+2{h}_{2}-{d}_{1}{h}_{2}-{d}_{2}{h}_{2}+2{h}_{3}-{d}_{2}{h}_{3}-{d}_{3}{h}_{3}\right)\) should be taken as.

Example 2.

We consider the coupled NLSE (Wu and Li 2020)

$$ \begin{gathered} iu_{t} + u_{xx} + 2u\left| u \right|^{2} + 2u\left| v \right|^{2} = 0, \hfill \\ iv_{t} + v_{xx} + 2v\left| u \right|^{2} + 2v\left| v \right|^{2} = 0. \left( {i = \sqrt { - 1} } \right) \hfill \\ \end{gathered} $$
(26)

when the following transformations are applied to this equations, in which \(\upxi =x+{h}_{3}t, \theta ={h}_{1}x+{h}_{2}t\)

$$ u(x,t) = e^{{i}{(\theta )}} U(\xi )\;{\text{and }}\;v(x,t) = e^{{i}{(\theta )}}V(\xi ) $$
(27)

we acquire the following ODE

$$ \begin{gathered} U^{\prime\prime} - MU + 2U^{3} + 2UV^{2} = 0, \hfill \\ V^{\prime\prime} - MV + 2VU^{2} + 2V^{3} = 0, \hfill \\ \end{gathered} $$
(28)

where \(M={h}_{1}^{2}+{h}_{2}, {h}_{3}=-2{h}_{1}.\) If \({U}{^{\prime\prime}}\) with \(U{V}^{2}\) and \({V}{^{\prime\prime}}\) with \(V{U}^{2}\) are balanced in Eq. (28), \({m}_{1}=1\) and \({m}_{2}=1\) are obtained. In this case, the solution functions are as follows:

$$ \begin{gathered} U\left( {\upxi } \right) = a_{ - 1} exp\left( {{{\varphi }}\left( {\upxi } \right)} \right) + a_{0} + a_{1} exp\left( { - {{\varphi }}\left( {\upxi } \right)} \right) \hfill \\ V\left( {\upxi } \right) = b_{ - 1} exp\left( {{{\varphi }}\left( {\upxi } \right)} \right) + b_{0} + b_{1} exp\left( { - {{\varphi }}\left( {\upxi } \right)} \right) \hfill \\ \end{gathered} $$
(29)

In the solution expressed by (29) \({a}_{-1},\;{a}_{0},\;{a}_{1},\;{b}_{-1},\;{b}_{0}\) are constants. If Eqs. (29) are substituted in Eq. (28), the following algebraic equation system is acquired:

$$ \begin{gathered} \lambda a_{ - 1} - Ma_{0} + 2a_{0}^{3} + \lambda \mu a_{1} + 12a_{ - 1} a_{0} a_{1} + 4a_{1} b_{ - 1} b_{0} + 2a_{0} b_{0}^{2} + 4a_{0} b_{ - 1} b_{1} + 4a_{ - 1} b_{0} b_{1} \hfill \\ = 0, 2\mu^{2} a_{ - 1} + 2a_{ - 1}^{3} + 2a_{ - 1} b_{ - 1}^{2} = 0, 3\lambda \mu a_{ - 1} + 6a_{ - 1}^{2} a_{0} + 2a_{0} b_{ - 1}^{2} + 4a_{ - 1} b_{ - 1} b_{0} \hfill \\ = 0, - Ma_{ - 1} + \lambda^{2} a_{ - 1} + 2\mu a_{ - 1} + 6a_{ - 1} a_{0}^{2} + 6a_{ - 1}^{2} a_{1} + 2a_{1} b_{ - 1}^{2} + 4a_{0} b_{ - 1} b_{0} + 2a_{ - 1} b_{0}^{2} \hfill \\ + 4a_{ - 1} b_{ - 1} b_{1} = 0, - Ma_{1} + \lambda^{2} a_{1} + 2\mu a_{1} + 6a_{0}^{2} a_{1} + 6a_{ - 1} a_{1}^{2} + 2a_{1} b_{0}^{2} + 4a_{1} b_{ - 1} b_{1} \hfill \\ + 4a_{0} b_{0} b_{1} + 2a_{ - 1} b_{1}^{2} = 0, 3\lambda a_{1} + 6a_{0} a_{1}^{2} + 4a_{1} b_{0} b_{1} + 2a_{0} b_{1}^{2} = 0, 2a_{1} + 2a_{1}^{3} + 2a_{1} b_{1}^{2} \hfill \\ = 0, \lambda b_{ - 1} + 4a_{0} a_{1} b_{ - 1} - Mb_{0} + 2a_{0}^{2} b_{0} + 4a_{ - 1} a_{1} b_{0} + 2b_{0}^{3} + \lambda \mu b_{1} + 4a_{ - 1} a_{0} b_{1} \hfill \\ + 12b_{ - 1} b_{0} b_{1} = 0, 2\mu^{2} b_{ - 1} + 2a_{ - 1}^{2} b_{ - 1} + 2b_{ - 1}^{3} = 0,3\lambda \mu b_{ - 1} + 4a_{ - 1} a_{0} b_{ - 1} + 2a_{ - 1}^{2} b_{0} \hfill \\ + 6b_{ - 1}^{2} b_{0} = 0, - Mb_{ - 1} + \lambda^{2} b_{ - 1} + 2\mu b_{ - 1} + 2a_{0}^{2} b_{ - 1} + 4a_{ - 1} a_{1} b_{ - 1} + 4a_{ - 1} a_{0} b_{0} + 6b_{ - 1} b_{0}^{2} \hfill \\ + 2a_{ - 1}^{2} b_{1} + 6b_{ - 1}^{2} b_{1} = 0,2a_{1}^{2} b_{ - 1} + 4a_{0} a_{1} b_{0} - Mb_{1} + \lambda^{2} b_{1} + 2\mu b_{1} + 2a_{0}^{2} b_{1} + 4a_{ - 1} a_{1} b_{1} \hfill \\ + 6b_{0}^{2} b_{1} + 6b_{( - 1)} b_{1}^{2} = 0,2a_{1}^{2} b_{0} + 3?b_{1} + 4a_{0} a_{1} b_{1} + 6b_{0} b_{1}^{2} = 0,2b_{1} + 2a_{1}^{2} b_{1} + 2b_{1}^{3} = 0. \hfill \\ \end{gathered} $$

If this algebraic equations system is solved, we obtain the following coefficients.

Case 1:

$$ \mu \ne 0,M = \frac{1}{2}\left( { - \lambda^{2} + 4\mu } \right),\lambda \ne 0,a_{ - 1} = \frac{{2\mu a_{0} }}{\lambda },a_{1} = 0,b_{1} = 0,b_{0} = \pm \frac{1}{2}\sqrt { - \lambda^{2} - 4a_{0}^{2} } ),a_{0} \ne 0,b_{ - 1} = \frac{{a_{ - 1} b_{0} }}{{a_{0} }} . $$
(30)

Case 2:

$$ \mu = 0,M = - \frac{{\lambda^{2} }}{2},a_{ - 1} = 0,\lambda \ne 0,a_{1} = \frac{{2a_{0} }}{\lambda },b_{1} = \pm \sqrt { - 1 - a_{1}^{2} } ,b_{0} = \frac{{\lambda b_{1} }}{2},b_{ - 1} = 0 . $$
(31)

Case 3:

$$ M = \frac{1}{2}\left( { - \lambda^{2} + 4\mu } \right),a_{ - 1} = 0,\lambda \ne 0,a_{1} = \frac{{2a_{0} }}{\lambda },b_{1} = \pm \sqrt { - 1 - a_{1}^{2} } ,b_{0} = \frac{{\lambda b_{1} }}{2},b_{ - 1} = 0 . $$
(32)

Case 4:

$$ \mu = 0,\lambda \ne 0,M = \lambda^{2} ,M \ne 0,a_{ - 1} = \frac{{\lambda \left( {2M + \lambda^{2} } \right)a_{0} }}{3M},a_{1} = 0,b_{1} = 0,a_{ - 1} \ne 0,b_{0} = \pm \frac{{{\text{i}}\sqrt { - 3M^{2} + 2M\lambda^{2} + \lambda^{4} + 6Ma_{0}^{2} } }}{\sqrt 6 \sqrt M } ,b_{ - 1} = \frac{{\lambda \left( {2M + \lambda^{2} } \right)b_{0} }}{3M} $$
(33)

Here, the coefficients found in (30)–(33) are also substituted in the solution of (29), then if the acquired solution (29) is also substituted in (27), the solutions of Eq. (26) will be as follows:

For Case 1

When \({\uplambda }^{2}-4\mu >0, \quad \mu \ne 0,\)

$$ u_{1} \left( {x,t} \right) = \left( { - \frac{{\sqrt { - 2M} a_{0} {\text{Tanh}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}{\lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{1} \left( {x,t} \right) = \left( { - \frac{{\sqrt {M\lambda^{2} + 4Ma_{0}^{2} } {\text{Tanh}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}{\sqrt 2 \lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(34)
$$ u_{2} \left( {x,t} \right) = \left( { - \frac{{\sqrt { - 2M} {\text{Coth}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)a_{0} }}{\lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{2} \left( {x,t} \right) = \left( { - \frac{{{\text{Coth}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)\sqrt {M\lambda^{2} + 4Ma_{0}^{2} } }}{\sqrt 2 \lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(35)

When \({\uplambda }^{2}-4\mu <0,\)

$$ u_{3} \left( {x,t} \right) = \left( {\frac{{\sqrt {2M} a_{0} {\text{Tan}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}{\lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{3} \left( {x,t} \right) = \left( {\frac{{\sqrt { - M\lambda^{2} - 4Ma_{0}^{2} } {\text{Tan}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}{\sqrt 2 \lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(36)
$$ u_{4} \left( {x,t} \right) = \left( {\frac{{\sqrt {2M} {\text{Cot}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)a_{0} }}{\lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{4} \left( {x,t} \right) = \left( {\frac{{{\text{Cot}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)\sqrt { - M\lambda^{2} - 4Ma_{0}^{2} } }}{\sqrt 2 \lambda }} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(37)

For Case 2

When \({\uplambda }^{2}-4\mu >0, \mu =0,\)

$$ u_{5} \left( {x,t} \right) = a_{0} \left( {1 + \frac{2}{{ - 1 + {\text{e}}^{{\sqrt { - 2M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}} }}} \right) e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{5} \left( {x,t} \right) = \left( {\frac{{\left( {1 + {\text{e}}^{{\sqrt { - 2M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}} } \right)\sqrt {M - 2a_{0}^{2} } }}{{\sqrt 2 \left( { - 1 + {\text{e}}^{{\sqrt { - 2M} \left( {\xi + C_{1} } \right)}} } \right)}}} \right) e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(38)

For Case 3

When \({\uplambda }^{2}-4\mu >0, \mu \ne 0,\)

$$ u_{6} \left( {x,t} \right) = a_{0} \left( {1 - \frac{2\mu }{{ - M + 2\mu + \sqrt { - M} \sqrt { - M + 2\mu } {\text{Tanh}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{6} \left( {x,t} \right) = \frac{1}{2}\sqrt {\frac{{ - M + 2\mu + 2a_{0}^{2} }}{M - 2\mu }} \left( {\sqrt { - 2M + 4\mu } - \frac{2\sqrt 2 \mu }{{\sqrt { - M + 2\mu } + \sqrt { - M} {\text{Tanh}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(39)
$$ u_{7} \left( {x,t} \right) = a_{0} \left( {1 - \frac{2\mu }{{ - M + 2\mu + \sqrt { - M} \sqrt { - M + 2\mu } {\text{Coth}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{7} \left( {x,t} \right) = \frac{1}{2}\sqrt {\frac{{ - M + 2\mu + 2a_{0}^{2} }}{M - 2\mu }} \left( {\sqrt { - 2M + 4\mu } - \frac{2\sqrt 2 \mu }{{\sqrt { - M + 2\mu } + \sqrt { - M} {\text{Coth}}\left( {\frac{{\sqrt { - M} \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(40)

When \({\uplambda }^{2}-4\mu <0,\)

$$ u_{8} \left( {x,t} \right) = a_{0} \left( {1 + \frac{2\mu }{{M - 2\mu + \sqrt M \sqrt { - M + 2\mu } {\text{Tan}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{8} \left( {x,t} \right) = \frac{1}{2}\sqrt {\frac{{ - M + 2\mu + 2a_{0}^{2} }}{M - 2\mu }} \left( {\sqrt { - 2M + 4\mu } - \frac{2\sqrt 2 \mu }{{\sqrt { - M + 2\mu } - \sqrt M {\text{Tan}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(41)
$$ u_{9} \left( {x,t} \right) = a_{0} \left( {1 + \frac{2\mu }{{M - 2\mu + \sqrt M \sqrt { - M + 2\mu } {\text{Cot}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{9} \left( {x,t} \right) = \frac{1}{2}\sqrt {\frac{{ - M + 2\mu + 2a_{0}^{2} }}{M - 2\mu }} \left( {\sqrt { - 2M + 4\mu } - \frac{2\sqrt 2 \mu }{{\sqrt { - M + 2\mu } - \sqrt M {\text{Cot}}\left( {\frac{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}}{\sqrt 2 }} \right)}}} \right)e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(42)

When \({\uplambda }^{2}-4\mu >0, \mu =0,\)

$$ u_{10} \left( {x,t} \right) = a_{0} {\text{e}}^{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}} e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
$$ v_{10} \left( {x,t} \right) = \left( {\frac{{{\text{ie}}^{{\sqrt M \left( {\left( {x + h_{3} t} \right) + C_{1} } \right)}} \sqrt {Ma_{0}^{2} } }}{\sqrt M }} \right) e^{{i\left( {h_{1} x + h_{2} t} \right)}} $$
(43)

3 Physical explanation

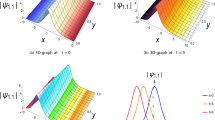
In plots Fig. 1, we show the evolution of the periodic solutions with the effects of free parameter \({h}_{3}\). However, in plots Fig. 2, we stress the effects of the parameter \(C\). It is observed in Fig. 2a, b the kink-like soliton and in Fig. 2c, d the corresponding double kink-like soliton and breather-like soliton is get out. Beside, when we increase the value of the parameter, we show out the breather-like soliton. These results could help to improve the communication in optical fibers (Fig. 3).

Fig. 1
figure 1

Plot evolution of the periodic analytic solution with the variation of \({h}_{3}\) parameter a \({h}_{3}=-0.15\), b \({h}_{3}=-1.15\), c \({h}_{3}=-15.15\) and d \({h}_{3}=-20.15\) for \({a}_{0}=0.25, \mu =0.4, \lambda =1.2, M=-0.64.\)

Full size image
Fig. 2
figure 2

Plot evolution of the analytic kink-like soliton solution and breather-like soliton with the variation of \(C\) parameter a, b \(C=-10\), c, d \(C=-20\) and \({a}_{0}=0.25, \mu =0.4, \lambda =0.2, {h}_{3}=0.5, M=0.64.\)

Full size image
Fig. 3
figure 3

Plot evolution of breather-like soliton with the variation of \(C\) parameter a, b \(C=110\) and \({a}_{0}=0.25, \mu =0.4, \lambda =0.2, {h}_{3}=0.5, M=0.64.\)

Full size image

4 Conclusion

We used the extended \(exp\left(-\varphi \left(\upxi \right)\right)\)-expansion method for find some optical solitons of (3 + 1)-dimensional and coupled NLSEs. The acquired solutions are dark, bright, combined optical solitons and exact solutions. Then, we observed that these solutions provided the equations through Mathematica 11.2. Apart from that, we have shown the graphics performance of some of the solutions found. The method can be used for many other nonlinear equations or combined equations.