Analyzing coupled-wave dynamics: lump, breather, two-wave and three-wave interactions in a (3+1)-dimensional generalized KdV equation

Abstract

In this study, we particularly address the generalized (3+1)-dimensional Kortewegde Vries (KdV) problem as one variation of the KdV equation. This equation can be utilized to simulate a wide range of physical events in a variety of domains, such as nonlinear optics, fluid dynamics, plasma physics, and other fields where coupled wave dynamics are significant. We first construct a Hirota bilinear form for the generalized KdV equation, and then we derive two different Bäcklund transformations (BT). The first Bäcklund transformation includes eleven arbitrary parameters, while the second form contains eight parameters. Rational and exponential traveling wave solutions with random wave numbers are found based on the suggested bilinear Bäcklund transformation. These solutions of the rational and exponential functions lead to the formation of dark and bright solitons. Moreover, we utilize the bilinear form of the equation to fully comprehend the behavior of lump-kink, breather, rogue, two-wave, three-wave, and multi-wave solutions. In-depth numerical simulations using 3-D profiles and contour plots are carried out while carefully taking into account relevant parameter values, offering more insights into the unique characteristics of the solutions that are obtained. Our results demonstrate the effectiveness and efficiency of the method used to obtain analytical solutions for nonlinear partial differential equations.

1 Introduction

Nature’s nonlinearity is a captivating phenomenon, and many scientists perceive nonlinear research as the most promising area for developing fundamental knowledge of nature. The study of an extensive range of nonlinear ordinary and partial differential equations is crucial to the mathematical modeling of complex processes that evolve over time. These equations are generated in a broad spectrum of domains, encompassing economics, elasticity, plasma physics, population ecology, and the physical and natural sciences [1, 2]. Soliton solutions to the aforementioned phenomena have consequently been a fascinating and exceptionally dynamic field of study for the past few decades, and the associated challenge has been the development of closed-form solutions to a broad range of nonlinear partial differential equations (NLPDEs). Closed-form solutions for solitary waves offer more internal information about these types of events. Consequently, a great deal of effort has been put forward by mathematics and physical scientists to obtain wave solutions of these NLPDEs, and several effective and potent techniques such as, modified extended tanh function method [3], Riccati sub-equation method [4], sinh-Gordon expansion technique [5], Bäcklund transformation [6], and extended transformed rational function approach [7], have been discovered.

A soliton is a single, self-sustaining wave which maintains its shape and speed while moving over a surface while not ever dispersing or dissipating. Because of their peculiar behavior, solitons are exceptionally stable and can retain their shape over extended distances. Planar wave-guides and optical fibres are two examples of waveguide structures where these solitons might occur. The physical relevance of soliton solutions stems from their capacity to counterbalance the opposing impacts of dispersion and nonlinearity. A pulse’s tendency to spread out over time due to dispersion causes it to expand and distort. Conversely, nonlinearity can cause a self-focusing effect that compresses the pulse, which lowers dispersion. A balanced coexistence of dispersion and nonlinearity is necessary for the emergence of solitons. Several researchers have used various mathematical models and techniques to investigate the theory of soliton. Wang [8] obtained Y-type soliton and complex multiple soliton solutions to the extended (3+1)-dimensional Jimbo–Miwa equation by employing Hirota bilinear method, Wang and Liu [9] explored some semi-domain soliton solutions for the fractal (3+1)-dimensional generalized Kadomtsev–Petviashvili–Boussinesq equation through Bernoulli sub-equation function approach, and Nisar et al. [10] investigated different NLPDEs and retrieved many solutions containing one-, two-, and triple-soliton solutions via the multiple Exp-function method.

The novel (2+1)-dimensional generalized Korteweg–de Vries (gKdV) equation emerged recently [11],

$$\begin{aligned} & u_{t}+6uu_x+u_{xxx}+u_x+\int _{-\infty }^x u_{yt}dx+u_y+u_{xxy}\nonumber \\ & \quad +3uu_y+3u_x\int _{-\infty }^x u_{y}dx=0, \end{aligned}$$

(1)

which, by taking into account the potential $u(x,y,t)=\phi _x(x,y,t)$, is similar to following equation:

$$\begin{aligned} & \varphi _{xt}+6\varphi _{x}\varphi _{xx}+\varphi _{xxxx}+\varphi _{xx}+\varphi _{yt}\nonumber \\ & \quad +\varphi _{xy} +\varphi _{xxxy}+3\varphi _{x}\varphi _{xy}+3\varphi _{xx}\varphi _y=0. \end{aligned}$$

(2)

Lu and Chen [11] looked into this equation and came up with several different soliton solutions as well as results about its integrability.

A new (3+1)-dimensional integrable gKdV equation was recently constructed by Ismaeel et al. [12], by changing the previous (2+1)-dimensional gKdV Eq. (1).

(3)

where, $u=u(x,y,z,t)$ and $\beta$, $\beta _1$, and $\gamma$, are any non-zero parameters. Three further terms have been added to Eq. (1), which are second-order derivatives, to generate Eq. (3). By examining the compatibility conditions, Ismaeel et al. [12] used the Painlevé test to show that Eq. (3) is Painlevé integrable only when $\beta =\beta _1$. Furthermore, by adjusting the relevant parameters, they investigated a set of lump and multi-soliton solutions.

Therefore, based on the compatibility conditions presented before, Eq. (3) becomes:

(4)

Over the past few years, a number of researchers have shown a significant deal of interest in discovering the solutions for generalized KdV equation. Hosseini et al. [13] discovered lump-type, complexiton, and soliton solutions for gKdv equation by utilizing the bilinear form of model, Xia et al. [14] discovered conservation laws and soliton solutions for generalized seventh order KdV equation by using a direct algebraic method, Khan et al. [15] applied hirota bilinear technique and found multiple bifurcation solitons and rogue waves of a generalized perturbed KdV equation, and Xu [16] used Nucci’s method to find the lax pais of a generalized seventh-order KdV equation and performed a singularity structure analysis to assess the equation’s integrability.

The Hirota bilinear transformation is a helpful mathematical method for researching nonlinear integrable systems, particularly soliton theory [17]. Since its invention, it has been used to transform nonlinear partial differential equations into a bilinear form, simplifying analysis and facilitating the methodical development of soliton solutions. Because it is algorithmic, applicable to a wide range of integrable systems, and intimately associated with the inverse scattering transform, this approach is efficient [18]. Apart from making it easier to find soliton solutions, this approach provides researchers with a uniform and systematic means to study and understand how solitons behave in various physical systems. Our goal is to utilize the gKdV equation’s bilinear representation to find Bäcklund transformation. In order to solve NLPDEs, the Bäcklund transformation is a helpful analytical technique that creates new solutions based on preexisting ones [19]. In comparison to more recent methods, the bilinear Bäcklund transformation provides a systematic and flexible method that maintains the integrability of the original equation, ensuring accurate solutions, even though it can be complex and requires a profound understanding of bilinear forms and transformations. Numerous equations, such as the sine-Gordon Eq. [20], the Kadomtsev–Petviashvili–Sawada–Kotera–Ramani equation [21], the Konopelchenko–Dubrovsky equation [22], and the Boussinesq equation [23], have been successfully solved using the Bäcklund transformation.

The computational techniques that are suggested here are straightforward, explicit, reliable, and minimize the amount of computational labor, which contributes to their broad applicability. With all these characteristics, our research deserves more attention because it is effective and influential in handling other nonlinear partial differential equations that arise in other scientific domains. Additionally, we’ll delve into various hypotheses using the provided model’s bilinear structure. Our investigation will encompass a range of conjectures, including those involving two, three, multi-wave, breather, rogue, and lump-cross-kink wave solutions. It is noteworthy that the aforementioned methodologies are never implemented in the past research for the model under consideration.

The article is formatted as follows: In Sect. 2, the Bäcklund transformation is examined, and outcomes for rational and exponential functions are shown. In Sect. 3, the bilinear form is used to analyze different wave forms and their dynamic nature. Lastly, a final synopsis of the work is provided.

2 Bäcklund transformation

By taking the following transformation,

$$\begin{aligned} u(x,y,z,t)=2(\ln {P})_{xx}, \end{aligned}$$

(5)

we can obtain the following bilinear representation of Eq. (4) by inserting Eq. (5) into Eq. (4),

$$\begin{aligned} & \big (D_{t}D_x+D_{y}D_t+D_{x}D_y+D_{x}^4+ D_{x}^3D_y+ D_{x}^2\nonumber \\ & \quad +\beta D_{x}D_z+\beta D_{y}D_z+\gamma D_{y}^2 \big )P \cdot P=0, \end{aligned}$$

(6)

the Hirota bilinear operator is given by,

where, $\Delta _1$, $\Delta _2$, $\Delta _3$ and $\Delta _4$ are integers. Also, the functions P and G are differentiable.

2.1 The first Bäcklund transformation

Let G(x, y, z, t) be an additional function that denotes the bilinear form’s solution,

$$\begin{aligned} & \big (D_{t}D_x+D_{y}D_t+D_{x}D_y+D_{x}^4+ D_{x}^3D_y+ D_{x}^2\nonumber \\ & +\beta D_{x}D_z+\beta D_{y}D_z+\gamma D_{y}^2 \big )G \cdot G=0, \end{aligned}$$

(7)

and by using [24], we consider the expression:

$$\begin{aligned} \begin{aligned} 2Q&=2[ \big (D_{t}D_x+D_{y}D_t+D_{x}D_y+D_{x}^4+ D_{x}^3D_y\\&\quad + D_{x}^2+\beta D_{x}D_z+\beta D_{y}D_z+\gamma D_{y}^2 \big ) G \cdot G]P^{2}\\&\quad - 2G^{2}[ \big (D_{t}D_x+D_{y}D_t+D_{x}D_y+D_{x}^4\\&\quad + D_{x}^3D_y+ D_{x}^2+\beta D_{x}D_z+\beta D_{y}D_z\\ &\quad +\gamma D_{y}^2 \big ) P\cdot P], \end{aligned} \end{aligned}$$

(8)

wherein the following list includes some of the characteristics associated with the Hirota Bilinear operator [25]:

$$\begin{aligned} \begin{aligned}&\big ( D_x D_t B\cdot B\big )A^2-B^2 \big ( D_x D_t A\cdot A\big )\\&\quad =2 D_x \big (D_t B\cdot A\big )\cdot A B,\\&\qquad \left( D_x^4 B\cdot B\right) A^2 -B^2 \left( D_x^4 A\cdot A\right) \\&\quad =2 D_x \left( D_x^3 B\cdot A\right) \cdot A B\\&\qquad +6 D_x \left( D_x^{2}B\cdot A\right) \cdot \big (D_x A\cdot B\big ),\\&\qquad 2\left( \left( D_x^3D_y B\cdot B\right) A^2 -\left( D_x^3D_y A\cdot A\right) B^2\right) \\&\quad =D_x[\left( 3D_x^2D_y B\cdot A\right) \cdot A B\\&\qquad +\left( 3D_x^2B\cdot A\right) \cdot \left( D_y A \cdot B\right) \\&\qquad +\left( 6D_xD_y B\cdot A\right) \cdot \left( D_x A \cdot B\right) ]\\&\qquad +D_y[ \left( D_x^{3} B\cdot A\right) \cdot \\&\qquad A B +\left( 3D_x^2 B\cdot A\right) \cdot \big (D_x A\cdot B\big )], \\&\qquad \left( D_x^2 B \cdot B \right) A^2-B^2 \left( D_x^2 A\cdot A\right) \\&\quad =2 D_x \big (D_x B\cdot A\big )\cdot A B, \\&\qquad \left( D_y^2 B \cdot B \right) A^2-B^2 \left( D_y^2 A\cdot A\right) \\&\quad =2 D_y \big (D_y B\cdot A\big )\cdot A B,\\&\qquad \left( D_p(D_q B.A\right) .A B=D_q\left( D_p B.A\right) .A B.\end{aligned} \end{aligned}$$

Using Eq. (8) and the previously indicated features, we obtain the following expression:

$$\begin{aligned}&2Q=2[ \big (D_{t}D_x+D_{y}D_t+D_{x}D_y+D_{x}^4\\&\qquad + D_{x}^3D_y+ D_{x}^2+\beta D_{x}D_z\\&\qquad +\beta D_{y}D_z+\gamma D_{y}^2 \big ) G \cdot G]P^{2}\\&\qquad -2G^{2}[ \big (D_{t}D_x+D_{y}D_t+D_{x}D_y\\&\qquad +D_{x}^4+ D_{x}^3D_y+ D_{x}^2+\beta D_{x}D_z\\&\qquad +\beta D_{y}D_z+\gamma D_{y}^2 \big ) P \cdot P]\\&\quad =2[(D_{t}D_x G\cdot G)P^{2}-G^{2}(D_{t}D_x P\cdot P)]\\&\qquad +2[(D_{t}D_y G\cdot G)P^{2}-G^{2}(D_{t}D_y P\cdot P)]\\&\qquad +2[(D_{x}D_y G\cdot G)P^{2}-G^{2}(D_{x}D_y P\cdot P)]\\&\qquad +2[(D_x^{4}G\cdot G)P^{2}-G^{2}(D_x^{4}P\cdot P)]\\&\qquad +2[(D_x^{3}D_y G\cdot G)P^{2}-G^{2}(D_x^{3}D_y P\cdot P)]\\&\qquad +2[(D_{x}^{2}G\cdot G)P^{2}-G^{2}(D_{x}^{2}P\cdot P)]\\&\qquad +2\beta [(D_{x}D_z G\cdot G)P^{2}-G^{2}(D_{x}D_z P\cdot P)]\\&\qquad +2\beta [(D_{y}D_z G\cdot G)P^{2}-G^{2}(D_{y}D_z P\cdot P)]\\&\qquad +2\gamma [(D_{y}^2 G\cdot G)P^{2}-G^{2}(D_{y}^2 P\cdot P)]\\&\quad =4D_{x}(D_{t}G\cdot P)\cdot P G+4D_{y}(D_{t}G\cdot P)\\&\qquad \cdot P G+4D_{x}(D_{y}G\cdot P)\cdot P G\\&\qquad +2[2(D_{x}(D_{x}^{3} G\cdot P)\cdot P G)\\&\qquad +6(D_{x}(D_{x}^2 G\cdot P).(D_{x} P\cdot G))]\\&\qquad +D_x[\left( 3D_x^2D_y G\cdot P\right) \cdot P G\\&\qquad +\left( 3D_x^2G\cdot P\right) \cdot \left( D_y P \cdot G\right) \\&\qquad +\left( 6D_xD_y G\cdot P\right) \cdot \left( D_x P \cdot G\right) ]\\&\qquad +D_y[ \left( D_x^{3}G\cdot P\right) \cdot P G +\left( 3D_x^2 G\cdot P\right) \\&\qquad \cdot \big (D_x P\cdot G\big )]+4[D_{x}(D_{x}G\cdot P)\cdot P G]\\&\qquad +4\beta [D_{x}(D_{z} G\cdot P)\cdot P G]\\&\qquad +4\beta [D_{y}(D_{z} G\cdot P)\cdot P G]\\&\qquad +4\gamma [[D_{y}(D_{y} G\cdot P)\cdot P G]\\&\quad =D_x[(4D_x^3+4D_x+3D_{x}^2 D_y+\chi _1 D_y\\&\qquad + \chi _2D_z+\chi _3D_t+\chi _4)G\cdot P]\cdot P G\\&\qquad +D_y[(4D_x+4\gamma D_y+D_{x}^3\\&\qquad -\chi _1D_x+\chi _5)G\cdot P]\cdot P G\\&\qquad +D_z[(4\beta D_x+4\beta D_y-\chi _2 D_x+\chi _6)G\cdot P]\cdot P G\\&\qquad +D_t[(4 D_y+4 D_x-\chi _3 D_x+\chi _7)G\cdot P]\cdot P G\\&\qquad +D_x[(3D_{x}^2+\chi _{8} D_{y}+\chi _{11}) G\cdot P]\cdot (D_{y}P\cdot G)\\&\qquad +D_x[(12D_{x}^2+6D_xD_y+\chi _9D_x) G\cdot P]\\&\qquad \cdot (D_{x}P\cdot G)\\&\qquad +D_y[(3D_{x}^2+\chi _{10}D_x-\chi _{11}) G\cdot P]\cdot (D_{x}P\cdot G). \end{aligned}$$

The given characteristics of the bilinear operator explain why the coefficients of $\chi _{i}, (i=1,2,3,\ldots ,11)$ in the previous formula are zero: $D_a P\cdot P=0$, $D_x(D_y P\cdot G)\cdot P G = D_y(D_x P\cdot G)\cdot P G$, $D_x P\cdot G =-D_x G\cdot P$. Consequently, the equation that represents the Bäcklund transform of Eq. (4) is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \left( 4D_x^3+4D_x+3D_{x}^2 D_y+\chi _1 D_y+ \chi _2D_z+\chi _3D_t+\chi _4\right) G\cdot P=0,\\ \left( 4D_x+4\gamma D_y+D_{x}^3-\chi _1D_x+\chi _5\right) G\cdot P=0,\\ \left( 4\beta D_x+4\beta D_y-\chi _2 D_x+\chi _6\right) G\cdot P=0,\\ \left( 4 D_y+4 D_x-\chi _3 D_x+\chi _7\right) G\cdot P=0,\\ \left( 3D_{x}^2+\chi _{8} D_{y}+\chi _{11}\right) G\cdot P=0,\\ \left( 12 D_{x}^2+6D_x D_y+\chi _9D_x\right) G\cdot P=0,\\ \left( 3D_{x}^2+\chi _{10}D_x-\chi _{11}\right) G\cdot P=0. \end{array}\right. \end{aligned}$$

(9)

For the bilinear form (7), we investigate the solution $P=1$. Now, the aforementioned system utilizes the following characteristic:

$$\begin{aligned} D_{p}^{q}G\cdot 1=\frac{\partial ^{p}}{\partial q^{p}} G. \end{aligned}$$

After that, the bilinear Bäcklund transformation Eq. (9) is transformed into a group of linear partial differential equations:

$$\begin{aligned} \left\{ \begin{array}{l} \left( 4G_{xxx}+4 G_x+3 G_{xxy}+\chi _1 G_y+\chi _2 G_z+\chi _3 G_t+\chi _4\right) =0,\\ \left( 4G_x+4\gamma G_y+G_{xxx}-\chi _1G_x+\chi _5\right) =0,\quad \left( 4\beta G_x+4\beta G_y-\chi _2 G_x+\chi _{6}\right) =0,\\ \left( 4G_{y}+4 G_x-\chi _3 G_x+\chi _{7}\right) =0,\quad \left( 3G_{xx}+\chi _{8} G_{y}+\chi _{11}\right) =0,\\ \left( 12 G_{xx}+6G_{xy}+\chi _9 G_x\right) =0, \quad \left( 3G_{xx}+\chi _{10}G_x-\chi _{11}\right) =0. \end{array}\right. \end{aligned}$$

(10)

2.1.1 Rational function solution

We consider a first order polynomial function solution as,

$$\begin{aligned} G(x,y,z,t)=k_{{1}}x+k_{{2}}y+k_{{3}}z+k_{{4}}t, \end{aligned}$$

(11)

where $k_1$, $k_2$, $k_3$, and $k_4$ are random constants. The following results from inserting the aforementioned equation into system (10):

$$\begin{aligned} \left\{ \begin{array}{l} k_{{1}}=-{\frac{k_{{2}}\chi _{{8}}}{\chi _{{10}}}},\quad \chi _{{4}}=-{\frac{k_{{2}}\chi _{{1}}\chi _{{10}}+k_{{3}}\chi _{{2}}\chi _{{10}}+k_{{4} }\chi _{{3}}\chi _{{10}}-4\,k_{{2}}\chi _{{8}}}{\chi _{{10}}}},\quad \chi _{{5}}=-{\frac{k_{{2} } \left( 4\,\gamma \,\chi _{{10}}+\chi _{{1}}\chi _{{8}}-4\,\chi _{{8}} \right) }{\chi _{{ 10}}}},\\ \chi _{{6}}={\frac{4\,\beta \,k_{{2}}\chi _{{8}}-4\,\beta \,k_{{2}}\chi _{{ 10}}+k_{{3}}\chi _{{2}}\chi _{{10}}}{\chi _{{10}}}},\quad \chi _{{7}}=-{\frac{k_{{2}} \left( \chi _{{3}}\chi _{{8}}-4\,\chi _{{8}}+4\,\chi _{{10}} \right) }{\chi _{{10}}}},\quad \chi _{ {9}}=0,\quad \chi _{{11}}=-k_{{2}}\chi _{{8}},\\ k_{{2}}=k_{{2}},k_{{3}}=k_{{3}},k_{{4}}=k_{{4}},\chi _{{1}}=\chi _{{1}},\chi _{{2 }}=\chi _{{2}},\chi _{{3}}=\chi _{{3}}, \chi _{{8}}=\chi _{{8}},\chi _{{10}}=\chi _{{10}}, \end{array}\right. \end{aligned}$$

thus, Eq. (4) has the following solution:

$$\begin{aligned} & u(x,y,z,t)\nonumber \\ & \quad =-2\,{\frac{k_{{2}}^2\chi _{{8}}^2}{(tk_{{4}}\chi _{{10}}-xk_{{2}}\chi _{{8}}+yk_{{2}}\chi _{{10}}+zk_{{3}}\chi _{{10}})^2}}.\nonumber \\ \end{aligned}$$

(12)

2.1.2 Exponential function solution

The following is considered the solution of the bilinear Form Eq. (7).

$$\begin{aligned} \begin{aligned}&G=1+k_{{5}}{\textrm{e}^{ax+by+gz+ht}}, \end{aligned} \end{aligned}$$

(13)

where the constants are represented by $a$, $b$, $g$, and $h$. The following results from inserting Eq. (13) into system (10):

$$\begin{aligned} \left\{ \begin{array}{l} b=-2\,a-\frac{1}{6}\,\chi _{{ 9}},\quad \beta ={\frac{-36\,{a}^{4}-6\,{a}^{3}\chi _{{9}}+144\,\gamma \,{a} ^{2}+24\,a\gamma \,\chi _{{9}}+\gamma \,{\chi _{{9}}}^{2}-36\,{a}^{2}-36\,ha-6\, a \chi _{{9}}-6\,h \chi _{{9}}}{6a \left( 6\,a+\chi _{{9}} \right) }},\\ \chi _{{1}}=-{\frac{-3\,{a}^{3}+24\,a\gamma +2\,\gamma \,\chi _{{ 9}}-12\,a}{3a}},\quad \chi _{{2}}=-{\frac{-36\,{a}^{4}-6\,{a}^{3}\chi _{{9}}+ 144\,\gamma \,{a}^{2}+24\,a\gamma \,\chi _{{9}}+\gamma \,{\chi _{{9}}}^{2}-36\,{a }^{2}-36\,ha-6\,a \chi _{{9}}-6\,h \chi _{{9}}}{9ag}},\\ \chi _{{3}}=-\frac{2}{3}\,{\frac{6\,a+ \chi _{{9}}}{a}},\quad \chi _{{8}}=18\,{\frac{{a}^{2}}{12\,a+\chi _{{9}}}},\quad \chi _{{10}}=-3 \,a. \end{array}\right. \end{aligned}$$

(14)

Thus, the solution to Eq. (4) can be obtained by substituting Eq. (14) in (5),

$$\begin{aligned} u(x,y,z,t)=2\,{\frac{k_{{5}}a^2{\textrm{e}^{ax-2\,ya-\frac{1}{6}\,\chi _{{9}}y+gz+ht}}}{(1+k_{{5}} {\textrm{e}^{ax-2\,ya-\frac{1}{6}\,\chi _{{9}}y+gz+ht}})^2}}. \end{aligned}$$

(15)

2.2 The second Bäcklund transformation

For Eq. (4), we employ the following exchange identity to obtain the second BT:

$$\begin{aligned}&\left( D_x^3D_y G\cdot G\right) P^2 -\left( D_x^3D_y P\cdot P\right) G^2 \nonumber \\&\quad =2D_y\left( D_x^3 G\cdot P\right) \cdot FG+6D_x\left( D_xD_yG\cdot P\right) \nonumber \\&\quad \cdot \left( D_x P \cdot G\right) . \end{aligned}$$

(16)

Now, by using this identity in Eq. (8) and following the similar procedure,

$$\begin{aligned}&Q=2D_{x}(D_{t}G\cdot P)\cdot P G+2D_{y}(D_{t}G\cdot P)\cdot P G\\&\qquad +2D_{x}(D_{y}G\cdot P)\cdot P G+2(D_{x}(D_{x}^{3} G\cdot P)\cdot P G)\\&\qquad +6(D_{x}(D_{x}^2 G\cdot P).(D_{x} P\cdot G)) +2D_y \left( D_x^{3}G\cdot P\right) \\&\qquad \cdot P G +6D_x\left( D_xD_y G\cdot P\right) \cdot \big (D_x P\cdot G\big )\\&\qquad +2[D_{x}(D_{x}G\cdot P)\cdot P G]\\&\qquad +2\beta [D_{x}(D_{z} G\cdot P)\cdot P G] +2\beta [D_{y}(D_{z} G\cdot P)\cdot P G]\\&\qquad +2\gamma [D_{y}(D_{y}G\cdot P)\cdot P G]\\&\quad =2D_x[(D_x^3+D_x+\chi _1 D_y\\&\qquad + \chi _2D_z+\chi _3D_t+\chi _4)G\cdot P]\cdot P G\\&\qquad +D_y[(D_x+\gamma D_y+D_{x}^3-\chi _1D_x+\chi _5)G\cdot P]\\&\qquad \cdot P G+D_z[(\beta D_x+\beta D_y-\chi _2 D_x+\chi _6)G\cdot P]\cdot P G\\&\qquad +D_t[( D_y+ D_x-\chi _3 D_x+\chi _7)G\cdot P] \\&\qquad \cdot PG+D_x[(3D_{x}^2+3D_xD_y\\&\qquad +\chi _8 D_x) G\cdot P]\cdot (D_{x}P\cdot G). \end{aligned}$$

Eight arbitrary parameters are suggested in this particular case. As a result,the Bäcklund transformation of Eq. (4) is,

$$\begin{aligned} \left\{ \begin{array}{l} \left( D_x^3+D_x+\chi _1 D_y+ \chi _2D_z+\chi _3D_t+\chi _4\right) G\cdot P=0,\\ \left( D_x+\gamma D_y+D_{x}^3-\chi _1D_x+\chi _5\right) G\cdot P=0,\\ \left( \beta D_x+\beta D_y-\chi _2 D_x+\chi _6\right) G\cdot P=0,\\ \left( D_y+ D_x-\chi _3 D_x+\chi _7\right) G\cdot P=0,\\ \left( 3D_{x}^2+3D_x D_y+\chi _8D_{x}\right) G\cdot P=0. \end{array}\right. \end{aligned}$$

(17)

Now, the bilinear Bäcklund transformation Eq. (17) is transformed into a group of linear partial differential equations,

$$\begin{aligned} \left\{ \begin{array}{l} \left( G_{xxx}+ G_x+\chi _1 G_y+\chi _2 G_z+\chi _3 G_t+\chi _4\right) =0,\\ \left( G_x+\gamma G_y+G_{xxx}-\chi _1G_x+\chi _5\right) =0,\\ \left( \beta G_x+\beta G_y-\chi _2 G_x+\chi _{6}\right) =0,\\ \left( G_{y}+ G_x-\chi _3 G_x+\chi _{7}\right) =0,\\ \left( 3G_{xx}+3G_{xy}+\chi _{8} G_{x}\right) =0. \end{array}\right. \end{aligned}$$

(18)

2.2.1 Rational function solution

We take the same rational function solution as Eq. (11), and after plugging it into Eq. (18), we obtain the following constraints:

$$\begin{aligned} \left\{ \begin{array}{l} k_{{2}}=k_{{1}}\chi _{{3}}-k_{{ 1}}-\chi _{{7}},\quad \\ \chi _{{4}}=-k_{{1}}\chi _{{1}}\chi _{{3}}+k_{{1}}\chi _{{1}}-k_{{3}}\chi _{{2 }}-k_{{4}}\chi _{{3}}+\chi _{{1}}\chi _{{7}}-k_{{1}},\\ \chi _{{5}}=-\gamma \,k_{{1}}\chi _{{3 }}+\gamma \,k_{{1}}+\gamma \,\chi _{{7}}+k_{{1}}\chi _{{1}}-k_{{1}},\quad \\ \chi _{{6}}=- \beta \,k_{{1}}\chi _{{3}}+\beta \,\chi _{{7}}+k_{{1}}\chi _{{2}},\quad \chi _{{8}}=0, \end{array}\right. \end{aligned}$$

therefore, the rational function solution is given as,

$$\begin{aligned} & u(x,y,z,t)\nonumber \\ & \quad =-2\,{\frac{k_{{1}}^2}{(yk_{{1}}\chi _{{3}}+tk_{{4}}+xk_{{1}}-yk_{{1}}-y \chi _{{7} }+zk_{{3}})^2}}.\nonumber \\ \end{aligned}$$

(19)

2.2.2 Exponential function solution

Similarly taking the same solution as Eq. (13), and solving for parameters results in,

$$\begin{aligned} \left\{ \begin{array}{l} b=a\chi _{{3}}-a, \quad \\ \beta =-{\frac{{a}^{3}\chi _{{3}}+a\gamma \,{\chi _{{3}}}^{2}-2\,a\gamma \,\chi _{{3 }}+a\gamma +a \chi _{{3}}+h \chi _{{3}}}{g \chi _{{3}}}},\\ \chi _{{1 }}={a}^{2}+\gamma \,\chi _{{3}}-\gamma +1,\quad \\ \chi _{{2}}=-{\frac{{a}^{3}\chi _{{3}}+a \gamma \,{\chi _{{3}}}^{2}-2\,a\gamma \,\chi _{{3}}+a\gamma +a \chi _{{3}}+h \chi _{{3}}}{g }},\quad \\ \chi _{{8}}=-3\,a \chi _{{3}}, \end{array}\right. \end{aligned}$$

therefore, by substituting the above solution set along with Eq. (13) into (5), the solution is,

$$\begin{aligned} u(x,y,z,t)=2\,{\frac{k_{{5}}a^2{\textrm{e}^{ay \chi _{{3}}+ax-ay+gz+ht}}}{(1+k_{{5}}{ \textrm{e}^{ay \chi _{{3}}+ax-ay+gz+ht}})^2}}. \end{aligned}$$

(20)

3 Interactional solutions

3.1 Two wave solutions

The following function is employed to obtain two-wave solutions to Eq. (4):

$$\begin{aligned} P(x,y,z,t)= & {n_1} e^{ (-\delta _1)}+{n_2} e^{ (\delta _1)}+{n_3} \sin (\delta _2)\nonumber \\ & +{n_4} \sinh (\delta _3), \end{aligned}$$

(21)

where, $\delta _1=({a_1} y+{b_1} t+{c_1} z+{d_1} x)$, $\delta _2=({a_2} y+{b_2} t+{c_2} z+{d_2} x)$, and $\delta _3=({a_3} y+{b_3} t+{c_3} z+d_3 x)$. Furthermore, (5) can be used to transform the bilinear form (6) into the following expression,

$$\begin{aligned} & P P_{xt}-P_x P_t+P P_{yt}-P_y P_t+P P_{xy}-P_x P_y+(P P_{xxxx}-4P_x P_{xxx}+3P_{xx}^2)\nonumber \\ & \quad +(P P_{xxxy}-3P_{x}P_{xxy}+3P_{xx}P_{xy}-P_{xxx}P_{y}) +P P_{xx}-P_x^2\nonumber \\ & \quad +\beta (P P_{xz}-P_x P_z)+\beta (P P_{yz}-P_{x} P_{y}) +\gamma (P P_{yy}-P_y^2)=0. \end{aligned}$$

(22)

Plugging Eq. (21) into Eq. (22) yields the following set of solutions:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {n_3}= 0,\quad {b_1}= \frac{6 {a_1}^4+12 {a_1}^3+{a_1}^2 (6 {a_2} ({a_2}+2)-\beta +7)+2 {a_1} {a_2} (\beta +5)-{a_2}^2 (\beta +5)}{({a_1}-{a_2})^2},\\ {b_2}= \frac{6 {a_1}^3 ({a_2}-1)+{a_1}^2 (18 {a_2}-\beta -9)+2 {a_1} {a_2} (3 {a_2} ({a_2}+1)+\beta +9)+{a_2}^2 (6 {a_2}-\beta +3)}{({a_1}-{a_2})^2},\\ {b_3}= \frac{6 {a_1}^4+12 {a_1}^3+{a_1}^2 (6 {a_2} ({a_2}+2)-\beta +7)+2 {a_1} {a_2} (\beta +5)-{a_2}^2 (\beta +5)}{({a_1}-{a_2})^2},\\ {a_3}= {a_1},\quad \gamma = -\frac{6 ({a_1}+1) ({a_1} ({a_1}+2)+{a_2} ({a_2}+2)+2)}{({a_1}-{a_2})^2}, \end{array}\right. \end{aligned}$$

(23)

plugging Eq. (23) into Eq. (21), gives,

$$\begin{aligned} & P(x,y,z,t)\nonumber \\ & \quad ={n_1} \exp \left( -\frac{t \left( 6 {a_1}^4+12 {a_1}^3+{a_1}^2 (6 {a_2} ({a_2}+2)-\beta +7)+2 {a_1} {a_2} (\beta +5)-{a_2}^2 (\beta +5)\right) }{({a_1}-{a_2})^2}-{a_1} y-{c_1} z-{d_1} x\right) \nonumber \\ & \quad +{n_2} \exp \left( \frac{t \left( 6 {a_1}^4+12 {a_1}^3+{a_1}^2 (6 {a_2} ({a_2}+2)-\beta +7)+2 {a_1} {a_2} (\beta +5)-{a_2}^2 (\beta +5)\right) }{({a_1}-{a_2})^2}+{a_1} y+{c_1} z+{d_1} x\right) \nonumber \\ & \quad +{n_4} \sinh \left( \frac{t \left( 6 {a_1}^4+12 {a_1}^3+{a_1}^2 (6 {a_2} ({a_2}+2)-\beta +7)+2 {a_1} {a_2} (\beta +5)-{a_2}^2 (\beta +5)\right) }{({a_1}-{a_2})^2}+{a_1} y+{c_3} z+{d_3} x\right) .\nonumber \\ \end{aligned}$$

(24)

Set 2:

$$\begin{aligned} \left\{ \begin{array}{l} {b_1}= -\frac{\left( {a_1}^2-2\right) \gamma }{{a_1}+1}-\beta +1,\quad {b_2}= \frac{({a_1} ({a_1}+4)+2) \gamma }{{a_1}+1}-\beta -3,\\ {n_1}= \frac{{n_3}^2}{4 {n_2}},\quad {n_4}= 0,\quad {a_2}= -{a_1}-2, \end{array}\right. \nonumber \\ \end{aligned}$$

(25)

plugging Eq. (25) into Eq. (21), gives,

$$\begin{aligned}&P(x,y,z,t)\nonumber \\&\quad =\frac{{n_3}^2 \exp \left( t \left( -\left( -\frac{\left( {a_1}^2-2\right) \gamma }{{a_1}+1}-\beta +1\right) \right) -{a_1} y-{c_1} z-{d_1} x\right) }{4 {n_2}}\nonumber \\&\qquad +{n_2} \exp \left( t \left( -\frac{\left( {a_1}^2-2\right) \gamma }{{a_1}+1}-\beta +1\right) +{a_1} y+{c_1} z+{d_1} x\right) \nonumber \\&\qquad +{n_3} \sin \left( t \left( \frac{({a_1} ({a_1}+4)+2) \gamma }{{a_1}+1}-\beta -3\right) \right. \nonumber \\&\qquad \left. +(-{a_1}-2) y+{c_2} z+{d_2} x\right) . \end{aligned}$$

(26)

Plugging in Eqs. (24) and (26) into Eq. (5) yields the solution to Eq. (4).

3.2 Three wave solutions

The following function is utilized to obtain three wave solutions for Eq. (4):

$$\begin{aligned} P(x,y,z,t)= & {l_1} \exp (\Lambda _1)+\exp (-\Lambda _1)+l_2 \cos (\Lambda _2)\nonumber \\ & +{l_3} \sin (\Lambda _3), \end{aligned}$$

(27)

where, $\Lambda _1={p_1} x+{p_2} y+{p_3} t+{p_4}+{q_1} z$, $\Lambda _2={p_5} x+{p_6} y+{p_7} t+{p_8}+{q_2} z$, and $\Lambda _3={p_{10}} y+{p_{11}} t+{p_{12}}+{p_9} x+{q_3} z$. By putting Eq. (27) into Eq. (22), the following solution set is obtained:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {l_2}= 0,\quad {p_{11}}= \beta (-{q_3})-24,\quad {p_{10}}= -3,\quad \\ \gamma = -6,\quad {p_3}= \beta (-{q_1})-2, \end{array}\right. \end{aligned}$$

(28)

the outcome of inserting this solution set into Eq. (27) is:

$$\begin{aligned} P(x,y,z,t)= & e^{ (-{p_1} x-{p_2} y-{p_4}-t (\beta (-{q_1})-2)-{q_1} z)}+{l_1} e^{{p_1} x+{p_2} y+{p_4}+t (\beta (-{q_1})-2)+{q_1} z}\nonumber \\ & +{l_3} \sin ({p_12}+{p_9} x+t (\beta (-{q_3})-24)+{q_3} z-3 y). \end{aligned}$$

(29)

Set 2:

$$\begin{aligned} \left\{ \begin{array}{l} {l_1}= \frac{{l_3}^2 \left( \gamma ({p_{10}}-1)^2-6 ({p_{10}}+1) ({p_{10}} ({p_{10}}+2)+5)\right) }{4 \gamma ({p_{10}}-1)^2+48 ({p_{10}} ({p_{10}}+2)+5)}, {l_2}= 0,\quad {p_{11}}= \frac{\gamma -\gamma {p_{10}} \left( {p_{10}}^2+{p_{10}}+3\right) }{{p_{10}} ({p_{10}}+2)+5}+\beta (-{q_3})-3,\\ {p_3}= -\frac{2 \gamma ({p_{10}}+1)}{{p_{10}} ({p_{10}}+2)+5}+\beta (-{q_1})+1, \end{array}\right. \end{aligned}$$

(30)

therefore, Eq. (27) yields,

$$\begin{aligned} & P(x,y,z,t)\nonumber \\ & \quad =\frac{{l_3}^2 \left( \gamma ({p_{10}}-1)^2-6 ({p_{10}}+1) ({p_{10}} ({p_{10}}+2)+5)\right) \exp \left( {p_1} x+t \left( -\frac{2 \gamma ({p_{10}}+1)}{{p_{10}} ({p_{10}}+2)+5}+\beta (-{q_1})+1\right) +{p_2} y+{p_4}+{q_1} z\right) }{4 \gamma ({p_{10}}-1)^2+48 ({p_{10}} ({p_{10}}+2)+5)}\nonumber \\ & \quad +\exp \left( -{p_1} x-t \left( -\frac{2 \gamma ({p_{10}}+1)}{{p_{10}} ({p_{10}}+2)+5} +\beta (-{q_1})+1\right) -{p_2} y-{p_4}-{q_1} z\right) \nonumber \\ & \quad +{l_3} \sin \left( t \left( \frac{\gamma -\gamma {p_{10}} \left( {p_{10}}^2+{p_{10}}+3\right) }{{p_{10}} ({p_{10}}+2)+5}+\beta (-{q_3})-3\right) +{p_{10}} y+{p_{12}}+{p_9} x+{q_3} z\right) . \end{aligned}$$

(31)

Plugging in Eqs. (29) and (31) into Eq. (5) yields the solution to Eq. (4).

3.3 Multi wave solutions

To obtain multi wave solutions to Eq. (4), the function used is as follows:

$$\begin{aligned} P(x,y,z,t)= & {n_2} \cos (\theta _1)+{n_1} \cosh (\theta _2)\nonumber \\ & +{n_3} \cosh (\theta _3), \end{aligned}$$

(32)

where, $\theta _1={a_1} y+{b_1} t+{c_1} z+x$, $\theta _2={a_2} y+{b_2} t+{c_2} z+x$, and $\theta _3={a_3} y+{b_3} t+{c_3} z+x$. By plugging Eq. (32) into Eq. (22) we get:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {n_1}= 0,\quad {n_2}= \frac{i {n_3} \sqrt{({a_3}-1)^2 \gamma +6 ({a_3}+1) ({a_3} ({a_3}+2)+5)}}{\sqrt{({a_3}-1)^2 (-\gamma )+12 {a_3} ({a_3}+2)+60}},\quad \\ {c_1}= -\frac{\frac{2 ({a_3}+1) \gamma }{{a_3} ({a_3}+2)+5}+{b_1}+3}{\beta },\\ {b_3}= \frac{\gamma -{a_3} \left( {a_3}^2+{a_3}+3\right) \gamma }{{a_3} ({a_3}+2)+5}+\beta (-{c_3})+1, \end{array}\right. \end{aligned}$$

(33)

upon rearranging these parameters in Eq. (32), the outcome is:

$$\begin{aligned} P(x,y,z,t)= & {n_3} \cosh \left( t \left( \frac{\gamma -{a_3} \left( {a_3}^2+{a_3}+3\right) \gamma }{{a_3} ({a_3}+2)+5}+\beta (-{c_3})+1\right) +{a_3} y+{c_3} z+x\right) \nonumber \\ & +\frac{i {n_3} \sqrt{({a_3}-1)^2 \gamma +6 ({a_3}+1) ({a_3} ({a_3}+2)+5)} \cos \left( {a_1} y-\frac{z \left( \frac{2 ({a_3}+1) \gamma }{{a_3} ({a_3}+2)+5}+{b_1}+3\right) }{\beta }+{b_1} t+x\right) }{\sqrt{({a_3}-1)^2 (-\gamma )+12 {a_3} ({a_3}+2)+60}}. \end{aligned}$$

(34)

Set 2:

$$\begin{aligned} \left\{ \begin{array}{l} {n_2}= -i {n_1},\quad {n_3}= 0,\quad {c_1}= -\frac{2 {b_1}+\gamma +6}{2 \beta },\quad {c_2}= -\frac{2 {b_2}+\gamma -2}{2 \beta }, \end{array}\right. \end{aligned}$$

(35)

then Eq. (32) yields,

$$\begin{aligned} P(x,y,z,t)= & {n_1} \cosh \left( {a_2} y+{b_2} t-\frac{z (2 {b_2}+\gamma -2)}{2 \beta }+x\right) -i {n_1} \cos \left( {a_1} y+{b_1} t-\frac{z (2 {b_1}+\gamma +6)}{2 \beta }+x\right) . \end{aligned}$$

(36)

Plugging Eqs. (34) and (36) into Eq. (5) yields the solution to Eq. (4).

3.4 Breather solutions

The following function is employed to obtain breather-wave solutions for Eq. (4):

$$\begin{aligned} P(x,y,z,t)={n_2} \exp (\theta _1)+\exp (-\theta _1)+{n_1} \cos (\theta _2),\nonumber \\ \end{aligned}$$

(37)

where, $\theta _1={q_1} ({a_1} y+{b_1} t+{c_1} z+d_1x)$, and $\theta _2={q_0} ({a_2} y+{b_2} t+{c_2} z+d_2x)$. By substituting Eq. (37) into Eq. (22), we obtain the following solution set:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {b_1}= \frac{4 \left( 5-6 {a_1}^2\right) {n_2}+{n_1}^2}{{n_1}^2-4 {n_2}}-\beta {c_1},\quad {b_2}= -\frac{3 \left( {n_1}^2-4 (4 {a_1} {n_2}+{n_2})\right) }{{n_1}^2-4 {n_2}}-\beta {c_2},\quad \gamma = \frac{24 ({a_1}+1) {n_2}}{{n_1}^2-4 {n_2}},\quad {a_2}= -1, \end{array}\right. \end{aligned}$$

(38)

the outcome of inserting this solution set into Eq. (37) is:

$$\begin{aligned} & P(x,y,z,t)={n_2} \exp \left( {q_1} \left( t \left( \frac{4 \left( 5-6 {a_1}^2\right) {n_2}+{n_1}^2}{{n_1}^2-4 {n_2}}-\beta {c_1}\right) +{a_1} y+{c_1} z+{d_1} x\right) \right) \nonumber \\ & \quad +\exp \left( -{q_1} \left( t \left( \frac{4 \left( 5-6 {a_1}^2\right) {n_2}+{n_1}^2}{{n_1}^2-4 {n_2}}-\beta {c_1}\right) +{a_1} y+{c_1} z+{d_1} x\right) \right) \nonumber \\ & \quad +{n_1} \cos \left( {q_0} \left( t \left( -\frac{3 \left( {n_1}^2-4 (4 {a_1} {n_2}+{n_2})\right) }{{n_1}^2-4 {n_2}}-\beta {c_2}\right) +{c_2} z+{d_2} x-y\right) \right) . \end{aligned}$$

(39)

Set 2:

$$\begin{aligned} \left\{ \begin{array}{l} {b_1}= \frac{{n_1}^2 \left( \frac{6 ({a_2}+1)}{\sqrt{-({a_2}+1)^2}}-\beta {c_1}+1\right) +4 {n_2} (\beta {c_1}+5)}{{n_1}^2-4 {n_2}},\quad \\ {b_2}= \frac{4 {n_2} \left( -\frac{6 ({a_2}+1)}{\sqrt{-({a_2}+1)^2}}+\beta {c_2}+3\right) +{n_1}^2 (3-\beta {c_2})}{{n_1}^2-4 {n_2}},\\ \gamma = 0,\quad {a_1}= \sqrt{-({a_2}+1)^2}-1, \end{array}\right. \end{aligned}$$

(40)

therefore the outcome of Eq. (37) is,

$$\begin{aligned} & P(x,y,z,t)\nonumber \\ & \quad ={n_2} \exp \left( {q_1} \left( \frac{t \left( {n_1}^2 \left( \frac{6 ({a_2}+1)}{\sqrt{-({a_2}+1)^2}}-\beta {c_1}+1\right) +4 {n_2} (\beta {c_1}+5)\right) }{{n_1}^2-4 {n_2}}+\left( \sqrt{-({a_2}+1)^2}-1\right) y+{c_2} z+{d_1} x\right) \right) \nonumber \\ & \quad +\exp \left( -{q_1} \left( \frac{t \left( {n_1}^2 \left( \frac{6 ({a_2}+1)}{\sqrt{-({a_2}+1)^2}}-\beta {c_1}+1\right) +4 {n_2} (\beta {c_1}+5)\right) }{{n_1}^2-4 {n_2}}+\left( \sqrt{-({a_2}+1)^2}-1\right) y+{c_2} z+{d_1} x\right) \right) \nonumber \\ & \quad +{n_1} \cos \left( {q_0} \left( \frac{t \left( 4 {n_2} \left( -\frac{6 ({a_2}+1)}{\sqrt{-({a_2}+1)^2}}+\beta {c_2}+3\right) +{n_1}^2 (3-\beta {c_2})\right) }{{n_1}^2-4 {n_2}}+{a_2} y+{c_2} z+{d_1} x\right) \right) . \end{aligned}$$

(41)

Plugging in Eqs. (39) and (41) into Eq. (5) yields the solution to Eq. (4).

3.5 Lump-cross kink solution

The following function is employed to obtain lump cross kink wave solutions for Eq. (4):

$$\begin{aligned} & P(x,y,z,t)\nonumber \\ & \quad ={k_1} e^{ ({b_{10}} x+{b_{11}} y+{b_{12}} t+z)}+{b_9}+g^2+h^2\text {/.}\, \nonumber \\ & \qquad \{g={b_1} x+{b_2} y+{b_4} t+z,h={b_5} x+{b_6} y+{b_8} t+z\}. \end{aligned}$$

(42)

By putting Eq. (42) into Eq. (22), gives the following solution set:

$$\begin{aligned} \left\{ \begin{array}{l} {k_1}= 0,\quad {b_4}= {b_8},\quad {b_6}= -1+i \sqrt{2},\quad {b_9}= \frac{2 \left( 2-5 i \sqrt{2}\right) }{3 \gamma },\quad \beta = -{b_8}-i \sqrt{2} \gamma -1, \end{array}\right. \end{aligned}$$

(43)

upon inserting Eq. (43) into Eq. (42), the outcome is,

$$\begin{aligned} & P(x,y,z,t)=({b_1} x+{b_2} y+{b_8} t+z)^2 +\left( {b_5} x+{b_8} t+\left( -1+i \sqrt{2}\right) y+z\right) ^2+\frac{2 \left( 2-5 i \sqrt{2}\right) }{3 \gamma }. \end{aligned}$$

(44)

Plugging in Eq. (44) into Eq. (5) yields the solution to Eq. (4).

3.6 Lump-cross two kink solutions

The following function is employed to obtain lump cross two kink wave solutions for Eq. (4):

$$\begin{aligned} & P(x,y,z,t)\nonumber \\ & \quad =({a_1} x+{a_2} y+{a_4} t+z)^2+{a_{11}} e^{ ({k_1} x+{k_2} y+{k_6} t+z)}\nonumber \\ & \qquad +{a_{12}} e^{ ({k_3} x+{k_4} y+{k_5} t+z)}\nonumber \\ & \qquad +{a_{13}}+({a_6} x+{a_7} y+{a_9} t+z)^2. \end{aligned}$$

(45)

By plugging Eq. (45) into Eq. (22), gives the following solution set:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {k_2}= \frac{\sqrt{\frac{{a_7}^4}{2}+{a_7}^3+{a_7}^2}}{{a_7}}-1,\quad {a_2}= -2,\quad {a_{12}}= 0,\quad {a_4}= -\frac{3 {a_7}^2}{2}-3 \sqrt{\frac{{a_7}^4}{2}+{a_7}^3+{a_7}^2}+{a_9},\\ {k_6}= -\frac{3}{2} \sqrt{\frac{{a_7}^4}{2}+{a_7}^3+{a_7}^2}+\frac{3 {a_7}}{2}+{a_9}+2,\quad {a_{13}}= \frac{4 \sqrt{2} \sqrt{{a_7}^2 ({a_7} ({a_7}+2)+2)}-4 {a_7}^2}{({a_7}+2)^2},\\ \gamma = -\frac{3 ({a_7} ({a_7}+2)+2) \left( {a_7}^2+\sqrt{2} \sqrt{{a_7}^2 ({a_7} ({a_7}+2)+2)}\right) }{2 {a_7} ({a_7}+2)^2},\\ \beta = \frac{{a_7} \left( {a_7} \left( {a_7} \left( 3 \sqrt{2} \sqrt{{a_7}^2 ({a_7} ({a_7}+2)+2)}+3 {a_7} ({a_7}+1)-2 {a_9}-2\right) +3 \sqrt{2} \sqrt{{a_7}^2 ({a_7} ({a_7}+2)+2)}-8 {a_9}-20\right) -8 ({a_9}+1)\right) -12 \sqrt{2} \sqrt{{a_7}^2 ({a_7} ({a_7}+2)+2)}}{2 {a_7} ({a_7}+2)^2}. \end{array}\right. \end{aligned}$$

Equation (45) yields the following result when this solution set is entered:

$$\begin{aligned} P(x,y,z,t)= & \left( {a_1} x+t \left( -\frac{3 {a_7}^2}{2}-3 \sqrt{\frac{{a_7}^4}{2}+{a_7}^3+{a_7}^2}+{a_9}\right) -2 y+z\right) ^2\nonumber \\ & +{a_{11}} \exp \left( t \left( -\frac{3}{2} \sqrt{\frac{{a_7}^4}{2}+{a_7}^3+{a_7}^2}+\frac{3 {a_7}}{2}+{a_9}+2\right) \right. \nonumber \\ & \left. +\left( \frac{\sqrt{\frac{{a_7}^4}{2}+{a_7}^3+{a_7}^2}}{{a_7}}-1\right) y+{k_1} x+z\right) \nonumber \\ & +({a_6} x+{a_7} y+{a_9} t+z)^2+\frac{4 \sqrt{2} \sqrt{{a_7}^2 ({a_7} ({a_7}+2)+2)}-4 {a_7}^2}{({a_7}+2)^2}. \end{aligned}$$

(46)

Set 2:

$$\begin{aligned} \left\{ \begin{array}{l} {k_4}= -2,\quad {a_7}= -\sqrt{1-{a_2} ({a_2}+2)}-1,\quad {k_2}= -2,\quad {k_5}= {a_9}+2,\quad {a_4}= {a_9},\\ {k_6}= {a_9}+2,{a_{13}}= \frac{4 \left( {a_2}^2+{a_2}+\sqrt{1-{a_2} ({a_2}+2)}-1\right) }{{a_2}^2},\quad \gamma = \frac{3 \left( {a_2}+\sqrt{1-{a_2} ({a_2}+2)}+3\right) }{2 ({a_2}+2)^2},\\ \beta = \frac{-{a_2} ({a_2} ({a_9}+4)+4 {a_9}+10)+6 \sqrt{1-{a_2} ({a_2}+2)}-4 {a_9}+2}{({a_2}+2)^2}, \end{array}\right. \end{aligned}$$

(47)

then Eq. (45), results in,

$$\begin{aligned} P(x,y,z,t)= & ({a_1} x+{a_2} y+{a_9} t+z)^2+{a_{11}} e^{({a_9}+2) t+{k_1} x-2 y+z}\nonumber \\ & +{a_{12}} e^{({a_9}+2) t+{k_3} x-2 y+z}+\frac{4 \left( {a_2}^2+{a_2}+\sqrt{1-{a_2} ({a_2}+2)}-1\right) }{{a_2}^2}\nonumber \\ & +\left( \left( -\sqrt{1-{a_2} ({a_2}+2)}-1\right) y+{a_6} x+{a_9} t+z\right) ^2. \end{aligned}$$

(48)

Plugging in Eqs. (46) and (48) into Eq. (5) yields the solution to Eq. (4).

3.7 Rogue wave solutions

The following function is utilized to obtain rogue wave solutions for Eq. (4):

$$\begin{aligned} & P(x,y,z,t)\nonumber \\ & \quad =({a_1} x+{b_1} y+{d_1} t+z)^2+({a_2} x\nonumber \\ & \qquad +{b_2} y+{d_2} t+z)^2\nonumber \\ & \qquad +{k_1} \cosh ({a_3} x+{b_3} y+{d_3} t+z)+{k_2}. \end{aligned}$$

(49)

Equation (49) can be plugged into Eq. (22) to yield the following solution set:

Set 1:

$$\begin{aligned} \left\{ \begin{array}{l} {b_2}= -\sqrt{1-{b_1} ({b_1}+2)}-1,\quad {k_2}= \frac{6 \left( 2 \left( \sqrt{1-{b_1} ({b_1}+2)}-1\right) +{b_1} \left( 2 \sqrt{1-{b_1} ({b_1}+2)}+{b_1} \left( {b_1}+\sqrt{1-{b_1} ({b_1}+2)}+3\right) \right) \right) }{{b_1}^2 ({b_1}+2)^2 \gamma },\\ {k_1}= 0,\quad \beta = \left( -{b_1}+\sqrt{1-{b_1} ({b_1}+2)}+1\right) \gamma -2, \end{array}\right. \end{aligned}$$

(50)

The outcome of inserting this solution set into Eq. (49) is:

$$\begin{aligned} P(x,y,z,t)= & ({a_1} x+{b_1} y+{d_1} t+z)^2+\left( {a_2} x+\left( -\sqrt{1-{b_1} ({b_1}+2)}-1\right) y+{d_2} t+z\right) ^2\nonumber \\ & +\frac{6 \left( 2 \left( \sqrt{1-{b_1} ({b_1}+2)}-1\right) +{b_1} \left( 2 \sqrt{1-{b_1} ({b_1}+2)}+{b_1} \left( {b_1}+\sqrt{1-{b_1} ({b_1}+2)}+3\right) \right) \right) }{{b_1}^2 ({b_1}+2)^2 \gamma }. \end{aligned}$$

(51)

Set 2:

$$\begin{aligned} \left\{ \begin{array}{l} {b_1}= -1+\frac{i}{\sqrt{3}},\quad {b_2}= -1+\frac{i}{\sqrt{3}},\quad {b_3}= -1-\frac{i}{\sqrt{3}},\quad {k_1}= -4,\quad \gamma = \frac{i \sqrt{3}}{4},\quad \beta = \frac{1}{2} i \left( \sqrt{3}+5 i\right) , \end{array}\right. \end{aligned}$$

(52)

subsequently, Eq. (49) yields,

$$\begin{aligned} & P(x,y,z,t)\nonumber \\ & \quad =\left( {a_1} x+{d_1} t+\left( -1+\frac{i}{\sqrt{3}}\right) y+z\right) ^2\nonumber \\ & \qquad +\left( {a_2} x+{d_2} t +\left( -1+\frac{i}{\sqrt{3}}\right) y+z\right) ^2\nonumber \\ & \qquad -4 \cosh \left( {a_3} x+{d_3} t+\left( -1-\frac{i}{\sqrt{3}}\right) y+z\right) \nonumber \\ & \qquad +{k_2}. \end{aligned}$$

(53)

Plugging in Eqs. (51) and (53) into Eq. (5) yields the solution to Eq. (4).

Fig. 1

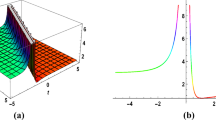
Visual depiction of Eq. (12) when $k_2=-1.2,k_4=2,k_3=3,\chi _8=-1,\chi _{10}=2,y=1,z=1$

Fig. 2

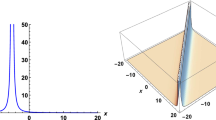
Visual depiction of Eq. (15) when $a=1,g=1,h=0.5,k_5=2,\chi _9=2,y=1.2,z=0.5$

Fig. 3

Visual depiction of Eq. (19) when $k_1=1,\chi _7=0.2,k_4=-0.02,k_3=-0.2,\chi _8=-1,\chi _3=-0.2,y=0.1,z=0.1$

4 Concluding remarks

This study investigated various methods for addressing the significant nonlinear equation (3+1)-dimensional generalized KdV equation, which is used to describe the waves on shallow water surfaces.

• First, two separate Bäcklund transformations with distinct exchange identities were carefully derived using the Hirota bilinear form. Eight parameters were used in the second transformation, whereas eleven were used in the first. By means of this conversion procedure, solutions with exponential and rational functions were acquired. Using the first Bäcklund transformation, a singular dark soliton was obtained as a result of the rational function solution (Fig. 1), and a bright soliton was obtained as a result of the exponential function solution (Fig. 2). Similarly, using the rational solution of the second Bäcklund transformation, a singular dark soliton was observed as a result of the rational function solution (Fig. 3), and a singular bright soliton was seen as a result of the exponential function solution (Fig. 4).

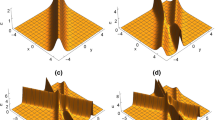
• Furthermore, a variety of solutions were obtained by applying the bilinear form and distinct ansatz, such as breather, rogue waves, lump cross kink wave solutions, and two-, three-, and multi-wave solutions. These solutions, which illustrate the unique characteristics and behaviors found in these wave solutions, are displayed in Figs. 5, 6, 7, 8, 9, 10 and 11. The solutions are significant because they provide insight into the intricate dynamics of nonlinear wave equations, advancing both theoretical knowledge and possible real-world applications in domains including fluid dynamics, optical fibres, and plasma physics.

One important characteristic that both dark and bright solitons have in common is their robustness, which is crucial for guaranteeing their usefulness in optical communications. These solutions can also continue to move at the same speed and form over extended distances. These findings indicate that further research should be conducted because our studies are useful in addressing additional nonlinear partial differential equations that arise in various scientific domains.

Fig. 4

Graphical representation of Eq. (20) when $a=-5,g=1,h=0.5,k_5=0.2,\chi _3=0.2,y=1,z=1$

Fig. 5

Visual depiction of two-wave solution when (A) ${n_4}= -0.1,{n_1}= 1,z= 1,{n_2}= -1,y= 1,{a_1}= -5,{a_2}= 1,\beta = 1.1,{d_1}= 0.5,{d_2}= -1.1,{c_3}= 1,{d_3}= -1,{c_1}= 1,{c_2}= 1$, (B) $z= 5,{n_2}= 1,\gamma = 0.2,y= 2,{a_1}= 1,{a_2}= 1,\beta = 1,{d_1}= 1,{d_2}= 1,{c_1}= 0.1,{c_2}= 0.1,{n_3}= 1.1$

Fig. 6

Visual depiction of three-wave solution when (A)${l_3}= 1,z= 1,{p_1}= 1,{p_4}= -1,{q_1}= -0.1,\gamma = -1,{p_9}= -1.1,y= 1,\beta = 1.2,\alpha = 5,{p_{12}}= -1.1,{p_{11}}= -0.1,{q_3}= 1.1,{p_3}= -1,{p_{10}}= 1,{p_2}= -0.2,{l_1}= 1.1$, (B)${l_3}= \frac{5}{9},z= 0,{p_1}= -0.1,{p_4}= -0.1,{q_1}= -0.1,\gamma = -0.1,{p_9}= -5.1,y= 0,\beta = 6.2,{p_{12}}= -5.1,{p_{11}}= -5.1,{q_3}= -5.1,{p_3}= -5.1,{p_2}= -5.1,{p_{10}}= -5.1$

Fig. 7

Visual depiction of Multi-wave solution when (A)${n_3}= 1,{c_1}= -0.7,{a_3}= -1,{c_3}= 1.51,y= 1,z= 1,\beta = -1.5,\gamma = -5,{b_3}= 12,{b_1}= 1,{a_1}= 2$, (B)${a_2}= -2.1,y= 1,z= 0,{n_1}= 5,\beta = -1.5,\gamma = -5,{b_1}= 1,{b_2}= -2,{a_1}= 2$

Fig. 8

Visual depiction of breather solution when (A)$y= 1,z= 1,{n_1}= 0.1,\beta = 0.01,{a_1}= 2,{q_0}= 1.2,{q_1}= 0.1,{d_1}= 1,{d_2}= 2,{c_1}= 0.2,{c_2}= 0.1,{n_2}= 0.1$, (B)${a_2}= 1,y= 1,z= 1,{n_1}= 0.1,\beta = 0.1,{q_0}= 0.2,{q_1}= 0.1,{d_1}= 1.01,{d_2}= 1.02,{c_1}= 2,{c_2}= -1,{n_2}= 0.1$

Fig. 9

Visual depiction of lump-kink solution when ${b_5}= -1.5,y= 1,{b_8}= 1.3,{b_2}= -0.5,\gamma = 0.02,{b_1}= 2.1,z= 0$

Fig. 10

Visual depiction of lump cross two kink wave solution when (A)${a_1}= -0.4,{a_9}= 1.1,{a_6}= -0.1,{a_11}= 0.6,y= 1,{k_1}= 1,{a_6}= 1,{a_1}= 1,{a_2}= 1,z= 1,{a_7}= -0.3$, (B)${a_{12}}= 1,{a_2}= 2,{a_1}= -1,{a_9}= -5,{a_6}= -0.1,{a_{11}}= 5,y= 1,z= 1,{k_1}= -0.5,{k_3}= -5.8$

Fig. 11

Visual depiction of rogue wave solution when (A)${d_2}= -0.2,{a_2}= 1,{d_2}= -0.1,y= 1,{b_1}= -1,{a_1}= -0.1,z= 5,{d_1}= 2,\gamma = 2$, (B)${d_2}= 1.2,{k_2}= -0.11,{a_2}= 1.1,{d_2}= -2.1,y= 1,{a_3}= 0,{a_1}= -1.1,z= 5,{d_1}= -2.5,{d_3}= 0$

Fig. 12

Plotting code for Fig. 1

Appendix

See the Fig. 12.