1 Introduction

Finding exact solutions of nonlinear equations plays an imperative role in understanding the processes and phenomena of many nonlinear models arising in fluids, dynamics, physical science, and nonlinear optical fibers. In the theory of solitons, different types of solutions such as bell-shaped, kink, cusp, periodic and others are identified by using suggested forms of solutions either in terms of exponential, trigonometric, or hyperbolic functions as in the cases of simplified bilinear method, tanh expansion, \((G'/G)\) expansion, Riccati expansion, sine–cosine function, sech–csch function, Kudryashov expansion, unified expansion, Lie symmetry, and many other methods ( [1,2,3,4,5,6,7,8,9,10]).

Recently, new types of solitons are produced by combining the Hirota bilinear method and the Cole–Hopf transformation \(u=a(\ln {f})_x\) or \(u=b(\ln {f})_{xx}\), see ( [11,12,13,14,15,16,17,18,19,20]). If f is chosen to be a polynomial, then the resulting solution u is identified as the lump soliton. If f is the combination of polynomial and sine/cosine, then u is of periodic-lump type. The breather-soliton waves are obtained if f is a combination of sine/cosine and the exponential functions. Finally, the two-wave soliton type can be obtained by combining sin–sinh or cos–cosh with the exponential functions.

In this paper, we investigate new features of solitary wave solutions to the generalized perturbed-KdV equation which reads as

$$\begin{aligned} u_t +\alpha u_x +\beta u u_x +\gamma u_{xxx}=0, \end{aligned}$$
(1.1)

where \(u=u(x,t)\) represents the free surface advancement, \(\alpha \) is the perturbation parameter known as the Coriolis effect, and \(\beta ,\ \gamma \) are the nonlinearity and dispersion factors, respectively. The perturbed-KdV model describes the physical mechanism of sound propagation in fluid and appears in the applications of aerodynamics, acoustics, and medical engineering. Special case of (1.1) has been discussed in [21], for \(\beta =\frac{3}{2}\) and \(\gamma =\frac{1}{6}\). The authors extracted different lumps and breather solutions but upon assigning a wrong choice of the Cole–Hopf transformation \(u=R(\ln {f(x,t)})_{xx}\) by taking \(R=2\).

The motivation of the current work is threefold: First, we derive the correct value of R that covers, in particular, the case of [21] and, in general, the case of (1.1). Second, we assign different choices of f(x, t), to construct new lump-soliton, lump-periodic, single-stripe soliton, breather waves, and two-wave solutions to (1.1). Finally, we investigate the impact of the involved model’s parameters on the propagation form of the retrieved solutions to the proposed model.

The paper is organized as follows: Section (2) deals with the construction of Hirota’s bilinear form to the perturbed-KdV equation. Then, we derive both lump and periodic-lump solutions in Sect. (3). The single-stripe soliton and breather-wave solutions are extracted in Sects. (4) and (5), respectively. The two-wave solutions are investigated in Sect. (6), and some dynamical aspects are discussed in Sect. (7). Finally, some concluding remarks based on the obtained results are presented in Sect. (8).

2 Hirota bilinear form of the perturbed-KdV equation

To find the Hirota’s form to (1.1), we apply the simplified bilinear method. First, we start with the following function

$$\begin{aligned} u(x,t)=e^{s x-r t}. \end{aligned}$$
(2.2)

Then, we substitute (2.2) in the linear terms of (1.1) to obtain the dispersion relation as

$$\begin{aligned} r=\alpha s+\gamma s^3. \end{aligned}$$
(2.3)

The second step is to bring the following function

$$\begin{aligned} k(x,t)=1+C\ e^{s x-\left( \alpha s+\gamma s^3\right) t}, \end{aligned}$$
(2.4)

and to apply one of the Cole–Hopf transformations. In particular, we consider

$$\begin{aligned} u(x,t)=R \left( \ln (k(x,t))\right) _{xx}. \end{aligned}$$
(2.5)

To find R, we insert (2.5) in (1.1) to get that

$$\begin{aligned} R=\frac{12\gamma }{\beta }. \end{aligned}$$
(2.6)

As the third step, we update the assumption of the function u to take the following action:

$$\begin{aligned} u(x,t)=\psi _{xx}(x,t). \end{aligned}$$
(2.7)

Substituting (2.7) in (1.1) and simplifying by integration with respect to x, we reach at the following relation regarding the new function \(\psi \)

$$\begin{aligned} \psi _{xt}+\alpha \psi _{xx}+\frac{\beta }{2}\left( \psi _{xx}\right) ^2+\gamma \psi _{xxxx}=0. \end{aligned}$$
(2.8)

Then, we choose \(\psi \) as

$$\begin{aligned} \psi (x,t)=\frac{12\gamma }{\beta } \ln (f(x,t)). \end{aligned}$$
(2.9)

Finally, we insert (2.9) in (2.8) to deduce the following relation:

$$\begin{aligned}&f f_{x t}- f_x f_t +\alpha f f_{x x}-\alpha f_{x}^2+\gamma f f_{x x x x}\nonumber \\&\quad -4\gamma f_x f_{x x x}+3\gamma f_{x x}^2=0. \end{aligned}$$
(2.10)

By using Hirota’s bilinear operators, (2.10) is written as

$$\begin{aligned} (D_x D_t+\alpha D_x ^2+\gamma D_x ^4)f.f=0, \end{aligned}$$
(2.11)

where D represents the Hirota bilinear operator defined as

$$\begin{aligned} D_x^{l}D_t^{k}f.g= & {} \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^l \left( \frac{\partial }{\partial t}\right. \nonumber \\&\left. -\frac{\partial }{\partial t'}\right) ^k f(x,t)g(x',t')|_{x'=x,t'=t}, \end{aligned}$$
(2.12)

and \(f,\ g \in \mathbf {C}^{\infty }(\mathbb {R}^{2})\).

3 Lump-type solutions

In this section, we derive two types of lump solutions to (1.1) by choosing f to be either quadratic function, or a combination of quadratic function and cosine function.

3.1 Lump soliton

To obtain lump soliton, we consider the following assumption

$$\begin{aligned} f=X^T A X+u_0, \end{aligned}$$
(3.13)

where \(X=(1,x,t)^T\), \(A=(a_{i,j})_{3\times 3}\) is a symmetric matrix, and \(a_{ij},u_0\) are real constants to be determined. By expanding (3.13), we get

$$\begin{aligned}&f(x,t)=a_{1,1}+ a_{2,1}t+ a_{3,1} x+x (a_{1,2}+ a_{2,2}t+ a_{3,2} x)\nonumber \\&\quad +t (a_{1,3}+ a_{2,3}t+ a_{3,3}x)+u_0. \end{aligned}$$
(3.14)

Next, we insert (3.14) in (2.10) and solve for the unknowns \(a_{ij},\ u_0\). By doing so, we obtain two cases:

Case I:

$$\begin{aligned} a_{2,3}= & {} -\alpha a_{2,2}-\alpha a_{3,3}, \\ u_0= & {} \frac{\alpha a_{1,2}^2+a_{3,1}(a_{1,3}+a_{2,1}+\alpha a_{3,1})+a_{1,2}(a_{1,3}+a_{2,1}+2\alpha a_{3,1})-a_{1,1}(a_{2,2}+a_{3,3})}{a_{2,2}+a_{3,3}}, \\ a_{3,2}= & {} 0, \end{aligned}$$

where \(a_{1,1},\ a_{1,2},\ a_{1,3},\ a_{2,1},\ a_{2,2},\ a_{3,1}\) and \(a_{3,3}\) are free parameters. Accordingly,

$$\begin{aligned} f=\frac{(a_{1,2}+ a_{3,1}+ (a_{2,2}+a_{3,3})t)(\alpha a_{1,2}+a_{1,3}+a_{2,1}+\alpha a_{3,1}+ (a_{2,2}+a_{3,3})(x-\alpha t))}{a_{2,2}+a_{3,3}}. \end{aligned}$$
(3.15)

Recalling (2.7), the first lump soliton to (1.1) is

$$\begin{aligned}&u_1(x,t)\nonumber \\&\quad =-\frac{12 \gamma (a_{2,2}+a_{3,3})^2}{\beta (\alpha a_{1,2}+a_{1,3}+a_{2,1}+\alpha a_{3,1}+(a_{2,2}+a_{3,3})(x-\alpha t))^2}.\nonumber \\ \end{aligned}$$
(3.16)

Case II:

$$\begin{aligned} a_{2,1}= & {} -\alpha a_{1,2}-a_{1,3}-\alpha a_{3,1}, \\ a_{2,3}= & {} a_{3,2}=0, \\ a_{3,3}= & {} -a_{2,2}. \end{aligned}$$

Thus,

$$\begin{aligned} f=u_0+a_{1,1}+(a_{1,2}+a_{3,1})(x-\alpha t), \end{aligned}$$
(3.17)

with \(a_{1,1},\ a_{1,2},\ a_{1,3},\ a_{2,2},\ a_{3,1}\) and \(u_0\) being free parameters. By this case, the second lump soliton is

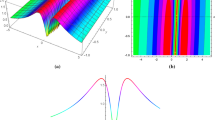
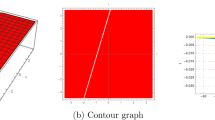
$$\begin{aligned} u_2(x,t)=-\frac{12 \gamma (a_{1,2}+a_{3,1})^2}{\beta (u_0+a_{1,1}+(a_{1,2}+a_{3,1})(x-\alpha t))^2}.\nonumber \\ \end{aligned}$$
(3.18)

In Fig. 1, we show the physical structure of the first lump soliton (3.16), which is similar in shape to (3.18).

Fig. 1
figure 1

2D and 3D plots of \(u_1(x,t)\) where \(\alpha =\beta =-1\), \(\gamma =1\), \(a_{2,2}=2\), \(a_{3,3}=a_{1,2}=a_{1,3}=a_{2,1}=a_{3,1}=1\)

Full size image

3.2 Lump-periodic solution

To construct lump-periodic solution to (1.1), f is to be chosen as a linear combination of quadratic and cosine functions, i.e.

$$\begin{aligned} f=X^T A X+\omega \cos {(p_1 x+p_2 t+p_3)}+ \sigma . \end{aligned}$$
(3.19)

We substitute (3.19) in (2.10) and look up for the coefficients of different polynomials of x, t and trigonometric functions. Then, we set each coefficient to zero and solve the resulting system to get the following output:

$$\begin{aligned} \omega= & {} \mp \frac{a_{1,2}+a_{3,1}}{p_1},\nonumber \\ p_2= & {} -\alpha p_1+\gamma p_1^3,\nonumber \\ a_{3,2}= & {} a_{2,3}=0,\nonumber \\ a_{3,3}= & {} -a_{2,2},\nonumber \\ a_{1,3}= & {} -\alpha a_{1,2}+3\gamma p_1^2 a_{1,2}- a_{2,1}- \alpha a_{3,1}+3 \gamma p_1^2 a_{3,1}.\nonumber \\ \end{aligned}$$
(3.20)

Let \(\triangle =p_1(x-\alpha t)+\gamma p_1^3 t+p_3\), \(\Box =\sigma +a_{1,1}+a_{1,2}(x-\alpha t)+ a_{3,1} x-\alpha a_{3,1} t\) and \(T=a_{1,2}+a_{3,1}\). Then, f has the following form

$$\begin{aligned}&f=\sigma + a_{1,1}+ a_{2,1} t+T x+ a_{2,2} x t\pm \frac{T \cos {(\triangle )}}{p_1}\nonumber \\&\quad +t((3 \gamma p_1^2-\alpha )T- a_{2,1}- a_{2,2}x). \end{aligned}$$
(3.21)

Therefore, the lump-periodic solution to (1.1) is

$$\begin{aligned} u_3(x,t)=\frac{12\gamma T\left( -T(\sin {(\triangle )}\mp 1)^2\mp p_1 \cos {(\triangle )}\left( \Box \pm \frac{\cos {(\triangle )}T}{p_1}+3\gamma p_1^2 T t\right) \right) }{\beta (\Box \pm \frac{T \cos {(\triangle )}}{p_1}+3\gamma p_1^2 T t)^2}. \end{aligned}$$
(3.22)

In Fig. 2, we present the physical structure of the lump-periodic solution (3.22).

Fig. 2
figure 2

2D and 3D plots of \(u_3(x,t)\) where \(\alpha =\beta =\gamma =1\), \(a_{1,1}=a_{1,2}=a_{3,1}=\sigma =p_1=p_3=1\)

Full size image

4 Single-stripe soliton solutions

The approach for finding single-stripe solitons is known as a simplified bilinear method. They are similar to those steps illustrated earlier and given by (2.2)-(2.6). However, it can be derived directly using (2.9) and assume f as

$$\begin{aligned} f=1+c e^{d_1 x+ d_2 t+d_3}, \end{aligned}$$
(4.23)

where \(d_i,\ i=1,2,3\) and \(c\ne 0\) are unknown real constants to be determined. Substituting of (4.23) in (2.10) gives that \(d_2=-\alpha d_1-\gamma d_1^3\), where \(d_1\) and \(d_3\) are arbitrary constants. Thus, the single-stripe soliton solution of (1.1) is

$$\begin{aligned} u_4(x,t)=\frac{12c\, \gamma \, e^{(x-\alpha t)d_1+\gamma t d_1^3+d_3} d_1^2}{\beta (e^{\gamma t d_1^3}+c\, e^{(x-\alpha t)d_1+d_3})^2}. \end{aligned}$$
(4.24)

5 Breather-wave solution

To find some families of breather-wave solutions, we consider the following test function

$$\begin{aligned} f\!=\!\epsilon _1 \cos {(p_2(x\!+\! b_2 t))}\!+\!\epsilon _2 e^{p_1(x+ b_1 t)}\!+\! e^{-p_1(x+ b_1 t)}.\nonumber \\ \end{aligned}$$
(5.25)

where \(\epsilon _i,\ p_i,\ b_i:\ i=1,2\) are real constants to be determined later. Substituting (5.25) in the bilinear form (2.10) and equating the coefficients of exponentials or trigonometric functions to zero, we get the following nonlinear algebraic system:

$$\begin{aligned} 0= & {} \alpha p_1^2 \epsilon _1 \epsilon _2+b_1 p_1^2 \epsilon _1 \epsilon _2+ \gamma p_1^4 \epsilon _1 \epsilon _2-\alpha p_2^2 \epsilon _1 \epsilon _2\\&\quad - b_2 p_2^2 \epsilon _1 \epsilon _2-6 \gamma p_1^2 p_2^2 \epsilon _1 \epsilon _2+ \gamma p_2^4 \epsilon _1 \epsilon _2, \\ 0= & {} \alpha p_1^2 \epsilon _1 +b_1 p_1^2 \epsilon _1 + \gamma p_1^4 \epsilon _1 -\alpha p_2^2 \epsilon _1- b_2 p_2^2 \epsilon _1 \\&\quad -6 \gamma p_1^2 p_2^2 \epsilon _1+ \gamma p_2^4 \epsilon _1, \\ 0= & {} 2\alpha p_1 p_2 \epsilon _1 \epsilon _2+b_1 p_1 p_2 \epsilon _1 \epsilon _2+ b_2 p_1 p_2 \epsilon _1 \epsilon _2\\&\quad +4 \gamma p_1^3 p_2 \epsilon _1 \epsilon _2- 4\gamma p_1 p_2^3 \epsilon _1 \epsilon _2, \\ 0= & {} -2\alpha p_1 p_2 \epsilon _1 -b_1 p_1 p_2 \epsilon _1 \\&\quad - b_2 p_1 p_2 \epsilon _1 -4 \gamma p_1^3 p_2 \epsilon _1+ 4\gamma p_1 p_2^3 \epsilon _1, \\ 0= & {} 4\alpha p_1^2 \epsilon _2 +4b_1 p_1^2 \epsilon _2+16 \gamma p_1^4 \epsilon _2 -\alpha p_2^2 \epsilon _1^2 \\&\quad -b_2 p_2^2 \epsilon _1^2 +4 \gamma p_2^4 \epsilon _1^2. \end{aligned}$$

Solving the above system leads to

$$\begin{aligned} b_1= & {} -\alpha -\gamma p_1^2+3 \gamma p_2^2,\\ b_2= & {} -\alpha -3\gamma p_1^2+\gamma p_2^2, \\ \epsilon _2= & {} -\frac{p_2^2 \epsilon _1^2}{4p_1^2}, \end{aligned}$$

with \(\epsilon _1,\ p_i: i=1,2\) being free parameters. Let \(\lambda _1=p_1(-x+\alpha t+\gamma t p_1^2-3\gamma t p_2^2)\) and \(\lambda _2=p_2(x-\alpha t-3\gamma t p_1^2+\gamma t p_2^2)\), and we get

$$\begin{aligned} f=\epsilon _1 \cos {(\lambda _2)}+ e^{\lambda _1}-\frac{p_2^2 \epsilon _1^2 e^{-\lambda _1}}{4p_1^2}. \end{aligned}$$
(5.26)

Accordingly, the breather-wave solution to (1.1) is

$$\begin{aligned} \begin{aligned} u_5(x,t)&=(12\gamma (-(p_1 e^{\lambda _1}+p_2 \epsilon _1 \sin {(\lambda _2)}+\frac{p_2^2 \epsilon _1^2 e^{-\lambda _1}}{4p_1})^2\\&\quad +(e^{\lambda _1}+\epsilon _1 \cos {(\lambda _2)} -\frac{p_2^2 \epsilon _1^2 e^{-\lambda _1}}{4p_1^2})(p_1^2 e^{\lambda _1}+\frac{p_2^2 \epsilon _1}{4}\\&\qquad (-4\cos {(\lambda _2)}-\epsilon _1 e^{-\lambda _1}))))/(\beta (e^{\lambda _1}+\epsilon _1 \cos {(\lambda _2)}\\&\quad -\frac{p_2^2 \epsilon _1^2 e^{-\lambda _1}}{4p_1^2})^2). \end{aligned}\nonumber \\ \end{aligned}$$
(5.27)

In Fig. 3, we present the physical structure of the breather-wave solution (5.27).

Fig. 3
figure 3

2D and 3D plots of \(u_5(x,t)\) where \(\beta =\gamma =-1\), \(\alpha =p_1=p_2=\epsilon _1=1\)

Full size image

6 Two-wave solution

To find the two-wave solution to the perturbed-KdV equation, we consider the following test function:

$$\begin{aligned}&f=\omega _1 e^{\mu t+x}+\omega _2 e^{-(\mu t+x)}+\omega _3 \sin {(c_1 t+x)}\nonumber \\&\quad +\omega _4 \sinh {(c_2 t+x)}. \end{aligned}$$
(6.28)

To get information about the values of \(\omega _j:\ (j=1,2,3,4),\ c_1,\ c_2\) and \(\mu \), we substitute (6.28) in Eq. (2.10). Then, we collect the coefficients of same terms and set each to zero to obtain the following system:

$$\begin{aligned} 0= & {} -2\alpha \omega _1 \omega _3-\mu \omega _1 \omega _3-c_1 \omega _1 \omega _3, \\ 0= & {} -4\gamma \omega _1 \omega _3+\mu \omega _1 \omega _3-c_1 \omega _1 \omega _3, \\ 0= & {} 2\alpha \omega _1 \omega _4+8\gamma \omega _1 \omega _4+\mu \omega _1 \omega _4+c_2 \omega _1 \omega _4, \\ 0= & {} 2\alpha \omega _2 \omega _3+\mu \omega _2 \omega _3+c_1 \omega _2 \omega _3, \\ 0= & {} -4\gamma \omega _2 \omega _3+\mu \omega _2 \omega _3-c_1 \omega _2 \omega _3, \\ 0= & {} 2\alpha \omega _2 \omega _4+8\gamma \omega _2 \omega _4+\mu \omega _2 \omega _4+c_2 \omega _2 \omega _4, \\ 0= & {} -2\alpha \omega _3 \omega _4-c_1 \omega _3 \omega _4-c_2 \omega _3 \omega _4, \\ 0= & {} -4\gamma \omega _3 \omega _4-c_1 \omega _3 \omega _4+c_2 \omega _3 \omega _4, \\ 0= & {} 4\alpha \omega _1 \omega _2+16\gamma \omega _1 \omega _2+4\mu \omega _1 \omega _2-\alpha \omega _4^2-4\gamma \omega _4^2\\&\quad -c_2 \omega _4^2-\alpha \omega _3^2+4 \gamma \omega _3^2-c_1 \omega _3^2. \end{aligned}$$

By solving the above system, we retrieve three solution’s sets:

Set(I): \(\omega _2=-\frac{\omega _4^2}{4\omega _1},\ \omega _3=0,\ c_2=-2\alpha -8\gamma -\mu \). Then, f explicitly is

$$\begin{aligned}&f=\omega _1 e^{x+\mu t}\nonumber \\&\quad -\frac{\omega _4^2 e^{-x-\mu t}}{4 \omega _1}+\omega _4 \sinh {(x-t(2\alpha +8\gamma +\mu ))}.\nonumber \\ \end{aligned}$$
(6.29)

Thus, the sixth recovery solution to (1.1) is

Fig. 4
figure 4

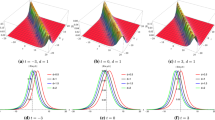
Propagations of \(u_6(x,t)\) for different values of: a The perturbation parameter \(\alpha \) where \(t=\beta =\gamma =\omega _1=\omega _4=1\). b The nonlinearity parameter \(\beta \) where \(t=\alpha =\gamma =\omega _1=\omega _4=1\). c The dispersion parameter \(\gamma \) where \(t=\alpha =\beta =\omega _1=\omega _4=1\)

Full size image
$$\begin{aligned} u_6(x,t)= & {} \frac{12\gamma }{\beta }-\frac{12\gamma (\omega _1 e^{x+\mu t}+\omega _4 \cosh {(x-t(2\alpha +8\gamma +\mu ))}+\frac{\omega _4^2 e^{-x-\mu t}}{4\omega _1})^2}{\beta (\omega _1 e^{x+\mu t}+\omega _4 \sinh {(x-t(2\alpha +8\gamma +\mu ))}-\frac{\omega _4^2 e^{-x-\mu t}}{4\omega _1})^2},\nonumber \\= & {} -\frac{96 \gamma \omega _1 \omega _4 e^{2 (t (\alpha +4 \gamma )+x)}}{\beta \left( \omega _4 e^{2 t (\alpha +4 \gamma )}-2 e^{2 x} \omega _1\right) {}^2}. \end{aligned}$$
(6.30)

Set(II): \(\omega _2=-\frac{\omega _3^2}{4\omega _1},\ \omega _4=0,\ \mu =-\alpha +2\gamma ,\ c_1=-\alpha -2\gamma \). Then, f explicitly is

$$\begin{aligned} f=\omega _1 e^{\zeta }-\frac{\omega _3^2 e^{-\zeta }}{4 \omega _1}+\omega _3 \sin {(\eta )}, \end{aligned}$$
(6.31)

where \(\zeta =x-t(\alpha -2\gamma )\) and \(\eta =x-t(\alpha +2\gamma )\). Hence, the seventh recovery solution to (1.1) is:

$$\begin{aligned} u_7(x,t)= & {} \frac{12\gamma (\omega _1 e^\zeta -\omega _3 \sin {(\eta )}-\frac{\omega _3^2 e^{-\zeta }}{4\omega _1})}{\beta (\omega _1 e^\zeta +\omega _3 \sin {(\eta )}-\frac{\omega _3^2 e^{-\zeta }}{4\omega _1})}-\frac{12\gamma (\omega _1 e^\zeta +\omega _3 \cos {(\eta )}+\frac{\omega _3^2 e^{-\zeta }}{4\omega _1})^2}{\beta (\omega _1 e^\zeta +\omega _3 \sin {(\eta )}-\frac{\omega _3^2 e^{-\zeta }}{4\omega _1})^2},\nonumber \\= & {} -\frac{96 \gamma \omega _1 \omega _3 e^{\alpha t+2 \gamma t+x} \left( 4 \omega _3 \omega _1 e^{\alpha t+2 \gamma t+x}+4 \omega _1^2 e^{4 \gamma t+2 x} \cos (\eta )+\omega _3^2 e^{2 \alpha t} \cos (\eta )\right) }{\beta \left( -\omega _3^2 e^{2 \alpha t}+4 \omega _3 \omega _1 e^{\alpha t+2 \gamma t+x} \sin (\eta )+4 \omega _1^2 e^{4 \gamma t+2 x}\right) {}^2}. \end{aligned}$$
(6.32)

Set(III): \(\omega _1=0,\ \omega _2=0,\ \omega _3=-\omega _4,\ c_1=-\alpha -2\gamma ,\ c_2=-\alpha +2\gamma \). Then, f explicitly is:

$$\begin{aligned} f=-\omega _4 \sin {(\eta )}+\omega _4 \sinh {(\zeta )}. \end{aligned}$$
(6.33)

Accordingly, the eighth recovery solution to (1.1) is

$$\begin{aligned}&u_8(x,t)=-\frac{12\gamma (-\omega _4 \cos {(\eta )}+\omega _4 \cosh {(\zeta )})^2}{\beta (-\omega _4 \sin {(\eta )}+\omega _4 \sinh {(\zeta )})^2}\nonumber \\&\quad +\frac{12\gamma (\omega _4 \sin {(\eta )}+\omega _4 \sinh {(\zeta )})}{\beta (-\omega _4 \sin {(\eta )}+\omega _4 \sinh {(\zeta )})} \end{aligned}$$
(6.34)

7 Dynamics of the perturbed KdV

In this section, we study the impact of the perturbation, nonlinearity, and dispersion parameters, \(\alpha \), \(\beta \), \(\gamma \), being acting on the propagation of the perturbed KdV. To achieve this goal, we consider the obtained solution depicted earlier as the function \(u_6(x,t)\). We investigate the physical structures to this function by plotting some curves for different values of the assigned parameters. Figure 4 shows the dynamics of propagating \(u_6\), and three observations can be drawn:

  • The propagation is symmetric when \(\alpha \) changes its sign.

  • The propagation has a reflexive relation when \(\beta \) changes its sign.

  • The propagation is reflexive due to the sign of \(\gamma \).

8 Conclusion

In this study, we derived the Hirota bilinear form for the generalized perturbed-KdV equation. Then, the Cole–Hopf transformations are used, and different selections of the involved test function are elaborated to retrieve novel types of solitons such as lumps, breather-wave, and multi-wave solutions. Also, the dynamics of the model’s parameters, perturbation, nonlinearity, and dispersion are investigated.

For future work, we aim to extend the use of Hirota’s bilinear methods to study other important nonlinear applications arising in physical and engineering fields and higher-dimensional models.