1 Introduction

Integrable equations possess soliton solutions—exponentially localized solutions in certain directions [1]. They can also possess positon solutions—a kind of periodic solutions [2]—and complexiton solutions—combinations of solitons and positons [3]. The Hirota bilinear forms [4] play an important role in presenting solitons, positons and complexitons.

In contrast to soliton solutions, lump solutions are a kind of rational function solutions, localized in all directions in the space. Particular examples of lump solutions are found for many integrable equations such as the KPI equation [5–8], the three-dimensional three-wave resonant interaction equation [9], the B-KP equation [10], the Davey–Stewartson II equation [7] and the Ishimori I equation [11]. There are general searches for rational function solutions to the KdV equation, the Boussinesq equation and the Toda lattice equation (see, e.g., [12–14]), systematically through the Wronskian and Casoratian determinant techniques for integrable equations [15, 16]. Generalized bilinear forms are also used to compute rational function solutions to the generalized KdV, KP and Boussinesq equations [17–19]. A natural question arises what kind of lump solutions can exist for nonlinear partial differential equations which possess generalized bilinear forms.

The (3+1)-dimensional generalized KP and BKP (gKP and gBKP) equations are as follows [20]:

$$\begin{aligned} u_{xxxy}+3(u_xu_y)_x+u_{tx}+u_{ty}-u_{zz}=0, \end{aligned}$$
(1.1)

and

$$\begin{aligned} u_{ty}-u_{xxxy}-3(u_xu_y)_x+3u_{xz}=0. \end{aligned}$$
(1.2)

Under the transformation \(u=2(\text {ln}f)_x\), they become the Hirota bilinear equations

$$\begin{aligned} (D_x^3D_y+D_tD_x+D_tD_y-D_z^2)f\cdot f=0, \end{aligned}$$
(1.3)

and

$$\begin{aligned} (D_tD_y-D_x^3D_y+3D_xD_z)f\cdot f=0, \end{aligned}$$
(1.4)

respectively. Here, \(D_t,D_x,D_y\) and \(D_z\) are Hirota bilinear derivatives [4], which have connections with Kac–Moody algebras and quantum field theory [21]. For the above bilinear gKP and gBKP equations, resonant solitons are presented, forming linear subspaces of solutions [20], and three-wave solutions are computed by using the multiple exp-function method [22].

In this paper, we would like to consider the following two generalized bilinear equations in (3+1)-dimensions, called the (3+1)-dimensional bilinear p-gKP and p-gBKP equations:

$$\begin{aligned} (D_{p,x}^3D_{p,y}+D_{p,t}D_{p,x}+D_{p,t}D_{p,y}-D_{p,z}^2)f\cdot f=0, \end{aligned}$$
(1.5)

and

$$\begin{aligned} (D_{p,t}D_{p,y}-D_{p,x}^3D_{p,y}+3D_{p,x}D_{p,z})f\cdot f=0, \end{aligned}$$
(1.6)

with p being an arbitrarily given natural number, often a prime number, and the generalized bilinear operators being defined by [23]:

$$\begin{aligned}&(D_{p,x_1}^{n_1}\cdots D_{p,x_M}^{n_M}f\cdot g)(x_1,\cdots ,x_M) \nonumber \\&\quad = \prod _{i=1}^M\bigl (\frac{\partial }{\partial {x_i}} +\alpha \frac{\partial }{\partial {x_i'}}\bigr )^{n_i} f(x_1,\cdots ,x_M)g(x_1',\cdots ,x_M' )\nonumber \\&\qquad \quad \times \, \bigl .\bigr |_{x_1'=x_1,\cdots ,x_M'=x_M}\nonumber \\&\quad = \prod _{i=1}^M \sum _{l_i=0}^{n_i} \alpha ^{l_i} {n_i \atopwithdelims ()l_i} \frac{\partial ^{n_i-l_i}}{\partial {x_i} ^{n_i-i_i} } f(x_1,\cdots ,x_M) \nonumber \\&\qquad \quad \times \frac{\partial ^{l_i} }{\partial {x_i}^{l_i}} g(x_1,\cdots ,x_M ), \qquad \quad \end{aligned}$$
(1.7)

where \(n_1,\cdots ,n_M\) are arbitrary nonnegative integers, and for an integer m, the m-th power of \(\alpha \) is computed as follows:

$$\begin{aligned}&\alpha ^m=(-1) ^{r(m)},\ \text {if}\ m\equiv r(m)\ \text {mod}\,p\nonumber \\&\quad \, \text {with}\ {0\le r(m)< p}. \end{aligned}$$
(1.8)

The choices for powers in (1.8) just give a rule to take the signs: \(+1\) or \(-1\). When \(p=2k\), \(k\in {\mathbb {N}}\), the two generalized bilinear Eqs. (1.5) and (1.6) simplify to the two Hirota bilinear Eqs. (1.3) and (1.4), respectively.

With symbolic computation with Maple, we will do a search for positive quadratic function solutions to the dimensionally reduced bilinear p-gKP and p-gBKP equations from taking \(z=x\) or \(z=y\) in Eqs. (1.5) and (1.6). To search for quadratic function solutions, we begin with

$$\begin{aligned}&f=g^2+h^2+a_{9}, \ g=a_1 x +a_2 y +a_3 t+a_4,\nonumber \\&h=a_5 x +a_6 y +a_7 t+a_{8}, \end{aligned}$$
(1.9)

where \(a_i\), \(1\le i\le 9\), are real parameters to be determined. In the two-dimensional space, a sum involving one square does not generate exact solutions which are rationally localized in all directions in the space, through the dependent variable transformations \(u=2(\text {ln}f)_x\) or \(u=2(\text {ln} f)_{xx}\). Noting that the generalized bilinear equations

$$\begin{aligned} P(D_{p,x},D_{p,y},D_{p,z},D_{p,t})f\cdot f=0 \end{aligned}$$

with a given polynomial P but different values of \(p\ge 2\) have the same set of quadratic function solutions, and the resulting quadratic function solutions will generate the same set of lump solutions to the corresponding nonlinear p-gKP and p-gBKP equations with different values of p. Because of the same set of solutions, our discussion will focus on the case of \(p=3\). The sufficient and necessary conditions to guarantee analyticity and localization of the corresponding rational function solutions will be explicitly presented. A few concluding remarks will be given at the end of the paper.

2 Lump solutions to the reduced p-gKP equations

2.1 Reduction with \(z=x\)

When \(p=3\), the (3+1)-dimensional bilinear p-gKP Eq. (1.5) reduces to the following generalized bilinear equation in (2+1)-dimensions:

$$\begin{aligned}&B_{p\text {-gKP}_x}(f):= (D_{3,x}^3D_{3,y} +D_{3,t}D_{3,x}\nonumber \\&\qquad \quad +D_{3,t} D_{3,y}- D_{3,x}^2)f\cdot f \nonumber \\&\quad =2( 3 f_{xx}f_{xy} - f_tf_x + f_{tx}f + f_{ty}f - f_tf_y \nonumber \\&\qquad \quad + {f_{x}}^2 - f_{xx}f) =0, \end{aligned}$$
(2.1)

under \(z=x\). Through the link between f and u:

$$\begin{aligned} u=2(\ln f)_{x}, \end{aligned}$$
(2.2)

the reduced bilinear p-gKP Eq. (2.1) is transformed into

$$\begin{aligned}&P_{p\text {-gKP}_x}(u)= \frac{9}{8} u^2 u_x v +\frac{3}{8} u^3 u_y +\frac{3}{4} u u_{xx}v \nonumber \\&\quad +\frac{3}{4} {u_x} ^2 v + \frac{3}{4} u ^2 u_{xy} +\frac{9}{4} u u_x u_y +\frac{3}{2} u_{xx}u_y \nonumber \\&\quad +\frac{3}{2} u_x u_{xy}-u_{xx} +u_{tx}+u_{ty}=0 , \end{aligned}$$
(2.3)

where \(u_y=v_x\). The transformation (2.2) is also a characteristic one in establishing Bell polynomial theories of integrable equations [24, 25], and the actual relation between the reduced p-gKP Eq. (2.3) and the reduced bilinear p-gKP Eq. (2.1) reads

$$\begin{aligned} P_{p\text {-gKP}_x}(u)= \Bigl [\frac{B_{p\text {-gKP}_x}(f)}{f^2}\Bigr ]_{x}. \end{aligned}$$
(2.4)

Therefore, if f solves the reduced bilinear p-gKP Eq. (2.1), then \(u=2(\ln f)_{x}\) will solve the reduced p-gKP Eq. (2.3).

For Eq. (2.1), a direct symbolic computation with f in (1.9) leads to the following set of constraining equations for the parameters:

$$\begin{aligned}&\Bigl \{ a_{{1}}=a_{{1}},\nonumber \\&\quad \ a_{{2}}={\frac{{a_{{1}}}^{2}a_{{3}}-a_{{1}}{ a_{{3}}}^{2}+2\,a_{{1}}a_{{5}}a_{{7}}-a_{{1}}{a_{{7}}}^{2}-a_{{3}}{a_{ {5}}}^{2}}{{a_{{3}}}^{2}+{a_{{7}}}^{2}}},\nonumber \\&\quad a_{{3}}=a_{{3}},\ a_{{4}}=a_{{4 }}, \quad a_{{5}}=a_{{5}},\nonumber \\&\quad \ a_{{6}}=-{\frac{{a_{{1}}}^{2}a_{{7}}{-}2\,a_{{1}}a_{ {3}}a_{{5}}{+}{a_{{3}}}^{2}a_{{5}}{-}{a_{{5}}}^{2}a_{{7}}+a_{{5}}{a_{{7}}} ^{2}}{{a_{{3}}}^{2}+{a_{{7}}}^{2}}},\nonumber \\&\quad a_{{7}}=a_{{7}},\ a_{{8}}=a_{{8}}, \nonumber \\&\quad a_ {{9}}= \frac{3({a_1}^2+{a_5}^2)^2 [(a_1-a_3)a_3+(a_5-a_7)a_7]}{ \left( a_{{1}}a_{{7}}-a_{{3}}a_{{5} } \right) ^{2}} \Bigr \} , \nonumber \\ \end{aligned}$$
(2.5)

which needs to satisfy the conditions

$$\begin{aligned} a_3a_7\ne 0,\ a_{{1}}a_{{7}}-a_{{3}}a_{{5}} \ne 0, \end{aligned}$$
(2.6)

to make the corresponding solutions f to be well defined. The condition

$$\begin{aligned} (a_1-a_3)a_3+(a_5-a_7)a_7 >0, \end{aligned}$$
(2.7)

guarantees the positiveness of f, and the condition

$$\begin{aligned} ({a_1}^2-{a_5}^2) (a_1a_7+a_3a_5)-2a_1a_5(a_1a_3-a_5a_7)\ne 0, \end{aligned}$$
(2.8)

guarantees the localization of u in all directions in the (x, y)-plane. The parameters in the set (2.5) generate a class of positive quadratic function solutions to the reduced bilinear p-gKP Eq. (2.1):

$$\begin{aligned}&f=\Bigl ( a_1x + {\frac{{a_{{1}}}^{2}a_{{3}}-a_{{1}}{ a_{{3}}}^{2}+2\,a_{{1}}a_{{5}}a_{{7}}-a_{{1}}{a_{{7}}}^{2}-a_{{3}}{a_{ {5}}}^{2}}{{a_{{3}}}^{2}+{a_{{7}}}^{2}}}\nonumber \\&y + a_3 t + a_4 \Bigr )^2 \nonumber \\&\quad \ \ +\Bigl ( a_{{5}}x -{\frac{{a_{{1}}}^{2}a_{{7}}-2\,a_{{1}}a_{ {3}}a_{{5}}+{a_{{3}}}^{2}a_{{5}}-{a_{{5}}}^{2}a_{{7}}+a_{{5}}{a_{{7}}} ^{2}}{{a_{{3}}}^{2}+{a_{{7}}}^{2}}}\nonumber \\&y+ a_7 t +a_{{8}} \Bigr )^2 \nonumber \\&\quad \ \ + \frac{3 ({a_1}^2+{a_5}^2)^2 [(a_1-a_3)a_3+(a_5-a_7)a_7]}{ \left( a_{{1}}a_{{7}}-a_{{3}}a_{{5} } \right) ^{2}} , \end{aligned}$$
(2.9)

and the resulting class of quadratic function solutions, in turn, yields a class of lump solutions to the reduced p-gKP Eq. (2.3) through the transformation (2.2):

$$\begin{aligned} u=\frac{4(a_1g+a_5h)}{f}, \end{aligned}$$
(2.10)

where the function f is defined by (2.9), and the functions of g and h are given as follows:

$$\begin{aligned} g= & {} a_1x \nonumber \\&+ {\frac{{a_{{1}}}^{2}a_{{3}}-a_{{1}}{ a_{{3}}}^{2}+2\,a_{{1}}a_{{5}}a_{{7}}-a_{{1}}{a_{{7}}}^{2}-a_{{3}}{a_{ {5}}}^{2}}{{a_{{3}}}^{2}+{a_{{7}}}^{2}}} y \nonumber \\&+ a_3 t + a_4 , \end{aligned}$$
(2.11)
$$\begin{aligned} h= & {} a_{{5}}x \nonumber \\&-{\frac{{a_{{1}}}^{2}a_{{7}}-2\,a_{{1}}a_{ {3}}a_{{5}}+{a_{{3}}}^{2}a_{{5}}-{a_{{5}}}^{2}a_{{7}}+a_{{5}}{a_{{7}}} ^{2}}{{a_{{3}}}^{2}+{a_{{7}}}^{2}}} y\nonumber \\&+ a_7 t +a_{{8}}. \end{aligned}$$
(2.12)

In this class of lump solutions, all six involved parameters of \(a_1,a_3,a_4,a_5,a_7\) and \( a_8\) are arbitrary, provided that the three conditions (2.6), (2.7) and (2.8) are satisfied, which guarantee the definedness, positiveness and localization in all directions in the space for the solutions, respectively.

2.2 Reduction with \(z=y\)

When \(p=3\), the (3+1)-dimensional bilinear p-gKP Eq. (1.5) reduces the following generalized bilinear equation:

$$\begin{aligned}&B_{p\text {-gKP}_y}(f):= (D_{3,x}^3D_{3,y} +D_{3,t}D_{3,x}+D_{3,t}D_{3,y}\nonumber \\&\qquad \quad - D_{3,y}^2)f\cdot f \nonumber \\&\quad =2( 3 f_{xx}f_{xy} - f_tf_x + f_{tx}f + f_{ty}f - f_tf_y \nonumber \\&\qquad \quad + {f_{y}}^2 - f_{yy}f)=0 , \end{aligned}$$
(2.13)

under \(z=y\). Through the link between f and u defined by (2.2), the reduced bilinear p-gKP Eq. (2.13) is transformed into

$$\begin{aligned} P_{p\text {-gKP}_y}(u)= & {} \frac{9}{8} u^2 u_x v +\frac{3}{8} u^3 u_y +\frac{3}{4} u u_{xx}v +\frac{3}{4} {u_x} ^2 v \nonumber \\&+ \frac{3}{4} u ^2 u_{xy} +\frac{9}{4} u u_x u_y +\frac{3}{2} u_{xx}u_y \nonumber \\&+\frac{3}{2} u_x u_{xy}-u_{yy} +u_{tx}+u_{ty}=0 , \nonumber \\ \end{aligned}$$
(2.14)

where \(u_y=v_x\). The actual relation between the reduced p-gKP Eq. (2.14) and the reduced bilinear p-gKP Eq. (2.13) reads

$$\begin{aligned} P_{p\text {-gKP}_y}(u)= \Bigl [\frac{B_{p\text {-gKP}_y}(f)}{f^2}\Bigr ]_{x}. \end{aligned}$$
(2.15)

Therefore, if f solves the reduced bilinear p-gKP Eq. (2.13), then \(u=2(\ln f)_{x}\) will solve the reduced p-gKP Eq. (2.14).

For Eq. (2.13), a direct symbolic computation with f defined by (1.9) yields the following set of constraining equations for the parameters:

$$\begin{aligned}&\Bigl \{ a_{{1}}={\frac{{a_{{2}}}^{2}a_{{3}}-a_{{2}}{a_{{3}}}^{2}+2\, a_{{2}}a_{{6}}a_{{7}}-a_{{2}}{a_{{7}}}^{2}-a_{{3}}{a_{{6}}}^{2}}{{a_{{ 3}}}^{2}+{a_{{7}}}^{2}}},\nonumber \\&\quad a_{{2}}=a_{{2}},\ a_{{3}}=a_{{3}},\ a_{{4}}=a_{{4 }},\Bigr . \nonumber \\&\quad a_{{5}}=-{\frac{{a_{{2}}}^{2}a_{{7}}-2\,a_{{2}}a_{{3}}a_{{6}}+{a_{ {3}}}^{2}a_{{6}}-{a_{{6}}}^{2}a_{{7}}+a_{{6}}{a_{{7}}}^{2}}{{a_{{3}}}^ {2}+{a_{{7}}}^{2}}},\nonumber \\&\quad a_{{6}}=a_{{6}},\ a_{{7}}=a_{{7}},\ a_{{8}}=a_{{8}}, \nonumber \\&\quad a_ {{9}}= \frac{3({a_1}^2+{a_5}^2)({a_1}a_2+{a_5}a_6 ) ({a_3}^2+{a_7}^2) }{ (a_{{2}}a_{{7}}-a_{{3}}a_{{6}})^2} \Bigr \} ,\nonumber \\ \end{aligned}$$
(2.16)

which needs to satisfy

$$\begin{aligned} a_3a_7\ne 0, a_{{2}}a_{{7}}{-}a_{{3}}a_{{6}} \ne 0 .\nonumber \\ \end{aligned}$$
(2.17)

Noting the expression of \(a_9\) in (2.16), the positiveness of f needs \(a_1{a_2}+a_5{a_6}>0 ,\) which is equivalent to

$$\begin{aligned} (a_2-a_3)a_3+(a_6-a_7)a_7>0, \end{aligned}$$
(2.18)

thanks to (2.17). The localization of f needs \(a_1a_6-a_2a_5\ne 0\), which equivalently requires

$$\begin{aligned} ({a_2}^2-{a_6}^2) (a_2a_7{+}a_3a_6){-}2a_2a_6(a_2a_3-a_6a_7)\ne 0. \nonumber \\ \end{aligned}$$
(2.19)

The parameters in the set (2.16) lead to a class of positive quadratic function solutions to the reduced bilinear p-gKP Eq. (2.13):

$$\begin{aligned}&f=\Bigl ( {\frac{{a_{{2}}}^{2}a_{{3}}-a_{{2}}{a_{{3}}}^{2}+2\, a_{{2}}a_{{6}}a_{{7}}-a_{{2}}{a_{{7}}}^{2}-a_{{3}}{a_{{6}}}^{2}}{{a_{{ 3}}}^{2}+{a_{{7}}}^{2}}}\nonumber \\&\quad x + a_2 y + a_3 t + a_4 \Bigr )^2\nonumber \\&\quad +\Bigl ( -{\frac{{a_{{2}}}^{2}a_{{7}}-2\,a_{{2}}a_{{3}}a_{{6}}+{a_{ {3}}}^{2}a_{{6}}-{a_{{6}}}^{2}a_{{7}}+a_{{6}}{a_{{7}}}^{2}}{{a_{{3}}}^ {2}+{a_{{7}}}^{2}}}\nonumber \\&\quad x +a_6 y+ a_7 t +a_{{8}} \Bigr )^2\nonumber \\&\quad \ \ + \frac{3({a_1}^2+{a_5}^2)({a_1}a_2+{a_5}a_6 ) ({a_3}^2+{a_7}^2) }{ (a_{{2}}a_{{7}}-a_{{3}}a_{{6}})^2} ,\qquad \end{aligned}$$
(2.20)

where \(a_1\) and \(a_5\) are defined as in (2.16), and the resulting class of quadratic function solutions, in turn, yields a class of lump solutions to the reduced p-gKP Eq. (2.14) through the transformation (2.2):

$$\begin{aligned} u=\frac{4(a_1g+a_5h)}{f}, \end{aligned}$$
(2.21)

where the function f is defined by (2.20), and the functions of g and h are given as follows:

$$\begin{aligned} g= & {} {\frac{{a_{{2}}}^{2}a_{{3}}-a_{{2}}{a_{{3}}}^{2}+2\, a_{{2}}a_{{6}}a_{{7}}-a_{{2}}{a_{{7}}}^{2}-a_{{3}}{a_{{6}}}^{2}}{{a_{{ 3}}}^{2}+{a_{{7}}}^{2}}} x \nonumber \\&+a_2 y + a_3 t + a_4 , \end{aligned}$$
(2.22)
$$\begin{aligned} h= & {} -{\frac{{a_{{2}}}^{2}a_{{7}}-2\,a_{{2}}a_{{3}}a_{{6}}+{a_{ {3}}}^{2}a_{{6}}-{a_{{6}}}^{2}a_{{7}}+a_{{6}}{a_{{7}}}^{2}}{{a_{{3}}}^ {2}+{a_{{7}}}^{2}}} x\nonumber \\&+a_{{6}} y+ a_7 t +a_{{8}} . \end{aligned}$$
(2.23)

In this class of lump solutions, all six involved parameters of \(a_2,a_3,a_4,a_6,a_7\) and \(a_8\) are arbitrary, provided that the conditions in (2.17), (2.18) and (2.19) are satisfied.

3 Lump solutions to the reduced p-gBKP equations

3.1 Reduction with \(z=x\)

When \(p=3\), the (3+1)-dimensional bilinear p-gBKP Eq. (1.6) reduces to the following generalized bilinear equation:

$$\begin{aligned}&B_{p\text {-gBKP}_x}(f):= (D_{3,t}D_{3,y} - D_{3,x}^3 D_{3,y}+3 D_{3,x}^2)f\cdot f \nonumber \\&\quad =2( f_{ty}f - f_tf_y -3 f_{xx}f _{xy} -3{ f_{x}}^2 +3 f_{xx}f ) =0, \nonumber \\ \end{aligned}$$
(3.1)

under \(z=x\). Through the link between f and u defined by (2.2), the reduced bilinear gBKP Eq. (3.1) is transformed into

$$\begin{aligned}&P_{p\text {-gBKP}_x}(u):= -\frac{9}{8} u^2 u_x v -\frac{3}{8} u^3 u_y -\frac{3}{4} u u_{xx} v \nonumber \\&\quad -\frac{3}{4} {u_x}^2 v-\frac{3}{4} u^2 u_{xy} -\frac{9}{4} u u_x u_y -\frac{3}{2} u_{xx}u_y \nonumber \\&\quad -\frac{3}{2} u_xu_{xy} +3u_{xx}+u_{ty} =0 , \end{aligned}$$
(3.2)

where \(u_y=v_x\). The actual relation between the reduced p-gKP equation and the reduced bilinear p-gKP equation reads

$$\begin{aligned} P_{p\text {-gBKP}_x}(u)= \Bigl [\frac{B_{p\text {-gBKP}_x}(f)}{f^2}\Bigr ]_{x}. \end{aligned}$$
(3.3)

Therefore, if f solves the reduced bilinear p-gBKP Eq. (3.1), then \(u=2(\ln f)_{x}\) will solve the reduced p-gBKP Eq. (3.2).

For Eq. (3.1), a direct symbolic computation with f in (1.9) yields the following set of constraining equations for the parameters:

$$\begin{aligned}&\Bigl \{ a_{{1}}=a_{{1}},\ a_{{2}}=a_{{2}},\ a_{{3}}=-{\frac{3({a_{{1}}} ^{2}a_{{2}}+2\,a_{{1}}a_{{5}}a_{{6}}-a_{{2}}{a_{{5}}}^{2})}{{a_{{2}}}^{ 2}+{a_{{6}}}^{2}}},\ a_{{4}}=a_{{4}}, \nonumber \\&\quad a_{{5}}=a_{{5}},\ a_{{6}}=a_{{6}},\ a_{ {7}}={\frac{3({a_{{1}}}^{2}a_{{6}}-2\,a_{{1}}a_{{2}}a_{{5}}-a_{{6}}{ a_{{5}}}^{2})}{{a_{{2}}}^{2}+{a_{{6}}}^{2}}},\ a_{{8}}=a_{{8}}, \nonumber \\&\quad a_{{9}}= \frac{{a_1}^3{a_2}^3+ ({a_1}^2{a_6}^ 2 +{a_1}{a_2} {a_5}{a_6} +{a_2}^2{a_5}^2 )(a_1a_2+a_5a_6)+ {a_5}^3{a_6}^3}{ \left( a_{{1}}a_{{6}}-a_{{2}}a_{{5}} \right) ^{2}} \Bigr \} , \end{aligned}$$
(3.4)

which needs to satisfy a determinant condition

$$\begin{aligned} a_{{1}}a_{{6}}-a_{{2}}a_{{5}}=\left| \begin{array}{cc} a_1 &{} a_2\\ a_5 &{} a_6 \end{array}\right| \ne 0. \end{aligned}$$
(3.5)

When \(a_9>0\), i.e.,

$$\begin{aligned}&{a_1}^3{a_2}^3+ ({a_1}^2{a_6}^ 2 +{a_1}{a_2} {a_5}{a_6} +{a_2}^2{a_5}^2 )(a_1a_2+a_5a_6)\nonumber \\&\quad + {a_5}^3{a_6}^3 >0, \end{aligned}$$
(3.6)

the corresponding quadratic function f, defined by (1.9), is positive. Now the parameters in the set (3.4) generate a class of positive quadratic function solutions to the reduced bilinear p-gBKP Eq. (3.1):

$$\begin{aligned}&f=\Bigl [ a_1x {+} a_2 y -{\frac{3({a_{{1}}} ^{2}a_{{2}}{+}2\,a_{{1}}a_{{5}}a_{{6}}{-}a_{{2}}{a_{{5}}}^{2})}{{a_{{2}}}^{ 2}+{a_{{6}}}^{2}}} t {+} a_4 \Bigr ]^2{+}\Bigl [ a_{{5}}x +a_6 y{+} {\frac{3({a_{{1}}}^{2}a_{{6}}-2\,a_{{1}}a_{{2}}a_{{5}}-a_{{6}}{ a_{{5}}}^{2})}{{a_{{2}}}^{2}+{a_{{6}}}^{2}}} t +a_{{8}} \Bigr ]^2\nonumber \\&\quad + \frac{{a_1}^3{a_2}^3+ ({a_1}^2{a_6}^ 2 +{a_1}{a_2} {a_5}{a_6} +{a_2}^2{a_5}^2 )(a_1a_2+a_5a_6)+ {a_5}^3{a_6}^3}{ \left( a_{{1}}a_{{6}}-a_{{2}}a_{{5}} \right) ^{2}} , \end{aligned}$$
(3.7)

and the resulting class of quadratic function solutions, in turn, yields a class of lump solutions to the reduced p-gBKP equation in (3.2) through the transformation (2.2):

$$\begin{aligned} u=\frac{4(a_1g+a_5h)}{f}, \end{aligned}$$
(3.8)

where the function f is defined by (3.7), and the functions of g and h are given as follows:

$$\begin{aligned}&g=a_1x +a_2 y\nonumber \\&\quad -{\frac{3({a_{{1}}} ^{2}a_{{2}}+2\,a_{{1}}a_{{5}}a_{{6}}-a_{{2}}{a_{{5}}}^{2})}{{a_{{2}}}^{ 2}+{a_{{6}}}^{2}}} t + a_4 , \end{aligned}$$
(3.9)
$$\begin{aligned}&h= a_{{5}}x+a_{{6}} y\nonumber \\&\quad + {\frac{3({a_{{1}}}^{2}a_{{6}}-2\,a_{{1}}a_{{2}}a_{{5}}-a_{{6}}{ a_{{5}}}^{2})}{{a_{{2}}}^{2}+{a_{{6}}}^{2}}} t +a_{{8}}. \end{aligned}$$
(3.10)

In this class of lump solutions, all six involved parameters of \(a_1,a_2,a_4,a_5,a_6\) and \(a_8\) are arbitrary, provided that the solutions are well defined and positive, i.e., if the conditions in (3.5) and (3.6) are satisfied. That determinant condition (3.5) precisely means that two directions \((a_1,a_2)\) and \((a_5,a_6)\) in the (x, y)-plane are not parallel, which is essential in formulating lump solutions in (2+1)-dimensions by using a sum involving two squares.

3.2 Reduction with \(z=y\)

When \(p=3\), the (3+1)-dimensional bilinear p-gBKP Eq. (1.6) reduces the following generalized bilinear equation:

$$\begin{aligned}&B_{p\text {-gBKP}_y}(f):= (D_{3,t}D_{3,y} - D_{3,x}^3 D_{3,y}\nonumber \\&\qquad +3 D_{3,x}D_{3,y})f\cdot f\nonumber \\&\quad =2( f_{ty}f - f_tf_y - 3 f_{xx}f_{xy} -3 f_xf_y + 3 f_{xy}f )=0 , \nonumber \\ \end{aligned}$$
(3.11)

under \(z=y\). Through the link between f and u defined by (2.2), the reduced bilinear p-gBKP Eq. (3.11) is transformed into

$$\begin{aligned}&P_{p\text {-gBKP}_y}(u):= -\frac{9}{8} u^2 u_xv -\frac{3}{8} u^3 u_y -\frac{3}{4} u u_{xx} v \nonumber \\&\qquad -\frac{3}{4} {u_x}^2 v -\frac{3}{4} u^2 u_{xy} -\frac{9}{4} uu_xu_y -\frac{3}{2} u_{xx}u_y\nonumber \\&\qquad -\frac{3}{2} u_xu_{xy} +3 u_{xy} + u_{ty} =0 , \end{aligned}$$
(3.12)

where \(u_y=v_x\). The actual relation between the reduced p-gBKP Eq. (3.12) and the reduced bilinear p-gBKP Eq. (3.11) reads

$$\begin{aligned} P_{p\text {-gBKP}_y}(u)= \Bigl [\frac{B_{p\text {-gBKP}_y}(f)}{f^2}\Bigr ]_{x}. \end{aligned}$$
(3.13)

Therefore, if f solves the reduced bilinear p-gBKP Eq. (3.11), then \(u=2(\ln f)_{x}\) will solve the reduced p-gBKP Eq. (3.12).

Fig. 1
figure 1

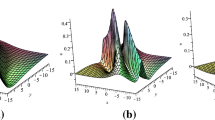
The 3d plots of the lump solutions via (2.10). Parameters adopted here are: \(a_1=4\), \(a_2=-12/5\), \(a_3=2\), \(a_4=0\), \(a_5=6\), \(a_6=86/5\), \(a_7=1\), \(a_8=0\) and \(a_9=4563/4\)

Full size image

For Eq. (3.11), a direct symbolic computation with f defined by (1.9) yields the following set of constraining equations for the parameters:

$$\begin{aligned}&\Bigl \{ a_{{1}}=-\frac{a_{{5}}a_{{6}}}{a_{{2}}}, \ a_{{2}}=a_{{2}},\ a_ {{3}}= \frac{3\,a_{{5}}a_{{6}}}{a_{{2}}},\ a_{{4}}=a_{{4}},\nonumber \\&\quad a_{{5}}=a_{ {5}},\ a_{{6}}{=}a_{{6}},\ a_{{7}}=-3\,a_{{5}}, a_{{8}}=a_{{8}},\ a_{{9}}=a_{{9 }} \Bigr \} ,\nonumber \\ \end{aligned}$$
(3.14)

where

$$\begin{aligned} a_2\ne 0 \end{aligned}$$
(3.15)

and all the other parameters are arbitrary. The parameters in this set lead to a class of positive quadratic function solutions to the reduced bilinear p-gBKP Eq. (3.1):

$$\begin{aligned} f= & {} \bigl ( { -{\frac{a_{{5}}a_{{6}} }{a_{{2}}}}x +a_{{2}}y +\frac{3\,a_{{5}}a_{{6}}}{a_{{2}}}}t +a_{{4}} \bigr ) ^{2}\nonumber \\&+ \bigl ( a_{{5}}x +a_{{6}}y -3\, a_{{5}}t +a_{{8}} \bigr ) ^{2}+a_{{9}}, \end{aligned}$$
(3.16)

and the resulting class of quadratic function solutions, in turn, yields a class of lump solutions to the reduced p-gBKP equation in (3.12) through the transformation (2.2):

$$\begin{aligned} u=\frac{4(a_1g +a_5h)}{f}, \end{aligned}$$
(3.17)

where the function f is defined by (3.16), and the functions of g and h are given as follows:

$$\begin{aligned}&g= -{\frac{a_{{5}}a_{{6}} }{a_{{2}}} } x +a_2 y + \frac{3\,a_{{5}}a_{{6}}}{a_{{2}}} t + a_4 ,\end{aligned}$$
(3.18)
$$\begin{aligned}&h= a_{{5}}x+a_{{6}} y -3\, a_5 t +a_{{8}} . \end{aligned}$$
(3.19)

In this class of rational function solutions, all six involved parameters of \(a_2,a_4,a_5,a_6,a_8\) and \(a_9\) are arbitrary, provided that the solutions are well defined, i.e., if the condition (3.15) is satisfied. Under the condition (3.15), the determinant condition, which guarantees that two directions \((a_1,a_2)\) and \((a_5,a_6)\) in the (x, y)-plane are not parallel, is equivalent to

$$\begin{aligned} a_5\ne 0. \end{aligned}$$
(3.20)

Therefore, the conditions on the parameters

$$\begin{aligned} a_2a_5\ne 0, \ a_9>0, \end{aligned}$$
(3.21)

will guarantee analyticity and localization of the solutions in (3.17) and thus present lump solutions to the reduced p-gBKP equation in (3.12).

Fig. 2
figure 2

The 3d plots of the lump solutions via (2.21). Parameters adopted here are: \(a_1=-68/13\), \(a_2=4\), \(a_3=3\), \(a_4=0\), \(a_5=184/13\), \(a_6=8\), \(a_7=2\), \(a_8=0\) and \(a_9=41625/13\)

Full size image
Fig. 3
figure 3

The 3d plots of the lump solutions via (3.8). Parameters adopted here are: \(a_1=1\), \(a_2=3\), \(a_3=96/25\), \(a_4=0\), \(a_5=5\), \(a_6=4\), \(a_7=-378/25\), \(a_8=0\) and \(a_9=14950/121\)

Full size image
Fig. 4
figure 4

The 3d plots of the lump solutions via (3.17). Parameters adopted here are: \(a_1=-3\), \(a_2=2\), \(a_3=9\), \(a_4=0\), \(a_5=6\), \(a_6=1\), \(a_7=-18\), \(a_8=0\) and \(a_9=4\)

Full size image

4 Concluding remarks

Based on the generalized bilinear formulation and Maple symbolic computation, we presented positive quadratic functions solutions to the (2+1)-dimensional reduced bilinear p-gKP and p-gBKP equations, and thus, lump solutions to the (2+1)-dimensional reduced p-gKP and p-gBKP equations associated with \(p=3\). The results actually work for all other values of \(p\ge 2\) as well [26]. The representatives of the considered reduced generalized bilinear equations and their corresponding nonlinear differential equations with \(p=3\) were computed explicitly as in the set of Eqs. (2.1), (2.13), (3.1) and (3.11) and the set of Eqs. (2.3), (2.14), (3.2) and (3.12), respectively. The 3d plots of the presented lump solutions with some special choices of the involved parameters can be found in Figs. 1, 2, 3 and 4, which show energy distribution.

We point out that resonant solutions, in terms of exponential functions, to generalized trilinear differential equations have been systematically analyzed [27]. It would be very interesting to determine when there exist positive polynomial solutions including quadratic function solutions to generalized multi-linear equations. This kind of polynomial solutions will generate lump solutions to the corresponding nonlinear equations through \(u= m (\ln f)_x\) or \(u= m (\ln f)_{xx}\), where m is a constant related to the multi-linearity of the associated multi-linear equations. Rogue wave solutions could be generated as well in terms of positive polynomial solutions, being a particularly interesting class of exact solutions with rational function amplitudes. Such wave solutions are used to describe significant nonlinear wave phenomena in both oceanography [28] and nonlinear optics [29], which received a great deal of recent attention in the mathematical physics community. To explore more soliton phenomena, it would be very interesting to consider multi-component and higher-order extensions of lump solutions, more importantly in (3+1)-dimensional cases and fully discrete cases.