1 Introduction

The topic of nonlinear Schrodinger equation (NLSE) has achieved some remarkable success for many decades, and different types of NLSEs are used in various domains to describe particular phenomena, such as optical solitons in fibers (Triki and Biswas 2011; Zhang and Si 2010; Biswas 2001; Rehman et al. 2021), matter waves in Bose–Einstein Delicacy (Bronski et al. 2001; Trombettoni and Smerzi 2001; Mihalache 2014; Sulaiman et al. 2021), pulses and beams in nonlinear photonics, as well as several others (Nore et al. 1993; Biswas 2003; Eslami and Mirzazadeh 2013; Bulut et al. 2019; Yavuz and Yokus 2020; Aceves et al. 1994). On the other side, the Korteweg-de Vries (KdV) equation describes the motion of shallow-water phenomena arising in quantum mechanics, plasma physics, nonlinear optics and other areas (Jin 2008; Khater et al. 2005; Wazwaz 2006; Biswas and Konar 2007; Karpman 1996).

The motivation of this study is to investigate the bidirectional-waves (Alquran 2021; Alquran et al. 2021) of a new combination of KdV–Schrodinger equations. The classical nonlinear coupled KdV–Schrodinger system has the following form Yavuz et al. (2021)

$$\begin{aligned} 0&= {} p_t+i p_{xx}+ i p q,\nonumber \\ 0&= {} q_t+6 q q_x + q_{xxx}-(|p|^2)_x, \end{aligned}$$
(1.1)

where \(p=p(x,t)\) is a complex-valued function and \(q=q(x,t)\) is a real-valued function.

The connection between unidirectional-wave and bidirectional-waves was investigated by Korsunsky (1994); Wazwaz (2017). They suggested a general two-mode (TM) nonlinear equations in the following form

$$\begin{aligned} u_{tt}-s^2 u_{xx}+\left( \frac{\partial }{\partial t}-a s \frac{\partial }{\partial x}\right) N(u,u_x,u_{xx},...)+\left( \frac{\partial }{\partial t}-b s \frac{\partial }{\partial x}\right) L(u_{xx},u_{xxx},...)=0. \end{aligned}$$
(1.2)

\(N=\) nonlinear terms, \(L=\) linear terms, \(s=\) phase velocity (\(s>0\)), \(a=\) nonlinearity parameter (\(|a|\le 1\)) and \(b=\) dispersion parameter (\(|b|\le 1\)). TM equations describe the propagation of bidirectional symmetric waves and their interaction is dependent on the phase-velocity parameter. For the TM equation (1.2), if we substitute \(s=0\) and integrate once with respect to the time-coordinate, we get the following standard single-mode (SM) equation

$$\begin{aligned} u_{t}+N(u,u_x,u_{xx},...)+L(u_{xx},u_{xxx},...)=0. \end{aligned}$$
(1.3)

It is clear that TM is a second-order in time, while SM is a first-order in time. TM belongs models with moving bidirectional waves, while SM belongs models with moving single wave.

In this manuscript, we adapting the Korsunsky-Wazwaz sense (1.2) to construct the two-mode version of (1.1). Accordingly, the two-mode coupled KdV–Schrodinger (TMcKdV-NLS) system takes the following form

$$\begin{aligned} 0&&= {} p_{tt}-s^2 p_{xx}+i \left( \frac{\partial }{\partial t}-\alpha _1 s \frac{\partial }{\partial x}\right) \{p q\}+ i \left( \frac{\partial }{\partial t}-\beta _1 s \frac{\partial }{\partial x}\right) \{p_{xx}\},\nonumber \\ 0&= {} q_{tt}-s^2 q_{xx}+\left( \frac{\partial }{\partial t}-\alpha _2 s \frac{\partial }{\partial x}\right) \{6 q q_x -(|p|^2)_x\} + \left( \frac{\partial }{\partial t}-\beta _2 s \frac{\partial }{\partial x}\right) \{q_{xxx}\}, \end{aligned}$$
(1.4)

where \(\alpha _1,\ \alpha _2\) are the nonlinearity parameters, \(\beta _1,\ \beta _2\) are the dispersions and s is the phase velocity. The model given in (1.4) is presented here for the first time, and our contribution is to find explicit solutions that help to explore the physical structures of TMcKdV-NLS. For more details about two-mode nonlinear equations see (Alquran et al. 2021a, b; Alquran and Yassin 2018)

2 Kudryashov-expansion solution for TMcKdV-NLS

Fig. 1
figure 1

3D left-right bidirectional waves of the real part solutions to the function p(x, t) with (\(d>0\))

Full size image
Fig. 2
figure 2

Contour plots of the left-right bidirectional waves of the real part solutions to the function p(x, t) with (\(d>0\))

Full size image
Fig. 3
figure 3

Profile solutions of the left-right bidirectional waves of the real part solutions to the function p(x, t) with (\(d>0\))

Full size image

In this section, we extract solitary wave solutions to TMcKdV-NLS by means of the Kudryashov-expansion method. Since the unknown field function \(p=p(x,t)\) is a complex-valued (Jaradat et al. 2018; Alquran and Jaradat 2019; Sulaiman et al. 2021), we write the solution of (1.4) as

$$\begin{aligned} p(x,t)=e^{i \eta }\ P(\zeta ), \end{aligned}$$
(2.5)

and the real-valued function \(q=q(x,t)\) as

$$\begin{aligned} q(x,t)= Q(\zeta ), \end{aligned}$$
(2.6)

where \(\eta =\lambda (x+w t)\) and \(\zeta =x-c t\). The new variables \(\eta \) and \(\zeta \) are regarded as wave transformations with speeds of w and c, respectively. Now, substitution of (2.5)–(2.6) in (1.4) produces

$$\begin{aligned} 0= & {} R_1(P(\zeta ),Q(\zeta ))+i\ R_2(P(\zeta ),Q(\zeta )),\nonumber \\ 0= & {} R_3(P(\zeta ),Q(\zeta )), \end{aligned}$$
(2.7)

where

$$\begin{aligned} R_1\left( P(\zeta ),Q(\zeta )\right)&= {} \left( c^2+2 c \lambda -s^2+3 \beta _1 \lambda s-\lambda w\right) P''(\zeta ) +\lambda (\alpha _1 s-w) P(\zeta ) Q(\zeta )\nonumber \\+ &\quad {} \lambda ^2 \left( s^2-\beta _1 \lambda s+w(\lambda -w)\right) P(\zeta ),\nonumber \\ R_2(P(\zeta ),Q(\zeta ))&= {} (c+\beta _1 s) P''(\zeta )+ (c+\alpha _1 s) P(\zeta ) Q(\zeta ) \nonumber \\+ &\quad {} \lambda \left( -c \lambda +2c w+2 s^2-3 \beta _1 \lambda s+2\lambda w\right) P(\zeta ),\nonumber \\ R_3(P(\zeta ),Q(\zeta ))&= {} \left( c^2-s^2\right) Q(\zeta )+(c+\alpha _2 s) \left( P^2(\zeta )-3 Q^2(\zeta )\right) - (c+\beta _2 s)Q''(\zeta ). \end{aligned}$$
(2.8)

Then, we solve the following system

$$\begin{aligned} R_1=R_1(P(\zeta ),Q(\zeta ))= & {} 0,\nonumber \\ R_2=R_2(P(\zeta ),Q(\zeta ))= & {} 0, \nonumber \\ R_3=R_3(P(\zeta ),Q(\zeta ))= & {} 0. \end{aligned}$$
(2.9)

First, by performing the linear combination, \(\lambda (\alpha _1 s-w) R_2- (c+\alpha _1 s) R_1\), we get

$$\begin{aligned} R_4=R_4(P(\zeta ))&= {} \left( \lambda \left( 2 c^2+\alpha _1 c s+\beta _1 s (3 c+2 \alpha _1 s+w)-\alpha _1 s w\right) \right. \nonumber \\& \left. \quad + (c^2-s^2) (c+\alpha _1 s)\right) P''(\zeta )\nonumber \\& \quad + c \lambda ^2 \left( s (\alpha _1 \lambda -\beta _1 \lambda +s-2 \alpha _1 w)+w^2\right) P(\zeta )\nonumber \\&\quad -\lambda ^2 \left( \alpha _1 s^3-2 s^2 (\alpha _1 \beta _1 \lambda +w)+s w (\alpha _1 \lambda +3 \beta _1 \lambda +\alpha _1 w)-2 \lambda w^2\right) P(\zeta )=0. \end{aligned}$$
(2.10)

Next, we only solve the new system

$$\begin{aligned} R_3= & {} R_3(P(\zeta ),Q(\zeta ))=0,\nonumber \\ R_4= & {} R_4(P(\zeta ))=0. \end{aligned}$$
(2.11)

The Kudryashov method (Jaradat and Alquran 2020; Jaradat et al. 2020; Kudryashov 2012; Alquran et al. 2019, 2021) suggests the following solutions to (2.11)

$$\begin{aligned} P(\zeta )= & {} \sum _{i=0}^{k_1} a_i Y^i,\nonumber \\ Q(\zeta )= & {} \sum _{i=0}^{k_2} b_i Y^i, \end{aligned}$$
(2.12)

where \(Y=Y(\zeta )\) satisfies the auxiliary differential equation

$$\begin{aligned} Y'=\mu Y(Y-1). \end{aligned}$$
(2.13)

The solution of (2.13) is

$$\begin{aligned} Y=\frac{1}{1+d \ e^{\mu \zeta }}. \end{aligned}$$
(2.14)

To determine the indices \(k_1,\ k_2\), we perform the balance procedure by equating the orders of P against \(P''\) in \(R_4\) and \(P^2\) against \(Q''\) in \(R_3\), to obtain \(k_1=k_2=2\). Now, by (2.13) and twice differentiation of the functions \(P,\ Q\) in (2.12), leads to

$$\begin{aligned} P''(\zeta )= & {} \mu ^2 Y (Y-1)\left( a_1 (2 Y-1)+2 a_2 Y (3 Y-2)\right) ,\nonumber \\ Q''(\zeta )= & {} \mu ^2 Y (Y-1) \left( b_1 (2 Y-1)+2 b_2 Y (3 Y-2)\right) . \end{aligned}$$
(2.15)

To this stage, we are ready to substitute (2.15) as well as (2.12) in the last system (2.11), then we collect the coefficients of the same powers of the variable Y, and set each coefficient to zero. The resulting system consists of many nonlinear algebraic equations in the unknowns \(a_0,\ a_1,\ a_2,\ b_0,\ b_1,\ b_2,\ \mu ,\ c,\ w\) and \(\lambda \). To be able solving this inconsistent system, we require some reasonable constraints. Trying many trials, we reached at the following condition

$$\begin{aligned} \alpha _1=\alpha _2=\beta _1=\beta _2=\gamma \ :\ |\gamma |\le 1. \end{aligned}$$
(2.16)

Accordingly, we deduce the following outputs

$$\begin{aligned} a_0&= {} \frac{a_1}{2}=-\mu \sqrt{\frac{1}{2} \sqrt{4 \lambda ^2+3 \mu ^4}+\mu ^2},\nonumber \\ a_2&= {} 0,\nonumber \\ b_0&= {} \frac{1}{6} \left( -\sqrt{4 \lambda ^2+3 \mu ^4}-2 \lambda -3 \mu ^2\right) ,\nonumber \\ b_1&= {} -b_2= 2\mu ^2,\nonumber \\ c&= {} -w=\sqrt{\lambda ^2+s^2-2 \lambda s \gamma }-\lambda ,\nonumber \\ \gamma &= {} \pm 1. \end{aligned}$$
(2.17)

We should alert here that the wave speed c in (2.17) has two values; \(c=s\) and \(c=-s\). Hence, the TMcKdV-NLS admits having bidirectional wave-solutions which are given by

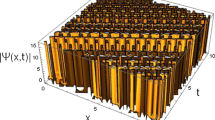
$$\begin{aligned} p(x,t)&= {} e^{i \lambda (x\mp s t)}\left( -\mu \sqrt{\frac{1}{2} \sqrt{4 \lambda ^2+3 \mu ^4}+\mu ^2} + \frac{2\mu \sqrt{\frac{1}{2} \sqrt{4 \lambda ^2+3 \mu ^4}+\mu ^2}}{1+d \ e^{\mu (x\pm s t)}}\right) ,\nonumber \\ q(x,t)&= {} \frac{1}{6} \left( -\sqrt{4 \lambda ^2+3 \mu ^4}-2 \lambda -3 \mu ^2\right) +\frac{2\mu ^2}{1+d \ e^{\mu (x\pm s t)}}-\frac{2\mu ^2}{\left( 1+d \ e^{\mu (x\pm s t)}\right) ^2}. \end{aligned}$$
(2.18)

Figures 1, 2 and 3 represent, respectively, the 3D plot of the bidirectional waves solution, the contour plot and profile solutions to the function p(x, t) as depicted in (2.18) where the Kudryashov parameter d is of a positive value. These bidirectional waves can be regarded as left-wave and right-wave for the reason that both are symmetric and having the same physical structure. On the other side, Figs. 4, 5 and 6 represent the graphical analysis of the reported bidirectional waves to the function q(x, t) with \(d>0\).

Fig. 4
figure 4

3D left-right bidirectional waves to the function q(x, t) with (\(d>0\))

Full size image
Fig. 5
figure 5

Contour plots of the left-right bidirectional waves to the function q(x, t) with (\(d>0\))

Full size image
Fig. 6
figure 6

Profile solutions of the left-right bidirectional waves to the function q(x, t) with (\(d>0\))

Full size image

3 Interaction of the bidirectional waves of TMcKdV-NLS

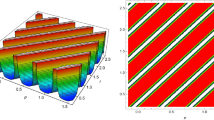
In this section we study graphically the impact of both the phase velocity s and the Kudryashov parameter d on the propagations of the obtained bidirectional waves to TMcKdV-NLS. Figure 7 shows the interactions of both left-wave and right-wave of the real-part of the function q(x, t) upon increasing the phase velocity s and having \(d>0\). While as, Fig. 8 shows the interactions of the case of increasing s and having \(d<0\).

Fig. 7
figure 7

Interactions of moving the left-right bidirectional waves to Re(p(x, t)) upon increasing the phase velocity \(s=1,\ 3,\ 5\) and \(d>0\)

Full size image
Fig. 8
figure 8

Interactions of moving the left-right bidirectional waves to Re(p(x, t)) upon increasing the phase velocity \(s=1,\ 3,\ 5\) and \(d<0\)

Full size image

Moreover, Fig. 9 is the interaction of left-right waves to the function q(x, t) when s is increasing and \(d>0\), and Fig. 10 is the case of s being increasing and \(d<0\).

Fig. 9
figure 9

Interactions of moving the left-right bidirectional waves to q(x, t) upon increasing the phase velocity \(s=1,\ 3,\ 5\) and \(d>0\)

Full size image
Fig. 10
figure 10

Interactions of moving the left-right bidirectional waves to q(x, t) upon increasing the phase velocity \(s=1,\ 3,\ 5\) and \(d<0\)

Full size image

4 Conclusion and future work

The new TMcKdV-NLS is introduced in this work for the first time. We observed some physical properties to the new model by providing 2D-3D graphical analysis. Some solutions are obtained to TMcKdV-NLS by means of the Kudryashov-expansion method.

As a future work, more solutions can be obtained to the proposed model by applying other numerical and analytical schemes. Also, N-solitons and lump solutions (Sulaiman and Yusuf 2021) can be investigated to such two-mode model.