1 Introduction

As a nonlinear wave, solitons have been a hot area of research in the integrable systems (Lü et al. 2016; Wazwaz 2016, 2017a; Liu et al. 2011; Lü and Ma 2016; Osman and Wazwaz 2018). For instance, optical solitons have been extensively studied in the telecommunication systems because of their potential applications in the longdistance optical fiber communication and all-optical ultrafast switching devices (Wang et al. 2015a, b, 2016a, b). Optical solitons have been formed in the balance between the group velocity dispersion and self-phase modulation (Szmytkowski 2012; Zhou et al. 2013; Guo and Zhao 2016; Liu et al. 2014, 2017; Lü and Lin 2016; Guo et al. 2015; Wazwaz 2016; Cai et al. 2017), so they could propagate over a long distance in a fiber without either attenuation or change of shape (Hasegawa and Tappert 1973a, b; Dai et al. 2017, 2016). To describe the propagation of the picosecond pulses in an optical fiber, the nonlinear Schrödinger (NLS) equation (Nakatsuka et al. 1981; Lan and Gao 2017; Zhao et al. 2016, 2017),

$$\begin{aligned} iu_z+u_{\tau \tau }+2|u|^2u=0, \end{aligned}$$
(1)

has been proposed, where \(i^2=-1\), u is the slowly-varying electric field function with respect to the scaled space coordinate z and time coordinate \(\tau \), while the subscripts mean the corresponding derivatives.

NLS equation has been regarded as the basic model to describe the phenomena in optical fibers, plasmas, cold atoms and oceans (Sun et al. 2015). Nonetheless, Eq. (1) only includes the basic effects such as the lowest-order dispersion and nonlinearity (Chai et al. 2015). When the intensity of the optical field gets stronger and the pulses get shorter in optics, one should consider the higher-order effects (Ankiewicz et al. 2014; Liu et al. 2016; Nakazawa et al. 2000; Lakoba and Kaup 1998; Bourkoff et al. 1987; Oliveira and Moura 1998). In fact, some high-order effects and dark solitons for the NLS equations have been discussed (Chowdury et al. 2015; Daniel et al. 1999; Guo et al. 2016; Wazwaz 2017b; Li et al. 2018; Zhang et al. 2017; Lan et al. 2016).

In this paper, a sextic NLS equation has been proposed to model the pulses propagating along a fiber (Ankiewicz et al. 2016; Sun 2017), i.e.,

$$\begin{aligned} \begin{aligned}&iq_x+\frac{1}{2}(q_{tt}+2q|q|^2)+\delta \left\{ q_{tttttt}+q^2[60|q_t|^2q^*+50q_{tt}(q^*)^2\right. \\&\quad +\,2q^*_{tttt}]+q[12q_{tttt}q^*+8q_tq^*_{ttt}+22|q_{tt}|^2+18q_{ttt}q^*_t+70q_t^2(q^*)^2]\\&\quad \left. +\,20q_t^2q^*_{tt}+10q_t(5q_{tt}q^*_t+3q_{ttt}q^*)+20q_{tt}^2q^*+10q^3[(q^*_t)^2+2q^*q^*_{tt}]+20q|q|^6\right\} =0, \end{aligned} \end{aligned}$$
(2)

where x and t are respectively the scaled space and time coordinates, q(x, t) is the envelope of the waves, \(*\) represents the complex conjugation, and \(\delta \) is a real parameter denoting the coefficient of the sextic-order dispersion. When \(\delta =0\), Eq. (2) becomes the basic NLS equation to describe the different nonlinear waves in the Heisenberg ferromagnetic spin chain, Bose–Einstein condensation and nonlinear optics (Sun 2017). Equation (2) has been presented in Ref. Ankiewicz et al. (2016) for the first time. Some different nonlinear waves (Ankiewicz et al. 2016) and breather-to-soliton transitions (Sun 2017) for Eq. (2) have been discussed. Here, the bilinear forms and analytic solutions for Eq. (2) will be obtained by using the modified Hirota bilinear method and symbolic computation.

However, to our knowledge, infinitely-many conservation laws, bilinear forms, soliton solutions and linear stability analysis for Eq. (2) have not been discussed through the modified Hirota method and symbolic computation. In Sect. 2, infinitely-many conservation laws for Eq. (2) will be constructed by virtue of the symbolic computation. In Sect. 3, bilinear forms, multi-soliton solutions for Eq. (2) will be obtained via the modified Hirota method. In Sect. 4, propagations and interactions between the solitons will be illustrated and discussed graphically. In Sect. 5, linear stability analysis will be presented. Conclusions will be given in Sect. 6.

2 Infinitely-many conservation laws for Eq. (2)

In this section, we will derive the Lax pair and infinitely-many conservation laws for Eq. (2). Based on the Ablowitz–Kaup–Newell–Segur system (Ablowitz et al. 1973), Lax pair for Eq. (2) can be written into the following form,

$$\begin{aligned} \Phi _t=M \Phi ,\,\,\,\Phi _x=N \Phi , \end{aligned}$$
(3)

where \(\Phi =(\varphi _1,\varphi _2)^T\) is a vector eigenfunction for Lax Pair (3), \(\varphi _1\) and \(\varphi _2\) are both the complex functions of x and t, while the superscript T signifies the vector transpose, the \(2\times 2\) matrices M and N can be defined by,

$$\begin{aligned} M=i\begin{pmatrix} \lambda &{} r \\ q &{} -\lambda \\ \end{pmatrix},\,\,\,N=i\begin{pmatrix} A &{} B \\ C &{} -A \\ \end{pmatrix}, \end{aligned}$$
(4)

where r, A, B and C are the complex functions of x and t, \(\lambda \) is a complex eigenvalue parameter. Based on the compatibility condition \(\Phi _{tx}=\Phi _{xt}\) and Lax Pair (4), we can get the zero-curvature equation as follows:

$$\begin{aligned} M_t-N_x+MN-NM=0. \end{aligned}$$
(5)

Substituting Matrices (4) into Eq. (5), we can get

$$\begin{aligned} A_t=-i\,q\,B+i\,r\,C,\,\,\,B_t=r_x-2\,i\,r\,A +2\,i\lambda \,B,\,\,\,C_t=q_x-2\,i\lambda \,C+2\,i\lambda \,q\,A. \end{aligned}$$
(6)

In order to facilitate the calculation of Lax Pair (3), A, B and C are expended into the forms as (Chai et al. 2015; Wang et al. 2015c),

$$\begin{aligned} A=\sum \limits _{j=0}^{6}{i\lambda ^j A_j},\,\,\,B=\sum \limits _{j=0}^{6}{i\lambda ^j B_j},\,\,\,C=\sum \limits _{j=0}^{6}{i\lambda ^j C_j}, \end{aligned}$$
(7)

where \(A_j{'}\)s, \(B_j{'}\)s and \(C_j{'}\)s are the complex functions of x and t. Substituting Expressions (7) into Eqressions (6) and equating the coefficients of the same powers of \(\lambda \), we have

$$\begin{aligned} \begin{aligned} A_0=&-\frac{1}{2}|q|^2-\delta \left\{ 10|q|^6+5q_t^2(q^*)^2+q_{tt}q^*_{tt}\right. \\&\left. +\,5q^2[(q^*)^2+q^*q^*_{tt}]-q_{ttt}q^*_t-q_tq^*_{ttt}+q_{tttt}q^*+q[10q_{tt}(q^*)^2+q^*_{tttt}]\right\} ,\\ A_1=&-2i\delta \left\{ q_{tt}q^*_t+6q|q|^2q^*_t-q_tq^*_{tt}-q_{ttt}q^*-q[6q_t(q^*)^2-q^*_{ttt}]\right\} ,\,\,\,A_3=-8i\delta (q_tq^*-qq^*),\\ A_2=&1+4\delta (3|q|^4-|q_t|^2+q_{tt}q^*+qq^*_{tt}),\,\,\,A_4=-16\delta |q|^2,\,\,\,A_5=0,\,\,\,A_6=32\delta ,\\ B_0&=-i\frac{1}{2}q^*_t-i\delta \left\{ 30|q|^4q^*+10q_{tt}q^*_tq^*+10q_t[(q^*_t)^2+q^*q^*_{tt}]+10q(2q^*_tq^*_{tt}+q^*q^*_{ttt})+q^*_{ttttt}\right\} ,\\ B_1&=q^*+2\delta \left\{ 6|q|^4q^*+4|q_t|^2q^*+2q_{tt}(q^*)^2+q[6(q^*_t)^2+8q^*q^*_{tt}]+q^*_{tttt}\right\} ,\,\,\,\,\,\,B_4=-16i\delta q^*_t,\\ B_2&=4i\delta (6|q|^2q^*_t+q^*_{ttt}),\,\,\,B_3=-8\delta (2|q|^2q^*+q^*_{tt}),\,\,\,B_5=32\delta q^*,\,\,\,B_6=0,\,\,\,C_j=B_j^*,\,\,r=q^*. \end{aligned} \end{aligned}$$

Our calculation indicates that Compatibility Condition (5) leads to Eq. (2). Thus, Eq. (2) is integrable in the Lax sense.

Next, based on Lax Pair (3), we will show how to derive the infinitely-many conservation laws for Eq. (2). Introducing three complex functions (Chai et al. 2015; Wang et al. 2015c)

$$\begin{aligned} \Lambda _1=\frac{\varphi _{1,t}}{\varphi _1},\,\,\,\Lambda _2= \frac{\varphi _{1,x}}{\varphi _1},\,\,\,\Lambda _3=\frac{\varphi _2}{\varphi _1}, \end{aligned}$$
(8)

and applying the compatibility condition \(\Lambda _{1,x}=\Lambda _{2,t}\) from Lax Pair (3), we have

$$\begin{aligned} \Lambda _{3,t}=i\,q-2\,i\lambda \,\Lambda _3-i\,r\Lambda _3^2,\,\,\, (\lambda +r\Lambda _3)_x=(A+B\Lambda _3)_t. \end{aligned}$$
(9)

Then, expanding the expansion of \(\Lambda _3\) with respect to \(\lambda \) as follows:

$$\begin{aligned} \Lambda _3=\sum \limits _{j=1}^{\infty }\frac{\chi _j}{\lambda ^j}, \end{aligned}$$
(10)

where \(\chi _{j}{'}\)s (\(j=\)1,2...) are all the complex functions of x and t. Substituting Expressions (7) and (10) into Eq. (9) and collecting the coefficients of the same powers of \(\lambda \) to be equal to zero, we get

$$\begin{aligned} \chi _1=\frac{1}{2}q,\,\,\,\chi _2=\frac{i}{4}q_t,\,\cdots ,\,\,\, \chi _{j+1}=\frac{i}{2}\left( \chi _{j,t}+iq^*\sum \limits _{o=1}^{j-1}\chi _o\chi _{j-o}\right) , \end{aligned}$$
(11)

and the infinite-many conservation laws for Eq. (2) as

$$\begin{aligned} \frac{\partial \Gamma _j}{\partial t}+\frac{\partial \Theta _j}{\partial x}=0,\,\,\,\Gamma _j=q\chi _j,\,\,\,\Theta _j=-i\sum \limits _{o=0}^7B_o\chi _{j+o}, \end{aligned}$$
(12)

where \(\Gamma _j{'}\)s and \(\Theta _j{'}\)s are all the complex functions of x and t, \(\Gamma _j{'}\)s represent the conserved densities and \(\Theta _j{'}\)s represent the fluxes.

3 Bilinear forms and soliton solutions for Eq. (2)

In order to detect the form of linearizable representation of Eq. (2), a transformation

$$\begin{aligned} q(x,t)=\frac{g}{f}, \end{aligned}$$
(13)

will be introduced, where f is a real function of x and t, while g is a complex one. Substituting Expression (13) into Eq. (2) and letting \(D_t^2 f\cdot f-2|g|^2=0\), the bilinear forms for Eq. (2) will be obtained as

$$\begin{aligned} \begin{aligned}&D_t^2 g\cdot g-h\,f=0,\,\,\,30g^*(D_t g\cdot g_{3t}+f_th_t)-15f_tg_t^*h-f\,\rho \,\varrho =0,\\&D_t^2 f\cdot f-2|g|^2=0,\,\,\,\left( i D_x+\frac{1}{2}D_t^2+\delta D_t^6\right) g\cdot f+\delta (5g_t^*h_t-10g_{2t}^*+5g^*h_{2t}+\rho \varrho )=0, \end{aligned} \end{aligned}$$
(14)

where the Hirota D-operator is defined as (Hirota 1991),

$$\begin{aligned} D_x^{n_1} D_t^{n_2}p\cdot q=\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^{n_1} \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^{n_2} p\left( x,y,t\right) q\left( x',t'\right) \left| _{x'=x,t'=t}\right. , \end{aligned}$$
(15)

p(x, t) is a function of x and t, \(q(x',t')\) is a function of the formal variables \(x'\) and \(t'\), while \(n_1\) and \(n_2\) are all the non-negative integers.

In order to obtain the soliton solutions for Eq. (2), f, g, h, \(\rho \) and \(\varrho \) are expended with respect to a small parameter \(\varepsilon \) as

$$\begin{aligned} \begin{aligned}&f=1+\varepsilon ^2f_2+\varepsilon ^4f_4+\ldots ,\,\,\,g=\varepsilon g_1+\varepsilon ^3g_3+\varepsilon ^5g_5+\ldots ,\\&h=h_0+\varepsilon ^2h_2+\varepsilon ^4h_4+\ldots ,\,\,\,\rho =\varepsilon \rho _1+\varepsilon ^3\rho _3+\varepsilon ^5\rho _5+\ldots ,\,\,\,\varrho =\varrho _0+\varepsilon ^2\varrho _2+\varepsilon ^4\varrho _4+\ldots , \end{aligned} \end{aligned}$$
(16)

where \(f_{\ell }\)’s (\(\ell =2,4,...\)), \(\rho _{\jmath }\)’s (\(\jmath =\)1,3,...), \(h_{k}\)’s and \(\varrho _{\iota }\)’s (\(\iota =\)0,2,...) are the real functions of x and t, while \(g_{\jmath }\)’s are the complex ones.

Truncating Expressions (16) as

$$\begin{aligned} f=1+\varepsilon ^2f_2,\,\,\,g=\varepsilon g_1,\,\,\,\rho =\varepsilon \rho _1,\,\,\,h=h_0+\varepsilon ^2h_2,\,\,\,\varrho =\varrho _0+\varepsilon ^2\varrho _2, \end{aligned}$$
(17)

and substituting Expressions (17) into Bilinear Forms (14) with \(\varepsilon =1\), the one-soliton solutions are obtained as

$$\begin{aligned} q=\frac{g_1}{1+f_2}, \end{aligned}$$
(18)

where

$$\begin{aligned} f_2=A e^{\xi +\xi ^*},\,\,\,g_1=e^{\xi },\,\,\,\xi =\frac{i}{2}\omega ^2(1+2\delta \omega ^4)x+\omega t,\,\,\,A=\frac{1}{(\omega +\omega ^*)^2},\,\,\,h_0=h_2=\varrho _0=\varrho _2=0, \end{aligned}$$

with \(\omega \)’s as the complex constants.

Next, truncating Expressions (16) as

$$\begin{aligned} \begin{aligned}&f=1+\varepsilon ^2f_2+\varepsilon ^4f_4,\,\,\,g=\varepsilon g_1+\varepsilon ^3g_3,\\&\rho =\varepsilon \rho _1+\varepsilon ^3\rho _3,\,\,\,h=h_0+\varepsilon ^2h_2+\varepsilon ^4h_4,\,\,\,\varrho =\varrho _0+\varepsilon ^2\varrho _2+\varepsilon ^4\varrho _4, \end{aligned} \end{aligned}$$
(19)

and substituting Expressions (19) into Bilinear Forms (14) with \(\varepsilon =1\), the two-soliton solutions are obtained as

$$\begin{aligned} q=\frac{g_1+ g_3}{1+ f_2+f_4}, \end{aligned}$$
(20)

where

$$\begin{aligned} \begin{aligned}&g_1=e^{\xi _1}+e^{\xi _2},\,\,\,g_3=A_{123}e^{\xi _1+\xi _2+\xi _1^*}+A_{124}e^{\xi _1+\xi _2+\xi _2^*},\,\,\,h_2=2A_{12}e^{\xi _1+\xi _2},\\&f_2=A_{13}e^{\xi _1+\xi _1^*}+A_{23}e^{\xi _2+\xi _1^*}+A_{14}e^{\xi _1+\xi _2^*}+A_{24}e^{\xi _2+\xi _2^*},\,\,\,f_4=A_{1234}e^{\xi _1+\xi _1^*+\xi _2+\xi _2^*},\\&\varrho _2=B_{12}e^{\xi _1+\xi _2},\,\,\,\rho _1=B_{34}(e^{\xi _1^*}+e^{\xi _2^*}),\,\,\,\rho _3=B_{134}e^{\xi _1+\xi _1^*+\xi _2^*}+B_{234}e^{\xi _2+\xi _1^*+\xi _2^*},\,\,\,\xi _j=k_jx+\omega _jt,\\&k_j=\frac{i}{2}\omega _j^2(1+2\delta \omega _j^4),\,\,\,A_{12}=\omega _1-\omega _2,\,\,\,A_{34}=\omega _1^*-\omega _2^*,\,\,\,A_{j,l+2}=\frac{1}{(\omega _j+\omega _j^*)^2},\,\,\,(j=1,2),\\&A_{123}=A_{12}A_{13}A_{23},\,\,\,A_{124}=A_{12}A_{14}A_{24},\,\,\,A_{1234}=A_{12}A_{13}A_{14}A_{23}A_{24}A_{34}\,\,\,(l=1,2), \end{aligned} \end{aligned}$$

with \(k_l\) and \(\omega _l\) as the complex constants.

4 Discussions on the soliton solutions

In this section, the solitons for Eq. (2) will be analyzed. From One-Soliton Solutions (18), q could be rewritten as,

$$\begin{aligned} |q|=|\omega _R|\text {sech}\left( \xi _R+\frac{1}{2}\ln A\right) , \end{aligned}$$
(21)

where the subscripts I and R are the imaginary and real parts, respectively. Here, the concept of characteristic line for the solitons’ propagation (Yang et al. 2016) will be introduced to determine the velocity. Letting \(\omega =a_m+ib_m\) with \(a_m\) and \(b_m\) being the real constants \((m=1,2,\cdots )\), the soliton amplitude \(\Delta =a_m\) will be derived. Through the method in Ref. Yang et al. (2016), the characteristic-line equation for each soliton is deduced to

$$\begin{aligned} -a_mb_m\left[ 1+2\delta (3a_m^4-10a_m^2b_m^2+3b_m^4)\right] x+a_mt+\frac{\ln A}{2}=\text {constant}. \end{aligned}$$

Then differentiating it on both sides with respect to x, the velocity of each soliton is

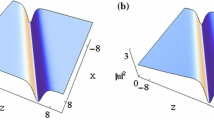
$$\begin{aligned} v=\frac{1}{b_m\left[ 1+2\delta (3a_m^4-10a_m^2b_m^2+3b_m^4)\right] }. \end{aligned}$$
(22)

Based on the above analysis, we find that the initial position and velocity of the soliton are related to the parameter \(\delta \), but the soliton’s amplitude is not affected by it. As seen in Fig. 1, we find that the one solitons propagate stably with the same amplitude and shape but different velocities and a certain degree of broadening or compressing.

Fig. 1
figure 1

One soliton via solutions (18) with \(\omega =0.8+0.7i\): a \(\delta =0.1\); b \(\delta =1\); c \(\delta =2\). d–f Trajectories of a–c at \(t=-2\), \(t=0\) and \(t=2\), respectively

Full size image
Fig. 2
figure 2

a Head-on interaction between the two solitons via solutions (20) with \(\omega _1=0.8+0.7i\), \(\omega _2=0.9+0.4i\) and \(\delta =1\). b Trajectories of (a) at \(t=-\,8\), 0 and 8

Full size image
Fig. 3
figure 3

a Overtaking interaction between the two solitons via solutions (20) with \(\omega _1=0.8+0.1i\), \(\omega _2=1.0+0.3i\) and \(\delta =1\). b Trajectories of a at \(t=-\,8\), 0 and 8

Full size image

Based on the asymptotic analysis, the two solitons will be analyzed as follows: When \(x\rightarrow -\infty \) (before the interaction),

$$\begin{aligned} \begin{aligned}&q\rightarrow q^{1-}=|\omega _{1R}|e^{i\xi _{1I}}\text {sech}\left( \xi _{1R}+\frac{1}{2}\ln A_{11}\right) , (\xi _1+\xi _1^*\rightarrow 0, \xi _2+\xi _2^*\rightarrow -\infty ),\\&q\rightarrow q^{2-}=|\omega _{2R}|e^{i\xi _{2I}}\text {sech}\left( \xi _{2R}+\frac{1}{2}\ln \frac{A_{1234}}{A_{11}}\right) , (\xi _2+\xi _2^*\rightarrow 0, \xi _1+\xi _1^*\rightarrow +\infty ), \end{aligned} \end{aligned}$$
(23)

where \(q^{1-}\) and \(q^{2-}\) denote the two solitons before the interaction. When \(t\rightarrow +\infty \) (after the interaction),

$$\begin{aligned} \begin{aligned}&q\rightarrow q^{1+}=|\omega _{1R}|e^{i\xi _{1I}}\text {sech}\left( \xi _{1R}+\frac{1}{2}\ln \frac{A_{1234}}{A_{22}}\right) , (\xi _1+\xi _1^*\rightarrow 0, \xi _2+\xi _2^*\rightarrow +\infty ),\\&q\rightarrow q^{2+}=|\omega _{2R}|e^{i\xi _{2I}}\text {sech}\left( \xi _{2R}+\frac{1}{2}\ln A_{22}\right) , (\xi _1+\xi _1^*\rightarrow 0, \xi _1+\xi _1^*\rightarrow -\infty ), \end{aligned} \end{aligned}$$
(24)

where \(q^{1+}\) and \(q^{2+}\) denote the two solitons after the interaction. Through the asymptotic analysis, we find that the interaction between the two solitons is elastic, which means that their amplitudes and shapes keep invariant after each interaction except for certain phase shifts, and this phenomenon can be confirmed in Figs. 2, 3, 4.

Fig. 4
figure 4

a Oscillation interaction between the two solitons via solutions (20) with \(\omega _1=1.2-0.731i\), \(\omega _2=0.8+0.532i\) and \(\delta =1/2\). b Trajectories of a at \(t=-\,8\), 0 and 8

Full size image
Fig. 5
figure 5

a Bound state via solutions (20) with \(\omega _1=1.2+0.0124i\), \(\omega _2=0.8+0.0486i\) and \(\delta =1\). b Trajectories of a at \(t=-\,8\), 0 and 8

Full size image

As shown in Fig. 2a, when the velocities for the two solitons satisfy the different signs, the head-on interaction happens. While the velocities of them are the same sign, the overtaking interaction is observed in Fig. 3a, where the soliton with a smaller amplitude moves faster and overtakes the larger one. Comparing Figs. 4a with 2a, we find that the two solitons present oscillation interaction when the distance between them decreases to a certain value, and the oscillation phenomenon is especially obvious at \(t=0\). Meanwhile, as seen in Figs. 2b–4b, we notice that those interactions are elastic. Bound state for the two solitons is formed as they have the equal velocity, and they attract and repulse each other periodically in Fig. 5.

5 Modulation instability

Based on the linear stability analysis (Zhao et al. 2016), we will investigate the Modulation instability (MI) of the stationary solutions for Eq. (2). The stationary solution for Eq. (2) has the following form,

$$\begin{aligned} q=q_0 e^{i(\kappa t+\theta x)}, \end{aligned}$$
(25)

where \(\theta =q_0^2+20\delta q_0^6-\kappa ^2(\frac{1}{2}+90\delta q_0^4)+30\delta \kappa ^4 q_0^2-\delta \kappa ^6\), \(q_0\) and \(\kappa \) are the real constants. In order to perform the linear stability analysis, we set Solutions (25) with a small perturbation term as follows (Zhao et al. 2016; Chai et al. 2015; Wang et al. 2015c):

$$\begin{aligned} q=(q_0 +\chi \tilde{q})e^{i(\kappa t+\varpi x)}, \end{aligned}$$
(26)

where \(\chi \) is a perturbation parameter, \(\tilde{q}\) is a function of x and t. In general, \(\tilde{q}\) can be set as (Chai et al. 2015; Wang et al. 2015c)

$$\begin{aligned} \tilde{q}=q_1 e^{i(\kappa _1 t-\theta x)}+q_2e^{-i(\kappa _1 t-\theta x)}, \end{aligned}$$
(27)

where \(q_1\) and \(q_2\) are both the coefficients of the linear combination, \(\kappa _1\) is a real disturbance wave numbers, while \(\theta \) is a real disturbance frequency. Substituting Eqs. (26) and (27) into Eq. (2), we have linear equations about \(q_1\) and \(q_2\) as follows:

$$\begin{aligned} \begin{aligned}&\Delta _{11}q_1+\Delta _{12}q_2=0,\\&\Delta _{21}q_1+\Delta _{22}q_2=0, \end{aligned} \end{aligned}$$
(28)

with

$$\begin{aligned} \begin{aligned} \Delta _{11}=&-2q_0^2\left\{ 1+2\delta \left[ \kappa _1^4-5\kappa _1^2(2q_0^2-3\varpi ^2)+15(2q_0^4-6q_0^2\varpi ^2+\varpi ^4)\right] \right\} ,\\ \Delta _{12}=&\kappa _1^2+2\delta \kappa _1^6-24\kappa _1^4q_0^2\delta +100\kappa _1^2q_0^4\delta -160q_0^6\delta \\&+\,2\kappa _1[1+6\delta \varpi (\kappa _1^4-10\kappa _1^2q_0^2+30q_0^4)]+\varpi ^2[1+30\delta (\kappa _1^4-8\kappa _1^2q_0^2+18q_0^4)]\\&+\,40\delta \kappa _1\varpi ^3(\kappa _1^2-6q_0^2)+30\delta \varpi ^4(\kappa _1^2-4q_0^2)+12\delta \kappa _1\varpi ^5+2\delta \varpi ^6-2(2q_0^2+\theta )+2\kappa ,\\ \Delta _{21}=&\kappa _1^2-4q_0^2+2\delta \kappa _1^6-24\kappa _1^4q_0^2\delta +100\kappa _1^2q_0^4\delta -160q_0^6\delta \\&-\,2\kappa _1[1+6\delta \varpi (\kappa _1^4-10\kappa _1^2q_0^2+30q_0^4)]+\varpi ^2[1+30\delta (\kappa _1^4-8\kappa _1^2q_0^2+18q_0^4)]\\&-\,40\delta \kappa _1\varpi ^3(\kappa _1^2-6q_0^2)+30\delta \varpi ^4(\kappa _1^2-4q_0^2)-12\delta \kappa _1\varpi ^5+2\delta \varpi ^6+2\theta +2\kappa ,\\ \Delta _{22}=&-2q_0^2\left\{ 1+2\delta \left[ \kappa _1^4-5\kappa _1^2(2q_0^2-3\varpi ^2)+15(2q_0^4-6q_0^2\varpi ^2+\varpi ^4)\right] \right\} . \end{aligned} \end{aligned}$$

Equation (28) have a nontrivial solutions if and only if the determinant

$$\begin{aligned} \begin{vmatrix}\Delta _{11}&\Delta _{12}\\ \Delta _{21}&\Delta _{22}\end{vmatrix}=0. \end{aligned}$$
(29)

Based on the above expression, we get the following dispersion relation as

$$\begin{aligned} \theta =\kappa _1\varpi [1+6\delta \kappa _1^4-20\delta \kappa _1^2 (3q_o^2-\varpi ^2)+6\delta (30q_0^4-20q_0^2\varpi ^2+\varpi ^4)]\pm \frac{1}{2}\sqrt{\Lambda }, \end{aligned}$$
(30)

with

$$\begin{aligned} \begin{aligned} \Lambda =&\left\{ \kappa _1^2-6q_0^2+2\delta \kappa _1^6-28\delta \varpi ^4q_0^2+140\delta \varpi ^2q_0^4-280\delta q_0^6\right. \\&\left. +\,\varpi ^2[1+30\delta (\kappa _1^4-10\kappa _1^2q_0^2+30q_0^4)]+30\delta \varpi ^4(\kappa _1^2-6q_0^2)+2\delta \varpi ^6+2\kappa \right\} \\&\times \,\left\{ \kappa _1^2-2q_0^2+2\delta \kappa _1^6-20\delta \varpi ^4q_0^2+60\delta \varpi ^2q_0^4-40\delta q_0^6\right. \\&\left. +\,\varpi ^2[1+30\delta (\kappa _1^4-6\kappa _1^2q_0^2+6q_0^4)]+30\delta \varpi ^4(\kappa _1^2-2q_0^2)+2\delta \varpi ^6+2\kappa \right\} . \end{aligned} \end{aligned}$$

If \(\Lambda \geqslant 0\), \(\theta \) is always a real number. Based on the case, the intensity of the small perturbation \(\tilde{q}\) will keep invariable along the fiber, which implies that the envelopes for Eq. (2) are stable against the disturbance of small perturbation. On the contrary, if \(\Lambda <0\), the \(\theta \) will be a complex one. Then the \(\tilde{q}\) will exponentially increase along the fiber, causing that the modulation instability will take place.

6 Conclusions

In this paper, Eq. (2) has been focused, which describes the pulses propagating along an optical fiber. With the help of the symbolic computation, we have derived Infinite-Many Conservation Laws (12) for Eq. (2). By virtue of the Hirota method and three auxiliary functions, we have obtained Bilinear Forms (14), One-Soliton Solutions (18) and Two-Soliton Solutions (20). From Expressions (21) and (22), we have found that the initial position and velocity of the soliton are related to the parameter \(\delta \) in Eq. (2), but the soliton’s amplitude is not affected by it. In Fig. 1, with the different values of \(\delta \), we have found that the one solitons propagate stably with the same amplitude and shape but different velocities and a certain degree of broadening or compressing. Figures 2, 3, 4 and 5 have illustrated the interactions between the two solitons: Head-on, overtaking, oscillating interactions and the bound state, respectively. Through the asymptotic analysis, interaction between the two solitons has been proved to be elastic. Based on the Linear stability analysis, we have derived the modulation instability condition for the soliton solutions.