Analytic solutions for the generalized complex Ginzburg–Landau equation in fiber lasers

Abstract

Generalized complex Ginzburg–Landau equation (GCGLE) can be used to describe the nonlinear dynamic characteristics of fiber lasers and has riveted much attention of researchers in ultrafast optics. In this paper, analytic solutions of the GCGLE are obtained via the modified Hirota bilinear method. Kink waves and period waves are presented by selecting the relevant parameters. The influence of the related parameters on them is analyzed and studied. The results indicate that the desired pulses can be demonstrated by effectively controlling the dispersion and nonlinearity of fiber lasers.

1 Introduction

Nonlinear partial differential equations have been widely studied all the time [1,2,3,4,5,6,7,8,9,10,11]. Among them, the generalized complex Ginzburg–Landau equation (GCGLE) is a class of general-purpose models with wide applications, which have attracted much attention in both physics and applied mathematics [12,13,14,15,16,17,18,19,20]. Researchers have got some achievements in different ways for the GCGLEs [21,22,23,24,25,26,27,28]. With the homotopy analysis method, the approximate solution of the GCGLE has been obtained [29]. Besides, the periodic attractors of the GCGLE have been identified [30]. Using the modified Hirota method, the soliton amplification of the GCGLE has been discussed [31]. The dissipative solitons of the GCGLE have also been studied [32]. In addition, the GCGLE with a linear dissipative term has been investigated [33]. In this paper, we study the following GCGLE,

$$\begin{aligned}&iu_{t}+Pu_{xx}+\varGamma u+Q|u|^{2}u+Q_{3}|u|^{4}u\nonumber \\&+\,Q_{1}u^{2}u_{x}^{*}+Q_{2}|u|^{2}u_{x}=0. \end{aligned}$$

(1)

Here, u(x, t) is a complex function of time t and spatial variable x and $*$ is the complex conjugate. The coefficients are $P=p_{1}(t)+ip_{2}(t), \varGamma =\gamma _{1}(t)+i\gamma _{2}(t), Q=q_{1}(t)+iq_{2}(t), Q_{3}=c_{1}(t)+ic_{2}(t), Q_{1}=d_{1}(t)+id_{2}(t)$, and $Q_{2}=s_{1}(t)+is_{2}(t)$. What is more, $p_{l}, \gamma _{l}, q_{l}, c_{l}, d_{l}$, and $s_{l}$ are complex-valued functions of t ($l=1,2$).

Kengne et al. [34] have studied Eq. (1) and presented a set of soliton solutions for this equation using the standard semidiscrete approximation method. Analytic solutions for Eq. (1) have been derived with the help of the double-mapping method combining the similarity method and F-expansion method [35]. In addition, other researchers have made explorations of relevant equations [36, 37]. Here, analytic solutions for Eq. (1) are obtained by using the modified Hirota bilinear method. Those solutions include periodic wave solutions and kink wave solutions.

This paper expands as follows: In Sect. 2, analytic solution is derived with the modified Hirota method. Then in Sect. 3, kink wave solutions, period solutions, and their interactions are presented, and the characteristics of those waves have been analyzed. Finally in Sect. 4, we make the summary of our discussions.

2 Analytic solutions for Eq. (1)

According to the modified Hirota method, we introduce the dependent variable transformations.

$$\begin{aligned}&u(x,t)=\frac{g(x,t)}{f(x,t)^{n}}, \nonumber \\&u(x,t)^{*}=\frac{g(x,t)^{*}}{f(x,t)^{n^{*}}}\ \left( n=\frac{1}{2}+i\alpha \right) . \nonumber \\&u_{t}=\frac{D_{n,t}g\cdot f}{f^{n+1}},\nonumber \\&u_{x}=\frac{D_{n,x}g\cdot f}{f^{n+1}},\ \ \ \ u_{x}^{*}=\frac{D_{n,x}^{*}g^{*}\cdot f}{f^{n^{*}+1}}, \end{aligned}$$

(2)

and

$$\begin{aligned} u_{xx}=\frac{D_{n,x}^{2}g\cdot f}{f^{n+1}}-\frac{n(n+1)g\cdot D_{x}^{2}f\cdot f}{2f^{n+2}}. \end{aligned}$$

Here $D_{n,x}^{*}g^{*}\cdot f$ is the complex conjugate operator of $D_{n,x}g\cdot f$, and they are defined by,

$$\begin{aligned}&D_{n,x}g\cdot f=\Big (\frac{\partial }{\partial x}-n\frac{\partial }{\partial x'}\Big )g(x,t)f(x',t')\bigg |_{x'=x,t'=t}\ ;\\&D_{n,x}^{*}g^{*}\cdot f=\Big (\frac{\partial }{\partial x}-n^{*}\frac{\partial }{\partial x'}\Big )g^{*}(x,t)f(x',t')\bigg |_{x'=x,t'=t}\ ;\\&D_{x}^{2}f\cdot f=\Big (\frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\Big )f(x,t)f(x',t')\bigg |_{x'=x,t'=t}\ ;\\&D_{n,x}^{2}g\cdot f=\Big (\frac{\partial }{\partial x}-n\frac{\partial }{\partial x'}\Big )^{2}g(x,t)f(x',t')\bigg |_{x'=x,t'=t}. \end{aligned}$$

Then Eq. (1) can be derived as,

$$\begin{aligned}&Q\frac{|g|^{2}g}{f^{n+n^{*}+n}}+Q_{3}\frac{|g|^{4}g}{f^{2n+2n^{*}+n}} +Q_{1}\frac{g^{2}D_{n,x}^{*}g^{*}\cdot f}{f^{2n+n^{*}+1}}\nonumber \\&\quad +\,Q_{2}\frac{|g|^{2}\cdot D_{n,x}g\cdot f}{f^{n+n^{*}+n+1}}\nonumber \\&\quad +\, i\cdot \Bigg (\frac{D_{n,t}g\cdot f}{f^{n+1}}\Bigg )+A=0, \end{aligned}$$

(3)

where

$$\begin{aligned} A= & {} P\Bigg [\frac{D_{n,x}^{2}g\cdot f}{f^{n+1}}-\frac{n(n+1)g\cdot D_{x}^{2}f\cdot f}{2f^{n+2}}\Bigg ]\nonumber \\&+\,\varGamma \frac{g}{f^{n}}. \end{aligned}$$

Both sides of Eq. (3) are multiplied by $f^{n}$. In addition, $n+n^{*}=1$, and Eq. (3) can be abbreviated as,

$$\begin{aligned}&\Bigg [A+i\cdot \Big (\frac{D_{n,t}g\cdot f}{f^{n+1}}\Big )\Bigg ]\cdot f^{n} +\,\frac{g\cdot B}{f^{2}}=0, \end{aligned}$$

(4)

where

$$\begin{aligned} B= & {} Q|g|^{2}f+Q_{3}|g|^{4}+Q_{1}gD_{n,x}^{*}g^{*}\cdot f\\&+Q_{2}g^{*}D_{n,x}g\cdot f. \end{aligned}$$

Connecting the coefficients $\frac{1}{f}$ and $\frac{1}{f^{2}}$, the following formulas can be obtained,

$$\begin{aligned}&\frac{1}{f}\Bigg [i\cdot D_{n,t}g\cdot f+PD_{n,x}^{2}g\cdot f+\varGamma g\cdot f\Bigg ]\nonumber \\&+\frac{1}{f^{2}}\Bigg [-\frac{1}{8}P(1+2i\alpha )(3+2i\alpha )D_{x}^{2}f\cdot f+B\Bigg ]g=0. \end{aligned}$$

Fig. 1

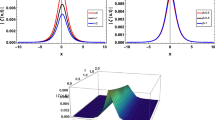
Propagation of kink waves. The parameters for analytic solution (8) are $\varepsilon =1, a_{1}=1, a_{2}=2, k_{1}=2, k_{2}=3, s_{2}(x)=1, \gamma _{1}(t)=0.001, \gamma _{2}(x)=0.002, s_{1}(t)=0.5, d_{1}(t)=0.2, d_{2}(t)=0.003$ with a $\alpha =0.031, q_{1}(t)=-0.78$, and $p_{2}(t)=0.023$; b $\alpha =0.38, q_{1}(t)=0.47$, and $p_{2}(t)=-0.31$

Fig. 2

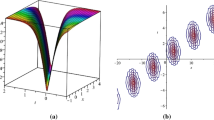
Interactions between kink waves and period waves. The parameters for analytic solution (8) are $\varepsilon =1, k_{1}=2, k_{2}=3, s_{2}(x)=1, \gamma _{1}(t)=0.001, \gamma _{2}(x)=0.002, s_{1}(t)=0.5, d_{1}(t)=0.2, d_{2}(t)=\sin (mt)$ with a $m=1.7, a_{1}=0.88, a_{2}=-1.3, \alpha =-1.5, p_{2}(t)=-2.8$, and $q_{1}(t)=0.71$; b $m=-1.4, a_{1}=1, a_{2}=-1.3, \alpha =-0.94, p_{2}(t)=2.8$, and $q_{1}(t)=0.69$

Then, the bilinear representation of Eq. (1) can be derived as,

$$\begin{aligned}&iD_{n,t}g\cdot f+PD_{n,x}^{2}g\cdot f+\varGamma g\cdot f=0, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{1}{8}P(1+2i\alpha )(3+2i\alpha )D_{x}^{2}f\cdot f=B. \end{aligned}$$

(6)

With the Hirota method, Eq. (2) can be solved by the following power series expansions for g(x, t) and f(x, t) as:

$$\begin{aligned} g(x,t)= & {} \varepsilon g_{1}(x,t)+\varepsilon ^{3}g_{3}(x,t)\nonumber \\&+ \, \varepsilon ^{5}g_{5}(x,t)+\cdots , \end{aligned}$$

(7a)

$$\begin{aligned} f(x,t)= & {} 1+\varepsilon ^{2}f_{2}(x,t)+\varepsilon ^{4}f_{4}(x,t)\nonumber \\&+ \,\varepsilon ^{6}f_{6}(x,t)+\cdots , \end{aligned}$$

(7b)

where $\varepsilon$ is a formal expression parameter, $g_{m}(x,t)(m=1,3,5,\ldots )$ are complex functions, and the $f_{j}(x,t)(j=2,4,6,\ldots )$ are the real ones. To obtain the analytic solution of Eq. (1), we set $g(x,t)=\varepsilon g_{1}(x,t)$, and $f(x,t)=1+\varepsilon ^{2}f_{2}(x,t)$. The analytic solution of Eq. (1) can be written as,

$$\begin{aligned} u(x,t)=e^{Q(x,t)}\varepsilon \Bigg [1+e^{Q(x,t)+Q^{*}(x,t)}\varepsilon ^{2} \sigma (t)\Bigg ]^{-\frac{1}{2}-i\alpha },\nonumber \\ \end{aligned}$$

(8)

where

$$\begin{aligned}&g_{1}(x,t)=e^{Q(x,t)},\ \ f_{2}(x,t)=\sigma (t)e^{Q(x,t)+Q^{*}(x,t)},\\&Q(x,t)=(a_{1}+ia_{2})x+[b_{1}(t)+ib_{2}(t)]t+(k_{1}+ik_{2}),\\&\sigma (t)=\frac{-a_{1}[s_{1}(t)+d_{1}(t)]+a_{2}[s_{2}(t)-d_{2}(t)]-q_{1}(t)}{a_{1}^{2}[-3p_{1}(t)+4\alpha ^{2}p_{1}(t)+8\alpha p_{2}(t)]},\\&b_{1}(t)=\frac{\int [-2a_{1}a_{2}p_{1}(t)-a_{1}^{2}p_{2}(t)+a_{2}^{2}p_{2}(t)-\gamma _{2}(t)]dt}{t},\\&b_{2}(t)=\frac{\int [a_{1}^{2}p_{1}(t)-a_{2}^{2}p_{1}(t)-2a_{1}a_{2}p_{2}(t)+\gamma _{1}(t)]dt}{t},\\&q_{2}(t)=-a_{1}[d_{2}(t)+s_{2}(t)]+a_{2}[d_{1}(t)-s_{1}(t)] \\&\quad +\, a_{1}^{2}\sigma (t)[8\alpha p_{1}(t)+3p_{2}(t)-4\alpha ^{2}p_{2}(t)],\\&p_{1}(t)=\frac{2(a_{2}-a_{1}\alpha )p_{2}(t)}{a_{1}},\\&\gamma _{2}(t)=\frac{2(a_{2}-2a_{1}\alpha )^{2}\sigma (t)p_{2}(t)+\sigma ^{\prime }(t)}{2\sigma (t)},\\&c_{1}(t)=\sigma (t)[s_{2}(t)-d_{2}(t)](a_{2}-2a_{1}\alpha )-\sigma (t)q_{1}(t),\\&c_{2}(t)=\sigma (t)[d_{1}(t)-s_{1}(t)](a_{2}-2a_{1}\alpha )-\sigma (t)q_{2}(t). \end{aligned}$$

Here, $a_{1}, a_{2}, b_{1}, b_{2}, k_{1}$, and $k_{2}$ are real-valued functions.

Fig. 3

Interactions between kink waves and period waves. The parameters for analytic solution (8) are $\varepsilon =1, k_{1}=2, k_{2}=3, s_{2}(x)=1, \gamma _{1}(t)=0.001, \gamma _{2}(x)=0.002, s_{1}(t)=\sin (mt), d_{1}(t)=0.2, d_{2}(t)=0.003$ with a $m=-1.7, a_{1}=0.094, a_{2}=-1.3, \alpha =0.97, p_{2}(t)=-0.47$, and $q_{1}(t)=0.97$; b $m=-1.2, a_{1}=-0.19, a_{2}=-1.8, \alpha =0.63, p_{2}(t)=2$, and $q_{1}(t)=0.88$

Fig. 4

Interactions between kink waves and period waves. The parameters of the former two are $\varepsilon =1, k_{1}=2, k_{2}=3, s_{2}(x)=3, \gamma _{1}(t)=0.001, \gamma _{2}(x)=0.0002, s_{1}(t)=2, d_{1}(t)=1, d_{2}(t)=2, p_{2}(t)=\sin (ct)$ with a $c=-0.7, a_{1}=-0.031, a_{2}=-1.7, \alpha =0.1$, and $q_{1}(t)=0.91$; b $c=-0.16, a_{1}=-0.69, a_{2}=0.063, \alpha =1.7$, and $q_{1}(t)=0.83$. And the parameters of the latter two are $\varepsilon =1, k_{1}=2, k_{2}=3, s_{2}(x)=3, \gamma _{1}(t)=0.001, \gamma _{2}(x)=0.0002, s_{1}(t)=2, d_{1}(t)=1, d_{2}(t)=2, p_{2}(t)=\sin (ct), q_{1}(t)=\cos (nt)$ with c $c=0.16, n=-0.094, a_{1}=1.2, a_{2}=-1.4$, and $\alpha =2$; d $c=-0.16, n=0.59, a_{1}=-0.063, a_{2}=1.1$, and $\alpha =-1.9$

Fig. 5

Interactions between kink waves and period waves. The parameters for analytic solution (8) are $\varepsilon =1, k_{1}=2, k_{2}=3, s_{2}(x)=3, \gamma _{1}(t)=0.001, \gamma _{2}(x)=0.0002, s_{1}(t)=2, d_{1}(t)=1, d_{2}(t)=2, p_{2}(t)=\sin (ct), q_{1}(t)=\cos (nt)$ with a $c=0.63, n=-1.3, a_{1}=1.9, a_{2}=-1.4$, and $\alpha =-0.31$; b $c=1.1, n=-0.19, a_{1}=0.16, a_{2}=-1.3$, and $\alpha =-1.9$; c $c=1.3, n=0.56, a_{1}=0.41, a_{2}=-1.6$, and $\alpha =-1.4$; d $c=2.5, n=0.44, a_{1}=0.75, a_{2}=0.13$, and $\alpha =-0.56$

3 Discusses on analytic solution (8)

In the following discussion, we analyze the influences of the related parameters on solution (8). Figure 1 shows the propagation of kink waves with different amplitudes and phases. We find that the phase is affected by $\alpha$, and the amplitude is affected by $\alpha$ and $q_{1}(t)$. As $|\alpha |$ and $q_{1}(t)$ decrease, the amplitude decreases. Moreover, the kink wave’s amplitudes are almost equal when the values of $\alpha$ are $\pm 0.023$. And the propagation velocities of kink waves increase with decreasing the value of $\alpha$.

Figure 2 shows the interactions between periodic waves and kink waves. Such a surprising feature of the interactions between periodic waves and kink waves is obtained firstly. And Fig. 2a is different with Fig. 2b in the amplitude, phase, and period. As $\alpha$ and $q_{1}(t)$ increase, the amplitudes of them increase. If we set $d_{2}(t)=A\sin mt$, the amplitude will also increase when the value of A increases. The phase and velocity of waves are associated with the values of $\alpha$ and $p_{2}(t)$. The velocity increases when the value of $\alpha$ decreases or the value of $p_{2}(t)$ increases. Additionally, the period of waves will increase if the value of m increases as $d_{2}(t)=\sin mt$.

Figure 3 shows the parallel transmission of periodic waves and kink waves. And here we set $s_{1}(t)=\sin mt$. The amplitude decreases when the values of $q_{1}(t)$ and $a_{2}$ increase, or the value of $a_{1}$ decreases. The phase is related to the value of $a_{2}$. In addition, the forward-direction (or backward-direction) wave shows the same feature, although the incident angles are different.

Figure 4a–c is generated by the interactions of kink waves, while Fig. 4d is the interaction of two period waves. The number of the interaction kink waves increases when the value of |c| increases because of the formula $p_{2}(t)=\sin ct$ we set. And the amplitude decreases when the value of $a_{1}$ or $\alpha$ decreases. Figure 4c, d is obtained if we set $q_{1}(t)=\cos nt$ and take $n, c, a_{1}, a_{2}, \alpha$ and $q_{1}(t)$ with different constants in the same time. The generation of Fig. 4c is the result of the synergy of two kink waves, while the generation of Fig. 4d is the result of the synergy of two periodic waves as $c, a_{1}, a_{2}, \alpha$, and n take different positive or negative values. Figure 4c shows the amplitude is also related to the value of n. Figure 4d shows the smaller the value of n is, the longer the period is.

Figure 5 shows the synergy of different number of periodic waves while $n, c, a_{1}, a_{2}$, and $\alpha$ take different constants. The amplitude sharply decreases when the values of $a_{1}$ and $a_{2}$ decrease, or the value of $\alpha$ increases. The periodic solution is symmetric about $t=0$ because we set $q_{1}(t)=\cos nt$. And the period become shorter when the value of c increases because $p_{2}(t)=\sin ct$.

4 Conclusion

In this paper, the GCGLE (1) has been investigated. With the modified Hirota bilinear method, analytic solution (8) has been obtained. The interactions between periodic waves and kink waves have been observed firstly. Influences on the interactions between them have been discussed by selecting the relevant parameters. The related conclusion is beneficial to the generation of pulses in fiber lasers.