Breathers and rogue waves of the fifth-order nonlinear Schrödinger equation in the Heisenberg ferromagnetic spin chain

Abstract

One-dimensional anisotropic Heisenberg ferromagnetic spin chain can be described by the fifth-order nonlinear Schrödinger equation, which is investigated in this paper. Through the Darboux transformation, we obtain the Akhmediev breathers (ABs), Kuznetsov–Ma (KM) solitons and rogue-wave solutions. Effects of the coefficients of the fourth-order dispersion, $\gamma$, and of the fifth-order dispersion, $\delta$, on the properties of ABs, KM solitons and rogue waves are discussed: (1) With $\gamma$ increasing, the AB exhibits stronger localization in time; (2) The propagation directions of an AB and a KM soliton change with the presence of $\delta$; and (3) Enhancement of $\gamma$ makes the existence time of the rogue waves shorter, while enhancement of $\delta$ increases the existence time of the rogue waves.

1 Introduction

Rogue waves are the large amplitude waves in the ocean which appear unexpectedly [1–3]. Notion of the rogue waves has been transferred into the realm of plasmas [4], Bose–Einstein condensation [5], Heisenberg ferromagnetic spin chain [6] and optical fibers [7]. The formation of rogue waves in nonlinear dispersive media can be described within the framework of nonlinear evolution equations, such as the nonlinear Schrödinger (NLS) equation [8–10, 13], which has the analytic solutions in the forms of certain types of breathers or solitons on the finite background, i.e., the Akhmediev breathers (ABs), Kuznetsov–Ma (KM) solitons and Peregrine solitons [8–12]. Such solutions allow the analytic studies into the conditions that support the emergence of rogue waves [8–12, 14, 15].

To describe the wave propagation more realistically, some models with the higher-order effects, such as the third- and fourth-order dispersion, self-steepening and symmetric perturbations, have been proposed [16, 17]. In this paper, via the Darboux transformation (DT) [18–21], we will investigate the analytic solutions in the forms of ABs, KM solitons and rogue waves of the fifth-order NLS equation as follows [22, 23]:

(1)

which works as a model corresponding to a one-dimensional anisotropic Heisenberg ferromagnetic spin chain, where $q(x,t)$ represents the envelope of the waves, $t$ and $x$, respectively, denote the scaled time and spatial coordinates, the asterisk represents the complex conjugation, and the real parameters $\alpha$, $\gamma$ and $\delta$ are, respectively, the coefficients of the third-order dispersion $q_{xxx}$, fourth-order dispersion $q_{xxxx}$ and fifth-order dispersion $q_{xxxx}$ [22, 23]. Infinitely, many conversation laws and $N$-soliton solutions of Eq. (1) have been obtained [22]. Lax pair and soliton solutions of Eq. (1) have been derived [23].

Special cases of Eq. (1) have been used to describe different nonlinear waves, depending on the particular applicative context (e.g., Bose–Einstein condensation, plasma physics, nonlinear optics and Heisenberg ferromagnetic spin chain): (1) With $\alpha =\gamma =\delta =0$, Eq. (1) can be reduced to the focusing NLS equation for the wave evolution in different physical systems [24, 26]; (2) when $\alpha \ne 0$ and $\gamma =\delta =0$, Eq. (1) can be reduced to the Hirota equation for the propagation of a subpicosecond or femtosecond pulse [10]; (3) for $\alpha =\delta =0$ and $\gamma \ne 0$, Eq. (1) can be reduced to a fourth-order dispersive NLS equation for the one-dimensional anisotropic Heisenberg ferromagnetic spin chain with the octuple–dipole interaction [27, 28]; and (4) with $\alpha =\gamma =0$ and $\delta \ne 0$, Eq. (1) can be reduced to a fifth-order NLS equation for the Heisenberg ferromagnetic spin system [22, 28]. Relevant issues can also be seen in [29–34].

However, to our knowledge, the breather and rogue-wave solutions of Eq. (1) have not been constructed through the DT. In Sect. 2, through the DT and limit process, the breathers and rogue-wave solutions of Eq. (1) will be derived. In Sect. 3, influence of $\gamma$ and $\delta$, the coefficients of the fourth-order dispersion and fifth-order dispersion, on the ABs, KM solitons and rogue waves will be discussed. Section 4 will be our conclusions.

2 Breather and rogue-wave solutions of Eq. (1) based on the DT

With the $2\times 2$ Ablowitz–Kaup–Newell–Segur matrix [24, 25], the Lax pair associated with Eq. (1) can be given as [23]

$$\begin{aligned} \varPsi _{x}=\mathbf {U}\varPsi ,\quad \varPsi _{t}=\mathbf {V}\varPsi , \end{aligned}$$

(2)

where $\varPsi =(\varPsi _{1}, \varPsi _{2})^{T}$ is the vector eigenfunction, $\varPsi _{1}$ and $\varPsi _{2}$ are the complex functions of $x$ and $t$, $T$ denotes the transpose of the matrix, and $\mathbf {U}$ and $\mathbf {V}$ are expressible in the form of [23]

$$\begin{aligned} \mathbf {U}= & {} i \left( \begin{array}{l@{\quad }l}\lambda &{} q^{*}(x,t) \\ q(x,t) &{} -\lambda \end{array}\right) ,\nonumber \\ \mathbf {V}= & {} \sum _{c=0}^{5}i\lambda ^{c} \left( \begin{array}{l@{\quad }l}A_{c}&{} B^{*}_{c} \\ B_{c} &{} -A_{c}\end{array}\right) , \end{aligned}$$

(3)

with

$$\begin{aligned} A_{0}= & {} \,-\frac{1}{2}|q|^2-3\gamma |q|^4-i\alpha \left( q^{*}_{x}q-q_{x}q^{*}\right) \\&-\,\gamma \left( q^{*}_{xx}q-|q_{x}|^2+q_{xx}q^{*}\right) \\&-\,i\delta \left( q^{*}_{xxx}q-q^{*}_{xx}q_{x}+q_{xx}q^{*}_{x}-q_{xxx}q^{*}\right) \\&-\,6i\delta \left( q^{*}_{x}q-q_{x}q^{*}\right) |q|^2,\\ B_{0}= & {} 2\alpha |q|^2 q+6\delta |q|^4 q+i\frac{1}{2}q_{x}+6i\gamma |q|^2 q_{x}\\&+\,\alpha q_{xx}+2\delta q^{*}_{xx}q^2+4\delta |q_{x}|^2q+6\delta (q_{x})^2q^{*}\\&+\,8\delta q_{xx}|q|^2+i\gamma q_{xxx}+\delta q_{xxxx},\\ A_{1}= & {} 2\alpha |q|^2+6\delta |q|^4-2i\gamma \left( q^{*}_{x}q-q_{x}q^{*}\right) \nonumber \\&+\,2\delta \left( q^{*}_{xx}q-|q_{x}|^2+q_{xx}q^{*}\right) ,\nonumber \\ B_{1}= & {} q+4\gamma |q|^2q-2i\alpha q_{x}-12i\delta |q|^2q_{x}\nonumber \\&+\,2\gamma q_{xx}-2i\delta q_{xxx},\nonumber \\ A_{2}= & {} 1+4\gamma |q|^2+4i\delta \left( q^{*}_{x}q-q_{x}q^{*}\right) ,\nonumber \\ B_{2}= & {} -\,4\alpha q-8\delta |q|^2q-4i\gamma q_{x}-4\delta q_{xx},\nonumber \\ A_{3}= & {} -\,4\alpha -8\delta |q|^2,\quad B_{3}=-8\gamma q+8i \delta q_{x},\nonumber \\ A_{4}= & {} -\,8\gamma ,\quad B_{4}=16\delta q,\quad A_{5}=16\delta ,\quad B_{5}=0,\nonumber \end{aligned}$$

where $\lambda$ is an eigenvalue of Lax Pair (2).

One can check that the compatibility condition $\mathbf {U}_{t}-\mathbf {V}_{x}+\mathbf {UV}-\mathbf {VU}=0$ is equivalent to Eq. (1). Considering the gauge transformation,

$$\begin{aligned} \varPsi [1]=\mathbf {D}[1] \varPsi , \end{aligned}$$

(4)

through which we can cast Lax Pair (2) into

$$\begin{aligned}&\varPsi [1]_{x}=\mathbf {U}[1]\varPsi [1], \mathbf {U}[1]=(\mathbf {D}[1]_{x}+\mathbf {D}[1] \mathbf {U})\mathbf {D}[1]^{-1},\nonumber \\ \end{aligned}$$

(5a)

$$\begin{aligned}&\varPsi [1]_{t}=\mathbf {V}[1]\varPsi [1], \mathbf {V}[1]=(\mathbf {D}[1]_{t}+\mathbf {D}[1] \mathbf {V})\mathbf {D}[1]^{-1},\nonumber \\ \end{aligned}$$

(5b)

where $[j]$ $(j=0,1,2,\ldots N)$ represents the $j$th-iteration, $N$ is a positive integer, $\mathbf {D}[1]$ is a $2\times 2$ matrix, $\varPsi [1]$ is a $2 \times 1$ vector eigenfunction, $\mathbf {D}[1]^{-1}$ denotes the inverse matrix of $\mathbf {D}[1]$, $\mathbf {U}[1]$ and $\mathbf {V}[1]$ are the $2\times 2$ matrices.

Cross differentiation of Lax Pair (2) leads to

$$\begin{aligned}&\mathbf {U}[1]_{t}-\mathbf {V}[1]_{x}+[\mathbf {U}[1],\mathbf {V}[1]]\nonumber \\&\quad =\mathbf {D}[1]({\mathbf {U}}_{t}-{\mathbf {V}}_{x}+[{\mathbf {U}},{\mathbf {V}}])\mathbf {D}[1]^{-1}, \end{aligned}$$

(6)

which implies that in order to keep Lax Pair (2) invariant under Transformation (4), we need to obtain a matrix $\mathbf {D}$[1] such that $\mathbf {U}[1]$ and $\mathbf {V}[1]$, respectively, possess the same forms as $\mathbf {U}$ and $\mathbf {V}$, while $q$, which works as the old potential of the Lax-pair representation in $\mathbf {U}$ and $\mathbf {V}$, is mapped into the new one $q[1]$ in $\mathbf {U}[1]$ and $\mathbf {V}[1]$.

Hereby, we assume the matrix $\mathbf {D}[1]$ in the form of

$$\begin{aligned} \mathbf {D}[1]= & {} \begin{pmatrix} \lambda &{} 0 \\ 0 &{} \lambda \end{pmatrix}-\begin{pmatrix} \varPsi _{1,1} &{} -\varPsi ^{*}_{2,1} \\ \varPsi _{2,1} &{} \varPsi ^{*}_{1,1} \end{pmatrix} \begin{pmatrix} \lambda _{1}&{} 0 \\ 0 &{} \lambda ^{*}_{1} \end{pmatrix}\nonumber \\&\times \begin{pmatrix} \varPsi _{1,1} &{} -\varPsi ^{*}_{2,1} \\ \varPsi _{2,1} &{} \varPsi ^{*}_{1,1} \end{pmatrix}^{-1}, \end{aligned}$$

(7)

where $\lambda _{1}$ is an eigenvalue of Lax Pair (2), $\varPsi _{1,1}$ and $\varPsi _{2,1}$ are the complex functions of $x$ and $t$. It can be verified that if $(\varPsi _{1,1}, \varPsi _{2,1})^{T}$ is an eigenfunction of Lax Pair (2) with the eigenvalue $\lambda =\lambda _{1}$, then $(-\varPsi ^{*}_{2,1}, \varPsi ^{*}_{1,1})^{T}$ is also an eigenfunction of Lax Pair (2) with the eigenvalue $\lambda =\lambda ^{*}_{1}$.

Via Expressions (5), the DT for Eq. (1) is given by

$$\begin{aligned} q[1]=q+2\frac{(\lambda ^{*}_{1}-\lambda _{1})\varPsi ^{*}_{1,1}\varPsi _{2,1}}{\varPsi _{1,1}\varPsi ^{*}_{1,1}+\varPsi _{2,1}\varPsi ^{*}_{2,1}}. \end{aligned}$$

(8)

To construct the breather and rogue-wave solutions of Eq. (1), we obtain the seed solutions first, as

$$\begin{aligned} q(x,t)=e^{(1+6\gamma )it}. \end{aligned}$$

(9)

The corresponding solutions for Lax Pair (2) at $\lambda =i h$ are

$$\begin{aligned} \varphi (h)=\left( \begin{array}{l} \left( i\mu _{1}e^{\varDelta }-i\mu _{2}e^{-\varDelta }\right) e^{-\frac{(1+6\gamma )it}{2}} \\ \left( \mu _{2}e^{\varDelta }-\mu _{1}e^{-\varDelta }\right) e^{\frac{(1+6\gamma )it}{2}} \end{array}\right) , \end{aligned}$$

(10)

where

$$\begin{aligned} \mu _{1}=\frac{(h-\sqrt{h^2-1})^{\frac{1}{2}}}{\sqrt{h^2-1}},\quad \mu _{2}=\frac{(h+\sqrt{h^2-1})^{\frac{1}{2}}}{\sqrt{h^2-1}}, \end{aligned}$$

$$\begin{aligned} \varDelta= & {} \sqrt{h^2-1}x+\left\{ [8 i h^3 \gamma + i h (1 + 4 \gamma )+ 16 h^4 \delta \right. \nonumber \\&\left. +\, 4 h^2 (\alpha + 2 \delta ) +2 (\alpha + 3 \delta )] \sqrt{h^2-1}\right\} t. \end{aligned}$$

Substituting Solutions (10) into DT (8), we obtain the breather solutions of Eq. (1) as follows:

$$\begin{aligned} q=e^{(1+6\gamma )it}-4ih\frac{\varPsi ^{*}_{1,1}\varPsi _{2,1}}{\varPsi _{1,1}\varPsi ^{*}_{1,1}+\varPsi _{2,1}\varPsi ^{*}_{2,1}}, \end{aligned}$$

(11)

where

$$\begin{aligned} \varPsi _{1,1}= & {} (i\mu _{1}e^{\varDelta }-i\mu _{2}e^{-\varDelta })e^{-\frac{(1+6\gamma )it}{2}},\nonumber \\ \varPsi _{2,1}= & {} (\mu _{2}e^{\varDelta }-\mu _{1}e^{-\varDelta })e^{\frac{(1+6\gamma )it}{2}}. \end{aligned}$$

Solutions (11) include the ABs $(0<h<1)$ and KM solitons $(1<h)$. When $0 < h < 1$, the AB, which exhibits the localization in $t$ but periodicity in $x$, can be observed. When $1<h$, the KM soliton appears. In contrast to the AB, the KM soliton is periodic in $t$ and localized in $x$. We note that $|q|^2(0,0)=(1+2h)^2$, which is the height of peaks of breathers.

Then, we consider what will happen with respect to a breather when its period goes to the infinity. Based on Solutions (11) and setting $h\rightarrow {1}$, we obtain the rogue-wave solutions of Eq. (1) as

$$\begin{aligned} q_{h\rightarrow {1}}=-e^{(1+6\gamma )it}\frac{G_{1}}{F_{1}}, \end{aligned}$$

(12)

where

$$\begin{aligned} G_{1}= & {} \left\{ -3 + 4 x^2 + 4 t^2 (1 + 36 \alpha ^2 + 24 \gamma + 144 \gamma ^2 \right. \\&\left. +\,360 \alpha \delta + 900 \delta ^2)+ 8 t \left[ -i (1 + 12 \gamma ) \right. \right. \\&\left. \left. +\,6 x (\alpha + 5 \delta )\right] \right\} ,\\ F_{1}= & {} 1 + 4 x^2 + 48 t x (\alpha + 5 \delta ) + 4 t^2 (1 + 36 \alpha ^2 \\&+\,24 \gamma + 144 \gamma ^2 + 360 \alpha \delta + 900 \delta ^2). \end{aligned}$$

The first-order rogue wave corresponds to a single wave with localization in $t$ and $x$. The peak height of that rogue wave is $|q|^2(0,0)=9$. Effects of $\gamma$ and $\delta$ on the properties of ABs, KM solitons and rogue waves will be discussed in Sect. 3.

Let $(\varPsi _{1,1}, \varPsi _{2,1})^{T}$, $(\varPsi _{1,2}, \varPsi _{2,2})^{T}$,$\ldots$, $(\varPsi _{1,N}, \varPsi _{2,N})^{T}$ be the $N$ distinct solutions of Lax Pair (2) at $\lambda _{1},\ldots , \lambda _{N}$, respectively, where ${\varPsi _{1,k}}$’s and ${\varPsi _{2,k}}$’s $(k=1,2,\ldots ,N)$ are the functions of $x$ and $t$, and $\lambda _{k}$’s are the eigenvalues of Lax Pair (2). Via the $N$ iteration of Expression (4) and (5), the $N$-fold DT for Eq. (1) is

$$\begin{aligned}&q[N]=q[0]\\&\quad +\,2\sum _{k=1}^{N}\frac{(\lambda ^{*}_{k}-\lambda _{k})\varPsi _{2,k}[k-1]\varPsi _{1,k}[k-1]^{*}}{\varPsi _{1,k}[k-1]\varPsi _{1,k}[k-1]^{*}+\varPsi _{2,k}[k-1]\varPsi _{2,k}[k-1]^{*}},\nonumber \\&\varPsi [N]=\mathbf {D}[N]\mathbf {D}[N-1]\cdots \mathbf {D}[1]\varPsi ,\nonumber \end{aligned}$$

(13)

with

$$\begin{aligned}&\mathbf {D}[k]=\left( \begin{array}{l@{\quad }l} \lambda &{} 0 \\ 0 &{} \lambda \end{array}\right) -\left( \begin{array}{l@{\quad }l} \varPsi _{1,k}[k-1] &{} -\varPsi _{2,k}[k-1]^{*} \\ \varPsi _{2,k}[k-1] &{} \varPsi _{1,k}[k-1]^{*} \end{array}\right) \nonumber \\&\times \left( \begin{array}{l@{\quad }l} \lambda _{k}&{} 0 \\ 0 &{} \lambda ^{*}_{k} \end{array}\right) \left( \begin{array}{l@{\quad }l} \varPsi _{1,k}[k-1] &{} -\varPsi _{2,k}[k-1]^{*} \\ \varPsi _{2,k}[k-1] &{} \varPsi _{1,k}[k-1]^{*} \end{array}\right) ^{-1},\nonumber \\&\left( \begin{array}{l} \varPsi _{1,k}[k-1] \\ \varPsi _{2,k}[k-1] \end{array}\right) \nonumber \\&\quad =(\mathbf {D}[k-1]\mathbf {D}[k-2]\cdots \mathbf {D}[1])|_{\lambda =\lambda _{k}}\left( \begin{array}{l} \varPsi _{1,k} \\ \varPsi _{2,k} \end{array}\right) ,\nonumber \\&q[0]=q, \quad \left( \begin{array}{l} \varPsi _{1,1}[0] \\ \varPsi _{2,1}[0] \end{array}\right) = \left( \begin{array}{l} \varPsi _{1,1} \\ \varPsi _{2,1} \end{array}\right) . \end{aligned}$$

(14)

When $N=2$, the $2$-fold DT can be expressed as

$$\begin{aligned} q[2]=q[1]+2\frac{(\lambda ^{*}_{1}-\lambda _{1})\varPsi _{1,2}[1]^{*}\varPsi _{2,2}[1]}{\varPsi _{1,2}[1]\varPsi _{1,2}[1]^{*}+\varPsi _{2,2}[1]\varPsi _{2,2}[1]^{*}}.\nonumber \\ \end{aligned}$$

(15)

Since all the eigenvalues in the standard Darboux scheme are the same, the explicit formulas for $\varPsi _{1,2}[1]$ and $\varPsi _{2,2}[1]$ cannot be obtained from the scheme. Instead, to obtain the second-order rogue-wave solutions of Eq. (1), we solve Lax Pair (2) with the $q$ function found at the previous step, $q=q[1]$, to obtain $\varPsi _{1,2}[1]$ and $\varPsi _{2,2}[1]$,

$$\begin{aligned} \varPsi _{1,2}[1]=e^{-\frac{(1+6\gamma )it}{2}}\frac{\mathcal {A}_{1}}{3F_{1}}, \varPsi _{2,2}[1]=e^{\frac{(1+6\gamma )it}{2}}\frac{\mathcal {A}_{2}}{3F_{1}},\nonumber \\ \end{aligned}$$

(16)

with

$$\begin{aligned} \mathcal {A}_{1}= & {} \left[ 3 - 12 x - 16 x^3+ 16 x^4 +16 t^4 (-i + 6 \alpha \right. \\&- 12 i \gamma + 30 \delta )(i +6 \alpha + 12 i \gamma + 30 \delta )^3\\&+\,32 t^3 (i + 6 \alpha + 12 i \gamma + 30 \delta )^2 \\&\times \, (i -3 \alpha + 12 i \gamma - 15 \delta \\&+\,x (-i + 12 \alpha - 12 i \gamma + 60 \delta )) \\&+\,8 t (-36 x^2 (\alpha + 5 \delta ) -3 (i + 7 \alpha + 20 i \gamma + 55 \delta )\\&+\,4 x^3 (i+ 12 \alpha + 12 i \gamma + 60 \delta )\\&-\,3 x (i + 8 \alpha + 28 i \gamma + 80 \delta )) +24 t^2 (-1- 48 \alpha ^2 \\&-\, 40 \gamma -336 \gamma ^2 + \alpha (2 i - 72 i \gamma - 720 \delta ) +50 i \delta \\&+\, 120 i \gamma \delta - 2400 \delta ^2 + 24 x^2 (\alpha + 5 \delta ) (i + 6 \alpha \\&+\, 12 i \gamma +30 \delta )-2 x (1 + 36 \alpha ^2 + 24 \gamma + 144 \gamma ^2 \\&+\, \left. 360 \alpha \delta + 900 \delta ^2))\right] ,\\ \mathcal {A}_{2}= & {} \left[ 3 + 12 x +16 x^3 + 16 x^4 +16 t^4 (-i + 6 \alpha \right. \\&-\,12 i \gamma + 30 \delta )(i +6 \alpha + 12 i \gamma + 30 \delta )^3\\&+\,32 t^3 (i + 6 \alpha + 12 i \gamma + 30 \delta )^2 \\&\times \, (-i +3 \alpha - 12 i \gamma + 15 \delta +x (-i + 12 \alpha \\&-\, 12 i \gamma + 60 \delta )) +8 t (36 x^2 (\alpha + 5 \delta ) +3 (i + 7 \alpha \\&+\, 20 i \gamma + 55 \delta ) +4 x^3 (i + 12 \alpha + 12 i \gamma + 60 \delta )\\&-\,3 x (i + 8 \alpha + 28 i \gamma + 80 \delta )) +24 t^2 (-1 - 48 \alpha ^2 \\&-\, 40 \gamma -336 \gamma ^2 + \alpha (2 i - 72 i \gamma - 720 \delta ) +50 i \delta \\&+\, 120 i \gamma \delta - 2400 \delta ^2 +24 x^2 (\alpha + 5 \delta ) \\&\times \,(i + 6 \alpha + 12 i \gamma +30 \delta )\\&+\,2 x (1 + 36 \alpha ^2 + 24 \gamma + 144 \gamma ^2 +360 \alpha \delta \\&+\, \left. 900 \delta ^2))\right] . \end{aligned}$$

By virtue of Expressions (15) and (16), we obtain the second-order rogue-wave solutions of Eq. (1) as

$$\begin{aligned} q[2]=e^{(1+6\gamma )it}\frac{G_{2}}{F_{2}}, \end{aligned}$$

(17)

where $G_{2}$ and $F_{2}$ are given in the Appendix.

3 Discussions

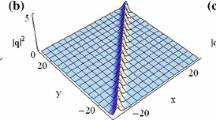
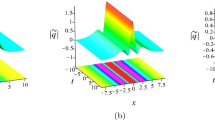
Figure 1 shows the propagation of an AB and a KM soliton without the presence of $\gamma$ and $\delta$. In the case $\gamma \ne 0$ and $\delta =0$, the propagation of ABs and KM solitons is shown in Figs. 2 and 3: As $\gamma$ increases, the AB exhibits stronger localization in $t$, while the distance between adjacent peaks keeps unchanged with $\gamma$ increasing, as seen in Fig. 2; for the KM soliton, as $\gamma$ increases, the distance between adjacent peaks decreases, as seen in Fig. 3. In the case $\gamma =0$ and $\delta \ne 0$, the propagation of an AB and a KM soliton is displayed in Fig. 4. We note that the propagation directions of the AB and KM soliton change with the presence of $\delta$.

Fig. 1

Breathers via Solutions (11) with $\alpha =0.01$, $\delta =0$, $\gamma =0$, a $h=0.2$ (the AB) b $h=1.2$ (the KM soliton)

Fig. 2

The ABs via Solutions (11) with $\alpha =0.01$, $\delta =0$, $h=0.2$ a $\gamma =0.5$ and b $\gamma =1$

Fig. 3

The KM solitons via Solutions (11) with $\alpha =0.01$, $\delta =0$, $h=1.2$ a $\gamma =0.02$ and b $\gamma =0.08$

Fig. 4

Breathers via Solutions (11) with $\alpha =0.01$, $\delta =0.03$, $\gamma =0$, a $h=0.2$ (the AB) b $h=1.2$ (the KM soliton)

Here, we investigate how $\gamma$ and $\delta$ affect the properties of rogue waves. With the presence of $\gamma$ and $\delta$, one case of the first-order rogue-wave solutions is shown in Fig. 5. With the increase in $\gamma$, properties of the first-order rogue waves can be shown in Fig. 6a. In Fig. 6b, it is found that the rogue wave can reach its peak and disappear more quickly with the increase in $\gamma$ at $x=0$. In other words, increasing the value of $\gamma$ makes the existence time of a first-order rogue wave shorter. We note that $t=0$ implies that $q(x,t)=\frac{-3+4x^2}{1+4x^2}$, which means that $\gamma$ and $\delta$ do not influence the envelope of the waves $q(x,t)$. With the comparison between Figs. 5 and 7, we find that increasing $\delta$ would lead to an increase in the existence time of a first-order rogue wave. Increasing the value of $\gamma$ makes the existence time of a second-order rogue wave shorter, while increasing $\delta$ would lead to an increase in the existence time of a second-order rogue wave. For simplicity, we do not include the figures here.

Fig. 5

The first-order rogue wave via Solutions (12) with $\alpha =0.01$, $\gamma =0.01$ and $\delta =0.01$

Fig. 6

a The same as Fig. 5 except that $\gamma =0.1$; b Comparison between (a) (short dashed curve) and Fig. 5 (solid curve) with $x=0$

Fig. 7

The same as Fig. 5 except that $\delta =0.05$

4 Conclusions

The ABs, KM solitons and rogue waves of the fifth-order NLS equation, i.e., Eq. (1), which works as a model corresponding to a one-dimensional anisotropic Heisenberg ferromagnetic spin chain, have been investigated. Through DT (8), the ABs, KM solitons and rogue-wave solutions, i.e., Solutions (11),  (12) and (17), have been obtained. Dependence of the properties of the ABs, KM solitons and rogue waves on the coefficients of the fourth-order dispersion, $\gamma$, and of the fifth-order dispersion, $\delta$, has been examined. Figure 1 has shown the propagation of an AB and a KM soliton without the presence of $\gamma$ and $\delta$. In the case $\gamma \ne 0$ and $\delta =0$: As $\gamma$ increases, the AB exhibits stronger localization in time, while the distance between the adjacent peaks keeps a unchanged with $\gamma$ increasing, as seen in Fig. 2; for a KM soliton, as $\gamma$ increases, the distance between the adjacent peaks decreases, as seen in Fig. 3. The propagation directions of an AB and a KM soliton change with the presence of $\delta$, as shown in Fig. 4. Figure 5 has displayed the first-order rogue wave with the presence of $\gamma$ and $\delta$. Figure 6 has shown that the enhancement of $\gamma$ makes the existence time of the first-order rogue wave shorter. With the comparison between Figs. 5 and 7, we have found that the enhancement of $\delta$ increases the existence time of the first-order rogue wave.

Appendix

$$\begin{aligned} G_{2}= & {} (e^{i t (1 + 6 \gamma )} (45 - 180 x^2 - 144 x^4\\&+\,64 x^6 +64 t^6 (1 + 36 \alpha ^2\\&+\, 24 \gamma + 144 \gamma ^2 +360 \alpha \delta + 900 \delta ^2)^3\\&+\,384 t^5 (1 + 36 \alpha ^2 + 24 \gamma + 144 \gamma ^2\\&+\,360 \alpha \delta \!+\!900 \delta ^2)^2 (-i (1 \!+\! 12 \gamma ) \!+\!6 x (\alpha \!+\! 5 \delta ))\\&+\,24 t (-16 i x^4 (1 + 12 \gamma )\\&+\, 24 i x^2 (1 \!+\! 28 \gamma ) \!+\!3 i (5 \!+\! 92 \gamma ) \!+\! 96 x^5 (\alpha \!+\! 5 \delta )\\&-\,16 x^3 (13 \alpha + 85 \delta )-18 x (13 \alpha + 105 \delta ))\\&+\,12 t^2 (-768 i x^3 (1 + 12 \gamma ) (\alpha + 5 \delta )\\&+\,192 i x (\alpha (-1 + 36 \gamma ) -5 (5 + 12 \gamma ) \delta )\\&+\,16 x^4 (1 + 180 \alpha ^2 + 24 \gamma + 144 \gamma ^2 +1800 \alpha \delta \\&+\, 4500 \delta ^2)\!-\!24 x^2 (5 \!+\! 204 \alpha ^2 \!+\! 152 \gamma \!+\! 1104 \gamma ^2 \\&+\,2520 \alpha \delta + 7500 \delta ^2) -3 (13 + 500 \alpha ^2 + 376 \gamma \\&+\, 1616 \gamma ^2 +5320 \alpha \delta + 7700 \delta ^2))\\&+\,48 t^4 (-11 - 10800 \alpha ^4 - 464 \gamma - 7200 \gamma ^2 \\&-\,48384 \gamma ^3\!- \!117504 \gamma ^4 \!-\!250560 \alpha ^3 \delta \!+\! 1800 \delta ^2 \\&-\,129600 \gamma \delta ^2- 1814400 \gamma ^2 \delta ^2-11070000 \delta ^4\\&-\,192 i x (1 + 12 \gamma ) (\alpha + 5 \delta ) (1 +36 \alpha ^2+ 24 \gamma \\&+\, 144\gamma ^2\!+\!360 \alpha \delta \!+\! 900 \delta ^2) \!-\!2160 \alpha \delta (1 \!+\! 56 \gamma \\&+\, 528\gamma ^2\!+\!3700 \delta ^2)\! -\!72 \alpha ^2 (7\!+ \!264 \gamma \!+\! 2160 \gamma ^2 \\&+\,29700 \delta ^2)+4 x^2 (1 + 6480\alpha ^4 + 6912 \gamma ^3 \\&+\,20736 \gamma ^4+ 129600 \alpha ^3 \delta +5400 \delta ^2 \\&+\, 4050000 \delta ^4\!+\!864 \gamma ^2 (1 \!+\! 900 \delta ^2) \!+\!2160 \!\times \!\alpha \delta \\&\times \, (1 \!+ \!24\gamma \!+ \!144 \gamma ^2\!+\!1500 \delta ^2) \!+\! 48 \gamma (1 \!+\! 2700 \delta ^2) \\&+\,216 \alpha ^2 (1 + 24\gamma + 144 \gamma ^2 +4500\delta ^2))) \\&+\,192 t^3 (24 x^3 (\alpha \!+\! 5 \delta ) (1\!+\! 60 \alpha ^2 \!+\!24 \gamma \!+\! 144 \gamma ^2\\&+ \,600 \alpha \delta \!+\!1500 \delta ^2)\!- \!4 i x^2 (1 \!+ \!12 \gamma ) (1 \!+\! 108 \alpha ^2\\&+\, 24 \gamma +144 \gamma ^2 + 1080 \alpha \delta + 2700 \delta ^2) \\&-i (1 + 84\gamma + 1584 \gamma ^2+ 8640 \gamma ^3\\&+\,36 \alpha ^2 (5 + 12 \gamma ) +1080 \alpha (3 + 20 \gamma ) \delta \\&+\,11700 \delta ^2 \!+\! 97200 \gamma \delta ^2) \!-\!6 x (252 \alpha ^3 \!+\! 4500 \alpha ^2 \delta \\&+\,5 \delta (7 + 264 \gamma + 2160\gamma ^2 +9900 \delta ^2) \\&+ \alpha (11 + 360 \gamma +2736 \gamma ^2 + 26100 \delta ^2))))), \end{aligned}$$

$$\begin{aligned} F_{2}= & {} (9 + 108 x^2 + 48 x^4 + 64 x^6 +48 t x ((51 - 8 x^2 \\&+\, 48 x^4) \alpha +5 (75- 40 x^2 + 48 x^4) \delta )\\&+\,2304 t^5 x (\alpha + 5 \delta ) (1+ 36 \alpha ^2 +24 \gamma + 144 \gamma ^2\\&+ 360 \alpha \delta +900 \delta ^2)^2+64 t^6 (1+ 36 \alpha ^2 + 24 \gamma \\&+\, 144 \gamma ^2 +360 \alpha \delta + 900 \delta ^2)^3 +12 t^2 \\&\times (-24 x^2 (1 + 60 \alpha ^2 + 56 \gamma + 528 \gamma ^2\\&+\,1080 \alpha \delta + 3900\delta ^2)+16 x^4 (1 + 180 \alpha ^2 + 24\gamma \\&+ \,144 \gamma ^2 +1800 \alpha \delta + 4500 \delta ^2)\\&+\,3 (11 + 556 \alpha ^2 + 456 \gamma + 4912 \gamma ^2+9080 \alpha \delta \\&+\, 37900 \delta ^2))+48 t^4 (9 - 5616 \alpha ^4 + 496 \gamma \\&+\, 10080 \gamma ^2+89856 \gamma ^3 + 297216 \gamma ^4\\&-\,146880 \alpha ^3 \delta + 23400 \delta ^2+388800 \gamma \delta ^2 \\&+\, 1296000 \gamma ^2 \delta ^2 -7830000 \delta ^4 -2160 \alpha \delta (-3\\&- \,40\gamma - 48 \gamma ^2+2500 \delta ^2)-72 \alpha ^2 (-5 - 24 \gamma \\&+ \,432 \gamma ^2 +18900 \delta ^2) +4 x^2 (1+ 6480 \alpha ^4 \\&+ \,6912 \gamma ^3 +20736 \gamma ^4 + 129600 \alpha ^3 \delta \\&+\,5400 \delta ^2 + 4050000 \delta ^4 +864 \gamma ^2 (1 + 900 \delta ^2) \\&+\,2160 \alpha \delta (1 + 24 \gamma + 144 \gamma ^2 +1500 \delta ^2) \\&+\, 48 \gamma (1 + 2700 \delta ^2) +216 \alpha ^2 (1 + 24 \gamma + 144\gamma ^2 \\&+\,4500 \delta ^2)))+1152 t^3 x (12 (-9 + 20 x^2) \alpha ^3\\&+\,180 (-13 + 20 x^2) \alpha ^2 \delta + \alpha (1 -72 \gamma - 1008\gamma ^2 \\&- \,15300 \delta ^2+4 x^2 (1 + 24\gamma + 144 \gamma ^2 + 4500 \delta ^2)) \\&+\,5 \delta (5+ 24 \gamma - 432 \gamma ^2- 6300\delta ^2 \\&+\,x^2 (4 + 96 \gamma + 576\gamma ^2 + 6000 \delta ^2)))). \end{aligned}$$