1 Introduction

In soliton theory [1–14], lump solutions have attracted more and more attention [15–20]. As a kind of rational function solutions, lump solutions localized in all directions in the space. Such integrable equations as the KPI equation [16, 17], the BKP equation  [18], the three-dimensional three wave resonant interaction equation [19], the Davey–Stewartson-II equation [17] and the Ishimori I equation [20] have been found to possess lump solutions.

Lump solutions can be studied based on the Hirota bilinear equations and their generalized counterparts. For example, a class of lump solutions to the KPI equation has been presented by making use of its Hirota bilinear form [16]. The resulting lump solutions contain six free parameters, two of which are due to the translation invariance of the KP equation and the other four of which satisfy a nonzero determinant condition guaranteeing analyticity and rational localization of the solutions. Further, based on generalized bilinear forms, lump solutions to dimensionally reduced p-gKP and p-gBKP equations in (2+1) dimensions have been computed [15]. The sufficient and necessary conditions to guarantee analyticity and rational localization of the solutions have been given.

In our previous work [21], a new Hirota bilinear equation has been proposed and studied, which reads

$$\begin{aligned}&(D_{t}D_{y}-D^{3}_{x}D_{y}-3\,D^{2}_{x}+3\,D^{2}_{z})f\cdot f=0, \end{aligned}$$
(1)

that is,

$$\begin{aligned}&2\,[(ff_{ty}-f_{t}f_{y}+f_{xxx}f_{y}\nonumber \\&\quad +\,3\,f_{xxy}f_{x} -3\,f_{xx}f_{xy}-ff_{xxxy}\nonumber \\&\quad -\,3(ff_{xx}-f^{2}_{x})+3(ff_{zz}-f^{2}_{z})]=0, \end{aligned}$$
(2)

where \(f=f(x,y,z,t)\), and the derivatives \(D_{t}D_{y}\), \(D^{3}_{x}D_{y}\), \(D^{2}_{x}\) and \(D^{2}_{z}\) are the Hirota bilinear operators [22] defined by

$$\begin{aligned} D_{x}^{\alpha }D_{t}^{\beta }(f\cdot g)=&\Big (\frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\Big )^{\alpha }\Big (\frac{\partial }{\partial t} -\frac{\partial }{\partial t'}\Big )^{\beta }\nonumber \\&\quad \times \, f(x,t)g(x',t')\Big |_{x'=x,t'=t.}\nonumber \end{aligned}$$

Bell polynomial theories (see, e.g., Refs. [23–27]) motivate us to consider a dependent variable transformation

$$\begin{aligned}&u=2\Big [\mathrm {ln}\,f(x,y,z,t)\Big ]_{x}=2\frac{f_x(x,y,z,t)}{f(x,y,z,t)}, \end{aligned}$$
(3)

and map Eq. (2) into

$$\begin{aligned} u_{yt}-u_{xxxy}-3\,(u_{x}u_{y})_{x}-3\,u_{xx}+3\,u_{zz}=0. \end{aligned}$$
(4)

Eq. (4) is a (3 + 1)-dimensional model, and it is clear that if f solves Eq. (2), then \(u=u(x,y,z,t)\) is a solution to Eq. (4) through the transformation (3).

Via applying to Eq. (2) the linear superposition principle [28, 29], two types of resonant N-wave solutions have been found and illustrated [21]. In this paper, we will search for positive quadratic function solutions to the dimensionally reduced Hirota bilinear Eq. (2) via taking \(z=y\) or \(z=t\) casesFootnote 1 , and begin with

$$\begin{aligned} f=g^{2}+h^{2}+a_{9}, \end{aligned}$$
(5)

and

$$\begin{aligned}&g=a_{1}x+a_{2}y+a_{3}t+a_{4},\\&h=a_{5}x+a_{6}y+a_{7}t+a_{8},\\ \end{aligned}$$

where \(a_{i}\) (\(1\le i \le 9\)) are all real parameters to be determined. To determine the lump solutions, we note that the conditions guaranteeing the well-definedness of f, positiveness of f and localization of u in all directions in the space need to be satisfied.

2 Lump solutions to reduction with \(z=y\)

With \(z=y\), the dimensionally reduced form of the Hirota bilinear Eq. (2) turns out to be

$$\begin{aligned}&2\,\left[ (ff_{ty}-f_{t}f_{y}+f_{xxx}f_{y}\right. \nonumber \\&\left. \quad +\, 3\,f_{xxy}f_{x} -3\,f_{xx}f_{xy}-ff_{xxxy}\right. \nonumber \\&\left. \quad -\,3(ff_{xx}-f^{2}_{x})+3(ff_{yy}-f^{2}_{y})\right] =0, \end{aligned}$$
(6)

which is transformed into

$$\begin{aligned} u_{yt}-u_{xxxy}-3\,(u_{x}u_{y})_{x}-3\,u_{xx}+3\,u_{yy}=0. \end{aligned}$$
(7)

through the link between f and u:

$$\begin{aligned} u=2\Big [\mathrm {ln}\,f(x,y,t)\Big ]_{x}=2\frac{f_x(x,y,t)}{f(x,y,t)}. \end{aligned}$$
(8)

Symbolic computation manipulation on a direct substitution of f in Eq. (5) into Eq. (6) leads to the following set of constraining equations for the parameters:

$$\begin{aligned} \Bigg \{&a_{1}=a_{1}, a_{2}=a_{2},\nonumber \\&a_{3}=\frac{3[a_{2}(a_{1}^2-a_{2}^2-a_{5}^2-a_{6}^2) +2a_{1}a_{5}a_{6}]}{a_{2}^2+a_{6}^2},\nonumber \\&a_{4}=a_{4}, a_{5}=a_{5}, a_{6}=a_{6},\nonumber \\&a_{7}=-\frac{3[a_{6}(a_{1}^2+a_{2}^2-a_{5}^2+a_{6}^2) -2a_{1}a_{2}a_{5}]}{a_{2}^2+a_{6}^2}, a_{8}=a_{8},\nonumber \\&a_{9}=-\frac{(a_{2}^2+a_{6}^2)(a_{1}^2+a_{5}^2) (a_{1}a_{2}+a_{5}a_{6})}{(a_{1}a_{6}-a_{2}a_{5})^2}\Bigg \}, \end{aligned}$$
(9)

which needs to satisfy the conditions

$$\begin{aligned}&a_{1}a_{6}-a_{2}a_{5}\ne 0, \end{aligned}$$
(10)
$$\begin{aligned}&a_{1}a_{2}+a_{5}a_{6}<0, \end{aligned}$$
(11)

to guarantee the well-definedness of f, the positiveness of f and the localization of u in all directions in the space. The parameters in the set (9) yield a class of positive quadratic function solution to Eq. (6) as

$$\begin{aligned} f&=\Bigg (a_{1}x+a_{2}y+\,\frac{3[a_{2}(a_{1}^2-a_{2}^2-a_{5}^2-a_{6}^2) +2a_{1}a_{5}a_{6}]}{a_{2}^2+a_{6}^2} t +a_{4}\Bigg )^2\nonumber \\&\quad +\,\Bigg (a_{5}x +a_{6}y -\,\frac{3[a_{6}(a_{1}^2+a_{2}^2-a_{5}^2+a_{6}^2) -2a_{1}a_{2}a_{5}]}{a_{2}^2+a_{6}^2}t +a_{8}\Bigg )^2\nonumber \\&\quad -\,\frac{(a_{2}^2+a_{6}^2)(a_{1}^2+a_{5}^2) (a_{1}a_{2}+a_{5}a_{6})}{(a_{1}a_{6}-a_{2}a_{5})^2}, \end{aligned}$$
(12)

which, in turn, generates a class of lump solutions to the dimensionally reduced Eq. (7) through transformation (8) as

$$\begin{aligned}&u^\mathrm{{(I)}}=\frac{4(a_{1}g+a_{5}h)}{f}, \end{aligned}$$
(13)

where the function f is defined by Eq. (12), and the functions g and h are given as follows:

$$\begin{aligned} g=&\,a_{1}x+a_{2}y\\&\,+\frac{3[a_{2}(a_{1}^2-a_{2}^2-a_{5}^2-a_{6}^2) +2a_{1}a_{5}a_{6}]}{a_{2}^2+a_{6}^2}t +a_{4},\\ h=&\,a_{5}x+a_{6}y\\&\,-\frac{3[a_{6}(a_{1}^2+a_{2}^2-a_{5}^2+a_{6}^2) -2a_{1}a_{2}a_{5}]}{a_{2}^2+a_{6}^2}t+a_{8}. \end{aligned}$$

Note here that six parameters \(a_{1}\), \(a_{2}\), \(a_{4}\), \(a_{5}\), \(a_{6}\) and \(a_{8}\) are involved in the solution u, among which, \(a_{4}\) and \(a_{8}\) are arbitrary, while the rests are demanded to satisfy conditions (10) and (11) to guarantee \(u^\mathrm{{(I)}}\) to be lump solutions.

3 Lump solutions to reduction with \(z=t\)

With \(z=t\), the dimensionally reduced form of the Hirota bilinear Eq. (2) reads

$$\begin{aligned}&2\,[(ff_{ty}-f_{t}f_{y}+f_{xxx}f_{y}+3\,f_{xxy}f_{x} -3\,f_{xx}f_{xy}\nonumber \\&\quad -ff_{xxxy} -3(ff_{xx}-f^{2}_{x})+3(ff_{yy}-f^{2}_{y})]=0, \end{aligned}$$
(14)

which is cast into

$$\begin{aligned}&u_{yt}-u_{xxxy}-3\,(u_{x}u_{y})_{x}-3\,u_{xx}+3\,u_{tt}=0. \end{aligned}$$
(15)

through the link between f and u, that is transformation (8).

For Eq. (14), a direct substitution of f gives rise to the following set of constraining equations for the parameters:

$$\begin{aligned} \Bigg \{a_{1}&=a_{1}, a_{2}=\frac{3[a_{3}(a_{1}^2-a_{3}^2-a_{5}^2-a_{7}^2) +2a_{1}a_{5}a_{7}]}{a_{3}^2+a_{7}^2}, \nonumber \\ a_{3}&=a_{3}, a_{4}=a_{4}, a_{5}=a_{5},\nonumber \\ a_{6}&=-\frac{3[a_{7}(a_{1}^2+a_{3}^2-a_{5}^2+a_{7}^2) -2a_{1}a_{3}a_{5}]}{a_{3}^2+a_{7}^2}, \nonumber \\ a_{7}&=a_{7}, a_{8}=a_{8}, \nonumber \\ a_{9}&=-\frac{3(a_{1}^2+a_{5}^2)(a_{1}a_{3}+a_{5}a_{7}) (a_{1}^2-a_{3}^2+a_{5}^2-a_{7}^2)}{(a_{1}a_{7}-a_{3}a_{5})^2}\Bigg \}, \end{aligned}$$
(16)

which needs to satisfy the conditions

$$\begin{aligned}&a_{1}a_{7}-a_{3}a_{5}\ne 0, \end{aligned}$$
(17)
$$\begin{aligned}&(a_{1}a_{3}+a_{5}a_{7})(a_{1}^2-a_{3}^2+a_{5}^2-a_{7}^2)<0, \end{aligned}$$
(18)

to guarantee the well-definedness of f, the positiveness of f and the localization of u in all directions in the space. The parameters in the set (16) yield a class of positive quadratic function solution to Eq. (14) as

$$\begin{aligned} f=&\Bigg (a_{1}x+\frac{3[a_{3}(a_{1}^2-a_{3}^2-a_{5}^2-a_{7}^2) +2a_{1}a_{5}a_{7}]}{a_{3}^2+a_{7}^2}y \nonumber \\&+a_{3} t+a_{4}\Bigg )^2\nonumber \\&+\Bigg (a_{5}x -\frac{3[a_{7}(a_{1}^2+a_{3}^2-a_{5}^2+a_{7}^2) -2a_{1}a_{3}a_{5}]}{a_{3}^2+a_{7}^2}y\nonumber \\&+a_{7}t+a_{8}\Bigg )^2\nonumber \\&-\frac{3(a_{1}^2+a_{5}^2)(a_{1}a_{3}+a_{5}a_{7}) (a_{1}^2-a_{3}^2+a_{5}^2-a_{7}^2)}{(a_{1}a_{7}-a_{3}a_{5})^2}, \end{aligned}$$
(19)

which, in turn, generates a class of lump solutions to the dimensionally reduced Eq. (15) through transformation (8) as

$$\begin{aligned}&u^\mathrm{{(II)}}=\frac{4(a_{1}g+a_{5}h)}{f}, \end{aligned}$$
(20)

where the function f is defined by Eq. (19), and the functions g and h are given as follows:

$$\begin{aligned} g=&\,a_{1}x+\frac{3[a_{3}(a_{1}^2-a_{3}^2-a_{5}^2-a_{7}^2) +2a_{1}a_{5}a_{7}]}{a_{3}^2+a_{7}^2}y\\&+a_{3}t+a_{4},\\ h=&\,a_{5}x -\frac{3[a_{7}(a_{1}^2+a_{3}^2-a_{5}^2+a_{7}^2) -2a_{1}a_{3}a_{5}]}{a_{3}^2+a_{7}^2}y\\&+a_{7}t+a_{8}. \end{aligned}$$

Note here that six parameters \(a_{1}\), \(a_{3}\), \(a_{4}\), \(a_{5}\), \(a_{7}\) and \(a_{8}\) are involved in the solution u, among which, \(a_{4}\) and \(a_{8}\) are arbitrary, while the rests are demanded to satisfy conditions (17) and (18) to guarantee \(u^\mathrm{{(II)}}\) to be lump solutions.

4 Lump dynamics and energy distribution

For the exact solution u(x, y, t) to Eqs. (7) and (15) to be lump ones, it is required that

$$\begin{aligned}&\lim _{x^2+y^2\rightarrow \infty }u(x,y,t)=0, \ \forall \ t\in \mathbb {R}. \end{aligned}$$

By virtue of transformation (8), a sufficient condition for u(x, y, t) to be a lump solution constraining on f(x, y, t) is

$$\begin{aligned}&\lim _{x^2+y^2\rightarrow \infty }f(x,y,t)=\infty , \ \forall \ t\in \mathbb {R}. \end{aligned}$$

All the solutions derived in this paper (\(u^\mathrm{{(I)}}\) and \(u^\mathrm{{(II)}}\)) satisfy this criterion, and they are rationally localized in all directions in the space.

Fig. 1
figure 1

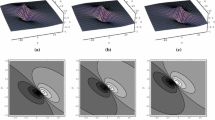
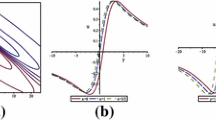
Lump dynamic characteristics of \(u^\mathrm{{(I)}}\) via Eq. (13) with \(a_{1}=1\), \(a_{2}=3\), \(a_{4}=0\), \(a_{5}=-4\), \(a_{6}=2\), \(a_{8}=0\) and \(t=0\): a 3-dimensional plot; b density plot; c x-curves and d y-curves

Full size image
Fig. 2
figure 2

Lump dynamic characteristics of \(u^\mathrm{{(II)}}\) via Eq. (20) with \(a_{1}=2\), \(a_{3}=3\), \(a_{4}=0\), \(a_{5}=1\), \(a_{7}=6\), \(a_{8}=0\) and \(t=0\): a 3-dimensional plot; b density plot; c x-curves and d y-curves

Full size image

The amplitude of a lump solution u is defined as max |u|, and the location of a lump solution is then defined as the place where the max |u| is attained. With these definitions, we know that the amplitude of \(u^\mathrm{{(I)}}\) is \(\frac{2|a_{1}a_{6}-a_{2}a_{5}|}{\sqrt{-(a_{1}a_{2}+a_{5}a_{6})(a_{2}^2+a_{6}^2)}}\) and initially located at

$$\begin{aligned} \left( \frac{\epsilon \sqrt{a_{1}^2+a_{5}^2}(a_{2}a_{8}-a_{4}a_{6})\pm \sqrt{a_{9}}(a_{1}a_{6}-a_{2}a_{5})}{\epsilon \sqrt{a_{1}^2+a_{5}^2}(a_{1}a_{6}-a_{2}a_{5})}, \frac{a_{4}a_{5}-a_{1}a_{8}}{a_{1}a_{6}-a_{2}a_{5}}\right) , \end{aligned}$$

where \(a_{i}\) (\(1\le i \le 9\)) are given in  (9) and the amplitude of \(u^\mathrm{{(II)}}\) is \(\frac{2|a_{1}a_{7}-a_{3}a_{5}|}{\sqrt{-3(a_{1}a_{3}+a_{5}a_{7})(a_{1}^2-a_{3}^2+a_{5}^2-a_{7}^2)}}\) and initially located at

$$\begin{aligned} \left( \frac{\epsilon \sqrt{a_{1}^2+a_{5}^2} (a_{2}a_{8}-a_{4}a_{6})\pm \sqrt{a_{9}}(a_{1}a_{6}-a_{2}a_{5})}{\epsilon \sqrt{a_{1}^2+a_{5}^2}(a_{1}a_{6}-a_{2}a_{5})}, \frac{a_{4}a_{5}-a_{1}a_{8}}{a_{1}a_{6}-a_{2}a_{5}}\right) , \end{aligned}$$

where \(a_{i}\) (\(1\le i \le 9\)) are given in  (16), and

$$\begin{aligned} \epsilon =\left\{ \begin{aligned}&1, \quad a_{5}>0, \\&-1, \quad a_{5}<0. \end{aligned} \right. \end{aligned}$$

The localized characteristics and energy distribution of the lump solutions can be seen clearly in Figs. 1 and 2 including 3-dimensional plots, density plots and 2-dimensional curves with particular choices of the involved parameters in the potential function u.

5 Concluding remarks

Lump solution is a type of rational solution, and another type of exact solution with rational function amplitudes is rogue wave solution, which attracts recent attention in describing nonlinear wave phenomena in oceanography and nonlinear optics [30, 31]. In this paper, we have derived two classes of lump solutions (see Eqs. 13 and 20) to the dimensionally reduced Eqs. (7) and (15), respectively, by searching for positive quadratic function solutions to the associated bilinear equations, i.e., Eqs. (6) and (14). This method can be used to search for rogue wave solutions, that is to say, rogue wave solutions could be generated as well in terms of positive polynomial solutions to the associated bilinear equations. Work of this aspect will be proceeded in our future papers.

It should be noticed that we have studied lump solutions to two types of dimensional reductions with \(z=y\) and \(z=t\) for Eq. (2), or correspondingly for Eq. (4). For the reduction with \(z=x\), Eq. (2) is reduced to

$$\begin{aligned}&2\,[(ff_{ty}-f_{t}f_{y}+f_{xxx}f_{y}+3\,f_{xxy}f_{x}\nonumber \\&\quad -3\,f_{xx}f_{xy}-ff_{xxxy}]=0, \end{aligned}$$
(21)

which is linked to

$$\begin{aligned}&u_{yt}-u_{xxxy}-3\,(u_{x}u_{y})_{x}=0, \end{aligned}$$
(22)

through the transformation (8). We have found no positive quadratic function solutions in terms of Eqs. (5)–(21) such that no lump solutions to Eq. (22) either. How to derive lump solutions or how to prove its nonexistence to Eq. (22) is a further question.