Vector spatiotemporal localized structures in (3 $+$ 1)-dimensional strongly nonlocal nonlinear media

Abstract

We investigate the (3 $+$ 1)-dimensional coupled nonlocal nonlinear Schrödinger equation in the inhomogeneous nonlocal nonlinear media and derive analytical vector spatiotemporal localized solution. Based on this solution, Gaussian solitons and some symmetric multipole patterns around the point $(x, y) =(0,0)$ can be constructed. The change trends of the amplitude and width of solitons are opposite, and they finally tend to a certain value. The compression and expansion of spatiotemporal localized structures are also studied in an exponential diffraction decreasing system.

1 Introduction

The characteristics of solitons are their sustainability in time, localization in space and stability along propagating distance. Different soliton structures have been investigated in various physical fields including plasma physics, condensed matter physics and nonlinear optics [1–11].

In optics, abundant localized structures in local and nonlocal nonlinear media have been intensively studied. In local nonlinear media, spatial and spatiotemporal soliton [12–15], vortex solitons [16], light bullet [17, 18] and breather [19, 20] have been produced and play important roles in dense wavelength division multiplexing, soliton supercontinuum generation, and new soliton lasers design, etc. In nonlocal nonlinear media, two-dimensional Hermite–Gaussian solitons [21] and rotating azimuthons [22] and three-dimensional necklace solitons [23] and Hermite–Bessel solitons [24] have also been extensively studied.

In the nonlocal nonlinear media, nonlocality means that the nonlinearity of a material at a particular point depends on the wave intensity at all other material points, and thus, the nonlinear term in the nonlocal nonlinear Schrödinger equation (NNSE) is the nonlocal form associated with a symmetric and real-valued response kernel. For the strongly nonlocal case, the NNSE can be simplified into the standard Snyder–Mitchell model (a linear model) [25].

The nonlocality produces some new interesting effects. In Refs. [26, 27], authors reported that nonlocality can prevent beam collapse and stabilize multidimensional solitons. Moreover, nonlocality can also promote the stability of vector solitons [28]. However, three-dimensional vector solitons are hardly reported in the inhomogeneous nonlocal nonlinear media. In this paper, we investigate a (3 $+$ 1)-dimensional coupled NNSE with variable coefficients and obtain analytical vector spatiotemporal localized solution. Based on this solution, the compression and expansion of spatiotemporal localized structures are studied in an exponential diffraction decreasing system.

2 Vector spatiotemporal localized solution

In general, an essential requirement of vector solitons is the absence of any interference between the single components. This requirement can either be realized by using beams of different polarization [29] or just mutually incoherent beams [30]. In (3 $+$ 1)-dimensional inhomogeneous nonlocal nonlinear media, the propagation of vector optical solitons is governed by the following coupled NNSE

$$\begin{aligned}&\text {i}u_t+\frac{\beta (t)}{2} \nabla ^2 u-\triangle n_1(\mathbf r ,t)u=\text {i}\gamma (t) u,\nonumber \\&\text {i}v_t+\frac{\beta (t)}{2} \nabla ^2 v-\triangle n_2(\mathbf r ,t)v=\text {i}\gamma (t) v, \end{aligned}$$

(1)

where $u(\mathbf r ,t)$ and $v(\mathbf r ,t)$ denote two normalized complex mode components with $\mathbf r =(x,y,z)$, x, y represent dimensionless transverse coordinates, t is the evolution coordinate, which corresponds to the propagation distance in optics and the time in BEC, the three-dimensional “transverse” Laplacian operator $\nabla =\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}$. Functions $\beta (t)$ and $\gamma (t)$ are coefficients of diffraction and gain/loss, respectively. The nonlocal nonlinear term $\triangle n_1(\mathbf r ,t)=S(t)\int _{-\infty }^{+\infty }R(\mathbf r -\mathbf r ')(a_1|u|^2+a|v|^2)\hbox {d}{} \mathbf r$ and $\triangle n_2(\mathbf r ,t)=S(t)\int _{-\infty }^{+\infty }R(\mathbf r -\mathbf r ')(a|u|^2+a_2|v|^2)\hbox {d}{} \mathbf r$ with the response function $R(\mathbf r -\mathbf r ')=\exp \left[ -\frac{|\mathbf r -\mathbf r '|^2}{\sigma ^2}\right] /(\pi \sigma ^2)$. The constants $a , a_1$ and $a_2$ determine the ratio of the coupling strengths of the cross-phase modulation to the self-phase modulation. The limit $\sigma \rightarrow 0$ corresponds to the case of local cubic nonlinearity, whereas $\sigma \rightarrow \infty$ corresponds to the strongly nonlocal case.

Fig. 1

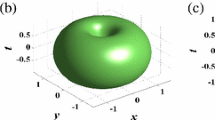
(Color online) Spatiotemporal localized structures of $I=|u|^2$ for $q=0.9$ at $t=50$: a–c $l=0,1,2$ with $m=0,n=1$, d–f $l=1,2,3$ with $m=n=1$, and g–i $l=2,3,4$ with $m=2,n=1$. Parameters are chosen as $a_1=0.98,a_2=a=1,\epsilon =1,s_0=0.03,\beta _0=0.5,\sigma =0.05,A_0=0.8,\omega _0=0.4,W_0=0.5,d_1=0,d_2=1$

Fig. 2

(Color online) Spatiotemporal multipole structures for $q=0$ at $t=50$: a–c $l=2,3,4$ with $m=1$ and d–f $l=4,5,6$ with $m=2$. Parameters are chosen as the same as those in Fig. 1

Fig. 3

(Color online) a The change of amplitude and width, b–d the compression and expansion of spatiotemporal structure corresponding to Fig. 1f at $t=8,50,120$. Parameters are chosen as the same as those in Fig. 1 except for $\omega _0=0.9$

Fig. 4

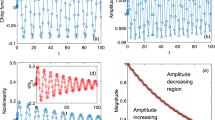
(Color online) a The change of amplitude and width, b–d the compression of spatiotemporal multipole structure with $m=2,l=5,n=1$ at $t=8,40,120$. Parameters are chosen as the same as those in Fig. 3 except for $\lambda =1$

By means of the following transformation

$$\begin{aligned} \left\{ \begin{array}{cc}u\\ v\end{array}\right\} =\left\{ \begin{array}{cc}\sqrt{|\frac{a_2-a}{a_1a_2-a^2}|}\\ \sqrt{|\frac{a_1-a}{a_1a_2-a^2}|}\end{array}\right\} \psi , \end{aligned}$$

(2)

Equation (1) changes into

$$\begin{aligned} \text {i}\psi _t+\frac{\beta (t)}{2} \nabla ^2 \psi -\triangle n(\mathbf r ,t)\psi =\text {i}\gamma (t)\psi . \end{aligned}$$

(3)

In the strongly nonlocal medium, the degree of nonlocality $\sigma$ is far more than wave characteristic width w. In this case, one expands the response function in Taylor’s series, and then the nonlinear refraction index in Eq. (3) is $\triangle n(\mathbf r ,t)\approx s(t)r^2$ with $r^2=x^2+y^2+z^2$.

Considering the relation between diffraction and nonlocal nonlinearity as

$$\begin{aligned} s(t)=\frac{\epsilon \beta (t)}{W^4(t)}, \end{aligned}$$

(4)

and using the transformation

$$\begin{aligned} \psi= & {} \frac{A_0}{W^{3/2}(t)}\Psi \left[ T\equiv \frac{\varOmega (t)\varTheta (t)}{W_0^2},X\equiv \frac{x}{W(t)}, \right. \nonumber \\ Y\equiv & {} \frac{y}{W(t)}, \left. Z\equiv \frac{z}{W(t)}\right] \exp \left[ \int _0^t \gamma (\tau ) \hbox {d}\tau \right. \nonumber \\&\left. -\,\text {i}\frac{s_0\varOmega (t)}{2}r^2\right] , \end{aligned}$$

(5)

with the width $W(t)=\frac{W_0}{\varOmega (t)}$, the chirp function $\varOmega (t)=[1-s_0\varTheta (t)]^{-1}$, the accumulated diffraction $\varTheta (t)=\int ^t_0\beta (\tau )\text {d}\tau$ and constants $A_0,W_0,s_0$, Eq. (3) changes into

$$\begin{aligned}&\text {i} \Psi _T+\frac{1}{2}(\Psi _{XX}+\Psi _{YY}+\Psi _{ZZ})\nonumber \\&\quad -\,\epsilon (X^2+Y^2+Z^2)\Psi =0, \end{aligned}$$

(6)

whose solutions have been reported in Ref. [23]. However, we follow the procedure in Ref. [23] to obtain more general solutions and use these general solutions to produce solutions of Eq. (1).

From transformations (2) and (5) with soliton solution of Eq. (6), we obtain exact solution of Eq. (1)

$$\begin{aligned}&\left\{ \begin{array}{cc}u\\ v\end{array}\right\} =\left\{ \begin{array}{cc}\sqrt{|\frac{a_2-a}{a_1a_2-a^2}|}\\ \sqrt{|\frac{a_1-a}{a_1a_2-a^2}|}\end{array}\right\} \frac{A_0k}{\omega ^{3/2}(t) W^{3/2}(t)}[\cos (m\phi )\nonumber \\&\quad +\,\text {i}q\sin (m\phi )]P_l^m(\cos \theta )\left[ d_1M\left( -n,l{+}\frac{3}{2},\frac{R^2}{\omega ^2(t)}\right) \right. \nonumber \\&\quad \left. +\,d_2U({-}n,l+\frac{3}{2},\frac{R^2}{\omega ^2(t)})\right] \left( \frac{R}{\omega (t)}\right) ^l\exp \left\{ \frac{1}{2}\right. \nonumber \\&\quad -\frac{R^2}{2\omega ^2}+\int _0^t \gamma (\tau ) \hbox {d}\tau +\text {i}\left[ b(t)\right. \nonumber \\&\quad \left. \left. -\frac{s_0\varOmega (t)}{2}r^2+c(t)R^2\right] \right\} , \end{aligned}$$

(7)

where $M(\cdot )$ and $U(\cdot )$ are Kummer M and U functions [31], $P_l^m(\cos \theta )$ are the associated Legendre function with the degree l and order m satisfying $l\ge m\ge 0$ [23], and $\cos (\theta )=Z/R$, $\omega (t)=\omega _0[1+(\lambda -1)\sin (2\varXi )], b(t){=}-\,\frac{(2n+l+3/2)\arctan [\sqrt{\lambda }\tan (2\varXi )]}{2\sqrt{\epsilon \lambda }\omega _0^4} ,c(t)=\frac{\sqrt{\epsilon }\omega _0^2(\lambda -1)\sin (4\varXi )}{1+\lambda -(\lambda -1)\cos (4\varXi )}$ with $R^2{=}X^2{+}Y^2{+}Z^2,\lambda {=}1/(2\epsilon \omega _0^4),\varXi (t){=}\sqrt{\epsilon }\omega _0^2T, k=\sqrt{\frac{2^{l-n+2}(2l+1)(l-m)!(2l+2n+1)!!}{4\pi \sqrt{\pi }(1+q^2)n!(l+m)![(2l+1)!!]^2}}$, the modulation depth of the pulse intensity $q\in [0,1]$, the azimuthal angle $\phi$ in the transverse plane (X, Y) and three constants $\omega _0,d_1$ and $d_2$.

3 Dynamical characteristics and evolution of spatiotemporal localized structures

In the following, the propagation behaviors of spatiotemporal localized structures are discussed in an exponential diffraction decreasing system [32, 33]

$$\begin{aligned} \beta (t)=\beta _{0}\exp ({-}\sigma t), \end{aligned}$$

(8)

where $\beta _{0}$ and $\sigma$ are two positive parameters related to diffraction. When $\sigma >0$, this system is the diffraction decreasing system.

At first, we discuss the case of $q=0.9$, and other parameters are chosen as $a_1=0.98,a_2=a=1,\epsilon =1,s_0=0.03,\beta _0=0.5,\sigma =0.05,A_0=0.8, \omega _0=0.4,W_0=0.5,d_1=0,d_2=1$. When $m=0$, Gaussian solitons are exhibited in Fig. 1a–c. In particular, if $l=0$, a sphere light bullet forms. With the addition of l, the sphere in Fig. 1a turns into a torus-shaped structure in Fig. 1b, and then a pair of drip-shaped structures appears above and below the torus-shaped structure in the middle [see Fig. 1c]. When $m=1$, some pair-like structures exist. With the addition of l, a pair of ellipsoids in Fig. 1d changes into a pair of torus-shaped structures in Fig. 1e, and then a pair of drip-shaped structures also appears above and below the pair of torus-shaped structures in the middle [see Fig. 1f]. When $m=2$, with the addition of l, some layer structures along the vertical direction are produced in Fig. 1g–i.

Next, we discuss spatiotemporal multipole structures for the case of $q=0$. Some symmetric multipole patterns around the point $(x, y) =(0,0)$ can be constructed in Fig. 2. When $m=0$, four solitons exhibit layout around the point $(x, y) =(0,0)$. With the addition of l, another layer of solitons appears gradually from Fig. 2b–c. When $m=1$, four solitons in Fig. 2a–c split into eight solitons in Fig. 2d–f; that is, every soliton splits into two parts. Similarly, with the addition of l, the layer of multipole soliton structures also increases from Fig. 2e, f.

At last, we discuss dynamical evolution of spatiotemporal localized structures. As an example, the compression and expansion of spatiotemporal structure corresponding to Fig. 1f are exhibited in Fig. 3. From Fig. 3a, the width and amplitude are decided by $W(z)\omega (z)$ and $\frac{A_0k}{\omega ^{3/2}(z)W^{3/2}(z)}$, respectively. Although W(z) changes as an exponential form in the exponential dispersion decreasing system (8), $\omega (z)$ changes with $\sin$-function as $\sin (2\varXi )$. Therefore, the amplitude and width change periodically and finally tend to some fixed values. Note that the change trends of the amplitude and width are opposite, namely, the amplitude reveals an adding oscillation and finally tends to a certain value, while the width exhibits a decreasing oscillation and finally tends to a certain value. These changes are verified by the evolutional plots shown in Fig. 3b–d. Spatiotemporal soliton is compressed from $z=8$ in Fig. 3b to $z=50$ in Fig. 3c and then is expanded from $z=50$ in Fig. 3c to $z=120$ in Fig. 3d.

Compared with these compression and expansion behaviors of spatiotemporal structure, we can also discuss the compression behavior (only compression and no expansion). As another example, we study spatiotemporal structure with $m=2,l=5,n=1$. When $\lambda =1$, the dispersion/diffraction of pulse is exactly balanced by the nonlinearity. In this case, $\omega (z)=\omega _0$ (constant); thus, the width and amplitude both change as an exponential form in the exponential dispersion decreasing system (8). Their changes are shown in Fig. 4a; that is, the width decreases and amplitude increases exponentially, and ultimately incline to some certain values. From Fig. 4b–d, the spatiotemporal multipole structure is compressed with the increase of the evolution coordinate.

4 Conclusions

In short, we investigate the (3 $+$ 1)-dimensional coupled NNSE in the inhomogeneous nonlocal nonlinear media and derive analytical vector spatiotemporal localized solution built out of spherical harmonics and Kummer’s functions. Based on this solution, Gaussian solitons and some symmetric multipole patterns around the point $(x, y) =(0,0)$ can be constructed. The change trends of the amplitude and width of solitons are opposite, and they finally tend to a certain value. The compression and expansion of spatiotemporal localized structures are also studied in a exponential dispersion decreasing system. These results may give new insight into laser devices emitting ultra-short pulses, all-optical networks and experimental realization in nonlocal nonlinear BEC.