1 Introduction

Gear transmission systems are crucial components with a wide range of applications and usually operate under complex conditions like high speed, heavy load, and variable torque. There have been several researches on the dynamic analysis of the gears to identify the parameters that ensure the stability of the system under different operational conditions. The goal is mainly to avoid severe vibration that lead to damage and breakage of the machinery, resulting in catastrophic failure. In many articles, different lumped parameter models are proposed and analyzed to study the complex nonlinear dynamic behavior of geared systems.

In the most basic case, the deformation of the shafts and bearings is neglected and a one-degree-of-freedom (DOF) model with rigid supports is formulated. It has been shown that in this model, the separation of teeth occurs in the vicinity of the parametric resonance tongues [34] where the presence of the clearance-type nonlinearity dictates system behavior [3]. Several works investigated the effect of different parameters on the nonlinear behavior of the system in this regime: Basins of attraction [23], bifurcation diagrams, Poincaré sections [17, 22], amplitude–frequency response, and largest Lyapunov exponent [22] are used to identify chaotic behaviors. The effect of logarithmic [21, 39] and fractal [13] estimation for backlash function are investigated. And the influence of the load [4] and backlash [41] on the time-varying mesh stiffness and dynamic transmission error is established. Some analytical methods are also employed to provide more comprehensive understanding of system’s dynamic: The Melnikov method is used to analyze [11] and control [28] homoclinic bifurcation. And the incremental harmonic balance method is used to determine excitation amplitude on the frequency–response curves [30].

Some research analyzed the performance of the geared system by including the effect of the bending of the shafts and the elasticity of the bearings [27], along with nonlinearity due to the backlash. In these studies, the coupled lateral–torsional vibration of gears is described by a three-DOF dynamic model, where the resilient elements of the supports are described by Voigt–Kelvin model: Phase trajectories, bifurcation diagram, and basin of attraction are used to study and compare the torsional vibration of gears with and without suspension [20]. The effects of internal and external excitation [18, 42] and gear eccentricity [19] on the jump discontinuity phenomenon are investigated. Specifically, the bifurcation diagram is plotted by choosing the stiffness of the suspension as the control parameter to demonstrate the importance of the deformation of the suspension [17]. In other studies, the effect of the bearing radial clearance is also included in the three-DOF dynamic model: The frequency response diagram is used to reveal the effect of the loading parameters on the system’s dynamic behavior [33]. Analytical [26] and numerical [14, 35, 36] methods are used to study the influence of internal and external excitation on the occurrence of bifurcation and chaotic motions. And experimental data and theoretical analysis [16] are used to study the effect of surface roughness [8] by using fractal estimation for expressing the clearance of bearings.

Other works analyzed the performance of geared systems by including the nonlinear effect of the supporting shaft, along with the nonlinearity due to the backlash. In these studies, phase plane, Poincaré map, bifurcation diagram [6, 7, 40], power spectra, the Lyapunov exponent [6, 7], and fractal dimensions [7] are used to provide an understanding of the operating conditions under which periodic, quasi-periodic, and chaotic motions occur. Specifically, the importance of including the nonlinearity of the supporting shaft in the lumped model is demonstrated by comparing the dynamic response of a gear set with linear and nonlinear suspensions [40].

In most of these studies (either with rigid, linear, or nonlinear suspensions), the nonlinear characteristics of the geared systems are analyzed by using the assumption that the system operates under constant speed and lightly loaded operational conditions, where the clearance between the gears are considered as the main source of the nonlinearity. Few attempts have been made to investigate the effect of the nonlinear suspension on the performance of the gears under the assumption that the gears in mesh do not separate [37], and the nonlinearity due to free play mode and impact phases does not participate in system’s response [32]. This condition is acceptable under steady state operational conditions of the constant speed and high load [10], where the gears in mesh remain in permanent contact regime [12].

In my previous work, the permanent contact condition was imposed upon a system with linear suspension, which reduced the governing differential equations of the system to a system of linear, parametrically excited coupled differential equations [2].Then the effect of the suspension on the number and location of the parametrically unstable tongues was investigated. In continuation of the prior results, the goal of this paper is to impose the permanent contact condition to the same system but with nonlinear suspension and investigate the effect of nonlinearity on the dynamic behavior of the system around the parametrically unstable tongues. To this end, the lumped parameter analysis method is used to drive the dimensionless governing system of equations for a one-stage spur gear pair with nonlinear suspension. The Poincaré–Lindstedt method is used to investigate the influence of the parameters on the stability and bifurcation, specifically around the unstable tongues. The results reveal that with the change of the control parameter, the meshing frequency, the system undergoes both pitchfork and hopf bifurcations around the primary and combination parametrically unstable tongues, respectively. Finally, numerical integrations are used to plot the Poincaré map and time response of the nonlinear system in order to validate the analytical results. The analytical results are provided for both hardening and softening cubic nonlinearity of the suspension, but the numerical results are provided only for the softening case since the experimental data reported mostly softening behavior for geared systems [3, 4, 8, 30, 34].

The remainder of this paper is organized accordingly. In Sect. 2, the dimensionless dynamic model of a spur gear pair with nonlinear suspension is provided. In Sect. 3, the Poincaré–Lindstedt method is used to demonstrate the pitchfork and hopf bifurcation around the unstable tongues by studying the eigenvalues of the Jacobian matrix. In Sect. 4, the results from numerical simulation are presented, demonstrating the behavior of the system under different operational conditions. The conclusion contains final remarks.

Fig. 1
figure 1

Schematic of pinion and gear in mesh with nonlinear suspension

Full size image

2 Generalized model of spur gear pairs in mesh

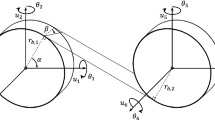
In this section, the lumped parameter technique is used to formulate the dynamic model of a single-stage spur gear in mesh with nonlinear suspension. As illustrated in Fig. 1, the gears in mesh are modeled as a pair of rigid disks with radii equal to the base circles (the circle from which the involute portion of the tooth profile is generated). For involute spur gear mesh, the mesh deformation is measured and the mesh force is transmitted along the line of action [5]. Therefore, the disks are connected along this line by a set of spring–damper [14]. The transmission shafts and the supporting mounts are modeled by a set of nonlinear springs and linear dampers [6, 7, 38, 40]. The cubic nonlinearity of the suspension in the rotor-bearing system is mainly caused by mid-plane stretching of the shaft [9, 15] or elasticity of the bearings [29] and has been studied in many articles.

In the above-mentioned model, each disk has one rotational and one translational DOF. Newton’s second law is used to construct the torsional and translational differential equations of motion for each disk.

$$\begin{aligned}&M_p {\ddot{x}}_p + C_p \dot{x}_p + K_p x_p + K_{po} x_p^3 \nonumber \\&\quad + C ( \dot{x}_p - \dot{x}_g + r_p {{\dot{\theta }}}_p - r_g {{\dot{\theta }}}_g - \dot{e}(t) )\nonumber \\&\quad + k(t) f (x_p - x_g + r_p\theta _p - r_g \theta _g - e(t)) = 0\end{aligned}$$
(1)
$$\begin{aligned}&M_g {\ddot{x}}_g + C_g \dot{x}_g + K_g x_g + K_{go} x_g^3 \nonumber \\&\quad - C ( \dot{x}_p - \dot{x}_g + r_p {{\dot{\theta }}}_p - r_g {{\dot{\theta }}}_g - \dot{e}(t) ) \nonumber \\&\quad - k(t) f (x_p - x_g + r_p\theta _p - r_g \theta _g - e(t)) = 0 \end{aligned}$$
(2)
$$\begin{aligned}&I_p {{\ddot{\theta }}}_p + r_p C ( \dot{x}_p - \dot{x}_g + r_p {{\dot{\theta }}}_p - r_g {{\dot{\theta }}}_g - \dot{e}(t) ) \nonumber \\&\qquad + r_p k(t) f (x_p - x_g + r_p\theta _p - r_g \theta _g - e(t)) \nonumber \\&\quad = + {\overline{T}}_p + {\widetilde{T}}_p \cos (\omega _p t) \end{aligned}$$
(3)
$$\begin{aligned}&I_g {{\ddot{\theta }}}_g - r_g C ( \dot{x}_p - \dot{x}_g + r_p {{\dot{\theta }}}_p - r_g {{\dot{\theta }}}_g - \dot{e}(t) ) \nonumber \\&\qquad - r_g k(t) f (x_p - x_g + r_p\theta _p - r_g \theta _g - e(t)) \nonumber \\&\quad = - {\overline{T}}_g - {\widetilde{T}}_g \cos (\omega _g t). \end{aligned}$$
(4)

In these equations, subscripts g and p designate the gear and pinion, respectively. The total difference between the translational displacement and rotational angle of the gears in mesh along the line of action can be expressed by the following equation, which is defined as dynamic transmission error [33].

$$\begin{aligned} x = x_p - x_g + r_p\theta _p - r_g \theta _g - e(t), \end{aligned}$$
(5)

where e(t) is known as the static transmission error, taking into account the effects of manufacturing errors and gear faults, [20]. To consider the fluctuation of the excitation torque and the applied load, both can be decomposed into averaging and fluctuating parts [11], so Eqs. (1)–(4) can be written in the following form.

$$\begin{aligned}&M_p {\ddot{x}}_p + C_p \dot{x}_p + K_p x_p + K_{po} x_p^3 + C \dot{x} + k(t) f (x)\nonumber \\&\quad = 0 \end{aligned}$$
(6)
$$\begin{aligned}&M_g {\ddot{x}}_g + C_g \dot{x}_g + K_g x_g + K_{go} x_g^3 - C \dot{x} - k(t) f (x)\nonumber \\&\quad = 0 \end{aligned}$$
(7)
$$\begin{aligned}&I_p {{\ddot{\theta }}}_p + r_p C x + r_p k(t) f (x)= +{\overline{T}}_p + {\widetilde{T}}_p \cos (\omega _p t) \end{aligned}$$
(8)
$$\begin{aligned}&I_g {{\ddot{\theta }}}_g - r_g C x - r_g k(t) f (x)= -{\overline{T}}_g - {\widetilde{T}}_g \cos (\omega _g t) , \end{aligned}$$
(9)

where \({\overline{T}}_p \) and \( {\overline{T}}_g \) are the average torques and \( {\widetilde{T}}_p \) and \( {\widetilde{T}}_g \) are the fluctuating torques. The time-varying gear mesh stiffness can be formulated as follows [16].

$$\begin{aligned} k(t) = K \Big ( 1+k_0 \cos (\omega t) \Big ) , \quad k_0 = \frac{k}{K}, \end{aligned}$$
(10)

where K and k are the average and amplitude of the harmonic components of the gear meshing stiffness, respectively. By subtracting Eq. (9) from Eq. (8), the governing torsional equations of motion reduce to the following equation [40].

$$\begin{aligned}&- {\ddot{x}}_p + {\ddot{x}}_g +{\ddot{x}} + \frac{C}{M} \dot{x} + \frac{K}{M} \big ( 1+k_0 \cos (\omega t) \big ) f(x)\nonumber \\&\quad = \frac{K}{M} F + \frac{K}{M} F_p \cos (\omega _p t) + \frac{K}{M} F_g \cos (\omega _g t) - {\ddot{e}}(t),\nonumber \\ \end{aligned}$$
(11)

where M is the equivalent mass, representing the total inertia of the gear pair, F is the average static force transmitted through the gear pair, and \( F_p \) and \( F_g \) are the fluctuating forces applied to the pinion and gear, expressed by the following equations.

$$\begin{aligned} M= & {} \frac{I_p I_g}{I_p r_g^2 + I_g r_p^2} , \;\;\; F = \frac{M}{K}\left( \frac{{\overline{T}}_p r_p}{I_p}+\frac{{\overline{T}}_g r_g}{I_g}\right) , \nonumber \\ F_p= & {} \frac{M}{K} \frac{{\widetilde{T}}_p r_p}{I_p} , \;\; \quad F_g = \frac{M}{K} \frac{{\widetilde{T}}_g r_g}{I_g}. \end{aligned}$$
(12)

By defining the following standard parameters

$$\begin{aligned} \omega _n = \sqrt{ \frac{K}{M} } , \;\;\; \zeta = \frac{C}{2\sqrt{KM}}, \end{aligned}$$
(13)

and the following static transmission error [28]

$$\begin{aligned} e(t) = E \cos (\omega t), \end{aligned}$$
(14)

one can write Eq. (11) in the following standard form.

$$\begin{aligned} \begin{aligned}&- {\ddot{x}}_p + {\ddot{x}}_g + {\ddot{x}} + 2 \zeta \omega _n \dot{x} + \omega _n^2 \big (1+k_0 \sin (\omega t) \big ) f(x)\\&\quad = \omega _n^2 F + \omega _n^2 F_p \cos (\omega _p t) + \omega _n^2 F_g \cos (\omega _g t)\\&\qquad + \omega ^2 E \cos (\omega t). \end{aligned} \end{aligned}$$
(15)

By defining the following dimensionless parameters [16]

$$\begin{aligned} {\hat{t}}= & {} \omega _n t, \nonumber \\ u= & {} \frac{x}{b} , \;\;\; u_p = \frac{x_p}{b}, \;\;\; u_g = \frac{x_g}{b}, \nonumber \\ {\varOmega }= & {} \frac{\omega \;}{\omega _n}, \;\;\; {\varOmega }_p = \frac{\omega _p}{\omega _n}, \;\;\; {\varOmega }_g = \frac{\omega _g}{\omega _n}, \end{aligned}$$
(16)

Equations (6),(7), and (15) are written in the following dimensionless form.

$$\begin{aligned}&m_p \hat{ {\ddot{u}} }_p + 2 \zeta _p \hat{ \dot{u} }_p + 2 \zeta \hat{ \dot{u} } + k_p u_p + \alpha _p u_p^3 \nonumber \\&\qquad + \big (1+k_o \cos ({\varOmega } {\hat{t}} ) \big ) f(u) = 0 \end{aligned}$$
(17)
$$\begin{aligned}&m_g \hat{ {\ddot{u}} }_g + 2 \zeta _g \hat{ \dot{u} }_g - 2 \zeta \hat{ \dot{u} } + k_g u_g + \alpha _g u_g^3\nonumber \\&\qquad - \big (1+k_o \cos ({\varOmega } {\hat{t}} ) \big ) f(u) = 0 \end{aligned}$$
(18)
$$\begin{aligned}&- \hat{ {\ddot{u}} }_p + \hat{ {\ddot{u}} }_g + \hat{ {\ddot{u}} } + 2 \zeta \hat{ \dot{u} } + \big (1+k_o \cos ({\varOmega } {\hat{t}} ) \big ) f(u) \nonumber \\&\quad = F + F_p \cos ({\varOmega }_p {\hat{t}} ) + F_g \cos ({\varOmega }_g {\hat{t}} )\nonumber \\&\qquad + {\varOmega }^2 E \cos ({\varOmega } {\hat{t}} ), \end{aligned}$$
(19)

where the ratio of the suspension system parameters over the gear pairs in mesh parameters is expressed as follows.

$$\begin{aligned} m_p= & {} \frac{M_p}{M} , \;\;\; m_g = \frac{M_g}{M}, \nonumber \\ k_p= & {} \frac{K_p}{K} , \;\;\; k_g = \frac{K_g}{K} ,\end{aligned}$$
(20)
$$\begin{aligned} \alpha _p= & {} \frac{b^2 K_{po}}{K} , \;\;\; \alpha _g = \frac{b^2 K_{go}}{K},\nonumber \\ \zeta _p= & {} \frac{C_p}{2 \sqrt{ K M} }, \;\;\; \zeta _g = \frac{C_g}{2 \sqrt{ K M} }. \end{aligned}$$
(21)

Finally, one can write Eqs. (18)–(19) in the following matrix form.

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} m_p &{} 0 &{} 0 \, \\ 0 &{} m_g &{} 0 \, \\ - 1 &{} 1 &{} 1 \, \end{bmatrix} \begin{bmatrix} \hat{ {\ddot{u}} }_p \\ \hat{ {\ddot{u}} }_g \\ \hat{ {\ddot{u}} } \end{bmatrix} + 2 \begin{bmatrix} \zeta _p &{} 0 &{} \zeta \, \\ 0 &{} \zeta _g &{} - \zeta \,\\ 0 &{} 0 &{} \zeta \, \end{bmatrix} \begin{bmatrix} \hat{ \dot{u} }_p \\ \hat{ \dot{u} }_g \\ \hat{ \dot{u} } \end{bmatrix} \\&\qquad + \begin{bmatrix} k_p &{} 0 &{} + \big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \\ 0 &{} k_g &{} -\big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \\ 0 &{} 0 &{} + \big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \end{bmatrix} \begin{bmatrix} u_p \\ u_g \\ f(u) \end{bmatrix} \\&\qquad + \begin{bmatrix} \alpha _p &{} 0 &{} 0 \\ 0 &{} \alpha _g &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} \begin{bmatrix} u_p^3 \\ u_g^3 \\ u^3 \end{bmatrix} \\&\quad = \begin{bmatrix} 0 \\ 0 \\ F + F_p \cos ({\varOmega }_p {\hat{t}} ) + F_g \cos ({\varOmega }_g {\hat{t}} ) + {\varOmega }^2 E \cos ({\varOmega } {\hat{t}} ) \end{bmatrix}, \end{aligned} \end{aligned}$$
(22)

with the following dimensionless backlash function

$$\begin{aligned} f(u) = {\left\{ \begin{array}{ll} u-1 &{} \quad +1< u \\ \quad 0 &{} -1 \le u \le +1 \\ u+1 &{} \quad u < -1 \end{array}\right. } \end{aligned}$$
(23)

Equation (22) is a damped, conservative, parametrically and externally excited nonlinear system of coupled equations.

3 Analytical calculations

The goal of this section is to use Poincaré–Lindstedt method to study the stability and bifurcation of the equilibria around the parametric unstable tongues. This is done under the assumption that the system operates under constant speed and relatively high load, for a symmetric system that both driving and driven shafts have the same parameters.

$$\begin{aligned} \begin{aligned}&m = m_p = m_g, \\&k = k_p = k_g, \\&\alpha = \alpha _p = \alpha _g. \end{aligned} \end{aligned}$$
(24)

By imposing the permanent contact condition, Eq. (22) becomes a system of damped nonlinear differential equations with periodic time-varying coefficients.

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} m &{} 0 &{} 0 \, \\ 0 &{} m &{} 0 \, \\ - 1 &{} 1 &{} 1 \, \end{bmatrix} \begin{bmatrix} \hat{ {\ddot{u}} }_p \\ \hat{ {\ddot{u}} }_g \\ \hat{ {\ddot{u}} } \end{bmatrix} + 2 \begin{bmatrix} \zeta _p &{} 0 &{} \zeta \, \\ 0 &{} \zeta _g &{} - \zeta \,\\ 0 &{} 0 &{} \zeta \, \end{bmatrix} \begin{bmatrix} \hat{ \dot{u} }_p \\ \hat{ \dot{u} }_g \\ \hat{ \dot{u} } \end{bmatrix} \\&\qquad + \begin{bmatrix} k &{} 0 &{} +\big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \\ 0 &{} k &{} - \big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \\ 0 &{} 0 &{} + \big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \end{bmatrix} \begin{bmatrix} u_p \\ u_g \\ u \end{bmatrix} + \begin{bmatrix} \alpha &{} 0 &{} 0 \\ 0 &{} \alpha &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} \begin{bmatrix} u_p^3 \\ u_g^3 \\ u^3 \end{bmatrix}\\&\quad = \begin{bmatrix} 0 \\ 0 \\ F + F_p \cos ({\varOmega }_p {\hat{t}} ) + F_g \cos ({\varOmega }_g {\hat{t}} ) + {\varOmega }^2 E \cos ({\varOmega } {\hat{t}} ) \end{bmatrix}\\&\qquad + \begin{bmatrix} + \big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big )\\ - \big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \\ + \big ( 1+ k_0 \cos ({\varOmega } {\hat{t}} ) \big ) \end{bmatrix}. \end{aligned} \end{aligned}$$
(25)

The following transformation of variables is used for the Poincaré–Lindstedt method to study the stability of the corresponding undamped homogenous system of equations, while the time varying and nonlinear terms are perturbed.

$$\begin{aligned} \tau = {\varOmega } {\hat{t}}, \quad u_p^{\prime } = \frac{du_p}{d\tau }, \quad u_g^{\prime } = \frac{du_g}{d\tau }, \quad u^{\prime } = \frac{du}{d\tau }, \end{aligned}$$
(26)

which results in the following system of equations.

$$\begin{aligned}&{\varOmega }^2 \begin{bmatrix} m &{} 0 &{} 0 \, \\ 0 &{} m &{} 0 \, \\ - 1 &{} 1 &{} 1 \, \end{bmatrix} \begin{bmatrix} u_p^{\prime \prime } \\ u_g^{\prime \prime } \\ u^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} +\big ( 1+ \epsilon \cos \tau \big ) \\ 0 &{} k &{} - \big ( 1+ \epsilon \cos \tau \big ) \\ 0 &{} 0 &{} + \big ( 1+ \epsilon \cos \tau \big ) \end{bmatrix} \begin{bmatrix} u_p \\ u_g \\ u \end{bmatrix}\nonumber \\&\quad + \epsilon \begin{bmatrix} \alpha &{} 0 &{} 0 \\ 0 &{} \alpha &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} \begin{bmatrix} u_p^3 \\ u_g^3 \\ u^3 \end{bmatrix} = 0, \end{aligned}$$
(27)

where \( \epsilon \) is a small parameter, and prime represents differentiation with respect to the new variable \( \tau \). Now, by expanding the variables in the following power series

$$\begin{aligned}&u_p = u_{0p} + u_{1p} \epsilon + u_{2p} \epsilon ^2 + u_{3p} \epsilon ^3 + \; ... \end{aligned}$$
(28)
$$\begin{aligned}&u_g = u_{0g} + u_{1g} \epsilon + u_{2g} \epsilon ^2 + u_{3g} \epsilon ^3 + \; ... \end{aligned}$$
(29)
$$\begin{aligned}&u = u_{0} + u_{1} \epsilon + u_{2} \epsilon ^2 + u_{3} \epsilon ^3 + \; ... \end{aligned}$$
(30)
$$\begin{aligned}&{\varOmega } = {\varOmega }_0 + {\varOmega }_1 \epsilon + {\varOmega }_2 \epsilon ^2 + {\varOmega }_3 \epsilon ^3 + \; ... \end{aligned}$$
(31)

substituting Eqs. (28)–(31) in Eq. (27), neglecting terms of \( O( \epsilon ^2 ) \), and collecting terms of the same power the following systems of equations are obtained.

$$\begin{aligned}&{\varOmega }_0^2 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{0p}^{\prime \prime } \\ u_{0g}^{\prime \prime } \\ u_{0}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} 1 \end{bmatrix} \begin{bmatrix} u_{0p} \\ u_{0g} \\ u_{0} \end{bmatrix} = 0 \end{aligned}$$
(32)
$$\begin{aligned}&{\varOmega }_0^2 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p}^{\prime \prime } \\ u_{1g}^{\prime \prime } \\ u_{1}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix}\nonumber \\&\quad = -2 {\varOmega }_0 {\varOmega }_1 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{0p}^{\prime \prime } \\ u_{0g}^{\prime \prime } \\ u_{0}^{\prime \prime } \end{bmatrix} - \begin{bmatrix} 1 \\ -1 \\ 1 \end{bmatrix} u_0 \cos \tau \nonumber \\&\qquad - \begin{bmatrix} \alpha &{} 0 &{} 0 \\ 0 &{} \alpha &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} \begin{bmatrix} u_p^3 \\ u_g^3 \\ u^3 \end{bmatrix}. \end{aligned}$$
(33)

Equation (32) is a linear homogenous system of equations with the following solution.

$$\begin{aligned} \begin{bmatrix} u_{0p} \\ u_{0g} \\ u_{0} \end{bmatrix} = \begin{bmatrix} A \\ B \\ C \end{bmatrix} e^{\lambda \tau }. \end{aligned}$$
(34)

By substituting Eq. (34) in Eq. (32), the following characteristic equation is obtained.

$$\begin{aligned}&\begin{bmatrix} m {\varOmega }_0^2 \lambda ^2 + k &{} 0 &{} +1\\ 0 &{} m {\varOmega }_0^2 \lambda ^2 + k &{} -1 \\ -{\varOmega }_0^2 \lambda ^2 &{} +{\varOmega }_0^2 \lambda ^2 &{} -{\varOmega }_0^2 \lambda ^2+1 \end{bmatrix} \begin{bmatrix} A \\ B \\ C \end{bmatrix} e^{\lambda \tau }\nonumber \\&\quad = 0, \end{aligned}$$
(35)

with the following eigenvalues and eigenvectors

$$\begin{aligned} \lambda _1^2= & {} \frac{k}{m {\varOmega }_0^2} i^2 , \quad \lambda _2^2 = \frac{2k-a}{2 m {\varOmega }_0^2} i^2 , \quad \lambda _3^2 = \frac{2k-b}{2 m {\varOmega }_0^2} i^2 \end{aligned}$$
(36)
$$\begin{aligned} v_1= & {} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} , v_2 = \begin{bmatrix} -2 \\ +2 \\ a \end{bmatrix} , v_3 = \begin{bmatrix} -2 \\ +2 \\ b \end{bmatrix}, \end{aligned}$$
(37)

where constants a and b are a function of system parameters m and k, and i represents the imaginary unit, satisfying \( i^2 = -1 \).

$$\begin{aligned}&a = -(m-k+2) + \sqrt{ { (m+k+2)^2 - 4 k m }} \end{aligned}$$
(38)
$$\begin{aligned}&b = -(m-k+2) - \sqrt{ { (m+k+2)^2 - 4 k m }} , \end{aligned}$$
(39)

and the following relationship holds between a and b.

$$\begin{aligned} a b = - 8 k. \end{aligned}$$
(40)

The eigenvectors of Eq. (32) are linearly independent, but the second and third eigenvectors are not orthogonal, which causes the lateral–torsional vibration coupling of the system. As shown below, in the special case of \( k = 1 \), the second and third eigenvectors are orthogonal and there is no coupling; however, in this work, the general form of Eq. (32) is solved for every value of k.

$$\begin{aligned} v_1 . v_2 = 0, \, v_1 . v_3 = 0, \, v_2 . v_3 = 8(1-k). \end{aligned}$$
(41)

For positive values of k and m, the following condition is always satisfied.

$$\begin{aligned} (m+k+2)^2 - 4 k m > 0. \end{aligned}$$
(42)

Therefore, the values of a and b and all the eigenvectors are real. Besides, the following terms are real and positive for any value of k and m.

$$\begin{aligned} \begin{aligned}&2k - a = (m+k+2) - \sqrt{ { (m+k+2)^2 - 4 k m }} \\&2k - b = (m+k+2) + \sqrt{ { (m+k+2)^2 - 4 k m }}. \end{aligned}\nonumber \\ \end{aligned}$$
(43)

Therefore, the three eigenvalues expressed by Eq. (36) are always complex, and for any value of the parameters, Eq. (32) has the following three natural frequencies.

$$\begin{aligned} \omega _{n1}^2 = \frac{k}{m {\varOmega }_0^2} , \quad \omega _{n2}^2 = \frac{2k-a}{2 m {\varOmega }_0^2} , \quad \omega _{n3}^2 = \frac{2k-b}{2 m {\varOmega }_0^2}, \end{aligned}$$
(44)

such that the following relationships holds between them.

$$\begin{aligned}&\omega _{n2}^2 \, \omega _{n3}^2 = \frac{k}{ m {\varOmega }_0^4} \end{aligned}$$
(45)
$$\begin{aligned}&\omega _{n1}^2 = {\varOmega }_0^2 \; \omega _{n2}^2 \, \omega _{n3}^2. \end{aligned}$$
(46)

By obtaining the eigenvalues and eigenvectors of Eq. (32), one can write the solution to this equation in the following form.

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} u_{0p} \\ u_{0g} \\ u_{0} \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \Big ( A_1 \cos ( \omega _{n1} \tau ) + A_2 \sin ( \omega _{n1} \tau ) \Big ) \\&\qquad \qquad \quad + \begin{bmatrix} -2 \\ +2 \\ a \end{bmatrix} \Big ( B_1 \cos ( \omega _{n2} \tau ) + B_2 \sin ( \omega _{n2} \tau ) \Big ) \\&\qquad \qquad \quad + \begin{bmatrix} -2 \\ +2 \\ b \end{bmatrix} \Big ( C_1 \cos ( \omega _{n3} \tau ) + C_2 \sin ( \omega _{n3} \tau ) \Big ). \\ \end{aligned}\nonumber \\ \end{aligned}$$
(47)

Substituting Eq. (47) in Eq. (33) results in the following equation.

$$\begin{aligned} \begin{aligned}&{\varOmega }_0^2 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p}^{\prime \prime } \\ u_{1g}^{\prime \prime } \\ u_{1}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix} \\&\quad = + \begin{bmatrix} + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 + 3 \alpha Y^2 B_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 + 3 \alpha Z^2 C_1 \\ + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 - 3 \alpha Y^2 B_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 - 3 \alpha Z^2 C_1 \\ 0 &{} + 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_1 &{} + 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_1 \end{bmatrix} \begin{bmatrix} \cos ( \omega _{n1} \tau ) \\ \cos ( \omega _{n2} \tau ) \\ \cos ( \omega _{n3} \tau ) \end{bmatrix} \\&\qquad - \begin{bmatrix} - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 - 3 \alpha Y^2 B_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 - 3 \alpha Z^2 C_2 \\ - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 + 3 \alpha Y^2 B_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 + 3 \alpha Z^2 C_2 \\ 0 &{} - 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_2 &{} - 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_2 \end{bmatrix} \begin{bmatrix} \sin ( \omega _{n1} \tau ) \\ \sin ( \omega _{n2} \tau ) \\ \sin ( \omega _{n3} \tau ) \end{bmatrix} \\&\qquad + \begin{bmatrix} -1 \\ + 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} - 1 ) \tau + B_2 \sin ( \omega _{n2} - 1 ) \tau \Big ) + \begin{bmatrix} -1 \\ + 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} + 1 ) \tau + B_2 \sin ( \omega _{n2} + 1 ) \tau \Big ) \\&\qquad + \begin{bmatrix} -1 \\ + 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} - 1 ) \tau + C_2 \sin ( \omega _{n3} - 1 ) \tau \Big ) + \begin{bmatrix} -1 \\ + 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} + 1 ) \tau + C_2 \sin ( \omega _{n3} + 1 ) \tau \Big ) \\&\qquad + (\text {some} \; \text {other} \; \text {nonresonant} \; \text {terms}). \end{aligned} \end{aligned}$$
(48)

Equation (48) contains harmonic functions with frequencies equal to

$$\begin{aligned} \omega _{n1} , \omega _{n2} , \omega _{n3} , \omega _{n2} \pm 1 , \omega _{n3} \pm 1, ... \end{aligned}$$
(49)

and parameters X, Y and Z are defined as follows.

$$\begin{aligned} \begin{aligned}&X^2 = (A_1^2 + A_2^2) + 8 (B_1^2 + B_2^2) + 8 (C_1^2 + C_2^2), \\&Y^2 = (A_1^2 + A_2^2) + 2 (B_1^2 + B_2^2) + 4 (C_1^2 + C_2^2), \\&Z^2 = (A_1^2 + A_2^2) + 4 (B_1^2 + B_2^2) + 2 (C_1^2 + C_2^2). \end{aligned} \end{aligned}$$
(50)

3.1 Primary parametric resonance caused by second natural frequency

In general, all harmonic terms with frequencies equal to the three natural frequencies in Eq. (48) are secular and must be removed. But in the following special case of the second natural frequency, more terms become secular [25].

$$\begin{aligned} \omega _{n2} - 1 = -\omega _{n2} \rightarrow \omega _{n2} = \frac{1}{2}. \end{aligned}$$
(51)

Imposing this condition upon Eq. (44) provides the emanating frequency of the first tongue related the second natural frequency.

$$\begin{aligned} {\varOmega }_0^2 = \frac{2 (2 k - a)}{m}. \end{aligned}$$
(52)

Inserting Eq. (52) into Eqs. (45) and (46) provides the other two natural frequencies.

$$\begin{aligned} \omega _{n1}^2 = \frac{k}{2 (2 k - a)}, \; \omega _{n2}^2 = \frac{1}{4}, \; \omega _{n3}^2 = \frac{km}{ (2 k - a)^2}.\nonumber \\ \end{aligned}$$
(53)

By substituting Eq. (53) in Eq. (48), the following matrix form of the secular terms is obtained.

$$\begin{aligned}&\begin{bmatrix} + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 + 3 \alpha Y^2 B_1 - \frac{a}{2} B_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 + 3 \alpha Z^2 C_1 \\ + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 - 3 \alpha Y^2 B_1 + \frac{a}{2} B_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 - 3 \alpha Z^2 C_1 \\ 0 &{} + 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_1 - \frac{a}{2} B_1 &{} + 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_1 \end{bmatrix}\end{aligned}$$
(54)
$$\begin{aligned}&\begin{bmatrix} - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 - 3 \alpha Y^2 B_2 - \frac{a}{2} B_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 - 3 \alpha Z^2 C_2 \\ - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 + 3 \alpha Y^2 B_2 + \frac{a}{2} B_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 + 3 \alpha Z^2 C_2 \\ 0 &{} - 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_2 - \frac{a}{2} B_2 &{} - 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_2 \end{bmatrix}. \end{aligned}$$
(55)

Imposing the zero determinant condition to these two matrices, where \( \alpha = 0 \), provides the two first-order multipliers of Eq. (31) for the transition curves of the unstable tongue. The negative and positive signs are related to sine and cosine multipliers associated to the left and right transition curves, respectively [2].

$$\begin{aligned} {\varOmega }_1 =\pm \frac{a(b+2m+4)}{2m{\varOmega }_0(a-b)}. \end{aligned}$$
(56)

The newborn nontrivial equilibria exist if and only if the first, second, or third column of both Eqs. (54) and (55) is in the column space of Eq. (35). For the column vector \( [a_{1j} \, a_{2j} \, a_{3j}]' \) where \( j = 1,2, \) or 3 Cramer’s rule can be used to determine the solvability condition as follows (page 399 of [25]).

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} a_{1j} &{} 0 &{} +1\\ a_{2j} &{} m {\varOmega }_0^2 \lambda ^2 + k &{} -1 \\ a_{3j} &{} +{\varOmega }_0^2 \lambda ^2 &{} -{\varOmega }_0^2 \lambda ^2+1 \end{bmatrix} = 0, \\&\begin{bmatrix} m {\varOmega }_0^2 \lambda ^2 + k &{} a_{1j} &{} +1\\ 0 &{} a_{2j} &{} -1 \\ -{\varOmega }_0^2 \lambda ^2 &{} a_{3j} &{} -{\varOmega }_0^2 \lambda ^2+1 \end{bmatrix} = 0, \\&\begin{bmatrix} m {\varOmega }_0^2 \lambda ^2 + k &{} 0 &{} a_{1j}\\ 0 &{} m {\varOmega }_0^2 \lambda ^2 + k &{} a_{2j} \\ -{\varOmega }_0^2 \lambda ^2 &{} +{\varOmega }_0^2 \lambda ^2 &{} a_{3j} \end{bmatrix} = 0. \end{aligned} \end{aligned}$$
(57)

For the special case expressed by Eq. (51), only the second column in both Eqs. (54) and (55) is in the column space of Eq. (35) and satisfies Eq. (57), for non-trivial \( B_1 \) and \( B_2 \), which results in two equations. These two equations can be written in the following simplified form by using the relationship between parameters a and b and the second natural frequency.

$$\begin{aligned}&\Big ( + 6 \alpha (B_1^2+B_2^2) - \frac{a(a-b)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \Big ) B_2 = 0 \end{aligned}$$
(58)
$$\begin{aligned}&\Big ( - 6 \alpha (B_1^2+B_2^2) + \frac{a(a-b)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \Big ) B_1 = 0. \end{aligned}$$
(59)

By defining the polar coordinates, \( B_1 = R_B \cos \theta _B \) and \( B_2 = R_B \sin \theta _B \), the alternate polar form of Eqs. (58) and (59) is obtained.

$$\begin{aligned}&\Big ( + 6 \alpha R_B^2 - \frac{a(a-b)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \Big ) R_B \sin \theta _B = 0 \end{aligned}$$
(60)
$$\begin{aligned}&\Big ( - 6 \alpha R_B^2 + \frac{a(a-b)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \Big ) R_B \cos \theta _B = 0. \end{aligned}$$
(61)

Solving Eqs. (60) and (61) results in the following five equilibrium points.

$$\begin{aligned}&R_{B1} = 0 \end{aligned}$$
(62)
$$\begin{aligned}&R^2_{B2,3} = \frac{a(a-b)}{12 \alpha {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \Big ) \theta _B = \frac{\pi }{2} , \frac{3 \pi }{2} \end{aligned}$$
(63)
$$\begin{aligned}&R^2_{B4,5} = \frac{a(a-b)}{12 \alpha {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \Big ) \theta _B = 0 , \pi , \end{aligned}$$
(64)

such that \( R_{1} \) corresponds to the trivial equilibria at origin, and each of \( R_{2,3} \) and \( R_{4,5} \) corresponds to two nontrivial equilibria located \( \pi \, (rad) \) apart from each other. The local stability of these equilibrium points is determined by the eigenvalues of the Jacobian matrix corresponding to Eqs. (58) and (59) [1, 24].

$$\begin{aligned} J = \begin{bmatrix} + 12 \alpha B_1 B_2 &{} + 6 \alpha (B_1^2+3B_2^2) - \frac{a(a-b)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \\ - 6 \alpha (3B_1^2+B_2^2) + \frac{a(a-b)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) &{} - 12 \alpha B_1 B_2 \end{bmatrix}. \end{aligned}$$
(65)

Alternatively, for a \( 2 \times 2 \) matrix the Trace (Tr) and Determinant (Det) of the Jacobian matrix can be used to form the characteristic equation.

$$\begin{aligned} \lambda ^2 - Tr(J) \lambda + Det(J) = 0. \end{aligned}$$
(66)

The Tr of Eq. (65) is equal to zero, and the value of the Det is expressed by the following equation.

$$\begin{aligned} \begin{aligned} Det&= 108 \alpha ^2 (B_1^2+B_2^2)^2 \\&\quad - 6 \alpha \frac{a(a-b)}{2 {\varOmega }_0 } \Big ( 4 {\varOmega }_1 (B_1^2+B_2^2) \\&\quad + \frac{a(b+2m+4)}{m {\varOmega }_0 (a-b) } (B_1^2-B_2^2) \Big ) \\&\quad + \frac{a^2(a-b)^2}{4 {\varOmega }_0^2 } \Big ( {\varOmega }_1^2 - \frac{a^2(b+2m+4)^2}{4m^2 {\varOmega }_0^2 (a-b)^2 } \Big ). \end{aligned} \end{aligned}$$
(67)

Since the value of Tr is equal to zero for every \( {\varOmega }_1 \), the eigenvalues of the Jacobian matrix have the same magnitude with opposite signs. So for the positive values of the Det, both eigenvalues are on the imaginary axis and the equilibria is stable (center); and for the negative values of the Det, both eigenvalues are on the real axis and the equilibria is unstable (saddle). Recall that a pitchfork bifurcation generically occurs when the Det of the Jacobean matrix become zero [31]. Transforming Eq. (67) into the polar coordinate and substituting Eqs. (62)–(64) in it yields the following expression for Det at the equilibrium points.

$$\begin{aligned}&\text {At} \, R_{B1} , \, Det = + \frac{a^2(a-b)^2}{4 {\varOmega }_0^2 } \Big ( {\varOmega }_1^2 - \frac{a^2(b+2m+4)^2}{4m^2 {\varOmega }_0^2 (a-b)^2 } \Big ) \end{aligned}$$
(68)
$$\begin{aligned}&\text {At} \, R_{B2,3} , \, Det = + \frac{a^3(b+2m+4)(a-b)}{2m {\varOmega }_0^3} \nonumber \\&\qquad \Big ( {\varOmega }_1+ \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ) \end{aligned}$$
(69)
$$\begin{aligned}&\text {At} \, R_{B4,5} , \, Det = - \frac{a^3(b+2m+4)(a-b)}{2m {\varOmega }_0^3} \nonumber \\&\qquad \Big ( {\varOmega }_1- \frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \Big ). \end{aligned}$$
(70)

The Det of the Jacobian matrix at the equilibrium points, expressed by Eqs. (68)–(70), for different values of \( {\varOmega }_1 \) are demonstrated in Fig. 2.

Fig. 2
figure 2

Det of the Jacobian matrix at the equilibrium points around the resonance tongue. The black stars mark the occurrence of pitchfork bifurcations, and the value of \( {\varOmega }_L \) and \( {\varOmega }_R \) is associated with the value of \( {\varOmega }_1 \) on the transition curves obtained in Eq. (56)

Full size image

Additionally, Eqs. (63) and (64) provide the square value of the equilibrium points which impose a condition on the value of \( {\varOmega }_1 \). Therefore, existence of the real equilibria requires that for the case of hardening cubic nonlinearity \( (\alpha > 0) \)

$$\begin{aligned}&R_{B1} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 \end{aligned}$$
(71)
$$\begin{aligned}&R_{B2,3} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 > -\frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \end{aligned}$$
(72)
$$\begin{aligned}&R_{B4,5} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 > +\frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } , \end{aligned}$$
(73)

and for the case of softening cubic nonlinearity \( (\alpha < 0) \)

$$\begin{aligned}&R_{B1} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 \end{aligned}$$
(74)
$$\begin{aligned}&R_{B2,3} \quad \text {Exist} \quad \forall \quad {\varOmega }_1< -\frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } \end{aligned}$$
(75)
$$\begin{aligned}&R_{B4,5} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 < +\frac{a(b+2m+4)}{2m {\varOmega }_0 (a-b) } . \end{aligned}$$
(76)

The corresponding bifurcation diagram for the hardening and softening cases is plotted in Fig. 3.

Fig. 3
figure 3

Supercritical and subcritical pitchfork bifurcations around the resonance tongue due to the second natural frequency are marked by green and yellow stars, respectively

Full size image

This analysis shows that for both hardening and softening nonlinearities, as one crosses the transition curves (for the constant value of \( \epsilon \)) subcritical and supercritical pitchfork bifurcations (birth of new equilibria) occur. As illustrated in Fig. 3, for the hardening nonlinearity Eqs. (71)–(73) requires that the origin is the only equilibria at the left-hand side of the unstable tongue. Additionally, Fig. 2 shows that by quasi-statically increasing the value of \( {\varOmega }_1 \) and approaching the left transition curve, Det of Jacobian matrix at \( R_{B1} \) and \( R_{B2,3} \) merge to zero. By crossing the left transition curve Det of the Jacobian matrix at \( R_{B1} \) and \( R_{B2,3} \) cross \( {\varOmega }_1 \) axis and a supercritical pitchfork bifurcation occurs, so the equilibria at the origin becomes unstable (saddle) and two new stable equilibria (centers) are born. Figure 2 shows that as \( {\varOmega }_1 \) increases more and crosses the right transition curve, Det of Jacobian matrix at \( R_{B1} \) and \( R_{B4,5} \) cross the \( {\varOmega }_1 \) axis and a subcritical pitchfork bifurcation occurs where the origin become stable (center) again and two new unstable equilibria (saddles) are born. Figure 3 shows that the same sequence of events happens in the case of softening nonlinearity.

The only difference is that Eqs. (74)–(76) require that origin is the only equilibria on the right-hand side of the unstable tongue and by quasi-statically decreasing \( {\varOmega }_1 \) and approaching the right transition curve, Det of \( R_{B1} \) and \( R_{B4,5} \) merge to zero and cause a supercritical pitchfork bifurcation. Greater decreases in the value of \( {\varOmega }_1 \) cause a subcritical pitchfork bifurcation where the left transition curve is crossed and Det of \( R_{B1} \) and \( R_{B2,3} \) approach zero and cross the \( {\varOmega }_1 \) axis.

3.2 Primary parametric resonance caused by third natural frequency

Alternatively, in the following special case of the third natural frequency, other terms in Eq. (48) become secular.

$$\begin{aligned} \omega _{n3} - 1 = - \omega _{n3} \rightarrow \omega _{n3} = \frac{1}{2}. \end{aligned}$$
(77)

Imposing this condition upon Eq. (44) provides the emanating frequency of the unstable tongue related the third natural frequency.

$$\begin{aligned} {\varOmega }_0^2 = \frac{2 (2 k - b)}{m}. \end{aligned}$$
(78)

Inserting Eq. (78) into Eqs. (45) and (46) provides the other two natural frequencies.

$$\begin{aligned} \omega _{n1}^2 = \frac{k}{2 (2 k - b)}, \; \omega _{n2}^2 = \frac{km}{ (2 k - b)^2 }, \; \omega _{n3}^2 = \frac{1}{4}.\nonumber \\ \end{aligned}$$
(79)

By substituting Eq. (79) in Eq. (48), the following matrix form of the secular terms is obtained.

$$\begin{aligned}&\begin{bmatrix} + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 + 3 \alpha Y^2 B_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 + 3 \alpha Z^2 C_1 - \frac{b}{2} C_1 \\ + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 - 3 \alpha Y^2 B_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 - 3 \alpha Z^2 C_1 + \frac{b}{2} C_1 \\ 0 &{} + 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_1 &{} + 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_1 - \frac{b}{2} C_1 \end{bmatrix}\end{aligned}$$
(80)
$$\begin{aligned}&\begin{bmatrix} - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 - 3 \alpha Y^2 B_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 - 3 \alpha Z^2 C_2 - \frac{b}{2} C_2 \\ - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 + 3 \alpha Y^2 B_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 + 3 \alpha Z^2 C_2 + \frac{b}{2} C_2 \\ 0 &{} - 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_2 &{} - 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_2 - \frac{b}{2} C_2 \end{bmatrix}. \end{aligned}$$
(81)

Similarly, imposing the zero determinant condition to Eqs, (80) and (81), where \( \alpha = 0 \), provides the two first-order multipliers of Eq. (31) for the transition curves of the unstable tongue. The negative and positive signs are related to sine and cosine multipliers associated to the left and right transition curves, respectively [2].

$$\begin{aligned} {\varOmega }_1 = \pm \frac{b(a+2m+4)}{2m{\varOmega }_0(b-a)}. \end{aligned}$$
(82)
Fig. 4
figure 4

Det of the Jacobian matrix at the equilibrium points around the resonance tongue. The black stars mark the occurrence of pitchfork bifurcations, and the value of \( {\varOmega }_L \) and \( {\varOmega }_R \) is associated with the value of \( {\varOmega }_1 \) on the transition curves obtained in Eq. (82)

Full size image
Fig. 5
figure 5

Supercritical and subcritical pitchfork bifurcations around the resonance tongue due to the third natural frequency, marked by green and yellow stars, respectively

Full size image

For the special case expressed by Eq. (77), only the third columns in Eqs. (80) and (81) are in the column space of Eq. (35) and satisfy Eq. (57) for non-trivial \( C_1 \) and \( C_2 \), which results in two equations. These two equations can be simplified as follows by using the relationship between parameters a, b and the third natural frequency.

$$\begin{aligned}&\Big ( + 6 \alpha (C_1^2+C_2^2) - \frac{b(b-a)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \Big ) C_2 = 0 \nonumber \\\end{aligned}$$
(83)
$$\begin{aligned}&\Big ( - 6 \alpha (C_1^2+C_2^2) + \frac{b(b-a)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \Big ) C_1 = 0. \nonumber \\ \end{aligned}$$
(84)

By defining the polar coordinates, \( C_1 = R_C \cos \theta _C \) and \( C_2 = R_C \sin \theta _C \), the alternate polar form of Eqs. (83) and (84) is obtained.

$$\begin{aligned}&\Big ( + 6 \alpha R_C^2 - \frac{b(b-a)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \Big ) R_C \sin \theta _C = 0 \end{aligned}$$
(85)
$$\begin{aligned}&\Big ( - 6 \alpha R_C^2 + \frac{b(b-a)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \Big ) R_C \cos \theta _C = 0. \end{aligned}$$
(86)

Solving Eqs. (85) and (86) results in the following five equilibrium points.

$$\begin{aligned}&R_{C1} = 0 \end{aligned}$$
(87)
$$\begin{aligned}&R^2_{C2,3} = \frac{b(b-a)}{12 \alpha {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \Big ) \quad \theta _C = \frac{\pi }{2} , \frac{3 \pi }{2} \end{aligned}$$
(88)
$$\begin{aligned}&R^2_{C4,5} = \frac{b(b-a)}{12 \alpha {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \Big ) \quad \theta _C = 0 , \pi , \end{aligned}$$
(89)

such that \( R_{C1} \) corresponds to the trivial equilibria at origin, and each of \( R_{C2,3} \) and \( R_{C4,5} \) corresponds to two nontrivial equilibria located \( \pi \, (rad) \) apart from each other. The local stability of these equilibrium points is determined by the eigenvalues of the Jacobian matrix corresponding to Eqs. (83) and (84) [1, 24].

$$\begin{aligned} J = \begin{bmatrix} + 12 \alpha C_1 C_2 &{} + 6 \alpha (C_1^2+3C_2^2) - \frac{b(b-a)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 - \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \\ - 6 \alpha (3C_1^2+C_2^2) + \frac{b(b-a)}{2 {\varOmega }_0} \Big ( {\varOmega }_1 + \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) &{} - 12 \alpha C_1 C_2 \end{bmatrix}. \end{aligned}$$
(90)

The Tr of Eq. (90) is equal to zero and the value of the Det is expressed by the following equation.

$$\begin{aligned} \begin{aligned}&Det = 108 \alpha ^2 (C_1^2+C_2^2)^2 \\&\quad - 6 \alpha \frac{b(b-a)}{2 {\varOmega }_0 } \Big ( 4 {\varOmega }_1 (C_1^2+C_2^2) \\&\quad - \frac{b(a+2m+4)}{m {\varOmega }_0 (b-a) } (C_1^2-C_2^2) \Big ) \\&\quad + \frac{b^2(b-a)^2}{4 {\varOmega }_0^2 } \Big ( {\varOmega }_1^2 - \frac{b^2(a+2m+4)^2}{4m^2 {\varOmega }_0^2 (b-a)^2 } \Big ). \end{aligned} \end{aligned}$$
(91)

Transforming Eq. (91) into the polar coordinate and substituting Eqs. (87)–(89) yields the following expression for Det at the equilibrium points.

$$\begin{aligned}&\text {At} \, R_{C1} , \, Det = + \frac{b^2(b-a)^2}{4 {\varOmega }_0^2 } \Big ( {\varOmega }_1^2 - \frac{b^2(a+2m+4)^2}{4m^2 {\varOmega }_0^2 (b-a)^2 } \Big ) \end{aligned}$$
(92)
$$\begin{aligned}&\text {At} \, R_{C2,3} , \, Det \nonumber \\&\quad = + \frac{b^3(a+2m+4)(b-a)}{2m {\varOmega }_0^3} \Big ( {\varOmega }_1 + \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ) \end{aligned}$$
(93)
$$\begin{aligned}&\text {At} \, R_{C4,5} , \, Det \nonumber \\&\quad = - \frac{b^3(a+2m+4)(b-a)}{2m {\varOmega }_0^3} \Big ( {\varOmega }_1 - \frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \Big ). \end{aligned}$$
(94)

The Det of the Jacobian matrix at equilibrium points for different values of \( {\varOmega }_1 \), expressed by Eqs. (92)–(94), are demonstrated in Fig. 4.

Fig. 6
figure 6

Eigenvalues of the Jacobian matrix at the origin around the combination parametric resonance tongue, expressed by Eq. (111). The black stars mark the occurrence of hopf bifurcations

Full size image
Fig. 7
figure 7

Supercritical and subcritical hopf bifurcations around the resonance tongue due to the summation of the second and third natural frequencies, marked by green and yellow stars, respectively

Full size image

Eqs. (88) and (89) provide the square value of the equilibrium points, imposing a condition on the value of \( {\varOmega }_1 \). In the case of hardening cubic nonlinearity \( (\alpha > 0) \), the existence of the real equilibria requires that

$$\begin{aligned}&R_{C1} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 \end{aligned}$$
(95)
$$\begin{aligned}&R_{C2,3} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 > -\frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \end{aligned}$$
(96)
$$\begin{aligned}&R_{C4,5} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 > +\frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) }, \end{aligned}$$
(97)

and for the case of softening cubic nonlinearity \( (\alpha < 0) \)

$$\begin{aligned}&R_{C1}\quad \text {Exist} \quad \forall \quad {\varOmega }_1 \end{aligned}$$
(98)
$$\begin{aligned}&R_{C2,3} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 < -\frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) } \end{aligned}$$
(99)
$$\begin{aligned}&R_{C4,5} \quad \text {Exist} \quad \forall \quad {\varOmega }_1 < +\frac{b(a+2m+4)}{2m {\varOmega }_0 (b-a) }. \end{aligned}$$
(100)

The corresponding bifurcation diagram for the hardening and softening cases is plotted in Fig. 5.

This analysis show that, as one crosses the transition curves of the unstable tongue (for the constant value of \( \epsilon \)), supercritical and subcritical pitchfork bifurcation occurs. For hardening nonlinearity, the origin is the only equilibria at the left-hand side of the unstable tongue, and by quasi-statically increasing the value of the \( {\varOmega }_1 \), Det of the Jacobian matrix at \( R_{C1} \) and \( R_{C2,3} \) cross the \( {\varOmega }_1 \) axis and results in a supercritical pitchfork bifurcation. As \( {\varOmega }_1 \) increases more, a subcritical pitchfork bifurcation occurs when Det of the Jacobian matrix at \( R_{C1} \) and \( R_{C4,5} \) cross the \( {\varOmega }_1 \) axis. Similarly, for the softening nonlinearity, the origin is the only equilibria at the right-hand side of the unstable tongue and by quasi-statically decreasing \( {\varOmega }_1 \), Det of \( R_{C1} \) and \( R_{C4,5} \) cross the \( {\varOmega }_1 \) axis and causes a supercritical pitchfork bifurcation. A subcritical pitchfork bifurcation occurs when Det of the Jacobian matrix at \( R_{C1} \) and \( R_{C2,3} \) cross the \( {\varOmega }_1 \) axis.

3.3 Combination parametric resonance of the summation type caused by second and third natural frequencies

In the following special case of the second and third natural frequencies, more terms in Eq. (48) become secular.

$$\begin{aligned} \begin{aligned}&\omega _{n2} - 1 = -\omega _{n3} \rightarrow \omega _{n2} + \omega _{n3} = 1 \\&\omega _{n3} - 1 = -\omega _{n2} \rightarrow \omega _{n2} + \omega _{n3} = 1. \end{aligned} \end{aligned}$$
(101)

Imposing this condition upon Eq. (44) results in the emanating frequency of the unstable tongue related to the combination parametric resonance.

$$\begin{aligned} {\varOmega }_0^2 = \frac{(m+k+2)}{m} + 2 \sqrt{ \frac{k}{m} }. \end{aligned}$$
(102)

By substituting Eq. (101) in Eq. (48), the following matrix form of the secular terms is obtained.

$$\begin{aligned}&\begin{bmatrix} + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 + 3 \alpha Y^2 B_1 - \frac{b}{2} C_1 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 + 3 \alpha Z^2 C_1 - \frac{a}{2} B_1\\ + 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_1 - \frac{3}{4} \alpha X^2 A_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_1 - 3 \alpha Y^2 B_1 + \frac{b}{2} C_1 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_1 - 3 \alpha Z^2 C_1 + \frac{a}{2} B_1 \\ 0 &{} + 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_1 - \frac{b}{2} C_1 &{} + 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_1 - \frac{a}{2} B_1 \end{bmatrix}\nonumber \\ \end{aligned}$$
(103)
$$\begin{aligned}&\begin{bmatrix} - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 - 3 \alpha Y^2 B_2 - \frac{b}{2} C_2 &{} + 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 - 3 \alpha Z^2 C_2 - \frac{a}{2} B_2 \\ - 2 m {\varOmega }_0 {\varOmega }_1 \omega _{n1}^2 A_2 + \frac{3}{4} \alpha X^2 A_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n2}^2 B_2 + 3 \alpha Y^2 B_2 + \frac{b}{2} C_2 &{} - 4 m {\varOmega }_0 {\varOmega }_1 \omega _{n3}^2 C_2 + 3 \alpha Z^2 C_2 + \frac{a}{2} B_2 \\ 0 &{} - 2 {\varOmega }_0 {\varOmega }_1 (a+4) \omega _{n2}^2 B_2 - \frac{b}{2} C_2 &{} - 2 {\varOmega }_0 {\varOmega }_1 (b+4) \omega _{n3}^2 C_2 - \frac{a}{2} B_2 \end{bmatrix}.\nonumber \\ \end{aligned}$$
(104)

Imposing the zero determinant condition to Eqs. (103) and (104), where \( \alpha = 0 \), results in two degenerate conics with a standard form of \( A x_1^2 + B x_1 x_2 + C x_2^2 = 0 \). Imposing the \( AB + 2AC + BC = 0 \) condition to these equations provides the two first-order multipliers of Eq. (31) for the transition curves of the unstable tongue. The negative and positive signs are related to sine and cosine multipliers associated to the left and right transition curves, respectively [2].

$$\begin{aligned} {\varOmega }_1 = \pm \frac{4k {\varOmega }_0}{(a-b)^2}. \end{aligned}$$
(105)
Fig. 8
figure 8

The effect of increasing the value of the parametric frequency on the eigenvalues of the Jacobian matrix at the origin, for the hardening nonlinearity

Full size image
Fig. 9
figure 9

Global bifurcation diagram for the hardening nonlinearity. The green and yellow stars mark the occurrence of supercritical and subcritical bifurcations, respectively

Full size image
Fig. 10
figure 10

Global bifurcation diagram for the softening nonlinearity. The green and yellow stars mark the occurrence of supercritical and subcritical bifurcations, respectively

Full size image

For the special case expressed by Eq. (101), none of the columns in Eqs. (103) and (104) are in the column space of Eq. (35), so no nontrivial equilibrium point is created in the combination parametric resonance tongue. But one can investigate the change of the stability of the origin by imposing Eq. (57) to the second and third columns of Eqs. (103) and (104), which results in four equations. These four equations can be simplified by using the relationship between parameters a, b and the second and third natural frequencies.

$$\begin{aligned}&\Big ( + 6 \alpha (B_1^2+B_2^2) + 12 \alpha (C_1^2+C_2^2) - \frac{a (a-b){\varOmega }_1}{2 {\varOmega }_0} \Big )B_2 \nonumber \\&\quad + k C_2 = 0 \end{aligned}$$
(106)
$$\begin{aligned}&\Big ( - 6 \alpha (B_1^2+B_2^2) - 12 \alpha (C_1^2+C_2^2) + \frac{a (a-b){\varOmega }_1}{2 {\varOmega }_0} \Big ) B_1 \nonumber \\&\quad + k C_1 = 0 \end{aligned}$$
(107)
$$\begin{aligned}&\Big ( + 12 \alpha (B_1^2+B_2^2) + 6 \alpha (C_1^2+C_2^2) + \frac{b (a-b){\varOmega }_1}{2 {\varOmega }_0} \Big )C_2 \nonumber \\&\quad + k B_2 = 0 \end{aligned}$$
(108)
$$\begin{aligned}&\Big ( - 12 \alpha (B_1^2+B_2^2) - 6 \alpha (C_1^2+C_2^2) - \frac{b (a-b){\varOmega }_1}{2 {\varOmega }_0} \Big )C_1 \nonumber \\&\quad + k B_1 = 0. \end{aligned}$$
(109)

The local stability of the origin is determined by the eigenvalues of the Jacobian matrix, corresponding to Eqs. (106)–(109).

$$\begin{aligned} J = \begin{bmatrix} 0 &{} - \frac{a (a-b){\varOmega }_1}{2 {\varOmega }_0} &{} 0 &{} k \\ + \frac{a (a-b){\varOmega }_1}{2 {\varOmega }_0} &{} 0 &{} k &{} 0 \\ 0 &{} k &{} 0 &{} + \frac{b (a-b){\varOmega }_1}{2 {\varOmega }_0} \\ k &{} 0 &{} - \frac{b (a-b){\varOmega }_1}{2 {\varOmega }_0} &{} 0 \end{bmatrix}.\nonumber \\ \end{aligned}$$
(110)

The four eigenvalues of Eq. (110) are obtained by the following equation.

$$\begin{aligned} \lambda ^2 = \pm \frac{a-b}{2 {\varOmega }_0} \sqrt{ \Big ( \frac{4k^2{\varOmega }_0^2}{(a-b)^2} - \frac{(a^2-b^2)}{2} {\varOmega }_1^2 \Big ) \pm \sqrt{ \Big ( \frac{4k^2{\varOmega }_0^2}{(a-b)^2} - \frac{(a^2-b^2)}{2} {\varOmega }_1^2 \Big )^2 - \Big ( \frac{4k^2{\varOmega }_0^2}{(a-b)^2} + ab {\varOmega }_1^2 \Big )^2 } }. \end{aligned}$$
(111)

As long as the following condition is satisfied, all the four eigenvalues expressed by Eq. (111) are purely imaginary with no real part, making the origin a center.

$$\begin{aligned} \Big ( \frac{4k^2{\varOmega }_0^2}{(a-b)^2} - \frac{(a^2-b^2)}{2} {\varOmega }_1^2 \Big )^2 - \Big ( \frac{4k^2{\varOmega }_0^2}{(a-b)^2} + ab {\varOmega }_1^2 \Big )^2 > 0. \end{aligned}$$
(112)

But, in the following region, Eq. (112) is violated and the eigenvalues have both real and imaginary parts, in that two of the eigenvalues have negative real parts and two have positive real parts. In this condition, the origin is an unstable spiral [31].

$$\begin{aligned} - \frac{4k{\varOmega }_0}{(a-b)^2}< {\varOmega }_1 < + \frac{4k{\varOmega }_0}{(a-b)^2}. \end{aligned}$$
(113)

The value of the four eigenvalues expressed by Eq. (111) for different values of \( {\varOmega }_1 \) is demonstrated in Fig. 6.

The corresponding bifurcation diagrams for the hardening and softening cases around the combination parametric resonance are plotted in Fig. 7.

Fig. 11
figure 11

Poincaré map for the softening nonlinearity within the primary parametric resonance tongue, corresponding to the second natural frequencies. The red dots mark the saddle at the origin, and the blue trajectory shows the location of the stable nontrivial equilibria (nodes) around the origin

Full size image

This analysis shows that, as one crosses the transition curves of the unstable tongue (for the constant value of \( \epsilon \)), supercritical and subcritical hopf bifurcation occurs. For the hardening nonlinearity, by quasi-statically increasing the value of \( {\varOmega }_1 \), and crossing the left-hand side transition curve of the unstable tongue, a supercritical hopf bifurcation occurs and a limit cycle is created around the origin. By further quasi-statically increasing the value of the \( {\varOmega }_1 \), the radius of this limit cycle increases, until by crossing the right hand-side transition curve of the unstable tongue, a subcritical hopf bifurcation occurs and the limit cycle is destroyed. The same sequence of events happens for the softening nonlinearity, only by quasi-statically decreasing the value of the \( {\varOmega }_1 \).

3.4 Overall bifurcation diagram

Figure 8 demonstrates how the eigenvalues of the Jacobian matrix at the origin change for the hardening case, while the value of \( {\varOmega } \) is increased. Figure 8a shows that starting from the primary unstable tongue, corresponding to the second natural frequency, the origin is a saddle as the eigenvalues have real values with positive and negative signs. Figure 8a shows that by increasing the value of \( {\varOmega } \), both of these real eigenvalues approach the origin. By crossing the right-hand side transition curve, the real eigenvalues cross the origin and become purely complex; in this case the origin become a center. Figure 8a shows that by further increasing the value of \( {\varOmega } \), the eigenvalues move further from the origin. By increasing \( {\varOmega } \) and crossing the left transition curve of the combination unstable tongue, corresponding to the summation of second and third natural frequencies, the eigenvalues leave the imaginary axis. At this point, the eigenvalues have both real and imaginary parts; due to the eigenvalues having positive real parts, the origin is an unstable spiral. Figure 8a shows that by increasing the value of \( {\varOmega } \), the imaginary parts of the eigenvalues get smaller while the real parts get larger. When reaching the middle of the combination unstable tongue, where \( {\varOmega }_1 = 0 \), the imaginary parts of the eigenvalues get very close to zero, but as is shown in Fig. 8b, by passing the middle of the combination unstable tongue, the imaginary part of the eigenvalues start to increase again while the real parts get smaller. This continues until by passing the right transition curve of the combination unstable tongue; the eigenvalues become purely complex again which makes the origin a center. Finally, Fig 8b shows that, by more increase in the value of \( {\varOmega } \) and crossing the left transition curve of the primary unstable tongue, corresponding to the third natural frequency, the origin become a saddle again; due to the real eigenvalues with positive and negative signs.

Figures 9 and 10 demonstrate the global bifurcation diagram of the hardening and softening nonlinear cases, respectively.

Fig. 12
figure 12

Poincaré map for the softening nonlinearity within the combination parametric resonance tongue, corresponding to the summation of the second and third natural frequencies. The orange dots mark the unstable spiral at the origin, and the blue trajectories show the limit cycle around the origin

Full size image
Fig. 13
figure 13

Poincaré map for the softening nonlinearity within the primary parametric resonance tongue, corresponding to the third natural frequencies. The red dots mark the saddle at the origin, and the blue trajectory shows the location of the stable nontrivial equilibria (nodes) around the origin

Full size image
Fig. 14
figure 14

System’s time response in linear (a) and nonlinear (b) regimes for the same parametric frequency inside the primary unstable tongue, corresponding to the second natural frequency. The light red represents the dead zone area where the separation of the teeth occurs

Full size image

4 Numerical simulations

In this section, the foregoing analytical analysis is compared with the results obtained from numerical integration, completed in MATLAB by using Runge–Kutta of the fourth-fifth order.

4.1 Poincaré map

Figures 11, 12, and 13 exhibit the Poincaré map for the homogeneous form of Eq. (25) for the softening nonlinearity, all for the surface of section at \( t = \omega _p / 2 \pi \). Figure 11 belongs to the system’s parameters inside the primary unstable tongue corresponding to the second natural frequency, showing that the origin is a saddle and there are two stable nodes around it, \( \pi \, (rad) \) apart from each other. This plot show that by increasing the value of \( {\varOmega } \), the two stable nodes get closer to the origin, consistent with the analytical results demonstrated by Fig. 10. Figure 11 belongs to the system’s parameters inside the combination unstable tongue corresponding to summation of the second and third natural frequencies, showing that the origin is an unstable spiral surrounded by a limit cycle. These plots show that by increasing the value of \( {\varOmega } \), the size of the limit cycle decreases. Figure 11 belongs to the system’s parameters inside the primary unstable tongue corresponding to the third natural frequency, showing that the origin is a saddle and there are two stable nodes around it, \( \pi \, (rad) \) apart from each other. These plots show that by increasing the value of \( {\varOmega } \), the two stable nodes move closer to the origin, consistent with the analytical results demonstrated by Fig. 10.

4.2 Time response

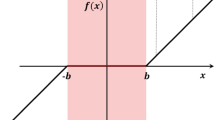
Figure 14 demonstrates the effect of softening nonlinear terms on the dynamic response of the non-homogeneous form of Eq. (25) inside the primary unstable tongue, corresponding to the second natural frequency. Comparing these two plots shows that, even inside the unstable tongues, by applying enough load on the system and choosing the right parameters for the suspension, the system response remains bounded and outside of the dead zone area, which is colored by light red. In this condition, the separation of the teeth in mesh and subsequent occurrence of the free play mode and impact phases can be avoided.

5 Conclusion

In this work, Poincaré–Lindstedt method is used to study the effect of nonlinear suspension on the dynamic behavior of geared systems, where the transmitting force is large enough for the gears in mesh to remain in permanent contact. Under this condition, the governing equations reduce to a system of nonlinear, parametrically excited coupled differential equations. In the absence of the nonlinear terms, the unbounded response of the system occurs only within the primary and combination parametric resonance tongues. The large amplitude oscillation results in the separation of the gears in mesh; subsequently the free play mode and impact phases should be considered in the dynamic response of the system. The analytical and numerical results in this paper show that, for the system with cubic nonlinear terms, and with the correct range of the parameters, the system’s response within the unstable tongues can remain bounded. Further results show that the bounded response of the system within the unstable tongues is due to the occurrence of the pitchfork bifurcation within the primary unstable tongues and hopf bifurcation within the combination unstable tongue. It is shown that the occurrence of the supercritical and subcritical pitchfork bifurcations follows the same pattern for both hardening and softening nonlinearity, only with a \( \pi /2 \, (rad) \) difference on the location of the newborn equilibria. The Poincaré map is presented only for the softening case, as the experimental data shows mostly softening nonlinear behaviors of the geared system. The Poincaré map confirms creation of both new equilibria within the primary unstable tongues and the limit cycle within the combination unstable tongue, which was predicted by Poincaré–Lindstedt method. It is demonstrated that by changing the parametric frequency the distance between the origin and nodes and also the radius of the limit cycle varies. Finally, the time response of the system for the parametric frequency inside the primary unstable tongue, corresponding to the second natural frequency, is provided. These plots show that small amplitude oscillation is possible even inside the unstable tongues by choosing the right parameters for the suspension, which prevent the separation of the gears in mesh.