Parametric stability of geared systems with linear suspension in permanent contact regime

Abstract

The prediction and control of excessive vibration are one of the most important concerns in the design and development of geared systems. For any gear set, parametric resonance is the main source of instability, resulting in the separation of gears in mesh and chaotic behavior. In many works, gears are modeled with rigid mountings, and various analytical and numerical approaches have been used to investigate the dynamic characteristics of the system in different regimes: permanent contact (no impact), free play, single-sided impact, and double-sided impact. Alternatively, in other works, the effect of the deformation of the mountings is included in the dynamic modeling; in almost all these studies, the dynamic characteristic of the system is investigated through direct numerical integration of the governing differential equations, and there is no analytical work to determine the effect of suspension on the parametric resonance of the system. Consequently, in this work, both analytical and numerical approaches, including the Poincare–Lindstedt method and Floquet theory, are used to investigate the dynamic characteristics of a one-stage spur gear pair with linear suspension in the permanent contact regime. It has been shown that, unlike systems with rigid mounting that have one set of unstable tongues, systems with suspension have three sets of unstable tongues. The results show that the additional sets of unstable tongues appear at higher parametric frequencies. Therefore, the rigid mounting assumption is accurate only for systems operating at low speeds; for systems operating at high speeds, the deformation of the suspension must be included in the dynamic modeling, as it significantly contributes to the parametric instability of the system.

1 Introduction

Gears are one of the most common mechanical parts widely used in rotary machinery and power transmission systems. Many researchers have investigated the dynamic characteristics of the geared systems under the influence of the internal excitation parameters like; time-varying stiffness and static transmission error, and external excitation like; fluctuation of the load and power, to design and develop optimal, silent, and reliable gear transmission systems. Originally, gears are designed to remain in permanent contact regime, where teeth in mesh do not separate while in motion, but due to the clearance between the teeth in mesh, for the lightly loaded operational condition [32] or bad range of the parameters [31], the teeth can separate. Consequently, alternating between permanent contact regime and free play mode while considering single- and double-sided impact has been one of the most intriguing topics in nonlinear dynamic analysis of the gears [32]. Under these conditions, gears in mesh can be considered as a non-smooth vibrio-impact system prone to chaotic behavior [11].

Many researchers have used the lumped parameter modeling technique to analyze gear pairs in mesh with the assumption that the mountings are rigid. In such a system, and with relatively large values of the forcing parameter, the permanent contact regime is achieved where the governing equations reduce to one linear parametrically time-varying differential equation [31], known as the Mathieu equation [13]. Consequently, parametric resonance has a dominant effect on the dynamic response of the gear pairs over the entire frequency range so that the large amplitude oscillation and separation of teeth occur in the vicinity of the resonance tongues [32]. Once tooth separation initiates, the permanent contact regime is no longer valid; the clearance between the teeth must be considered in the modeling, and the system will behave in a nonlinear fashion [1]. In general, the clearance between the teeth in mesh is expressed by a non-smooth piecewise linear function. Some researchers have used analytical methods such as the Multiple Time-Scales method [31] and the Harmonic Balance method [1] to develop a generalized solution for the gear platform, while permanent contact regime, Free play mode, single- and double-sided impact phases are carefully taken into consideration. This is while some others used a third-order polynomial [10], Fourier series [1], logarithmic function [19], or fractal law [5] to approximate the clearance between the teeth in mesh for ease of calculation. Consequently, the Melnikov method is used to predict [10] and control [28] the threshold values of the parameters for the occurrence of the homoclinic bifurcation and transition to chaotic behavior. The Incremental Harmonic Balance method is used to analyze and compare the frequency response of the system where single and multi-order harmonics are included [29]. Numerical integration is used to identify the chaotic behavior with reference to basins of attraction [21], bifurcation diagram, and maximum Lyapunov exponent [20]. The lumped parameter analysis is also used in fault simulation analysis by including gear profile error, [2] surface wear [9, 15], and fillet crack [12] in the dynamic modeling of the system. In some recent studies, the effect of the backlash size [37], applied force [3], and oil film [36] on the equivalent stiffness of gears in mesh are included to provide more enhanced dynamic models.

Alternatively, there are fewer papers that demonstrate the importance of including the defamation of the mountings in the lumped parameter modeling. In these studies, the effect of the operational speed [4] or the stiffness of the suspension [18] on the periodic, quasi-periodic and chaotic motions are studied with reference to the phase plane [35], bifurcation diagram [33], basins of attraction [18], and Lyapunov exponents [4]. The effect of known applied load rather than constant operational speed on system dynamic is studied with reference to the frequency response [30]. The effect of eccentricity on the nonlinear behavior of the system is studied with reference to the frequency spectrum [17] and bifurcation diagram [40]. The effect of damping coefficient, static transmission error, and external excitation on the jumping discontinuity is studied with reference to frequency response [39]. The effect of bearing clearance [14] and surface roughness [6] on the dynamic behavior of gears is studied with reference to phase diagram and Poincare map. The deformation of the suspension is also included in the fault simulation analysis, such that the effect of tooth crack [16, 22, 23] root crack [7], and wear [38] on the vibration response of the geared platforms is investigated. Finally, in some recent fault simulation studies even the lateral [7, 22, 38] and lateral–torsional [16] deformations of the mountings and the gyroscopic effect [23] are included in the dynamic modeling.

Even though these works provide insight into the effect of suspension on gear dynamics, there are still two missing components in the current studies. First, all the prior works use only direct numerical integration of the governing differential equations to plot the Poincare map, phase portray, bifurcation diagram, and other numeric-based approaches to investigate the dynamic characteristics of the gear sets. However, there is no research that uses an analytical approach to provide an in-depth understanding of the effect of suspension on the dynamic response of gears. Secondly, all prior works investigate the effect of the suspension along with the nonlinearity caused by the backlash, where the separation of teeth in mesh plays an important role in the nonlinear behavior of the system [26]. No works have investigated the dynamic behavior of the geared systems under constant speed and heavy-load operational conditions, where the governing equations of the system become linear [31] and the parametric resonance is the main source of instability and separation of teeth in mesh [32].

Consequently, in this paper, the Poincare–Lindstedt method and Floquet theory are used to study the dynamics of geared system with linear suspension, assuming that the gears in mesh remain in permanent contact regime, a condition that can be acceptable under constant speed and high load operational condition [8]. In such conditions, the governing differential equations of the system reduce into a linear periodically time-varying system of coupled equations. Then the effect of deformation of the mountings on the number and location of the unstable tongues is investigated which is clearly excluded in previous studies. Identification of parametric resonance is an important task in geared systems as it causes an increase in the amplitude of the oscillation and separation of the teeth in mesh, where the nonlinear effect of the clearance between the gears in mesh must be considered.

This paper is organized by sections: Sect. 2 describes the tribological characteristics of the gears in mesh. Section 3 formulates the dynamic equations of the spur gear pair in mesh with linear suspension. Section 4 utilizes the Poincare–Lindstedt method to analyze the stability of the perturbed system while the damping and external forcing terms are dropped out. Section 5 use Floquet theory to compute and characterize the dynamic behavior of the system for different parametric frequencies. Section 6 compares the numerical results with the analytical results obtained in the previous sections. And final remarks are presented in the conclusion.

2 Tribological characteristics

The tribological characteristics of the gears in mesh greatly influence the dynamic behavior and vibrations of geared systems, including the time-varying meshing stiffness, static transmission error and backlash. In this section, more detail is provided on the nature and the mathematical expressions of these characteristics.

2.1 Time-varying gear mesh stiffness

The concept of equivalent tooth mesh stiffness is helpful in the lumped mass modeling of the gears [14]. Under the assumption of constant velocity operational conditions, the gear stiffness coefficient can be described as a periodic function of time with fundamental frequency equal to the meshing frequency.

$$\begin{aligned} k(t) = K \Big ( 1+k_0 \cos (\omega t) \Big ) , \quad k_0 = \frac{k}{K} \end{aligned}$$

(1)

where K is the average value of the equivalent stiffness, k is the amplitude of the oscillation about K, and $\omega$ is the meshing frequency. The harmonic term in Eq. (1) is the most important source of internal excitation in geared systems such that an increase or decrease in the value of $k_0$ directly affects the amplitude of the vibration [6].

2.2 Static transmission error

Static transmission error, or meshing error, is an important source of noise in gear systems, defined as the difference between the actual and the ideal positions of the driven gear along the pressure line. This is mainly due to geometrical manufacturing errors from perfect involute form and teeth deformations during the operation [25]. Since the mean angular velocities of the gears are constant, the static transmission error can be approximated by a periodic function.

$$\begin{aligned} e(t) = E \cos (\omega t) \end{aligned}$$

(2)

where E is the comprehensive error amplitude and the fundamental frequency $\omega$ is the meshing frequency [10].

2.3 Backlash function

Backlash, looseness, or play is usually used to represent the gear clearances, which is the gap between the gear pair along the circumference. This can be due to manufacturing error, wear of the tooth surface, or mounting error. Theoretically, a gear pair with zero backlash is ideal, but in practice some backlash is necessary in order to avoid the jamming phenomenon, reduction of interference and to provide some space for ease of assembly, better lubrication, elastic deflection under the load, and thermal expansion. Typically, backlash is achieved by reducing the tooth thickness in the manufacturing process or by increasing the distance of the center of the mountings. In different works, the backlash width is approximated either by a constant value, time-varying function, normal distribution or fractal expression [14]. Here, a constant value (b) is incorporated to model the gear tooth backlash width. In any case, the gear backlash function is usually represented by a non-smooth piecewise linear, non-differentiable and symmetric function, which is the main source of nonlinearity in the geared system, defined by the following equation.

$$\begin{aligned} f(x) = {\left\{ \begin{array}{ll} x-b &{} \quad +b< x \\ 0 &{}\quad -b \le x \le +b \\ x+b &{} \quad x < -b \end{array}\right. } \end{aligned}$$

(3)

where x is the dynamic transmission error, 2b is the total non-dimensional backlash width, and b is known as half backlash. Figure 1 shows that if enough load transmits through the geared system, the minimum value of x remains greater than b and the system operates in permanent contact condition, where the effect of backlash does not participate in the dynamic response of the system [31].

Fig. 1

Backlash function

3 Generalized model of spur gear pairs in mesh

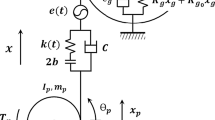
In this section, the lumped parameter technique is used to formulate the dynamic model of a single-stage spur gear in mesh with linear suspension. As illustrated in Fig. 2, the gears in mesh are modeled as a pair of rigid disks with radiuses equal to the base circles connected by a spring–damper set along the line of the action and the transmission shafts and the supporting mounts are modeled by a set of linear spring–dampers. It is assumed that only one tooth pair is in mesh at a time and all the parameters are represented in Table 1.

Fig. 2

Schematic of pinion and gear in mesh with linear suspension

Table 1 System parameters

For this system, each disk has one rotational and one translational degree of freedom. Newton’s Second Law is used to construct the torsional and translational differential equation of motion for each disk [6, 14].

$$\begin{aligned}&M_p {\ddot{x}}_p + C_p {\dot{x}}_p + K_p x_p + C ( {\dot{x}}_p - {\dot{x}}_g + r_p {\dot{\theta }}_p - r_g {\dot{\theta }}_g - {\dot{e}}(t) ) \nonumber \\&\quad +\, k(t) f (x_p - x_g + r_p\theta _p - r_g \theta _g - e(t)) = 0 \end{aligned}$$

(4)

$$\begin{aligned}&M_g {\ddot{x}}_g + C_g {\dot{x}}_g + K_g x_g - \,C ( {\dot{x}}_p - {\dot{x}}_g + r_p {\dot{\theta }}_p-\, r_g {\dot{\theta }}_g - {\dot{e}}(t) ) \nonumber \\&\quad - \,k(t) f (x_p - x_g + r_p\theta _p - r_g \theta _g - e(t)) = 0 \end{aligned}$$

(5)

$$\begin{aligned}&I_p {\ddot{\theta }}_p + r_p C ( {\dot{x}}_p - {\dot{x}}_g + r_p {\dot{\theta }}_p - r_g {\dot{\theta }}_g - {\dot{e}}(t) ) \nonumber \\&\quad + \, r_p k(t) f (x_p - x_g + r_p\theta _p- r_g \theta _g - e(t)) = + T_p(t) \end{aligned}$$

(6)

$$\begin{aligned}&I_g {\ddot{\theta }}_g - r_g C ( {\dot{x}}_p - {\dot{x}}_g +\, r_p {\dot{\theta }}_p - r_g {\dot{\theta }}_g - {\dot{e}}(t) ) \nonumber \\&\quad -\, r_g k(t) f (x_p - x_g + r_p\theta _p - r_g \theta _g - e(t)) = - T_g(t) \end{aligned}$$

(7)

where subscripts p and g stand for pinion and gear, respectively. The total difference between the rotation angle of the gears in mesh can be expressed by the following equation, which is defined as the difference between the dynamic and static transmission errors.

$$\begin{aligned} x = x_p - x_g + r_p\theta _p - r_g \theta _g - e(t). \end{aligned}$$

(8)

For considering the fluctuation of the excitation torque and the applied load, both can be decomposed into averaging and fluctuating parts [10], so Eqs. (4)–(7) can be written in the following form.

$$\begin{aligned}&M_p {\ddot{x}}_p + C_p {\dot{x}}_p + K_p x_p + C {\dot{x}} + k(t) f (x) = 0 \end{aligned}$$

(9)

$$\begin{aligned}&M_g {\ddot{x}}_g + C_g {\dot{x}}_g + K_g x_g - C {\dot{x}} - k(t) f (x) = 0 \end{aligned}$$

(10)

$$\begin{aligned}&I_p {\ddot{\theta }}_p + r_p C x + r_p k(t) f (x) = + {\overline{T}}_p + {\widetilde{T}}_p \cos (\omega _p t) \end{aligned}$$

(11)

$$\begin{aligned}&I_g {\ddot{\theta }}_g - r_g C x - r_g k(t) f (x) = - {\overline{T}}_g - {\widetilde{T}}_g \cos (\omega _g t) \end{aligned}$$

(12)

where ${\overline{T}}_p$ and ${\overline{T}}_g$ are the average torques and ${\widetilde{T}}_p$ and ${\widetilde{T}}_g$ are the fluctuating torques. By subtracting Eq. (12) from Eq. (11), the governing torsional equations of motion reduce to one equation.

$$\begin{aligned} \begin{aligned}&- {\ddot{x}}_p + {\ddot{x}}_g +{\ddot{x}} + \frac{C}{M} {\dot{x}}\\&\quad + \frac{K}{M} \big ( 1+k_0 \cos (\omega t) \big ) f(x) = \frac{K}{M} F\\&\quad + \frac{K}{M} F_p \cos (\omega _p t) + \frac{K}{M} F_g \cos (\omega _g t) - {\ddot{e}}(t) \end{aligned} \end{aligned}$$

(13)

where M is the equivalent mass representing the total inertia of the gear pair, F is the average static force transmitted through the gear pair and $F_p$ and $F_g$ are the fluctuating forces applied on the pinion and gear, expressed by the following equations.

$$\begin{aligned} M= & {} \frac{I_p I_g}{I_p r_g^2 + I_g r_p^2} , \;\;\quad F = \frac{M}{K}\left( \frac{{\overline{T}}_p r_p}{I_p}+\frac{{\overline{T}}_g r_g}{I_g}\right) \nonumber \\ F_p= & {} \frac{M}{K} \frac{{\widetilde{T}}_p r_p}{I_p} , \;\; \quad F_g = \frac{M}{K} \frac{{\widetilde{T}}_g r_g}{I_g} \end{aligned}$$

(14)

Now, by defining the following standard parameters

$$\begin{aligned} \omega _n = \sqrt{ \frac{K}{M} } , \;\;\; \zeta = \frac{C}{2\sqrt{KM}} \end{aligned}$$

(15)

and using Eq. (2), one can write Eq. (13) in the following standard form

$$\begin{aligned} \begin{aligned}&- {\ddot{x}}_p + {\ddot{x}}_g + {\ddot{x}} + 2 \zeta \omega _n {\dot{x}}\\&\quad + \omega _n^2 \big (1+k_0 \sin (\omega t) \big ) f(x) = \omega _n^2 F \\&\quad + \omega _n^2 F_p \cos (\omega _p t) + \omega _n^2 F_g \cos (\omega _g t) + \omega ^2 E \cos (\omega t) \end{aligned} \end{aligned}$$

(16)

By defining the following dimensionless parameters

$$\begin{aligned} {\hat{t}}= & {} \omega _n t \nonumber \\ u= & {} \frac{x}{b} , \;\;\; u_p = \frac{x_p}{b}, \;\;\; u_g = \frac{x_g}{b} \nonumber \\ \Omega= & {} \frac{\omega \;}{\omega _n}, \;\;\; \Omega _p = \frac{\omega _p}{\omega _n}, \;\;\; \Omega _g = \frac{\omega _g}{\omega _n}, \end{aligned}$$

(17)

Equations (9),(10) and (16) are written in the following dimensionless form.

$$\begin{aligned}&m_p \hat{ {\ddot{u}} }_p + 2 \zeta _p \hat{ {\dot{u}} }_p + 2 \zeta \hat{ {\dot{u}} } + k_p u_p\nonumber \\&\qquad + \big (1+k_0 \cos (\Omega {\hat{t}} ) \big ) f(u) = 0 \end{aligned}$$

(18)

$$\begin{aligned}&m_g \hat{ {\ddot{u}} }_g + 2 \zeta _g \hat{ {\dot{u}} }_g - 2 \zeta \hat{ {\dot{u}} } \nonumber \\&\qquad + k_g u_g - \big (1+k_0 \cos (\Omega {\hat{t}} ) \big ) f(u) = 0 \end{aligned}$$

(19)

$$\begin{aligned}&\qquad - \hat{ {\ddot{u}} }_p + \hat{ {\ddot{u}} }_g + \hat{ {\ddot{u}} } \nonumber \\&\qquad + 2 \zeta \hat{ {\dot{u}} } + \big (1+k_0 \cos (\Omega {\hat{t}} ) \big ) f(u) \nonumber \\&\quad = F + F_p \cos (\Omega _p {\hat{t}} ) + F_g \cos (\Omega _g {\hat{t}} ) \nonumber \\&\qquad + \Omega ^2 E \cos (\Omega {\hat{t}} ) \end{aligned}$$

(20)

where the ratio of the parameter corresponded to the suspension system over the parameter corresponded to the gear pairs in mesh are expressed as follow.

$$\begin{aligned} m_p= & {} \frac{M_p}{M} , \;\;\; m_g = \frac{M_g}{M} , \nonumber \\ k_p= & {} \frac{K_p}{K} , \;\;\; k_g = \frac{K_g}{K} \nonumber \\ \zeta _p= & {} \frac{C_p}{2 \sqrt{ K M} }, \;\;\; \zeta _g = \frac{C_g}{2 \sqrt{ K M} } \end{aligned}$$

(21)

One can write Eqs. (18)–(20) in the following matrix form.

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} \quad m_p &{} 0 &{} 0 \, \\ \quad 0 &{} m_g &{} 0 \, \\ - 1 &{} 1 &{} 1 \, \end{bmatrix} \begin{bmatrix} \hat{ {\ddot{u}} }_p \\ \hat{ {\ddot{u}} }_g \\ \hat{ {\ddot{u}} } \end{bmatrix} + 2 \begin{bmatrix} \zeta _p &{} 0 &{} \quad \zeta \, \\ 0 &{} \zeta _g &{} - \zeta \,\\ 0 &{} 0 &{} \quad \zeta \, \end{bmatrix} \begin{bmatrix} \hat{ {\dot{u}} }_p \\ \hat{ {\dot{u}} }_g \\ \hat{ {\dot{u}} } \end{bmatrix} \\&\qquad + \begin{bmatrix} k_p &{} 0 &{} \quad + \big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \\ 0 &{} k_g &{} \quad -\big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \\ 0 &{} 0 &{} \quad + \big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \end{bmatrix} \begin{bmatrix} u_p \\ u_g \\ f(u) \end{bmatrix} \\&\quad = \begin{bmatrix} 0 \\ 0 \\ F + F_p \cos (\Omega _p {\hat{t}} ) + F_g \cos (\Omega _g {\hat{t}} ) + \Omega ^2 E \cos (\Omega {\hat{t}} ) \end{bmatrix} \end{aligned} \end{aligned}$$

(22)

with the following dimensionless backlash function

$$\begin{aligned} f(u) = {\left\{ \begin{array}{ll} u-1 &{} \quad +1< u \\ \quad 0 &{} -1 \le u \le +1 \\ u+1 &{} \quad u < -1 \end{array}\right. } \end{aligned}$$

(23)

Equation (22) is a damped conservative system and the non-symmetric nature of this system is due to the choice of the coordinates.

4 Analytical calculations

The purpose of this section is to use analytical methods to obtain the parameter space that the parametric resonance causes the instability of the system, increase in the amplitude of the oscillation, and consequently the separation of the teeth in mesh. By assuming that the system is symmetric such that both driving and driven shafts have the same parameters

$$\begin{aligned} \begin{aligned}&m = m_p = m_g \\&k = k_p = k_g \\&\zeta = \zeta _p = \zeta _g \end{aligned} \end{aligned}$$

(24)

and by imposing the permanent contact condition, Eq. (22) reduces to a system of linear differential equations with periodic time-varying coefficients.

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} \quad m &{} 0 &{} 0 \, \\ \quad 0 &{} m &{} 0 \, \\ - 1 &{} 1 &{} 1 \, \end{bmatrix} \begin{bmatrix} \hat{ {\ddot{u}} }_p \\ \hat{ {\ddot{u}} }_g \\ \hat{ {\ddot{u}} } \end{bmatrix} + 2 \begin{bmatrix} \zeta &{} 0 &{} \quad \zeta \, \\ 0 &{} \zeta &{} - \zeta \, \\ 0 &{} 0 &{} \quad \zeta \, \end{bmatrix} \begin{bmatrix} \hat{ {\dot{u}} }_p \\ \hat{ {\dot{u}} }_g \\ \hat{ {\dot{u}} } \end{bmatrix} \\&\quad + \begin{bmatrix} k &{} 0 &{} \quad +\big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \\ 0 &{} k &{} \quad - \big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \\ 0 &{} 0 &{} \quad + \big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \end{bmatrix} \begin{bmatrix} u_p \\ u_g \\ u \end{bmatrix} \\&\quad = \begin{bmatrix} 0 \\ 0 \\ F + F_p \cos (\Omega _p {\hat{t}} ) + F_g \cos (\Omega _g {\hat{t}} ) + \Omega ^2 E \cos (\Omega {\hat{t}} ) \end{bmatrix} \\&\quad + \begin{bmatrix} + \big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big )\\ - \big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \\ + \big ( 1+ k_0 \cos (\Omega {\hat{t}} ) \big ) \end{bmatrix}. \end{aligned} \end{aligned}$$

(25)

To study the stability of the corresponding undamped homogenous system, the time-varying terms is perturbed as follows.

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \quad m &{} 0 &{} 0 \, \\ \quad 0 &{} m &{} 0 \, \\ - 1 &{} 1 &{} 1 \, \end{bmatrix} \begin{bmatrix} \hat{ {\ddot{u}} }_p \\ \hat{ {\ddot{u}} }_g \\ \hat{ {\ddot{u}} } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} +\big ( 1+ \epsilon \cos (\Omega {\hat{t}} ) \big ) \\ 0 &{} k &{} - \big ( 1+ \epsilon \cos (\Omega {\hat{t}} ) \big ) \\ 0 &{} 0 &{} + \big ( 1+ \epsilon \cos (\Omega {\hat{t}} ) \big ) \end{bmatrix} \begin{bmatrix} u_p \\ u_g \\ u \end{bmatrix} = 0 \end{aligned}\nonumber \\ \end{aligned}$$

(26)

where $\epsilon$ is a small parameter and the following transformation of the variable is used to implement the Poincare–Lindstedt method.

$$\begin{aligned} \tau = \Omega {\hat{t}}, \quad u_p^{\prime } = \frac{\mathrm{{d}}u_p}{\mathrm{{d}}\tau },\quad u_g^{\prime } = \frac{\mathrm{{d}}u_g}{\mathrm{{d}}\tau }, \quad u^{\prime } = \frac{\mathrm{{d}}u}{\mathrm{{d}}\tau } \end{aligned}$$

(27)

which results in the following system of equations.

$$\begin{aligned} \begin{aligned} \Omega ^2 \begin{bmatrix} \quad m &{} 0 &{} 0 \, \\ \quad 0 &{} m &{} 0 \, \\ - 1 &{} 1 &{} 1 \, \end{bmatrix} \begin{bmatrix} u_p^{\prime \prime } \\ u_g^{\prime \prime } \\ u^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} +\big ( 1+ \epsilon \cos \tau \big ) \\ 0 &{} k &{} - \big ( 1+ \epsilon \cos \tau \big ) \\ 0 &{} 0 &{} + \big ( 1+ \epsilon \cos \tau \big ) \end{bmatrix} \begin{bmatrix} u_p \\ u_g \\ u \end{bmatrix} = 0 \end{aligned}\nonumber \\ \end{aligned}$$

(28)

where prime represents differentiation with respect to the new variable $\tau$. Now, by expanding the variables in the following power series

$$\begin{aligned}&u_p = u_{0p} + u_{1p} \epsilon + u_{2p} \epsilon ^2 + u_{3p} \epsilon ^3 + \; \cdots \end{aligned}$$

(29)

$$\begin{aligned}&u_g = u_{0g} + u_{1g} \epsilon + u_{2g} \epsilon ^2 + u_{3g} \epsilon ^3 + \; \cdots \end{aligned}$$

(30)

$$\begin{aligned}&u = u_{0} + u_{1} \epsilon + u_{2} \epsilon ^2 + u_{3} \epsilon ^3 + \; \cdots \end{aligned}$$

(31)

$$\begin{aligned}&\Omega = \Omega _0 + \Omega _1 \epsilon + \Omega _2 \epsilon ^2 + \Omega _3 \epsilon ^3 + \; \cdots \end{aligned}$$

(32)

substituting Eqs. (29)–(32) in Eq. (28), neglecting terms of $O( \epsilon ^3 )$, and collecting terms of the same power the following system of equations is obtained.

$$\begin{aligned}&\Omega _0^2 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{0p}^{\prime \prime } \\ u_{0g}^{\prime \prime } \\ u_{0}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} \quad 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} \quad 1 \end{bmatrix} \begin{bmatrix} u_{0p} \\ u_{0g} \\ u_{0} \end{bmatrix} = 0 \end{aligned}$$

(33)

$$\begin{aligned}&\Omega _0^2 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p}^{\prime \prime } \\ u_{1g}^{\prime \prime } \\ u_{1}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} \quad 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} \quad 1 \end{bmatrix} \begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix}\nonumber \\&\quad = -2 \Omega _0 \Omega _1 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{0p}^{\prime \prime } \\ u_{0g}^{\prime \prime } \\ u_{0}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} u_0 \cos \tau \end{aligned}$$

(34)

$$\begin{aligned}&\Omega _0^2 \begin{bmatrix} \quad m &{} 0 &{} 0 \\ \quad 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{2p}^{\prime \prime } \\ u_{2g}^{\prime \prime } \\ u_{2}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} \quad 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} \quad 1 \end{bmatrix} \begin{bmatrix} u_{2p} \\ u_{2g} \\ u_{2} \end{bmatrix} = \nonumber \\&\quad - ( \Omega _1^2 + 2 \Omega _0 \Omega _2 ) \begin{bmatrix} \quad m &{} 0 &{} 0 \\ \quad 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{0p}^{\prime \prime } \\ u_{0g}^{\prime \prime } \\ u_{0}^{\prime \prime } \end{bmatrix} \nonumber \\&\quad - 2 \Omega _0 \Omega _1 \begin{bmatrix} \quad m &{} 0 &{} 0 \\ \quad 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p}^{\prime \prime } \\ u_{1g}^{\prime \prime } \\ u_{1}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} u_1 \cos (\tau ). \end{aligned}$$

(35)

Equation (33) is a linear homogenous system of equations with the following solution.

$$\begin{aligned}&\begin{bmatrix} u_{0p} \\ u_{0g} \\ u_{0} \end{bmatrix} = \begin{bmatrix} A \\ B \\ C \end{bmatrix} e^{\lambda \tau }. \end{aligned}$$

(36)

By substituting Eq. (36) in Eq. (33), the corresponding eigenvalues and eigenvectors of the system are obtained as follows.

$$\begin{aligned} \lambda _1^2= & {} \frac{k}{m \Omega _0^2} i^2 , \quad \lambda _2^2 = \frac{2k-a}{2 m \Omega _0^2} i^2 , \quad \lambda _3^2 = \frac{2k-b}{2 m \Omega _0^2} i^2\nonumber \\ \end{aligned}$$

(37)

$$\begin{aligned}&\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} , \begin{bmatrix} -2 \\ +2 \\ a \end{bmatrix} , \begin{bmatrix} -2 \\ +2 \\ b \end{bmatrix} \end{aligned}$$

(38)

where constants a and b are a function of the system parameters; m and k, and i represent the imaginary unit, satisfying $i^2 = -1$.

$$\begin{aligned}&a = -(m-k+2) + \sqrt{ { (m+k+2)^2 - 4 k m }} \end{aligned}$$

(39)

$$\begin{aligned}&b = -(m-k+2) - \sqrt{ { (m+k+2)^2 - 4 k m }}. \end{aligned}$$

(40)

Such that the following relationships holds between a and b.

$$\begin{aligned}&a b = - 8 k. \end{aligned}$$

(41)

There is no gyroscopic or nonconservative forces participating in Eq. (33) and the non-symmetric nature of the system is due to the choice of coordinates. According to the Spectral Theorem, such a real, non-symmetric system cannot be diagonalized, which results in more complexity of the mathematical calculations. Even though the eigenvectors of the system are linearly independent, the second and third eigenvectors are not orthogonal, which causes the lateral-tortional vibration coupling of the system. As shown below, in the special case of $k = 1$, the second and third eigenvectors are orthogonal and there is no coupling; however, in this work, the general form of Eq. (33) is solved for every value of k.

$$\begin{aligned} v_1 v_2 = 0, \, v_1 v_3 = 0, \, v_2 v_3 = 8(1-k). \end{aligned}$$

(42)

For different values of k and m, the following condition is required to have real values for a and b.

$$\begin{aligned} (m+k+2)^2 - 4 k m > 0. \end{aligned}$$

(43)

In Fig. 3, the regions that Eq. (43) is satisfied is in blue highlights, and the regions where it is not satisfied is in red highlights. Since only positive values are allocated to k and m, then Eq. (43) is always satisfied and Eqs. (39) and (40) are real. So, the three eigenvectors represented by Eq. (38) are real for any value of k and m.

Fig. 3

Regions that Eq. (43) is satisfied

And, since the following equations are positive for any value of k and m.

$$\begin{aligned} \begin{aligned}&2k - a = (m+k+2) - \sqrt{ { (m+k+2)^2 - 4 k m }} \\&2k - b = (m+k+2) + \sqrt{ { (m+k+2)^2 - 4 k m }} \end{aligned} \end{aligned}$$

(44)

the three eigenvalues expressed by Eq. (37) are always complex. Therefore, for any value of the parameters, Eq. (33) has three natural frequencies.

$$\begin{aligned} \omega _{n1}^2= & {} \frac{k}{m \Omega _0^2} , \quad \omega _{n2}^2 = \frac{2k-a}{2 m \Omega _0^2} , \quad \omega _{n3}^2 = \frac{2k-b}{2 m \Omega _0^2} \end{aligned}$$

(45)

such that the following relationship holds between them.

$$\begin{aligned}&\omega _{n2}^2 \, \omega _{n3}^2 = \frac{k}{ m \Omega _0^4} \end{aligned}$$

(46)

$$\begin{aligned}&\omega _{n1}^2 = \Omega _0^2 \; \omega _{n2}^2 \, \omega _{n3}^2 \end{aligned}$$

(47)

By having the eigenvalues and eigenvectors of Eq. (33), one can write the solution of this equation as follows.

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} u_{0p} \\ u_{0g} \\ u_{0} \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \Big ( A_1 \cos ( \omega _{n1} \tau ) + A_2 \sin ( \omega _{n1} \tau ) \Big ) \\&\quad + \begin{bmatrix} -2 \\ +2 \\ a \end{bmatrix} \Big ( B_1 \cos ( \omega _{n2} \tau ) + B_2 \sin ( \omega _{n2} \tau ) \Big ) \\&\quad + \begin{bmatrix} -2 \\ +2 \\ b \end{bmatrix} \Big ( C_1 \cos ( \omega _{n3} \tau ) + C_2 \sin ( \omega _{n3} \tau ) \Big ). \\ \end{aligned} \end{aligned}$$

(48)

Substituting Eq. (48) in Eq. (34) results in the following equation.

$$\begin{aligned}&\Omega _0^2 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p}^{\prime \prime } \\ u_{1g}^{\prime \prime } \\ u_{1}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} \quad 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} \quad 1 \end{bmatrix} \begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix} = \nonumber \\&\quad + 2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 &{} -2m \omega _{n2}^2 &{} -2m \omega _{n3}^2 \\ m \omega _{n1}^2 &{} +2m \omega _{n2}^2 &{} +2m \omega _{n3}^2 \\ 0 &{} (a+4) \omega _{n2}^2 &{} (b+4) \omega _{n3}^2 \end{bmatrix}\begin{bmatrix} A_1 \cos ( \omega _{n1} \tau ) \\ B_1 \cos ( \omega _{n2} \tau ) \\ C_1 \cos ( \omega _{n3} \tau ) \end{bmatrix}+ 2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 &{} -2m \omega _{n2}^2 &{} -2m \omega _{n3}^2 \\ m \omega _{n1}^2 &{} +2m \omega _{n2}^2 &{} +2m \omega _{n3}^2 \\ 0 &{} (a+4) \omega _{n2}^2 &{} (b+4) \omega _{n3}^2 \end{bmatrix}\begin{bmatrix} A_2 \sin ( \omega _{n1} \tau ) \\ B_2 \sin ( \omega _{n2} \tau ) \\ C_2 \sin ( \omega _{n3} \tau ) \end{bmatrix} \nonumber \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} - 1 ) \tau + B_2 \sin ( \omega _{n2} - 1 ) \tau \Big )+ \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} + 1 ) \tau + B_2 \sin ( \omega _{n2} + 1 ) \tau \Big ) \nonumber \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} - 1 ) \tau + C_2 \sin ( \omega _{n3} - 1 ) \tau \Big ) + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} + 1 ) \tau + C_2 \sin ( \omega _{n3} + 1 ) \tau \Big ) \end{aligned}$$

(49)

which contains harmonic functions with frequencies equal to

$$\begin{aligned} \omega _{n1} , \omega _{n2} , \omega _{n3} , \omega _{n2} \pm 1 , \omega _{n3} \pm 1. \end{aligned}$$

(50)

Generally, primary and combination resonance can appear in a parametrically excited system with many degrees of freedom [34]. In the next two sections, it is explained how Eq. (49) can be used to determine the corresponding unstable tongues.

4.1 First tongues

4.1.1 Primary parametric resonance due to the second natural frequency

In general, all of the harmonic terms with frequencies equal to the three natural frequencies in Eq. (49) are secular terms and must be removed [24]. But in the following special case of the second natural frequency, more terms become secular [27].

$$\begin{aligned} \omega _{n2} - 1 = -\omega _{n2} \rightarrow \omega _{n2} = \frac{1}{2}. \end{aligned}$$

(51)

Imposing this condition on Eq. (45) results in the emanating frequency of the first tongue related the second natural frequency.

$$\begin{aligned} \Omega _0^2 = \frac{2 (2 k - a)}{m}. \end{aligned}$$

(52)

Inserting Eq. (52) into Eqs. (46) and (47) results in the other two natural frequencies.

$$\begin{aligned} \omega _{n1}^2 = \frac{k}{2 (2 k - a)}, \; \omega _{n2}^2 = \frac{1}{4}, \; \omega _{n3}^2 = \frac{km}{ (2 k - a)^2}. \end{aligned}$$

(53)

By substituting Eq. (53) in Eq. (49), the following matrix form of the secular terms is obtained.

$$\begin{aligned}&2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 &{} - 2 m \omega _{n2}^2 - \dfrac{a}{4 \Omega _0 \Omega _1} &{} -2 m \omega _{n3}^2 \\ m \omega _{n1}^2 &{} \quad 2 m \omega _{n2}^2 + \dfrac{a}{4 \Omega _0 \Omega _1} &{} \quad 2 m \omega _{n3}^2 \\ 0 &{} (a + 4) \omega _{n2}^2 - \dfrac{a}{4 \Omega _0 \Omega _1} &{} (b + 4) \omega _{n3}^2 \end{bmatrix}\begin{bmatrix} A_1 \cos ( \omega _{n1} \tau ) \\ B_1 \cos ( \omega _{n2} \tau ) \\ C_1 \cos ( \omega _{n3} \tau ) \end{bmatrix} \nonumber \\&\quad + 2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 &{} - 2 m \omega _{n2}^2 + \dfrac{a}{4 \Omega _0 \Omega _1} &{} -2 m \omega _{n3}^2 \\ m \omega _{n1}^2 &{} \quad 2 m \omega _{n2}^2 - \dfrac{a}{4 \Omega _0 \Omega _1} &{} \quad 2 m \omega _{n3}^2 \\ 0 &{} (a + 4) \omega _{n2}^2 + \dfrac{a}{4 \Omega _0 \Omega _1} &{} (b + 4) \omega _{n3}^2 \end{bmatrix} \begin{bmatrix} A_2 \sin ( \omega _{n1} \tau ) \\ B_2 \sin ( \omega _{n2} \tau ) \\ C_2 \sin ( \omega _{n3} \tau ) \end{bmatrix} = 0.\nonumber \\ \end{aligned}$$

(54)

To remove these secular terms, the determinant of each matrix in Eq. (54) must be equal to zero. These conditions provide the two first-order multipliers of Eq. (32) for the transition curves of the first tongue corresponded to the second natural frequency.

$$\begin{aligned} \Omega _1 =\pm \frac{a(b+2m+4)}{2m\Omega _0(a-b)}. \end{aligned}$$

(55)

In Eq. (55), the positive and negative signs are related to cosine and sine multipliers associated with the left and right transition curves, respectively. At this point, substituting the solution of Eq. (49) in Eq. (35) and removing the secular terms provide the two second-order multipliers of Eq. (55) for the transition curves of the first tongue corresponded to the second natural frequency. Zero-determinant conditions for multipliers of both cosine and sine terms results in the following value for both the left and right transition curves.

$$\begin{aligned} \begin{aligned} \Omega _2&= \frac{ \Omega _{0} }{16 m (a-b) \omega _{n1}^2 } \Big ( b(a+2m+4) ( \beta _3 + \beta _4 ) \omega _{n2}^2 \\&\quad - a(b+2m+4) ( \beta _2) \omega _{n3}^2 \Big ) - \frac{\Omega _{1}^2 }{ 2 \Omega _{0}}. \end{aligned} \end{aligned}$$

(56)

The value of $\beta _i$ will be defined later in Eq. (77).

4.1.2 Primary parametric resonance due to the third natural frequency

Alternatively, in the following special case of the third natural frequency, other terms in Eq. (49) become secular

$$\begin{aligned} \omega _{n3} - 1 = -\omega _{n3} \rightarrow \omega _{n3} = \frac{1}{2}. \end{aligned}$$

(57)

Imposing this condition on Eq. (45) gives the emanating frequency of the first tongue related to the third natural frequency.

$$\begin{aligned} \Omega _0^2 = \frac{2 (2 k - b)}{m}. \end{aligned}$$

(58)

Inserting Eq. (58) into Eqs. (46) and (47) provides the other two natural frequencies.

$$\begin{aligned} \omega _{n1}^2= & {} \frac{k}{2 (2 k - b)}, \; \omega _{n2}^2 = \frac{km}{ (2 k - b)^2 }, \; \omega _{n3}^2 = \frac{1}{4}.\nonumber \\ \end{aligned}$$

(59)

By substituting these three natural frequencies in Eq. (49), the following matrix form of the secular terms is obtained.

$$\begin{aligned}&2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 &{} -2 m \omega _{n2}^2 &{} - 2 m \omega _{n3}^2 - \dfrac{b}{4 \Omega _0 \Omega _1} \\ m \omega _{n1}^2 &{} \quad 2 m \omega _{n2}^2 &{} \quad 2 m \omega _{n3}^2 + \dfrac{b}{4 \Omega _0 \Omega _1} \\ 0 &{} (a + 4) \omega _{n2}^2 &{} (b + 4) \omega _{n3}^2 - \dfrac{b}{4 \Omega _0 \Omega _1} \end{bmatrix}\begin{bmatrix} A_1 \cos ( \omega _{n1} \tau ) \\ B_1 \cos ( \omega _{n2} \tau ) \\ C_1 \cos ( \omega _{n3} \tau ) \end{bmatrix} \nonumber \\&\quad + 2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 &{} -2 m \omega _{n2}^2 &{} - 2 m \omega _{n3}^2 + \dfrac{b}{4 \Omega _0 \Omega _1} \\ m \omega _{n1}^2 &{} \quad 2 m \omega _{n2}^2 &{} \quad 2 m \omega _{n3}^2 - \dfrac{b}{4 \Omega _0 \Omega _1} \\ 0 &{} (a + 4) \omega _{n2}^2 &{} 2 (b + 4) \omega _{n3}^2 + \dfrac{b}{4 \Omega _0 \Omega _1} \end{bmatrix}\begin{bmatrix} A_2 \sin ( \omega _{n1} \tau ) \\ B_2 \sin ( \omega _{n2} \tau ) \\ C_2 \sin ( \omega _{n3} \tau ) \end{bmatrix} = 0.\nonumber \\ \end{aligned}$$

(60)

Similarly, the zero-determinant condition results in two first-order multipliers of Eq. (32) for the transition curves of the first tongue corresponding to the third natural frequency.

$$\begin{aligned} \Omega _1 = \pm \frac{b(a+2m+4)}{2m\Omega _0(b-a)}. \end{aligned}$$

(61)

In Eq. (68), the negative and positive signs are obtained from the zero-determinant condition of the cosine and sine terms, which are associated with the left and right transition curves, respectively. At this point, substituting the solution of Eq. (49) in Eq. (35) and removing the secular terms provide the two second-order multipliers of Eq. (32) for the transition curves of the first tongue corresponding to the third natural frequency. Zero-determinant conditions for multipliers of both cosine and sine terms results in the same value for the left and right transition curves.

$$\begin{aligned} \begin{aligned} \Omega _2&= \frac{ \Omega _{0} }{16 m (a-b) \omega _{n1}^2 } \Big ( b(a+2m+4) ( \beta _4 ) \omega _{n2}^2 \\&\quad - a(b+2m+4) ( \beta _1 + \beta _2) \omega _{n3}^2 \Big ) - \frac{\Omega _{1}^2 }{ 2 \Omega _{0}}. \end{aligned} \end{aligned}$$

(62)

The value of $\beta _i$ will be defined later in Eq. (77).

4.1.3 Combined parametric resonance of summation type

For the following special case of the second and third natural frequency, more terms in Eq. (49) become secular.

$$\begin{aligned} \begin{aligned}&\omega _{n2} - 1 = -\omega _{n3} \rightarrow \omega _{n2} + \omega _{n3} = 1 \\&\omega _{n3} - 1 = -\omega _{n2} \rightarrow \omega _{n2} + \omega _{n3} = 1. \end{aligned} \end{aligned}$$

(63)

Imposing this condition on Eq. (45) gives the emanating frequency of the first tongue related to the combined parametric resonance.

$$\begin{aligned} \Omega _0^2 = \frac{m+k+2}{m} + 2 \sqrt{ \frac{k}{m} }. \end{aligned}$$

(64)

Figure 4 shows the values of the natural frequencies for different normalized stiffness ratios resulting from substituting Eq. (64) in Eq. (45).

which shows that for the emanating frequency provided by Eq. (64), the summation of the second and third natural frequencies is always equal to one. Imposing Eqs. (63)–(49) results in the following matrix form of the secular terms.

$$\begin{aligned} \begin{aligned}&2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 A_1 &{} - 2 m \omega _{n2}^2 B_1 - \frac{b}{4 \Omega _0 \Omega _1} C_1 &{} - 2 m \omega _{n3}^2 C_1 - \frac{a}{4 \Omega _0 \Omega _1} B_1 \\ m \omega _{n1}^2 A_1 &{} + 2 m \omega _{n2}^2 B_1 + \frac{b}{4 \Omega _0 \Omega _1} C_1 &{} + 2 m \omega _{n3}^2 C_1 + \frac{a}{4 \Omega _0 \Omega _1} B_1 \\ 0 &{} (a + 4) \omega _{n2}^2 B_1 - \frac{b}{4 \Omega _0 \Omega _1} C_1 &{} (b + 4) \omega _{n3}^2 C_1 - \frac{a}{4 \Omega _0 \Omega _1} B_1 \end{bmatrix}\begin{bmatrix} \cos ( \omega _{n1} \tau ) \\ \cos ( \omega _{n2} \tau ) \\ \cos ( \omega _{n3} \tau ) \end{bmatrix} \\&\quad + 2 \Omega _0 \Omega _1 \begin{bmatrix} m \omega _{n1}^2 A_2 &{} - 2 m \omega _{n2}^2 B_2 + \frac{b}{4 \Omega _0 \Omega _1} C_2 &{} - 2 m \omega _{n3}^2 C_2 + \frac{a}{4 \Omega _0 \Omega _1} B_2 \\ m \omega _{n1}^2 A_2 &{} + 2 m \omega _{n2}^2 B_2 - \frac{b}{4 \Omega _0 \Omega _1} C_2 &{} + 2 m \omega _{n3}^2 C_2 - \frac{a}{4 \Omega _0 \Omega _1} B_2 \\ 0 &{} (a + 4) \omega _{n2}^2 B_2 + \frac{b}{4 \Omega _0 \Omega _1} C_2 &{} (b + 4) \omega _{n3}^2 C_2 + \frac{a}{4 \Omega _0 \Omega _1} B_2 \end{bmatrix}\begin{bmatrix} \sin ( \omega _{n1} \tau ) \\ \sin ( \omega _{n2} \tau ) \\ \sin ( \omega _{n3} \tau ) \end{bmatrix} = 0. \end{aligned} \end{aligned}$$

(65)

Fig. 4

Natural frequencies at combined parametric resonance frequency, for $m = 1$

Imposing the zero-determinant condition to multipliers of the cosine and sine terms in Eqs, (65) results in the following equations.

$$\begin{aligned}&+ b (a+2m+4) \omega _2^2 B_2^2+ 8 m \Omega _0 \Omega _1 (b-a) \omega _2^2 \omega _3^2 B_2 C_2- a (b+2m+4) \omega _3^2 C_2^2 = 0 \end{aligned}$$

(66)

$$\begin{aligned}&- b (a+2m+4) \omega _2^2 B_1^2 + 8 m \Omega _0 \Omega _1 (b-a) \omega _2^2 \omega _3^2 B_1 C_1 + a (b+2m+4) \omega _3^2 C_1^2 = 0. \end{aligned}$$

(67)

Each one of Eqs. (66) and (67) form a degenerate conic with the standard form of $A x_1^2 + B x_1 x_2 + C x_2^2 = 0$. Imposing the condition of $AB + 2AC + BC = 0$ on these equations provides the two first-order multipliers of Eq. (32) for the transition curves of the unstable tongue. The negative and positive signs are related to sine and cosine multipliers associated with the left and right transition curves, respectively.

$$\begin{aligned} \Omega _1 = \pm \frac{4k \Omega _0}{(a-b)^2}. \end{aligned}$$

(68)

At this point, substituting the solution of Eq. (49) in Eq. (35) and removing the secular terms provides the two second-order multipliers of Eq. (32) for the transition curves of the first tongue of combined parametric resonance. Zero-determinant condition for the multipliers of both cosine and sine terms results in the same value for the left and right transition curves.

$$\begin{aligned} \begin{aligned} \Omega _2&= \frac{ \Omega _{0} }{16 m (a-b) \omega _{n1}^2 } \Big ( b(a+2m+4) ( \beta _4 ) \omega _{n2}^2 \\&\quad - a(b+2m+4) ( \beta _2 ) \omega _{n3}^2 \Big ) - \frac{\Omega _{1}^2 }{ 2 \Omega _{0}}. \end{aligned} \end{aligned}$$

(69)

The value of $\beta _i$ will be defined later in Eq. (77).

4.2 Second tongues

To find the second tongues associated with the second and third natural frequencies and combined resonance, the general form of Eq. (49) must be solved, where the following conditions hold.

$$\begin{aligned}&\omega _{n2} \ne \frac{1}{2}, \quad \omega _{n3} \ne \frac{1}{2}, \omega _{n2} + \omega _{n3} \ne 1. \end{aligned}$$

(70)

Under this condition, for every value of k and m the determinant of the secular terms is nonzero, and the only way to remove them is the following condition.

$$\begin{aligned} \Omega _1 = 0. \end{aligned}$$

(71)

This means that for all of the higher-order tongues, the first-order multiplier of the transition curve expressed by Eq. (32) is zero. Imposing Eq. (71) upon Eq. (49) results in the following non-homogeneous linear system of equations.

$$\begin{aligned}&\Omega _0^2 \begin{bmatrix} \quad m &{} 0 &{} 0 \\ \quad 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{1p}^{\prime \prime } \\ u_{1g}^{\prime \prime } \\ u_{1}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} \quad 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} \quad 1 \end{bmatrix} \begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix} =\nonumber \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} - 1 ) \tau + B_2 \sin ( \omega _{n2} - 1 ) \tau \Big ) \nonumber \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} + 1 ) \tau + B_2 \sin ( \omega _{n2} + 1 ) \tau \Big ) \nonumber \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} - 1 ) \tau + C_2 \sin ( \omega _{n3} - 1 ) \tau \Big )\nonumber \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} + 1 ) \tau + C_2 \sin ( \omega _{n3} + 1 ) \tau \Big ). \nonumber \\ \end{aligned}$$

(72)

The homogenous and particular solutions of Eq. (72) are in the following form.

$$\begin{aligned}&\begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix}_{H} = \begin{bmatrix} E \\ F \\ G \end{bmatrix} e^{\lambda \tau } \end{aligned}$$

(73)

$$\begin{aligned}&\begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix}_{P} = \begin{bmatrix} \quad U_p \\ \quad U_g \\ U \end{bmatrix} e^{D i \tau } \end{aligned}$$

(74)

Such that i represents the imaginary unit, satisfying the equation $i^2 = -1$. Therefore, the general solution of Eq. (72) is obtained as follows.

$$\begin{aligned}&\begin{bmatrix} u_{1p} \\ u_{1g} \\ u_{1} \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \Big ( E_1 \cos ( \omega _{n1} \tau ) + E_2 \sin ( \omega _{n1} \tau ) \Big ) \nonumber \\&\quad + \begin{bmatrix} -2 \\ \quad 2 \\ \quad a \end{bmatrix} \Big ( F_1 \cos ( \omega _{n2} \tau ) + F_2 \sin ( \omega _{n2} \tau ) \Big ) \nonumber \\&\quad + \begin{bmatrix} -2 \\ \quad 2 \\ \quad b \end{bmatrix} \Big ( G_1 \cos ( \omega _{n3} \tau ) + G_2 \sin ( \omega _{n3} \tau ) \Big ) \nonumber \\&\quad + \begin{bmatrix} \quad \alpha _1 \\ - \alpha _1 \\ \quad \beta _1 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} - 1 ) \tau + B_2 \sin ( \omega _{n2} - 1 ) \tau \Big ) \nonumber \\&\quad + \begin{bmatrix} \quad \alpha _2 \\ - \alpha _2 \\ \quad \beta _2 \end{bmatrix} \frac{a}{2} \Big ( B_1 \cos ( \omega _{n2} + 1 ) \tau + B_2 \sin ( \omega _{n2} + 1 ) \tau \Big ) \nonumber \\&\quad + \begin{bmatrix} \quad \alpha _3 \\ - \alpha _3 \\ \quad \beta _3 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} - 1 ) \tau + C_2 \sin ( \omega _{n3} - 1 ) \tau \Big ) \nonumber \\&\quad + \begin{bmatrix} \quad \alpha _4 \\ - \alpha _4 \\ \quad \beta _4 \end{bmatrix} \frac{b}{2} \Big ( C_1 \cos ( \omega _{n3} + 1 ) \tau + C_2 \sin ( \omega _{n3} + 1 ) \tau \Big ) \nonumber \\ \end{aligned}$$

(75)

where

$$\begin{aligned}&\alpha _j = \frac{ \Omega _0^2 D_j^2 }{ ( k - m \Omega _0^2 D_j^2 ) ( 1 - \Omega _0^2 D_j^2 ) - 2 \Omega _0^2 D_j^2 } \end{aligned}$$

(76)

$$\begin{aligned}&\beta _j = \frac{ (m+2) \Omega _0^2 D_j^2 - k }{ ( k - m \Omega _0^2 D_j^2 ) ( 1 - \Omega _0^2 D_j^2 ) - 2 \Omega _0^2 D_j^2 } \nonumber \\&j = 1, 2, 3, 4 \end{aligned}$$

(77)

and

$$\begin{aligned} \begin{aligned}&D_1 = ( \omega _{n2} -1 ) , \quad D_2 = ( \omega _{n2} + 1 ) \\&D_3 = ( \omega _{n3} -1 ) , \quad D_4 = ( \omega _{n3} + 1 ). \\ \end{aligned} \end{aligned}$$

(78)

Substituting Eqs. (48) and (75) in Eq. (35) results in

$$\begin{aligned} \begin{aligned}&\Omega _0^2 \begin{bmatrix} m &{} 0 &{} 0 \\ 0 &{} m &{} 0 \\ -1 &{} 1 &{} 1 \end{bmatrix} \begin{bmatrix} u_{2p}^{\prime \prime } \\ u_{2g}^{\prime \prime } \\ u_{2}^{\prime \prime } \end{bmatrix} + \begin{bmatrix} k &{} 0 &{} \quad 1 \\ 0 &{} k &{} -1 \\ 0 &{} 0 &{} \quad 1 \end{bmatrix} \begin{bmatrix} u_{2p} \\ u_{2g} \\ u_{2} \end{bmatrix} = \\&\quad + \begin{bmatrix} 2 m \Omega _0 \Omega _2 \omega _{n1}^2 &{} - 4 m \Omega _0 \Omega _2 \omega _{n2}^2 - \frac{a}{4} ( \beta _1 + \beta _2) &{} - 4 m \Omega _0 \Omega _2 \omega _{n3}^2 - \frac{b}{4} ( \beta _3 + \beta _4) \\ 2 m \Omega _0 \Omega _2 \omega _{n1}^2 &{} + 4 m \Omega _0 \Omega _2 \omega _{n2}^2 + \frac{a}{4} ( \beta _1 + \beta _2) &{} + 4 m \Omega _0 \Omega _2 \omega _{n3}^2 + \frac{b}{4} ( \beta _3 + \beta _4) \\ 0 &{} 2 \Omega _0 \Omega _2 (a+4) \omega _{n2}^2 - \frac{a}{4} ( \beta _1 + \beta _2) &{} 2 \Omega _0 \Omega _2 (b+4) \omega _{n2}^3 - \frac{b}{4} ( \beta _3 + \beta _4) \end{bmatrix} \begin{bmatrix} A_1 \cos ( \omega _{n1} \tau ) \\ B_1 \cos ( \omega _{n2} \tau ) \\ C_1 \cos ( \omega _{n3} \tau ) \end{bmatrix} \\&\quad + \begin{bmatrix} 2 m \Omega _0 \Omega _2 \omega _{n1}^2 &{} - 4 m \Omega _0 \Omega _2 \omega _{n2}^2 - \frac{a}{4} ( \beta _1 + \beta _2) &{} - 4 m \Omega _0 \Omega _2 \omega _{n3}^2 - \frac{b}{4} ( \beta _3 + \beta _4) \\ 2 m \Omega _0 \Omega _2 \omega _{n1}^2 &{} + 4 m \Omega _0 \Omega _2 \omega _{n2}^2 + \frac{a}{4} ( \beta _1 + \beta _2) &{} + 4 m \Omega _0 \Omega _2 \omega _{n3}^2 + \frac{b}{4} ( \beta _3 + \beta _4) \\ 0 &{} 2 \Omega _0 \Omega _2 (a+4) \omega _{n2}^2 - \frac{a}{4} ( \beta _1 + \beta _2) &{} 2 \Omega _0 \Omega _2 (b+4) \omega _{n2}^3 - \frac{b}{4} ( \beta _3 + \beta _4) \end{bmatrix} \begin{bmatrix} A_2 \sin ( \omega _{n1} \tau ) \\ B_2 \sin ( \omega _{n2} \tau ) \\ C_2 \sin ( \omega _{n3} \tau ) \end{bmatrix}\\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( F_1 \cos ( \omega _{n2} - 1 ) \tau + F_2 \sin ( \omega _{n2} - 1 ) \tau \Big ) + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{2} \Big ( F_1 \cos ( \omega _{n2} + 1 ) \tau + F_2 \sin ( \omega _{n2} + 1 ) \tau \Big ) \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( G_1 \cos ( \omega _{n3} - 1 ) \tau + G_2 \sin ( \omega _{n3} - 1 ) \tau \Big ) + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{2} \Big ( G_1 \cos ( \omega _{n3} + 2 ) \tau + G_2 \sin ( \omega _{n3} + 2 ) \tau \Big ) \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{4} \beta _1 \Big ( B_1 \cos ( \omega _{n2} - 2 ) \tau + B_2 \sin ( \omega _{n2} - 2 ) \tau \Big ) + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{a}{4} \beta _2 \Big ( B_1 \cos ( \omega _{n2} + 2 ) \tau + B_2 \sin ( \omega _{n2} + 2 ) \tau \Big ) \\&\quad + \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{4} \beta _3 \Big ( C_1 \cos ( \omega _{n3} - 2 ) \tau + C_2 \sin ( \omega _{n3} - 2 ) \tau \Big )+ \begin{bmatrix} -1 \\ \quad 1 \\ -1 \end{bmatrix} \frac{b}{4} \beta _4 \Big ( C_1 \cos ( \omega _{n3} + 2 ) \tau + C_2 \sin ( \omega _{n3} + 2 ) \tau \Big ) \end{aligned} \end{aligned}$$

(79)

which contains harmonic functions with frequencies equal to

$$\begin{aligned} \omega _{n1} , \omega _{n2} , \omega _{n3} , \omega _{n2} \pm 1 , \omega _{n3} \pm 1, \omega _{n2} \pm 2 , \omega _{n3} \pm 2.\nonumber \\ \end{aligned}$$

(80)

4.2.1 Primary parametric resonance due to the second natural frequency

As before, the harmonic terms with frequencies equal to the first three terms in Eq. (79) are secular and must be removed. But in the following special case of the second natural frequency, more terms in Eq. (79) become secular.

$$\begin{aligned} \omega _{n2} - 2 = -\omega _{n2} \rightarrow \omega _{n2} = 1. \end{aligned}$$

(81)

Imposing this condition upon Eq. (45) provides the emanating frequency of the second tongue corresponding to the second natural frequency.

$$\begin{aligned} \Omega _0^2 = \frac{ 2 k - a }{2 m}. \end{aligned}$$

(82)

By inserting Eq. (82) in Eqs. (46) and (47), the other two natural frequencies are obtained.

$$\begin{aligned} \omega _{n1}^2 = \frac{2k}{ 2 k - a }, \; \omega _{n2}^2 = 1, \; \omega _{n3}^2 = \frac{4km}{ ( 2 k - a )^2}. \end{aligned}$$

(83)

By substituting these three natural frequencies in Eq. (79), collecting the secular terms, and imposing the zero-determinant condition, one can find the second-order multipliers of the left and right transition curves for the second tongue corresponding to the second natural frequency.

$$\begin{aligned} \Omega _2&= \frac{\Omega _0}{16 m (b-a) \omega _{n1}^2 } \Big ( a ( 2m+b+4 ) (2 \beta _1+ \beta _2) \omega _{n3}^2 \nonumber \\&\quad - b (2 m + a + 4) (\beta _3 + \beta _4) \omega _{n2}^2 \Big ) \end{aligned}$$

(84)

$$\begin{aligned} \Omega _2&= \frac{\Omega _0}{16 m (b-a) \omega _{n1}^2 } \Big ( a ( 2m+b+4 ) ( \beta _2 ) \omega _{n3}^2 \nonumber \\&\quad - b (2 m + a + 4) (\beta _3 + \beta _4) \omega _{n2}^2 \Big ). \end{aligned}$$

(85)

4.2.2 Primary parametric resonance due to the third natural frequency

Alternatively, for the following special case of the third natural frequency, more terms in Eq. (79) become secular.

$$\begin{aligned} \omega _{n3} - 2 = -\omega _{n3} \rightarrow \omega _{n3} = 1. \end{aligned}$$

(86)

Imposing this condition upon Eq. (45) provides the emanating frequency of the second tongue corresponding to the third natural frequency.

$$\begin{aligned} \Omega _0^2 = \frac{ 2 k - b }{2 m} \end{aligned}$$

(87)

By inserting Eq. (87) in Eqs. (46) and (47), the other two natural frequencies are obtained.

$$\begin{aligned} \omega _{n1}^2 = \frac{2k}{ 2 k - b }, \; \omega _{n2}^2 = \frac{4km}{ (2 k - b)^2}, \; \omega _{n3}^2 = 1. \end{aligned}$$

(88)

By substituting these three natural frequencies in Eq. (79), collecting the secular terms, and imposing the zero-determinant condition to the multipliers of the cosine and sine terms, the second-order multiplier of the transition curves for the second tongue corresponding to the third natural frequency are obtained.

$$\begin{aligned} \Omega _2&= \frac{ \Omega _0 }{16 m (b-a) \omega _{n1}^2 } \Big ( a ( 2m+b+4 ) (\beta _1+ \beta _2) \omega _{n3}^2 \nonumber \\&\quad - b (2 m + a + 4) (2 \beta _3 + \beta _4) \omega _{n2}^2 \Big ) \end{aligned}$$

(89)

$$\begin{aligned} \Omega _2&= \frac{ \Omega _0 }{16 m (b-a) \omega _{n1}^2 } \Big ( a ( 2m+b+4 ) (\beta _1+ \beta _2) \omega _{n3}^2 \nonumber \\&\quad - b (2 m + a + 4) ( \beta _4 ) \omega _{n2}^2 \Big ). \end{aligned}$$

(90)

4.2.3 Combined parametric resonance of summation type

For the following special case of the second and third natural frequency, more terms in Eq. (79) become secular.

$$\begin{aligned} \begin{aligned}&\omega _{n2} - 2 = -\omega _{n3} \rightarrow \omega _{n2} + \omega _{n3} = 2 \\&\omega _{n3} - 2 = -\omega _{n2} \rightarrow \omega _{n2} + \omega _{n3} = 2. \end{aligned} \end{aligned}$$

(91)

Imposing this condition upon Eq. (45) results in the emanating frequency of the second tongue relating to the combined parametric resonance.

$$\begin{aligned} \Omega _0^2 = \frac{1}{4} \Big ( \frac{m+k+2}{m} + 2 \sqrt{ \frac{k}{m} } \, \Big ). \end{aligned}$$

(92)

As before, substituting these three natural frequencies in Eq. (79), collecting the secular terms, and imposing the zero-determinant condition, result in two degenerate conics. Imposing the condition of $AB + 2AC + BC = 0$ to these equations provides the second-order multiplier of the transition curves for the second tongue corresponding to the combined parametric resonance.

$$\begin{aligned} \begin{aligned} \Omega _2&= \frac{ \Omega _0 }{8 m (b-a) \omega _{n1}^2 } \Big ( \pm \frac{2ab (2 m + a + 4) (2 m + b + 4)\omega _{n2}^2\omega _{n3}^2 \beta _1 \beta _3 }{ b (2 m + b + 4)\omega _{n3}^2 \beta _3 - a (2 m + a + 4)\omega _{n2}^2 \beta _1 } \\&\quad + a ( 2m+b+4 ) (\beta _1+ \beta _2) \omega _{n3}^2 - b (2 m + a + 4) ( \beta _3 + \beta _4) \omega _{n2}^2 \Big ). \end{aligned} \end{aligned}$$

(93)

Fig. 5

Unstable tongues corresponded to the second, third and combined natural frequencies

Fig. 6

Floquet multipliers

4.3 General formulas

In general, the emanating frequencies and the corresponding natural frequencies related to the second natural frequency can be obtained by the following general equations.

$$\begin{aligned}&\omega _{n2} - n = -\omega _{n2} \rightarrow \omega _{n2} = \frac{n}{2} \nonumber \\&\Omega _0^2 = \frac{ 2 ( 2 k - a ) }{ n^2 m } \nonumber \\&\omega _{n1}^2 = \frac{n^2k}{ 2 ( 2 k - a ) }, \; \omega _{n2}^2 = \frac{n^2}{4}, \; \omega _{n3}^2 = \frac{ n^2 k m }{ (2 k - a)^2} \nonumber \\&\quad n = 1, 2, 3, \, \ldots \end{aligned}$$

(94)

Similarly, the general form of the emanating frequencies and the corresponding natural frequencies related to the third natural frequency can be obtained by the following equations.

$$\begin{aligned}&\omega _{n3} - n = -\omega _{n3} \rightarrow \omega _{n3} = \frac{n}{2} \nonumber \\&\Omega _0^2 = \frac{ 2 ( 2 k - b ) }{ n^2 m } \nonumber \\&\omega _{n1}^2 = \frac{n^2 k }{ 2 ( 2 k - b ) }, \; \omega _{n2}^2 = \frac{n^2 k m }{ ( 2 k - b )^2 }, \; \omega _{n3}^2 = \frac{n^2}{4}\nonumber \\&\quad n = 1, 2, 3, \, \ldots \end{aligned}$$

(95)

Finally, the general form of the emanating frequencies for the combined parametric resonance can be obtained by the following equations.

$$\begin{aligned}&\omega _{n2} - n = -\omega _{n3} \rightarrow \omega _{n2} + \omega _{n3} = n \nonumber \\&\omega _{n3} - n = -\omega _{n2} \rightarrow \omega _{n2} + \omega _{n3} = n \nonumber \\&\Omega _0^2 = \frac{1}{n^2} \Big ( \frac{m+k+2}{m} + 2 \sqrt{ \frac{k}{m} } \, \Big ) \nonumber \\&\quad n = 1, 2, 3, \, \ldots \end{aligned}$$

(96)

Figure 5 demonstrates that all the unstable tongues in the parametric frequency space. The red and orange tongues correspond to the second and third natural frequencies, respectively, and the green tongues correspond to the combined parametric resonance. The analytical calculations in this section clearly show that the first natural frequency does not cause any parametric resonance.

5 Floquet theory

In this section, it is shown how Floquet theory is used to verify the analytical results. To this end, the governing undamped homogenous differential equations of the three DOF model is written in the state-space form as a system of first-order ordinary differential equations.

$$\begin{aligned} {\dot{x}} = A(t) x. \end{aligned}$$

(97)

The corresponding fundamental matrix of Eq. (97) is defined by the fundamental system of solutions where each column of this matrix is a linearly independent solution for Eq. (97).

$$\begin{aligned} X(t) = \begin{bmatrix} x_{11}(t) &{} x_{21}(t) &{} \ldots &{} x_{n1}(t) \\ x_{12}(t) &{} x_{22}(t) &{} \ldots &{} x_{n2}(t) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ x_{1n}(t) &{} x_{2n}(t) &{} \ldots &{} x_{nn}(t) \end{bmatrix}. \end{aligned}$$

(98)

Additionally, Eq. (97) is a system of linear differential equations with a time periodic coefficient matrix, and T is the minimal period of the coefficient matrix as it is the smallest constant positive number satisfying the following condition.

$$\begin{aligned} A(t+T) = A(t). \end{aligned}$$

(99)

The main idea of Floquet theory is that for a linear time periodic system, there is a transition matrix C that maps the state of the system from a particular time to the state of the system after one period.

$$\begin{aligned} X(t+T) = X(t) C. \end{aligned}$$

(100)

Fig. 7

Root locus of unstable cases corresponded to the second natural frequency

Such that C is a nonsingular constant matrix known as the Monodromy matrix, and according to the reducibility of the linear periodic systems, it contains complete information about the system. For a $6 \times 6$ system, the Monodromy matrix can be constructed by integrating the equations of motion for six linearly independent initial conditions. By choosing the identity matrix as the set of linear-independent initial conditions at time $t = 0$

$$\begin{aligned} X(0) = I_n. \end{aligned}$$

(101)

Equation (100) simplifies to the following solution space.

$$\begin{aligned} C = X(T). \end{aligned}$$

(102)

Consequently, numerical methods can be used to integrate Eq. (97) with initial conditions expressed by Eq. (101) for one period of oscillation. Therefore, the following Monodromy matrix is constructed out of the six solution vectors.

Fig. 8

Root locus of unstable cases corresponded to the third natural frequency

Fig. 9

Root locus of unstable cases corresponded to the combined resonance

Fig. 10

Stability chart of three DOF model for k = 0.5

Fig. 11

Stability chart of three DOF model for k = 1

Fig. 12

Stability chart of three DOF model for k = 5

$$\begin{aligned} C = \begin{bmatrix} x_{11}(T) &{} x_{21}(T) &{} x_{31}(T) &{} x_{41}(T) &{} x_{51}(T) &{} x_{61}(T) \\ x_{12}(T) &{} x_{22}(T) &{} x_{32}(T) &{} x_{42}(T) &{} x_{52}(T) &{} x_{62}(T) \\ x_{13}(T) &{} x_{23}(T) &{} x_{33}(T) &{} x_{43}(T) &{} x_{53}(T) &{} x_{63}(T) \\ x_{14}(T) &{} x_{24}(T) &{} x_{34}(T) &{} x_{44}(T) &{} x_{54}(T) &{} x_{64}(T) \\ x_{15}(T) &{} x_{25}(T) &{} x_{35}(T) &{} x_{45}(T) &{} x_{55}(T) &{} x_{65}(T) \\ x_{16}(T) &{} x_{26}(T) &{} x_{36}(T) &{} x_{46}(T) &{} x_{56}(T) &{} x_{66}(T) \\ \end{bmatrix}.\nonumber \\ \end{aligned}$$

(103)

According to Floquet Theory, Eq. (97) is stable if all the eigenvalues of the Monodromy matrix, known as Floquet Multipliers, lie on the unit circle [13]. The Monodromy matrix for this system has six eigenvalues, which are demonstrated in Figs. 6, 7, 8 and 9. Figure 6 represents the real, imaginary, and absolute values of all the eigenvalues for different values of the parametric frequency, and Figs. 7, 8 and 9 represent the root locus of the eigenvalues on the unit circle only for the unstable cases.

Figure 6 shows that two of the eigenvalues are always on the unit circle and do not cause instability. These two eigenvalues correspond to the first natural frequency of the system. This is while, for some parameters, the other four eigenvalues leave the unit circle. Figures 7 and 8 show that there are cases that only two of these eigenvalues are real and one of them falls outside of the unit circle. These cases of instability correspond to the second and third natural frequencies. Figure 9 shows that there are cases that none of the eigenvalues are real and two of them fall outside the unit circle. These cases of instability correspond to the combined parametric frequency.

6 Simulation

In this section, the fourth–fifth-order Runge–Kutta numerical integration algorithm is used to examine the accuracy of the analytical results.

6.1 Stability chart

Figures 10, 11, 12, 13, 14 and 15 show the first two unstable tongues corresponding to the second and third natural frequencies and combined parametric resonance, where the stiffness of the suspension is increased gradually. In these plots the colored area is obtained using Floquet theory, such that the red areas correspond to the second natural frequency, the orange areas correspond to the third natural frequency, and the green regions correspond to parametric combination resonances. The black solid lines are plotted by using the analytical formula obtained by the Poincare–Lindstedt method.

Fig. 13

Stability chart of three DOF model for k = 10

Fig. 14

Stability chart of three DOF model for k = 15

Fig. 15

Stability chart of three DOF model for k = 20

Fig. 16

Emanating frequency of the first tongues

Fig. 17

Slope of the first tongues

Figures 10, 11, 12, 13, 14 and 15 demonstrate agreement between the analytical and numerical calculations. By increasing the value of the stiffness of the suspension, all the unstable tongues shift toward higher frequencies. This is while, the width of the tongues corresponding to the second natural frequency increase, the width of the tongues corresponding to the third natural frequency decrease, and the width of the tongues corresponding to the combined parametric frequency increase first and then start decreasing. To have a better sense about the location and width of the unstable tongues, Eqs. (52), (58), (68) are used to plot the value of the emanating frequencies of the first tongues in Fig. 16. Eqs. (55) and (68) are used to plot the slope of the second and third natural frequencies in Fig. 17.

Fig. 18

Time response for $\zeta = 0.05, k = 20, k_0 = 0.3, F = 1, \Omega = 1.5$

Fig. 19

Time response for $\zeta = 0.05, k = 20, k_0 = 0.3, F = 2, \Omega = 1.5$

Fig. 20

Time response for $\zeta = 0.05, k = 20, k_0 = 0.3, F = 3, \Omega = 1.5$

Fig. 21

Time response for $\zeta = 0.05, k = 20, k_0 = 0.3, F = 3, \Omega = 1.9$

Figures 16 and 17 show that by choosing relatively high values for the stiffness of the suspension, the emanating frequency and the slope of the first unstable tongue related to the second natural frequency both merge to constant values. At the same time the emanating frequency and the slope of the first unstable tongue related to the third natural frequency and combined parametric frequency merge to infinity and zero, respectively. This means that for high values of the suspension stiffness, when the mountings are assumed to be rigid, the unstable tongues corresponding to the third natural frequency and combined parametric resonance vanish.

6.2 Time response

Figures 18, 19, 20 and 21 demonstrate the effect of changing the average transmitting force on the time response of the system. Figure 18 shows that for low values of the transmitting force, the system enters the dead zone area, so the permanent contact condition is violated, and the linear model is not valid. Under this condition, the effect of the backlash and impact phase must be considered. Figure 19 shows that for the larger values of the transmitting force, the time response of the system shifts up and remains outside of the dead zone area. In these conditions, the stability of the system can be determined by the stability chart demonstrated in Fig. 15. Figure 20 shows that by applying a larger transmitting force, the response of the system moves further from the dead zone area and the system is more resistant to external disturbances. Figure 21 shows that, even with large values of the transmitting force, if the system parameters are not designed properly the parametric resonance causes an increase in the amplitude of the vibration, entering into the dead zone area, and violation of the permanent contact regime.

7 Conclusion

It is well known that for a gear set with a rigid mounting assumption there is only one set of unstable tongues, and many researchers have investigated the dynamic behavior of this type of system around the unstable tongues. This is while, no studies have examined the effect of deformation of the mountings on the parametric stability of gears. Therefore, the purpose of this work is to investigate the effect of suspension on the number and location of parametric unstable tongues. The Poincare–Lindstedt method and Floquet theory are used to find the parameter space where the primary and combined parametric resonances occur.

The results of the analytical calculations show that a gear set with suspension has three natural frequencies, but only two of them participate in parametric resonance. There are two sets of unstable tongues associated with the second and third natural frequencies, and one set of unstable tongues associated with their summation. Alternatively, the numerical analysis shows that a gear set with linear suspension has a total of six Floquet multipliers. Two of these multipliers remain inside the unit circle for every value of the parametric frequency and do not cause instability. These two multipliers are associated with the first natural frequency obtained by analytical calculation. According to the numerical results, the instability of the system is related to the four other Floquet multipliers, which are associated with the second and third natural frequencies obtained by the analytical calculation. There are frequencies that two of these multipliers are real and one of them falls outside the unit circle, which corresponds to the primary parametric resonances. For some other frequencies, all four multipliers are complex when two of them fall outside of the unit circle, which corresponds to the parametric combination resonance of the summation type.

The results show that, unlike a gear set with rigid mounting that has only one set of unstable tongues, a gear set with suspension has three sets of unstable tongues. Of significance is that the location and width of all the unstable tongues depend on the stiffness of the suspension, and by increasing the values of the stiffness, these changes are observed: The primary resonance tongues corresponding to the second natural frequency expand and converge to the parameters associated with the unstable tongues of a gear set with rigid mountings. The primary resonance tongues corresponding to the third natural frequency become narrower and shift toward higher frequencies. The tongues corresponding to the combined parametric resonance first expand and then begin to narrow as they shift toward higher frequencies.

Finally, the results presented here demonstrate that the rigid mounting assumption is accurate only for gear sets under low-speed operational conditions; in these cases, both models with rigid mountings and suspension predict the same set of unstable tongues. This is while for gears operating at higher speeds, the deformation of the mounting must be included in the dynamic modeling because it causes two sets of additional unstable tongues within this region.