Vibro-impact dynamics of large-scale geared systems

Abstract

This work is concerned with the analysis of vibro-impact responses observed in large-scale nonlinear geared systems. Emphasis is laid on the interactions between the high-frequency internal excitation generated by the meshing process, i.e. the static transmission error and time-varying mesh stiffness, and low-frequency external excitations. To this end, a three-dimensional finite element model of a pump equipped with a reverse spur gear pair (gear ratio $1\!:\!1$) is built. The model takes into account the flexibility of the kinematic chain, the bearings and the housing and the gear backlash nonlinearity. A reduced-order model is solved with the Harmonic Balance Method coupled to an arc-length continuation algorithm which allows one to compute the periodic solutions of the system. The onset and disappearance of vibro-impact responses is studied through the computation of grazing bifurcations. Results show that the coupling between the external excitation and the time-varying mesh stiffness term greatly modifies the characteristics of the responses in terms of number and periodicity of impacts and contact loss duration.

1 Introduction

Gears are key components of numerous mechanical systems used to adapt and transmit speed and torques. They can be found in automotive transmissions, wind turbines [1], geared turbofan engines [2] and pumps [3, 4], to name a few. It is well known that geared systems are prone to vibration and noise issues. The meshing process, associated with the contact between gear teeth, generates an internal excitation characterized by a transmission error and time-varying mesh stiffness. The transmission error is defined as the difference between the actual position of the output gear and the position it would occupy if the gear pair were perfectly conjugate [5]. Under standard operating conditions, gear teeth are in permanent contact. However, a gap, or gear backlash, is necessary to allow for assembly and operation. Some specific operating conditions may therefore lead to contact loss and repeated impacts between gear teeth [6]. In both cases, the resulting dynamic mesh load is transmitted through the shafts to the housing. The vibratory state of the latter generates a high frequency, multi-harmonic noise, known as whining noise [7] in case of permanent contact, or rattle [8]/hammering noise [9] when impacts occur.

Most nonlinear gear dynamics studies in the literature resort to using lumped parameter, torsional models of the gear pair without considering the flexibility of other components [10,11,12,13], although some consider the shafts with a lumped torsional stiffness [14, 15] and the bearings [16, 17]. Such models are limited to a single, up to a dozen of degrees of freedom (DoF) and are quite restrictive in their assumptions. More recently, a few studies used FE models with beam elements to model the shafts [18, 19]. Both types of models suffer from a limited predictability as the effects of the housing on the driveline dynamic behaviour are neglected [20]. Furthermore, these models cannot be used to retrieve the displacement field of the housing which is essential to compute the vibro-impact-induced noise.

The most common numerical methods used in nonlinear gear dynamics studies are time integration techniques such as Runge–Kutta (RK) schemes [11, 21, 22] and the Harmonic Balance [15, 18, 23,24,25,26]. RK-based integrators are found in numerous studies as they provide the means to investigate both periodic and non-periodic responses. However, gear dynamics are characterized by stiff equations due to the contact between gear teeth and high-frequency excitations generated by the meshing process. Small time steps are thus required to ensure sufficient accuracy. Besides, taking into account the whole system usually involves considering other sources of excitation. These other sources are generally low-frequency excitations, so that time integration has to be carried out over long time intervals. All these reasons, coupled to the need to compute the transient response, lead to hefty computational efforts when employing direct time integration methods.

The HBM, on the other hand, relies on solving the equations of motion in the frequency domain by approximating the solutions with Fourier series. In contrast to time integration methods, the transient response does not need to be computed and problems associated with considering both low- and high-frequency excitations are avoided. The accuracy of the solution and computational effort directly depends on the truncation order of the Fourier series. However, the HBM framework offers ways to efficiently reduce the number of equations in the frequency domain, e.g. either by using only a subset of harmonics, as is the case with systems with dry friction where only odd harmonics contribute to the response [27], or by dynamically adapting the truncation order [28,29,30].

All excitations acting on the system are also seldom taken into account [4, 31]. Garambois et al. [4] used a FE model of a kinematic chain with beam elements and a linear model of the gear mesh, i.e. without considering the backlash nonlinearity, to study the coupling between the internal excitation and the fluctuating torques. They showed that such coupling induces a spectral enrichment as well as an increased RMS value of the dynamic response resulting in a marked influence on the perceived radiated noise.

The main contributions of the present work can be summarized as follows:

• To propose a general numerical strategy to compute the nonlinear dynamic response of a geared system with backlash nonlinearity. The strategy can be applied to systems of varying complexity, from single degree of freedom models to large-scale FE models including, for the first time, a detailed, high fidelity 3D model of the housing.

• To take into account complex loading scenario, consisting of the various multiharmonic excitations stemming from different physics (contact between gear teeth, aerodynamic forces, rotor unbalance, etc.).

• To carry out an in-depth study of the coupling between these excitations, more specifically between the low-frequency aerodynamic and unbalance forces and the parametric high-frequency gear excitation.

The structure of the paper is as follows: Sect. 2 describes the FE model and reduced-order model of the studied system. In Sect. 3, the numerical methods used to solve the equations of motion are introduced. The results are discussed in Sects.  4, and 5 draws the main conclusions and suggests directions for future research.

2 Model description

2.1 Mathematical model

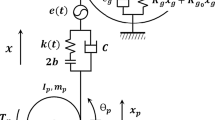
The system under investigation in this study is an industrial pump consisting of two counter-rotating shafts coupled by a spur gear pair without tooth profile modifications whose gear ratio is $1\!:\!1$ with 76 teeth. The input and output shafts thus have the same rotational speed $\varOmega$. The design characteristics of the gear pair are reported in Table 1. Since their first mode is far above the frequency range of interest, each gear blank is considered as a rigid disk with lumped mass and inertia. Each gear thus possesses six degrees of freedom (three translations and three rotations) located at its centre, as depicted in Fig. 1. More details on the contact modelling are given in Sect. 2.3.

Table 1 Characteristics of the gear pair

Fig. 1

Local frame of the gear pair

Fig. 2

Schematic representation of the system (a) and view of the FE model of the housing (b)

Each shaft is supported by two ball bearings modelled by linear axial and radial stiffness elements. 3D quadratic tetrahedral elements are used to generate the FE mesh of the shafts and the housing. They are described, respectively, by around 400,000 and 2.4 million degrees of freedom. Figure 2a depicts a schematic representation of the system, and Fig. 2b shows the geometry and mesh of the housing.

Several excitations are considered in the analysis. The external aerodynamic loading stemming from the pumping process is a narrowband random process approximated as a multi-harmonic periodic excitation. Due to the pump geometry, only even harmonics are significant. Both forces and torques are applied on twelve centreline nodes (six on each shaft) that are rigidly linked to the FE mesh of the shafts, as depicted in Fig. 2a.

$$\begin{aligned} {{\textbf {f}}}_\mathrm{{ex}}^\mathrm{{\,aero}} = \sum _{k=1}^\infty \tilde{{\textbf {f}}}_\mathrm{{ex},2k}^\mathrm{{\,aero}}\text {e}^{i2k\varOmega t} \end{aligned}$$

(1)

In the following, two harmonic components are considered, corresponding to up to harmonic $H_4$ of the shafts rotation $\varOmega$. Figure 3 shows an example of the applied aerodynamic forcing, computed in the time domain with an in-house CFD software. Its amplitude is equal to approximately $15\%$ of the applied torque $T=2.5$ N$\cdot$m. One can also see that the forcing exhibits a phase shift equal to $\pi /2$ between the input and output shafts and are of opposite signs.

An additional excitation $f_\mathrm{{unb}}$ in the form of a mass unbalance:

$$\begin{aligned} f_\mathrm{{unb},x}&= -m_\mathrm{{unb}}\varOmega ^2 \sin {\varOmega t}, \end{aligned}$$

(2)

$$\begin{aligned} f_\mathrm{{unb},y}&= -m_\mathrm{{unb}}\varOmega ^2 \cos {\varOmega t}, \end{aligned}$$

(3)

is uniformly distributed along the shafts with a phase shift equal to $\pi /2$ between the input and output shafts. The values considered is the following are $m_\mathrm{{unb}}=30\cdot 10^{-6}$ kg$\cdot$m for the input shaft and $m_\mathrm{{unb}}=20\cdot 10^{-6}$ kg$\cdot$m for the output shaft.

Fig. 3

Example of aerodynamic forcing. The blue solid line and red solid line correspond to the forcing on the input and output shafts, respectively

Considering the shaft geometry and operating speed, rotation and gyroscopic effects are neglected. The equation of motion of the system can therefore be written in the following form:

$$\begin{aligned} {{\textbf {M}}}\ddot{{{\textbf {u}}}} + {{\textbf {K}}}{{\textbf {u}}} + {{\textbf {f}}}_{nl}({{\textbf {u}}}) = {{\textbf {f}}}_{ex}, \end{aligned}$$

(4)

where ${{\textbf {M}}}$ and ${{\textbf {K}}}$ are, respectively, the mass and stiffness matrices and ${{\textbf {u}}}$ is the vector of displacements of each DoF. ${{\textbf {f}}}_{ex}$ is the vector of external periodic forcing, and ${{\textbf {f}}}_{nl}$ is the vector of nonlinear forces (cf. Sect. 2.3). Note that obvious time dependence is omitted in the notations for the sake of clarity.

2.2 Reduced-order model

The above-described FE model consists of about 3 million DoF. A direct calculation of the system’s response with classical numerical strategies would lead to intractable computations. As a first step, the FE model is thus approximated by building a representative reduced-order model.

In this work, we rely on a component mode synthesis (CMS) technique [32,33,34]. CMS methods rely on defining a number of substructures with $n_i$ internal DoF $q_i$ and $n_c$ contact DoF $q_c$ at the interface between substructures. The internal DoF are then reduced using a set of $n_{CM}$ component modes. Since only internal DoF are reduced, CMS-based reduction methods are particularly well suited when the contact interfaces comprise a small number of DoF. In our case, the contact interface only consists of the twelve DoF used to model the gear pair (see Fig. 1) which lead to a significantly smaller model. The Craig–Bampton (CB) [35] method is employed hereafter, which consists in computing a reduction basis spanned by fixed-interface modes and static constraint modes. First, the mass and stiffness matrices are partitioned into internal and contact DoF:

$$\begin{aligned} {{\textbf {K}}} = \begin{bmatrix} {{\textbf {K}}}_{ii} &{} {{\textbf {K}}}_{ic} \\ {{\textbf {K}}}_{ci} &{} {{\textbf {K}}}_{cc} \end{bmatrix}&\text { and }&{{\textbf {M}}} = \begin{bmatrix} {{\textbf {M}}}_{ii} &{} {{\textbf {M}}}_{ic} \\ {{\textbf {M}}}_{ci} &{} {{\textbf {M}}}_{cc} \end{bmatrix}. \end{aligned}$$

(5)

Fixed-interface modes are computed by solving the following eigenvalue problem:

$$\begin{aligned} \left( {{\textbf {K}}}_{ii}-\omega ^2{{\textbf {M}}}_{ii}\right) \pmb {\phi }={{\textbf {0}}}. \end{aligned}$$

(6)

Static constraint modes are computed by applying a unit displacement on each contact DoF, sequentially:

$$\begin{aligned} {\varvec{\varPsi }} = -{{\textbf {K}}}_{ii}^{-1}{{\textbf {K}}}_{ic} \end{aligned}$$

(7)

The reduction matrix ${{\textbf {T}}}$ is then formed by concatenating the fixed-interface and static constraint modes:

$$\begin{aligned} {{\textbf {T}}} = \begin{bmatrix} \pmb {\varPhi } &{} \pmb {\varPsi } \\ {{\textbf {0}}} &{} {{\textbf {I}}} \end{bmatrix} \end{aligned}$$

(8)

A Galerkin projection then yields $n_r = n_c + n_{CM}$ equations of motion in the reduced subspace written in matrix form:

$$\begin{aligned} \underbrace{{{\textbf {T}}}^T{{\textbf {M}}}{{\textbf {T}}}}_{{{\textbf {M}}}_r}\ddot{{{\textbf {q}}}} + \underbrace{{{\textbf {T}}}^T{{\textbf {K}}}{{\textbf {T}}}}_{{{\textbf {K}}}_r}{{\textbf {q}}} + \underbrace{{{\textbf {T}}}^T{{\textbf {f}}}_\mathrm{{nl}}}_{f_\mathrm{{nl}}^r}({{\textbf {T}}}{{\textbf {q}}})&= \underbrace{{{\textbf {T}}}^T{{\textbf {f}}}_\mathrm{{ex}}}_{f_\mathrm{{ex}}^r} \end{aligned}$$

(9)

where ${{\textbf {M}}}_r$, ${{\textbf {K}}}_r$ are the mass and stiffness matrices of the reduced-order model. $f_\mathrm{{nl}}^r$ and $f_\mathrm{{ex}}^r$ are the vectors of nonlinear forces and external forces, respectively.

2.3 Contact modelling

The contact between gear teeth acts in the normal direction of the tooth profile. The displacement along the line of action describes the relative deformation and contact gap between gear teeth. This relative deformation can be retrieved from the generalized coordinates ${{\textbf {q}}}$ of the reduced-order model by using a projection vector ${{\textbf {G}}}$ of size $n_r$ defined in the local frame of the gear pair (see. Fig. 1):

$$\begin{aligned} \pmb {\varDelta } = {{\textbf {G}}}^T{{\textbf {q}}}. \end{aligned}$$

(10)

Only the restriction of ${{\textbf {G}}}$ to the gear DoF ${{\textbf {q}}}_c =~\left( u_1,u_2,\right. \left. u_3,\theta _1,\theta _2,\theta _3,u_4,u_5,u_6,\theta _4,\theta _5,\theta _6\right)$ has nonzero elements, i.e.:

$$\begin{aligned} {{\textbf {G}}}|_{q_c} =&\left( 0,\, 1,\, \tan \beta ,\, r_{b,1}\tan \alpha \tan \beta ,\, -r_{b,1}\tan \beta ,\,\right. \nonumber \\&\left. r_{b,1},\,0,\, -1,\, -\tan \beta ,\,\right. \nonumber \\&\left. r_{b,2}\tan \alpha \tan \beta ,\, -r_{b,2}\tan \beta ,\, r_{b,2} \right) ^T, \end{aligned}$$

(11)

where $\alpha$ and $\beta$ are the pressure and helix angles and $r_{b,1}$ and $r_{b,2}$ are the base radii of the pinion and the gear, respectively.

Depending on the relative displacement on the line of action, the following behaviours can be observed:

• a linear behaviour, corresponding to permanent contact between gear teeth, when the vibration amplitude is smaller than the static deflection,

• single-sided impacts when oscillations are larger than the static deflection, yet small enough not to cross the gear backlash,

• double-sided impacts when the amplitude of the dynamic response is sufficient to cross the gear backlash and lead to impacts on the reverse flank of the adjacent tooth.

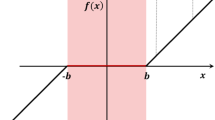
The transmitted torque induces a static deflection $q_s(\theta )$ corresponding to the static transmission error (STE), which depends on the angular position of the gear pair. When the gear pair rotates, the STE generates a displacement excitation which is periodic under stationary operating conditions. The nonlinear contact force $f_\mathrm{{nl}}$ acting between gear teeth can be linearized around the static equilibrium, i.e. $q_s(t)$, to define a time-varying mesh stiffness $k_m(t)$. Contact loss can therefore occur at a threshold g(t) (see Fig. 4):

$$\begin{aligned} g(t) = b + q_s(t) - \frac{F_s}{k_m(t)}, \end{aligned}$$

(12)

where b is the constant half backlash and $F_s$ is the transmitted load.

Fig. 4

Nonlinear force model

The nonlinear mesh force acting along the line of action is expressed as:

$$\begin{aligned} f^{LoA}_\mathrm{{nl}}\left( q,t\right)= & {} k_m(t)\left( {{\textbf {G}}}^T{{\textbf {q}}}-g\right) {\mathcal {H}}\left( {{\textbf {G}}}^T{{\textbf {q}}}-g\right) \nonumber \\{} & {} + k_m(t)\left( {{\textbf {G}}}^T{{\textbf {q}}}+g\right) {\mathcal {H}}\left( -{{\textbf {G}}}^T{{\textbf {q}}}-g\right) ,\nonumber \\ \end{aligned}$$

(13)

where ${\mathcal {H}}$ is the Heaviside step function. The generalized nonlinear force vector is thus written as:

$$\begin{aligned} {{\textbf {f}}}_\mathrm{{nl}}^{\,r}\left( q,t\right) = {{\textbf {G}}} f^{LoA}_\mathrm{{nl}}\left( q,t\right) \end{aligned}$$

(14)

The STE and mesh stiffness are computed with an in-house code based on the Reissner–Mindlin thick plate theory [36]. Due to the symmetry of the gears, an angular sector corresponding to one tooth (one mesh period) is discretized and the contact equations are solved in static conditions for each angular position.

Under stationary operating conditions, the signals are periodic and can be expressed as truncated Fourier series:

$$\begin{aligned} q_s(t)&= \sum \limits _{k=0}^{H_{q_s}} q_s^{c,k}\cos (k\varOmega t) + q_s^{s,k}\sin (k\varOmega t) \end{aligned}$$

(15)

$$\begin{aligned} k_m(t)&= \sum \limits _{k=0}^{H_{k_m}} k_m^{c,k}\cos (k\varOmega t) + k_m^{s,k}\sin (k\varOmega t) \end{aligned}$$

(16)

In the following, three harmonics are used both for the STE and mesh stiffness. Figure 5 shows the STE and mesh stiffness over two mesh period computed with an input torque $T=2.5$ N$\cdot$m. For more realistic results, tooth profile and helix errors corresponding to a quality class 6 (ISO 1328-1:2013) are taken into account in the computation.

Fig. 5

Static transmission error (a) and time-varying mesh stiffness (b) reconstructed with three harmonics at an input torque $T=2.5$ N$\cdot$m

2.4 Damping modelling

There exist numerous sources of energy dissipation and damping mechanisms in geared system, which makes them quite difficult to model accurately. Equivalent viscous damping terms acting at the gear mesh are commonly used in single degree of freedom gear models [11, 37]. In order to generalize this idea, a constant modal damping is defined with the modal basis of the underlying reduced linear system where the gears are coupled with the average mesh stiffness $\overline{k_m}$, i.e.:

$$\begin{aligned} \left( \left[ {{\textbf {K}}}_{r} + \overline{k_m}{{\textbf {G}}}{{\textbf {G}}}^T\right] -\omega _{r,j}^2{{\textbf {M}}}_{r}\right) \pmb {\phi }_r^{contact}={{\textbf {0}}}. \end{aligned}$$

(17)

It is thus possible to write the modal damping matrix ${{\textbf {C}}}_r^m$ in the reduced modal subspace:

$$\begin{aligned} {{\textbf {C}}}_r^m = {\textbf {diag}}\left( 2\xi _j\omega _{r,j}\right) , \end{aligned}$$

(18)

where $\omega _{r,j}$ is the eigenfrequency of the j-th mode of the reduced-order model and $\xi _j=5\%$ in the following. The damping matrix in the reduced subspace finally reads:

$$\begin{aligned} {{\textbf {C}}}_r = {{\textbf {M}}}_r^T \mathbf {\varPhi }_r {{\textbf {C}}}_r^{mod} \mathbf {\varPhi }_r^T{{\textbf {M}}}_r, \end{aligned}$$

(19)

where matrix $\mathbf {\varPhi }_r$ is formed with the mass-normalized eigenvectors of Eq. (17). Note that more sophisticated damping models, i.e. impact damping [38, 39], can easily be implemented since the physical gear DoFs are retained in the reduced-order model.

3 Computational strategy

3.1 Harmonic balance method

The general idea behind the HBM consists in approximating a periodic solution ${{\textbf {q}}}$ of Eq. (4) with truncated Fourier series:

$$\begin{aligned} {{\textbf {q}}} = \textrm{Re} \left( \sum \limits _{k=0}^{\infty } \tilde{{{\textbf {q}}}}_k \textrm{e}^{ik\varOmega t}\right) \approx \textrm{Re} \left( \sum \limits _{k=0}^{H} \tilde{{{\textbf {q}}}}_k \textrm{e}^{ik\varOmega t}\right) , \end{aligned}$$

(20)

where $\tilde{{{\textbf {q}}}}$ contains the coefficients of the one-sided Fourier transform. Substituting Eq. (20) into Eq. (4) and applying a Galerkin procedure yields a residual which consists of a set of $n(H+1)$ nonlinear algebraic equations:

$$\begin{aligned} {{\textbf {R}}}(\tilde{{{\textbf {q}}}},\varOmega ) = {{\textbf {Z}}}(\varOmega )\tilde{{{\textbf {q}}}} + \tilde{{{\textbf {f}}}}_\mathrm{{nl}}(\tilde{{{\textbf {q}}}}) - \tilde{{{\textbf {f}}}}_{ex} = {{\textbf {0}}}, \end{aligned}$$

(21)

where ${{\textbf {Z}}}(\varOmega )$ is the dynamic stiffness matrix duplicated on each considered harmonic:

$$\begin{aligned} {{\textbf {Z}}}(\varOmega ) = \varOmega ^2\nabla ^2\otimes {{\textbf {M}}} + \varOmega \nabla \otimes {{\textbf {C}}} + {{\textbf {I}}}_{H+1}\otimes {{\textbf {K}}}. \end{aligned}$$

(22)

where $\otimes$ is the Kronecker product and $\nabla$ the frequency domain differential operator:

$$\begin{aligned} \nabla = {\textbf {diag}}(0,i,2i,\dots ,Hi). \end{aligned}$$

(23)

It is worth noting that the present study only investigates period-one solutions. Subharmonic responses can be computed by modifying the Fourier base used in the HBM formulation [24, 40].

The Fourier coefficients of the nonlinear forces are evaluated using Eq. (14) and the alternating frequency/time (AFT) scheme [41] whose principle is summarized in Fig. 6.

Fig. 6

Illustration of the AFT procedure

Eq. (21) can be solved using a Newton–Raphson-based iterative solver to yield the solution at a given frequency. In order to compute the response in a given frequency range, the frequency $\varOmega$ is treated as an unknown and the response curve is parameterized by its curvilinear abscissa to avoid difficulties with vertical tangents at turning points. An arc-length continuation procedure is also implemented. The arc-length continuation is a predictor/corrector scheme (see Fig. 7) which relies on finding an approximate solution $\tilde{{{\textbf {Q}}}}_{(p)} = \left( \tilde{{{\textbf {q}}}} \,\, \varOmega \right) _{(p)}^T$ based on the previously computed solution point $\tilde{{{\textbf {Q}}}}_{(k)}$ and iteratively performing corrections on the predicted solution until convergence is reached. A thorough description of the numerical methods employed in this work can be found in [15, 26].

Fig. 7

Illustration of the arc-length continuation

3.2 Condensation on the nonlinear degrees of freedom

The nonlinear force stemming from the contact between gear teeth and backlash nonlinearity only act on a small set of DoF, i.e. the twelve DoF representing the gear pair. It is possible to exploit this sparsity to only retain the nonlinear DoF as unknowns of the problem and greatly reduce the computational time [42]. The equations of motion are first partitioned into nonlinear (subscript ’nl’) and linear (subscript ’ln’) DoF:

$$\begin{aligned} \begin{bmatrix} {{\textbf {Z}}}_\mathrm{{ln},\textrm{ln}} &{} {{\textbf {Z}}}_\mathrm{{ln},\textrm{nl}}\\ {{\textbf {Z}}}_\mathrm{{nl},\textrm{ln}} &{} {{\textbf {Z}}}_\mathrm{{nl},\textrm{nl}} \end{bmatrix} \begin{pmatrix} \tilde{{{\textbf {q}}}}_\mathrm{{ln}} \\ \tilde{{{\textbf {q}}}}_\mathrm{{nl}} \end{pmatrix} + \begin{pmatrix} {{\textbf {0}}} \\ \tilde{{{\textbf {F}}}}_\mathrm{{nl}} \end{pmatrix} = \begin{pmatrix} \tilde{{{\textbf {F}}}}_{ex,\mathrm{{ln}}} \\ \tilde{{{\textbf {F}}}}_{ex,\mathrm{{nl}}} \end{pmatrix}, \end{aligned}$$

(24)

which yields:

$$\begin{aligned} {{\textbf {Z}}}_r\tilde{{{\textbf {q}}}}_\mathrm{{nl}} + \tilde{{{\textbf {F}}}}_\mathrm{{nl}} = \tilde{{{\textbf {F}}}}_{r}, \end{aligned}$$

(25)

where ${{\textbf {Z}}}_r$ is the Schur complement of the linear part of the dynamic stiffness matrix and $\tilde{{{\textbf {F}}}}_{r}$ is the condensed external forcing vector:

$$\begin{aligned} \begin{aligned} {{\textbf {Z}}}_r&= {{\textbf {Z}}}_\mathrm{{nl},\textrm{nl}} - {{\textbf {Z}}}_\mathrm{{nl},\textrm{ln}}{{\textbf {Z}}}_\mathrm{{ln},\textrm{ln}}^{-1}{{\textbf {Z}}}_\mathrm{{ln},\textrm{nl}}, \\ \tilde{{{\textbf {F}}}}_{r}&= \tilde{{{\textbf {F}}}}_\mathrm{{ex},\textrm{nl}} - {{\textbf {Z}}}_\mathrm{{nl},\textrm{ln}}{{\textbf {Z}}}_\mathrm{{ln},\textrm{ln}}^{-1}\tilde{{{\textbf {F}}}}_\mathrm{{ex},\textrm{ln}}. \end{aligned} \end{aligned}$$

(26)

The Jacobian matrix can be expressed by direct differentiation of Eq. (26) with respect to the unknowns:

$$\begin{aligned} \partial _\varOmega {{\textbf {Z}}}_r&= \partial _\varOmega {{\textbf {Z}}}_\mathrm{{nl,nl}}\nonumber \\&- \left( \partial _\varOmega {{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}{{\textbf {Z}}}_\mathrm{{ln,nl}} \right. \nonumber \\&+{{\textbf {Z}}}_\mathrm{{nl,ln}}\partial _\varOmega {{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}{{\textbf {Z}}}_\mathrm{{ln,nl}} \nonumber \\&\left. +{{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}\partial _\varOmega {{\textbf {Z}}}_\mathrm{{ln,nl}}\right) , \end{aligned}$$

(27)

$$\begin{aligned} \partial _\varOmega \tilde{{{\textbf {F}}}}_{r}&= \,\partial _\varOmega \tilde{{{\textbf {F}}}}_\mathrm{{ex,nl}}\nonumber \\&-\left( \partial _\varOmega {{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}\tilde{{{\textbf {F}}}}_\mathrm{{ex,ln}} \right. \nonumber \\&+{{\textbf {Z}}}_\mathrm{{nl,ln}}\partial _\varOmega {{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}\tilde{{{\textbf {F}}}}_\mathrm{{ex,ln}} \nonumber \\&+\left. {{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}\partial _\varOmega \tilde{{{\textbf {F}}}}_\mathrm{{ex,ln}} \right) . \end{aligned}$$

(28)

The above expressions involve the inverse of the linear part of the dynamic stiffness matrix ${{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}$. This can lead to heavy computational effort as the number of linear degrees of freedom increases, even with the preliminary CMS reduction described in Sect. 2.2. To keep the computational time to a minimum, the inverse ${{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}$ is not computed explicitly. Instead, the terms $\partial _\varOmega {{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}$, ${{\textbf {Z}}}_\mathrm{{nl,ln}}\partial _\varOmega {{\textbf {Z}}}_\mathrm{{ln,ln}}^{-1}$ and ${{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_{ln,ln}^{-1}$ are evaluated by solving three linear systems [43]:

$$\begin{aligned} {{\textbf {Z}}}_\mathrm{{ln,ln}}^T{{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-T} =&\,\, {{\textbf {Z}}}_\mathrm{{nl,ln}}^T, \nonumber \\ {{\textbf {Z}}}_\mathrm{{ln,ln}}^T {{\textbf {Z}}}_\mathrm{{nl,ln}}\partial _\varOmega {{\textbf {Z}}}_\mathrm{{ln,ln}}^{-T} =&- \partial _\varOmega {{\textbf {Z}}}_\mathrm{{ln,ln}}^{T}{{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-T},\\ {{\textbf {Z}}}_\mathrm{{ln,ln}}^T\partial _\varOmega {{\textbf {Z}}}_\mathrm{{nl,ln}}{{\textbf {Z}}}_\mathrm{{ln,ln}}^{-T} =&\,\, \partial _\varOmega {{\textbf {Z}}}_\mathrm{{nl,ln}}^T.\nonumber \end{aligned}$$

(29)

3.3 Detection of grazing bifurcations

The non-smoothness of the nonlinear contact force can give rise to discontinuity-induced bifurcations [44]. Of particular importance in this paper are grazing bifurcations, characterized by impacts with zero normal velocity, which mark the onset and disappearance of vibro-impacting orbits. It is usual in bifurcation analysis to define test functions whose zeros indicate bifurcation points. In this work, grazing bifurcations are detected by monitoring the changes of sign of $\phi _\mathrm{{GR}}$ defined as:

$$\begin{aligned} \phi _\mathrm{{GR}} = 1 - 2\,{\mathcal {H}}\left( 1-\bigg \langle {\mathcal {H}} \left( {{\textbf {G}}}^T{{\textbf {q}}}-g(t)\right) \bigg \rangle \right) , \end{aligned}$$

(30)

where $\langle \bullet \rangle$ denotes the mean value over one fundamental period. Before a grazing bifurcation, the gear teeth are in permanent contact and, assuming ${\mathcal {H}}(0) = 0$, $\phi _\mathrm{{GR}}$ equals 1. As soon as the teeth lose contact, the value of $\phi _\mathrm{{GR}}$ switches to $-1$ until contact is re-established over the whole rotation period. Thus, a grazing bifurcation corresponding to the onset (resp. disappearance) of vibro-impacting orbits is detected when $\phi _\mathrm{{GR}}$ switches from 1 to $-$1 (resp. from $-$1 to 1). The accuracy of the detection depends directly on the number of harmonics retained in the HBM approximation and on the number of harmonics used to describe the mesh stiffness and static transmission error.

4 Results and discussion

4.1 Preliminary analysis

The accuracy of the reduced-order model is dependent on dimension of the reduced subspace, i.e. the number of fixed-interface modes used to approximate the dynamics of the linear part of the system. This number ought to be large enough to describe the vibration behaviour resulting from all excitations. The frequency range in which the reduced-order model is valid is dictated by the maximum frequency of the internal excitation, since its acts at a significantly higher frequency than the external excitation and all fixed-interface modes are considered up to truncation order $n_{CM}$.

In the following, the validity of the reduced-order model is evaluated using the concept of mesh energy $\rho$ [20] defined for each mode of the underlying linear system by Eq. (31):

$$\begin{aligned} \rho _j = \frac{\pmb {\phi }_j^T \left[ \overline{k_m} {{\textbf {G}}}{{\textbf {G}}}^T\right] \pmb {\phi }_j}{\pmb {\phi }_j^T \left[ {{\textbf {K}}}+\overline{k_m} {{\textbf {G}}}{{\textbf {G}}}^T\right] \pmb {\phi }_j}, \end{aligned}$$

(31)

with:

• $\pmb {\phi }_j$ the eigenvector of the j-th mode,

• ${{\textbf {G}}}$ the projection vector defined by Eq. (11),

• $\left[ {{\textbf {K}}}\right]$ the stiffness matrix of the system without coupling between gear teeth.

Modes with a high mesh energy can be excited by the high-frequency internal excitation. It is therefore necessary to ensure those modes are correctly described by the reduced-order model. In the following, we consider 3 harmonics of the internal mesh excitation, corresponding to harmonics $H_Z$, $H_{2Z}$ and $H_{3Z}$ of the shaft rotation. Figure 8 shows the Campbell diagram of the underlying linear system, i.e. with the gears coupled by the average mesh stiffness $\overline{k_m}$. Excitation orders are shown in solid black lines, and the modes are plotted as horizontal lines with energy-dependent colours. For readability reasons, only modes with a mesh energy greater than 3% are plotted. One can see that several modes have a significant mesh energy. The mode with most mesh energy ($\rho = 32\%)$ lies at 4 kHz. The highest frequency of a mode with mesh energy is 5 kHz. By keeping $n_{CM}=250$ component modes in the reduction, Fig. 9 shows that the reduced-order model is valid until more than $\varOmega = 9$ kHz.

Fig. 8

Campbell diagram of the underlying linear system. Excitation orders corresponding to the internal excitation are plotted in solid black lines. The colour of the horizontal lines corresponds to the mesh energy of the corresponding mode. (Color figure online)

The response being approximated by Fourier series, the accuracy directly depends on the number of retained harmonics. As such, harmonics present in the excitation must be included. The TVMS is a multi-harmonic parametric excitation which is expected to induce a coupling between the external excitation, leading to additional harmonics in the response. In our case, the frequency of the external excitation is significantly lower (up to harmonic $H_4$ of the shaft rotation) than that of the internal excitation (harmonics kZ, $k\in {\mathbb {N}}$ of the shaft rotation). Sidebands around each considered mesh harmonic should therefore be retained in the Fourier series for an accurate description of the response.

Fig. 9

Relative error on the frequency of the modes of the linearized reduced-order model with respect to those of the full FE model

With large-scale systems, each additional harmonic can lead to a significant increase in the computational time. Thus, a convergence study with all excitation sources is first carried out to determine the smallest set of harmonic to consider for the analysis. Figure 10 shows the evolution of the standard deviation (SD) of the mesh load, computed with Eq. (13), with respect to the rotational frequency of the shafts for several number of harmonics. The complete list can be found in Table 2. One can see that convergence in term of mesh load is reached with 20 harmonics. Most features of the forced response curve are well captured once all harmonics of the internal excitation ($H_{kZ}$, $k\in {\mathbb {N}}$ of the shaft rotation) are included in the computation. However, it is clear that the coupling between internal and external excitations severely affects the primary resonance peak and more harmonics need to be taken into account for a satisfying accuracy.

Figure 11 depicts the frequency of all detected grazing bifurcations with respect to the number of harmonics. The vertical dashed lines correspond to a $\pm 1$% error centred on the most converged computation. It appears that carrying out the computation with an insufficient number of harmonics leads to the inaccurate detection of vibro-impact responses. For instance, the computation with 5 harmonics cannot detect the grazing bifurcations occurring at low frequencies. Furthermore, one can see that satisfying accuracy is reached with 14 harmonics, which is smaller than the number of harmonics required for a good description of the forced response curve. A set of 20 harmonics is therefore used throughout the rest of this paper. All computations were performed on a PC equipped with an AMD Ryzen 9 5950X CPU (16 cores, 32 threads) with a base clock speed equal to 3.4 GHz and 64 Gb RAM. The total computation time depends on the continuation step size, number of harmonics and sampling in the AFT procedure. With the parameters used in this paper, the average computation time is 11 s per solution point.

4.2 Coupling between internal and external excitations

In order to highlight the coupling between internal and external excitations in the nonlinear regime, we carry out three analyses with an input torque $T =2.5$ N$\cdot$m corresponding to a static mesh load $F_s=70$ N:

• the first one corresponds to a forced response computation considering only the internal excitation,

• the second one considers only the external excitation (aerodynamic loading and mass unbalance) and STE with a constant mesh stiffness (the average value over one vibration cycle),

• the third one includes all excitations.

Fig. 10

Convergence of the standard deviation of the dynamic mesh load with respect to the number of retained harmonics. Diamond markers correspond to grazing bifurcation points. (Color figure online)

Fig. 11

Convergence of grazing bifurcations with respect to the number of retained harmonics. The vertical dashed lines correspond to a $\pm 1$% error centred on the most converged computation with 24 harmonics

Figure 12 depicts the evolution of the dynamic mesh load with respect to the rotational frequency for all cases. The regions where the response exhibits vibro-impacts are delimited by coloured diamond markers denoting grazing bifurcations. It appears that including low-frequency external excitation leads to a higher amplitude of the dynamic response away from resonances, both at low and high frequencies. Furthermore, contrary to the resonances at $\varOmega = 1085$ rpm and $\varOmega = 1580$ rpm which are almost unaffected, the primary resonance peak is modified. Its amplitude decreases from 93 N when only the internal excitation is considered to 88 N with all excitations. Besides, its shape is also significantly impacted by the coupling between internal and external excitations, leading to smaller amplitude-jump instabilities.

Fig. 12

Evolution of the standard deviation of the mesh load with respect to the rotational speed. Computation with all excitations (red), all excitations except the TVMS and external excitations (blue) and internal excitation only (purple). Coloured diamond markers represent grazing bifurcations. (Color figure online)

Figure 13 shows the frequency at which grazing bifurcations occur for the considered excitation scenario. One can see that the external excitation leads to an increase in the frequency range exhibiting vibro-impacts, as grazing bifurcations occurring at $\varOmega = 1000$ rpm and $\varOmega = 1300$ rpm appear more spread. Overall, the span of vibro-impact regions increases by 14% when all excitations are considered.

4.3 Influence of the excitations on the vibro-impact characteristics

Figure 14 depicts the evolution of the standard deviation of the mesh load with respect to the rotational speed. One can see three main resonance peaks located at $\varOmega = 1070$ rpm, $\varOmega = 1570$ rpm and $\varOmega = 3000$ rpm, corresponding to the excitation of the mode with highest mesh energy by the three harmonics of the internal excitation $H_{3Z}$, $H_{2Z}$ and $H_{Z}$, respectively.

Five grazing bifurcations are observed on the forced response curve. In the following, they are referred to with their number of appearance with respect to the rotational speed. For clarity, regions of the forced response curve exhibiting vibro-impacts are highlighted in blue. The first grazing bifurcation around $\varOmega = 994$ rpm marks the onset of a vibro-impact region spanning $\varDelta \varOmega =260$ rpm until the second grazing bifurcation at $\varOmega = 1255$ rpm. A small interval of responses with permanent contact conditions can be observed following this bifurcation until the appearance of a third grazing bifurcation at $\varOmega = 1295$ rpm. The responses exhibit vibro-impacts until a speed $\varOmega = 2202$ rpm where the fourth grazing bifurcation occurs, leading to another small interval without vibro-impacts. At $\varOmega = 2378$ rpm, the forced response curve exhibits a grazing bifurcation responsible for the appearance of vibro-impacting responses over the rest of the frequency range of interest.

Fig. 13

Frequency location of grazing bifurcations for all considered cases. Grazing bifurcations, represented by diamond markers, associated with both ends of a vibro-impact region are plotted in the same color

Fig. 14

Forced response curve with both internal and external excitations. Blue diamond markers denote grazing bifurcations, and blue highlights denote vibro-impacting responses

Fig. 15

Time series of the dynamic mesh load (a, b) and dynamic transmission error (d, e) and harmonic content of the dynamic mesh load (c) at $\varOmega = 2970$ rpm. Close-ups of the dynamic mesh load (b) and dynamic transmission error (e). Black dashed lines correspond to the gap limit, i.e. teeth flanks

Time responses can be evaluated from the Fourier coefficients computed with the HBM. Figure 15 depicts the time series of the dynamic mesh load computed with Eq. (13) and the dynamic transmission error computed with Eq. (10) at $\varOmega = 2970$ rpm, where the most energetic mesh mode is excited by the first harmonic of the internal excitation $H_{Z}$. Figure 15a, b shows that the dynamic mesh load goes to zero, indicating a contact loss, repeatedly during the rotation period. This induces impacts on the teeth flanks. Note that the mesh load is always positive or null. This indicates that impacts always occur on the active tooth flanks and that the vibration amplitude is never high enough to cross the gear backlash. This is confirmed by Fig. 15d which shows the dynamic transmission error over two fundamental periods. The response exhibits a low-frequency modulation due to the aerodynamic loads (harmonic $H_2$ of the shaft rotation, also visible in Fig. 15c) with a peak-to-peak amplitude equal to 4 $\mu$m which is much smaller than the gear backlash $b = 40$ $\mu$m.

Figure 15c shows the harmonic content of the dynamic mesh load at $\varOmega = 2970$ rpm. One can see that the response is strongly multi-harmonic with harmonics of the mesh frequency ($H_{Z}$, $H_{2Z}$ and $H_{3Z}$), low-frequency harmonics stemming from the aerodynamic forcing ($H_{2}$ and $H_{4}$). Sidebands generated by interactions between the aerodynamic forcing and the time-varying mesh stiffness can be observed only around mesh harmonics $H_{Z}$ and $H_{2Z}$. Sidebands around harmonics $H_{3Z}$ and $H_{4Z}$ do not appear for they were not considered in the computation. Note that the amplitude of the sidebands is of the same order of magnitude as the $H_2$ harmonic.

Figure 15e is a close-up of Fig. 15d. The black dashed line represents the gap limit corresponding to the teeth flanks with the STE. It appears clearly that impacts occur once every fundamental period of the STE, i.e. 76 times per shaft rotation. Note that due to the low-frequency modulation, the impact velocity varies periodically. This results in significant variations of the dynamic mesh load, as evidenced in Fig. 15b. The smallest impacts generate a mesh load equal to 180 N while the largest ones generate a mesh load equal to 260 N. This corresponds to a variation of 44% of the dynamic mesh load occurring twice per shaft rotation.

Figure 16 shows the time series and harmonic content of the dynamic mesh load computed with Eq. (13) and the time series of the dynamic transmission error computed with Eq. (10) at $\varOmega = 6875$ rpm. At this rotational speed, the frequency of the internal excitation is too high to excite the mesh modes. The small dynamic amplification visible in Fig. 14 is induced by the excitation of a shaft mode by the external excitation. One can see from Fig. 16a that the gear response is governed by the second harmonic of the shaft rotation induced by the aerodynamic forcing, with the amplitude of the mesh harmonics relatively small. The peak-to-peak amplitude of the mesh load is significantly smaller than the one at $\varOmega = 2970$ rpm (160 N instead of 275 N).

Fig. 16

Time series of the dynamic mesh load (a, b) and dynamic transmission error (d, e) and harmonic content of the dynamic mesh load (c) at $\varOmega = 6875$ rpm. Close-ups of the dynamic mesh load (b) and dynamic transmission error (e). Black dashed lines correspond to the gap limit, i.e. teeth flanks

Fig. 17

Time series of the dynamic transmission error at $\varOmega = 1700$ rpm where the response exhibits one impact per period (a) and two impacts per period (b). The black dashed line corresponds to the gap limit

Fig. 18

Time series of the dynamic transmission error at $\varOmega = 1070$ rpm where the response exhibits permanent contact (a), one impact per period (b), two impacts per period (c) and three impacts per period (d). The black dashed line corresponds to the gap limit

This is confirmed by Fig. 16c which shows the harmonic content of the dynamic mesh load at $\varOmega = 6875$ rpm. Compared to the results at $\varOmega = 2970$ rpm, harmonics $H_{2}$ and $H_{4}$ appears much more prominent, with harmonic $H_{2}$ of the same order of magnitude as the mesh harmonics. Furthermore, the amplitude sidebands around each mesh harmonic are quite noticeably smaller.

Figure 16e shows that vibro-impacts still occur once per mesh period with 76 impacts per shaft rotation. However, Fig. 16a clearly shows intermittent phases of vibro-impacts induced by the low frequency modulation. Phases of permanent contact lasting several mesh periods ($\approx 22\%$ of the shaft rotation) alternate with phases of vibro-impacts, lasting approximately $28\%$ of the shaft rotation, twice per shaft rotation.

The same analysis can be carried out over the whole forced response curve. Figure 17a, b shows two close-ups of the time series of the dynamic transmission error at $\varOmega = 1700$ rpm. At this rotational speed, the external excitation-induced modulation does not lead to alternating phases of permanent contact and phases with 1 impact per period of the internal excitation (1-IPP). Instead, the modulation induces a change in the number of impacts per period during the rotation of the shafts. The dynamic response exhibits 1-IPP during around 20% of the shaft rotation and 2-IPP for the rest of the rotation. Note that the change in the number of IPP is governed by the external excitation so that it occurs twice per shaft rotation in the following sequence:

• 2-IPP (40% of the rotation),

• 1-IPP (10% of the rotation),

• 2-IPP (40% of the rotation),

• 1-IPP (10% of the rotation).

The response at $\varOmega = 2970$ rpm exhibits an even more complex vibro-impacting behaviour. Figure 18 shows close-ups of the time series of the dynamic transmission error at $\varOmega = 1070$ rpm, corresponding to the resonance of the most energetic mesh mode excited by the third harmonic of the internal excitation $H_{3Z}$.

One can see that, since the response is governed by the third harmonic of the internal excitation, the response exhibits sequentially permanent contact, 1-IPP, 2-IPP and 3-IPP with continuous, smooth transitions between each type of behaviour in the following sequence:

• Permanent contact (14.5% of the rotation),

• 1-IPP (4% of the rotation),

• 2-IPP (5.25% of the rotation),

• 3-IPP (17% of the rotation),

• 2-IPP (5.25% of the rotation),

• 1-IPP (4% of the rotation),

• Permanent contact (14.5% of the rotation),

• 1-IPP (4% of the rotation),

• 2-IPP (5.25% of the rotation),

• 3-IPP (17% of the rotation),

• 2-IPP (5.25% of the rotation),

• 1-IPP (4% of the rotation).

5 Concluding remarks

Gears are an essential component of a plethora of mechanical systems present in almost all industrial sectors. A thorough understanding of their dynamic behaviour is thus of crucial importance to achieve efficient designs to meet the ever more stringent demands of the industry. Such demands often require that all components be included in the mechanical analyses to obtain representative models. Besides, mechanical systems are often a significant source of noise that ought to be reduced as much as possible. Thus, it is of vital importance to model the flexibility of the housing and to employ numerical methods able to deal with the considerable increase in the dimension of the system.

In this regard, this paper proposed a computational strategy to study the periodic solutions of large-scale geared system. It is based on a spectral technique, the harmonic balance method, coupled to an arc-length continuation algorithm. The industrial-scale model is reduced in two steps. Firstly, the Craig–Bampton method allows one to a few hundreds of degrees of freedom. Secondly, the number of equations in the spectral domain is reduced to twelve via an exact explicit condensation on the gear degrees of freedom. The proposed methodology is able to compute the periodic solutions of high-fidelity models of geared systems composed of several millions of degrees of freedom. The dynamic response at the gear can then be used to reconstruct the response of all degrees of freedom, allowing one to retrieve the dynamic response of the housing which can be used to evaluate the radiated sound.

Besides, retaining the gear degrees of freedom as physical coordinates with the Craig–Bampton reduction allows one to modify the gear and carry out an optimization of the gear design parameters to minimize the dynamic response without having to compute an updated reduced order model.

The main findings of this paper show that the parametric mesh stiffness induces a coupling with the low frequency external excitation generated by the pumping process of the pump under study. This coupling induces an enrichment of the harmonic content of the dynamic transmission error with sidebands around each gear mesh harmonic. As a result, depending on the rotational speed and dynamic amplifications due to mesh modes and/or shaft modes, one can observe either alternating phases of permanent contact and vibro-impacts or transitions between responses with 1 impact per period and 2 impacts per period. Future work will focus on computing the radiated noise and evaluating the effect of these modulations on the acoustic perception.

Appendix

See Table 2.

Table 2 List of harmonics used in the convergence study