Effects of the gear eccentricities on the dynamic performance of a planetary gear set

Abstract

Gear eccentricities are one of the practical types of the manufacturing errors that affect the dynamic performance of a planetary gear train (PGT). Previous research about the effects of the gear eccentricities is abundant, and many of them focus on the parallel shaft gear set. However, almost none of them have considered the influence of the gear eccentricities on the mesh stiffness. In fact, the existence of the gear eccentricities can change the center distance and the mesh positions of a meshing gear pair, which will directly affect the mesh stiffness. Situation can be even more complex for the PGT with either sun gear eccentricities or planet gear eccentricities or both of them. Based on that, a new dynamic model of a PGT with gear eccentricities is established. The planar motions of the PGT and the mesh stiffness are integrated and solved simultaneously where the mesh stiffness is determined by the actual mesh positions of the meshing gear pair. The mesh stiffness is calculated by the energy potential method. The time-varying center distance caused by the gear eccentricities is also considered, which can result in the change of line of action, pressure angle, contact ratio and mesh positions. The influence of gear eccentricities on the dynamic performance of a 4-planet PGT is studied. Some useful results are derived at last.

1 Introduction

Planetary gear trains (PGTs) are widely used in the industry applications (e.g., wind turbine, aerospace, etc.) due to their significant advantages including compactness, high power density, as well as the reduced noise and vibration. There have been numerous studies on the PGTs in various aspects. Most attentions are attracted on the vibration, load sharing and noise of PGTs as they are the primary concerns in applications.

The primary advantage of a PGT is that it can carry more load than a parallel shaft gear set as the power is split nearly equally among planets. To achieve this objective, it is essential to guarantee the equal load sharing among planets. As a result, strict restrictions on the manufacturing and assembly tolerances, such as the pinhole position errors, the tooth profile errors and the gear eccentricity errors (i.e., gear eccentricities) [1,2,3], are required for the PGTs. Moreover, gear eccentricities can induce dynamic excitation and complex modulations which will further influence the overall dynamic performance [4]. A series of papers were completed by Hidaka who studied the dynamic behavior of a PGT showing that the load sharing in a three-planet gear set is perfectly equal if one of the central members is allowed to float [5, 6]. Kahraman et al. [1, 2] established a lumped parameter model to investigate the influence of the carrier pin hole and planet run-out errors on the planet load sharing under dynamic condition. They divided manufacturing errors into three groups: time-invariant and assembly-independent errors, time-invariant and assembly-dependent errors, as well as time-varying and assembly-dependent errors. Cheon and Parker [7] analyzed the effects of gear eccentricity errors and other manufacturing errors on bearing forces and critical tooth stress by using a hybrid finite element method. Meanwhile, Chaari et al. [4] and Chen and Shao [8] studied the dynamic behavior of a PGT with the gear eccentricity errors, tooth profile errors considering the gyroscopic effect. They indicated that the gear mesh frequency was modulated by the gear eccentricity errors, and for larger eccentricity errors the transmission would deteriorate with the gear mesh frequency drowned in the defect signal. Inalpolat and Kahraman [9] introduced a discrete dynamic model to predict the modulation sidebands of the PGTs. Their model was formed by assuming that the mesh interface displacement excitations were amplitude- and frequency-modulated due to the gear eccentricity errors. However, the influence of gear eccentricity errors on the mesh stiffness was not discussed. Kim et al. [10] noticed that the existence of gear eccentricities and bearing deformations can change the center distance, line of action (LOA), pressure angle and contact ratio of a meshing gear pair. They proposed a dynamic model that firstly regards them as time-varying variables in literature. However, they used the traditional mesh stiffness model (square wave form) proposed by Kahraman et al. [1] that is independent on the actual mesh positions. Recently, Gu and Velex [11] proposed an original lumped parameter model to study the dynamic load sharing characteristics of a PGT with the pinhole position errors and gear run-out errors where the tooth excitation associated with tooth mesh were derived from the instantaneous contact condition.

In most of the above-mentioned lumped parameter models, gear eccentricity errors were usually simulated as the displacement excitations by projecting eccentricity errors on the LOA and offline of action (OLOA) [10,11,12]. Some researchers have already noticed that gear eccentricity errors can induce time-varying LOA, pressure angle and contact ratio, and discovered that the dynamic response of gear transmission system may be modulated. However, almost all of them treated the mesh stiffness model as the same as the case without gear eccentricities. The influence of gear eccentricities on the mesh stiffness was completely neglected. In fact, gear eccentricities can change the center distance and mesh positions of a meshing gear pair, which will directly affect the mesh stiffness. Situation can be even more complex for the PGT with either sun gear eccentricities or planet gear eccentricities or both of them. Hence, in this paper, a new dynamic model of an N-planet PGT with gear eccentricity errors is proposed. The eccentricity errors are intrinsically incorporated into the dynamic model of the PGT by considering the time-varying distance caused by the gear eccentricity errors. The mesh stiffness is calculated based on the potential energy method according to the actual mesh positions of a meshing gear pair. Dynamic characteristics of a 4-planet PGT with gear eccentricity errors will be presented base on the proposed model.

Fig. 1

Lumped parameter model of an N-planet planetary gear set

2 Dynamic model of a planetary gear set with gear eccentricities

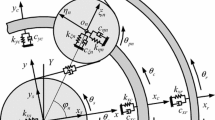
Figure 1 shows the overall dynamic model of an N-planet planetary gear set. Each component (sun, ring, carrier and every planet) is represented by a rigid disk with three degrees of freedom (DOF), i.e., translations in the horizontal and vertical directions, and rotation along its central axis. The coordinate is built on a rotating carrier reference frame with a constant carrier rotating speed $\Omega _{c}$, which is fixed to the carrier with origin O. The translations of component j in the horizontal and vertical direction are denoted by $x_{j}$ and $y_{j}$, respectively (j = s, c, r and pn representing the sun, the carrier, the ring and the nth planet respectively). The infinitesimal rotation $\theta _{j}$ is fluctuating around the relative nominal rotation (rigid body motion) of the $j\hbox {th}$ component with a rotating speed $w_{j}$ in the rotating reference, whereas the absolute rotating speed of jth component in the static reference is $w_{j}+\Omega _{c}$. Therefore, the gross rotation of component j is $w_{j}t+\theta _{j}$ in the rotating reference. The elastic linear support of each component is represented by two linear springs in two perpendicular directions, which are denoted by $k_{jx}$ and $k_{jy}$, respectively. The torsional constraint on the each center member (sun, ring, and carrier) is denoted by the stiffness $\hbox {k}_{j\theta }$. The nth sun–planet and ring-planet mesh behaviors are represented by time-varying springs parallel to their corresponding LOA, denoted as kspn and krpn.

The sun gear is assumed as the input element and rotates in the anticlockwise direction. The carrier is the output element, and the ring gear keeps fixed. The mass and the polar moment of inertia of each member of the PGT are denoted as $m_{j}$ and $I_{j}$, respectively. The base radius of each member is indicated by $r_{bj}$, and the distance between the centers of sun/ring and planets is indicated by $R_{c}$.

2.1 Actual mesh positions and mesh deformations of a meshing gear pair

For involute spur gear mesh, the mesh force is transmitted along LOA and the deformation is also measured along the LOA direction. When eccentricity error occurs on either the sun, or the planet, or the ring gear, its base circle will rotate around its corresponding rotating center. Consequently, the LOA is changing with the rotation of base circle. In the dynamic model of PGT, it is assumed that the mesh force is in the new LOA direction. In addition, bearing deformations will lead to the translation of the gears that will also influence the direction of LOA. For the sake of completeness, bearing deformations are included in this study. Apart from the gear eccentricities and the bearing deformations, no other factors are considered to affect the LOA.

Figure 2 shows the planar motions of the sun gear and the nth planet. Line $N_{s}N_{pn}$ is the original LOA, which should be tangent with the base circles of sun gear ($r_{bs}$) and $n\hbox {th}$ planet ($r_{bpn}$). As the sun gear and the planet rotate, the contact region of the conjugated tooth pair moves and the mesh deformation of the nth planet–sun at a specific time instant t is obtained by calculating the overlap between the two un-deformed gear teeth. Once the positions of the planet and the sun gear are known, the mesh deformation of the nth planet–sun at t can be determined according to the geometry of the gear teeth [13]. In order to calculate the mesh deformation, an arbitrary initial position needs to be set as the reference. Similar to most of the other studies [13, 14], the moment when the 1st planet firstly contacts at pitch point with the sun is defined as the initial state. The initial positions of other sun–planet meshes are determined according to the phasing relationship, which depends on the direction of planet rotation. Detailed discussions about it can be found in [14].

Fig. 2

Planar motions of the sun and the nth planet

The eccentricity error of each component in PGT is defined by two parameters, the amplitude $e_{j}$ and the initial phase angle $\varepsilon _{j}$, as illustrated in Fig. 2. If one or more members of PGT have the eccentricity error, for example, if the nth planet has eccentricity amplitude of $e_{pn}$, and the sun gear has eccentricity amplitude of $e_{s}$, the geometric center of the sun will translate from $O_{s}$ to ${O}'_s$, and the planet from $O_{pn}$ to ${O}'_{pn}$. The LOA will be changed from line $N_{s}N_{pn}$ to line ${N}'_s {N}'_{pn}$. An overlap or gap will thus be generated between the gear meshes in the new LOA. So, in the initial condition of PGT, some of the sun–planet meshes may be in contact, while some others in separation.

Fig. 3

Variations of mesh positions and LOA with eccentric sun and planet gears

Fig. 4

Equivalent motions of the final positions of the gear centers

Under a certain load, the sun has translational motions $x_{s}$, $y_{s}$ and rotational motion $w_{s}t+\theta _{s}$, whereas the nth planet has translational motions $x_{pn}$, $y_{pn}$ and rotational motion $w_{pn}t +\theta _{pn}$. The rotational motion of the sun will move its geometric center from ${O}'_s$ to ${O}'''_s$, whereas the rotational motion of the nth planet will move its geometric center from ${O}'_{pn}$ to ${O}'''_{pn}$. In addition, the translational motions of the sun will further move ${O}'''_s$ to ${O}''_s$ and the translational motions of the nth planet will further move ${O}'''_{pn}$ to ${O}''_{pn}$. These center movements are shown in Fig. 3. In a word, the final positions of gear centers are achieved by two successive steps, i.e., rotational motion from $O_{j}'$ to $O_{j}'''$ and translational motions from $O_{j}'''$ to $O_{j}''$, as shown in Fig. 4.

It can be noticed that the center distance and the pressure angle between the nth planet and the sun or ring gear have changed because of the bearing deformations and gear eccentricities. At a specific time t, the mesh deformation is determined by the overlap (or gap) between the conjugated tooth pair. The new center distance of the sun–planet or the ring-planet is given as:

$$\begin{aligned} {d}'_{in} =\sqrt{d_{in\_x}^2 +d_{in\_y}^2 } \end{aligned}$$

(1)

where

$$\begin{aligned} d_{in\_x}= & {} R_c \cos \varphi _n +x_{pn} -x_i \nonumber \\&+\, e_{pn} \cos (w_p t+\varepsilon _{pn} +\theta _{pn} )\nonumber \\&-\,e_i \cos (w_i t+\theta _i +\varepsilon _i ) \end{aligned}$$

(2)

$$\begin{aligned} d_{in\_y}= & {} R_c \sin \varphi _n +y_{pn} -y_i\nonumber \\&+\,e_{pn} \sin (w_p t+\varepsilon _{pn} +\theta _{pn} )\nonumber \\&-\,e_i \sin (w_i t+\theta _i +\varepsilon _i ) \end{aligned}$$

(3)

where $i=s$ for the sun–planet and $i=r$ for the ring-planet. $\varphi _{n}$ is the spacing angle of nth planet as illustrated in Fig. 1.

The new pressure angle is

$$\begin{aligned} \alpha ^{\prime }_{in} = a \hbox { cos} \frac{r_{bi}+s_{1}r_{bp}}{d^{\prime }_{in}} \end{aligned}$$

(4)

where $s_{1}$ = 1 for $i=s$ and $s_{1} = -1$ for $i=r$. The roll angle is used to locate the contact point of the conjugated tooth pair. The length of $\delta _{ipn}$ along the new LOA is given by

$$\begin{aligned} \delta _{ipn} = r_{bi} \beta _{in} + s_{1}r_{bp}\beta ^{i}_{pn}+s_{2}d^{\prime }_{in} \hbox { sin }\alpha ^{\prime }_{in} \end{aligned}$$

(5)

where the roll angle of the sun/ring gear is,

$$\begin{aligned} \beta _{in}= \alpha ^{\prime }_{in} - \alpha _{i} + s_{2}(\varphi ^{i}_{n} - \varphi _{n}) + \theta ^{0}_{in} + s_{1} (w_{i}t+ \theta _{i})\nonumber \\ \end{aligned}$$

(6)

and the roll angle of the nth planet is,

$$\begin{aligned} \beta ^{i}_{pn}= & {} \alpha ^{\prime }_{in} - \alpha _{i}+\textit{s}_2(\varphi ^i_n-\varphi _n)+\theta ^{i0}_{pn}+\textit{s}_1(\textit{w}_p{t}+\theta _{pn}\nonumber \\ \end{aligned}$$

(7)

where $s_{2} = -1$ for $i=s$ representing the sun–planet mesh and $s_{2}$ = 1 for $i=r$ representing the ring-planet mesh. $\varphi _{n}^{i}$ is the angle between the line connecting the centers of the nth planet and the ith member (i.e., the sun or the ring) and the horizontal axis. $\theta _{in}^0$ is the initial roll angle of the ith member meshing with the nth planet when there is no error. $\theta _{pn}^{i0}$ is the initial roll angle of the nth plant meshing with the ith member when there is no error.

2.2 Calculation of the mesh stiffness based on the actual mesh positions

Mesh stiffness is an important intrinsic excitation to the gear transmission systems. Even if there are no manufacturing errors or assembly errors, gear transmission systems will still exhibit vibration problem due to the fluctuation of the number of tooth pair in the mesh zone [15, 16]. For the PGT, mesh stiffness will also affect its stability, natural frequency and vibration characteristic [17,18,19,20]. For ideal gear meshes, mesh stiffness is a periodic function whose period is the time interval of two neighboring teeth entering into the contact zone. As one of the inputs to the dynamic equations of motion, mesh stiffness should be obtained before solving equations.

The mesh stiffness of a conjugated gear pair can be calculated by the analytical methods [21,22,23], or the finite element methods [24, 25], or the hybrid methods [26, 27]. The general approach to acquire the mesh stiffness is to fix the driven gear and adjust the position of driving gear to make them in contact. Then, the gears are loaded and the mesh stiffness value at this angular position can be calculated. Rotating the driving gear to the other angular positions and repeating the previous steps, the mesh stiffness values at these new positions can be obtained. When the sun, planets and ring have eccentricity errors, if the normal mesh stiffness is still used, the following problems arise: (1) the introduction of the eccentricity error will make the theoretical geometric center of the component considered rotating in a circle rather than fixed. Therefore, LOA will change with the theoretical geometric center circulating around the rotating center. Meanwhile, the contact ratio is no longer constant and the period of the mesh stiffness is time varying as the center distance between gear centers is changing; (2) supposing the angular position of the driving gear is known, the actual contact positions of the conjugated tooth pair with the gear eccentricities will differ from that of the case without the gear eccentricities, which will further change the magnitude variation of the mesh stiffness.

The mesh stiffness of a conjugated gear pair is related to the deflection of each tooth treated as a non-uniform cantilever beam fixed to the rigid fillet foundation, the deflection of the rigid tooth caused by the flexible fillet foundation (i.e., gear body), and the hertz contact deformation. The elastic deformation of one tooth as a beam contains bending, shearing, and axial deformations. Since the mesh stiffness is usually calculated when the conjugated tooth pair is in contact, its value will be different in different contact positions. In this study, a more realistic method is taken into consideration. The mesh stiffness is obtained based on the un-deformed gear profile as shown in Fig. 5. Intersections between the LOA and teeth profiles of the mating tooth pair are the acting points of the mesh force.

Fig. 5

Calculation of the mesh stiffness of an eccentric planetary gear set a mesh position of the eccentric planetary gear set, b non-uniform cantilever beam model of the spur gear tooth

The bending, shearing and axial compressive stiffness of an external spur gear (i.e., the sun and planets of the PGT as shown in Fig. 1) tooth under a mesh force F are given as [23]:

$$\begin{aligned} \frac{1}{k_{b}}= & {} \int \nolimits _{0}^{d} \frac{[F(d-x) \hbox {cos }\alpha _{1}- Fh \hbox { sin } \alpha _{1}]^{2}}{2EI_{x}} \mathrm{d}\alpha \nonumber \\= & {} \int \nolimits _{-\alpha 1}^{\alpha 2} \frac{3\Big \{1+ \hbox {cos }\alpha _{1}[(\alpha _{2}-\alpha )\hbox {sin }\alpha - \hbox {cos }\alpha ]\Big \}^{2}\, (\alpha _{2}-\alpha )\hbox {cos }\alpha }{2EL\left[ \hbox {sin }\alpha + (\alpha _{2}- \alpha )\hbox {cos }\alpha \right] ^{3}} \mathrm{d}\alpha \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} \frac{1}{K_{s}}= & {} \int \nolimits ^{0}_{d} \frac{1.2\, \hbox {cos}^{2}\,\alpha _{1}}{GA_{x}} \mathrm{d}x\nonumber \\= & {} \int \nolimits _{-\alpha _{1}}^{\alpha _{2}}\frac{1.2\,(1+\nu )(\alpha _{2}-\alpha )\hbox {cos }\alpha \hbox { cos}^{2}\alpha _{1}}{GL\left[ \hbox {sin }\alpha + (\alpha _{2}- \alpha )\hbox {cos }\alpha \right] } \mathrm{d}\alpha \nonumber \\ \end{aligned}$$

(9)

$$\begin{aligned} \frac{1}{K_{a}}= & {} \int _0^d {\frac{\sin ^{2}\alpha _1 }{EA_x }} \mathrm{d}x\nonumber \\= & {} \int _{-\alpha _1 }^{\alpha _2 } {\frac{(\alpha _2 -\alpha )\cos \alpha \sin ^{2}\alpha _1 }{2EL\left[ {\sin \alpha +(\alpha _2 -\alpha )\cos \alpha } \right] }} \mathrm{d}\alpha \nonumber \\ \end{aligned}$$

(10)

where $\alpha _{2}$ is the half base tooth angle shown in Fig. 5b. $\alpha _{1}$ is related with the roll angle in Eqs. (6) and (7). That is, for the sun gear $\alpha _{1} = \beta _{sn}- \alpha _{s2}$, and for the nth planet $\alpha _{1}=\beta _{pn}^s- \alpha _{p2}$. $\alpha _{s2}$ and $\alpha _{p2}$ are the half base tooth angles of the sun and planet. The derivations of the bending, shearing and axial compressive stiffness of an internal spur gear (i.e., the ring of the PGT as shown in Fig. 1) is similar to those of the external spur gear and will not be detailed here. Explicit explanations can be found in [28]. It should be noted that the upper limit of the integral should be replaced by the actual roll angle of the ring gear.

The total stiffness of a meshing tooth pair from a meshing gear pair (sun–planet or ring-planet) is represented by

$$\begin{aligned} K_{ip}= & {} 1\Big /\left( \frac{1}{K_{bi}}+\frac{1}{K_{si}}+\frac{1}{K_{ai}}+\frac{1}{K_{fi}}\right. \nonumber \\&\left. +\,\frac{1}{K_{bp}}+\frac{1}{K_{sp}}+\frac{1}{K_{ap}}+\frac{1}{K_{fp}}+\frac{1}{K_\mathrm{h}}\right) \end{aligned}$$

(11)

where $K_\mathrm{h}$ is the hertz contact stiffness; $K_{f}$ is the stiffness due to the fillet foundation, and $i=s$ or r, representing the sun and the ring respectively. Their expressions can be found in [23].

Table 1 Parameters of the planetary gear train

Fig. 6

Comparisons between the mesh stiffnesses and mesh forces obtained by the proposed model and the model in [1] with $e_{s} = 20$ $\upmu$m and $f_{m}=3500$ Hz a stiffness of the 1st planet–sun mesh, b stiffness of the 1st planet-ring mesh, c mesh force of the 1st planet–sun mesh, d mesh force of the 1st planet-ring mesh

Fig. 7

Comparisons between the mesh stiffnesses obtained by the proposed model and traditional model with $e_{p1} = 300\,\upmu$m and $f_{m}=3500$ Hz a stiffness of the 1st planet–sun mesh, b enlarged view of (a), c stiffness of the 1st planet-ring mesh, d enlarged view of (c)

Fig. 8

Comparisons between the amplitude spectrums of the 1st planet’s torsional vibration $\theta _{p1}$ obtained by the proposed model and traditional model with $e_{s} = 300\,\upmu$m and $f_{m}=3500$ Hz

Fig. 9

Amplitude spectrums of the 1st planet’s torsional vibration $\theta _{p1}$ with $e_{s} = 200\,\upmu$m, $e_{p1}= 200\,\upmu$m and $f_{m}=3500$ Hz obtained by the a traditional model, b proposed model

The total stiffness of a meshing gear pair is the sum of the stiffness of all meshing tooth pairs. With the time-varying center distance and the elastic tooth deformations considered, the contact ratio should be recalculated. Whether the teeth are in contact or not depends on the actual roll angles of the sun/ring gear and the planet gear. The total mesh stiffness of the nth planet–sun mesh is,

$$\begin{aligned} k_{spn} =\left\{ \begin{array}{ll} \sum \limits _{k=1}^M k_{spn}^{k}, &{}\quad \gamma _{{snl}} \!\le \! \beta _{sn}^k \!\le \! \,\gamma _{snu},\,\gamma _{{pnl}} \!\le \! \beta _{pns}^k \!\le \! \gamma _{pnu} \\ 0, &{}\quad \mathrm{else} \end{array} \right. \!\!\!\! \end{aligned}$$

(12)

where

$$\begin{aligned} \gamma _{snl}= & {} \left( {{d}'_{sn} \sin ({a}'_{sn} )-\sqrt{r_{as}^2 -r_{bs}^2 }} \right) \Big /r_{bp} \end{aligned}$$

(13)

$$\begin{aligned} \gamma _{snu}= & {} \hbox {tan} \left( a \hbox { cos} \frac{r_{bs}}{r_{as}}\right) \end{aligned}$$

(14)

$$\begin{aligned} \gamma _{pnl}= & {} \left( d'_{sn} \hbox { sin}(\alpha ^{\prime }_{sn}) + \sqrt{r_{ap}^{2}- r_{bp}^{2}}\right) \Big / r_{bs} \end{aligned}$$

(15)

$$\begin{aligned} \gamma _{pnu}= & {} \hbox {tan}\left( \alpha \hbox { cos} \frac{r_{bp}}{r_{ap}}\right) \end{aligned}$$

(16)

and M is the total number of tooth pair in mesh of the nth planet–sun mesh. $k_{spn}^k$ is the mesh stiffness of the kth tooth pair of the nth planet–sun mesh. $r_{as}$ and $r_{ap}$ are the radii of addendum circles of the sun and the planet, respectively. The total mesh stiffness of the nth planet-ring mesh is

$$\begin{aligned} k_{rpn} =\left\{ \begin{array}{ll} \sum \limits _{k=1}^{{M}'} k_{rpn}^k,&{} \quad \rho _{{rnl}} \le \beta _{rn}^k \le \hbox { }\rho _{rnu} ,\,\rho _{{rnl}} {\le } \beta _{pnr}^k {\le } \rho _{rnu} \\ 0,&{}\quad \mathrm{else} \\ \end{array} \right. \!\!\!\!\!\!\nonumber \\ \end{aligned}$$

(17)

where

$$\begin{aligned} \rho _{rnl}= & {} \left( \sqrt{r^{2}_{ar}-r^{2}_{ar}} - d^{\prime }_{rn} \hbox { sin}(a^{\prime }_{rn})\right) \Big / r_{bp} \end{aligned}$$

(18)

$$\begin{aligned} \rho _{snu}= & {} \hbox {tan} \left( a \hbox { cos} \frac{r_{bp}}{r_{ap}}\right) \end{aligned}$$

(19)

$$\begin{aligned} \gamma _{pnl}= & {} \hbox {tan} \left( a \hbox { cos} \frac{r_{br}}{r_{ar}}\right) \end{aligned}$$

(20)

$$\begin{aligned} \gamma _{pnu}= & {} \left( \sqrt{r^{2}_{ap}-r^{2}_{bp}}- d^{\prime }_{rn} \hbox { sin}(a^{\prime }_{rn})\right) \Big / r_{bs} \end{aligned}$$

(21)

$M'$ is the total number of tooth pair in mesh of the nth planet-ring mesh. $k_{rpn}^k$ is the mesh stiffness of the kth tooth pair of the nth planet-ring mesh. $r_{ar}$ is the radius of addendum circle of the ring.

2.3 Lumped parameter model of a planetary gear set

The lumped parameter model of an N-planet PGT is shown in Fig. 1. The dynamic mesh force between an engaged gear pair is

$$\begin{aligned} F_{ipn} = K_{ipn} \delta _{ipn} \end{aligned}$$

(22)

The total number of DOF in this model is 3$N+9$. Based on the force and moment equilibrium, the governing equations of motion of this model are

$$\begin{aligned}&m_c (\ddot{x}_c -2\Omega _c \dot{y}_c -\Omega _c^2 x_c )\nonumber \\&\quad +\sum _{n=1}^N {k_p (x_c -x_{pn} -R_c \theta _c \sin \varphi _n )} +k_c x_c =0 \nonumber \\&m_c (\ddot{y}_c +2\Omega _c \dot{x}_c -\Omega _c^2 y_c )\nonumber \\&\quad +\sum _{n=1}^N {k_p (y_c -y_{pn} +R_c \theta _c \cos \varphi _n )} +k_c y_c =0 \nonumber \\&I_c \ddot{\theta }_c -\sum _{n=1}^N k_p (x_c -x_{pn} -R_c \theta _c \sin \varphi _n )R_c \sin \varphi _n \nonumber \\&\quad +\sum _{n=1}^N {k_p (y_c -y_{pn} +R_c \theta _c \cos \varphi _n )R_c \cos \varphi _n } \nonumber \\&\quad +\,k_{c\theta } \theta _c =T_c \nonumber \\&m_r (\ddot{x}_r -2\Omega _c \dot{y}_r {-}\Omega _c^2 x_r )\,{-}\sum _{n=1}^N {F_{rpn} \sin \varphi _{rn} }\,{+}\,k_r x_r =0 \nonumber \\&m_r (\ddot{y}_r \,{+}\,2\Omega _c \dot{x}_r {-}\Omega _c^2 y_r )\,{+}\sum _{n=1}^N {F_{rpn} \cos \varphi _{rn} } +k_r y_r =0 \nonumber \\&I_r \ddot{\theta }_r +\sum _{n=1}^N {F_{rpn} r_{br} +k_{r\theta } \theta _r =0} \nonumber \\&m_s (\ddot{x}_s {-}2w_c \dot{y}_s {-}w_c^2 x_s )\,{-}\sum _{n=1}^N {F_{spn} \sin \varphi _{sn} } {+}k_s x_s =0 \nonumber \\&m_s (\ddot{y}_s {+}2w_c \dot{x}_s {-}w_c^2 y_s )\,{+}\sum _{n=1}^N {F_{spn} \cos \varphi _{sn} } {+}k_s y_s =0 \nonumber \\&I_s \ddot{\theta }_s +\sum _{n=1}^N {F_{spn} r_{bs} +\,k_{s\theta } \theta _s =T_s } \nonumber \\&m_p (\ddot{x}_{pn} -2\Omega _c \dot{y}_{pn} +\Omega _c^2 (x_{pn} +\,R_c \cos \varphi _n ))\nonumber \\&\quad +\,F_{spn} \sin \varphi _{sn} +F_{rpn} \sin \varphi _{rn} -k_p (x_c -x_{pn} \nonumber \\&\quad -\,R_c \theta _c \sin \varphi _n )=0 \nonumber \\&m_p (\ddot{y}_{pn} +2\Omega _c \dot{x}_{pn} -\Omega _c^2 (y_{pn} +R_c \sin \varphi _n ))\nonumber \\&\quad -\,F_{spn} \cos \varphi _{sn} -F_{rpn} \cos \varphi _{rn} \nonumber \\&\quad -\,k_p (y_c -y_{pn} +R_c \theta _c \cos \varphi _n )=0 \nonumber \\&\quad I_p \ddot{\theta }_{pn} +F_{spn} r_{bp} -F_{rpn} r_{bp} =0 \end{aligned}$$

(23)

where $\varphi _{sn}=\varphi _n^s - {a}'_{sn}, \varphi _{rn}=\varphi _n^r +{a}'_{rn}$, $k_{j}$ ($j=c$, r, s and p representing the carrier, ring, sun and planets, respectively) is the radial stiffness of the corresponding bearing. $k_{j\theta }$ is the torsional stiffness. $T_{c}$ and $T_{s}$ are the external torques applied on the carrier and the sun gear, respectively.

Fig. 10

Comparisons between the time-history LSR curves calculated by the proposed model and the traditional model with $e_{s} = 300\,\upmu$m and $f_{m}=3000$ Hz: a LSR of the sun–planet, b enlarged view of (a)

3 Results and discussion

A 4-planet PGT is used to study the dynamic characteristics of the system with gear eccentricity errors. The sun gear is the input element and rotates in the anticlockwise direction. The carrier is the output element and the ring gear keeps fixed. The input torque on the sun gear is 600 Nm, and the output torque on the carrier is 2000 Nm. The mesh frequency of the PGT is set as $f_{m}$=3500 Hz. The values of key system parameters are shown in Table 1. Unless otherwise explicitly stated, these parameters’ values are used for all of the following simulations. The mesh stiffnesses of the sun–planet and the ring-planet are calculated based on the potential energy method according to the actual mesh positions of the conjugated (meshing) gear pair introduced in Sect. 2. A fixed step four order Runge–Kutta method is adopted to solve the differential equations of motion of the PGT.

3.1 Effects of eccentricity error on the mesh stiffness, dynamic response and load sharing characteristics

In the first case, a light load and small gear eccentricities are applied on the PGT. The external load on the sun gear is set as 30 Nm .The amplitude of sun gear eccentricity is set as $e_{s} = 30\,\upmu \hbox {m}$, and all the other bodies are assumed to have no eccentricity error (i.e., $e_{pi}=e_{r}$ = 0). Results from the proposed model will be compared with those from the traditional method in [1] in order to exhibit the new findings. In [1], the mesh stiffness is approximately simulated by rectangular waves and the eccentricity error is considered as a displacement excitation. In this model, the mesh stiffness is calculated based on the potential energy method according to the actual mesh positions induced by the gear eccentricity errors as well as the bearing deformations.

The simulated time-history mesh stiffness curves of the 1st planet–sun mesh and 1st planet-ring mesh are shown in Fig. 6a, b. The mesh forces of the 1st planet–sun mesh 1st and planet-ring mesh are shown in Fig.6c, d. It can be found that the mesh stiffnesses and mesh forces yielded by both methods agree well except slight differences in amplitudes. This is because the load is light, the amplitudes of gear eccentricities are small, and the geometric centers of gears translate in a small range. Therefore, gear actual mesh positions are slightly affected. The fact that these two models generate similar results in case of small translations validates the proposed model to a certain extent.

A larger sun gear eccentricity ($e_{s} = 300\,\upmu \hbox {m}$) is considered this time to investigate its influence on the mesh stiffness and dynamic behavior of the PGT. The mesh stiffnesses calculated from both methods are shown in Fig. 7. It can be seen that in the traditional model, the mesh stiffness wave in each mesh cycle is same, whereas in the proposed method, the amplitude and frequency of the mesh stiffness wave in each mesh cycle are periodically changing depending on the rotation of the eccentric sun gear. The amplitude difference is due to the periodic change of the actual mesh positions, whereas the frequency difference is due to the varying contact zones defined by Eqs. (13)–(16) for the sun–planet mesh and Eqs. (18)–(21) for the ring-planet mesh. These phenomena demonstrate that the influence of large gear eccentricity on the mesh stiffness is obvious, and the proposed model is more realistic and accurate than the traditional model to yield the mesh stiffness.

Fig. 11

Influence of the amount of 1st planet eccentricity amplitude $e_{p1}$ on the a maximum LSR of the 1st planet–sun, b mesh stiffness of the 1st planet–sun, c amplitude spectrum of the 1st planet’s torsional vibration ($f_{m}$=3500 Hz)

Figure 8 compares the amplitude spectrums of the 1st planet’s torsion vibration $\theta _{p1}$ simulated by the proposed model and traditional model [1] with sun eccentricity $e_{s} = 300\,\upmu \hbox {m}$. The abscissa ranges from 3000 to 15000 Hz to highlight the mesh frequency (3500 Hz) and its harmonics. There are sidebands appearing around the gear mesh frequency and its harmonics in the spectrums from both models. Compared with the results of traditional model, the amplitude of the second harmonic of mesh frequency is smaller and the sidebands $2f_{m}\,\pm \,f_{s}$ are larger in results of proposed model. More sidebands $2f_{m}\,\pm \,2f_{s}$ are found in the spectrum obtained from the proposed model. The sidebands are symmetric about the second harmonic of mesh frequency in the spectrum obtained from the traditional model, whereas there are asymmetric in the proposed model. Meanwhile, the same phenomenon appears near the third and fourth harmonics of mesh frequency. This is because, in the proposed model, the calculated mesh stiffness is much more complex than the rectangular-shape mesh stiffness approximated by the traditional model. Its amplitude and frequency are different for each mesh cycle. Hence, the 1st planet’s torsional vibration $\theta _{p1}$ is complicatedly modulated under the sinusoidal displacement excitation and complex mesh stiffness excitation.

Fig. 12

Maximum LSR of the 1st plane-sun with eccentric planet 1 under different initial phase angles

Fig. 13

LSR of the PGT with two eccentric planets a two neighboring eccentric planets with $e_{p1} = 100\,\upmu$m and $e_{p2} = 100\,\upmu$m, b two diametrically opposed eccentric planets with $e_{p1} = 100\,\upmu$m and $e_{p3} = 100\,\upmu$m

Dynamic characteristics of the PGT with sun gear and one planet having eccentricity errors are also analyzed. Eccentricity errors with $e_{s} = 200\,\upmu \hbox {m}, e_{p1} = 200\,\upmu \hbox {m}$ at $\varepsilon _{s} = \varepsilon _{p1} = 0$ are applied to the PGT. Spectrums of the 1st planet’s torsional vibration $\theta _{p1}$ obtained by both models are plotted in Fig. 9. Similarly, the frequency ranges are limited from 3000 to 15000 Hz. Major differences can be seen around the second, third and fourth harmonics of mesh frequency. In the spectrum of traditional method, only $2f_{m}\pm f_{s}$ and $2f_{m}\pm f_{p}$ $(f_{p}=f_{m}/Z_{p})$ appear around the $2f_{m}$, whereas in the proposed method, the side frequencies are much more abundant. Apart from the $2f_{m}\pm {nf}_{s}$ and $2f_{m}\pm {nf}_{p}$ (n is integer), there are many other sidebands $2f_{m}\pm {nf}_{s}\pm f_{1}$ around the $2f_{m}$, where $f_{1}$ is the greatest common divisor of $f_{s}$ and $f_{p}$. It should be noted that the amplitude spectrum characteristics may be different for other rotational speeds and planet arrangements such as 3-planet or 5-planet etc.

Dynamic load sharing ratio (LSR) is a parameter evaluating the dynamic load sharing among planets and the dynamic factor of a PGT. It is defined as the ratio of the actual dynamic load and the designed static load [1]. For a specific planet n, the dynamic LSR includes the sun–planet LSR and the ring-planet LSR, denoted by $L_{spn}$ and $L_{rpn}$ respectively. Figure 10 shows the dynamic LSR of a sun–planet with $e_{s}$ = 300 um. It is found that the maximum dynamic LSR calculated by the proposed method is larger than that by the traditional method.

Figure 11a depicts the variation of maximum dynamic LSR under 7 different amounts of 1st planet eccentricity error $e_{p1}$. Figure 11b, c shows the time-history mesh stiffness curves and the frequency responses of 1st planet’s torsional vibration $\theta _{p1}$ under three different amounts of 1st planet eccentricity error $e_{p1}$. The maximum dynamic LSR of the 1st planet–sun is nearly linearly growing with the amplitude of gear eccentricity $e_{p1}$ increasing from 0 to $400\,\upmu \hbox {m}$. There is a positive correlation between the peak-to-peak value of mesh stiffness and the amplitude of the eccentricity error as shown in Fig. 11b. In Fig. 11c, the larger the amplitude of the 1st planet eccentricity, the more abundant of the side frequencies around the mesh frequency harmonics, and the larger of the amplitudes of these side frequency components. Therefore, the transmission efficiency of the PGT declines as the eccentricity error increases.

3.2 Load sharing characteristics of the PGT under different assembly configurations

Eccentricity error is a time-varying and assembly-dependent error [1, 2]. Under different assembly configurations, load sharing characteristics of the PGT are performed. We first consider that only the 1st planet has the eccentricity error ($e_{p1} = 100\,\upmu \hbox {m}$). Figure 12 shows the variation of the maximum dynamic load sharing ratio $L_{sp1}$ of the PGT when the initial phase angle $\varepsilon _{p1}$ varies from 0$^\circ$ to 360$^\circ$. It can be found that $L_{sp1}$ is not constant and ranged from 2.07 to 2.26. The reason for the variation is that the dynamic LSR is the product of the load sharing ratio and the dynamic factor. Since the tangential component of the planet eccentric error (for the nth planet, the tangential direction is perpendicular to the line connecting the center of the sun and the center of the nth planet) leads to the unequal load sharing among planets, the static LSR reaches its maximum value whenever the 1st planet rotates to the position where the eccentricity error is in the tangential direction. The dynamic factor is a periodic function with the frequency $f_{m}$. Although the initial phase angle will not influence the maximum value of the static LSR, it will affect the phase difference between the maximum static LSR and the dynamic factor and further influence the maximum dynamic LSR.

Next, we consider that two planets have eccentricity errors, which can be divided into two cases, i.e., two neighboring planets or two diametrically opposed planets having eccentricity errors. Assuming planets 1 and 2 (i.e., neighboring planets), or planets 1 and 3 (i.e., diametrically opposed planets), have the same amplitude of eccentricity error, which is $100\,\upmu \hbox {m}$. Their initial phase angles are allowed to range from 0$^\circ$ to 360$^\circ$ incrementally. In Fig. 13a, when the initial phase angle of planet 2 is 90$^\circ$ larger than that of planet 1, the PGT gets a better dynamic load sharing characteristic. However, when the initial phase angle of planet 2 is 90$^\circ$ less than that of planet 1, the PGT gets a worse dynamic load sharing characteristic. In Fig. 13b, when the initial phase angle of planet 1 is equal to that of planet 3, a better dynamic load sharing characteristic can be achieved. The dynamic LSR of the first case is ranged from 1.85 to 2.85, whereas the dynamic LSR of the second case is ranged from 1.87 to 2.42. The above results indicate that the initial phase angle of the gear eccentricity error will affect the dynamic characteristics of the PGT significantly. Therefore, appropriate assembly configuration can help to achieve better dynamic LSR. For example, for a 4-planet PGT consisting of two eccentric planets and two perfect planets, the two eccentric planets should be installed adjacently with their initial phase positions perpendicular to each other, or installed diagonally with their initial phase positions in the same direction.

4 Conclusion

In this study, a new dynamic model of the PGT with gear eccentricities is established. The main improvement of the proposed model against previous models is that the influence of gear eccentricities on the mesh stiffness of a meshing gear pair (sun–planet or ring-planet) is considered. A 4-planet planetary gear is used as an example to analyze the dynamic characteristics (i.e., 1st planet’s torsional vibration and LSR) of the PGT with various amounts and initial phase angles of the gear eccentricities. Meanwhile, the influence of gear eccentricities on the mesh stiffness of the meshing gear pair with gear eccentricities is quantitatively discussed. Although the eccentricity error is exclusively analyzed in this paper, other manufacturing errors, such as the pinion position error, can be easily incorporated in this model.

The main conclusions are listed below.

• (1) The eccentricity error of a meshing gear pair within the PGT will lead to cycle-to-cycle variations in the magnitude and frequency of mesh stiffness, which would result in complex modulation phenomenon on the dynamic response of PGT.

• (2) The increase in the magnitude of gear eccentricity error will not only deteriorate the dynamic LSR of PGT, but also affect the dynamic transmission of PGT.

• (3) The assembly configuration of the planet eccentricity error has great influence on the dynamic LSR of PGT. Simulation results illustrate that appropriate assembly configuration can help to achieve better dynamic LSR.