1 Introduction

High contact ratio gears (HCRG) are generally referred as a spur gear mesh with a contact ratio between two and three. This means there are at least two tooth pairs in contact at all times during the gear mesh, whereas conventional low contact ratio gears (LCRG) alternate between one and two pairs in contact [1]. HCRG have been received much concern especially in the military application fields, because they have the advantages of higher power-to-weight ratio, higher load-carrying capacity, smoother running, and lower noise attributes, etc. [2, 3].

Though HCRG have many significant advantages, it would be expected that HCRG would be more sensitive to tooth spacing errors and tooth profile modifications because of the multiple tooth contacts. In the past few decades, most of research on HCRG has mainly been concentrated on tooth load sharing, stress analysis, and tooth profile modification. Staph [4] discussed the effects of gear parameters on several performance factors of HCRG and gave a method to tooth load sharing in HCRG. Cornell and Westervelt [1] developed a dynamic model for calculating the dynamic tooth loads and root stresses for HCRG. Based on the compliance equations of the loaded teeth, Rosen and Frint [2] presented an analytical method to calculate the HCRG tooth load sharing. Similar methods were also adopted by Elkholy [5], Tavakoli and Houser [6], and Mohanty [7]. Wang and Howard [8] used finite element analysis (FEA) to calculate the load sharing ratio, contact stress and the maximum tooth root stress of HCRG. Rameshkumar [3] studied the load sharing ratio, bending stress, contact stress, and deflection for LCRG/HCRG in a tracked vehicle final drive with FEA. Recently, Sánchez et al. [9, 10] proposed a load distribution model based on the minimum elastic potential (MEP) criteria for the calculations of contact stress and tooth root stress for HCRG and helical gears. Subsequently, they again presented an enhanced model for the calculations of the meshing stiffness and the loading sharing ratio for HCRG and LCRG considering the hertzian deflections [11]. Ye and Tsai [12] employed a loaded tooth contact analysis (LTCA) method to explore the contact characteristics of HCRG with and without flank modification in consideration of tip corner contact and shaft misalignment.

The gear teeth under heavily loaded condition are prone to deflection, which will result in the increase in vibration and noise of the mechanical systems. Tooth profile modification is regarded as one of the most effective ways to reduce the dynamic loads and vibrations of gear systems. Most of the literature on profile modification has been focused on the LCRG, but fewer contributions deal with the HCRG. Lee et al. [13] investigated the effects of linear profile modification and applied loading on the dynamic load and tooth root stress of HCRG. Whereafter, they examined and compared both linear and parabolic tooth profile modification of HCRG under various loading conditions [14]. It has been found that parabolic profile modification prevails over linear profile modification for HCRG because of it lower sensitivity to manufacturing errors. Yildirim [15, 16] proposed a new type of double relief which can be viewed as a superposition of a short and a long relief combining the advantages of these two limiting profile modifications. The research revealed that the overall performance of such double relief is superior to that of conventional single slope relief. Wang and Howard [17], and Velex [18] further confirmed that double profile relief can improve the dynamic behavior of HCRG. Faggioni et al. [19] developed a Random-Simplex optimization algorithm in search of the optimal profile modification to reduce gear vibration, using the peak to peak of the STE or the vibration level as the objective functions.

Many researchers have devoted themselves to the dynamic characteristics of low contact ratio spur and helical gears, and a great many useful results have been gained, such as periodic solution, sub-harmonic resonance, super-harmonic resonance, periodic coexistence and chaos. There is a great amount of literature on gear dynamics and dynamic modeling of gear systems. Özgüven and Houser [20] first reviewed the linear dynamic models of geared systems comprehensively. Wang et al. [21] gave an overview of the nonlinear vibration of geared systems. Özgüven and Houser [22] used a single degree of freedom (SDOF) nonlinear model for the dynamic analysis of a gear pair, including the effects of TVMS, damping, gear errors, profile modifications and backlash. Based on this research, Özgüven [23] developed a six degrees of freedom (DOFs) model for the dynamic analysis of a gear system including shaft and bearing dynamics, and studied the effect of lateral-torsional vibration coupling on the dynamics of gears. Kahraman and Singh [24,25,26] proposed a series of studies for the influence of several factors on the frequency responses of nonlinear geared system based on the 1DOF and 3 DOFs models, such as time-variant mesh stiffness, gear backlash, bearing clearances, and external/internal excitations. Their results have laid a solid foundation for the work of the subsequent researchers. Blankenship et al. [27, 28] examined analytically and experimentally the nonlinear dynamic behavior of a mechanical oscillator with periodical time-varying parameters and clearance. Theodossiades et al. [29, 30] applied the piecewise-linear technique and multi-scale method to determine periodic steady-state motions and their stability properties. Al-shyyab and kaharman [31, 32] presented a nonlinear dynamic model of a typical multi-mesh gear train to investigate period-one, sub-harmonic and chaotic motions by using multi-term Harmonic Balance Method (HBM). Vaishya and Singh [33, 34] earlier developed a SDOF dynamic model considering sliding friction between the teeth in contact. Velex and Sainsot [35] pointed out the potentially significant contribution of tooth friction to translational vibrations of pinions and gears, especially in the case of HCRG. He et al. [36, 37] proposed a new multi-degree of freedom (MDOF) spur gear model including realistic time-varying stiffness and sliding friction, and emphatically analyzed the effect of sliding friction on the system dynamic responses. Huang et al. [38] conducted the effects of rough surfaces on the dynamic performances of HCRG, in which the STE is described by the fractal theory.

In conclusion, few studies have been done on the dynamic characteristics of HCRG, especially in nonlinear dynamics. Nevertheless, the modeling theories and analytical methods about LCRG can apply equally to HCRG. Based on this idea, a MDOF nonlinear dynamic model for HCRG is established including the TVMS, STE, gear backlash and bearing radial clearance. The TVMS for HCRG is calculated based on an improved energy model, which considers the misalignment of root circle and base circle, and the realistic transition curve. The bifurcation and chaotic characteristics of HCRG are studied systematically and comprehensively using the numerical integral method. The results can provide the theoretical support for the design and vibration control of HCRG.

The structure of this study is organized as follows: the nonlinear dynamic model and equations of motion of the system are presented in Sect. 2, where the TVMS of HCRG is given. In Sect. 3, the equations of motion of the system are solved by the numerical integral method, and then the bifurcation and chaotic characteristics under different control parameters are examined. Finally, some brief conclusions are given in Sect. 4.

2 Nonlinear dynamic modeling of HCRG

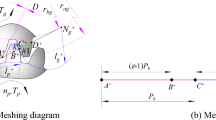
The nonlinear dynamic model of HCRG with multiple clearances is shown in Fig. 1 [25]. The gear pair is modeled as two disks connected by mesh stiffness, mesh damping, backlash and transmission error along the line of action (LOA). The gears are supported by two flexible rolling element bearings. Neglecting the effects of the friction between the teeth, only the lateral vibrations in the LOA direction and the torsional vibrations of two gears are considered. In this model, \( T_{i} \) (i = 1: pinion; 2: gear) are the constant external torques applied on pinion and gear, respectively; \( m_{i} \), \( I_{i} \) and \( R_{i} \) indicate the masses, moments of inertial and base radiuses of two gears, respectively; \( F_{\text{b}i} \) are the bearing radial preloads; \( k_{\text{b}i} \) and \( c_{\text{b}i} \) are the equivalent bearing stiffness and damping; \( k_{\text{m}} \) is the mesh stiffness of gear pair; \( c_{\text{m}} \) is the gear mesh damping; 2 \( b_{n} \) is the gear backlash; \( b_{1} \) and \( b_{2} \) are half the bearing radial clearances; \( e\left( t \right) \) represents the STE; The essential motions of the system can be described by four degrees of freedom, namely, two torsional motions \( \theta_{1} \) and \( \theta_{2} \), and tow translational motions \( y_{1} \) and \( y_{2} \).

Fig. 1
figure 1

Nonlinear dynamic model with multiple clearances

Full size image

2.1 Equations of motion of the system

According to Newtonian laws of motion, the system differential equations of motion can be expressed as follows:

$$ \left\{ {\begin{array}{l} { m_{1} {\ddot{y}}_{1} + c_{{\text{b}}1} \dot{y}_{1} + k_{{\text{b}}1} f_{{\text{b}}1} \left( {y_{1} } \right) + c_{{\text{m}}} \dot{\delta } + k_{{\text{m}}} f_{{\text{m}}} \left( \delta \right) = - F_{{\text{b}}1} } \hfill \\ {m_{2} {\ddot{y}}_{2} + c_{{\text{b}}2} {\dot{y}}_{2} + k_{{\text{b}}2} f_{{\text{b}}2} \left( {y_{2} } \right) - c_{\text{m}} \dot{\delta } - k_{\text{m}} f_{\text{m}} \left( \delta \right) = F_{{\text{b}}2} } \hfill \\ {I_{1} \ddot{\theta }_{1} + R_{1} c_{\text{m}} \dot{\delta } + R_{1} k_{\text{m}} f_{\text{m}} \left( \delta \right) = T_{1} } \hfill \\ {I_{2} \ddot{\theta }_{2} + R_{2} c_{\text{m}} \dot{\delta } + R_{2} k_{\text{m}} f_{\text{m}} \left( \delta \right) = - T_{2} } \hfill \\ \end{array} } \right. $$
(1)

where \( \delta \) is called the relative displacement between pinion and gear along the LOA, which is defined as the difference between the dynamic transmission error (DTE) and the STE \( e\left( t \right) \).

$$ \delta = R_{1} \theta_{1} - R_{2} \theta_{2} + y_{1} - y_{2} - e\left( t \right) $$
(2)

The STE \( e\left( t \right) \) is a kind of displacement excitation due to gear manufacturing error, which is usually indicated by first-order harmonic function.

$$ e\left( t \right) = e_{0} + e_{\text{a}} \sin \left( {\omega_{\text{m}} t + \varphi } \right) $$
(3)

where \( e_{0} \) is the mean value, \( e_{\text{a}} \) indicates the fluctuation amplitude, \( \varphi \) represents the initial phase, and \( \omega_{\text{m}} \) is the meshing frequency of gear pair, \( \omega_{\text{m}} = \omega_{1} z_{1} = \omega_{2} z_{2} \).

\( f_{\text{m}} \left( \delta \right) \) is the nonlinear displacement function of gear backlash, which can be expressed as:

$$ f_{\text{m}} \left( \delta \right) = \left\{ {\begin{array}{*{20}l} {\delta - b_{n} } \hfill & { \left( {\delta > b_{n} } \right)} \hfill \\ 0 \hfill & {\left( {\left| \delta \right| \le b_{n} } \right)} \hfill \\ {\delta + b_{n} } \hfill & {(\delta < - b_{n} )} \hfill \\ \end{array} } \right. $$
(4)

Similarly, the nonlinear displacement function of the bearing radial clearance \( f_{\text{b}i} \left( {y_{i} } \right) \), which can be written as follows:

$$ f_{\text{b}i} \left( {y_{i} } \right) = \left\{ {\begin{array}{*{20}l} {y_{i} - b_{i} } \hfill & {\left( {y_{i} > b_{i} } \right)} \hfill \\ 0 \hfill & {\left( {\left| {y_{i} } \right| \le b_{i} } \right)} \hfill \\ {y_{i} + b_{i} } \hfill & {(y_{i} < - b_{i} )} \hfill \\ \end{array} } \right., \quad i = 1,2 $$
(5)

Equation (1) can be further simplified into the following three-DOF equations in terms of the variable δ.

$$ \left\{ {\begin{array}{*{20}l} {m_{1} \ddot{y}_{1} + c_{\text{b}1} \dot{y}_{1} + k_{\text{b}1} f_{\text{b}1} \left( {y_{1} } \right) + c_{\text{m}} \dot{\delta } + k_{\text{m}} f_{\text{m}} \left( \delta \right) = - F_{\text{b}1} } \hfill \\ {m_{2} \ddot{y}_{2} + c_{\text{b}2} \dot{y}_{2} + k_{\text{b}2} f_{\text{b}2} \left( {y_{2} } \right) - c_{\text{m}} \dot{\delta } - k_{\text{m}} f_{\text{m}} \left( \delta \right) = F_{\text{b}2} } \hfill \\ {m_{\text{e}} \left( {\ddot{\delta } - \ddot{y}_{1} + \ddot{y}_{2} } \right) + c_{\text{m}} \dot{\delta } + k_{\text{m}} f_{\text{m}} \left( \delta \right) = F_{\text{m}} - m_{\text{e}} \ddot{e}\left( t \right) } \hfill \\ \end{array} } \right. $$
(6)

where \( m_{\text{e}} \) is the equivalent mass of gear pair, \( m_{\text{e}} = I_{1} I_{2} /(I_{1} R_{2}^{2} + I_{2} R_{1}^{2} ) \); \( F_{\text{m}} \) is the average force transmitted by the gear pair, \( F_{\text{m}} = T_{1} /R_{1} = T_{2} /R_{2} \); \( c_{\text{m}} = 2_{\text{m}} \sqrt {k_{0} \cdot m_{\text{e}} } \), \( k_{0} \) is the average mesh stiffness and m is the mesh damping ratio.

For the convenience of analysis, the differential equations (6) should be dimensionless. Introducing nominal dimension \( b_{c} \) and dimensionless time \( \tau = \omega_{n} t \), where \( \omega_{n} = \sqrt {k_{0} /m_{\text{e}} } \) is the natural frequency of gear pair, the dimensionless displacement, velocity and acceleration can be expressed as, respectively.

$$ \begin{aligned} &\delta = ub_{c} ,\quad \dot{\delta } = \dot{u}\omega_{n} b_{c} ,\quad \ddot{\delta } = \ddot{u}\omega_{n}^{2} b_{c} ,\quad y_{i} = \bar{y}_{i} b_{c} ,\quad \\&\dot{y}_{i} = \dot{\bar{y}}_{i} \omega_{n} b_{c} ,\quad \ddot{y}_{i} = \ddot{\bar{y}}_{i} \omega_{n}^{2} b_{c} ,\quad \left( {i = 1, \, 2} \right) \end{aligned} $$
(7)

Substituting Eqs. (7) into (6) yields the following dimensionless equations expressed in matrix form.

$$ \begin{aligned}& \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ { - 1} & 1 & 1 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{\bar{y}}_{1} } \\ {\ddot{\bar{y}}_{2} } \\ {\ddot{u}} \\ \end{array} } \right\} + 2\left[ {\begin{array}{*{20}c} {\zeta_{11} } & 0 & {\zeta_{13} } \\ 0 & {\zeta_{22} } & { - \zeta_{23} } \\ 0 & 0 & {\zeta_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{\bar{y}}_{1} } \\ {\dot{\bar{y}}_{2} } \\ {\dot{u}} \\ \end{array} } \right\} \\&\quad+ \left[ {\begin{array}{*{20}c} {k_{11} } & 0 & {k_{13} } \\ 0 & {k_{22} } & { - k_{23} } \\ 0 & 0 & {k_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\bar{f}_{\text{b}1} (\bar{y}_{1} )} \\ {\bar{f}_{\text{b}2} (\bar{y}_{2} )} \\ {f_{\text{m}} \left( u \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} { - \bar{F}_{\text{b}1} } \\ {\bar{F}_{\text{b}2} } \\ {\bar{F}_{\text{m}} + \bar{F}_{\text{eh}} } \\ \end{array} } \right\} \end{aligned} $$
(8)

where \( \zeta_{ii} = c_{\text{b}i} /\left( {2m_{i} \omega_{n} } \right) \), \( \zeta_{i3} = c_{\text{m}} /\left( {2m_{i} \omega_{n} } \right) \left( {i = 1, 2} \right) \), \( \zeta_{33} = c_{\text{m}} /\left( {2m_{\text{e}} \omega_{n} } \right) \), \( k_{ii} = k_{\text{b}i} /\left( {m_{i} \omega_{n}^{2} } \right) \), \( k_{i3} = k_{\text{m}} /\left( {m_{i} \omega_{n}^{2} } \right) \left( {i = 1, 2} \right) \), \( k_{33} = k_{\text{m}} /\left( {m_{\text{e}} \omega_{n}^{2} } \right) \), \( \bar{F}_{\text{m}} = F_{\text{m}} /(m_{\text{e}} \omega_{n}^{2} b_{c} ) \), \( \bar{F}_{\text{b}i} = F_{\text{b}i} /(m_{i} \omega_{n}^{2} b_{c} ) \left( {i = 1, 2} \right) \), \( \bar{F}_{\text{eh}} = F_{\text{e}} \varOmega^{2} \sin \left( {\varOmega \tau } \right) \), \( F_{\text{e}} = e_{\text{a}} /b_{c} \), \( \varOmega = \omega_{\text{m}} /\omega_{n} \).

The dimensionless nonlinear displacement functions for backlash and bearing radial clearance are re-written as, respectively.

$$ f_{\text{m}} \left( u \right) = \left\{ {\begin{array}{*{20}l} {u - b} \hfill & {\left( {u > + b} \right)} \hfill \\ 0 \hfill & { \left( {\left| u \right| \le b} \right)} \hfill \\ {u + b } \hfill & {(u < - b)} \hfill \\ \end{array} } \right.;\quad b = b_{n} /b_{c} $$
(9)
$$ \bar{f}_{\text{b}i} \left( {\bar{y}_{i} } \right) = \left\{ {\begin{array}{*{20}l} {\bar{y}_{i} - \bar{b}_{i} } \hfill & {\left( {\bar{y}_{i} > \bar{b}_{i} } \right)} \hfill \\ 0 \hfill & {\left( {\left| {\bar{y}_{i} } \right| \le \bar{b}_{i} } \right)} \hfill \\ {\bar{y}_{i} + \bar{b}_{i} } \hfill & {(\bar{y}_{i} < - \bar{b}_{i} )} \hfill \\ \end{array} } \right.;\quad \bar{b}_{i} = b_{i} /b_{c} , \quad i = 1, 2 $$
(10)

2.2 Calculation of time-varying mesh stiffness

As is well known, TVMS changes periodically with the number of meshing teeth pair and the position of contact point. It is shown that TVMS is one of the main sources exciting the vibration of the gear system. There are many methods to calculate the TVMS, involving analytical method, finite element method (FEM), analytical-FE approach, and photo-elasticity technique. Considering the misalignment of gear root circle and base circle, and the accurate transition curve, Ma et al. [39] presented an improved mesh stiffness model, as shown in Fig. 2. Based the ANSYS software, Wang [7] developed an approach to predict the TVMS by establishing the contact elements. Wan et al. [40] also presented an improved TVMS algorithm by judging the relationship between the teeth number and 42. Saxena et al. [41] proposed an analytical method to calculate the TVMS of the spur gear for different spall shapes, size and location considering sliding friction. Karma1 and Agarwal [42] calculated the mesh stiffness of high contact ratio spur gear and load sharing using the energy method. Raghuwanshi and Parey [43] measured the mesh stiffness of cracked spur gear using photo-elasticity technique. However, in these researches, the gear tooth is mostly modeled as a non-uniform cantilever beam on the base circle. In fact, the root circle and base circle are misaligned, which would affect the accuracy of TVMS.

Fig. 2
figure 2

Geometric model of the tooth profile [39]

Full size image

To calculate the mesh stiffness conveniently and effectively, the improved potential energy method in [39] is adopted to calculate the TVMS of HCRG. Based on the elastic mechanics and beam theory, the bending stiffness \( k_{\text{b}} \), shear stiffness \( k_{\text{s}} \) and axial compressive stiffness \( k_{\text{a}} \) can be obtained as follows:

$$ \begin{aligned} \frac{1}{{k_{\text{b}} }} &= \int_{{\frac{\pi }{2}}}^{\alpha } {\frac{{\left[ {\cos \beta \left( {y_{\beta } - y_{1} } \right) - x_{\beta } \sin \beta } \right]^{2} }}{{EI_{y1} }}} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma \\&\quad+ \int_{{\tau_{c} }}^{\beta } {\frac{{\left[ {\cos \beta \left( {y_{\beta } - y_{2} } \right) - x_{\beta } \sin \beta } \right]^{2} }}{{EI_{y2} }}} \frac{{{\text{d}}y_{2} }}{{{\text{d}}\tau }}{\text{d}}\tau \end{aligned} $$
(11)
$$ \frac{1}{{k_{\text{s}} }} = \int_{{\frac{\pi }{2}}}^{\alpha } {\frac{{1.2\cos^{2} \beta }}{{GA_{y1} }}} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma + \int_{{\tau_{c} }}^{\beta } {\frac{{1.2\cos^{2} \beta }}{{GA_{y2} }}} \frac{{{\text{d}}y_{2} }}{{{\text{d}}\tau }}{\text{d}}\tau $$
(12)
$$ \frac{1}{{k_{\text{a}} }} = \int_{{\frac{\pi }{2}}}^{\alpha } {\frac{{\sin^{2} \beta }}{{EA_{y1} }}} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\gamma }}{\text{d}}\gamma + \int_{{\tau_{c} }}^{\beta } {\frac{{\sin^{2} \beta }}{{EA_{y2} }}} \frac{{{\text{d}}y_{2} }}{{{\text{d}}\tau }}{\text{d}}\tau $$
(13)

The Hertzian contact stiffness \( k_{\text{h}} \) and fillet-foundation stiffness \( k_{\text{f}} \) can be given by

$$ \frac{1}{{k_{\text{h}} }} = \frac{{4\left( {1 - \upsilon^{2} } \right)}}{\pi EL} $$
(14)
$$ \frac{1}{{k_{\text{f}} }} = \frac{{\cos^{2} \beta }}{EL}\left\{ {L^{*} \left( {\frac{{u_{\text{f}} }}{{S_{\text{f}} }}} \right)^{2} + M^{*} \left( {\frac{{u_{\text{f}} }}{{S_{\text{f}} }}} \right) + P^{*} \left( {1 + Q^{*} \tan^{2} \beta } \right)} \right\} $$
(15)

Note that the detailed definitions of the symbols in Eqs. (11–15) can be found in Refs. [39, 44].

When a gear pair are meshing, the total potential energy U stored in a meshing tooth pair is the summation of Hertzian energy \( U_{\text{h}} \), bending energy \( U_{\text{b}} \), shear energy \( U_{\text{s}} \), axial compressive energy \( U_{\text{a}} \) and fillet-foundation deformation energy \( U_{\text{f}} \) of each tooth, which can be expressed as:

$$ \begin{aligned} U & = \frac{{F^{2} }}{{2k_{\text{s}} }} = U_{\text{h}} + U_{{{\text{b}}1}} + U_{{{\text{s}}1}} + U_{{{\text{a}}1}} + U_{{{\text{f}}1}} + U_{{{\text{b}}2}} + U_{{{\text{s}}2}} + U_{{{\text{a}}2}} + U_{{{\text{f}}2}} \\ & = \frac{{F^{2} }}{2}\left( {\frac{1}{{k_{\text{h}} }} + \frac{1}{{k_{{{\text{b}}1}} }} + \frac{1}{{k_{{{\text{s}}1}} }} + \frac{1}{{k_{\text{a1}} }} + \frac{1}{{k_{{{\text{f}}1}} }} + \frac{1}{{k_{\text{b2}} }} + \frac{1}{{k_{\text{s2}} }} + \frac{1}{{k_{\text{a2}} }} + \frac{1}{{k_{\text{f2}} }}} \right) \\ \end{aligned} $$
(16)

where \( k_{\text{s}} \) represents the total mesh stiffness of a pair of contact teeth, subscripts 1 and 2 represent pinion and gear, respectively.

Accordingly, the single-tooth-pair mesh stiffness can be give as:

$$ k_{\text{s}} = 1/\left( {\frac{1}{{k_{\text{h}} }} + \frac{1}{{k_{{{\text{b}}1}} }} + \frac{1}{{k_{{{\text{s}}1}} }} + \frac{1}{{k_{\text{a1}} }} + \frac{1}{{k_{{{\text{f}}1}} }} + \frac{1}{{k_{\text{b2}} }} + \frac{1}{{k_{\text{s2}} }} + \frac{1}{{k_{\text{a2}} }} + \frac{1}{{k_{\text{f2}} }}} \right) $$
(17)

For multiple tooth pairs, the total mesh stiffness is parallel combination of the mesh stiffnesses of all tooth pairs in contact, which can be written as:

$$ k_{\text{m}} \left( t \right) = \mathop \sum \limits_{i = 1}^{N} \left( {\frac{1}{{k_{h} }} + \frac{1}{{k_{\text{b}1,i} }} + \frac{1}{{k_{\text{s}1,i} }} + \frac{1}{{k_{\text{a}1,i} }} + \frac{1}{{k_{\text{f}1,i} }} + \frac{1}{{k_{\text{b}2,i} }} + \frac{1}{{k_{\text{s}2,i} }} + \frac{1}{{k_{\text{a}2,i} }} + \frac{1}{{k_{\text{f}2,i} }}} \right)^{ - 1} $$
(18)

where N indicates the number of meshing tooth pair at the same time, N = 2 or 3 for HCRG.

The basic parameters of HCRG for this study are listed in Table 1. Based on the improved potential energy method, the TVMS of HCRG throughout a whole meshing period can be obtain. For the convenience of calculation, the TVMS is expanded into an eighth-order Fourier series form about \( \theta_{1} \left(^\circ \right) \) (see Fig. 3).

$$ k_{\text{m}} \left( {\theta_{1} } \right) = k_{0} + \mathop \sum \limits_{j = 1}^{8} \left[ {k_{\text{a}j} \cos \left( {j\omega_{\theta } \theta_{1} } \right) + k_{\text{b}j} \sin \left( {j\omega_{\theta } \theta_{1} } \right)} \right] $$
(19)

where \( k_{0} \) is the average value of stiffness; \( k_{\text{a}j} \) and \( k_{\text{b}j} \) are the coefficients of harmonic terms, as listed in Table 2. \( \omega_{\theta } = 2\pi z_{1} /360 \), \( z_{1} \) is the tooth number of pinion.

Table 1 Basic parameters of HCRG
Full size table
Fig. 3
figure 3

Fitting curve of TVMS of HCRG

Full size image
Table 2 Coefficients of harmonic terms of mesh stiffness (N/m)
Full size table

By changing the coordinate, the TVMS \( k_{\text{m}} \left( {\theta_{1} } \right) \) can be converted into another form about time t to facilitate the subsequent calculation.

$$ k_{\text{m}} \left( t \right) = k_{0} + \mathop \sum \limits_{j = 1}^{8} \left[ {k_{\text{a}j} \cos \left( {j\omega_{\text{m}} t} \right) + k_{\text{b}j} \sin \left( {j\omega_{\text{m}} t} \right)} \right] $$
(20)

where \( \omega_{\text{m}} \) is the above-mentioned meshing frequency of gear pair.

3 Numerical simulation and discussion

Due to the existence of time-varying stiffness, gear backlash, and bearing radial clearance, the gear system is a complex system with strong nonlinearity and time variation. In order to understand comprehensively the dynamic features of HCRG, excitation frequency Ω, mesh damping ratio ξm, gear backlash b, error fluctuation Fe, and bearing radial clearances \( \bar{b}_{1} , \bar{b}_{2} \) are selected as bifurcation parameters to study the influence on the system responses. The system equations of motion are solved by the 4th–5th order Runge–Kutta numerical integration method, and its nonlinear dynamic characteristics are systematically analyzed through the bifurcation diagrams, LLE charts, time-domain waveforms, FFT spectra, Poincaré maps and phase diagrams. The main geometric parameters of HCRG are seen in Table 1, and the invariant parameters of this simulation are listed as follows: input power \( P \) = 200 kW, nominal dimension \( b_{c} \) = 10 μm, equivalent bearing stiffness \( k_{\text{b}1} \) = \( k_{\text{b}2} \) = 3.5e8 N/m, bearing damping \( c_{\text{b}1} \) = 1.90e3 N s/m, \( c_{\text{b}2} \) = 2.06e3 N s/m; the initial values of control parameters are set as: error fluctuation \( e_{\text{a}} \) = 5 μm, gear backlash \( b_{n} \) = 40 μm, bearing radial clearances \( b_{i} \) = 10 μm, and mesh damping ratio ζm= 0.04.

3.1 Effects of excitation frequency Ω

Excitation frequency Ω reflects the rotational speed of pinion or gear, and is one of the key parameters that affect the dynamic behaviors of the mechanical transmission system. Figure 4a presents the bifurcation diagram of the relative torsional displacement u with the change of excitation frequency Ω. The corresponding LLE chart is shown in Fig. 4b. It can be seen from the bifurcation diagram and the LLE chart in Fig. 4 that there exist kinds of motion forms within the different ranges of values of the excitation frequency, such as period-1, period-2, multi-period, and chaotic motions. When Ω ∈ [0.2, 1.046], the system is in period-1 motion state and the LEEs are negative values. In the frequency range of Ω ∈ [1.047, 1.282], the system undergoes a series of transitions among quasi-periodic, multi-period and chaotic motions and there appears zero, positive and negative values in the LEE chart, which will be subsequently discussed in detail. When Ω ∈ [1.283, 1.685], the system response changes from period-1 motion to period-2 motion and the corresponding LEEs show negative. When Ω ∈ [1.686, 2.32], the system enters into chaotic region by crisis way, when the LEEs hold positive. Eventually, the system response converges to period-1 motion by inverse period-doubling bifurcation and the corresponding LEEs change from positive to negative. Moreover, the phenomenon of frequency hopping occurs at the point of Ω = 0.906, where the LEE is − 0.008686.

Fig. 4
figure 4

Bifurcation diagram and largest Lyapunov exponent chart with the change of Ω

Full size image

Figure 5 shows the partial enlarged view and the corresponding LEE chart at the range of Ω ∈ [1.0, 1.3]. It is quite clear that the system exhibits complex nonlinear behaviors. In order to reveal the evolution process of the system responses more clearly, the phase diagrams and Poincaré maps under different excitation frequencies are listed in Fig. 6. When Ω is less than 1.047, the system is in period-1 motion state and the corresponding LEEs show negative, as seen in Figs. 6a and 5b. As Ω is increased to 1.055, the system turns into quasi-periodic motion from period-1 motion by Hopf bifurcation. As displayed in Fig. 6b, the phase diagram shows a closed curve band with a certain thickness and Poincaré map is a closed smooth curve. Besides, the LEE is equal to zero in Fig. 5b. All these characteristics reveal that the system is in quasi-periodic motion state. As Ω is further increased, the thickness of phase diagram gradually becomes larger and the Poincaré maps show some twisted-closed curves, which mean that chaotic motion is about to occur, as can be observed from Fig. 6d, f, h, where the LEEs are 0. When Ω increases to 1.163, the system enters into chaotic region until Ω value is equal to 1.263, as can be identified from Fig. 6j, k, where the LEEs are 0.00391 and 0.01079. As Ω is changed from 1.264 to 1.282, it can be inferred from Fig. 6l, n that the system returns to quasi-periodic motion, where the LEEs are 0. Finally, the system leaves quasi-periodic motion, and then comes into period-1 motion by crisis way, as shown in Fig. 6o. In addition, from Fig. 6c, e, g, i, m, there also exist several transient multi-period motion windows between these quasi-periodic regions, which are period-7, period-18, period-11, period-15 and period-19 motions. The corresponding LEEs are − 0.001638, − 0.006928, − 0.002968, − 0.005638 and − 0.005116, respectively.

Fig. 5
figure 5

Partial enlarged view and largest Lyapunov exponent at the range of Ω ∈ [1.0, 1.3]

Full size image
Fig. 6
figure 6

Evolution process of the system responses at the range of Ω ∈ [1.0, 1.3]

Full size image

From the above analysis, when the excitation frequency of the system is in the intervals of Ω ∈ [0.2, 1.046], [1.283, 1.685] and [2.32, 3.0], the HCRG manifests as simple period-1 or period-2 motions, which are the better working areas of the system. This will contributes to improve the system stability, reduce the vibration and avoid the chaos.

3.2 Effects of gear backlash b

Considering these factors like gear lubrication, tooth elastic deformation, thermal expansion and so on, a certain amount of gear backlash must be reserved between the non-working tooth profiles. However, the existence of gear backlash can result in the teeth separation and impact. Thus, it is vital to explore the effects of gear backlash on the dynamic behaviors of the system and to select a proper gear backlash. Here, gear backlash b is used as a control parameter and the remaining parameters are kept unchanged. Excitation frequency is taken as Ω = 1.08, 1.283, 1.685, 1.70. The bifurcation diagrams of the system with the change of gear backlash are shown in Fig. 7.

Fig. 7
figure 7

Bifurcation diagrams with the change of b under different excitation frequencies

Full size image

It can be seen from Fig. 7 that, when the remaining parameters are invariant and the excitation frequency takes different values, the system behaves as some simple periodic properties under smaller gear backlashes, e.g., period-1 and period-2 motions, which are favor of the system stability. With the increase in gear backlash b, the bifurcation features of the system obviously change. For example, when Ω = 1.283, as shown in Fig. 7b, the system goes through the following switching process: period-1 motion → quasi-periodic motion → period-8 motion → period-4 motion → transient quasi-periodic motion → period-1 motion, as can be identified by Figs. 8, 9, 10, 11, 12 and 13. As Ω increases, the range of periodic motion of the system is gradually narrowing and that of chaotic motion is increasing in Fig. 7c, d, which are adverse to the system stability. The response analyses under the other excitation frequencies are similar to Fig. 7b, so they are not repeated here.

Fig. 8
figure 8

Dynamic response curves at b = 0.3. a Time-domain waveform, b phase diagram and Poincaré map and c FFT spectrum

Full size image
Fig. 9
figure 9

Dynamic response curves at b = 0.6. a Time-domain waveform, b phase diagram and Poincaré map and c FFT spectrum

Full size image
Fig. 10
figure 10

Dynamic response curves at b = 0.75. a Time-domain waveform, b phase diagram and Poincaré map and c FFT spectrum

Full size image
Fig. 11
figure 11

Dynamic response curves at b = 0.82. a Time-domain waveform, b phase diagram and Poincaré map and c FFT spectrum

Full size image
Fig. 12
figure 12

Dynamic response curves at b = 0.87. a Time-domain waveform, b phase diagram and Poincaré map and c FFT spectrum

Full size image
Fig. 13
figure 13

Dynamic response curves at b = 4.0. a Time-domain waveform, b phase diagram and Poincaré map and c FFT spectrum

Full size image

The above analysis shows that the HCRG keeps periodic motion under smaller gear backlash and the system runs smoothly. Therefore, in the design process of HCRG, while ensuring good lubrication of gears, a proper gear backlash should be selected, which is of great significance to reduce the vibration and noise of gear transmission system.

3.3 Effects of mesh damping ratio ζm

To obtain the effects of mesh damping ratio ζm on the system nonlinear dynamics and to adjust the system structure, mesh damping ratio ζm is used as the analysis parameter and the other parameters are kept invariant. Excitation frequency is taken as Ω = 1.08, 1.283, 1.685, 1.70. Figure 14 shows the bifurcation diagrams of the system with the change of ζm in this range of ζm ∈ [0.03, 0.17].

Fig. 14
figure 14

Bifurcation diagrams with the change of ζm under different excitation frequencies

Full size image

It can be seen from the bifurcation diagrams in Fig. 14 that, when the remaining parameters are invariant and the excitation frequency takes various values, the system shows different bifurcation behaviors with the decrease of ζm. As shown in Fig. 14a, b, the system directly changes from period-1 motion to quasi-periodic motion by Hopf bifurcation. From Fig. 14c, d, the system first bifurcates into period-2 motion from period-1 motion and then enters into chaotic motion by crisis. For instance, when Ω = 1.08, with the reduction of ζm, the system first undergoes the transition from period-1 motion to quasi-periodic motion, then enters into period-7 motion region, and finally returns to quasi-periodic motion, as can be identified from Fig. 15. From the overall bifurcation diagrams, the system eventually converges to period-1 motion under higher mesh damping ratio. Therefore, the higher mesh damping ratio will contribute to enhance the system stability and avoid the chaotic motion. The response analyses of the other bifurcation diagrams are similar, so they are not repeated here.

Fig. 15
figure 15

Evolution process of the system responses at Ω = 1.08

Full size image

3.4 Effects of error fluctuation F e

Owing to multi-tooth meshing all the time, HCRG is very sensitive to tooth profile errors. Therefore, it is necessary to investigate the influence of error fluctuation on the nonlinear behavior of the system. Figure 16 presents the bifurcation diagrams of the system using error fluctuation Fe as a varying parameter under different excitation frequencies Ω = 1.5, 1.6, 1.7, 2.0. As can be seen from the bifurcation figures in Fig. 16, with the increase in error fluctuation, the system bifurcates into period-2 motion from period-1 motion and then suddenly enters into chaotic motion region. Furthermore, the region of the simple periodic motion is gradually decreasing with increasing the excitation frequency.

Fig. 16
figure 16

Bifurcation diagrams with the change of Fe under different excitation frequencies

Full size image

Meanwhile, Fig. 17 shows the changes of the system response with the excitation frequency under different error fluctuation values. It can be clearly seen form the bifurcation diagrams in Fig. 17 that the error fluctuation has a significant effects on the nonlinear behaviors of HCRG. When the error fluctuation Fe = 0, namely, the gears have perfect involute profiles, the dynamic response curve is continuous and no bifurcation phenomenon occurs, as shown in Fig. 17a. As Fe is further increased, the system gradually presents complex nonlinear behaviors, involving jump discontinuity, quasi-periodic response, bifurcation, chaotic response, etc. The nonlinear analysis for Fig. 17c has been done in Sect. 3.1. Comparing Fig. 17c with Fig. 17d, it can be found that, with the increase of Fe, the total range of chaotic window is gradually enlarging and the vibration amplitudes obviously increase, which are not good for the system stability. Figure 18 presents the amplitude-frequency spectra under four different error fluctuation values when Ω = 0.5 (namely, the same rotating speed). It can be seen that the dimensionless amplitudes at the fundamental frequency positions Ω = 0.5 are increasing with the increase of Fe. Accordingly, special attention should be paid to the manufacturing and processing of HCRG to attain the highest quality gears possible, so that the influence of tooth random errors can be minimized. The response analysis of the system about Fe = 0.8 is similar to that of Fe = 0.5, so it is not repeated again here.

Fig. 17
figure 17

Effects of error fluctuation on bifurcation and chaos characteristics

Full size image
Fig. 18
figure 18

Amplitude–frequency spectra at Ω = 0.5

Full size image

3.5 Effects of bearing radial clearance \( \bar{b}_{1} , \bar{b}_{2} \)

The bearing radial clearance is also one of the main factors that cause the nonlinear behaviors of the geared systems. Therefore, it is also very important to study the influence of bearing radial clearance on the system nonlinear dynamics and to select a suitable bearing clearance. Figure 19 shows the bifurcation diagrams of the system using the bearing radial clearance as a bifurcation parameter when Ω takes different values 0.906, 1.08, 1.283 and 1.685, and the other parameters remain invariant.

Fig. 19
figure 19

Bifurcation diagrams with the change of \( \bar{b}_{1} , \bar{b}_{2} \) under different excitation frequencies

Full size image

It can be clearly found from the bifurcation diagrams in Fig. 19 that the bearing radial clearance has a much weaker effect on the system nonlinear behavior when compared with gear backlash. When the bearing radial clearance is in the region of \( \bar{b}_{1} , \bar{b}_{2} \) ∈ [0, 3], the system is in a same motion state in most regions. When Ω = 0.906, the system is always in period-1 motion state, as shown in Fig. 19a. When Ω = 1.08, the system is in quasi-periodic state at a small scope of \( \bar{b}_{1} , \bar{b}_{2} \) ∈ [0, 0.14], and then enters a larger region with a stable period-7 motion, as can be seen from Fig. 19b. When Ω = 1.283, as illustrated in Fig. 19c, the system performs quasi-periodic motion at a very narrow range of \( \bar{b}_{1} , \bar{b}_{2} \) ∈ [0, 0.03], then rapidly comes into stable period-1 motion region. When Ω = 1.685, the system maintains stable period-2 motion all the time, though the bifurcation diagram shows some burrs, as displayed in Fig. 19d. The common phenomenon of the weak coupling effect about bearing radial clearance is further validated by different parameter combinations.

The above analysis shows that the bearing radial clearance only produce weak and ignorable coupling effects on the nonlinear features of the system. From the point of view of convenient modeling, the effect of nonlinearity of bearing radial clearance may be neglected in this study. However, to satisfy bearing lubrication and prevent the interference between raceway and rolling elements, the bearing radial clearance should be reasonably chosen according to the recommended scopes of the corresponding standard.

4 Conclusions

This paper establishes a nonlinear dynamic model for HCRG, which contains several nonlinear factors, such as TVMS, STE, gear backlash and bearing radial clearance. Based on the improved potential energy model, the TVMS of HCRG is calculated and then fitted into a Fourier series form. The system equations of motion are normalized and then solved using the 4th–5th order Runge–Kutta numerical integration method. The influence of excitation frequency, gear backlash, mesh damping ratio, error fluctuation, and bearing radial clearance on the nonlinear dynamic characteristics of the system is comprehensively analyzed by the bifurcation diagrams, time-domain waveforms, FFT spectra, Poincaré maps, phase diagrams as well as LLE charts.

The main conclusions can be summarized as follows:

  1. 1.

    The HCRG exhibits rich bifurcation and chaotic characteristics under the influence of multiple factors. With the change of excitation frequency, the system shows complex motion states, including simple periodic, multi-periodic, quasi-periodic and chaotic motions and so on. It is found that there are three typical routes to chaos in the response, i.e., period-doubling bifurcation to chaos, quasi-period to chaos and crisis to chaos.

  2. 2.

    The smaller gear backlash and larger mesh damping ratio will contribute to improve the system stability and reduce the vibration and noise, which is of great significance for guiding the dynamic design of the HCRG.

  3. 3.

    The bearing radial clearance has a weaker influence on the system nonlinear behaviors and no bifurcation behavior could be observed under this bifurcation parameter.

  4. 4.

    The error fluctuation has significant effects on the nonlinear behaviors of the HCRG. With the increase in error fluctuation, the system responses become more and more complicated and the range of periodic motion decreases step by step, which goes against the system stability. Therefore, the HCRG with high degree of accuracy will help to avoid chaos and enhance the system stability.