Global bifurcation and chaos analysis in nonlinear vibration of spur gear systems

Abstract

The global homoclinic bifurcation and transition to chaotic behavior of a nonlinear gear system are studied by means of Melnikov analytical analysis. It is also an effective approach to analyze homoclinic bifurcation and detect chaotic behavior. A generalized nonlinear time varying (NLTV) dynamic model of a spur gear pair is formulated, where the backlash, time varying stiffness, external excitation, and static transmission error are included. From Melnikov method, the threshold values of the control parameter for the occurrence of homoclinic bifurcation and onset of chaos are predicted. Additionally, the numerical bifurcation analysis and numerical simulation of the system including bifurcation diagrams, phase plane portraits, time histories, power spectras, and Poincare sections are used to confirm the analytical predictions and show the transition to chaos.

1 Introduction

Gears are one of the most common and important components in industrial rotating machinery and power transmission systems. The prediction and control of the gear vibrations have become important concerns in various engineering fields. Due to the high sensitivity of the gear pair to its control parameters, the vibratory response can be very complex and not easy to control. An attempt to design and develop silent gears system requires a good understanding of the dynamic behavior of the system. Over a long time, gear transmission systems were investigated with linear vibration theories, without considering nonlinear parameters [1]. The more accurate evaluation and the experimental investigations of the dynamic response have indicated that the vibration of geared systems should be considered with nonlinear vibration theories. A gear system with backlash, transmission error, and time varying stiffness is a nonlinear vibration system, which display some complicated phenomena such as regular vibrations, nonperiodic motions or even chaotic motions [2–16]. With the development of nonlinear dynamics theories, the nonlinear characteristics of these systems such as stability, periodic solutions, bifurcations, and chaos, have become the most interesting research areas. As a consequence, many studies have focused on analyzing nonlinear dynamics of the gear system or the related researches.

For instance, Sato et al. [2] established a nonlinear model of the gear system with the time dependence of tooth stiffness and backlash. They investigated the bifurcation of periodic response and chaotic behavior by using a shooting method. Kahraman and Blankenship [3, 4] performed some experiments on a spur gear pair and observed various nonlinear phenomena including gear tooth contact loss, period doubling and chaos. Raghothama and Narayanan [5] investigated nonlinear vibrations of a geared rotor-bearing system with time varying mesh stiffness and backlash. Periodic motions were obtained by the incremental harmonic balance method (IHBM). The chaotic motions were investigated numerically, and the Lyapunov exponents were computed. Theodossiades and Natsiavas [6, 7] analyzed the motor driven gear systems and predicted chaotic behaviors. De Souza et al. [8] used a numerical simulation method to demonstrate the existence of chaotic solutions in the gear systems. Bifurcation diagrams were calculated to determine regions of chaotic vibrations. Luczko [9] investigated a nonlinear model with the backlash and time varying stiffness to describe vibration of a one stage gearbox. The possibility of existence of quasi-periodic or chaotic response for some regions of the parameters was studied. Different types of vibration were illustrated by plots of time histories, phase portraits, and bifurcation diagrams. The study was done numerically using numerical integration and spectrum analysis.

Effects of the frictional force and backlash on the multidegree of freedom nonlinear dynamic gear system, which incorporate time varying stiffness, were investigated by Siyu et al. [10]. The chaotic motions were investigated numerically. The system exhibited a chaos in different regions of the control parameter. Wang [11] studied a gear pair associated with friction, backlash, and time varying gear meshing stiffness. A numerical simulation was applied. Bifurcation, chaos, and their corresponding largest Lyapunov exponents of the gear system are investigated and the critical parameters are identified. Also, Chang Jian and Chen [12–15] presented a series of investigations in bifurcation and chaotic responses of a gear bearing system. The results provided an understanding of the operating conditions in the gear systems and, therefore, serve as a useful reference in designing and controlling such systems.

From the above mentioned references, one finds that three kinds of methods, including experimental [3, 4], analytical [5], and numerical methods [2, 5–15], have been adopted to analyze the bifurcation and chaos in the nonlinear dynamics of the gear systems. Due to the complexity of the gear system and also the difficulty and limitation of the analytical methods, the numerical method was commonly used to analyze the gear systems, but they cannot provide any analytical expression of the solutions. Although a significant amount of research has been devoted to the nonlinear dynamics of the gear systems, few attempts have been made to investigate analytical solutions of the system. Melnikov analysis is one of the few analytical methods to provide an approximate criterion for the occurrence of homoclinic bifurcation and chaos in the nonlinear systems. Since Melnikov’s analysis is considered standard, it has been used by different authors today [16–18]. According to this theory, the existence of the transversal intersection of the stable and unstable manifolds of a saddle fixed point implies the existence of the chaotic behaviors [16–24]. The current study performs a nonlinear analysis of a spur gear pair. The chaotic motions of the gear system are studied analytically with the Melnikov method. The critical curves separating the periodic and chaotic regions are drawn. Also, the dynamic behaviors of the gear system are numerically computed and characterized using phase diagrams, power spectrums, Poincare maps, and bifurcation diagrams, which verify the analytical results.

The rest of paper is organized as follows. In Sect. 2, a nonlinear dynamic model of a spur gear pair is formulated, where the backlash, time varying stiffness, external excitation, and static transmission error are included. In Sect. 3, the unperturbed system is analyzed in which the damping and forcing terms are dropped out. The conditions for existence of chaos behavior in terms of homoclinic bifurcation by using Melnikov analysis are performed. In Sect. 4, the threshold values of the control parameter for the occurrence of homoclinic bifurcation and onset of chaos are obtained for various models. The influence of the parameters on the character and level of vibrations are studied. The theoretical predictions are verified with direct numerical simulations by construction of the bifurcation diagrams and computation of the plane phase portraits, time histories, power spectra, and Poincare section. Finally, Sect. 5 presents some brief conclusions.

2 Dynamic model and equations of motion

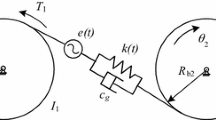
For the purpose of illustration, a generalized model of a spur gear pair system is considered. It is assumed that the transmission shafts and the bearing of the gear system are inflexible, so that the parametric and nonlinear effects in the meshing are accentuated. Figure 1 shows a generalized model for a single mesh gear system, which the gear mesh is modeled as a pair of rigid disks connected by a spring damper set along the line of action. The gears are represented by their base circles with radius r _a and r _b , respectively. I _a  and I _b are the mass moments of inertia of the gears. K and c represent the time varying mesh stiffness and a constant mesh damping. The backlash function f _h , is usually used to represent gear clearances and an internal displacement excitation e(t), is also applied to the gear mesh interface to represent manufacturing errors. T _a , and T _b are external torques acting on the driver and driven gear, respectively. In addition, the total rotation angle of each gear is assumed to result from a constant angular velocity term plus a small variation that represent the vibratory angular displacements from the mean position. This means that

$$ \varphi_{a}(t) = \omega_{a}t + \theta_{a}(t)\quad \mbox{and} \quad \varphi_{b}(t) = \omega_{b}t + \theta_{b}(t) $$

(1)

where ω _a and ω _b are the constant angular velocities of the gears. Under these assumptions, the differential equations of the torsional motion can be written as follows:

$$\begin{aligned} &I_{a}\frac{d^{2}\theta_{a}}{dt^{2}} + c\biggl(r_{a} \frac{d\theta_{a}}{dt} - r_{b}\frac{d\theta_{b}}{dt} - \frac{de}{dt} \biggr)r_{a} \\ &\quad {}+ r_{a}k(t)f_{h}\bigl(r_{a} \theta_{a} - r_{b}\theta_{b} - e(t)\bigr) = T_{a} \end{aligned}$$

(2a)

$$\begin{aligned} &I_{b}\frac{d^{2}\theta_{b}}{dt^{2}} - c\biggl(r_{a} \frac{d\theta_{a}}{dt} - r_{b}\frac{d\theta_{b}}{dt}- \frac{de}{dt} \biggr)r_{b} \\ &\quad {} - r_{b}k(t)f_{h}\bigl(r_{a} \theta_{a} - r_{b}\theta_{b} - e(t)\bigr) = - T_{b} \end{aligned}$$

(2b)

An input torque T _a is applied to the driver gear rotating at ω _a , and the mean braking torque T _b to the driven gear with angular velocity ω _b . The excitation torque T _a , fluctuates significantly between low and high values. Therefore, the T _a can be decomposed into the average torque transmitted through the gear pair T _ma and the fluctuating external torque excitation T _p (t) parts. Such excitations are typically at low frequencies ω _p which are the first few multiples of the input shaft frequency. Also, output torque T _b is assumed to be constant to simplify the dynamic problem, i.e., T _b (t)=T _mb . T _a  can be expressed via Fourier series as follows [25, 26]:

$$ T_{a}(t) = T_{ma} + \sum _{r = 1}^{\infty} T_{pr}\cos (r \omega_{p}t + \varphi_{pr}) $$

(3)

Moreover, the mesh stiffness of the gear is a periodic function depending on the number and position of the teeth in contact. Since the stiffness is periodically time varying with the mesh frequency, its analytical formulation can be obtained by means of a Fourier expansion [27]:

$$\begin{aligned} k(t) = k(t + 2\pi /\omega_{k}) = k_{m} + \sum _{r = 1}^{\infty} k_{r}\cos (r \omega_{k}t + \phi_{kr}) \end{aligned}$$

(4)

where ω _k =n _a ω _a =n _b ω _b is the mesh frequency, n _a  and n _b are the teeth number of each gear. The model takes into account the static transmission error e(t) applied along the line of action to model any manufacturing errors, and teeth deformations. Since the mean angular velocities of the gears are constant, the static transmission error can be approximated as time periodic function. Its fundamental frequency is the meshing frequency. As a result, static transmission error can be expressed in a Fourier series in the form [28]:

$$ e(t) = e(t + 2\pi /\omega_{e}) = \sum _{r = 1}^{\infty} e_{r}\cos (r \omega_{e}t + \phi_{er}) $$

(5)

The gear pair is bound to have some backlash, which may be designed for better lubrication and to reduce interference, or caused by wear and mounting errors. The gear backlash is essentially a discontinuous and nondifferentiable function, which is the main source of nonlinearity in the system. The backlash function f _h defined by the following equation:

$$ f_{h} = \left \{ \begin{array}{l} r_{a}\theta_{a} - r_{b}\theta_{b} - e(t) - (1 - \alpha )b \\ \quad b < r_{a}\theta_{a} - r_{b}\theta_{b} - e(t) \\ \alpha (r_{a}\theta_{a} - r_{b}\theta_{b} - e(t)) \\ \quad {-} b \le (r_{a}\theta_{a} - r_{b}\theta_{b} - e(t)) \le b \\ r_{a}\theta_{a} - r_{b}\theta_{b} - e(t) + (1 - \alpha )b \\ \quad b < - (r_{a}\theta_{a} - r_{b}\theta_{b} - e(t)) \end{array} \right . $$

(6)

where 2b represents the total backlash.

Fig. 1

A spur gear pair model

Equations (2a), (2b) can be reduced to a single equation by introducing a new variable $\tilde{x} = r_{a}\theta_{a} - r_{b}\theta_{b} - e(t)$, which is the difference between the dynamic transmission error and the static transmission error.

$$ m\frac{d^{2}\tilde{x}}{dt^{2}} + c\frac{d\tilde{x}}{dt} + k(t)f_{h}( \tilde{x}) = \hat{F}_{m} + \hat{F}_{e}(t) + \hat{F}_{p}(t) $$

(7)

with

$$\begin{aligned} &f_{h}(\tilde{x}) = \left \{ \begin{array}{l@{\quad}l} \tilde{x} - (1 - \alpha )b & b < \tilde{x} \\ \alpha \tilde{x} & - b \le \tilde{x} \le b \\ \tilde{x} + (1 - \alpha )b & b < - \tilde{x} \end{array} \right . \\ & m = \frac{I_{a}I_{b}}{I_{b}r_{a}^{2} + I_{a}r_{b}^{2}},\qquad \hat{F}_{e}(t) = - m\frac{d^{2}e(t)}{dt^{2}} \\ &\hat{F}_{m} = m\biggl(\frac{T_{ma}r_{a}}{I_{a}} + \frac{T_{mb}r_{b}}{I_{b}} \biggr) \\ & \begin{aligned} \hat{F}_{p} &= \sum _{r = 1}^{\infty} m\biggl(\frac{r_{a}}{I_{a}} \biggr)T_{pr}\cos (r\omega_{p}t + \phi_{pr}) \\ &= \sum_{r = 1}^{\infty} \hat{F}_{pr} \cos (r\omega_{p}t + \phi_{pr}) \end{aligned} \end{aligned}$$

Here, m is the equivalent mass representing the total inertia of the gear pair, $\hat{F}_{m}$ is the average force transmitted through the gear pair, $\hat{F}_{p}(t)$ is the fluctuating force related to the input torque excitation, and the internal excitation term $\hat{F}_{e}(t)$ arises from the gear static transmission error. Dimensionless equation of motion can be obtained by defining:

$$\begin{aligned} &x = \tilde{x}/b, \qquad \omega_{n} = \sqrt{k_{m}/m}, \qquad \tau = \omega_{n}t \\ &\varOmega_{k} = \omega_{k}/\omega_{n},\qquad \varOmega_{e} = \omega_{e}/\omega_{n}, \qquad \varOmega_{p} = \omega_{p}/\omega_{n} \\ &\tilde{\mu} = c/2m\omega_{n}, \qquad \tilde{k}_{pr} = k_{r}/2m\omega_{n}^{2} \\ &\tilde{F}_{m} = \hat{F}_{m}/bk_{m},\qquad \tilde{F}_{pr} = \hat{F}_{pr}/bk_{m},\qquad \tilde{F}_{er} = e_{r}/b \end{aligned}$$

The dimensionless equation of the gear pair could be written as

$$\begin{aligned} &\frac{d^{2}x}{d\tau^{2}} + 2\tilde{\mu} \frac{dx}{d\tau} \\ &\qquad {}+ \Biggl(1 + 2 \sum_{r = 1}^{\infty} \tilde{k}_{pr}\cos (r\varOmega_{k}\tau + \phi_{kr}) \Biggr)f_{h}(x) \\ &\quad = \tilde{F}_{m} + \sum_{r = 1}^{\infty} \tilde{F}_{pr}\cos (r\varOmega_{p}\tau + \phi_{pr}) \\ &\qquad {}+ \sum_{r = 1}^{\infty} (r \varOmega_{e})^{2}\tilde{F}_{er}\cos (r \varOmega_{e}\tau + \phi_{er}) \end{aligned}$$

(8)

where

$$f_{h}(x) = \left \{ \begin{array}{l@{\quad}l} x - (1 - \alpha ) & 1 < x \\ \alpha x & {-} 1 \le x \le 1 \\ x + (1 - \alpha ) & 1 < - x \end{array} \right . $$

f _h (x) is the nonlinear displacement function due to backlash. The third-order approximation polynomial can express the gear backlash clearance function f _h (x). Therefore the third-order polynomial is taken to do the following analysis in this study. The particular case of α=0 for a gear pair system is studied. The approximated polynomial can be written as f _h (x)=−0.1667x+0.1667x ³. Figure 2(a) and (b) shows the f _h (x) and approximated function, respectively.

Fig. 2

(a) Schematic of the backlash function, f _h (x). (b) The approximated of the f _h (x) based on a third-order polynomial

Substituting f _h (x) into Eq. (8), the equation of motion of the system can be obtained as

$$\begin{aligned} &\frac{d^{2}x}{d\tau^{2}} + 2\tilde{\mu} \frac{dx}{d\tau} + \Biggl(1 + 2\sum _{r = 1}^{\infty} \tilde{k}_{pr}\cos (r \varOmega_{k}\tau + \phi_{kr}) \Biggr) \\ &\qquad {}\times\bigl( - 0.1667x + 0.1667x^{3}\bigr) \\ &\quad = \tilde{F}_{m} + \sum_{r = 1}^{\infty} \tilde{F}_{pr}\cos (r\varOmega_{p}\tau + \phi_{pr}) \\ &\qquad {}+ \sum_{r = 1}^{\infty} (r \varOmega_{e})^{2}\tilde{F}_{er}\cos (r \varOmega_{e}\tau + \phi_{er}) \end{aligned}$$

(9)

The proposed study is focused on the homoclinic bifurcation and chaos of Eq. (9), which represents a generalized nonlinear time varying (NLTV) dynamic model of a spur gear pair. Both analytical and numerical solution techniques are employed to solve this equation.

3 Global homoclinic bifurcation and chaos prediction

Homoclinic bifurcation is the occurrence of transverse intersection of the stable and unstable manifolds of a saddle fixed point and is a global bifurcation. In particular, it is defined as mechanisms responsible for prediction of the chaotic behavior. The Melnikov method is one of the few analytical tools to study the global bifurcation of the system, and it gives a procedure for analyzing and estimating when a chaotic behavior of a nonlinear dynamical system is expected [16–18]. In the following subsections, in order to apply this technique the fixed points and the homoclinic orbits of the unperturbed system are derived. Then the conditions of existence of chaos behavior in terms of homoclinic bifurcation by using Melnikov analysis are performed.

3.1 Analysis of the unperturbed system

In this subsection, we derive the homoclinic orbits, stable, and unstable manifolds of the unperturbed system. In order to apply the Melnikov technique and to carry out this study, we need to consider the average force, the excitation terms, the mesh stiffness, and damping term as small perturbations to the Hamiltonian system. Scaling $\tilde{F}_{m} = \varepsilon f_{m}$, $\tilde{F}_{pr} = \varepsilon f_{pr}$, $\tilde{F}_{er} = \varepsilon f_{er}$, $\tilde{\mu} = \varepsilon \mu$ and $\tilde{k}_{pr} = \varepsilon k_{pr}$, the perturbed equation of Eq. (9) can be rewritten as

$$\begin{aligned} \begin{aligned}[b] &\dot{x} = y \\ &\dot{y} = - 2\varepsilon \mu \dot{x} + \Biggl(1 + 2\sum _{r = 1}^{\infty} \varepsilon k_{pr}\cos (r \varOmega_{k}\tau + \phi_{kr}) \Biggr) \\ &\quad\ {}\times\bigl(0.1667x - 0.1667x^{3}\bigr) \\ &\quad\ {}+\varepsilon \Biggl(f_{m} + \sum_{r = 1}^{\infty} f_{pr}\cos (r\varOmega_{p}\tau + \phi_{pr}) \\ &\quad\ {} + \sum_{r = 1}^{\infty} (r \varOmega_{e})^{2}f_{er}\cos (r \varOmega_{e}\tau + \phi_{er})\Biggr) \end{aligned} \end{aligned}$$

(10)

where ε is a small parameter. When ε=0, Eq. (10) becomes

$$\begin{aligned} \begin{aligned} &\dot{x} = y \\ &\dot{y} = \bigl(0.1667x - 0.1667x^{3}\bigr) = \bigl(ax - cx^{3}\bigr) \end{aligned} \end{aligned}$$

(11)

which is referred to as the unperturbed system. The unperturbed system (11) is a planar Hamiltonian system with a potential and Hamiltonian function as

$$\begin{aligned} &U(x) = - \frac{ax^{2}}{2} + \frac{cx^{4}}{4} \end{aligned}$$

(12)

$$\begin{aligned} &H(x,y) = \frac{y^{2}}{2} + U(x) = \frac{1}{2}y^{2} - \frac{a}{2}x^{2} + \frac{c}{4}x^{4} \end{aligned}$$

(13)

The potential and the Hamiltonian function of the unperturbed system are shown in Fig. 3(a) and (b), respectively. The unperturbed system has three equilibrium points: (0,0) and (${\pm} \sqrt{\frac{a}{c}},0$). From the linear stability analysis, the Jacobian matrix and eigenvalues of the system are obtained as

$$\begin{aligned} &J = \left (\begin{array}{c@{\quad}c} 0 & 1 \\ (a - 3cx^{2}) & 0 \end{array} \right ) \\ &\quad{\Rightarrow}\quad \mbox{eigenvalue}\ \lambda = \frac{1}{2}\bigl( \pm \sqrt{4\bigl(a - 3cx^{2}\bigr)}\bigr) \end{aligned}$$

(14)

So, the eigenvalues of the fixed point (0,0) are obtained as $\lambda_{1,2} = \pm \sqrt{a}$, that is, λ ₁<0<λ ₂, and hence is a saddle. The eigenvalues of the remaining two fixed points (${\pm} \sqrt{\frac{a}{c}},0$) are $\lambda_{1,2} = \pm i\sqrt{2a}$, purely imaginary, and are thus center. Thus, the saddle point is connected to itself by two homoclinic orbits and defined as

$$\begin{aligned} \bigl(x_{h}(\bar{\tau} ),y_{h}(\bar{\tau} ) \bigr)& = \biggl( \pm \sqrt{\frac{2a}{c}} \sec h\bigl(\sqrt{a} (\bar{\tau} ) \bigr), \\ &\quad \mp \sqrt{\frac{2}{c}} a\sec h\bigl(\sqrt{a} (\bar{\tau} )\bigr) \tanh \bigl(\sqrt{a} (\bar{\tau} )\bigr)\biggr) \end{aligned}$$

(15)

where $\tau - \tau_{0} = \bar{\tau}$. Stable manifolds ($W_{s}^{ \pm}$) and unstable manifolds ($W_{u}^{ \pm}$) of the homoclinic orbits are indicated in Fig. 4. Periodic orbits are depicted outside and inside of the homoclinic orbit. In the following parts, we use Melnikov’s method to study how the dynamics of the perturbed system are changed under homoclinic bifurcation and how the chaotic dynamics are performed.

Fig. 3

(a) Potential function and, (b) Hamiltonian function of the unperturbed system

Fig. 4

Phase portrait and the homoclinic orbits of unperturbed system

3.2 Melnikov analysis for gear model equation

The stable and unstable manifolds ($W_{s}^{ \pm}$ and $W_{u}^{ \pm}$) of the homoclinic orbits for the unperturbed system have been obtained. When the perturbation terms are added to the unperturbed system, the closed homoclinic orbits break, and may have transverse manifolds. It is a global homoclinic bifurcation and implies the existence of the chaotic behaviors. The Melnikov method provides the estimate in the parameter space for the appearance of homoclinic bifurcation, and hence for transition to chaos. In this section, we give the conditions for existence of the homoclinic bifurcation and chaos by using the Melnikov method. According to this theory, the existence of transversal intersection of the stable and unstable manifolds of the homoclinic orbits implies the existence of the chaotic behaviors. Hence, the homoclinic bifurcation for our model is analyzed by transforming Eq. (10) into the vector form as

$$ \begin{aligned} &\dot{x} = p_{1}(x,y) + \varepsilon q_{1}(x,y,\tau ) \\ &\dot{y} = p_{2}(x,y) + \varepsilon q_{2}(x,y,\tau ) \end{aligned} $$

(16)

where

$$\begin{aligned} &p_{1}(x,y) = y\qquad q_{1}(x,y,\tau ) = 0 \\ & p_{2}(x,y) = \bigl(ax - cx^{3}\bigr) \\ & q_{2}(x,y,\tau ) \\ &\quad = - 2\mu \dot{x} + 2\sum_{r = 1}^{\infty} k_{pr} \cos (r\varOmega_{k}\tau + \phi_{kr}) \bigl(ax - cx^{3}\bigr)\\ &\qquad {}+ f_{m} + \sum_{r = 1}^{\infty} f_{pr}\cos (r\varOmega_{p}\tau + \phi_{pr}) \\ &\qquad {}+ \sum_{r = 1}^{\infty} (r \varOmega_{e})^{2}f_{er}\cos (r \varOmega_{e}\tau + \phi_{er}) \end{aligned}$$

The Melnikov function measuring the distance between the stable and unstable manifolds of the perturbed system in the Poincare section is defined as follows [18]:

$$\begin{aligned} M(\tau_{0}) &= \int_{ - \infty}^{ + \infty} p \bigl(X_{h}(\tau - \tau_{0})\bigr) \wedge q \bigl(X_{h}(\tau - \tau_{0}),\tau \bigr)\,d\tau \\ &= \int_{ - \infty}^{ + \infty} p\bigl(X_{h}(\tau ) \bigr) \wedge q\bigl(X_{h}(\tau ),\tau + \tau_{0}\bigr)\,d \tau \end{aligned}$$

(17)

where X _h =(x _h ,y _h ) represents homoclinic orbits, and p∧q=p ₁ q ₂−p ₂ q ₁. Substituting Eq. (16) into Eq. (17), the Melnikov integral could be rewritten as

$$\begin{aligned} & \begin{aligned} M(\tau_{0}) &= \int_{ - \infty}^{ + \infty} y_{h}\Biggl( - 2\mu y_{h} + 2\sum_{r = 1}^{\infty} k_{pr} \cos \bigl(r\varOmega_{k} (\tau + \tau_{0}) + \phi_{kr}\bigr) \bigl(ax_{h} - cx_{h}^{3}\bigr) + f_{m} \\ &\quad {}+ \sum_{r = 1}^{\infty} f_{pr} \cos \bigl(r\varOmega_{p}(\tau + \tau_{0}) + \phi_{pr}\bigr) {}+ \sum_{r = 1}^{\infty} (r \varOmega_{e})^{2}f_{er}\cos \bigl(r \varOmega_{e}(\tau + \tau_{0}) + \phi_{er}\bigr) \Biggr) \,d\tau \end{aligned} \\ &\quad \begin{aligned}[b] {\Rightarrow}\quad M(\tau_{0}) &= \int_{ - \infty}^{ + \infty} \biggl[ \mp \sqrt{ \frac{2}{c}} a\sec h(\sqrt{a} \tau )\tanh (\sqrt{a} \tau )\biggr] \Biggl( - 2\mu \biggl[ \mp \sqrt{\frac{2}{c}} a\sec h(\sqrt{a} \tau )\tanh (\sqrt{a} \tau )\biggr] \\ &\quad {}+\sum_{r = 1}^{\infty} 2k_{pr} \cos \bigl(r\varOmega_{k}(\tau + \tau_{0}) + \phi_{kr}\bigr) \\ &\quad {}\times \biggl(a\biggl[ \pm \sqrt{\frac{2a}{c}} \sec h\bigl(\sqrt{a} ( \tau )\bigr)\biggr] - c\biggl[ \pm \sqrt{\frac{2a}{c}} \sec h\bigl(\sqrt{a} (\tau )\bigr) \biggr]^{3}\biggr) + f_{m} \\ &\quad {} + \sum_{r = 1}^{\infty} f_{pr}\cos \bigl(r\varOmega_{p}(\tau + \tau_{0}) + \phi_{pr}\bigr) + \sum_{r = 1}^{\infty} (r \varOmega_{e})^{2}f_{er}\cos \bigl(r \varOmega_{e}(\tau + \tau_{0}) + \phi_{er}\bigr) \Biggr)\,d\tau \end{aligned} \end{aligned}$$

(18)

Considering only the first harmonics term (r=1), and evaluating the integral, the Melnikov function can be written as

$$\begin{aligned} M^{ \pm} (\tau_{0}) & = - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} + 4a\sqrt{\frac{a}{c^{2}}} k_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\sin (\varOmega_{k}\tau_{0} + \phi_{k1})\varOmega_{k}^{2}}{2a^{3/2}} \\ &\quad {}- 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\sin (\varOmega_{k}\tau_{0} + \phi_{k1})\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\quad {}\pm \sqrt{\frac{2}{c}} f_{p1}\pi \sec h\biggl( \frac{\pi \varOmega_{p}}{2\sqrt{a}} \biggr)\sin (\varOmega_{p}\tau_{0} + \phi_{p1})\varOmega_{p} \pm \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\sin (\varOmega_{e}\tau_{0} + \phi_{e1})\varOmega_{e}^{3} \end{aligned}$$

(19)

According to Melnikov theory, M(τ ₀)=0 and $\frac{dM(\tau_{0})}{d\tau_{0}} \ne 0$ are conditions that the stable and unstable manifolds intersect transversally. So, if M(τ ₀) has a simple zero, the global homoclinic bifurcation occurs, which is indicative of chaotic vibration. From this relation, the threshold values of the parameters for occurrence of the homoclinic bifurcation are obtained.

4 Numerical simulations and analysis

In this section, we study the occurrence of the homoclinic bifurcation and chaos both analytically and numerically. We give the numerical simulation to demonstrate the theoretical results from Melnikov analysis obtained in the previous section. Different reduced models of the geared systems are considered in practice. The homoclinic bifurcation in case of internal excitation, external excitation, parametric excitation, and combination excitation of internal, external, and parametric excitation is obtained and the threshold curves are plotted. The conditions and system parameters are also investigated at which these models can imply the existence of chaotic behavior.

4.1 Gear model with manufacturing error term

A gear system with the manufacturing error is considered as the first example case. Here, we study the gear pair system on the condition of internal excitation term (the manufacturing error). The external excitation and time varying stiffness terms are ignored, i.e., $\tilde{k}_{pr} = \tilde{F}_{pr} = 0$. When only internal forces excite the system, Eq. (9) reduces to:

$$\begin{aligned} &\frac{d^{2}x}{d\tau^{2}} + 2\tilde{\mu} \frac{dx}{d\tau} + f_{h}(x) \\ &\quad = \tilde{F}_{m} + \sum_{r = 1}^{\infty} (r\varOmega_{e})^{2}\tilde{F}_{er}\cos (r \varOmega_{e}\tau + \phi_{er}) \end{aligned}$$

(20)

According to Eq. (19) and by considering the first harmonic term (r=1), M(τ ₀)^± can be simplified as follows:

$$\begin{aligned} &M^{ \pm} (\tau_{0}) \\ &\quad = - \frac{8}{3} \frac{\mu (a)^{2}}{c\sqrt{a}} \pm \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr) \\ &\qquad {}\times\sin (\varOmega_{e}\tau_{0} + \phi_{e1})\varOmega_{e}^{3} \\ &\quad = A' \pm F'\sin (\varOmega_{e}\tau_{0} + \phi_{e1}) \end{aligned}$$

(21)

The condition for transverse intersection of the stable and unstable manifolds can be written as

$$\begin{aligned} &\bigl\vert A' \bigr\vert \le \bigl\vert F' \bigr\vert \\ &\quad {\Rightarrow}\quad \biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert \le \biggl\vert \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3} \biggr\vert \end{aligned}$$

(22)

This equation provides the condition for the occurrence of chaos. Equality sign corresponds to the tangential intersections of the homoclinic orbits. Using Eq. (22) and choosing f _e1 as the control parameter, the conditions for transverse intersection of the stable and unstable manifolds are obtained as

$$ \begin{aligned} &f_{e1} \ge f_{e1(1)} = \frac{8}{3\sqrt{2}} \frac{\vert \mu \vert \sqrt{c} (a)^{2}}{\pi \varOmega_{e}^{3}c\sqrt{a}} \cos h\biggl(\frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\quad \mbox{or}\quad \\ &f_{e1} \le f_{e1(2)} = - \frac{8}{3\sqrt{2}} \frac{\vert \mu \vert \sqrt{c} (a)^{2}}{\pi \varOmega_{e}^{3}c\sqrt{a}} \cos h\biggl(\frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr) \end{aligned} $$

(23)

These conditions provide a domain on the parameter space where the system has transverse homoclinic orbits resulting in possible chaotic behavior. Figure 5 shows the Melnikov threshold curves for chaos in the (f _e1–Ω _e ) plane for μ=7. In the region between threshold curves f _e1(1), and f _e1(2), Melnikov function does not change its sign and is an indication of no transverse intersection of the stable and unstable manifolds. In the no-shaded regions that are above the threshold curve f _e1(1), and below the threshold curve f _e1(2), both M ⁺(τ ₀) and M ⁻(τ ₀) change their sign. As a result, in these regions transverse intersection of the stable and unstable manifolds occurs, and onset of chaos is expected.

Fig. 5

Threshold curves for homoclinic bifurcation in the (f _e1–Ω _e ) plane for μ=7

For instance, in Ω _e =0.5, when the control parameter f _e1 is increased from a zero value in the shaded region, transverse intersection of the stable and unstable manifolds ($W_{s}^{ \pm}$ and $W_{u}^{ \pm}$) occurs for f _e1≥20. Since the Melnikov function can change its sign (it has simple zeros), chaos may occur.

To verify the analytical predictions, a series of numerical simulations of Eq. (20) has been performed. The nonlinear equation (20) is integrated numerically using the fourth-order Runge–Kutta method. Figure 6 presents the bifurcation diagram of the spur gear system using the $\tilde{F}_{e1}$ $(\tilde{F}_{e1} = \varepsilon f_{e1})$, as a bifurcation parameter. The values of the parameters Ω _e =0.5, f _m =1, μ=7, ε=0.01 and initial conditions x=0.01 and $\dot{x} = 0.01$ are chosen. A transition from periodic motion to the chaotic dynamics are seen when $\tilde{F}_{e1}$ is increased from 0 to 0.3. It can be observed that the gear system exhibits a 1T-periodic response at low values of the internal excitation term $\tilde{F}_{e1}$, i.e., $\tilde{F}_{e1} \le 0.21$. However, as $\tilde{F}_{e1}$ is increased from 0.21 to 0.23, the 1T-periodic motion is replaced by 2T-periodic motion through a period doubling bifurcation. As the control parameter $\tilde{F}_{e1}$ is further increased, the 2T-periodic motion transits to periodic motion with a period of 4T. With the increase of the control parameter $\tilde{F}_{e1}$, period doubling occurs, and a bifurcation cascade leads to chaos. Finally, for $\tilde{F}_{e1} \ge 0.235$, the gear system performs nonperiodic or chaotic motion.

Fig. 6

Bifurcation diagram using $\tilde{F}_{e1}$ $(\tilde{F}_{e1} = \varepsilon f_{e1})$ as control parameter

For a better clarity, we show the transition to chaos through the numerical simulation for five values of f _e1 chosen in the shaded and no shaded regions (f _e1=18, f _e1=22, f _e1=23, f _e1=24, and f _e1=28 (see Fig. 5)). Transverse intersections of the stable and unstable manifolds of both the homoclinic orbits are seen in f _e1≥20, which is above the threshold value. Figures 7–11 illustrate the time histories, phase plane diagrams, Poincare sections, and Fourier spectras for this gear model at points 1–5, respectively. According to Fig. 5, point 1 corresponds to the point situated below threshold values (in the shaded region), and is associated with the 1T-periodic motion (see Fig. 6). The numerical simulations of Eq. (20) are performed for this point. The time history, phase plane diagram, Poincare section, and Fourier spectra are shown in Fig. 7. These figures show the periodic response and confirm the prediction of a periodic motion obtained by the Melnikov function. With the increasing f _e1 and crossing the critical value, the system loses its stability and consequently, the system begins to execute the chaotic behavior. The numerical analysis is carried out for the parameters associated with points 2 and 3. They correspond to the points situated in the transient region (Fig. 5) and are associated with the 2T and 4T-periodic motion (Fig. 6). Figures 8 and 9 illustrate the time histories, phase planes, Poincare sections, and Fourier spectras for these points.

Fig. 7

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for f _e1=18

Fig. 8

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for f _e1=22

Fig. 9

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for f _e1=23

Finally, the numerical analysis of Eq. (20) is carried out for the parameters associated with points 4 and 5 (f _e1=24 and f _e1=28) situated above threshold value. The investigated corresponds to the chaotic motion. The chaotic trajectories are obtained by numerical integration. The time histories, phase planes, Poincare sections, and Fourier spectras corresponding to the chaotic response are presented in Figs. 10 and 11. Chaotic behavior is clearly visible. The numerical computations confirm the analytical prediction of chaos for the applied value of f _e1.

Fig. 10

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for f _e1=24

Fig. 11

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for f _e1=28

Now we consider the effect of the parameter μ for the occurrence of homoclinic bifurcation and chaos in the system. Both analytical and numerical solution techniques are employed. Analytical solutions are constructed by the Melnikov method. Using Eq. (22) and choosing μ as a control parameter, the conditions for transverse intersection of the stable and unstable manifolds are given by

$$\begin{aligned} \begin{aligned} &\mu \le \mu_{(1)} = \frac{3c}{8a^{2}}\sqrt{\frac{2a}{c}} \vert f_{e1} \vert \pi \sec h\biggl(\frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\quad \mbox{and} \\ &\mu \ge \mu_{(2)} = - \frac{3c}{8a^{2}}\sqrt{\frac{2a}{c}} \vert f_{e1} \vert \pi \sec h\biggl(\frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr) \varOmega_{e}^{3} \end{aligned} \end{aligned}$$

(24)

The threshold curves for chaos in the (μ–Ω _e ) plane for f _e1=30 are shown in Fig. 12. In the region between the threshold curves μ ₍₁₎ and μ ₍₂₎, both M ⁺(τ ₀) and M ⁻(τ ₀) change their sign. As a result, in this region, transverse intersection of the stable and unstable manifolds occurs, and onset of chaos is expected. In the shaded regions that are above the threshold curve μ ₍₁₎ and below the threshold curve μ ₍₂₎, Melnikov function does not change sign and is an indication of no transverse intersection of the stable and unstable manifolds.

Fig. 12

Threshold curves for homoclinic bifurcation in the (μ−Ω _e ) plane for f _e1=30

The influence of the parameter $\tilde{\mu}\ (\tilde{\mu} = \varepsilon \mu)$ is also illustrated in the bifurcation diagram shown in Fig. 13. We fix the values of the parameters as Ω _e =0.7, f _e1=30, f _m =1, ε=0.01 and initial conditions as x=0.01 and $\dot{x} = 0.01$. It can be observed that the gear system exhibits chaotic motion at low values of the dimensionless damping term $\tilde{\mu}$. However, as $\tilde{\mu}$ is increased, the nonperiodic motion is replaced by nT-periodic motion. 4T and 2T periodic motions are clearly visible in Fig. 13. Finally, as the damping $\tilde{\mu}$ is further increased, the 2T-periodic motion transits to a motion with period of 1T.

Fig. 13

Bifurcation diagram using $\tilde{\mu}\ (\tilde{\mu} = \varepsilon \mu)$ as control parameter

Also, we show the transition to chaos through the numerical simulation for three values of μ=15, μ=13.5, and μ=12 (see Figs. 12 and 13). It can be observed that point 1 (μ=15,Ω _e =0.7), lies out of chaos, point 2 (μ=13.5,Ω _e =0.7) and point 3 (μ=12,Ω _e =0.7), lie in the chaotic area. Point (1) corresponds to the point situated above threshold value, the Melnikov function does not change its sign and is associated with the periodic motion. The numerical simulations are performed for the parameter sets associated with this point. The time history, phase plane diagram, Poincare section and Fourier spectra are shown in Fig. 14. These figures show the periodic response and confirm the prediction of a periodic motion was obtained by Melnikov theory.

Fig. 14

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for μ=15

In the next computational step, we have taken μ=13.5 (point 2). It corresponds to the point situated in transient region (see Fig. 12) and is associated with the 2T-periodic motion (see Fig. 13). Figure 15 illustrates the time history, phase plane, Poincare section, and Fourier spectra for the parameter μ=13.5. Observe that for this point the 2T-periodic motion occurs.

Fig. 15

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for μ=13.5

Finally, the numerical analysis is carried out for the parameter μ=12. Based on Fig. 12, the function changes its sign for μ=12. The investigated point corresponds to the chaotic motion. The chaotic trajectories are obtained by numerical integration. The time history, phase plane, Poincare section, and Fourier spectra corresponding to the chaotic response are presented in Fig. 16. Chaotic behavior is clearly visible. The numerical computations confirm the prediction of analytical chaos for applied value of μ.

Fig. 16

(a) Time history, (b) phase plane, (c) Poincare section, and (d) Fourier spectra for μ=12

We have also plotted the dependence of the excitation f _e1 for homoclinic chaos for different values of the damping parameter μ in a frequency range 0<Ω _e <2.5. The surfaces are shown in Fig. 17(a). As it can be observed from this figure, as μ increases, the threshold f _e1 for the onset of chaos obtained by the Melnikov technique increases in a frequency range 0<Ω _e <2.5. We have also plotted in Fig. 17(b) the dependence of the parameter μ on the frequency 0<Ω _e <2.5 for different values of f _e1. In the parameter region, between the threshold curves transverse intersection of the stable and unstable manifolds occurs, onset of chaos is expected. One clear observation from this figure is that, the threshold μ increases when f _e1 increases. These conditions provide a domain on the parameter spaces where the system has transverse homoclinic orbits resulting in possible chaotic behavior. So, these results play an important role in the formation of the chaotic regions and could be used for the analysis and dynamic design of the gear system parameters.

Fig. 17

Threshold surfaces for homoclinic bifurcation in the parameter space for: (a) control parameter f _e1, (b) control parameter μ

4.2 Gear model with time varying stiffness and manufacturing error

This section focuses on the analysis of the approximate model of the gear pair which represents a gear pair with the static transmission error excitation and the mesh stiffness variation. The governing equation is given by substituting $\tilde{F}_{p}(t) = 0$ in Eq. (9) and reduces to:

$$\begin{aligned} &\frac{d^{2}x}{d\tau^{2}} + 2\tilde{\mu} \frac{dx}{d\tau} \\ &\qquad {}+ \Biggl(1 + 2\sum_{r = 1}^{\infty} \tilde{k}_{pr}\cos (r\varOmega_{k}\tau + \phi_{kr}) \Biggr)f_{h}(x) \\ &\quad = \tilde{F}_{m} + \sum_{r = 1}^{\infty} (r\varOmega_{e})^{2}\tilde{F}_{er}\cos (r \varOmega_{e}\tau + \phi_{er}) \end{aligned}$$

(25)

According to Eq. (19) and by considering the first harmonic term (r=1), M(τ ₀)^± can be simplified as follows:

$$\begin{aligned} &M^{ \pm} (\tau_{0}) \\ &\quad = - \frac{8}{3} \frac{\mu (a)^{2}}{c\sqrt{a}} + 4a\sqrt{\frac{a}{c^{2}}} k_{p1} \\ &\qquad {}\times\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\sin (\varOmega_{k}\tau_{0} + \phi_{k1})\varOmega_{k}^{2}}{2a^{3/2}} \\ &\qquad {}- 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \\ &\qquad {}\times \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\sin (\varOmega_{k}\tau_{0} + \phi_{k1})\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\qquad {}\pm \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\sin (\varOmega_{e}\tau_{0} + \phi_{e1})\varOmega_{e}^{3} \\ & \begin{aligned}[b] \quad {\Rightarrow}\quad M^{ \pm} (\tau_{0}) &= A' + \bigl(B' + C' \bigr) \sin (\varOmega_{k}\tau_{0} + \phi_{k1}) \\ &\quad {}\pm F'\sin (\varOmega_{e} \tau_{0} + \phi_{e1}) \end{aligned} \end{aligned}$$

(26)

In the gear dynamic models, the dimensionless excitation frequencies Ω _e and Ω _k are equal. The phase angles ϕ _k1 and ϕ _e1 will be neglected to simplify the dynamic problem. Thus, the condition for transverse intersection of the stable and unstable manifolds can be written as

$$\begin{aligned} &\bigl\vert A' \bigr\vert \le \bigl\vert B' + C' \pm F' \bigr\vert \\ & \begin{aligned}[b] \quad {\Rightarrow}\quad \biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert &\le \biggl| 4a\sqrt{\frac{a}{c^{2}}} k_{p1}\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} \\ &\quad {} -8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \pm \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3} \biggr| \end{aligned} \end{aligned}$$

(27)

Using Eq. (27) and choosing f _e1 as control parameter, the conditions for transverse intersection of the stable and unstable manifolds $W_{s}^{ +}$ and $W_{u}^{ +}$ are obtained as:

$$\begin{aligned} f_{e1} &\ge f_{e1(1)} = \biggl( - 4a\sqrt{\frac{a}{c^{2}}} k_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} + 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\quad {}+ \biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert \biggr)\Big/\biggl(\sqrt{\frac{2}{c}} \pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr) \end{aligned}$$

(28a)

or

$$\begin{aligned} f_{e1} &\le f_{e1(2)} = \biggl( - 4a\sqrt{\frac{a}{c^{2}}} k_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} + 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\quad {}- \biggl| {-} \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr|\biggr)\Big/\biggl(\sqrt{ \frac{2}{c}} \pi \sec h\biggl(\frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr) \varOmega_{e}^{3}\biggr) \end{aligned}$$

(28b)

Also, the conditions for transverse intersection of the stable and unstable manifolds $W_{s}^{ -}$ and $W_{u}^{ -}$ are obtained as:

$$\begin{aligned} f_{e1} &\le f_{e1(3)} = \biggl(4a\sqrt{\frac{a}{c^{2}}} k_{p1}\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} -8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\quad {}- \biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert \biggr)\Big/\biggl(\sqrt{\frac{2}{c}} \pi \sec h\biggl(\frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr) \end{aligned}$$

(28c)

or

$$\begin{aligned} f_{e1} &\ge f_{e1(4)} = \biggl(4a\sqrt{\frac{a}{c^{2}}} k_{p1}\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} - 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\quad {}+ \biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert \biggr)\Big/\biggl(\sqrt{\frac{2}{c}} \pi \sec h\biggl(\frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr) \end{aligned}$$

(28d)

The threshold curves for chaos in the (f _e1–Ω), (f _e1–k _p1), and (f _e1–μ) plane are shown in Fig. 18. Figure 18(a) shows the Melnikov threshold curves for chaos in the (f _e1–Ω) plane for k _p1=10, and μ=10. In the regions above, the threshold curve f _e1(1), and below the threshold curve f _e1(2), M ⁺(τ ₀) changes its sign. As a result, in these regions transverse

Fig. 18

Threshold curves for homoclinic bifurcation: (a) in the (f _e1–Ω) plane, (b) in the (f _e1–k _p1) plane, (c) in the (f _e1–μ) plane

intersection of the stable and unstable manifolds $W_{s}^{ +}$ and $W_{u}^{ +}$ occurs. In the regions below, the threshold curve f _e1(3), and above the threshold curve f _e1(4), M ⁻(τ ₀) changes its sign, and the transverse intersection of the stable and unstable manifolds $W_{s}^{ -}$ and $W_{u}^{ -}$ occurs. These conditions provide a domain on the parameter spaces where the system has transverse homoclinic orbits resulting in possible chaotic behavior. Thus, in the shaded and dotted regions, both M ⁺(τ ₀) and M ⁻(τ ₀) change their sign. Consequently, in these regions transverse intersections of the manifolds $W_{s}^{ +}$ and $W_{u}^{ +}$ and $W_{s}^{ -}$ and $W_{u}^{ -}$ occur. Transverse intersections of $W_{s}^{ +}$ and $W_{u}^{ +}$ happen alone in the dotted regions. Since, in these regions only M ⁺(τ ₀) changes its sign and the sign of M ⁻(τ ₀) remains the same. In the shaded regions, M ⁻(τ ₀) alone changes its sign.

This implies that in these regions the transverse intersection of the manifolds $W_{s}^{ -}$ and $W_{u}^{ -}$ occurs. In the no shaded and no dotted regions, both M ⁺(τ ₀) and M ⁻(τ ₀) do not change their sign, and this is an indication of no transverse intersection of the stable and unstable manifolds.

Also, the Melnikov threshold curves in the (f _e1–k _p1) plane for Ω=1, and μ=10, and the threshold curves in the (f _e1–μ) plane for Ω=1, and k _p1=10, are shown in Fig. 18(b) and (c), respectively. We have also plotted the threshold surfaces in the parameter space (f _e1,k _p1,μ) and (f _e1,Ω,μ) in Figs. 19 and 20.

Fig. 19

Threshold surfaces for homoclinic bifurcation in the parameter space (f _e1, k _p1,μ) for Ω=1

Fig. 20

Threshold surfaces for homoclinic bifurcation in the parameter space (f _e1,Ω,μ) for k _p1=10

Using Eq. (27) and choosing k _p1 as control parameter, the conditions for transverse intersection of the stable and unstable manifolds $W_{s}^{ +}$ and $W_{u}^{ +}$ are obtained as:

$$\begin{aligned} k_{p1} &\ge k_{p1(1)} = \biggl(\biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert - \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr) \Big/\biggl(4a\sqrt{\frac{a}{c^{2}}} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} \\ &\quad {}- 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}c\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}}\biggr) \end{aligned}$$

(29a)

or

$$\begin{aligned} k_{p1} &\le k_{p1(2)} = \biggl( - \biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert - \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr) \Big/\biggl(4a\sqrt{\frac{a}{c^{2}}} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} \\ &\quad {}- 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}c\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}}\biggr) \end{aligned}$$

(29b)

Also, the conditions for transverse intersection of the stable and unstable manifolds $W_{s}^{ -}$ and $W_{u}^{ -}$ are obtained as:

$$\begin{aligned} k_{p1} &\ge k_{p1(3)} = \biggl(\biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert + \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr) \Big/\biggl(4a\sqrt{\frac{a}{c^{2}}} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} \\ &\quad {}- 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}c\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}}\biggr) \end{aligned}$$

(29c)

or

$$\begin{aligned} k_{p1} &\le k_{p1(4)} = \biggl( - \biggl\vert - \frac{8}{3}\frac{\mu (a)^{2}}{c\sqrt{a}} \biggr\vert + \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr) \Big/\biggl(4a\sqrt{\frac{a}{c^{2}}} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} \\ &\quad {}- 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}c\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}}\biggr) \end{aligned}$$

(29d)

These conditions provide a domain on the parameter spaces where the system has transverse homoclinic orbits resulting in possible chaotic behavior. The threshold curves for control parameter k _p1 in the (k _p1–f _e1), (k _p1–μ), and (k _p1–Ω) plane are shown in Fig. 21. We have also plotted the threshold surfaces in the parameter space (k _p1,f _e1,μ) for Ω=1, and (k _p1,Ω,μ) for f _e1=10 in Figs. 22 and 23, respectively.

Fig. 21

Threshold curves for homoclinic bifurcation: (a) in the (k _p1–f _e1) plane for Ω=1, and μ=10, (b) in the (k _p1–μ) plane for Ω=1, and f _e1=10, (c) in the (k _p1–Ω) plane for f _e1=10, and μ=10

Fig. 22

Threshold surfaces for homoclinic bifurcation in the parameter space (k _p1,f _e1,μ)

Fig. 23

Threshold surfaces for homoclinic bifurcation in the parameter space (k _p1,Ω,μ)

Using Eq. (27) and choosing μ as control parameter, the conditions for transverse intersection of the stable and unstable manifolds $W_{s}^{ +}$ and $W_{u}^{ +}$ are obtained as:

$$\begin{aligned} &{-}\biggl|\biggl(4a\sqrt{\frac{a}{c^{2}}} k_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} - 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2} ck_{p1}\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\qquad {}+ \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr)\Big/ \frac{3c\sqrt{a}}{8(a)^{2}} \biggr| = \mu_{(1)} \le \mu \end{aligned}$$

(30a)

and

$$\begin{aligned} \mu \le \mu_{(2)} &= \biggl|\biggl(4a\sqrt{\frac{a}{c^{2}}} k_{p1}\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} - 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\quad {}+ \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr)\Big/ \frac{3c\sqrt{a}}{8(a)^{2}} \biggr| \end{aligned}$$

(30b)

Also, the conditions for transverse intersection of stable and unstablemanifolds $W_{s}^{ -}$ and $W_{u}^{ -}$ are obtained as:

$$\begin{aligned} & {-}\biggl|\biggl(4a\sqrt{\frac{a}{c^{2}}} k_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} - 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\qquad {}-\sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr)\Big/ \frac{3c\sqrt{a}}{8(a)^{2}} \biggr| = \mu_{(3)} \le \mu \end{aligned}$$

(30c)

and

$$\begin{aligned} \mu \le \mu_{(4)} &= \biggl|\biggl(4a\sqrt{\frac{a}{c^{2}}} k_{p1}\frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}}{2a^{3/2}} - 8a\sqrt{\frac{1}{c}} \biggl(\frac{a}{c} \biggr)^{3/2}ck_{p1} \frac{\pi \csc h(\frac{\pi \varOmega_{k}}{2\sqrt{a}} )\varOmega_{k}^{2}(4a + \varOmega_{k}^{2})}{24a^{5/2}} \\ &\quad {}- \sqrt{\frac{2}{c}} f_{e1}\pi \sec h\biggl( \frac{\pi \varOmega_{e}}{2\sqrt{a}} \biggr)\varOmega_{e}^{3}\biggr)\Big/ \frac{3c\sqrt{a}}{8(a)^{2}} \biggr| \end{aligned}$$

(30d)

The threshold curves for the control parameter μ in the (μ–f _e1), (μ–k _p1), and (μ–Ω) plane are shown in Fig. 24. We have also plotted the threshold surfaces in the parameter space (μ,f _e1,k _p1) for Ω=1 and (μ,f _e1,Ω) for k _p1=10 in Figs. 25 and 26.

Fig. 24

Threshold curves for homoclinic bifurcation: (a) in the (μ–f _e1) plane for Ω=1, and k _p1=10, (b) in the (μ–k _p1) plane for Ω=1, and f _e1=10, (c) in the (μ–Ω) plane for f _e1=10, and k _p1=10

Fig. 25

Threshold surfaces for homoclinic bifurcation in the parameter space (μ,k _p1,f _e1)

Fig. 26

Threshold surfaces for homoclinic bifurcation in the parameter space (μ,f _e1,Ω)

4.3 A generalized nonlinear time varying (NLTV) model of gear

The approximate analytical solutions given in the above section are constructed only for one harmonic excitation term $\tilde{F}_{e}$. However, it is necessary to consider the generalized nonlinear model included the backlash, time varying stiffness, external excitation, and manufacturing error in the analysis. This section focuses on the study of Eq. (9), which represents a generalized nonlinear time varying (NLTV) dynamic model of a spur gear pair. By considering the first harmonic term (r=1), M(τ ₀)^± can be represented by Eq. (19). Mesh frequency Ω _k is higher than Ω _p . The dimensionless frequencies Ω _p , Ω _e , and Ω _k are assumed as: Ω _k =Ω _e =1 and Ω _p =0.1. The phase angles ϕ _p1, ϕ _k1, and ϕ _e1 will be neglected to simplify the dynamic problem. The conditions where Melnikov function can change its sign are obtained numerically. The regions for transverse intersection of the stable and unstable manifolds of $W_{s}^{ +}$ and $W_{u}^{ +}$ and $W_{s}^{ -}$ and $W_{u}^{ -}$ in the parameter space (f _e1,μ,k _p1) are shown in Fig. 27(a), and (b), respectively. Also, Fig. 28 shows the regions for transverse intersection of the stable and unstable manifolds in the parameter space (f _p1,μ,k _p1), resulting in possible chaotic dynamics. More precisely, these conditions play an important role in order to identify the chaotic region and could be used for the analysis and dynamic design of the gear system parameters.

Fig. 27

Homoclinic bifurcation regions in the parameter space (f _e1,μ,k _p1) for f _p1=10: (a) for transverse intersection of manifolds $W_{s}^{ +}$ and $W_{u}^{ +}$, (b) for transverse intersection of manifolds $W_{s}^{ -}$ and $W_{u}^{ -}$

Fig. 28

Homoclinic bifurcation regions in the parameter space (f _p1,μ,k _p1) for f _e1=10: (a) for transverse intersection of manifolds $W_{s}^{ +}$ and $W_{u}^{ +}$, (b) for transverse intersection of manifolds $W_{s}^{ -}$ and $W_{u}^{ -}$

5 Conclusions

In the present paper, the dynamic behavior and global homoclinic bifurcation of the generalized nonlinear time varying (NLTV) model of a spur gear pair has been studied. The Melnikov method has been applied to predict the threshold values of the gear system parameters for the occurrence of the homoclinic bifurcation and transition to chaotic behavior. Threshold curves were drawn on different parameter spaces and effects of different parameters have been studied. The analytical predictions have been verified through numerical simulation and good agreement is observed. Analyzing and predicting the chaotic behaviors of a gear system are useful. These results provide some idea and play an important role in order to analyze and dynamic design of the gear system parameters. The system parameters should be chosen, so that the system is not chaotically excited.