Introduction

Flow driven by rotating disks is apparently the most distinguished and of particular interest research part in the study of fluid mechanics, the reason behind this is because of its emerging numerous scientific applications associated with engineering, for instance, rotating machinery, lubrication, computer storage devices, turbine systems and jet motors. That is why the circulating disk flow phenomenon captured the interest of researchers globally. Von Karman was among the first one who has debated the laminar and steady flow of viscous Newtonian fluid over a disk which is rotating infinitely in 1921 [1]. He developed an authentic similarity transformation by means of which the Navier–Stokes equations are reduced to coupled ODEs, and thus the approximated solution of the ODEs is obtained via method of momentum integral. The results are more accurate when Cochran [2] gave an asymptotic series solution to Von Karman’s problem in 1934 by considering z positive and motion of the fluid is on the side of the plane as the nature of the fluid is infinite in extent and the only boundary is \(z = 0\). Rogers and Lance [3] improved the outcomes in 1960. They studied the fluid flow due to the infinite disk rotation in a state of solid rotation at infinity and concluded that when the fluid is revolving in a similar sense as disk at infinity then in all cases physically acceptable solutions exist and these solutions occur only in the presence of uniform suction which is operating on disk in the case when the fluid spins opposite to that of disk. In 1966, Benton [4] pointed out the mistakes in previous work and described the exact non-steady velocity and pressure fields given by appropriate power-series expansion in the angle of rotation with the help of coefficients which are the functions of similarity variables. Millsaps and Pohlhausen [5] investigated the solution of energy equation and transfer the heat for a variety of Prandtl numbers at a constant temperature due to disk rotation in 1952. The thermal boundary condition with the wall temperature of a power-law distribution for a free rotatory disk was scrutinized by Dorfman and Serazetdinov [6]. The new analytical solution of Nusselt number was given by Shevchuk [7] in the shape of a function of an arbitrary power-law and for specifying it as a boundary condition. Turkyilmazoglu [8] provided full analytical solutions of the conducting and viscous incompressible fluid flow through a porous disk which is spinning with a uniform angular speed. Flow by the virtue of rotating rough and porous disk is analyzed numerically and mathematically by Turkyilmazoglu and Senel [9]. Matkowsky and Siegmann [10] examined the similarity equations of Karman for the fluid which is flowing between two coaxial infinite disks that rotates in opposite directions but having equal rotation rates. Sandilya et al. [11] deal with the gas flow and transfer of mass and gave the numerical simulation between two co-axially rotating disks. Turkyilmazoglu further explored the fluid flow together with heat which is induced simultaneously by two stretchable and co-axially rotating disks having constant distance [12]. Awati et al. [13] did a series analysis of two stretching disks which are co-axially infinite of an axis-symmetric flow and enlarged the validity of the series solution for larger values of Reynolds number up to infinity. Ahmed et al. [14] investigated the Maxwell fluid for axisymmetric rotating flow between two disks which are spiraling co-axially by considering Cattaneo–Christov heat flux conduction model and concluded that in all directions the velocity components are decreasing with the Deporah number. Imtiaz et al. [15] have explored the Jeffrey fluid flow with respect to non-Fourier heat flux due to the rotation of disk and in occurrence of homogenous-heterogeneous reactions. They have computed the convergent series solutions of nonlinear equations by the method of homotopy analysis and concluded that radial velocity decays with the influence of Deborah number and also with the rise in Prandtl number the temperature reduces. Mahanthess et al. [16] assumed the nanofluid flow in the presence of heat source which is thermally as well as exponentially space based near the disk which is infinite and stretching in radial direction. The heat and mass for nonlinear mixed convection in stagnation-point flow around the solid cylinder of an impinging jet surrounded in a porous medium has been researched by Hong et al. [17]. Pahlevaninejad et al. [18] did the hydrodynamic and thermal analysis in a wavy microchannel for non-Newtonian nanofluid. Wakif et al. [19] numerically inspected the influences of externally applied uniform magnetic field upon the onset of convection in a layer of nanofluid which is conducting electrically and based upon two-phase non-homogeneous by incorporating the influences Brownian motion as well as thermophoresis of the particles of nanofluids within the mechanism of thermal transportation. Nayak et al. [20] did a comparative analysis upon examining the differential quadrature numerically by means of nanofluid fluid flow which is steady and mixed convection as well over a thin needle of an isothermal carrying the nanomaterials of metallic as well as metallic oxide. Zaib et al. [21] calculated the dual similarity solutions by analyzing the characteristics of entropy generation in the direction of thermally radiated MHD upon the incompressible mixed convection fluid flow of ferrofluid particles from a plate which is vertically flat under the influence of viscous dissipation and joule heating. Qasim et al. [22] scrutinized the two-dimensional Jeffrey fluid flow within the boundary layer on a disk which is stretching radially and in the occurrence of nonlinear thermal radiation. Wakif et al. [23] numerically computed the influence of magnetic field which is uniformly transverse by considering the water and metallic as a base and nanoparticles upon using Buongioron’s non-homogeneous mathematical model. Rashad and Hakiem [24] has assumed the temperature-dependent viscosity and examined the influence of radiation upon non-darcy free convection by means of cylinder which is placed vertically and in a porously saturated fluid. Some interesting researches about the nanofluid about the different geometries has been provided by Sheikholeslami et al. [25,26,27,28,29,30,31,32], Raza et al. [33] and Waqas et al. [34], respectively. Sheikholeslami et al. [35, 36] further did the modeling numerically for nanomaterial through circular channel as well as space which is porous and includes magnetic forces.

A considerable trend toward the flow and transfer of heat by means disk rotation near the Newtonian fluid got the prominent attention. Zandbergen and Dijkstra [37] gave valuable information by conveying more precisely the idea of single and double disk problems simultaneously. The fluid having variable viscosity is based on applied stress and is known as non-Newtonian fluid. It has its own importance and significance, for example, quicksand, cornflour, water, polymer solutions, melts, rubber, grease etc. Some interesting researches about the Reiner-Rivlin model have been provided by Attia [38] by transferring the heat of rotatory disk flow via porous medium with suction and injection of a non-Newtonian fluid. Sahoo [39] has calculated the influences of partial slip, joule heating viscous dissipation of an electrically conducting non-Newtonian fluid on a Karman’s flow and heat problem and Osalusi et al. [40] extended it further in the occurrence of hall and ion-slip currents. Rashaida [41] gave a better concept of the behavior of a Bingham fluid flow on a disk rotation in the laminar boundary layer by operating two district procedures: laboratory investigations and numerical simulation with support of flow visualization and particle image velocimetry (PIV). Several types of fluids satisfy the psuedo-plastic and dilatant properties which are known as power-law fluid. Mitschka [42] extended the Karman’s theory toward the power-law fluid. Mitschka and Ulbricht [43] have computed the solution numerically for the flow produced by disk rotation in liquids by taking viscosity which is dependent on shear with the power-law indices in the limit \(0.2 \le n \le 1.5.\) R. Smith and Greif [44] has obtained the mass transfer about rotating disks and cones for non-Newtonian laminar power-law fluids and rendered the exact results for the velocity field. Andersson et al. [45] re-examined the work in [43] to check the reliability of the numerically approached technique and concluded that when we reduce the index of power-law \(n\) the boundary layer thickness increases in the parameter range from 2.0 to 0.2. Nitin and Chhabra [46] have numerically solved the continuity and momentum equations for two-dimensional steady power-law fluids on a disk having thin circulation which is placed normally on the path of flow. They obtained the wide-ranging results on total drag coefficients which are the functions of Reynolds number Re, disk-to-cylinder diameter ratio \(e\) and the index of power-law \(n\) in the ranges, i.e., \(1 \le {\text{Re}} \le 100, 0.02 \le e \le 0.5\) and \(0.4 \le n \le 1\), respectively. Andersson and Korte [47] studied the power-law fluid over an infinite rotation of disk constantly with the consideration of a uniformly applied magnetic field. Denier and Hewitt [48] in 2003 debated the asymptotic matching constraints for power-law boundary layer rheology fluid flow which is driven with the help of a plane whose rotation is infinite in an otherwise static system by addressing the problem for pseudo-plastic and dilatant fluids. Kabeir et al. [49] have applied the group theoretic technique for combinedly transfer of heat and mass for naturally convective MHD non-Darcy toward a cylinder which is impermeably horizontal by considering non-Newtonian power-law fluid model embedded in saturatedly porous medium under the influence of mass and thermal diffusion, thermal radiation, magnetic field and inertial resistance, respectively. In 2010, Kabeir et al. [50] made an advancement in the power-law fluid through transferring heat and mass by considering MHD stagnation-point power-law fluid phenomenon about the surface which is stretchable together with the influence of radiation, chemical reaction and soret and dufour. Ming et al. [51] handled the power-law for steady flow and heat transfer on a disk rotation with the supposition that both thermal conductivity and viscosity obey the same function and further extended it in the existence of uniform magnetic field [52]. In 2016, Ming et al. [53] introduced a generalized heat transfer Fourier model that is when the thermal conductivity dependent on temperature gradient, the influences of the index of power-law and local Prandtl number upon velocity, pressure and temperature are calculated particularly, the conductivity of heat and the coefficient of viscosity are conversed. In 2014, Griffiths et al. [54] checked the boundary layer stability especially for the pseudo-plastic fluids on a rotatory disk which satisfies the power-law fluids. Griffiths [55] pondered the generalized Newtonian fluid cause of a rotating disk and provided the solutions for power-law, Bingham and Carreau modeled fluids, respectively.

It can be seen that not enough articles are available for flow and transfer of heat between two co-axially rotation of disks of power-law fluid with the occurrence of non-uniform heat source/sink. So, it encouraged us to examine the stretching phenomenon and its influences for the flow and transfer of heat for two disks which are rotating as well as stretchable with the aim of power-law fluid model and in the presence of non-uniform heat source/sink. The corresponding equations are firstly altered into nonlinear combined differential equations and later tackled by RK-shooting. The missing initial guesses are calculated by the Newton–Raphson method. Finally, the validities of some physical quantities on heat and flow properties are explained in detail.

Physical model and mathematical formulation

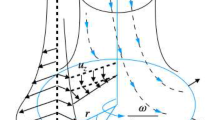
The steady axial-symmetric laminar flow between two infinite disks which are placed parallel where the lower one placed at \(z = 0\) and the upper one at \(z = h\) and in the presence of non-uniform heat source/sink have been assumed. The disk rotation toward \(r = 0\) is coaxial and of particular interest here with respect to constant stretching radial rates \(s_{1}\) and \(s_{2}\) along with constant angular velocities \(\varOmega_{1}\) and \(\varOmega_{2}\). The cylindrical coordinate system has been chosen and it can be seen in Fig. 1. In cylindrical coordinate systems, the velocity components such as \(\left( {u, v,w} \right)\) are taken in the directions of \(\left( {r, \varphi , z} \right)\), respectively.

Fig. 1
figure 1

The flow geometry

Full size image

The physically modeled PDEs can be written as [51].

$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0$$
(1)
$$u\frac{\partial u}{\partial r} - \frac{{v^{2} }}{r} + w\frac{\partial u}{\partial z} = \frac{1}{\rho }\frac{\partial }{\partial z}\left( {\mu \frac{\partial u}{\partial z}} \right)$$
(2)
$$u\frac{\partial v}{\partial r} + \frac{uv}{r} + w\frac{\partial v}{\partial z} = \frac{1}{\rho }\frac{\partial }{\partial z}\left( {\mu \frac{\partial v}{\partial z}} \right)$$
(3)
$$u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} = \frac{1}{{\rho c_{\rm p} }}\frac{\partial }{\partial z}\left( {\kappa \frac{\partial T}{\partial z}} \right) + \frac{1}{{\rho c_{\rm p} }}q^{\prime\prime\prime}$$
(4)

where \(T\) indicates temperature for the fluid \(\rho\) represents density, \(\mu\) is the dynamic viscosity, \(c_{\rm p}\) denotes specific heat at constant pressure and \(k\) implies the thermal conductivity of the fluid.

The viscosity \(\mu = \mu_{0} \left\{ {\left( {\frac{\partial u}{\partial z}} \right)^{2} + \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right\}^{{{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\text n} - 1} \right)} 2}} \right. \kern-0pt} 2}}}\) and \(k = k_{0} \left\{ {\left( {\frac{\partial u}{\partial z}} \right)^{2} + \left( {\frac{\partial v}{\partial z}} \right)^{2} } \right\}^{{{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\text n} - 1} \right)} 2}} \right. \kern-0pt} 2}}}\) thermal conductivity obey the power-law properties which is successfully implemented by the authors in [51, 52, 56]. Here \(\mu_{0}\) is the consistency coefficient for fluid, \(k_{0}\) which refers to a positive constant and \(n\) is an index of power-law. Here \(n = 1\) indicates Newtonian fluid and \(\mu = \mu_{0} , k = k_{0}\). The parameter of non-uniform heat source/sink \(q^{''' }\) is defined by the following relation [57,58,59]:

$$q^{\prime\prime\prime} = \frac{{k\varOmega_{1} }}{\nu }\left[ {\frac{{A^{*} \left( {T_{1} - T_{2} } \right)}}{{\varOmega_{1} r}}u + B^{*} \left( {T - T_{2} } \right)} \right]$$

In which \(A^*\) and \(B^*\) represents the parameters of space and temperature-dependent heat source/sink, respectively. The positive and negative values of these parameters denote internal heat generation and absorption.

The proper boundary conditions subject to (1–4) are

$$u = rs_{1} , \, v = r\varOmega_{1} , \, w = 0, \, T = T_{1} ,{\text{ at }}z = 0,$$
(5)
$$u = rs_{2}, \, v = r\varOmega_{2} , \, w = 0, \, T = T_{2} ,{\text{ at }}z = h,$$
(6)

Here \(T_{1}\) is the temperature corresponding to the lower wall and \(T_{2}\) with respect to the upper wall.

Similarity variables

The similarity transformation for this type of flow problem can be defined as follows:

$$\begin{aligned} \xi = z\left( {\frac{{\varOmega_{1}^{2 - {\text n}} }}{{{{\mu_{0} } \mathord{\left/ {\vphantom {{\mu_{0} } \rho }} \right. \kern-0pt} \rho }}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {\left( {n + 1} \right)}}} \right. \kern-0pt} {\left( {n + 1} \right)}}}} r^{{{{\left( {1 - {\text n}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {\text n}} \right)} {\left( {1 + {\text n}} \right)}}} \right. \kern-0pt} {\left( {1 + {\text n}} \right)}}}} , \, u = \varOmega_{1} rF\left( \xi \right), \, v = \varOmega_{1} rG\left( \xi \right), \hfill \\ w = \left( {\frac{{\varOmega_{1}^{1 - 2{\text n}} }}{{{{\mu_{0} } \mathord{\left/ {\vphantom {{\mu_{0} } \rho }} \right. \kern-0pt} \rho }}}} \right)^{{ - {1 \mathord{\left/ {\vphantom {1 {\left( {{\text n} + 1} \right)}}} \right. \kern-0pt} {\left( {n + 1} \right)}}}} r^{{{{\left( {{\text n} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\text n} - 1} \right)} {\left( {{\text n} + 1} \right)}}} \right. \kern-0pt} {\left( {{\text n} + 1} \right)}}}} \, H\left( \xi \right), \, T = T_{2} + \left( {T_{1} - T_{2} } \right)\theta . \hfill \\ \end{aligned}$$
(7)

Introducing (7) into (1–4), we get the following set of ODEs:

$$H^{\prime} = - 2F - \frac{1 - n}{1 + n}\xi F^{\prime}$$
(8)
$$F^{2} - G^{2} + \left( {H + \frac{1 - n}{1 + n}\xi F} \right)F^{\prime} = \left\{ {F^{\prime}\left( {\left( {F^{\prime}} \right)^{2} + \left( {G^{\prime}} \right)^{2} } \right)^{{{{\left( {{\text n} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\text n} - 1} \right)} 2}} \right. \kern-0pt} 2}}} } \right\}^{\prime }$$
(9)
$$2FG + \left( {H + \frac{1 - n}{1 + n}\xi F} \right)G^{\prime} = \left\{ {G^{\prime}\left( {\left( {F^{\prime}} \right)^{2} + \left( {G^{\prime}} \right)^{2} } \right)^{{{{\left( {{\text n} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\text n} - 1} \right)} 2}} \right. \kern-0pt} 2}}} } \right\}^{\prime }$$
(10)
$$\left( {H + \frac{1 - n}{1 + n}\xi F} \right)\theta^{\prime} = \frac{1}{Pr}\left[ {\left\{ {\theta^{\prime}\left( {\left( {F^{\prime}} \right)^{2} + \left( {G^{\prime}} \right)^{2} } \right)^{{{{\left( {{\text n} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {{\text n} - 1} \right)} 2}} \right. \kern-0pt} 2}}} } \right\}^{\prime } + \left\{ {A^{*} F + B^{*} \theta } \right\}} \right]$$
(11)

The boundary conditions are converted into

$$F\left( 0 \right) = S_{1} , \, G\left( 0 \right) = 1, \, H\left( 0 \right) = 0, \, \theta \left( 0 \right) = 1$$
(12)
$$F\left( 1 \right) = S_{2} , \, G\left( 1 \right) = \varOmega , \, H\left( 1 \right) = 0, \, \theta \left( 1 \right) = 0,$$
(13)

Here \(S_{1} = \frac{{s_{1} }}{{\varOmega_{1} }}\) and \(S_{2} = \frac{{s_{2} }}{{\varOmega_{1} }}\) are the parameters for stretching, \(\varOmega = \frac{{\varOmega_{2} }}{{\varOmega_{1} }}\) means rotation and \({ \Pr } = \frac{{\mu_{0} c_{\rm p} }}{{\kappa_{0} }}\), a Prandtl number. The skin friction coefficients at \(z = 0\) in radial \(C_{\rm Fr}\) as well as in tangential \(C_{{\rm F}\varphi }\) directions and local Nusselt number \({\text{Nu}}_{\text{r}}\) can be expressed as:

$$C_{\rm Fr} = \frac{{\tau_{\rm rz} }}{{\rho \left( {\varOmega_{1} r} \right)^{2} }}, \, C_{{\rm G}\varphi } = \frac{{\tau_{\varphi {\rm z}} }}{{\rho \left( {\varOmega_{1} r} \right)^{2} }}, \, Nu_{\rm r} = \frac{{rq_{\rm w} }}{{k\left( {T_{1} - T_{2} } \right)}},$$
(14)

The quantities \(\tau_{\rm rz} , \tau_{\varphi {\rm z}}\) represent the shear stresses in radial as well as in tangential directions and \(q_{\rm w}\) is the constant heat flux which are defined by the following relations:

$$\begin{aligned} \tau_{\rm rz} & = \left[ {\mu \left\{ {\left( {\frac{\partial u}{\partial z}} \right) + \frac{1}{r}\left( {\frac{\partial w}{\partial \varphi }} \right)} \right\}} \right]_{{\rm z} = 0} = \left[ {\mu \left( {\frac{\partial u}{\partial z}} \right)} \right]_{{\rm z} = 0} , \\ \tau_{{\rm r}\varphi } & = \left[ {\mu \left\{ {\left( {\frac{\partial v}{\partial z}} \right) + \frac{1}{r}\left( {\frac{\partial w}{\partial \varphi }} \right)} \right\}} \right]_{{\rm z} = 0} = \left[ {\mu \left( {\frac{\partial v}{\partial z}} \right)} \right]_{{\rm z} = 0} , \\ q_{\rm w} & = \left[ { - k\left( {\frac{\partial T}{\partial z}} \right)} \right]_{z = 0} . \\ \end{aligned}$$
(15)

Upon using the similarity transformation the (7) leads to

$$\begin{aligned} \text{Re}_{\rm r}^{{\frac{1}{{\text n} + 1}}} C_{\rm Fr} & = \left[ {F^{\prime 2} \left( 0 \right) + G^{\prime 2} \left( 0 \right)} \right]^{{\frac{{\text n} - 1}{2}}} F^{\prime}\left( 0 \right), \\ \text{Re}_{\rm r}^{{\frac{1}{{\text n} + 1}}} C_{{\rm G}\varphi } & = \left[ {F^{\prime 2} \left( 0 \right) + G^{\prime 2} \left( 0 \right)} \right]^{{\frac{{\text n} - 1}{2}}} G^{\prime}\left( 0 \right), \\ \text{Re}_{\rm r}^{{ - \frac{1}{{\text n} + 1}}} Nu_{\rm r} & = - \theta^{\prime}\left( 0 \right). \\ \end{aligned}$$
(16)

where \(\text{Re}_{\rm r} = \frac{{\varOmega_{1}^{2 - {\text n}} r^{2} }}{{{{\mu_{0} } \mathord{\left/ {\vphantom {{\mu_{0} } \rho }} \right. \kern-0pt} \rho }}}\) is the local Reynolds number.

Adopted numerical technique

Shooting method is adopted to obtain the solution of ODEs (8–11) subject to (12–13) in MATLAB software. The implementation of shooting method is based upon these steps [60]. Firstly, the boundary value problem (BVP) is required to transform into initial value problem (IVP) by setting the higher-order derivative terms to some functions so that the equations are reduced to first-order ODEs. Secondly, the missing initial conditions at the initial value of the provided interval are taken and then integrate the differential equation numerically at boundary point as an IVP, this leads to the determination of missing initial conditions. Thirdly, the validation of assumed missing initial conditions can be assured upon finding the dependent variable at the value which is given on the boundary, if there is still difference then we need to guess another value, this process can be continued until the desired level of accuracy is obtained between the given and computed missing initial conditions. Finally, RK-method is then applied for finding the solution of the system of first-order IVP subject to provided and computed missing initial conditions.

Thus, the above-mentioned solution scheme can be applied on our proposed problem as given below:

The given BVP corresponds to boundary conditions and is transformed to first-order IVP by setting the derivates as

$$y_{1} = F, \, y_{2} = F^{\prime}, \, y_{3} = G, \, y_{4} = G^{\prime}, \, y_{5} = H, \, y_{6} = \theta , \, y_{7} = \theta^{\prime}.$$
(17)

Then Eqs. (8) to (11) are expressed in terms of seven first-order ODEs with respect to seven variables, i.e., \(y_{\rm N} \left( {N = 1,2, \ldots ,7} \right)\)

$$\begin{aligned} y_{1}^{\prime } & = y_{2} , \\ y_{2}^{\prime } & = \frac{1}{n}\left( {y_{2}^{2} + y_{4}^{2} } \right)^{{\frac{1 - {\text n}}{2}}} \left\{ \begin{aligned} \left[ {1 + \left( {n - 1} \right)\left( {y_{2}^{2} + y_{4}^{2} } \right)^{ - 1} y_{4}^{2} } \right]\left[ {y_{1}^{2} - y_{3}^{2} + \left( {y_{5} + \frac{1 - n}{1 + n}\xi y_{1} } \right)y_{2} } \right] \hfill \\ - \left( {n - 1} \right)\left( {y_{2}^{2} + y_{4}^{2} } \right)^{ - 1} y_{2} y_{4} \left[ {2y_{1} y_{3} + \left( {y_{5} + \frac{1 - n}{1 + n}\xi y_{1} } \right)\xi y_{4} } \right] \hfill \\ \end{aligned} \right\}, \,\\ y_{3}^{\prime } & = y_{4} , \\ y_{4}^{\prime } & = \frac{1}{n}\left( {y_{2}^{2} + y_{4}^{2} } \right)^{{\frac{1 - {\text n}}{2}}} \left\{ \begin{aligned} \left[ {1 + \left( {n - 1} \right)\left( {y_{2}^{2} + y_{4}^{2} } \right)^{ - 1} y_{2}^{2} } \right]\left[ {2y_{1} y_{3} + \left( {y_{5} + \frac{1 - n}{1 + n}\xi y_{1} } \right)y_{4} } \right] \hfill \\ - \left( {n - 1} \right)\left( {y_{2}^{2} + y_{4}^{2} } \right)^{ - 1} y_{2} y_{4} \left[ {y_{1}^{2} - y_{3}^{2} + \left( {y_{5} + \frac{1 - n}{1 + n}\xi y_{1} } \right)y_{2} } \right] \hfill \\ \end{aligned} \right\}, \,\\ y_{5}^{\prime } & = - 2y_{1} - \frac{1 - n}{1 + n}\xi y_{2} , \\ y_{6}^{\prime } & = y_{7} , \\ y_{7}^{\prime } & = \left( {y_{2}^{2} + y_{4}^{2} } \right)^{{\frac{1 - {\text n}}{2}}} y_{7} \left\{ \begin{aligned} \left( {{ \Pr } - \frac{n - 1}{n}} \right)\left( {y_{5} + \frac{1 - n}{1 + n}\xi y_{1} } \right) - \left( {A^{*} \mathop y\nolimits_{{_{1} }} + B^{*} \mathop y\nolimits_{{_{6} }} } \right) - \frac{n - 1}{n}\left( {y_{2}^{2} + y_{4}^{2} } \right)^{ - 1} \hfill \\ \times \left( {y_{1}^{2} y_{2} - y_{2} y_{3}^{2} + 2y_{1} y_{3} y_{4} } \right) \hfill \\ \end{aligned} \right\}\\ \end{aligned}$$
(18)

Boundary conditions are:

$$y_{1} \left( 0 \right) = S_{1} , \, y_{2} \left( 0 \right) = a, \, y_{3} \left( 0 \right) = 1, \, y_{4} \left( 0 \right) = b, \, y_{5} \left( 0 \right) = 0, \, y_{6} \left( 0 \right) = 1, \, y_{7} \left( 0 \right) = c, \, y_{1} \left( 1 \right) = S_{2} , \, y_{3} \left( 1 \right) = \varOmega , \, y_{5} \left( 1 \right) = 0, \, y_{6} \left( 1 \right) = 0.$$
(19)

Here \(a,b,c\) are the missing initial conditions which can be determined from \(y_{1} \left( 1 \right) = S_{2} , \, y_{3} \left( 1 \right) = \varOmega ,{\text{ and }}y_{6} \left( 1 \right) = 0.\) For instance, in order to compare our results for \(n = 0.8\) with those in Ref. [43, 45, 51], Tables 1-4 are drawn by setting the involved parameters as \(S_{1} = S_{2} = \varOmega = A^{*} = B^{*} = 0\) and upon taking step size of 0.01. Then after performing the 15 iterations by means of Newton–Raphson method, the values for missing initial conditions \(\left( {F^{\prime}\left( 0 \right), - G^{ '} \left( 0 \right), \theta^{\prime}\left( 0 \right)} \right)\) that is \(\left( {a = 0.5038, b = 0.6361, c = 0.4111} \right)\) which are correct up to 4 decimal places with that of previous iterated value and are matched up to approximately 4 decimal places with those in Ref. [43, 45, 51]. Similarly, if we change the values of any of involved parameters we need to follow the same process as we just described. Hence, RK-method can be implemented for finding the solution of first-order IVP with respect to given conditions and calculated missing initial conditions. This means that proposed numerically technique is extremely effective in solving such type of highly nonlinear differential equations. Thus further outcomes are deliberated in Results and discussion section.

Table 1 Comparison of \(F^{\prime}\left( 0 \right)\) in non-stretching and non-rotation disk case \(S_{1} = S_{2} = \varOmega = A^* = B^* = 0, Pr = 1\)
Full size table
Table 2 Comparison of \(- G^{'} \left( 0 \right)\) in non-stretching and non-rotation disk case \(S_{1} = S_{2} = \varOmega = A^{*} = B^{*} = 0, Pr = 1\)
Full size table
Table 3 Comparison of \(- H^{'} \left( 1 \right)\) in non-stretching and non-rotation disk case \(S_{1} = S_{2} = \varOmega = A^* = B^* = 0, Pr = 1\)
Full size table
Table 4 Comparison of \(\theta^{\prime}\left( 0 \right)\) in non-stretching and non-rotation disk case \(S_{1} = S_{2} = \varOmega = A^{*} = B^{*} = 0, Pr = 1\)
Full size table

Results and discussion

This part of the paper demonstrates the numerical results with respect to velocity components such as radial \(F\left( \xi \right)\), tangential \(G\left( \xi \right)\), axial \(- H\left( \xi \right)\) and temperature θ(ξ) profiles for various non-dimensional physical quantities that are rotation parameter Ω, stretching parameters \((S_{1} ,S_{2} )\), Prandtl number Pr and index of power-law \(n\). Comprehensive discussion for shear thickening \(\left( {n > 1} \right)\) and shear thinning \((n < 1)\) alongside with that of physical parameters are studied by their graphical representations.

In order to elucidate the reliability and efficiency of the proposed technique, the comparison of the computed results with those in Ref. [43, 45, 51] can be seen in Tables 1–4 for different power-law indexes. The excellent agreement can be observed. Where \(F^{\prime}\left( 0 \right)\), \(G^{\prime}\left( 0 \right)\) and \(- H^{'} \left( 1 \right)\) indicate the wall-gradients and axial inflow, respectively, and \(\theta^{\prime}\left( 0 \right)\) specifies the heat flux. Furthermore, in order to examine the variations in skin friction and local Nusselt number Table 5 is constructed for different values of stretching parameters \(\left( {S_{1} , S_{2} } \right)\varvec{ }\) together with rotation parameter \(\left( \varOmega \right)\). It is seen that the values of skin friction in the case of shear thinning are smaller from shear thickening but for the values of local Nusselt number opposite trend is observed. Thus from Table 5 it is observed that, from non-stretching of disks \(\left( {S_{1} = 0.0, S_{2} = 0.0} \right)\) to faster stretching rate of upper disk than lower disk \(\left( {S_{1} = 0.2, S_{2} = 0.6} \right)\) and faster stretching rate of lower disk than upper disk \(\left( {S_{1} = 0.6, S_{2} = 0.2} \right)\), the effects of the stretching of a material change the results significantly in comparison with that of solid rotating disks.

Table 5 The values of radial direction skin friction and local Nusselt number when \(A^{*} = B^{*} = 0, Pr = 1\)
Full size table

Effects of rotation

Figures 2–5 illustrate how the velocity and temperature fields vary with a stationary to increasing \(\varOmega\) along ξ in the case when the disks are stretching with a constant rate that is \(S_{1}\) = \(S_{2} =\) 0.4. It should be reminded here \(\varOmega = 0\) describes that upper disk is stationary, and \(\varOmega > 0\) refers to the rotation of disks in a similar direction. Figure 2 is plotted to show the effects of rotation on radial velocity for shear thickening and shear shinning. It is noticed that the rotation parameter enhances the radial component of velocity in both shear-thickening and shear-thinning cases. Further, it is also depicted that the radial velocity under the circumstances of shear thickening is greater than the shear-thinning case. Figure 3 deals to predict the tangential velocity behavior against the rotation parameter in the occurrence of shear thickening and shear thinning. Tangential velocity in both situations (shear thickening and shear thinning) increases. It is also seen that for small values of rotation parameter the tangential velocity for shear-thickening case is higher than the shear-thinning case but however for larger values of rotation parameter this behavior gets reversed. It is due to the increasing resistance effects on the tangential motion of the fluid which is caused by shear-thickening behavior while this resistance is lower for the radial motion when power-law index and rotation parameters are increased. In Fig. 4, axial velocity is plotted to show the rotation effects for shear-thickening and shear-thinning. Axial velocity profile presents the behavior similar to tangential velocity but the change in axial velocity is very small. The effects of rotation in the case of shear-thinning and shear-thickening are shown in Fig. 5. This temperature profile predicts the two different effects of the parameter of rotation for shear-thickening and shear-thinning fluids. Temperature is found as an increasing function with respect to the parameter of rotation in the case of shear thickening while decreasing function of parameter of rotation in case of shear thinning.

Fig. 2
figure 2

Radial velocity \(F\) distributions when \(\varOmega = 0, 0.2, 0.4, 0.6, S_{1} = S_{2} = 0.4, {\text{Pr}} = 1, \,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 3
figure 3

Tangential velocity \(G\) distributions when \(\varOmega = 0, 0.2, 0.4, 0.6, S_{1} = S_{2} = 0.4, {\text{Pr}} = 1, \,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 4
figure 4

Axial velocity \(- H\) distributions when \(\varOmega = 0, 0.2, 0.4, 0.6,S_{1} = S_{2} = 0.4, {\text{Pr}} = 1, \,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 5
figure 5

Temperature \(\theta\) distributions when \(\varOmega = 0, 0.2, 0.4, 0.6, S_{1} = S_{2} = 0.4, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image

Effects of stretching

Figures 6–13 are plotted against the dimensionless similarity variable \(\xi\) for the velocities \(\left( {F, G, H} \right)\) and temperature \(\left( \theta \right)\) profiles in order to predict the stretching effects of upper and lower plates when the disks rotate by the rate that is \(\varOmega = 0.4\) and also upon fixing \({ \Pr } = 1\). Figures 6–9 explain the no stretching \(\left( {S_{2} = 0 } \right)\) to faster stretching rate \(\left( {S_{2} = 0.2, 0.4, 0.6 } \right)\) of upper disk when lower disk is stretching at a rate of 0.2. It is noted that radial and axial velocities (Figs. 6 and 8) are increasing function of the stretching parameter \(S_{2}\) while tangential velocity and temperature (Figs. 7 and 9) are declining functions along \(\xi\). It can be observed that in the case of radial and axial velocities when upper disk is not stretching the shear thinning \(\left( {n = 0.8} \right)\) is smaller from shear thickening \(\left( {n = 1.2} \right)\) but this trend gets reversed by the rise in stretching rate of upper disk and the fluid is naturally drawn from slower stretching disk to that of faster stretching disk. On the other hand, whenever stretching is functioning at upper disk the vertical flow changes its direction due to which flow is eventually thrown from faster to slower stretching disk this leads to reduction in the flow in tangential direction. Furthermore, a decrease in the temperature profile is seen from Fig. 9.

Fig. 6
figure 6

Radial velocity \(F\) distributions when \(\varOmega = 0.4, S_{1} = 0.2,S_{2} = 0, 0.2, 0.4, 0.6, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 7
figure 7

Tangential velocity \(G\) profiles when \(\varOmega = 0.4, S_{1} = 0.2, S_{2} = 0, 0.2, 0.4, 0.6, {\text{Pr}} = 1, \,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 8
figure 8

Axial velocity \(- H\) distributions when \(\varOmega = 0.4, S_{1} = 0.2, S_{2} = 0, 0.2, 0.4, 0.6, {\text{Pr}} = 1, \,\,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 9
figure 9

Temperature \(\theta\) distributions when \(\varOmega = 0.4, S_{1} = 0.2, S_{2} = 0, 0.2, 0.4, 0.6, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 10
figure 10

Radial velocity \(F\) when \(\varOmega = 0.4, S_{1} = 0, 0.2, 0.4, 0.6, S_{2} = 0.2, {\text{Pr}} = 1, \,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 11
figure 11

Tangential velocity \(G\) when \(\varOmega = 0.4, S_{1} = 0, 0.2, 0.4, 0.6, S_{2} = 0.2, {\text{Pr}} = 1, \,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 12
figure 12

Axial velocity \(- H\) when \(\varOmega = 0.4,S_{1} = 0, 0.2, 0.4, 0.6, S_{2} = 0.2, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 13
figure 13

Temperature \(\theta\) distribution when \(\varOmega = 0.4, S_{1} = 0, 0.2, 0.4, 0.6, S_{2} = 0.2, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image

Figures 10–13 indicate the effects of the stretching rate of lower disk on the profiles of velocity and temperature when the upper disk stretches by a constant rate that is 0.2. Again an increasing trend can be noted for the radial and axial components of the velocity whereas tangential component of velocity and temperature is decaying along \(\xi\). The shear thickening becomes greater from shear thinning with the increase in lower disk stretching rate in the case of radial and axial velocities but the reduction for shear thinning in the case of tangential velocity and temperature is on higher note than that of shear thickening. Physically it can be expressed as the larger values of the \(\left( {S_{1} , S_{2} } \right)\) leads to the greater stretching rates of the respective disks due to which radial and axial velocities escalates. Furthermore, the rotational velocity is in inverse relationship with that of tangential velocity which causes deduction in the tangential velocity for larger values of \(\left( {S_{1} , S_{2} } \right)\). Thus, the radial as well as axial velocities escalates significantly and the flow move toward the upper disk whenever stretching is operative at lower and upper disks while for tangential velocity as well as for temperature profiles this trend gets reversed.

Influence of power-law index

The influence of the index of power-law n can be observed from Figs. 14–17 when disks are stretching and rotating that is \(S_{1}\) = \(S_{2}\) = 0.4 and \(\varOmega = 0.6\). It is seen that the extreme value of radial velocity enhances and moving toward the center with the enhancement in the index of power-law. The shear which is driven by the motion in tangential direction decayed. Axial flow and temperature are escalating while the power-law index increasing. The effects for shear-thickening fluid are more noticeable in comparison with that of shear-thinning fluid.

Fig. 14
figure 14

Radial velocity \(F\) when \(\varOmega = 0.6, S_{1} = S_{2} = 0.4, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 15
figure 15

Tangential velocity \(G\) when \(\varOmega = 0.6,S_{1} = S_{2} = 0.4, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 16
figure 16

Axial velocity \(- H\) when \(\varOmega = 0.6, S_{1} = S_{2} = 0.4, {\text{Pr}} = 1,\, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 17
figure 17

Temperature \(\theta\) distribution when \(\varOmega = 0.6, S_{1} = S_{2} = 0.4, {\text{Pr}} = 1, \,A^{*} = B^{*} = 0.1.\)

Full size image

Effects of Prandtl number

Figure 18 explains the temperature for dilatant \(\left( {n = 1.2} \right)\) and pseudo-plastic \(\left( {n = 0.8} \right)\) with respect to the influence of Prandtl number. It is clearly distinguished that temperature decreases alongside the variable of similarity ξ. By increasing the \({ \Pr }\) which causes reduction in the temperature it is because of the reason that Prandtl number is linked with the momentum and thermal diffusities and with the augmentation in the Prandtl number which leads to the reduction in the thermal diffusivity and due to which temperature decreases. The reduction for shear thickening is more obvious from shear thinning.

Fig. 18
figure 18

Temperature \(\theta\) distributions when \(Pr = 1.0, 10.0, 50.0, 100.0,\) \(\varOmega = 0.6, S_{1} = S_{2} = 0.4, \,A^{*} = B^{*} = 0.1.\)

Full size image

Effects of parameters heat source/sink

The influence of the parameters of heat source/sink on temperature profile \(\theta\) when P \(r = 1,\) \(\varOmega = 0.6, S_{1}\) = \(S_{2} = 0.4\) has been deliberated in Fig. 19. It can be examined that the \(\theta\) is escalating along the dimensionless similarity variable \(\xi\) for the rising values of temperature-dependent heat source/sink parameters \(\left( {A^{*} , B^{*} } \right)\). Physically it can be interpreted as, the positivity of \(A^{*}\) and \(B^{*}\) refers to heat source which performs like heat generators due to which heat energy has been released toward the flow and it causes rise in temperature profile. The negativity of \(A^{*}\) and \(B^{*}\) indicates the heat sink which behaves as heat absorbers, the energy is absorbed for the negative values of \(A^{*}\) and \(B^{*}\). The heat source/sink effected the shear-thinning fluid \(n = 0.8\) dramatically.

Fig. 19
figure 19

Temperature \(\theta\) distributions when \(Pr = 1,\) \(\varOmega = 0.6, S_{1} = S_{2} = 0.4.\)

Full size image

Skin friction and local Nusselt number

The skin friction in radial \({\text{Re}}_{\rm r}^{{\frac{1}{{\text n} + 1}}} C_{\text{Fr}}\) as well as in tangential \({\text{Re}}_{\rm r}^{{\frac{1}{{\text n} + 1}}} C_{{\rm G}\varphi }\) directions and local Nusselt number \({\text{Re}}_{\rm r}^{{ - \frac{1}{{\text n} + 1}}} {\text{Nu}}_{\rm r}\) are plotted in Figs. 20–23 along the parameter \(S_{1}\) and for different values of \(S_{2}\) for shear-thickening and shear-thinning fluids by setting other parameters as \(\varOmega = 0.2, \, {\text{Pr}} = 1.0\). The effects of skin friction in radial direction are elucidated in Fig. 20 where both the fluids, i.e., shear thickening and shear thinning are describing almost the similar behavior and are increasing along \(S_{1} .\) The skin friction in tangential direction in Fig. 21 demonstrated the opposite trend to that of Fig. 20. The upshots of local Nusselt number are revealed in Fig. 22. The shear-thickening and shear-thinning fluids are increasing along \(S_{1}\) by increase in \(S_{2} .\) The increase in shear-thinning fluid is extremely on higher note. Figure 23 delibrates the influence of local Nusselt number along \(S_{1}\) for diverse values of \(Pr\) by setting \(S_{2} = 0.4, \varOmega = 0.2.\) Upon rising in the values of Prandtl number, the effects in shear-thinning fluid are slightly greater than shear-thickening fluid.

Fig. 20
figure 20

Skin friction in radial direction w. r. t. \(S_{1}\) when \(S_{2} = 0.0, 0.2, 0.4, 0.6\) and \(\varOmega = 0.2, Pr = 1.0,\, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 21
figure 21

Skin friction in tangential direction w. r. t. \(S_{1}\) when \(S_{2} = 0.0, 0.2, 0.4, 0.6\) and \(\varOmega = 0.2 Pr = 1.0, A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 22
figure 22

Local Nusselt number w. r. t. \(S_{1}\) when \(S_{2} = 0.0, 0.2, 0.4, 0.6\) and \(\varOmega = 0.2 Pr = 1.0, \,A^{*} = B^{*} = 0.1.\)

Full size image
Fig. 23
figure 23

Local Nusselt number corresponding to \(S_{1}\) when \(Pr = 1.0, 10.0, 50.0, 100.0, S_{2} = 0.4\) and \(\varOmega = 0.2, A^{*} = B^{*} = 0.1.\)

Full size image

Conclusions

This current study is dedicated to inspect the steady flow and transfer of heat of power-law fluid for two co-axially stretchable rotatory disks in the existence of various rates of stretching and rotation. The PDEs are converted to ODEs by means of suitable similarity transformation. The influence of rotation, stretching parameters, index of power-law and Prandtl number upon the profiles of velocity and temperature are explained for pseudo-plastic and dilatant fluids. Newly calculated results which are obtained from shooting method and already existing outcomes are rendered. In addition, graphical representation and tabular comparison certify that shooting method is truly operative to such problems and many more. The applied technique can also be useful to other nonlinear problems. Hence, the key points of current study are given below:

  • The effect of the rotation of disks which causes increases in the radial, tangential and axial flow except the temperature where shear thinning is toward downside.

  • Increasing the rates of stretching which causes a notable rise in the radial as well as axial velocities, but the tangential and temperature profiles are in decreasing trend.

  • By the increase in the stretching rate of upper disk which results the maximum in vertical velocity.

  • In the situation when upper disk is stretch the effect is to revert the radial direction of flow from bottom to upper disk.

  • The velocity and temperature distributions are increasing excluding the tangential component which is declining by rise in the index of power-law.

  • The temperature is affected by the increasing Prandtl number and heat transfer is decaying but it escalates with the escalation in space and temperature-dependent heat source/sink parameters \(\left( {A^{*} , B^{*} } \right)\).

  • Skin friction in the radial direction increases along \(S_{1}\) for increasing values of \(S_{2 }\) but in tangential direction it decreases.

  • The local Nusselt number escalates along \(S_{1}\) with the escalation in \(S_{2}\) and in \({\text{Pr }}\), respectively.