Chemical reactive flow of Jeffrey fluid due to a rotating disk with non-Fourier heat flux theory

Abstract

The present paper explores non-Fourier heat flux theory for Jeffrey fluid flow subject to a rotating disk. The current analysis is executed in the presence of homogeneous–heterogeneous reactions. Relevant system of equations is constructed and appropriate transformations lead to self-similar forms. Convergent series solutions are computed for the resulting nonlinear differential system by homotopy analysis method. Graphical illustrations thoroughly demonstrate the features of involved pertinent parameters. Skin friction coefficients are also obtained and discussed graphically. Current computations reveal that the radial velocity experience declines with the decay of Deborah number. Further, fluid temperature declines for higher Prandtl number.

Introduction

Non-Newtonian fluids flow is becoming extremely important topic owing to its emerging applications in polymer extrusion, lubrication using greases and heavy oils, papers coating, mercury and plasma, liquid alloys, nuclear fuel slurries, biological procedures, reactor cooling, food processing, heat exchanger and few others. Examples of these fluids include paints, ice cream, polymers, shampoos, mud, etc. Variety of such fluid models has been proposed amongst which one of the subclass that explains the features of relaxation and retardation time is Jeffrey fluid. These fluids comprise quite complicated intrinsic relationship in between the stress and strain rate as compared with widely known Navier–Stokes equation. These equations illustrate behavior of viscous fluids but are considered inadequate for description of non-Newtonian fluid types. Many researchers have proposed Jeffrey fluid model in the literature due to rheological properties of these fluids [1,2,3,4,5,6,7,8,9].

The heat transfer phenomena occur as a result of temperature alteration between two different bodies or various parts of same body. Such heat and mass transference appears commonly in numerous manufacturing and industrial phenomena including nuclear processes, pharmaceutical, marine engineering, petroleum and refining industries, etc. Although the well-known Fourier heat conduction law [10] has been preferred over energy transfer model in many pertinent situations despite of its significant inadequacies that it yields parabolic equation for temperature profile. Later, Cattaneo [11] suggested the generalized Fourier model by adding an attribute of the thermal relaxation time. Such consideration enables heat transportation by propagation of some thermal waves with finite speed. Christov [12] proposed the generalized Cattaneo equation with time derivative being replaced by upper convected derivative. Further related studies on Cattaneo–Christov theory can be found in articles by [13,14,15,16,17].

The fluid flow in rotating media has much promising applications in industry that includes aerodynamical engineering, air cleaning machines, food processing technology, in electric power generating systems, medical equipment and gas turbines. Pioneer work over the flow induced by a rotating disk has been conducted by Von Karman [18]. He introduced transformations to convert Navier–Stokes equations to ordinary differential equations. Later Cochran [19] found out more reliable solution to Von Karman problem. Millsaps and Pohlhausen [20] carried out the analysis of heat transfer using isothermal disk for the collection of Prandtl numbers. Bachok et al. [21] explored nanofluid flow initiated by a rotation of disk. Impacts of roughness on mass and heat transfer for viscous fluid flow induced by porous disk have been observed by Turkyilmazoglu and Senel [22]. The laminar flow generated by the two parallel disks has been analyzed by Jiji and Ganatos [23]. Flow in magnetite nanoparticles by stretchable rotating disks with partial slip effect was examined by Hayat et al. [24]. Recent research concerning the flow analysis by rotating disk includes those of Turkyilmazoglu [25], Khan et al. [26], Lin et al. [27] and Griffiths [28]. Ming et al. [29] and Hayat et al. [30] explored Darcy–Forchheimer flow of carbon nanotubes due to a convectively heated rotating disk with homogeneous–heterogeneous reactions.

In chemical reacting systems, reactions are comprised of both homogeneous–heterogeneous reactions like biochemical systems, catalysis and combustion. Homogeneous reactions occur in fluid while heterogeneous reactions take place on some catalyst surface. Some reactions have zero capacity to occur on their own or they are carried out with the involvement of some catalyst. Some general applications of such reactions include hydrometallurgical industry and polymers, dispersion and fog formation, food processing, ceramics production and few others. Merkin [31] analyzed viscous liquid flow with heterogeneous–homogeneous reactions, and surface reaction is observed to be dominating near to the plate. Chaudhary and Merkin [32] investigated the effect of heterogeneous and homogeneous reactions with equal diffusivities. Shaw et al. [33] found out the influence of chemical reactions in flow of micropolar fluid near the permeable sheet. Bachok et al. [34] analyzed the aspect of homogeneous–heterogeneous reactions impact on stretched viscous fluid flow. Significance of homogeneous–heterogeneous reactions in Darcy–Forchheimer three-dimensional rotating flow of carbon nanotubes was observed by Hayat et al. [35].

The phenomenon of heat transfer has numerous applications in industry and engineering processes, e.g., nuclear reactor cooling, energy production, cooling of electronic devices, transportations, microelectronics and fuel cells. Flow due to rotating surfaces has promising applications in engineering and industrial sectors such as lubrication, air cleaning machine, electric power generating system, turbo machinery, gas turbine, food processing technology and centrifugal machinery. The interaction between the homogeneous and heterogeneous reactions is very complex involving the production and consumption of reactant species at different rates both within the fluid and on the catalytic surfaces such as reactions occurring in food processing, hydrometallurgical industry, manufacturing of ceramics and polymer production, fog formation and dispersion, chemical processing equipment design, crops damage via freezing, cooling towers and temperature distribution and moisture over agricultural fields and groves of fruit trees. Motivated by above mentioned work, we intend to model and examine steady boundary layer flow of Jeffrey fluid due to a rotating disk. Cattaneo–Christov heat flux and homogeneous–heterogeneous reactions are also factored in mathematical formulation of problem. System of equations is first formulated and then computational analysis is executed via homotopy analysis method (HAM) [36,37,38,39,40,41,42,43,44]. HAM is one of the most efficient methods in solving different type of nonlinear equations such as coupled, decoupled, homogeneous and non-homogeneous. Many previous analytic methods have some restrictions in dealing with nonlinear equations. Unlike perturbation method, HAM is independent of any small or large parameters. Also HAM provides us with great freedom to choose initial guesses and auxiliary parameters to control and adjust the convergence region which is a main lack of other several techniques. Behavior of pertinent parameters against fluid flow, temperature and concentration fields is interpreted graphically. Skin friction is main interest of this work and is also examined graphically.

Formulation

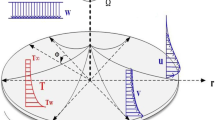
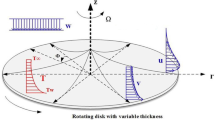
Consider the steady Jeffrey fluid flow with Cattaneo–Christov heat flux. Here, flow is initiated by a disk rotating with an angular velocity $\Omega$ about z-axis. Cylindrical coordinate frame $(r,\theta ,z)$ is opted for the model development. All three velocity components (u, v, w) are independent of azimuthal coordinate θ due to axisymmetric flow. The disk surface temperature and ambient fluid temperature are maintained at $T_{\mathrm{w }}$ and $T_{\infty },$ respectively (see Fig. 1).

Fig. 1

Geometry of the problem

We assume the model for homogeneous and heterogeneous reactions as suggested by Merkin and Chaudhary [32]. For cubic autocatalysis, homogeneous reaction is considered in the following fashion [30]:

$$\begin{aligned} A+2B\rightarrow 3B,\quad {\hbox {rate}}=k_{\mathrm{c }}ab^{2}, \end{aligned}$$

(1)

while on catalyst surface heterogeneous reaction is

$$\begin{aligned} A\rightarrow B, \quad {\hbox {rate}}=k_{\mathrm{s }}a, \end{aligned}$$

(2)

where chemical species A, B have concentrations a, b, respectively, while $k_{\mathrm{c }}$ and $k_{\mathrm{s }}$ and are rate constants. Also the reactions are assumed to be isothermal. Then, continuity, momentum, energy and concentration equations [7] are given as

$$\begin{aligned}\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(3)

$$\begin{aligned}&u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{v^{2}}{r} =\frac{\upsilon }{1+\alpha } \\&\quad \left[ \frac{\partial ^{2}u}{\partial z^{2}} +\lambda _{1}\left\{ \frac{\partial u}{\partial z}\frac{\partial ^{2}u}{ \partial r\partial z}+u\frac{\partial ^{3}u}{\partial r\partial z^{2}}+\frac{ \partial w}{\partial z}\frac{\partial ^{2}u}{\partial z^{2}}\right\} \right] \\&\quad +\frac{\upsilon \lambda _{1}}{1+\alpha }\left[ w\frac{\partial ^{3}u}{ \partial z^{3}}-\frac{1}{r}\left( \frac{\partial v}{\partial z}\right) ^{2}- \frac{v}{r}\frac{\partial ^{2}v}{\partial z^{2}}\right] , \end{aligned}$$

(4)

$$\begin{aligned}&u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{uv}{r} =\frac{\upsilon }{1+\alpha } \\&\quad \left[ \frac{\partial ^{2}v}{\partial z^{2}} +\lambda _{1}\left\{ \frac{\partial u}{\partial z}\frac{\partial ^{2}u}{ \partial r\partial z}+u\frac{\partial ^{3}v}{\partial r\partial z^{2}}+\frac{ \partial w}{\partial z}\frac{\partial ^{2}v}{\partial z^{2}}\right\} \right] \\&\quad +\frac{\upsilon \lambda _{1}}{1+\alpha }\left[ w\frac{\partial ^{3}v}{ \partial z^{3}}+\frac{1}{r}\frac{\partial v}{\partial z}\frac{\partial u}{ \partial z}+\frac{v}{r}\frac{\partial ^{2}u}{\partial z^{2}}\right] , \end{aligned}$$

(5)

$$\begin{aligned}\rho c_{\mathrm{p }}\left( w\frac{\partial T}{\partial z}+u\frac{\partial T}{\partial r }\right) =-{{\varvec{\nabla }} \cdot \mathbf{q}}, \end{aligned}$$

(6)

$$\begin{aligned}w\frac{\partial a}{\partial z}+u\frac{\partial a}{\partial r}=D_{\mathrm{A }}\frac{ \partial ^{2}a}{\partial z^{2}}-k_{\mathrm{c }}ab^{2}, \end{aligned}$$

(7)

$$\begin{aligned}w\frac{\partial b}{\partial z}+u\frac{\partial b}{\partial r}=D_{\mathrm{B }}\frac{ \partial ^{2}b}{\partial z^{2}}+k_{\mathrm{c }}ab^{2}, \end{aligned}$$

(8)

where u, v, w are the velocity components, $\upsilon$ the kinematic viscosity, $\lambda _{1}$ the retardation time, α the ratio of relaxation to retardation time, $\rho$ the density, $c_{\mathrm{p }}$ the specific heat, $D_{\mathrm{A }}$ and $D_{\mathrm{B }}$ stands for diffusion coefficients and T denotes the temperature. Cattaneo–Christov model for heat flux ${\mathbf {q}}$ is presented as [12]

$$\begin{aligned} {\mathbf {q}}+\lambda _{2}\left( \frac{\partial {\mathbf {q}}}{\partial t}+\left( {{\varvec{\nabla }} }\cdot{\mathbf {V}}\right) {\mathbf {q+V}}\cdot{{\varvec{\nabla }} {\mathbf{q}}}-{\mathbf {q}}\cdot {{\varvec{\nabla }} {\mathbf{V}}}\right) =-k{{\varvec{\nabla }} }T. \end{aligned}$$

(9)

For steady incompressible fluid situation, we have

$$\begin{aligned} {\mathbf {q}}+\lambda _{2}\left( {\mathbf {V}}\cdot{{\varvec{\nabla }} {\mathbf{q}}}-{\mathbf {q}}\cdot {{\varvec{\nabla }} {\mathbf{V}}}\right) =-k{{\varvec{\nabla }} }T, \end{aligned}$$

(10)

where k is the thermal conductivity and $\lambda _{2}$ is thermal relaxation time.

Eliminating ${\mathbf {q}}$ from Eqs. (6) and (10), we get

$$\begin{aligned} \rho c_{\mathrm{p }}\left( u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z }\right)&= k\frac{\partial ^{2}T}{\partial z^{2}}-\lambda _{2}\left[ w^{2} \frac{\partial ^{2}T}{\partial z^{2}}+u^{2}\frac{\partial ^{2}T}{\partial r^{2}}\right. \\&\quad +2uw\frac{\partial ^{2}T}{\partial r\partial z}+\frac{\partial T}{ \partial r}+\left( w\frac{\partial u}{\partial z}+u\frac{\partial u}{ \partial r}\right) \\&\quad\left. +\left( w\frac{\partial w}{\partial z}+u\frac{\partial w}{\partial r }\right) \frac{\partial T}{\partial z}\right] . \end{aligned}$$

(11)

with boundary conditions

$$\begin{aligned} u(r,z)&= 0,\;\;v(r,z)=r\Omega ,\;\;T=T_{\mathrm{w }}, \\D_{\mathrm{A }}\frac{\partial a}{\partial z}&=k_{\mathrm{s }}a,\;\;D_{\mathrm{B }}\frac{\partial b}{\partial z} =-k_{\mathrm{s }}a\;\;{\text {at}}\;z=0, \\&u \rightarrow 0,\;\;v\rightarrow 0,\;\;T\rightarrow T_{\infty }, \\&a\rightarrow a_{0},\;\;b\rightarrow 0\;{\text {as}}\;z\rightarrow \infty . \end{aligned}$$

(12)

here $a_{0}$ is positive dimensional constant.

Consider the following transformations

$$\begin{aligned} u&= r\Omega f^{\prime }(\zeta ),\;\;v=r\Omega g(\zeta ), \\ w&= - \sqrt{2\Omega \nu }f(\zeta ),\;\;\zeta =\sqrt{\frac{2\Omega }{\nu }}z, \\ \theta (\zeta )&= \frac{T-T_{\infty }}{T_{\mathrm{w }}-T_{\infty }},\;\; a=a_{0}\Phi (\zeta ),\;\;b=a_{0}\xi (\zeta ). \end{aligned}$$

(13)

Using the above transformations, Eqs. (3–8) and (11) with the boundary conditions Eq. (12) reduce to the following non-dimensional form

$$\begin{aligned}&f^{\prime \prime \prime }-\frac{1+\alpha }{2}\left( 2ff^{\prime \prime }-f^{\prime 2}+g^{2}\right) \\&\quad +\beta \left( f^{\prime \prime 2}-f^{\prime }f^{\prime \prime \prime }-2ff^{\prime \prime \prime \prime }-g^{\prime 2}-gg^{\prime \prime }\right) =0, \end{aligned}$$

(14)

$$\begin{aligned}&g^{\prime \prime }+\left( 1+\alpha \right) \left( fg^{\prime }-f^{\prime }g\right) \\&\quad +\beta \left( 2f^{\prime \prime }g^{\prime }-f^{\prime }g^{\prime \prime }-2fg^{\prime \prime \prime }+f^{\prime \prime \prime }g\right) =0, \end{aligned}$$

(15)

$$\begin{aligned}\frac{1}{\Pr }\theta ^{\prime \prime }+f\theta ^{\prime }-2\gamma \left( f^{2}\theta ^{\prime \prime }+ff^{\prime }\theta ^{\prime }\right) =0, \end{aligned}$$

(16)

$$\begin{aligned}\frac{1}{Sc}\Phi ^{\prime \prime }+f\Phi ^{\prime }-\frac{1}{2}k_{1}\Phi \xi ^{2}=0, \end{aligned}$$

(17)

$$\begin{aligned}\frac{\delta }{Sc}\xi ^{\prime \prime }+f\xi ^{\prime }+\frac{1}{2}k_{1}\Phi \xi ^{2}=0, \end{aligned}$$

(18)

$$\begin{aligned} f(0)&= 0,\;\;f^{\prime }(0)=0,\;\;f^{\prime }(\infty )\rightarrow 0, \\ g(0)&= 1,\;\;g(\infty )\rightarrow 0, \\ \theta (0)&= 1,\;\;\theta (\infty )\rightarrow 0, \\ \Phi ^{\prime }(0)&= k_{2}\Phi (0),\;\;\Phi (\infty )\rightarrow 1, \\ \delta \xi ^{\prime }(0)&= -k_{2}\Phi (0),\;\;\xi (\infty )\rightarrow 0, \end{aligned}$$

(19)

where Pr the Prandtl number, β the Deborah number, $\gamma$ the dimensionless thermal relaxation time, $\delta$ the ratio of diffusion coefficients, Sc the Schmidt number, $k_{1}$ the homogeneous reaction and $k_{2}$ is heterogeneous reaction parameter. Also these parameters are defined as

$$\begin{aligned} \beta&= \Omega \lambda _{1},\;\;\Pr =\frac{\rho c_{\mathrm{p }}\nu }{k},\;\; \gamma =\Omega \lambda _{2},\;\;{\text {Sc}}=\frac{\upsilon }{D_{\mathrm{A }}}, \\ \delta&= \frac{D_{\mathrm{A }}}{D_{\mathrm{B }}},\;\;k_{1}=\frac{a_{0}^{2}k_{\mathrm{c }}}{\Omega }, \;\; k_{2}=\frac{k_{\mathrm{s }}\sqrt{\upsilon }}{D_{\mathrm{A }}\sqrt{2\Omega }}. \end{aligned}$$

(20)

The diffusion coefficients $D_{\mathrm{A }}$ and $D_{\mathrm{B }}$ are supposed to be of comparable size, and hence, the ratio of diffusion coefficients reduces to 1, i.e., $\delta =1$ and thus [29]

$$\begin{aligned} \Phi (\zeta )+\xi (\zeta )=1. \end{aligned}$$

(21)

Then, Eqs.(17) and (18) become

$$\begin{aligned} \frac{1}{Sc}\Phi ^{\prime \prime }+f\Phi ^{\prime }-\frac{1}{2}k_{1}\Phi (1-\Phi )^{2}=0, \end{aligned}$$

(22)

with boundary conditions

$$\begin{aligned} \Phi ^{\prime }(0)=k_{2}\Phi (0),\quad \Phi (\infty )\rightarrow 1. \end{aligned}$$

(23)

Local skin friction coefficients $C_{\mathrm{f }}$ and $C_{\mathrm{g }}$ along the radial and azimuthal directions at disk are

$$\begin{aligned} C_{\mathrm{f }}=\frac{\left. \tau _{\mathrm{rz }}\right| _{z=0}}{\rho (r\Omega )^{2}},\quad C_{\mathrm{g }}=\frac{\left. \tau _{\uptheta {\mathrm{z}}}\right| _{z=0}}{\rho (r\Omega )^{2}}, \end{aligned}$$

(24)

where $\tau _{\mathrm{rz }}$ is the surface radial stress and $\tau _{\uptheta \mathrm{z}}$ is surface tangential stress and are defined as

$$\begin{aligned} \tau _{\mathrm{rz }}= \frac{\mu }{1+\alpha }\left[ \frac{\partial u}{\partial z} +\lambda _{1}\left\{ 3\frac{\partial u}{\partial r}\frac{\partial u}{ \partial z}+2\frac{\partial v}{\partial r}\frac{\partial v}{\partial z}- \frac{v}{r}\frac{\partial v}{\partial z}+\frac{\partial w}{\partial z}\frac{ \partial u}{\partial z}\right\} \right] , \end{aligned}$$

(25)

$$\begin{aligned} \tau _{\uptheta {\mathrm{z}}}= \frac{\mu }{1+\alpha }\left[ \frac{\partial v}{\partial z }+\lambda _{1}\left\{ \frac{\partial v}{\partial r}\frac{\partial u}{ \partial z}-2\frac{v}{r}\frac{\partial u}{\partial z}+\frac{3u}{r}\frac{ \partial v}{\partial z}\right\} \right] . \end{aligned}$$

(26)

In a view of Eq. (13), dimensionless form of Eq. (24) is as follows

$$\begin{aligned} C_{\mathrm{f }}\left( \frac{\mathop {\mathrm{Re}}\nolimits }{2}\right) ^{1/2}= \frac{1}{1+\alpha }\left[ f^{\prime \prime }(0)+3\beta g^{\prime }(0)\right] , \end{aligned}$$

(27)

$$\begin{aligned} C_{\mathrm{g }}\left( \frac{\mathop {\mathrm{Re}}\nolimits }{2}\right) ^{1/2}= \frac{1}{1+\alpha }\left[ g^{\prime }(0)-\beta f^{\prime \prime }(0)\right] . \end{aligned}$$

(28)

Solutions procedure

Zeroth-order deformation problems

The $f_{0}, g_{0}, \theta _{0}$ and $\Phi _{0}$ be initial approximations taken in the forms:

$$\begin{aligned} f_{0}(\zeta )&= 0,\;\;g_{0}(\zeta )=e^{-\upzeta },\\ \theta _{0}(\zeta ) &= e^{-\upzeta },\;\;\Phi _{0}(\zeta )=1-\frac{1}{2} e^{-{\text{k}}_{2}\upzeta }, \end{aligned}$$

(29)

with linear operators ${\mathcal {L}}_{1}, {\mathcal {L}}_{2},{\mathcal {L}}_{3}, {\mathcal {L}}_{4}$ as

$$\begin{aligned} {\mathcal {L}}_{1}&= f^{\prime \prime \prime }-f^{\prime },\;\;{\mathcal {L}} _{2}=g^{\prime \prime }-g, \\ {\mathcal {L}}_{3}&= \theta ^{\prime \prime }-\theta ,\;\;{\mathcal {L}}_{4}=\Phi ^{\prime \prime }-\Phi , \end{aligned}$$

(30)

where the linear operators have the properties

$$\begin{aligned}&{\mathcal {L}}_{1}\left[ c_{1}+c_{2}e^{\zeta }+c_{3}e^{-\zeta }\right] =0, \\&{\mathcal {L}}_{2}\left[ c_{4}e^{\zeta }+c_{5}e^{-\zeta }\right] =0, \\&{\mathcal {L}}_{3}\left[ c_{6}e^{\zeta }+c_{7}e^{-\zeta }\right] =0, \\&{\mathcal {L}}_{4}\left[ c_{8}e^{\zeta }+c_{9}e^{-\zeta }\right] =0, \end{aligned}$$

(31)

where $c_{\mathrm{i }}\,(i=1-9)$ are arbitrary constants. The nonlinear operators ${\mathcal {N}}_{1}, {\mathcal {N}}_{2}, {\mathcal {N}}_{3}, {\mathcal {N}}_{4}$ are given by

$$\begin{aligned} {\mathcal {N}}_{1}&= \frac{\partial ^{3}{\hat{f}}(\zeta ,q)}{\partial \zeta ^{3}} +\frac{1+\alpha }{2} \\&\quad\left( \left( {\hat{g}}(\zeta ,q)\right) ^{2}+2{\hat{f}} (\zeta ,q)\frac{\partial ^{2}{\hat{f}}(\zeta ,q)}{\partial \zeta ^{2}}-\left( \frac{\partial {\hat{f}}(\zeta ,q)}{\partial \zeta }\right) ^{2}\right) \\&\quad+\beta \left( \left( \frac{\partial ^{2}{\hat{f}}(\zeta ,q)}{\partial \zeta ^{2}}\right) ^{2}-2{\hat{f}}(\zeta ,q)\right. \\&\quad\frac{\partial ^{3}{\hat{f}}(\zeta ,q)}{\partial \zeta ^{3}}-\frac{\partial {\hat{f}}(\zeta ,q)}{\partial \zeta }\frac{ \partial ^{3}{\hat{f}}(\zeta ,q)}{\partial \zeta ^{3}} \\&\quad\left. -{\hat{g}}(\zeta ,q)\frac{\partial ^{2}{\hat{g}}(\zeta ,q)}{\partial \zeta ^{2}}-\left( \frac{\partial {\hat{g}}(\zeta ,q)}{\partial \zeta }\right) ^{2}\right) , \end{aligned}$$

(32)

$$\begin{aligned} {\mathcal {N}}_{2}&= \frac{\partial ^{2}{\hat{g}}(\zeta ,q)}{\partial \zeta ^{2}} +\left( 1+\alpha \right) \left( {\hat{f}}(\zeta ,q)\frac{\partial {\hat{g}} (\zeta ,q)}{\partial \zeta }\right. \\&\quad\left. -\frac{\partial {\hat{f}}(\zeta ,q)}{\partial \zeta }{\hat{g}}(\zeta ,q)\right) \\&\quad+\beta \left( 2\frac{\partial ^{2}{\hat{f}}(\zeta ,q)}{\partial \zeta ^{2}}\frac{\partial {\hat{g}}(\zeta ,q)}{\partial \zeta }+\frac{\partial ^{3}{\hat{f}}(\zeta ,q)}{\partial \zeta ^{3}}{\hat{g}}(\zeta ,q)\right. \\&\quad\left. -\frac{\partial {\hat{f}}(\zeta ,q)}{\partial \zeta }\frac{\partial ^{2}{\hat{g}}(\zeta ,q)}{\partial \zeta ^{2}}-2{\hat{f}}(\zeta ,q)\frac{\partial ^{3}{\hat{g}}(\zeta ,q)}{\partial \zeta ^{3}}\right) , \end{aligned}$$

(33)

$$\begin{aligned} {\mathcal {N}}_{3}&= \frac{1}{\Pr }\frac{\partial ^{2}{\hat{\theta }}(\zeta ,q)}{\partial \zeta ^{2}}+{\hat{f}}(\zeta ,q)\frac{\partial {\hat{\theta }}(\zeta ,q)}{ \partial \zeta } \\&\quad-2\gamma \left( {\hat{f}}(\zeta ,q)\frac{\partial {\hat{f}} (\zeta ,q)}{\partial \zeta }\frac{\partial {\hat{\theta }}(\zeta ,q)}{\partial \zeta }+\left( {\hat{f}}(\zeta ,q)\right) ^{2}\frac{\partial ^{2}{\hat{\theta }} (\zeta ,q)}{\partial \zeta ^{2}}\right) , \end{aligned}$$

(34)

$$\begin{aligned} {\mathcal {N}}_{4}&= \frac{1}{Sc}\frac{\partial ^{2}{\hat{\Phi }}(\zeta ,q)}{\partial \zeta ^{2}}+{\hat{f}}(\zeta ,q)\frac{\partial {\hat{\Phi }}(\zeta ,q)}{ \partial \zeta } \\&\quad-\frac{1}{2}k_{1}{\hat{\Phi }}(\zeta ,q)(1-{\hat{\Phi }}(\zeta ,q))^{2}. \end{aligned}$$

(35)

The zeroth-order deformation problem is presented as:

$$\begin{aligned}(1-q){\mathcal {L}}_{1}\left[ {\hat{f}}(\zeta ,q)-f_{0}(\zeta )\right] =q\hbar _{\mathrm{f }}{\mathcal {N}}_{1}\left[ {\hat{g}}(\zeta ,q),{\hat{f}}(\zeta ,q)\right] , \end{aligned}$$

(36)

$$\begin{aligned}(1-q){\mathcal {L}}_{2}\left[ {\hat{g}}(\zeta ,q)-g_{0}(\zeta )\right] =q\hbar _{\mathrm{g }}{\mathcal {N}}_{2}\left[ {\hat{f}}(\zeta ,q),{\hat{g}}(\zeta ,q)\right] , \end{aligned}$$

(37)

$$\begin{aligned}(1-q){\mathcal {L}}_{3}\left[ {\hat{\theta }}(\zeta ,q)-\theta _{0}(\zeta )\right] =q\hbar _{\uptheta }{\mathcal {N}}_{3}\left[ {\hat{f}}(\zeta ,q),{\hat{\theta }}(\zeta ,q),{\hat{g}}(\zeta ,q)\right] , \end{aligned}$$

(38)

$$\begin{aligned}(1-q){\mathcal {L}}_{4}\left[ {\hat{\Phi }}(\zeta ,q)-\Phi _{0}(\zeta )\right] =q\hbar _{\Phi }{\mathcal {N}}_{4}\left[ {\hat{\Phi }}(\zeta ,q),{\hat{f}}(\zeta ,q), {\hat{g}}(\zeta ,q)\right] , \end{aligned}$$

(39)

$$\begin{aligned} {\hat{f}}(0,q)&= 0,\;\;{\hat{f}}^{\prime }(0,q)=0,{\hat{g}}(0,q)=1, \\ {\hat{\theta }}(0,q)&= 1,{\hat{\Phi }}^{\prime }(0,q)=k_{2}{\hat{\Phi }} (0,q), \\ {\hat{f}}^{\prime }(\infty ,q)&= 0,{\hat{g}}(\infty ,q)=0,{\hat{\theta }}(\infty ,q)=0,{\hat{\Phi }}(\infty ,q)=1, \end{aligned}$$

(40)

in which $\hbar _{\mathrm{f }}, \hbar _{\mathrm{g }}, \hbar _{\uptheta }$ and $\hbar _{\Phi }$ are nonzero auxiliary parameters while $q \epsilon [0\,1]$ is the embedding parameter.

mth-order deformation problems

The problems at this order are presented as

$$\begin{aligned} {\mathcal {L}}_{1}\left[ f_{\mathrm{m }}(\zeta ,q)-\chi _{\mathrm{m }}f_{{\mathrm{m }}-1}(\zeta )\right]= \hbar _{\mathrm{f }}{\mathcal {R}}_{{\mathrm{f,m}}}(\zeta ), \end{aligned}$$

(41)

$$\begin{aligned} {\mathcal {L}}_{2}\left[ g_{\mathrm{m }}(\zeta ,q)-\chi _{\mathrm{m }}g_{{\mathrm{m }}-1}(\zeta )\right]= \hbar _{\mathrm{g }}{\mathcal {R}}_{{\mathrm{g,m}}}(\zeta ), \end{aligned}$$

(42)

$$\begin{aligned} {\mathcal {L}}_{3}\left[ \theta _{\mathrm{m }}(\zeta ,q)-\chi _{\mathrm{m }}\theta _{{\mathrm{m }}-1}(\zeta ) \right]= \hbar _{\uptheta }{\mathcal {R}}_{\uptheta ,{\mathrm{m}}}(\zeta ), \end{aligned}$$

(43)

$$\begin{aligned} {\mathcal {L}}_{4}\left[ \Phi _{\mathrm{m }}(\zeta ,q)-\chi _{\mathrm{m }}\Phi _{{\mathrm{m }}-1}(\zeta )\right]= \hbar _{\Phi }{\mathcal {R}}_{\Phi ,{\mathrm{m }}}(\zeta ), \end{aligned}$$

(44)

$$\begin{aligned} f_{\mathrm{m }}(0)&= f_{\mathrm{m }}^{\prime }(0)=g_{\mathrm{m }}(0)= \theta _{\mathrm{m }}(0)=0, \Phi _{\mathrm{m }}^{\prime }(0)-k_{2}\Phi _{\mathrm{m }}(0)=0, \\ f_{\mathrm{m }}^{\prime }(\infty )&= g_{\mathrm{m }}(\infty )=\theta _{\mathrm{m }}(\infty )=\Phi _{\mathrm{m }}(\infty )=0, \end{aligned}$$

(45)

$$\begin{aligned}&{\mathcal {R}}_{{\mathrm{f,m}}}\left( \zeta \right) = f_{{\mathrm{m }}-1}^{\prime \prime \prime }+ \frac{1+\alpha }{2}\mathop {\displaystyle \sum }\limits _{k=0}^{m-1} \\&\quad \left[ 2f_{\mathrm{k }}f_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime \prime }-f_{\mathrm{k }}^{\prime }f_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime }+g_{\mathrm{k }}g_{{\mathrm{m }}-1-{\mathrm{k }}}\right] \\&\quad +\beta \mathop {\displaystyle \sum }\limits _{k=0}^{m-1}\left[ f_{\mathrm{k }}^{\prime \prime }f_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime \prime }-f_{\mathrm{k }}^{\prime }f_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime \prime \prime }\right. \\&\quad \left. -2f_{\mathrm{k }}f_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime \prime \prime \prime }-g_{\mathrm{k }}^{\prime }g_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime }-g_{\mathrm{k }}g_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime \prime }\right] , \end{aligned}$$

(46)

$$\begin{aligned}&{\mathcal {R}}_{{\mathrm{g,m}}}(\zeta ) =g_{{\mathrm{m }}-1}^{\prime \prime }+\left( 1+\alpha \right) \\&\quad \mathop {\displaystyle \sum }\limits _{k=0}^{m-1}\left[ f_{\mathrm{k }}g_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime }-f_{\mathrm{k }}^{\prime }g_{{\mathrm{m }}-1-{\mathrm{k }}}\right] \\&\quad +\beta \mathop {\displaystyle \sum }\limits _{k=0}^{m-1}\left[ 2f_{\mathrm{k }}^{\prime \prime }g_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime }-f_{\mathrm{k }}^{\prime }g_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime \prime }\right. \\&\quad \left. -2f_{\mathrm{k }}g_{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime \prime \prime }+f_{\mathrm{k }}^{\prime \prime \prime }g_{{\mathrm{m }}-1-{\mathrm{k }}}\right] , \end{aligned}$$

(47)

$$\begin{aligned}&{\mathcal {R}}_{\uptheta,{\mathrm{m}}}(\eta )=\frac{1}{\Pr }\theta _{{\mathrm{m }}-1}^{\prime \prime }-\mathop {\sum\limits_{{\text{k}}=0}^{m-1}}\left[\vphantom{\left( f_{{\mathrm{m }}-1-{\mathrm{l}}}^{\prime }\mathop {\sum\limits_{{\text{j}}=0}^{l}}f_{\mathrm{l}-{\mathrm{j}}}^{\prime }\theta _{\mathrm{j }}+f_{{\mathrm{j }}-1-{\mathrm{l}}}\mathop {\displaystyle \sum }\limits _{{\text{j}}=0}^{l}f_{l-{\text{j}}}^{\prime }\theta _{\mathrm{j }}^{\prime }\right)} f_{\mathrm{k }}\theta _{{\mathrm{m }}-1-{\mathrm{k }}}^{\prime }-2\gamma\right. \\&\quad \left. \left( f_{{\mathrm{m }}-1-{\mathrm{l}}}^{\prime }\mathop {\sum\limits_{{\text{j}}=0}^{l}}f_{\mathrm{l}-{\mathrm{j}}}^{\prime }\theta _{\mathrm{j }}+f_{{\mathrm{j }}-1-{\mathrm{l}}}\mathop {\displaystyle \sum }\limits _{{\text{j}}=0}^{l}f_{{\text{l}}-{\text{j}}}^{\prime }\theta _{\mathrm{j }}^{\prime }\right) \right] , \end{aligned}$$

(48)

$$\begin{aligned}{\mathcal {R}}_{\Phi ,{\mathrm{m}}}(\zeta )=\frac{1}{Sc}\Phi _{{\text{m}}-1}^{\prime \prime }+\mathop {\displaystyle \sum }\limits _{{\text{k}}=0}^{m-1}\left[ f_{{\mathrm{m}}-1-{\mathrm{k}}}\Phi _{\mathrm{k }}^{\prime }-\frac{1}{2} k_{{\text{1}}}\left( \Phi _{{\mathrm{m}}-1-{\mathrm{l}}}\mathop {\displaystyle \sum }\limits _{{\text{j}}=0}^{l}\Phi _{{\mathrm{l}}-{\mathrm{j}}}\Phi _{\mathrm{j }}-2\Phi _{{\mathrm{m}}-1-{\mathrm{l}}}\Phi _{\mathrm{l }}\right) \right] -\frac{1}{2}k_{{\text{1}}}, \end{aligned}$$

(49)

$$\begin{aligned}\chi _{\mathrm{m }}=\left\{ \begin{array}{ll} 0,&\quad m\le 1 \\ 1,&\quad m>1 \end{array} \right. . \end{aligned}$$

(50)

The general solutions of Eqs. (41)–(45) can be expressed as

$$\begin{aligned} f_{\mathrm{m }}(\zeta )&= f_{\mathrm{m }}^{*}(\zeta )+c_{1}+c_{2}e^{\zeta }+c_{3}e^{-\zeta }, \\ g_{\mathrm{m }}(\zeta )&= g_{\mathrm{m }}^{*}(\zeta )+c_{4}e^{\zeta }+c_{5}e^{-\zeta }, \\ \theta _{\mathrm{m }}(\zeta )&= \theta _{\mathrm{m }}^{*}(\zeta )+c_{6}e^{\zeta }+c_{7}e^{-\zeta }, \\ \Phi _{\mathrm{m }}(\zeta )&= \Phi _{\mathrm{m }}^{*}(\zeta )+c_{8}e^{\zeta }+c_{9}e^{-\zeta }, \end{aligned}$$

(51)

$$\begin{aligned} c_{1}&= -f_{\mathrm{m }}^{*}(0)-\left. \frac{\partial f_{\mathrm{m }}^{*}(\zeta )}{ \partial \zeta }\right| _{\zeta =0}, \\ c_{3}&= \left. \frac{\partial f_{\mathrm{m }}^{*}(\zeta )}{\partial \zeta }\right| _{\zeta =0},\;\; c_{5}=-g_{\mathrm{m }}^{*}(0),\;\;c_{7}=-\theta _{\mathrm{m }}^{*}(0), \\ c_{9}&= \frac{1}{1+k_{2}}\left[ \left. \frac{\partial \Phi _{\mathrm{m }}^{*}(\zeta )}{\partial \zeta }\right| _{\zeta =0}-k_{2}\Phi _{\mathrm{m }}^{*}(0) \right] , \\&c_{2}&=&c_{4}=c_{6}=c_{8}=0. \end{aligned}$$

(52)

in which $f_{\mathrm{m }}^{*}(\zeta ), g_{\mathrm{m }}^{*}(\zeta ), \theta _{\mathrm{m }}^{*}(\zeta )$ and $\Phi _{\mathrm{m }}^{*}(\zeta )$ denote special solutions.

Convergence of the derived series solutions

We observe that Eqs. (36)–(39) contain some auxiliary parameters. The auxiliary parameters $\hbar _{\mathrm{f }}, \hbar _{\mathrm{g }}, \hbar _{\uptheta }$ and $\hbar _{\Phi }$ play an important role for adjusting the convergence of series solutions. The convergence rate of derived series solutions depend highly upon these parameters. To find appropriate values of involved auxiliary parameters, $\hbar$-curves are sketched in Fig. 2. Clearly, the range for admissible values of $\hbar _{\mathrm{f }}, \hbar _{\mathrm{g }}, \hbar _{\uptheta }$ and $\hbar _{\Phi }$ are $-1.8\le \hbar _{\mathrm{f }}\le -1.2, -1.8\le \hbar _{\mathrm{g }}\le -0.7, -1.7\le \hbar _{\uptheta }\le -0.9$ and $-1\le \hbar _{\Phi }\le -0.1$. Further, the performed computations show that series solutions converge in the whole region of $\zeta$ when $\ \hbar _{\mathrm{f }}=-1.4, \hbar _{\mathrm{g }}=-1, \hbar _{\uptheta }=-1.3$ and $\hbar _{\Phi }=-0.2$ (see Table 1).

Fig. 2

$\hbar$-curves for $f^{\prime \prime }(0),g^{\prime }(0),\theta ^{\prime }(0)$ and $\Phi ^{\prime }(0)$

Table 1 HAM solution converges when $\alpha =\beta =0.1, \Pr =1.2, \gamma =0.3, k_{1}=k_{2}=0.2$ and Sc = 0.4

Analysis of the results

This section provides physical insight into role of the pertinent parameters on the velocities $f^{\prime }(\zeta )$ and $g(\zeta )$, the temperature $\theta \left( \zeta \right)$ and concentration $\Phi \left( \zeta \right)$ . Behavior of few involved parameters like α and Deborah number $\beta$ on both the velocities $f^{\prime }(\zeta )$ and $g(\zeta )$ is displayed in Figs. 3–5. A change in radial velocity profile with variation in α is elucidated in Fig. 3. Increasing value of $\alpha$ reduces the retardation time that means particles require much time to return back from the perturbed to an equilibrium system. This in turn decreases the momentum boundary layer. Effects of α on azimuthal velocity $g(\zeta )$ are demonstrated in Fig. 4. It shows considerable reduction in $g(\zeta )$ as α grows from $\alpha =0.1$ to $\alpha =0.7$. In Fig. 5, radial velocity curves $f^{\prime }(\zeta )$ are sketched for the varying β. There is an increasing trend in velocity profile when β is increased. It is because of the fact that Deborah number and retardation time are directly related to one another (i.e., $\beta =\Omega \lambda _{1}$).

Fig. 3

Variation in $f^\prime (\zeta )$ by changing α

Fig. 4

Variation in $g(\zeta )$ by changing α

Fig. 5

Variation in $f^\prime (\zeta )$ by changing β

Figure 6 shows impact of Prandtl number Pr on temperature profile $\theta \left( \zeta \right)$. Since thermal diffusivity is inversely related to Pr therefore temperature $\theta \left( \zeta \right)$ rises with the decrease in Pr. Temperature profiles $\theta \left( \zeta \right)$ are presented for various values of α in Fig. 7. As $\alpha$ is increased it causes retardation time to decrease while the relaxation time increases. As a result of this arise in temperature $\theta \left( \zeta \right)$ is observed. A quite significant enhancement in temperature with decrease in Deborah number β is indicated in Fig. 8.

Fig. 6

Variation in $\theta (\zeta )$ by changing Pr

Fig. 7

Variation in $\theta (\zeta )$ by changing α

Fig. 8

Variation in $\theta (\zeta )$ by changing β

Figure 9 illustrates the fluctuation in concentration profile for varying values of strength of homogeneous reaction parameter $k_{1}$. Larger value of $k_{1}$ causes faster consumption of the reactants which in turn reduces the concentration. Contrary to the effect of $k_{1}$, heterogeneous reaction parameter $k_{2}$ increases the concentration $\Phi \left( \zeta \right)$ (see Fig. 10). An impact of Sc over the concentration profile $\Phi \left( \zeta \right)$ is accounted in Fig. 11. Larger value of Sc indicates that the momentum diffusivity is dominating to mass diffusivity, causes enhancement in the fluid concentration.

Fig. 9

Variation in $\Phi (\zeta )$ by changing $k_{1}$

Fig. 10

Variation in $\Phi (\zeta )$ by changing $k_{2}$

Fig. 11

Variation in $\Phi (\zeta )$ by changing Sc

Impact of α on radial skin friction coefficient $C_{\mathrm{f }}\left( \frac{ \mathop {\mathrm{Re}}\nolimits }{2}\right) ^{1/2}$ via Deborah number β is illustrated in Fig. 12. Here, $C_{\mathrm{f }}\left( \frac{\mathop {\mathrm{Re}}\nolimits }{2}\right) ^{1/2}$ decreases by increasing the values of α and β. Figure 13 portrays the variation of α on azimuthal skin friction coefficient $C_{\mathrm{g }}\left( \frac{\mathop {\mathrm{Re}}\nolimits }{2}\right) ^{1/2}$ against β. Here, it is seen that azimuthal skin friction coefficient enhances for larger values of α and it decreases with the enhancement in β.

Fig. 12

Variation in $C_{\mathrm{f }}(\mathop {\mathrm{Re}}\nolimits /2)^{1/2}$ with α

Fig. 13

Variation in $C_{\mathrm{g }}(\mathop {\mathrm{Re}}\nolimits /2)^{1/2}$ with α

Figure 14 is sketched to inspect the surface concentration via α for various values of Schmidt number Sc. One can clearly observe that $\Phi \left( 0\right)$ decreases with an increase in α.

Fig. 14

Variation in $\Phi (0)$ with Sc

Table 2 is organized for the authentication of present numerical computations. For this, we have calculated the numerical values for the Nusselt number $-\theta ^{\prime }(0)$ in limiting cases. The attained outcomes match in an outstanding way with those of Turkyimazoglu [25] and Khan et al. [26] which confirms the accuracy of the applied analytical scheme.

Table 2 Comparison of numerical values of $-\theta ^{\prime }(0)$ when $\gamma =\beta =\alpha =0$ and $\Pr =1$

Concluding remarks

Here, the effect of chemical reactions on Jeffrey fluid flow induced by rotating disk is analyzed. Further, inclusion of Cattaneo–Christov model modifies flow characteristics. Following results are outlined

• Deborah number contributes to an enhancement in velocity profiles.

• Both radial and azimuthal velocities decrease with an increment in α.

• Fluid temperature rises with an increase in α while it reduces when Pr and β are increased.

• Influence of homogeneous reaction parameter $k_{1}$ on concentration is qualitatively opposite to that of heterogeneous reaction parameter.

• Magnitude of surface concentration decreases for increasing values of α.

• Skin friction coefficients are found to decline upon increasing β.