1 Introduction

The novel properties of tiny particles suspended in a base fluid have led many scientists to great strides in the production of chemical reactors, heat exchangers, pharmaceutical equipment and hybrid-powered engines. The enhancement of the thermal properties of fluids due to the presence of nanosized particles was firstly buttressed by Choi [1]. In this framework, the nanofluids have emerged as promising fluids in enhancing the intrinsic thermophysical properties related explicitly to the heat transfer characteristics. These aforementioned thermal features were deliberated thoroughly by many renowned researchers, such as Xuan et al. [2], Das et al. [3], Azmi et al. [4], Animasaun et al. [5] and Wakif et al. [6]. Indeed, the enhancement of heat transfer across flowing or stagnant fluids or cooling can be encountered widely in numerous vital applications, such as chemical reactors, heat exchangers, pharmaceutical process, hybrid-powered engines, nuclear reactor cooling, electronics cooling, solar energy applications, copper wires annealing and phase change processes. According to Khan and Pop [7], Khan et al. [8] and Imtiaz et al. [9], the cooling rate in the aforesaid process shows an important role regarding the final product in the diversified industrial world. Meanwhile, an increase in the velocity slip has been shown to be a factor sufficient enough to greatly reduce the heat transfer rate in the non-Newtonian blood flows conveying gold nanoparticles as reported by Animasaun et al. [10]. In another work, Animasaun et al. [11] demonstrated that the heat transfer rate is an increasing property of thermoelectric in the case of water conveying 29-nm \( {\text{CuO}} \) spherical nanoparticles. Similarly, Wakif et al. [12] controlled passively the volumetric fraction of nanoparticles at the boundaries through the revised Nield’s condition [13, 14] to determine the temperature gradient in the flow of alumina–water-based nanofluids (\( {\text{Al}}_{2} {\text{O}}_{3} \)–\( {\text{H}}_{2} {\text{O}} \)). The significant effect of the other pertinent physical factors such as the bioconvection phenomenon and the gyrotactic microorganisms as well as the thermophoresis and the haphazard motion of nanoparticles in the flow of various nanofluids have been discussed extensively by Sivaraj et al. [15], Makinde and Animasaun [16, 17].

Lately, the heat and mass transport phenomena affected by a laminar boundary layer flow past over a stretching surface are relevant to diversified fields of several industrial and engineering processes due to their useful practice involved in such fields, such as cooling and heating manufacturing systems. An augmentation in the heat transfer rate is quite essential from an economic point of view, as long as this thermal enhancement participates significatively in the minimization of the processing time as well as in the perfection of the working efficiency. On the other hand, the mixed convection mechanism can arise when the thermal buoyancy effect participates also in the promotion of heat transfer in the fluidic mediums. In view of the above relevance of heat transport phenomena and mixed convection process, many researchers succeeded in accomplishing society and industry-friendly outcomes by carrying out extensive studies (e.g., analytical, numerical and experimental investigations) in the related areas. For instance, the examination of mixed convective flow with entropy generation in a heated skewed enclosure of \( {\text{Cu}} \)–water nanofluids has been performed numerically by Nayak et al. [18]. The impact of homogeneous–heterogeneous kinds of chemical reactions on the transportation of thermal energy was outlined by Hayat et al. [19]. Interesting exclusive reports on heat transfer during the dynamics of two-dimensional or three-dimensional flows of various nanofluids induced by either linear/nonlinear or exponential stretching/shrinking surfaces subject to linear or nonlinear thermal radiation, chemical reaction, Cattaneo–Christov heat flux and mixed convection flow with the convective boundary condition have been reported by Nayak et al. [20,21,22,23,24,25,26]. In addition, the conveyance of heat via the mixed convective flows of Sisko non-Newtonian fluids was presented by Tanveer et al. [27]. Besides, the heat transfer in stagnation point flows under the combined effect of Joule heating and viscous dissipation was reported by Khan et al. [28]. In another related study, the nature of heat transfer across the nanofluid flows over a stretchable porous surface was illustrated by Kameswarn et al. [29]. The relationship between the heat transfer aspects and the viscous dissipation in the three-dimensional radiative nanofluid flows in the presence of Lorentz force was discussed by Nayak [30]. Interestingly, Nadeem et al. [31] investigated the MHD oblique flows of Walter’s B type nanofluids past over a convective surface. An excellent study was accomplished by Afridi and Qasim [32] to scrutinize the entropy generation and heat transfer characteristics for the radiative flows over a heated thin needle.

In another flow geometry, Soid et al. [33] scrutinized numerically the stability of a two-dimensional laminar forced convection nanofluid flow along an incessantly moving thin needle. As the main findings, they notified that the presence of solid nanoparticles in a viscous fluidic medium declines the skin friction factor and upsurges the heat transfer rate. Based on the well-known boundary value problem solver (bvp4c), Waini et al. [34] performed a detailed stability analysis concerning the flow and heat transfer characteristics of an incompressible viscous fluid flowing over a moving heated thin needle with the prescribed surface heat flux. This motivating scientific research work has been extended recently by the same authors to the case of hybrid nanofluids, in order to analyze the behaviors of skin friction coefficient and local Nusselt number as well as the velocity and temperature profiles toward a steady mixed convection hybrid nanofluid flow past a vertical thin needle with the prescribed surface heat flux. After analyzing physically the admissibility of all solutions, Waini et al. [35] concluded that the skin friction coefficient and the local Nusselt number on the needle surface have the tendency to be heightened meaningfully by mounting the volume fraction of copper nanoparticles and diminishing the needle size.

Based on the literature search presented above, there are no outlined analyses dealing numerically with the flow of metallic and metallic oxide nanofluids over an isothermal needle using the generalized differential quadrature method (GDQM). However, no such investigations are yet declared considering the comparison of metallic and metallic oxide nanofluid flows with their heat transfer characteristics. Keeping this intention into mind, our main objective here is to examine numerically the mixed convection flows and thermal characteristics of metallic and metallic oxide nanofluids over an isothermal thin needle. The novelty of the present work is to explore the comparison of mixed convection flows and thermal characteristics of many metallic nanofluids (\( {\text{Al}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Al}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Zn}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Zn}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) and metallic oxide nanofluids (\( {\text{Al}}_{2} {\text{O}}_{3} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Al}}_{2} {\text{O}}_{3} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{CuO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{CuO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{ZnO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{ZnO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)). As a practical use, the physical problem under consideration has relevance in medicine, electronics, optics, solar cells, catalysis, arterials, manufacturing, smart computers, renewable energy, and many others. The involved system of nonlinear differential equations is tackled numerically using the generalized differential quadrature method (GDQM). Also, the numerical outcomes are compared tabularly with those of the existing literature. Besides this, the influence of the embedded physical parameters is deliberated in detail with the help of various graphical and tabular demonstrations.

2 Problem Statement

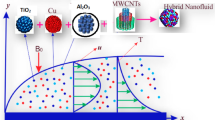
In this work, we consider a steady, laminar and incompressible convective flows of metallic/metallic oxide water/ethylene glycol-based nanofluids (\( {\text{Al}} \)–\( {\text{H}}_{2} {\text{O}} \),\( {\text{Al}}_{2} {\text{O}}_{3} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Al}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Al}}_{2} {\text{O}}_{3} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{CuO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{CuO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Zn}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{ZnO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Zn}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{ZnO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) over a vertical heated thin needle in a variable external stream. The schematic illustration of the present boundary layer flow along with the dimensional Cartesian coordinates is presented clearly in Fig. 1. In the present problem, the isothermal wall temperature \( T_{\text{w}} \) on the exterior surface of the needle is inserted in the mathematical description as an appropriate thermal boundary condition among the physical constraints to control the gravitational buoyancy effect. Further, the presence of an axial pressure gradient inside the boundary layer flow region is taken into account due to the variable axial free stream velocity \( U\left( x \right)\left( { = u_{\infty } x^{1/2} } \right) \). Also, it is assumed that the used base fluids (\( {\text{H}}_{2} {\text{O}} \), \( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) and nanoparticles (\( \text{Al} \), \( {\text{Cu}} \), \( {\text{Zn}} \), \( {\text{Al}}_{2} {\text{O}}_{3} \), \( {\text{CuO}} \), \( {\text{ZnO}} \)) are assumed to be always in thermal equilibrium.

Fig. 1
figure 1

Schematic diagram of the flow problem and coordinate system

Full size image

Keeping in mind the aforementioned assumptions together with the boundary layer and Boussinesq approximation, the relevant transport conservation equations for continuity, momentum, and energy governing the present problem can be formulated explicitly by adopting the Tiwari and Das’s approach [36] for the single-phase homogeneous nanofluid model. According to Chen and Smith [37], the governing partial differential equations (PDEs) are itemized in the steady form as follows

$$ \frac{{\partial \left( {ru} \right)}}{\partial x} + \frac{{\partial \left( {rv} \right)}}{\partial r} = 0, $$
(1)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial r} = - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial p}{\partial x} + \upsilon_{\text{nf}} \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r}} \right) + \frac{{\left( {\rho \beta_{\text{T}} } \right)_{\text{nf}} }}{{\rho_{\text{nf}} }}\,g\,\left( {T - T_{\infty } } \right)\,, $$
(2)
$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial r} = \frac{{k_{\text{nf}} }}{{\left( {\rho C} \right)_{{p{\text{nf}}}} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right), $$
(3)
$$ - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial p}{\partial x} = U\left( x \right)\frac{{{\text{d}}U\left( x \right)}}{{{\text{d}}x}}. $$
(4)

Physically, the above PDEs are exposed to the following boundary conditions:

$$ u = \,0,{\text{v}} = 0,T = T_{\text{w}} \;{\text{at}}\;r = R\left( x \right), $$
(5)
$$ u \to U\left( x \right),T \to T_{\infty } \,{\text{as}}\;r \to \infty . $$
(6)

Here, \( u \) and \( v \) represent the velocity components in the axial and radial directions, respectively, \( \upsilon_{\text{nf}} \) and \( \rho_{\text{nf}} \) denote the kinematic viscosity and density of nanofluids, respectively, \( \beta_{\text{T}} \) designates the thermal expansion coefficient, \( T \) refers to the nanofluid temperature within the boundary layer, \( T_{\infty } \) stands for the ambient temperature and \( T_{{{\text{w}} }} \) for the wall temperature and \( g \) indicates the gravitational acceleration.

In addition, the physical meanings of the other symbols and control parameters used in this paper are specified appropriately and summarized successfully in the nomenclature table.

By making use of the Brinkman’s model [38], the dynamic viscosity of the used nanofluids can be estimated by:

$$ \mu_{\text{nf}} = \frac{{\mu_{f} }}{{\left( {1 - \phi } \right)^{2.5} }}. $$
(7)

Moreover, the effective values of the density \( \rho_{\text{nf}} \), the heat capacitance \( \left( {\rho C_{P} } \right)_{\text{nf}} \) and the thermal expansion coefficient \( \beta_{\text{nf}} \) of nanofluids are given by Pourmehran et al. [39] as follows:

$$ \rho_{\text{nf}} = \left( {1 - \phi } \right)\rho_{\text{f}} + \phi \rho_{\text{s}} , $$
(8)
$$ \left( {\rho C_{p} } \right)_{\text{nf}} = \left( {\text{1} - \phi } \right)\left( {\rho C_{p} } \right)_{\text{f}} + \phi \left( {\rho C_{p} } \right)_{\text{s}} , $$
(9)
$$ \left( {\rho \beta_{\text{T}} } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho \beta_{\text{T}} } \right)_{\text{f}} + \phi \left( {\rho \beta_{\text{T}} } \right)_{\text{s}} . $$
(10)

Based on the Maxwell Garnett theory (MGT) [40], the effective thermal conductivity of studied mixtures can be assessed as:

$$ \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = 1 + \frac{{3\left( {\frac{{k_{\text{s}} }}{{k_{\text{f}} }} - 1} \right)\phi }}{{\left( {\frac{{k_{\text{s}} }}{{k_{\text{f}} }} + 2} \right) - \left( {\frac{{k_{\text{s}} }}{{k_{\text{f}} }} - 1} \right)\phi }}. $$
(11)

Here, it is worth noting that the subscripts \( \left( {{\text{nf}},{\text{f}},{\text{s}}} \right) \) represent the nanofluid, the base fluid and the solid nanoparticles, respectively.

For more clarification, the principal thermophysical properties of water \( \left( {{\text{H}}_{2} {\text{O}}} \right) \), ethylene glycol \( \left( {{\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{ 2} } \right) \), aluminum \( \left( {\text{Al}} \right) \), copper \( \left( {\text{Cu}} \right) \), zinc \( \left( {\text{Zn}} \right) \), alumina \( \left( {{\text{Al}}_{2} {\text{O}}_{3} } \right) \), copper oxide \( \left( {\text{CuO}} \right) \) and zinc oxide \( \left( {\text{ZnO}} \right) \) are enlisted in Table 1.

Table 1 Properties of some base fluids and metallic/metallic oxide nanoparticles
Full size table

By introducing the stream function formulation with the following transformations,

$$ \begin{aligned} & u = \frac{1}{r}\frac{\partial \psi }{\partial r},\quad {\text{v}} = - \frac{1}{r}\frac{\partial \psi }{\partial x},\quad \psi = x\upsilon_{\text{f}} F\left( \xi \right) \\ & T - T_{\infty } = \left( {T_{\text{w}} - T_{\infty } } \right)\varTheta \left( \xi \right),\\ & U\left( x \right) = u_{\infty } x^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \xi = \left( {\frac{{u_{{_{\infty } }} }}{{\upsilon_{\text{f}} }}} \right)\frac{{r^{2} }}{{x^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} \\ \end{aligned} $$
(12)

Equations (1)–(4) in association with the boundary conditions (5) and (6) readily take the forms:

$$ 8P_{1} \xi F^{\prime \prime \prime } + 8P_{1} F^{\prime \prime } + P_{2} \varGamma \varTheta + 4FF^{\prime \prime } - 2F^{\prime 2} + \frac{1}{2} = 0, $$
(13)
$$ P_{3} \xi \,\varTheta^{\prime\prime} + P_{3} \varTheta^{\prime} + \frac{1}{2}\Pr F\varTheta^{\prime} = 0, $$
(14)
$$ F = 0,\quad F^{\prime} = 0,\quad \varTheta = 1\;{\text{at}}\;\xi = a, $$
(15)
$$ F^{\prime} \to \frac{1}{2},\varTheta \to 0\;{\text{as}}\;\xi \to \infty . $$
(16)

As mentioned earlier, it can be noted here that the velocity components \( \left( {u,{\text{v}}} \right) \) are obviously verified the continuity equation given above by Eq. (1). By combining the expression of the similarity variable \( \xi \) with that of the free stream velocity \( U\left( x \right) \), the shape and size of the thin needle can be done by the function \( R\left( x \right) = \left( {a\upsilon_{\text{f}} x/U\left( x \right)} \right)^{1/2} \). Here, the limiting situation \( \xi = a \) corresponds to the surface of revolution of the thin needle. Moreover, the physical quantities \( P_{1} \), \( P_{2} \) and \( P_{3} \) appeared in Eqs. (13) and (14) are given by:

$$ P_{1} = \frac{{\mu_{r} }}{{\rho_{r} }},\quad P_{2} = \frac{{\left( {\rho \beta_{\text{T}} } \right)_{r} }}{{\rho_{r} }},\quad P_{3} = \frac{{k_{r} }}{{\text{(}\rho C_{p} \text{)}_{r} }}, $$
(17)

where

$$\begin{aligned} &\mu_{r} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},\quad \rho_{r} = \,\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }},\\ &\left( {\rho C_{p} } \right)_{r} = \frac{{\left( {\rho C_{p} } \right)_{\text{nf}} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }},\quad \left( {\rho \beta_{\text{T}} } \right)_{r} = \frac{{\left( {\rho \beta_{T} } \right)_{\text{nf}} }}{{\left( {\rho \beta_{T} } \right)_{f} }},\quad k_{r} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}.\end{aligned} $$
(18)

Furthermore, the mixed convection parameter \( \varGamma \) highlighted in Eq. (13) is taken into account in this investigation to measure the relative importance of the free convection phenomenon over the forced convection mechanism. This parameter is expressed mathematically by:

$$ \varGamma = \frac{{{\text{Gr}}_{x} }}{{\text{Re}_{x}^{2} }}, $$
(19)

in which

$$ {\text{Gr}}_{x} = \frac{{g\beta_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)x^{3} }}{{\upsilon_{\text{f}}^{2} }}, $$
(20)
$$ \text{Re}_{x} = \frac{U\left( x \right)x}{{\upsilon_{\text{f}} }}. $$
(21)

Here, the local parameters \( {\text{Gr}}_{x} \) and \( {\text{Re}}_{x} \) represent Grashof and Reynolds numbers, respectively.

For isothermal wall needle and no-slip conditions, the reduced expressions of the skin friction \( C_{{{\text{f}}x}} \) coefficient and Nusselt number \( {\text{Nu}}_{x} \) are defined locally by:

$$ \text{Re}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} C_{{{\text{f}}x}} = 8\sqrt a \,\mu_{r} \,F^{\prime\prime}\left( a \right), $$
(22)
$$ {\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} {\text{Nu}}_{x} = - 2\sqrt a k_{r} \,\varTheta^{\prime}\left( a \right). $$
(23)

In order to reduce the implementation complexity of the current physical problem, it is more useful to introduce the following simplifications:

$$ \left\{ {\begin{array}{*{20}l} {\eta = \xi - a, \, } \\ {\chi = {\eta \mathord{\left/ {\vphantom {\eta {\eta_{\infty } , \, }}} \right. \kern-0pt} {\eta_{\infty } , \, }}} \\ \begin{aligned} F\left( \xi \right) = F\left( {\eta + a} \right) = f\left( \eta \right), \hfill \\ f\left( \eta \right) = f\left( {\eta_{\infty } \chi } \right) = G\left( \chi \right), \hfill \\ \end{aligned} \\ \begin{aligned} \varTheta \left( \xi \right) = \varTheta \left( {\eta + a} \right) = \theta \left( \eta \right), \hfill \\ \theta \left( \eta \right) = \theta \left( {\eta_{\infty } \chi } \right) = H\left( \chi \right), \hfill \\ \end{aligned} \\ \end{array} } \right. $$
(24)

in which \( \eta_{\infty } \) is the appropriate asymptotical value taken by the boundary layer thickness.

In view of the above considerations, Eqs. (13) and (14) along with their corresponding boundary conditions (15) and (16) are transformed to the following nonlinear differential system:

$$ \, \left( {S_{1} } \right){ : }\left\{ {\begin{array}{*{20}l} {f = f^{\prime } = 0 \, } \hfill & {{\text{at}}\quad \eta = 0, \, } \hfill \\ {8P_{1} \left( {\eta + a} \right)f^{\prime \prime \prime } + 8P_{1} f^{\prime \prime } + P_{2} \varGamma \theta + 4ff^{\prime \prime } - 2f^{\prime 2} + \frac{1}{2} = 0} \hfill & {{\text{for}}\quad \eta > 0, \, } \hfill \\ {f^{\prime } \to {1 \mathord{\left/ {\vphantom {1 {2 \, }}} \right. \kern-0pt} {2 \, }}} \hfill & {{\text{as}}\quad \eta \to \infty , \, } \hfill \\ {\theta = 1 \, } \hfill & {{\text{at}}\quad \eta = 0, \, } \hfill \\ {P_{3} \left( {\eta + a} \right)\,\theta^{\prime \prime } + P_{3} \theta^{\prime } + \frac{1}{2}\Pr f\theta^{\prime } = 0 \, } \hfill & {{\text{for}}\quad \eta > 0, \, } \hfill \\ {\theta \to 0 \, } \hfill & {{\text{as}}\quad \eta \to \infty . \, } \hfill \\ \end{array} } \right. $$
(25)

After incorporating the reduced similarity variable \( \chi \) in Eq. (25), the differential system \( \left( {S_{1} } \right) \) can be simplified furtherly as follows:

$$ \left( {S_{2} } \right){ : }\left\{ {\begin{array}{*{20}l} {G = G\prime = 0 \, } \hfill & {{\text{at}}\quad \chi = 0, \, } \hfill \\ {\frac{{8P_{1} \left( {\eta_{\infty } \chi + a} \right)}}{{\eta_{\infty }^{3} }}G^{\prime \prime \prime } + \frac{{8P_{1} }}{{\eta_{\infty }^{2} }}G^{\prime \prime } + P_{2} \varGamma H + \frac{4}{{\eta_{\infty }^{2} }}GG^{\prime \prime } - \frac{2}{{\eta_{\infty }^{2} }}G^{\prime 2} + \frac{1}{2} = 0} \hfill & {{\text{for}}\quad \chi > 0, \, } \hfill \\ {G^{\prime } \to {{\eta_{\infty } } \mathord{\left/ {\vphantom {{\eta_{\infty } } {2 \, }}} \right. \kern-0pt} {2 \, }}} \hfill & {{\text{as}}\quad \chi \to 1, \, } \hfill \\ {H = 1 \, } \hfill & {{\text{at}}\quad \chi = 0, \, } \hfill \\ {\frac{{P_{3} \left( {\eta_{\infty } \chi + a} \right)}}{{\eta_{\infty }^{2} }}\,H^{\prime \prime } + \frac{{P_{3} }}{{\eta_{\infty } }}H^{\prime } + \frac{\Pr }{{2\eta_{\infty } }}GH^{\prime } = 0 \, } \hfill & {{\text{for}}\quad \chi > 0, \, } \hfill \\ {H \to 0 \, } \hfill & {{\text{as}}\quad \chi \to 1. \, } \hfill \\ \end{array} } \right. $$
(26)

By virtue of Eq. (24), the reduced physical quantities \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x}} \) and \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \) can be written in the following dimensionless form:

$$ \text{Re}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} C_{{{\text{f}}x}} = 8\sqrt a \,\mu_{r} \,f^{\prime\prime}\left( 0 \right) = \frac{{8\sqrt a \,\mu_{r} }}{{\eta_{\infty }^{2} }}\,G^{\prime\prime}\left( 0 \right), $$
(27)
$$ {\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} {\text{Nu}}_{x} = - 2\sqrt a k_{r} \,\theta^{\prime}\left( 0 \right) = - \frac{{2\sqrt a k_{r} }}{{\eta_{\infty } }}\,H^{\prime}\left( 0 \right). $$
(28)

3 Methodology and Validation of Results

As underlined above, the present nanofluid flow model constitutes a nonlinear case problem in the computational fluid mechanics and heat transfer areas. Also, the set of nonlinear ODEs signposted in the differential system \( \left( {S_{2} } \right) \)  besides their proper boundary conditions can be simulated numerically rather than solved analytically for sundry values of the embedded physical parameters \( \left( {\phi ,a, \varGamma } \right) \) by discretizing spatially the computational domain \( \left[ {0,1} \right] \) and adopting a powerful collocation technique based on non-uniform grid points. Hence, to accomplish this objective and get admissible physical results, the desired solutions for velocity and temperature fields can be computed numerically in terms of the functions \( G\left( \chi \right) \) and \( H\left( \chi \right) \) by resolving accurately the system \( \left( {S_{2} } \right) \) with the successful employment of the generalized differential quadrature method (GDQM) along with the modified Gauss–Lobatto collocation grid points \( \left\{ {\chi_{i} /0 \le \chi_{i} \le 1 \;{\text{and }}\;1 \le \chi_{i} \le N} \right\} \), whose spatial positions can be localized geometrically by the following expression [43, 46,47,48,49,50,51]:

$$ \chi_{i} = \frac{1}{2} - \frac{1}{2}\cos \left( {\frac{\pi i - \pi }{N - 1}} \right), $$
(29)

where \( N \) is the total number of collocation points.

For more description of the proposed numerical procedure, the readers can refer to the interesting mathematical findings reported by Shu [52], in which the numerical collocation method GDQM is well illustrated and explained through various problem situations.

After discretization, the functions \( \left\{ {G^{\prime } \left( \chi \right),G^{\prime \prime } \left( \chi \right),G^{\prime \prime \prime } \left( \chi \right),H^{\prime } \left( \chi \right),H^{\prime \prime } \left( \chi \right)} \right\} \) can then be evaluated at any collocation point \( \chi_{i} \) as:

$$ \left\{ {\begin{array}{*{20}c} {G^{\left( n \right)} \left( {\chi_{i} } \right){ = }\sum\limits_{j = 1}^{N} {d_{ij}^{\left( n \right)} \, } G_{j} } & {{\text{for}}\quad 1 \le i,j \le N,} \\ {H^{\left( n \right)} \left( {\chi_{i} } \right){ = }\sum\limits_{j = 1}^{N} {d_{ij}^{\left( n \right)} } H_{j} } & {{\text{for}}\quad 1 \le i,j \le N.} \\ \end{array} } \right. $$
(30)

Here, the superscript \( \left( n \right) \) represents the derivative order with respect to \( \chi \).

Generally, the elements \( d_{ij}^{\left( n \right)} \) used in Eq. (30) denote the weighting coefficients for the \( n{\text{th}} \)-order derivative, where \( G_{j} = G\left( {\chi_{j} } \right) \) and \( H_{j} = H\left( {\chi_{j} } \right) \). According to Shu [52], the coefficients \( d_{ij}^{\left( n \right)} \) for the first-order derivative \( \left( {{\text{i}}.{\text{e}}., n = 1} \right) \) are defined as follows:

$$ \left\{ {\begin{array}{*{20}l} {d_{ij}^{\left( 1 \right)} = \frac{{\mathop \prod \limits_{k = 1,\;k \ne i}^{N} \left( {\chi_{i} - \chi_{k} } \right)}}{{\left( {\chi_{i} - \chi_{j} } \right)\mathop \prod \limits_{k = 1,\;k \ne j}^{N} \left( {\chi_{j} - \chi_{k} } \right)}}} \hfill & {{\text{for}}\;i \ne j\;{\text{and}}\;1 \le i,\quad j \le N,} \hfill \\ {d_{ij}^{\left( 1 \right)} = - \mathop \sum \limits_{k = 1,k \ne i}^{N} d_{ik}^{\left( 1 \right)} } \hfill & {{\text{for}}\;i = j\;{\text{and}}\;1 \le i,\quad j \le N. \, } \hfill \\ \end{array} } \right. $$
(31)

As far as the evaluation of the weighting coefficients \( d_{ij}^{\left( 1 \right)} \) is concerned, the other coefficients \( d_{ij}^{\left( n \right)} \) corresponding to the higher derivative orders \( \left( {{\text{i}}.{\text{e}}., n \ge 2} \right) \) can be derived straightforwardly from \( d_{ij}^{\left( 1 \right)} \) by utilizing the following recursive expressions:

$$ \left\{ {\begin{array}{*{20}c} {d_{ij}^{\left( n \right)} = n\left( {d_{ii}^{{\left( {n - 1} \right)}} d_{ij}^{\left( 1 \right)} - \frac{{d_{ij}^{{\left( {n - 1} \right)}} }}{{\chi_{i} - \chi_{j} }}} \right)} & {{\text{for}}\quad i \ne j\;{\text{and}}\;1 \le i,\quad j \le N,} \\ {d_{ij}^{\left( n \right)} = - \mathop \sum \limits_{k = 1,k \ne i}^{N} d_{ik}^{\left( n \right)} } & {{\text{for}}\quad i = j\;{\text{and}}\;1 \le i,\quad j \le N .} \\ \end{array} } \right. $$
(32)

Accordingly, the discretized form of the differential system, \( \left( {S_{2} } \right) \) can be written in the following form:

$$ \left( {S_{3} } \right) :\;\left\{ {\begin{array}{*{20}l} {G_{1} = 0 \, } & {} \\ {\sum\limits_{j = 1}^{N} {d_{1j}^{\left( 1 \right)} } G_{j} = 0, \, } & {} \\ {L_{G} \left( {G_{i} ,H_{i} } \right) + NL_{G} \left( {G_{i} ,H_{i} } \right) + \frac{1}{2} = 0} & {{\text{for}} \; 3 \le i \le N - 1,} \\ {\sum\limits_{j = 1}^{N} {d_{Nj}^{\left( 1 \right)} } G_{j} - {{\eta_{\infty } } \mathord{\left/ {\vphantom {{\eta_{\infty } } {2 = 0, \, }}} \right. \kern-0pt} {2 = 0, \, }}} & {} \\ {H_{1} - 1 = 0, \, } & {} \\ {L_{H} \left( {G_{i} ,H_{i} } \right) + NL_{H} \left( {G_{i} ,H_{i} } \right) = 0 \, } & {{\text{for}}\;2 \le i \le N - 1,} \\ {H_{N} = 0, \, } & {} \\ \end{array} } \right. $$
(33)

where

$$ L_{G} \left( {G_{i} ,H_{i} } \right) = \frac{{8P_{1} \left( {\eta_{\infty } \chi_{i} + a} \right)}}{{\eta_{\infty }^{3} }}\left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 3 \right)} } G_{j} } \right) + \frac{{8P_{1} }}{{\eta_{\infty }^{2} }}\left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 2 \right)} } G_{j} } \right) + P_{2} \varGamma H_{i} , $$
(34)
$$ NL_{G} \left( {G_{i} ,H_{i} } \right) = \frac{4}{{\eta_{\infty }^{2} }}G_{i} \left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 2 \right)} } G_{j} } \right) - \frac{2}{{\eta_{\infty }^{2} }}\left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 1 \right)} } G_{j} } \right)\left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 1 \right)} } G_{j} } \right), $$
(35)
$$ L_{H} \left( {G_{i} ,H_{i} } \right) = \frac{{P_{3} \left( {\eta_{\infty } \chi_{i} + a} \right)}}{{\eta_{\infty }^{2} }}\,\left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 2 \right)} } H_{j} } \right) + \frac{{P_{3} }}{{\eta_{\infty } }}\,\left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 1 \right)} } H_{j} } \right), $$
(36)
$$ NL_{H} \left( {G_{i} ,H_{i} } \right) = \frac{\Pr }{{2\eta_{\infty } }}G_{i} \left( {\sum\limits_{j = 1}^{N} {d_{ij}^{\left( 1 \right)} } H_{j} } \right). $$
(37)

In order to get the desired numerical outcomes for the velocity and temperature distributions with an absolute accuracy of the order of \( 10^{ - 11} \), the resulting nonlinear algebraic system \( \left( {S_{3} } \right) \) is solved iteratively by applying the Newton–Raphson method (NRM) and taking \( \left( {\eta_{\infty } ,N} \right) = \left( {10,400} \right) \) as the greatest key values permitting to achieve the preferred convergence criterion asymptotically with a higher level of exactness.

After generating the discrete solutions \( \left\{ {\left( {G_{i} ,H_{i} } \right)/1 \le i \le N} \right\} \) accurately through the numerical procedures GDQM and NRM, correspondingly, the reduced engineering quantities \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x}} \) and \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \) described by Eqs. (27) and (28) can be deduced numerically as follows:

$$ \text{Re}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} C_{{{\text{f}}x}} = \frac{{8\sqrt a \,\mu_{r} }}{{\eta_{\infty }^{2} }}\,\left( {\sum\limits_{j = 1}^{N} {d_{1j}^{\left( 2 \right)} } G_{j} } \right), $$
(38)
$$ {\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} {\text{Nu}}_{x} = - \frac{{2\sqrt a k_{r} }}{{\eta_{\infty } }}\,\left( {\sum\limits_{j = 1}^{N} {d_{1j}^{\left( 1 \right)} } H_{j} } \right). $$
(39)

Also, the discretized forms \( \big\{ \big( {f^{\prime}\left( {\eta_{i} } \right),\theta \left( {\eta_{i} } \right)} \big)/0 \le \eta_{i} \le \eta_{\infty } \big\} \) of the dimensionless velocity and temperature fields \( \left\{ {f^{\prime}\left( \eta \right),\theta \left( \eta \right)} \right\} \) can be deduced as follows:

$$ f^{\prime } \left( {\eta_{i} } \right) = \frac{{\sum\nolimits_{j = 1}^{N} {d_{ij}^{\left( 1 \right)} \, } G_{j} }}{{\eta_{\infty } }}, $$
(40)
$$ \theta \left( {\eta_{i} } \right) = H_{i} , $$
(41)

where \( \eta_{i} = \eta_{\infty } \chi_{i} \) and \( 1 \le i \le N \).

In order to authenticate the physical significance of the resulting boundary layer flow upshots generated by the proposed GDQM code’s execution, multiple numerical implementations of various testing comparisons with Chen and Smith [37], Grosan and Pop [53] and Trimbitas et al. [54] are carried out successfully for the reduced engineering quantities \( \left\{ {f^{\prime\prime}\left( a \right),\theta^{\prime}\left( a \right)} \right\} \) as shown in Tables 2, 3 and 4. A thorough analysis of these tabular results proves obviously that the differential quadrature outcomes are at a reasonable level of agreement with the existing results testified in [37, 53, 54].

Table 2 Comparison of our numerical results for \( f^{\prime\prime}\left( a \right) \) with those of the literature for various values of \( a \), when \( \varGamma = 0 \)
Full size table
Table 3 Comparison of our numerical results for \( \theta^{\prime}\left( a \right) \) with those of the literature for various values of \( { \Pr } \), when \( \varGamma = 0 \) and \( a = 0.1 \)
Full size table
Table 4 Comparison of our numerical results for \( \theta^{\prime}\left( a \right) \) with those of the literature, for various values of \( a \), when \( \varGamma = 0 \) and \( { \Pr } = 0.733 \)
Full size table

4 Results and Discussion

Herein, we are concerned with addressing the comportments of the dimensionless velocity and temperature fields as well as the trends of skin friction coefficient and Nusselt number against any variation in the involved physical parameters, namely the volume fraction of nanoparticles \( \phi \), the needle size \( a \) and the mixed convection parameter \( \varGamma \). For that reason, our main focus in the plotted Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 is to scrutinize the behavior of each embedded parameter toward the development of steady laminar mixed convection of various kinds of metallic- and metallic oxide-based nanofluids flowing over an impermeable and isothermal thin needle in a variable external stream. Effectively, to realize such an objective, in which the water \( \left( {{\text{H}}_{2} {\text{O}}} \right) \) and ethylene glycol \( \left( {{\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} } \right) \) are used as appropriate base fluids for the nanomaterials \( {\text{Al}} \), \( {\text{Cu}} \), \( {\text{Zn}} \), \( {\text{Al}}_{2} {\text{O}}_{3} \), \( {\text{CuO}} \) and \( {\text{ZnO}} \).

Fig. 2
figure 2

Effect of \( \phi \) on \( f^{\prime}\left( \eta \right) \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

Figure 2 describes the behavior of velocity fields \( \left\{ {\left( {\eta_{i} ,f^{\prime}\left( {\eta_{i} } \right)} \right)/0 \le \eta_{i} \le \eta_{\infty } } \right\} \) for copper–water-based nanofluids (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)) and copper–ethylene glycol-based nanofluids (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) in response to different volume fractions \( \phi \) at a fixed needle size \( \left( {a = 10^{ - 2} } \right) \) and mixed convection parameter \( \left( {\varGamma = 1} \right) \). From this graphical representation, it is noted that an increase in the volume fraction yields a minor boost in the flow velocity for both metallic nanofluids (i.e., \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)), which leads to a slight shrink in the velocity boundary layer region. In fact, these dynamical findings prove that the nanofluid velocity grows sharply near the needle surface and then rises asymptotically far from the needle wall to reach locally the dimensionless value of the free stream velocity \( f^{\prime}\left( {\eta \to \eta_{\infty } } \right) = 1/2 \). In other words, velocity profiles show an increasing trend with respect to the similarity variable \( \eta \) as we go away from the needle surface. Physically, it is well known that the nanoparticle loading leads to a significant increasing trend in the wall velocity gradient and leading thereafter to more contact with the needle surface. This tendency can be explained by the increasing trend of the effective values of dynamic viscosity and density of metallic/metallic oxide nanofluids toward the volume fraction of nanoparticles, which provokes a non-negligible change in the nanofluid velocity distribution throughout the nanofluidic medium.

Basically, the dynamical evolution of velocity profiles due to the increment in the needle size \( a \) is represented visibly in Fig. 3. As a first remark, it is perceived that the arisen attenuation in the nanofluid flow velocity can be controlled properly by adjusting increasingly the value of the needle size \( a \) of both metallic nanofluids \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), when the other governing parameters are fixed at \( \phi = 0.01 \) and \( \varGamma = 5 \) as demonstrated graphically in the aforesaid illustration. Secondly, this slowdown has an enlarging impact on the velocity boundary layer thickness. The basis of such a declining trend is explicated by the augmentation in the contact surface between the thin needle and the surrounding water–ethylene glycol-based nanofluid as long as the thin needle size \( a \) is heightened discretely from \( 10^{ - 2} \) to \( 0.2 \). On the other hand, it now turns out that the geometrical parameter \( a \) acts as a drag force that strengthens thereby the decline in the nanofluid flow velocity.

Fig. 3
figure 3

Effect of \( a \) on \( f^{\prime}\left( \eta \right) \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

For both metallic nanofluids \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), it is evidently revealed from Fig. 4 that the intensification in the mixed convection parameter \( \varGamma \) contributes significantly to a hastening in the mounting tendency of the nanofluid velocity once the volume fraction \( \phi \) and the needle size parameter \( a \) are fixed at \( \phi = 0.01 \) and \( a = 0.1 \). Besides, it is worth pointing out that the relevant physical quantity \( \varGamma \) defined by Eq. (19) represents rather the ratio of the local thermal Grashof number \( {\text{Gr}}_{x} \) to the squared value of the local Reynolds number \( {\text{Re}}_{x} \). This non-local parameter plays an important role in the quantification of the effective dominance of either the natural convection process or the forced convection heat transport. Generally, it is noticed graphically that the larger values of the mixed convection parameter \( \varGamma \) yield a greater enhancement in the free convection heat transfer process. Physically, this increasing thermal behavior of the parameter \( \varGamma \) is responsible for speeding up the nanofluid velocity because of the rapid intensification in the thermal buoyancy forces. The present physical findings emphasize that the nanofluid velocity profiles schemed for copper–water-based nanofluids (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)) show an exceptional dynamical feature compared to those of the copper–ethylene glycol-based nanofluids (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)), in which the metallic nanofluid velocity near the needle surface becomes higher than the free stream velocity \( \left( {{\text{i}}.{\text{e}}.,f^{\prime}\left( \eta \right) > 1/2} \right) \) as witnessed graphically in Fig. 4. Moreover, the visualization of two comparative velocity profiles proves that the velocity profiles of \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) comprise multiple expanded overshoots near the needle surface, while those ascertainments are not seen in the velocity profiles of \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \). Further, the peaks observed in the velocity profiles of \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) for the higher values of the mixed convection parameter \( \varGamma \) (e.g., 20, 50, 100) exhibit a heightening trend with the elevation in the parameter \( \varGamma \), indicating that the maximum value of velocity decreases as moving away from the needle surface. Furthermore, it is worth mentioning here that the velocity profiles of \( Cu \)–\( C_{2} H_{6} O_{2} \) point out a significantly increasing tendency with the increasing values of the parameter \( \varGamma \). However, this augmenting feature still tiny compared with the results depicted for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \), due to the higher dynamic viscosity of ethylene glycol \( \left( {C_{2} H_{6} O_{2} } \right) \).

Fig. 4
figure 4

Effect of \( \varGamma \) on \( f^{\prime}\left( \eta \right) \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

It is worth noticing that Fig. 5 is portrayed to explain not merely the thermal behavior of \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) but also to compare this physical feature with that of \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), when the volume fraction \( \phi \) of \( {\text{Cu}} \) nanoparticles is varied increasingly from 0 to 0.2 and the other controlling parameters are maintained fixed at \( a = 10^{ - 2} \) and \( \varGamma = 1 \). Clearly, it is revealed that the temperature distribution of both metallic nanofluids underlines a noticeable augmentation with the rise in the volume fraction \( \phi \), due to the enhancement in thermal conductivity of the homogeneous mixture (i.e., nanoparticles + base fluid). Consequently, this fact leads to a large thickening in the thermal boundary layer region of \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) compared with that of \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \).

Fig. 5
figure 5

Effect of \( \phi \) on \( \theta \left( \eta \right) \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

In another context, the graphical results represented in Fig. 6 clarified that the nanofluid temperature throughout the thermal boundary layer region can also be enriched considerably just by augmenting slightly the needle size \( a \), so as the values of both parameters \( \phi \) and \( \varGamma \) still unaffected and kept fixed at \( \phi = 0.01 \) and \( \varGamma = 5 \). Accordingly, a larger thermal boundary layer thickness is detected for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \) with the escalating values of the parameter \( a \). However, the temperature increment rate near the needle surface is more pronounced for \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \) compared with that of \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \).

Fig. 6
figure 6

Effect of \( a \) on \( \theta \left( \eta \right) \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

Furtherly, Fig. 7 is plotted to interpret the thermal impact of the increasing values of the mixed convection parameter \( \varGamma \) toward the temperature distribution in a homogeneous medium characterized by \( \phi = 0.01 \) and \( a = 0.1 \) and comprised metallic nanofluids, such as \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \). Unlike the thermal tendency of both parameters \( \phi \) and \( a \), it is found that the nanofluid temperature reduces with the rising values of the mixed convection parameter \( \varGamma \). Due reverse behavior is due to the intensification in the thermal buoyancy forces, which act as a driving factor for the metallic nanofluid flows and their heat transfer characteristics. In addition, the thermal boundary layer exhibits a prompt drop in the thickness with the higher values of the control parameter \( \varGamma \). Accordingly, the heat transfer rate at the needle surface will favorably be affected by the increasing values of \( \varGamma \). These physical happenings are analyzed in detail with the aid of further graphical results.

Fig. 7
figure 7

Effect of \( \varGamma \) on \( \theta \left( \eta \right) \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

The noteworthy influence of the needle size \( a \) on the reduced skin friction coefficient \( {\text{Re}}_{x}^{1/2} C_{fx} \) against continuous values of the volume fraction \( \phi \) of \( {\text{Cu}} \) nanoparticles is displayed graphically in Fig. 8 for copper–water (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)) and copper–ethylene glycol (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) metallic nanofluids. Apparently, the physical quantity of interest \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x}} \) discloses a faster-declining trend with the progressive incrementation in the needle size \( a \) because of the resulting hydrodynamic resistance, which prevents the nanofluid flow to take place in the medium. For this reason, the nanofluid velocity slows down with the widening of the contact areas between the needle surface and the adjacent nanofluidic medium. However, the reduced engineering quantity \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x }} \) shows an opposite tendency with respect to the increasing values of the volume fraction \( \phi \), indicating that the presence of \( {\text{Cu}} \) nanoparticles in a fluidic medium including water \( \left( {{\text{H}}_{2} {\text{O}}} \right) \) or copper–ethylene glycol \( \left( {{\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} } \right) \) has a strengthening impact on the surface drag forces. On the contrary, it is recorded from Fig. 9 that the increasing adjustment of the mixed convection parameter \( \varGamma \) can be considered as an interesting gateway for escalating the wall shear stress, whose magnitude is generally greater for copper–water (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)) than for copper–ethylene glycol (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)).

Fig. 8
figure 8

Effect of \( a \) on \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x}} \) against continuous values of \( \phi \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image
Fig. 9
figure 9

Effect of \( \varGamma \) on \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x}} \) against continuous values of \( \phi \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

The heat transfer features of copper–water (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)) and copper–ethylene glycol (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) metallic nanofluids against varying values of the needle size \( a \) and diversified solid volume fractions \( \phi \) are divulged more evidently in Fig. 10 in terms of the reduced local Nusselt number \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \). Based on the obtained graphical results, it is asserted that any improvement in the heat transfer rate at the needle surface can be achieved straightforwardly either by reducing the needle size \( a \) or by augmenting the volume fraction \( \phi \) of \( {\text{Cu}} \) nanoparticles. However, the heat transfer behavior of \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \) elucidated in Fig. 11 shows a reverse characteristic in response to diverse values of the mixed convection parameter \( \varGamma \) compared to the previous situation, so as any deep reinforcement applied to the mixed convection parameter \( \varGamma \) permits to accomplish a prominent enhancement effect on the local wall heat transfer rate. Consequently, the thermal buoyancy forces speed up the motion of metallic nanofluids. Henceforth, these convection forces exhibit a strengthening effect on the heat transfer rate at the needle surface. Also, it is concluded that the copper–ethylene glycol-based nanofluids (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \) show an interesting thermal performance compared with that of the copper–water-based nanofluids (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)).

Fig. 10
figure 10

Effect of \( a \) on \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \) against continuous values of \( \phi \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image
Fig. 11
figure 11

Effect of \( \varGamma \) on \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \) against continuous values of \( \phi \) for \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) and \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)

Full size image

As shown below, Table 5 summarizes the proper values of the reduced local skin friction coefficient \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x}} \) derived numerically for several metallic nanofluids (\( {\text{Al}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Al}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Zn}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Zn}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) and metallic oxide nanofluids (\( {\text{Al}}_{2} {\text{O}}_{3} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Al}}_{ 2} {\text{O}}_{3} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{CuO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{CuO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{ZnO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{ZnO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) against diverse values of the solid volume fraction \( \phi \). Generally, it is proved from this tabular demonstration that an increase in the solid volume fraction \( \phi \) strengthens the resulting values of the physical quantity \( Re_{x}^{1/2} C_{fx} \) (i.e., the wall shear stress) for the above-declared metallic as well as metallic oxide nanofluids. So, the skin friction coefficient is an increasing function of the solid volume fraction \( \phi \). Based on the slope linear regression method (SLRM) suggested by Shah et al. [55], it is revealed that the rate of increase in the local skin friction that due to an increase in the volume fraction \( Slp \) is maximum in the flow of \( {\text{Zn}} \)–\( {\text{H}}_{2} {\text{O}} \), which is nearly of \( S = 20.3869 \), while a minimum increase occurs in the flow of \( {\text{Al}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \) with an average characteristic slope of about \( S = 11.6945 \).

Table 5 Skin friction characteristics for various metallic and metallic oxide nanofluids in response to different solid volume fractions \( \phi \)
Full size table

Furthermore, Table 6 recapitulates the various numerical outcomes arising from the reduced local Nusselt number \( Re_{x}^{ - 1/2} Nu_{x} \) of various metallic nanofluids (\( {\text{Al}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Al}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{Zn}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Zn}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) and metallic oxide nanofluids (\( {\text{Al}}_{2} {\text{O}}_{3} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{Al}}_{ 2} {\text{O}}_{3} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{CuO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{CuO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \), \( {\text{ZnO}} \)–\( {\text{H}}_{2} {\text{O}} \), \( {\text{ZnO}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) against varying values of the solid volume fractions \( \phi \). From the thermal effectiveness point of view, it is worth highlighting that the rise in the solid volume fraction \( \phi \) elevates meaningfully the heat transfer rate for both above-mentioned metallic and metallic oxide nanofluids. So, the physical quantity of interest \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \) is an increasing function of the solid volume fraction \( \phi \). Also, it is found that the maximum rate of increase in the involved thermal quantity \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \) due to an increase in the solid volume fraction \( \phi \) is ascertained in the flow of \( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \) with an estimated slope reaching the typical value \( S = 13.0189 \). However, this rate shows the tiniest increase in the flow of \( {\text{ZnO}} \)–\( {\text{H}}_{2} {\text{O}} \) with an approximate slope of \( S = 4.3721 \).

Table 6 Heat transfer characteristics for various metallic and metallic oxide nanofluids in response to different solid volume fractions \( \phi \)
Full size table

5 Concluding Remarks

In this study, the mixed convection heat transfer features of the laminar flows of some Newtonian metallic/metallic oxide nanofluids along a vertical isothermal thin needle have been investigated numerically using a robust quadrature algorithm GDQM-NRM for water \( \left( {{\text{H}}_{2} {\text{O}}} \right) \)–ethylene glycol \( \left( {{\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} } \right) \)-based nanofluids conveying various metallic nanoparticles (e.g., \( {\text{Al}} \), \( {\text{Cu}} \), \( {\text{Zn}} \)) and metallic oxide nanomaterials (e.g., \( {\text{Al}}_{2} {\text{O}}_{3} \), \( {\text{CuO}} \), \( {\text{ZnO}} \)). In summary, the major outcomes of the present investigation are itemized as follows:

  • Greater values of the needle size \( a \) permit to slow down the motion metallic and metallic oxide nanofluids.

  • Generally, the velocity boundary layer thickness is an increasing function with the needle size.

  • An augmentation in the solid volume fraction \( \phi \) promotes the motion of metallic and metallic oxide and then leads to a squeeze in the velocity boundary layer.

  • Copper–water-based nanofluids (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)) exhibit a distinctive dynamical behavior compared with copper–ethylene glycol-based nanofluids (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) in their velocity profiles.

  • Velocity peaks appeared in the profiles of \( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \) will get lowered thereafter, indicating that the maximum velocity declines as moving away from the surface of the needle surface.

  • Copper–water-based nanofluids (\( {\text{Cu}} \)–\( {\text{H}}_{2} {\text{O}} \)) have a significantly increasing tendency toward their velocity profiles unlike the features of copper–ethylene glycol-based nanofluids (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)).

  • Nanofluid temperature can be elevated either by rising the solid volume fraction \( \phi \) and the needle size \( a \) or by diminishing the mixed convection parameter \( \varGamma \).

  • Local skin friction coefficient and heat transfer rate characteristics disclose a remarkable drop due to the increment in the needle size \( a \), while a reverse trend is visualized in response to the solid volume fraction \( \phi \) and the mixed convection parameter \( \varGamma \).

  • Compared with the other metallic and metallic oxide nanofluids, zinc–water-based nanofluids (\( {\text{Zn}} \)–\( {\text{H}}_{2} {\text{O}} \)) show the maximum rate of increase in the physical quantity \( {\text{Re}}_{x}^{1/2} C_{{{\text{f}}x}} \) with respect to the \( Zn \) nanomaterial loading.

  • Among the other metallic and metallic oxide nanofluids, copper–ethylene glycol-based nanofluids (\( {\text{Cu}} \)–\( {\text{C}}_{2} {\text{H}}_{6} {\text{O}}_{2} \)) exhibit the highest rate of enhancement in the thermal quantity \( {\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} \) with respect to the \( {\text{Cu}} \) nanoparticle loading.