Introduction

The problem of impinging flow over a porous foam has received a sustained attention in engineering literature [1,2,3,4]. This is due to the wide application of this flow configuration in heat sinks [5] and chemical reactors [6]. In particular, the use of stagnation-point flows over surfaces covered by a porous medium is common in catalytic chemical reactors [7, 8]. Since temperature and concentration of species have pronounced effects upon the performance of catalytic reactors, accurate prediction of these quantities is of primary importance in reactor design. For heterogenous catalysts covered by porous inserts, this requires precise analysis of transport phenomena in the porous medium through considering the combined modes of heat and mass transfer.

The basic problem of convective heat transfer in a porous foam placed on a flat solid surface and subject to an impinging flow has been studied extensively, e.g. [9,10,11]. For conciseness reasons, here, those studies are not reviewed, and the reader is referred to the previous works of the authors for comprehensive reviews of the literature [12,13,14]. It is, nonetheless, emphasised that most previous investigations of stagnation-point flow through porous media assumed local thermal equilibrium in porous media, see, for example, [15,16,17]. This assumption although offering a mathematical convenience can jeopardise the accuracy of analysis in porous media that include chemical reactions [18, 19]. Therefore, the less restrictive assumption of local thermal non-equilibrium should be in place, instead. This requires addition of two energy equations for the solid and fluid phases of the porous medium and thus makes the problem mathematically involved. Such analysis was conducted by Jang and Tzeng [20], who considered impinging cooling of porous metallic foam heat sink under local thermal non-equilibrium. These authors found that implementation of a highly porous foam can boost the heat transfer from the flat plate by a factor of two or three [20]. In a subsequent work, the same group of authors repeated the analysis experimentally and confirmed their numerical findings [21]. Later, Wong and Saeid [22] advanced this heat transfer study through inclusion of buoyancy effects and considering mixed convection in their numerical investigation. They conducted an extensive parametric study and showed that thermal conductivity ratio and Biot number in the porous medium are the key parameters for maintaining the system under local thermal equilibrium [22]. The results of Wong and Saeid further indicated that increasing the porosity of the metal foam can lead to higher values of Nusselt number. Later, Wong used a similar numerical setting in an experimental and numerical study of impinging flow on a porous block and demonstrated an overall similarity between the experimentally recorded and computationally predicted temperature fields [23]. The same problem under turbulent flow regime was investigated numerically by Hwang and Yang [24], who reported that the qualitative trends in heat transfer behaviour of the system are similar to that under laminar flow.

Currently, there exist several studies on mixed convection in stagnation-point flow in porous media. Marafie et al. [25] conducted a numerical work on this problem by applying a finite element technique. In keeping with Jang and Tzeng [20], Marafie et al. [25] showed that addition of the impinging flow enhances the rate of heat transfer by more than two times. These authors showed that there is a critical height of the porous block. Thickening the porous block prior to reaching the critical height results in increasing the Nusselt number. However, further thickening of the block beyond the critical thickness leads to reduction of Nusselt number [25]. Harris et al. [26] presented a similarity analysis of the boundary layer flows at the stagnation-point upon a porous block located vertically. A computational study about mixed convection in jet flows over a porous insert showed that increases in Reynolds number and jet width render higher values of the mean Nusselt number [27]. It was further demonstrated that Nusselt number is enhanced by reducing the gap between the impinging flow and the heated part [27].

In the work of Kokubun and Fachini [3], an analytical solution was presented for the impinging flows over an infinitely long, horizontally positioned porous plate, experiencing different types of thermal boundary conditions. This investigation revealed that a dimensionless parameter, involving information about the transfer characteristics of the fluid and porous solid, governs the process of heat transfer. A numerical and experimental study was conducted by Feng et al. [5] on the problem of stagnation-point flow over a heated porous plate. They investigated a metal porous medium and a finned metal foam and showed that increases in the metal foam thickness reduce the heat transfer coefficient. However, such trend was not observed for the metal finned foam [5]. In a relatively recent study, Buonomo et al. [28] analysed the heat transfer process as a laminar jet vertically interacts with a horizontal, confined porous plate in an axisymmetric setting. Buonomo et al. [28] showed that Peclet number dominates the assisting and opposing configurations of free and forced convection. Makinde [29] and Rosca and Pop [30] examined mixed convection in stagnation-point flows impinging on a vertical porous plate. Magnetic effects and radiation of heat were also included in the analysis of mixed convection inside vertical, porous inserts [31]. An important common point in almost all studies on mixed convection in porous media is consideration of flat porous plates, and thus, curved porous configurations have been rarely investigated.

Nonlinear convection was included in a recent numerical work by Qayyum et al. [32], who analysed the nonlinear convection of a nanofluid over a heated stretching surface. Nonlinearity was included in the problem by considering nonlinear temperature and concentration terms in the form of \(\left( {T - T_{\infty } } \right)^{2}\) and \(\left( {C - C_{\infty } } \right)^{2}\) in the buoyancy term of momentum equation. Similar studies were conducted by Qayyum et al. [33] and Hayat et al. [34], who further included a heat source that was linearly dependent upon the fluid temperature. It is essential to note that the works of Qayyum et al. [32, 33] and Hayat et al. [34] were not concerned with flows inside porous media. Other recent investigations of nonlinear convection in boundary layer flows include those of Hayat et al. [35] and Khan et al. [36]. It appears that currently there is no study on nonlinear convection in porous media.

The present study aims to fill the gaps identified in the preceding review of the literature. Towards this goal, nonlinear mixed convection of heat and mass in a stagnation-point flow developed over a cylinder embedded in porous media is investigated numerically. To establish a direct connection to catalytic chemical reactors, it is assumed that a simple surface reaction takes place at the external surface of the cylinder.

Theoretical and numerical methods

Configuration of the problem, governing equations and assumptions

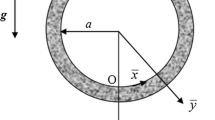
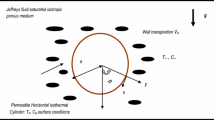
A schematic of the problem under investigation is shown in Fig. 1. A cylinder with radius a centred at \(r = 0\) has been coated by a catalyst and embedded in a porous medium. Surface temperature on the external wall of the cylinder is maintained constant. The external flow over the cylinder includes an axisymmetric radial stagnation-point flow with the strain rate of \(\bar{k}\). The current analysis considers the following assumptions.

Fig. 1
figure 1

Schematics of the investigated problem: a vertical cylinder embedded in porous media under radial stagnation flow

Full size image

  • The fluid flow is under steady-state condition. It is also laminar and incompressible, while the cylinder is infinitely long and features zero permeability.

  • The catalytic reactions on the surface of the cylinder are temperature independent and of zeroth order [37,38,39].

  • Soret and Dufour effects on the transport of heat and mass are taken into account.

  • The porous medium around the cylinder is under local thermal non-equilibrium (LTNE) and is also homogenous and isotropic.

  • Thermal radiation and frictional dissipation of the flow kinetic energy are ignored. However, gravitational effects and nonlinear convection of heat and mass are considered.

  • Density and heat conductivity as well as porosity and specific heat capacities are constant. As a result, the thermal dispersion in the porous medium is negligibly small.

  • Pore-scale Reynolds number is moderate, and therefore, Forchheimer term in the model of momentum transfer is ignored.

It is clarified that zeroth-order surface reactions are often used to approximate the kinetics of many catalytic reactions [40]. Hence, they are of practical importance.

Assuming a nonlinear, double-diffusive mixed convection and by employing a cylindrical coordinate, the governing equations and boundary conditions can be written in the following forms.

The conservation of mass is as follows:

$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0.$$
(1)

Momentum transfer in the radial direction is governed by

$$\frac{1}{{\varepsilon^{2} }}\left( {u\frac{\partial u}{\partial r} + w\frac{\partial u}{\partial z}} \right) = - \frac{1}{\rho }\frac{\partial p}{\partial r} + \frac{\upsilon }{\varepsilon }\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r} - \frac{u}{{r^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }} } \right) - \frac{\upsilon }{{k_{1} }}u,$$
(2)

and that in the axial direction, it is given by [35, 36]

$$\begin{aligned} & \frac{1}{{\varepsilon^{2} }}\left( {u\frac{\partial w}{\partial r} + w\frac{\partial w}{\partial z}} \right) = - \frac{1}{\rho }\frac{\partial p}{\partial z} + \frac{\upsilon }{\varepsilon }\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} w}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }} } \right) \mp g\left[ {\beta_{1} \left( {T_{\text{f}} - T_{\infty } } \right) + \beta_{2} \left( {T_{\text{f}} - T_{\infty } } \right)^{2} } \right] \\ & \quad + g\left[ {\beta_{3} \left( {C - C_{\infty } } \right) + \beta_{4} \left( {C - C_{\infty } } \right)^{2} } \right] - \frac{\upsilon }{{k_{1} }}w. \\ \end{aligned}$$
(3)

Equation (3) includes the nonlinear terms appearing as body forces on the right-hand side. The transfer of heat in the fluid phase reduces to

$$\begin{aligned} & u\frac{{\partial T_{\text{f}} }}{\partial r} + w\frac{{\partial T_{\text{f}} }}{\partial z} = \alpha_{\text{f}} \left( {\frac{{\partial^{2} T_{\text{f}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{f}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{f}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{f}} }}{{\partial z^{2} }} } \right) + \frac{{h_{\text{sf}} \cdot a_{\text{sf}} }}{{\rho \cdot C_{\text{p}} }}\left( {T_{\text{s}} - T_{\text{f}} } \right) \\ & \quad + \frac{{D k_{\text{T}} }}{{C_{\text{s}} \cdot C_{\text{p}} }}\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} C}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} C}}{{\partial z^{2} }} } \right). \\ \end{aligned}$$
(4)

The last term on the left-hand side of Eq. (4) denotes Dufour effect [37, 38]. The transfer of heat in the solid phase of the porous medium is expressed by

$$k_{\text{s}} \left( {\frac{{\partial^{2} T_{\text{s}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{s}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{s}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{s}} }}{{\partial z^{2} }} } \right) - h_{\text{sf}} \cdot a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) + \left[ {Q_{1} \left( {T_{\text{s}} - T_{\infty } } \right) + Q_{2} \left( {T_{\text{s}} - T_{\infty } } \right)^{2} } \right] = 0.$$
(5)

The following equation governs the transport of chemical species throughout the porous medium in which the thermal diffusion of mass (Soret effect) has been considered [38, 39]:

$$u\frac{\partial C}{\partial r} + w\frac{\partial C}{\partial z} = D\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} C}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} C}}{{\partial z^{2} }} } \right) + \frac{{D k_{\text{T}} }}{{ T_{\text{m}} }}\left( {\frac{{\partial^{2} T_{\text{f}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{f}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{f}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{f}} }}{{\partial z^{2} }} } \right).$$
(6)

In Eqs. (4–6), the subscripts “f” and “s” denote the fluid and solid phase of the porous medium, respectively.

The boundary conditions of momentum equations are given as follows.

$$r = a: \;\;w = 0,\;\;u = 0,$$
(7)
$$r = \infty : \; w = 2\bar{k}z , \;\; u = - \bar{k}\left( {r - \frac{{a^{2} }}{r}} \right),$$
(8)

The no-slip condition over the external wall of the cylinder is represented by Eq. (7). Further, Eq. (8) implies that the solution of viscous flow behaves similar to that for Hiemenz flow, the potential flow solution as \(r \to \infty\) [41,42,43]. This can be verified by starting from the continuity equation in the followings. \(- \frac{1}{r}\frac{\partial (ru)}{\partial r} = \frac{\partial w}{\partial z}{\text{Constant}} = 2\bar{k}z\), and integrating in \(r\) and \(z\) directions with boundary conditions, \(w = 0\) when \(z = 0\) and \(u = 0\) when \(r = a\).

The boundary conditions for the transport of thermal energy are given by

$$\begin{aligned} r = a{:} \;\; T_{\text{f}} & = T_{\text{w}} = {\text{Constant}}, \\ T_{\text{s}} & = T_{\text{w}} = {\text{Constant}}, \\ \end{aligned}$$
(9)
$$\begin{aligned} r = \infty{:} \;\; T_{\text{f}} & = T_{\infty } , \\ T_{\text{s}} & = T_{\infty } , \\ \end{aligned}$$

where \(T_{\text{w}}\) is the temperature of the surface of cylinder and \(T_{\infty }\) is that of the freestream flow.

The boundary condition for mass transfer is given by

$$\begin{aligned} r & = a{:}\;\; \frac{\partial C}{\partial r} = - \frac{{k_{\text{R}} }}{D} = {\text{Constant}}, \\ r & = \infty{:} \;\; C \to C_{\infty } \\ \end{aligned}$$
(10)

where \(D\) is the Fickian diffusion coefficient, \(k_{\text{R}}\) is the kinetic constant pertinent to a zeroth-order heterogenous reaction [38, 39], and \(C_{\infty }\) denotes the concentration of species in the freestream.

Self-similar analysis

The governing Eqs. (1–6) are reduced by applying the following similarity transformations.

$$u = - \frac{{\bar{k} \cdot a}}{\sqrt \eta }f(\eta ),\quad w = \left[ {2\bar{k}f^{\prime } (\eta )} \right]z,\quad p = \rho_{\text{f}} \bar{k}^{2} a^{2} P,$$
(11)

where \(\eta = \left( {\frac{r}{a}} \right)^{2}\) is the non-dimensional radial variable. Relations (11) satisfy the continuity of mass [Eq. (1)], and substitution into momentum equations [Eqs. (2), (3)] renders the following system of coupled, ordinary differential equations.

$$\left[ {\eta f ^{\prime \prime \prime } + f ^{\prime \prime } } \right] + \frac{1}{{\varepsilon^{2} }}{\text{Re}}\left[ {1 + ff ^{\prime } - \left( {f ^{\prime } } \right)^{2} } \right] + \lambda \left[ {1 - f ^{\prime } } \right] \mp \lambda_{1} \theta_{\text{f}} \left[ {1 + \beta_{\text{t}} \cdot \theta_{\text{f}} } \right] + \lambda_{1} \cdot N^{*} \cdot \phi \left[ {1 + \beta_{\text{C}} \cdot \phi } \right] = 0,$$
(12)
$$P - P_{0} = - \frac{1}{{2\varepsilon^{2} }}\left( {\frac{{f^{2} }}{\eta }} \right) - \frac{1}{\varepsilon }\left[ {\left( {\frac{{f ^{\prime } }}{\text{Re}}} \right) + \frac{\lambda }{\text{Re}}\mathop \smallint \limits_{1}^{\eta } \frac{f}{\eta }{\text{d}}\eta } \right] - 2\left[ {\frac{1}{{\varepsilon^{2} }} + \frac{\lambda }{\text{Re}}} \right]\left( {\frac{z}{a}} \right)^{2} ,$$
(13)

where \({\text{Re}} = \frac{{\bar{k} \cdot a^{2} }}{2\upsilon }\) shows the Reynolds number of the freestream, \(\lambda = \frac{{a^{2} }}{{4k_{1} }}\) is the permeability parameter, \(\lambda_{1} = \frac{\text{Gr}}{{\text{Re}^{2} }} = \frac{{g \cdot \beta_{1} (T_{\text{w}} - T_{\infty } )}}{{4a\bar{k}^{2} }}\) is the dimensionless mixed convection parameter, \(\beta_{\text{t}} = \frac{{\beta_{2} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{\beta_{1} }}\) is the nonlinear mixed convection parameter for temperature, \(\beta_{\text{C}} = \frac{{\beta_{4} \cdot C_{\infty } }}{{\beta_{3} }}\) denotes the nonlinear mixed convection parameter for concentration, \(N^{*} = \frac{{\beta_{3} \cdot C_{\infty } }}{{\beta_{1} \left( {T_{\text{w}} - T_{\infty } } \right)}}\) represents the ratio of concentration to thermal buoyancy forces, and prime represents the differentiation with respect to the radial variable \(\eta\).

Considering the transport of momentum, the boundary conditions for Eq. (12) reduce to

$$\eta = 1{:} \;\; f^{\prime } (1) = 0,\;\;f(1) = 0,$$
(14)
$$\eta \to \infty{:} \;\;f^{\prime } (\infty ) = 1.$$
(15)

The following transformation is introduced [43, 44], to non-dimensionalise the energy equation,

$$\theta_{\text{f}} (\eta ) = \frac{{T_{\text{f}} (\eta ) - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}.$$
(16)

By substituting Eqs. (11) and (16) into Eq. (4) and through ignoring the dissipation terms, the following relation is developed

$$\eta \theta^{\prime \prime }_{\text{f}} + \theta^{\prime }_{\text{f}} + {\text{Re}} \cdot { \Pr } \cdot \left( {f \cdot \theta^{\prime }_{\text{f}} } \right) + {\text{Bi}}\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right) + {\text{Df}} \cdot { \Pr }\left[ {\eta \phi^{\prime \prime } + \phi^{\prime } } \right] = 0 ,$$
(17)

where \({\text{Bi}} = \frac{{h_{\text{sf}} a_{\text{sf}} \cdot a}}{{4k_{\text{f}} }}\) is the Biot number and \({\text{Df}} = \frac{{D \cdot k_{\text{T}} }}{{C_{\text{s}} \cdot C_{\text{p}} }}\frac{{C_{\infty } }}{{\left( {T_{\text{w}} - T_{\infty } } \right)\upsilon }}\) is the Dufour number, and the pertinent boundary conditions can be written as:

$$\eta = 1{:}\;\; \theta_{\text{f}} (1) = 1$$
(18a)
$$\eta \to \infty{:} \;\; \theta_{\text{f}} (\infty ) = 0$$
(18b)

Substitution of Eqs. (11) and (16) into Eq. (5) results in

$$\eta \theta ^{\prime \prime }_{\text{s}} + \theta^{\prime }_{\text{s}} - {\text{Bi}} \cdot \gamma \left( {\theta_{\text{s}} - \theta_{\text{f}} } \right) + Q_{\text{h}} \cdot \gamma \cdot \theta_{\text{s}} \left[ {1 + \beta_{\text{h}} \cdot \theta_{\text{s}} } \right] = 0,$$
(19)

where \(\gamma = \frac{{k_{\text{f}} }}{{k_{\text{s}} }}\) is the modified conductivity ratio, \(Q_{\text{h}} = \frac{{Q_{1} a^{2} }}{{4k_{\text{f}} }}\) denotes the heat source parameter, and \(\beta_{\text{h}} = \frac{{Q_{2} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{Q_{1} }}\) is the nonlinear heat source parameter, while the boundary conditions are expressed by:

$$\eta = 1{:}\;\; \theta_{s} (1) = 1$$
(20a)
$$\eta \to \infty{:}\;\; \theta_{\text{s}} (\infty ) = 0$$
(20b)

Transformation (21) is used, to non-dimensionalise the mass transfer Eq. (6),

$$\phi (\eta ) = \frac{{C(\eta ) - C_{\infty } }}{{C_{\infty } }}.$$
(21)

By substituting Eqs. (14) and (16) into Eq. (6), the following equation is developed

$${ \Pr }\left[ {\eta \phi^{\prime \prime } + \phi^{\prime } } \right] + {\text{Sr}} \cdot {\text{Sc}}\left[ {\eta \theta^{\prime \prime }_{\text{f}} + \theta^{\prime }_{\text{f}} } \right] + {\text{Re}} \cdot { \Pr } \cdot {\text{Sc}}\left( {f \cdot \phi^{\prime } } \right) = 0$$
(22)

where \({\text{Sc}} = \frac{\upsilon }{D}\) is the Schmidt number and \({\text{Sr}} = \frac{{D \cdot k_{\text{T}} }}{{T_{\text{m}} }}\frac{{\left( {T_{\text{w}} - T_{\infty } } \right)}}{{C_{\infty } \cdot \alpha }}\) is the Soret number, and the boundary conditions are:

$$\eta = 1{:}\;\; \phi^{\prime } (1) = - \gamma^{*}$$
(23a)
$$\eta \to \infty{:} \;\;\phi (\infty ) = 0$$
(23b)

where \(\gamma^{*} = \frac{{k_{\text{R}} \cdot a}}{2D}\frac{1}{{C_{\infty } }}\) is the Damköhler number. Numerical solutions for Eqs. (12), (17), (19) and (22) along with the boundary conditions (14–15), (18), (20), (23) are developed by employing an implicit, iterative tri-diagonal finite difference method [45].

Nusselt and Sherwood numbers

The rate of heat transfer for the fluid phase and the local convection coefficient are defined as

$$h = \frac{{q_{\text{w}} }}{{T_{\text{w}} - T_{\infty } }} = \frac{{ - k_{\text{f}} \left( {\frac{{\partial T_{\text{f}} }}{\partial r}} \right)_{{{\text{r}} = {\text{a}}}} }}{{T_{\text{w}} - T_{\infty } }} = - \frac{{2k_{\text{f}} }}{a}\frac{{\partial \theta_{\text{f}} (1)}}{\partial \eta },$$
(24)

and

$$q_{\text{w}} = - \frac{{2k_{\text{f}} }}{a}\frac{{\partial \theta_{\text{f}} (1)}}{\partial \eta }T_{\text{w}} - T_{\infty } .$$
(25)

Thus, Nusselt number calculated on the external surface of the cylinder is expressed by

$${\text{Nu}} = \frac{h \cdot a}{{2k_{\text{f}} }} = - \theta^{\prime } (1).$$
(26)

In a similar way, the local rate of mass transfer and mass transfer coefficient are given by

$$k_{\text{m}} = \frac{{q_{\text{m}} }}{{C_{\text{w}} - C_{\infty } }} = \frac{{ - D\left( {\frac{\partial C}{\partial r}} \right)_{{{\text{r}} = {\text{a}}}} }}{{C_{\text{w}} - C_{\infty } }} = - \frac{2D}{a}\frac{\partial \phi (1)}{\partial \eta }.$$
(27)

and

$$q_{\text{m}} = - \frac{2D}{a}\frac{\partial \phi \left( 1 \right)}{\partial \eta }C_{\text{w}} - C_{\infty } .$$
(28)

Therefore, Sherwood number can be written as

$${\text{Sh}} = \frac{{k_{\text{m}} \cdot a}}{2D} = - \phi^{\prime } (1).$$
(29)

Grid independency and validation

To ensure achieving numerical results that are grid independent, values of the surface-averaged Nusselt and Sherwood number were computed for grid sizes of \(51 \times 18\), \(102 \times 36\), \(204 \times 72\), \(408 \times 144\) and \(816 \times 288\). As shown in Table 1, there are no considerable changes in the average Nusselt and Sherwood numbers for the (\(\eta ,\varphi\)) mesh sizes of (\(204 \times 72\)), (\(408 \times 144\)) and (\(816 \times 288\)). Hence, a (\(408 \times 144\)) grid in \(\eta - \varphi\) directions was chosen for the computational domain of the current work. To capture the sharp gradients of velocity, temperature and concentration around the external surface of the cylinder, a non-uniform grid was applied in \(\eta\) direction, while a homogeneous mesh was used in the angular direction. In the current work, the computational domain extends to \(\varphi_{ \hbox{max} } = 360^\circ\) and \(\eta_{ \hbox{max} } = 15\). It is important to note that \(\eta_{ \hbox{max} }\) essentially corresponds to \(\eta \mathop \to \limits_{{}} \infty .\) This is because for all cases investigated in this work, \(\eta_{ \hbox{max} }\) is located outside the concentration, momentum and thermal boundary layers. It is assumed that when the disparity between the two consecutive iterations becomes less than \(10^{ - 7}\), the convergence criterion in the numerical simulations has been met, and thus, the iterative process is stopped. On the basis of the utilised numerical method, the numerical error is deemed to be of \(O(\Delta \eta )^{2}\) [45].

Table 1 Verification of grid independency at \({\text{Df}} = 1.0, \;{\text{Bi}} = 0.1,\;{\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; \lambda = 10,\; {\text{Sc}} = 0.1\)
Full size table

Tables 2 and 3 show that for very large permeability and porosity of one (a clear region) and when the mass transfer and gravitational effects are suppressed, the numerical simulations developed in “Theoretical and numerical methods” section reduce to those of Wang [46] and Gorla [47] for the impinging flow on a circular cylinder. Also, although not shown in this section, it was verified that for large Biot numbers, the current LTNE results become identical to those developed in an earlier work of the authors under LTE condition [12]. This rational trend provides another evidence for correctness of the current simulations.

Table 2 Validation of the numerical method by comparison between the current simulations and those of Wang [36] for large porosity and permeability
Full size table
Table 3 Comparison between the current simulations and those of Gorla [37] for very large porosity and permeability
Full size table

Results and discussion

Temperature and concentration fields

Figure 2a depicts the radial distribution of non-dimensionalised axial velocity (\(f^{\prime }\)) for different Reynolds numbers. As expected, there is a hydrodynamic boundary layer over the cylinder in which flow velocity features an overshoot. In keeping with the classical behaviours of viscous flows at low Reynolds number, the hydrodynamic boundary layer grows in thickness as Reynolds number decreases. Figure 2a also shows that the amplitude of the overshoot increases for lower values of Reynolds number. The observed overshoot is because of the influence of buoyancy forces upon the fluid velocity, which becomes more noticeable in low-momentum flows. Figure 2b further elaborates on this by showing the radial variation in axial velocity for different mixed convection parameters. At low values of mixed convection parameter, for which the flow approaches forced convection, there is almost no velocity overshoot and a typical profile of forced convection boundary layer is recaptured. However, by increasing the share of natural convection at higher values of mixed convection parameter, the velocity overshoot grows in magnitude. Interestingly, as the numerical value of mixed convection exceeds 10, the thickness of the hydrodynamic boundary layer becomes nearly indifferent to this value. This along with the trend observed in Fig. 2a confirms that the boundary layer thickness in the current problem is dominated by Reynolds number.

Fig. 2
figure 2

Variation in velocity related to w component \(f^{\prime } (\eta )\) for varying a Reynolds number, b dimensionless mixed convection parameter, \({\text{Df}} = 0.1,\;{\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\;{\text{Re}} = 5.0, \;{\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image

Figure 3 shows the effects of nonlinear mixed convection upon the profiles of dimensionless axial velocity. Both parts of this figure indicate that strengthening of nonlinear convection results in higher amplitudes of velocity overshoot in the hydrodynamic boundary layer. Yet, in agreement with that discussed earlier, the boundary layer thickness remains independent of nonlinear mixed convection. This is an important result as it illustrates the influence of nonlinear mixed convection upon the hydrodynamics of the problem. Figure 3b implies that such influences can be significant. Figure 3 clearly shows that the influences of nonlinear mixed convection parameter for concentration (\(\beta_{\text{c}}\)) are stronger than those of nonlinear mixed convection for temperature (\(\beta_{\text{T}}\)). The reason for this difference is not immediately obvious and is most probably due to the strongly nonlinear nature of momentum transport in mixed convection, as reflected by Eq. (12). Unlike conventional mixed convection modelling, the current problem models the buoyancy effects of temperature and concentration difference through strongly nonlinear terms [see Eq. (3)]. This can lead to complex interactions between transport of momentum and those of heat and mass [Eqs. (4), (5), (6)] and imbalance the effects of mixed convection parameters upon momentum transfer.

Fig. 3
figure 3

Variation in velocity related to w component \(f^{\prime } (\eta )\) for different values of a nonlinear mixed convection parameter for temperature, b nonlinear mixed convection parameter for concentration, \({\text{Df}} = 0.1,\;{\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image

The effects of Reynolds number and permeability of the porous medium on the dimensionless temperature of the fluid phase are shown in Fig. 4. According to Fig. 4a, at any radial distance from the surface of the cylinder, increases in Reynolds number result in reduction in the dimensionless temperature of the fluid. It should be noted that according to the definition of dimensionless temperature (Eq. 6), lower values of this quantity imply a fluid temperature close to that of the impinging flow and the values of dimensionless temperature close to unity indicate proximity to the wall temperature. Figure 4a shows that at any radius, increases in Reynolds number result in the reduction in fluid temperature. It also shows that the thickness of thermal boundary layer decreases at higher values of Reynolds number. It will be later shown that this trend is associated with an increase in the rate of heat transfer. This is to be expected as, in general, increases in Reynolds number and reduction in the thickness of thermal boundary layer intensify the convective heat transfer [48]. Figure 4b shows that increases in mixed convection parameter lead to reduction in the dimensionless temperature of the fluid and formation of thinner thermal boundary layer. Hence, convective heat transfer is stronger at higher values of mixed convection parameter. Once again, this is an anticipated result as Reynolds number, and therefore, the strength of forced convection is kept constant in Fig. 4b. Thus, increases in mixed convection strengthen the contribution of natural convection with the heat transfer process.

Fig. 4
figure 4

Variation in dimensionless fluid temperature \(\theta_{\text{f}} (\eta )\) for varying a Reynolds number, b dimensionless mixed convection parameter, \({\text{Df}} = 0.1,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image

Figure 5 depicts the effects of \(\beta_{\text{c}}\) and \(\beta_{\text{T}}\) on the dimensionless temperature of the fluid. According to this figure, increases in either of \(\beta_{\text{c}}\) or \(\beta_{\text{T}}\) result in the reduction in dimensionless temperature and lessen the thickness of thermal boundary layer. It follows that the increases in the nonlinear convection parameters intensify the rate of heat transfer. Comparison of Fig. 5a, b shows that the influences of \(\beta_{\text{c}}\) upon the reduction in boundary layer thickness are stronger than those of \(\beta_{\text{T}} .\) This can be attributed to the behaviour observed in Fig. 3 in which variations in \(\beta_{\text{c}}\) affect the velocity field more significantly in comparison with \(\beta_{\text{T}} .\) Larger velocities induced at higher values of \(\beta_{\text{c}}\) strengthen mixed convection of heat and induce higher rates of heat transfer and smaller thicknesses of the thermal boundary layer. Figure 5b further shows that increases in \(\beta_{\text{c}}\) lead to a slight decrease in the thickness of thermal boundary layer. This implies that by intensifying nonlinear mixed convection, the characteristics of thermal boundary layer approach those of forced convection.

Fig. 5
figure 5

Variation in dimensionless fluid temperature \(\theta_{\text{f}} (\eta )\) for different values of a nonlinear mixed convection parameter for temperature, b nonlinear mixed convection parameter for concentration, \({\text{Df}} = 0.1,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3, \;\beta_{\text{h}} = 0.1\)

Full size image

The effects of Dufour and Biot number on the dimensionless temperature of the fluid are shown in Fig. 6. According to this figure, variation in Dufour number leaves modest effects on the fluid temperature. Magnification of Dufour effect slightly increases the dimensionless temperature of fluid and hence renders lower rates of heat transfer. Yet, variation in Biot number appears to feature more pronounced impacts on the fluid temperature. Figure 6a clearly shows that dimensionless fluid temperatures are smaller at lower values of Biot number. This is to be expected, as a low Biot number implies high thermal conductivity of the porous medium, which is a well-known factor in enhancement of heat transfer in porous media [49].

Fig. 6
figure 6

Variation in dimensionless fluid temperature \(\theta_{\text{f}} (\eta )\) for varying a Dufour number, b Biot number, \({\text{Df}} = 0.1, \;{\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5, \;{\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image

Figure 7a shows that changes in Reynolds number have no considerable effect on the dimensionless temperature of the porous solid phase. However, variation in heat source parameter can significantly alter the porous solid temperature (Fig. 7b). As shown in Fig. 8a, Biot number has also a significant effect on the temperature of the porous solid phase. At lower Biot numbers, the thermal conductivity of the porous solid is much larger than the convective cooling of the fluid medium. Hence, the solid phase approaches thermal equilibrium with the external surface of the cylinder. Increases in the Biot number and therefore strengthening the heat exchanges between the two phases of solid and fluid in the porous medium cause a drop in the temperature of the porous solid.

Fig. 7
figure 7

Variation in dimensionless solid temperature \(\theta_{\text{s}} (\eta )\) for varying a Reynolds number, b heat source parameter, \({\text{Df}} = 0.1,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0, \;{\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image
Fig. 8
figure 8

a Response of dimensionless solid temperature \(\theta_{\text{s}} (\eta )\) to changes in the value of Biot number, b response of \(\phi (\eta )\) for different values of Reynolds number, \({\text{Df}} = 0.1,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image

Figure 8b illustrates the radial distribution of dimensionless concentration for varying values of Reynolds number. This figure shows a similar behaviour to that observed in Fig. 4a, wherein dimensionless temperature drops by increases in Reynolds number. In both cases, increasing Reynolds number leads to reduction in the boundary layer thickness (thermal and concentration) and increases in the rate of transport (as shown in the following section).

It should be noted that these results are further supported by the analogy between heat and mass transfer. Figure 9 shows the effects of mixed convection and nonlinear convection parameters upon the radial profiles of concentration. Higher values of mixed and nonlinear convection parameters (\(\beta_{\text{c}}\)) cause reductions in the thickness of the concentration boundary layer. Once again, these findings are in qualitative agreement with those of temperature variation. Nonetheless, the effects of \(\beta_{\text{c}}\) on the thermal boundary layer appear to be stronger than those on the concentration boundary layer. Figure 10 shows that depending upon the sign of Soret number, thermal diffusion can either enhance or suppress mass transfer process. For the set of parameters shown in Fig. 10, positive values of Soret number tend to increase the value of dimensionless concentration and reduce the rate of mass transfer, while the negative values of Soret number have the opposite effect.

Fig. 9
figure 9

Response of dimensionless concentration \(\phi (\eta )\) to different values of a dimensionless mixed convection parameter, b nonlinear mixed convection parameter for concentration, \({\text{Df}} = 0.1,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0, \;{\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image
Fig. 10
figure 10

Response of dimensionless concentration \(\phi (\eta )\) to different values of Soret number \({\text{Df}} = 0.1,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image

Deviation from local thermal equilibrium and Nusselt and Sherwood numbers

Deviation from the state of local thermal equilibrium in porous media with chemical reactions has been already reported [18, 19, 50,51,52,53,54]. However, many numerical works still use local thermal equilibrium for reactive flows in porous media. Here, a systematic examination of the local thermal equilibrium of the system is put forward to identify the trends in deviation from local thermal equilibrium. Figure 11 shows surface plots of the temperature difference between the solid and fluid phase in the porous medium against Biot number and radial coordinate and for different values of a few pertinent parameters. Biot number is known to be a key dimensionless parameter in evaluation of local thermal equilibrium and is therefore chosen as one of the main variables. In Fig. 11, the values of temperature difference close to one indicate strong tendency towards local thermal non-equilibrium. However, as the temperature difference approaches zero, local thermal equilibrium conditions are retained. As anticipated for all investigated cases, lower values of Biot number push the system towards local thermal non-equilibrium. This is because of the poor heat exchanges between the porous solid and fluid at smaller Biot numbers that allow for the development of a sizeable temperature difference between the two.

Fig. 11
figure 11

Temperature difference between the fluid and porous solid phase, for different values of a Reynolds number, b dimensionless mixed convection parameter, c permeability parameter, \({\text{Df}} = 0.1,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\;\lambda_{1} = 10,\;\beta_{\text{t}} = 0.1,\; \beta_{\text{c}} = 0.3,\; \beta_{\text{h}} = 0.1\)

Full size image

Figure 11 shows that for all values of Biot number, there is a finite temperature difference close to the surface of the solid. This region marks the thermal boundary layer, and as shown in Fig. 11a, it is thicker at lower values of Reynolds number. Outside this region and for larger radii, the temperature difference increases slightly which is due to small changes in the temperature of porous solid. Figure 11a further shows that increasing Reynolds number intensifies the deviation from local thermal equilibrium, while Fig. 11b, c indicates that increases in mixed convection and permeability parameters have the same effect.

The values of the surface-averaged Nusselt and Sherwood number calculated for several different parameters are shown in Tables 4–6. Values of surface-averaged Nusselt and Sherwood number vary slightly by changes in the nonlinear heat generations (see Table 4). However, they are quite sensitive to changes in permeability parameter. Also, as discussed earlier, increases in Reynolds number and nonlinear convection parameters (\(\beta_{\text{c}}\) and \(\beta_{\text{T}}\)) magnify the values of Nusselt and Sherwood number (see Table 5). The extent of these magnifications is quite strong for Reynolds number and \(\beta_{\text{c}}\) but rather insignificant for \(\beta_{\text{T}} .\) Finally, as shown in Table 6, increases in Biot and Dufour number reduce Nusselt and Sherwood number. Nonetheless, depending upon its sign, Soret effect can either increase or reduce Nusselt number [55,56,57,58].

Table 4 Impact of Prandtl and Schmidt number on the surface-averaged Sherwood, Nusselt and Bejan number, \({\text{Df}} = 1.0,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\; \lambda_{1} = 1.0,\; \beta_{\text{t}} = 0.1,\; N^{*} = 1.0,\;\beta_{\text{c}} = 0.1\)
Full size table
Table 5 Impact of Reynolds number and nonlinear convection parameters on the surface-averaged Sherwood, Nusselt and Bejan number, \({\text{Df}} = 1.0,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 10,\; {\text{Sc}} = 0.1,\;\lambda = 10,\; \lambda_{1} = 10,\; \beta_{\text{t}} = 0.1,\; N^{*} = 50,\;\beta_{\text{c}} = 0.1\)
Full size table
Table 6 Impact of Dufour, Soret and Biot number on the surface-averaged Sherwood, Nusselt and Bejan number, \({\text{Df}} = 1.0,\; {\text{Bi}} = 0.1,\; {\text{Sr}} = 0.5,\; {\text{Re}} = 5.0,\; {\text{Sc}} = 0.1,\;\lambda = 10,\; \lambda_{1} = 1.0,\; \beta_{\text{t}} = 10, \;N^{*} = 50,\;\beta_{\text{c}} = 0.1\)
Full size table

Conclusions

Combined transport of heat and mass through mixed convection set by the impingement of a flow over a vertical cylinder embedded in a porous medium was considered. The surface of cylinder was coated with a catalytic material leading to the occurrence of a heterogenous chemical reaction. Nonlinear convection of heat and mass and nonlinear heat generations were considered, and the formulation of the problem included Soret and Dufour effects. The nonlinear governing equations were reduced to a system of ordinary differential equations by using similarity variables. A finite difference method was then used to solve the coupled, nonlinear ordinary differential equations. The findings of this study can be summarised as follows.

  • Increasing Reynolds number results in the reduction in the thicknesses of thermal and concentration boundary layers. Consequently, it enhances the value of Nusselt and Sherwood number.

  • Higher values of nonlinear mixed convection parameters make the boundary layers thinner and therefore enhance the rate of heat and mass transfer.

  • The effects of nonlinear mixed convection parameter for concentration appeared to be stronger than those of thermal mixed convection.

  • Soret and Dufour numbers were found to be influential on the value of Sherwood and Nusselt number. Nonetheless, their effects are either comparable or less than the influences of nonlinear mixed convection.

  • Deviation of the porous system from local thermal equilibrium was systematically examined. This showed that increases in Reynolds and mixed convection parameters push the system towards local thermal non-equilibrium.

Th current study clearly demonstrated the potential significance of nonlinear mixed convection. Future studies will focus on exploring the complex interaction between momentum transfer and nonlinear convection of heat and mass.