Introduction

A peristaltic pump is a type of positive displacement pump with two cavities, one for suction and the other for discharge, especially used for many types of liquid. During the operation of such a pump, fluid flows into the suction cavity and out of the discharge cavity as it collapses, the main constraint being that the volume of fluid remains constant in any given cycle. The whole process is known as peristalsis and can be observed extensively in biological systems such as the gastrointestinal tract, as well as in heart–lung machines, which are used to maintain normal blood circulation during bypass surgery or kidney dialysis. In fluid mechanics literature, pioneering work on peristalsis in relation to mechanical pumping was carried out by Latham [1], after which Shapiro et al. [2] were the first to study peristaltic transport of Newtonian fluids in the wave frame of reference, while Fung and Yih [3] again studied peristalsis but in the laboratory frame. At the start of the 20th century, Mishra and Ramachandra [4] reported on peristaltic flow in channels with asymmetry generated by peristaltic waves of different amplitudes, concluding that, in comparison with a symmetric channel, a thinner reflux layer, lower trapping zone, and lower flux were obtained. Meanwhile, peristaltic flow of different phases has also been discussed [5,6,7].

In the current technological era, a main area of focus has been improving heat transfer and decreasing the thermal conductivity of fluids such as water, oil, and ethylene–glycol mixtures. It is well known that the conductivity of some solids is always higher than that of liquids, thus the main effect of addition of particles into such fluids is to enhance their heat transfer features. However, such addition of particles of different sizes faces two main hurdles:

  1. (a)

    The increased pressure drop in the system.

  2. (b)

    The inhomogeneity of the mixed system.

As a result, scientists have focused on addition of nanoparticles, whose similar size to that of the fluid molecules in the base fluids offers two main advantages:

  1. (i)

    The particles can move along with the molecules in the fluid; i.e., they act like the fluid;

  2. (ii)

    They remain stable for long times because of the very low differential effect of gravity.

Such a combination of nanosized particles suspended in a conductive base fluid is known as a nanofluid, as explained in detail by Buongiorno [8], who showed that the relative velocity can be easily expressed as the sum of the velocity of the base fluid and its relative slip velocity, leading to the requirement for a realistic model for these two components of the effects in nanofluids. The findings of that work include that:

  • In a nanofluid, two very important factors are Brownian diffusion and thermophoresis of the nanoparticles, and the slip effect of the base liquid;

  • A two-part inhomogeneous equilibrium model can be developed to described the Brownian diffusion and thermophoresis;

  • The energy transfer by nanoparticles can be considered to be negligible (although other literature disagrees in this regard);

  • Results for the correlation structure can be obtained, in good agreement with other literature.

The nanoparticles suspended in the base fluid are usually made of metals, oxides, carbides, or carbon nanotubes, while the base fluid mat be water or ethylene glycol, as used by different authors, or some type of oil. The first use of the term “nanofluid” was by Choi [9], a pioneering researcher on this topic. Choi concluded that nanofluids represent a unique type of material and proposed that high-thermal-conductivity nanofluids could be analyzed with the help of the HM (Hamilton and Crosser) model for the studied copper–water nanofluid. This was also verified experimentally by Masuda [10] for another type of particles, viz. Al2O3. That author also explained some very prominent benefits of nanofluids with copper nanophase and explained them analytically, including the unexpected reduction in the pumping power required for a heat exchanger when using a nanofluid; For example, if heat source power of 10 W m−2 K−1 achieves heat transfer of 2 W m−2 K−1, the same can be achieved with a reduced heat source power of 3 W m−2 K−1 when using a nanofluid.

Carbon nanotubes (CNTs) are another important type of nanoparticles; they are another form of carbon, being similar to graphite, which is seen extensively in daily life, e.g., in lead pencils. CNTs are hollow cylindrical tubes with size 10,000 times smaller than a human hair but stronger than steel. They are also highly electrically conductive, which could make them an extremely cost-effective replacement for metal wires. The semiconducting properties of CNTs make them candidates for use in next-generation computer chips. Nanotubes were discovered by Iijima [11] and Baughman et al. [12]. There are two main types of nanotubes, viz. single-walled nanotubes (SWNTs) and multiwalled nanotubes (MWNTs). A single-walled carbon nanotube is just like a regular straw, having only one layer or wall. Multiwalled carbon nanotubes are formed from a collection of nested tubes of increasing diameter. Carbon nanotubes exhibit extraordinary thermal conductivity, electrical conductivity, and mechanical properties, finding applications as additives for structural materials used in golf clubs, boats, aircraft, bicycles, etc. Mixing CNTs into solids [13,14,15,16] or fluids [17,18,19,20,21,22,23] can effectively enhance the thermal and mechanical properties of the base material, leading to wide study of their use in heat transfer applications [24,25,26,27].

Magnetohydrodynamics (MHD) is the study of the magnetic properties of electrically conducting fluids. Examples of such magnetofluids include plasmas, liquid metals, and salt water or electrolytes [28,29,30,31,32,33,34,35,36,37,38].

Despite the studies cited above, peristaltic flow containing CNT nanoparticles in an induced magnetic field in a permeable channel has not been studied using the Crosser model; The objective of this paper is to fill this gap in the literature.

Mathematical formulation

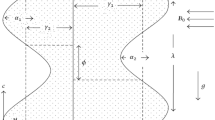
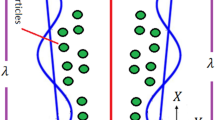
Consider the flow of a nanofluid containing SWCNTs with zigzag, chiral, and armchair shape in salt water as base fluid in a channel with a permeable wall having width \(d_{1} + d_{2}\). An external uniform constant transverse magnetic field \(H_{0}\) is applied, inducing a magnetic field H\(\left( {h_{{X}} \left( {X,Y,t} \right), H_{0} + h_{{Y}} \left( {X,Y,t} \right),0} \right)\) and a total magnetic field \(H^{ + } \left( {h_{{X}} \left( {X,Y,t} \right), H_{0} + h_{{Y}} \left( {X,Y,t} \right),0} \right)\). The undulations in the channel profile [39,40,41] lead to

$$\begin{aligned} & Y = \bar{H}_{1} = d_{1} + a_{1} { \cos }\left( {\frac{2\pi }{\lambda }\left( {\bar{X} - c_{1} \bar{t}} \right)} \right), \\ & Y = \bar{H}_{2} = - d_{2} - b_{1} \cos \left( {\frac{2\pi }{\lambda }\left( {\bar{X} - c_{1} \bar{t}} \right) + \omega } \right). \\ \end{aligned}$$
(1)

In Eq. (1), \(a_{1}\) and \(b_{1}\) are wave amplitudes, \(\lambda\) is the wavelength, \(\omega\) is the amplitude ratio, \(d_{1} + d_{2}\) is the channel width, \(c_{1}\) is the wave speed, \(\bar{t}\) is time, \(\bar{X}\) is the direction of wave propagation while Y is perpendicular to as shown in Fig. 1.

Fig. 1
figure 1

Flow diagram

Full size image

A mathematical model in the general form can be expressed as follows:

$$\nabla \varvec{ } \cdot {\mathbf{H}} = 0, \nabla \varvec{ } \cdot {\mathbf{E}} = 0,$$
(2)
$$\nabla \wedge {\mathbf{H}} = {\mathbf{J}},\quad {\mathbf{J}} = \sigma \left\{ {{\mathbf{E}} + \mu_{\text{e}} \left( {{\mathbf{V}} \wedge {\mathbf{H}}} \right)} \right\},$$
(3)
$$\nabla \wedge {\mathbf{E}} = - \mu_{\text{e}} \frac{{\partial {\mathbf{H}}}}{{\partial {\mathbf{t}}}}.$$
(4)

The continuity equation can be written as

$$\nabla \varvec{ }. {\mathbf{V}} = 0.$$
(5)

The equations of motion are

$$\rho_{\text{nf}} \left( {\frac{{\partial \varvec{V}}}{\partial t} + \varvec{V} \cdot \nabla \varvec{V}} \right) = - \nabla p + \mu_{\text{nf}} \nabla^{2} \varvec{V} + \left( {\rho \beta } \right)_{\text{nf}} g\alpha \left( {T - T_{0} } \right) - \nabla \left( {\frac{1}{2}\mu_{\text{e}} \left( {\varvec{H}^{ + } } \right)^{2} } \right) - \mu_{\text{e}} \left( {\varvec{H}^{ + } \cdot \nabla } \right)\varvec{H}.$$
(6)

The energy equation can be expressed as

$$\left( {\rho c} \right)_{\text{nf}} \left( {\frac{{\partial {\mathbf{T}}}}{\partial t} + {\mathbf{V}} \cdot \nabla {\mathbf{T}}} \right) = k_{\text{nf}} {\nabla }^{2} T + Q_{0} - \frac{\partial q}{\partial y} ,$$
(7)

where

$$q = \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y} .$$
(8)

Expanding in a Taylor’s series about \(T_{\infty }\) and ignoring higher-order terms yields

$$T^{4} \approx 4T_{\infty }^{3} T - 3T_{\infty }^{4} .$$
(9)

Combining Eqs. (2)–(4) provides

$$\frac{{\partial {\mathbf{H}}^{ + } }}{\partial t} = \nabla \wedge \left( {{\mathbf{V}} \wedge {\mathbf{H}}^{ + } } \right) + \frac{1}{\xi }\nabla^{2} {\mathbf{H}}^{ + } .$$
(10)

Using the static wave structures

$$x = X - ct, y = Y, u = U - c, v = V,$$
(11)

and applying the transformations

$$\begin{aligned} & \bar{p} = \frac{{a^{2} }}{{\mu_{{\text{f}}} c\lambda }}p,\,\bar{u} = \frac{\lambda }{ac}u,\,\bar{v} = \frac{v}{c},\,\bar{y} = \frac{y}{\lambda },\,\bar{x} = \frac{x}{a},\,\bar{t} = \frac{c}{\lambda }t,\,D_{\text{a}} = \frac{k}{{a^{2} }}, \\ & \text{Re} = \frac{\rho ca}{{\mu_{\text{f}} }},\,\delta = \frac{a}{\lambda },\,\bar{\theta } = \frac{{T - T_{0} }}{{T_{0} }},\,\bar{\varPhi } = \frac{\varPhi }{{H_{0} a}},\,\bar{\varPsi } = \frac{\varPsi }{ca},\,R_{\text{m}} = \sigma \mu_{\text{e}} ac, \\ & \overline{{h_{{\text{x}}} }} = \bar{\varPhi }_{{\bar{\text{x}}}} ,\,\overline{{h_{{\text{y}}} }} = - \bar{\varPhi }_{{{\bar{{\text{y}}}}}} ,\,G_{\text{r}} = \frac{{\rho_{\text{f}} g\alpha a^{2} }}{{\mu_{\text{f}} c}}\left( {T_{0} } \right),\,S_{1} = \frac{{H_{0} }}{c}\sqrt {\frac{{\mu_{\text{e}} }}{\rho }} , \\ & \alpha_{\text{nf}} = \frac{k}{{\left( {\rho c} \right)_{\text{f}} }}, \tau = \frac{{\left( {\rho c} \right)_{\text{p}} }}{{\left( {\rho c} \right)_{\text{f}} }}. \\ \end{aligned}$$
(12)

in Eq. (11) and taking \({\delta \to 0} ,\) the following dimensionless system of equations without bars is obtained:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(13)
$$\frac{{{\text{d}}p}}{{{\text{d}}x}} = \frac{{\partial^{3} \varPsi }}{{\partial y^{3} }}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right) + \text{Re} S_{1}^{2} \varPhi_{\text{yy}} + \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}\frac{{G_{\text{r}} }}{\text{Re}}\theta ,$$
(14)
$$\frac{{{\text{d}}p}}{{{\text{d}}y}} = 0,$$
(15)
$$\varPhi_{\text{yy}} = R_{\text{m}} \left( {E - \frac{\partial \varPsi }{\partial y}} \right),$$
(16)
$$\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} - N} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + Q_{0} \theta = 0.$$
(17)

Applying Eq. (16) in Eq. (14) yields

$$\frac{{{\text{d}}p}}{{{\text{d}}x}} = \frac{{\partial^{3} \varPsi }}{{\partial y^{3} }}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right) + \text{Re} S_{1}^{2} R_{\text{m}} \left( {E - \frac{\partial \varPsi }{\partial y}} \right) + \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}G_{\text{r}} \theta .$$
(18)

Differentiating Eq. (18) with respect to y yields

$$\frac{{\partial^{4} \varPsi }}{{\partial y^{4} }}\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right) + \text{Re} S_{1}^{2} R_{\text{m}} \left( { - \frac{{\partial^{2} \varPsi }}{{\partial y^{2} }}} \right) + \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}\frac{{G_{\text{r}} }}{\text{Re}}\frac{\partial \theta }{\partial y} = 0.$$
(19)

The nondimensional boundary conditions can be expressed as

$$\varPsi = \frac{F}{2}, \frac{\partial \varPsi }{\partial y} = - 1 - \frac{{\sqrt {D_{\text{a}} } }}{\alpha }\frac{{\partial^{2} \varPsi }}{{\partial y^{2} }}\quad {\text{at}}\,\,y = h_{1} ,$$
(20)
$$\varPsi = - \frac{F}{2},\, \frac{\partial \varPsi }{\partial y} = - 1 + \frac{{\sqrt {D_{\text{a}} } }}{\alpha }\frac{{\partial^{2} \varPsi }}{{\partial y^{2} }}\quad {\text{at}}\,\,y = h_{2} ,$$
(21)
$$\theta = 0\quad {\text{at}}\,\,y = h_{1} ,\,\theta = 1\quad {\text{at}}\,\,y = h_{2} ,$$
(22)
$$\varPhi = 0\quad {\text{at}}\,\, y = h_{1} ,\quad \varPhi = 0\,\,{\text{at}}\,\,y = h_{2} .$$
(23)

The pressure rise ∆p, magnetic factor hx, and current density Jz can be expressed nondimensionally as

$$\Delta p = \mathop \int \limits_{0}^{1} \left( {\frac{{{\text{d}}p}}{{{\text{d}}x}}} \right){\text{d}}x,$$
(24)
$$h_{\text{x}} = \frac{\partial \varPhi }{\partial y},$$
(25)
$$J_{{\text{z}}} = - \frac{{\partial h_{{\text{x}}} }}{\partial y}.$$
(26)

Meanwhile, the thermophysical relations are

$$\rho_{\text{nf}} = \left( {1 - \phi } \right)\rho_{\text{f}} + \phi \rho_{\text{s}} ,$$
(27)
$$\left( {\rho C_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho C_{\text{p}} } \right)_{\text{f}} + \phi \left( {\rho C_{\text{p}} } \right)_{\text{s}} ,$$
(28)
$$\beta_{\text{nf}} = \frac{{\left( {1 - \phi } \right)\left( {\rho \beta } \right)_{\text{f}} + \phi \left( {\rho \beta } \right)_{\text{s}} }}{{\rho_{\text{nf}} }},$$
(29)
$$\alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}.$$
(30)

Based on existing literature [42], one can write

$$\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} = \left( {1 - A_{1} \phi } \right),$$
(31)

where \(A_{1}\) is defined as

$$A_{1} = \frac{{0.312\gamma^{*} - 0.5}}{{\ln 2\gamma^{*} - 1.5}} + 2 - \frac{1.872}{{\gamma^{*} }},$$
(32)

with

$$\gamma^{*} = \frac{{\sqrt {\tilde{a}^{2} + \tilde{b}^{2} + \tilde{c}^{2} } }}{{\tilde{a}\tilde{b}\tilde{c}}},$$
(33)
$$\tilde{b} = \tilde{c} = \tilde{d}/2,$$
(34)
$$\tilde{a} \gg \tilde{b} = \tilde{c},$$
(35)

in which \(\tilde{d}\) is the diameter of the CNT particles of different shapes, given by

$$\tilde{d} = \frac{{a^{*} }}{\pi }\sqrt {n^{*2} + n^{*} m^{*} + m^{*2} } ,$$
(36)

where \(a^{*} = 0.246\,{\text{nm}}.\)

The Hamilton and Crosser models [43] are chosen, expressed as follows:

$$\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{K_{\text{s}} + \left( {n^{**} - 1} \right)K_{\text{f}} - \left( {n^{**} - 1} \right)\left( {K_{\text{f}} - K_{\text{s}} } \right)\phi }}{{K_{\text{s}} + \left( {n^{**} - 1} \right)K_{\text{f}} + \phi \left( {K_{\text{f}} - K_{\text{s}} } \right)}},$$
(37)
$$n^{**} = \frac{3}{{^{\alpha } }},$$
(38)
$$\psi = \frac{{\pi^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \left( {6V_{\text{p}} } \right)^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} }}{{A_{\text{p}} }},$$
(39)

where \(V_{\text{p}} = \pi r^{2} h\) is the volume and \(A_{\text{p}} = 2\pi r\left( {r + h} \right)\) is the surface area of a particle and \(r = \tilde{b} = \tilde{c}\), \(h = \tilde{a}\). The thermophysical properties are presented in Table 1.

Table 1 Thermophysical properties
Full size table

Analytical results

Using routine manipulations, these analytical results can be expressed as follows:

$$\theta = \text{csch} \left( {\frac{{\left( {h_{1} - h_{2} } \right)\sqrt {Q_{0} } }}{{\sqrt { - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} + N} }}} \right)\sinh \left( {\frac{{\sqrt {Q_{0} } \left( {h_{1} - y} \right)}}{{\sqrt { - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} + N} }}} \right),$$
(40)
$$\varPsi = C_{3} + C_{4} y + \frac{1}{\text{Re}}\left( \begin{array}{ll} \frac{{M_{1} C_{2} \mathrm{e}^{{ - {\text{M}}_{11} }} }}{{R_{\text{m}} S_{1}^{2} }} + \frac{{M_{1} C_{1} \mathrm{e}^{{{\text{M}}_{11} y}} }}{{R_{\text{m}} S_{1}^{2} }} - \hfill \\ \frac{{M_{2} G_{\text{r}} \left( {M_{9} } \right)^{3/2} \text{Cosh} \left( {M_{6} } \right)\text{Cosh} \left( {M_{5} } \right)\text{Csch} \left( {M_{7} } \right)}}{{M_{13} }} \hfill \\ + \frac{{M_{2} G_{\text{r}} \left( {M_{9} } \right)^{3/2} \text{Csch} \left( {M_{7} } \right)\text{Sinh} \left( {M_{6} } \right)\text{Sinh} \left( {M_{5} } \right)}}{{M_{13} }} \hfill \\ \end{array} \right),$$
(41)
$$\varPhi = \left. \begin{array}{ll} \frac{{M_{1}^{3/2} \mathrm{e}^{{{\text{M}}_{11} \text{y}}} \left( { - C_{1} + C_{2} \mathrm{e}^{{ - 2{\text{M}}_{11} {\text{y}}}} } \right)}}{{\text{Re}^{3/2} \sqrt {R_{\text{m}} } S_{1}^{3} }} - \frac{1}{2}C_{4} R_{\text{m}} y^{2} + \frac{1}{2}ER_{\text{m}} y^{2} + C_{5} + yC_{6} - \hfill \\ \frac{{M_{2} G_{\text{r}} M_{9}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} R_{\text{m}} \text{Cosh} \left( {M_{5} } \right)\text{Csch} \left( {M_{7} } \right)\text{Sinh} \left( {M_{6} } \right)}}{{\text{Re} M_{13} }} + \hfill \\ \frac{{M_{2} G_{\text{r}} M_{9}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} R_{\text{m}} \text{Cosh} \left( {M_{6} } \right)\text{Csch} \left( {M_{7} } \right)\text{Sinh} \left( {M_{5} } \right)}}{{\text{Re} M_{13} }} \hfill \\ \end{array} \right\},$$
(42)

The mean volume flow rate \(Q\) is

$$Q = 1 + F.$$
(43)

The pressure gradient \({\text{d}}p/{\text{d}}x\), axial induced magnetic field \(h_{\text{x}}\), and current density \(j_{\text{z}}\) are given as

$$\left. {\frac{{{\text{d}}p}}{{{\text{d}}x}} = - \frac{{\left( \begin{array}{ll} 2\text{Csch} \left( {M_{7} } \right)\sinh \left( {\frac{{M_{7} }}{2}} \right) \hfill \\ \left( \begin{array}{ll} G_{\text{r}} M_{2} \left( {N - M_{3} } \right)\left( \begin{array}{ll} \sqrt {D_{\alpha } } \left( {\mathrm{e}^{{{\text{h}}_{1} {\text{M}}_{11} }} - \mathrm{e}^{{^{{{\text{h}}_{2} {\text{M}}_{11} }} }} } \right)M_{10} \sinh \left( {\frac{{M_{7} }}{2}} \right)\left( {N - M_{3} } \right) + \hfill \\ \left( {\mathrm{e}^{{{\text{h}}_{1} {\text{M}}_{11} }} + \mathrm{e}^{{{\text{h}}_{2} {\text{M}}_{11} }} } \right)\sqrt {\text{Re} } \sqrt {R_{\text{m}} } S_{1} \alpha \sinh \left( {\frac{{M_{7} }}{2}} \right)\sqrt {M_{1} } \left( {N - M_{3} } \right) \hfill \\ 2\left( {\mathrm{e}^{{{\text{h}}_{1} {\text{M}}_{11} }} - \mathrm{e}^{{{\text{h}}_{2} {\text{M}}_{11}}} } \right)\alpha M_{1} \hfill \\ \end{array} \right) \hfill \\ \sqrt {N1 - M_{3} } \sqrt {Q_{0} } \left( {NM_{10} - M_{10} M_{3} - M_{1} Q_{0} } \right) \hfill \\ \end{array} \right) \hfill \\ \end{array} \right)}}{{\left( \begin{array}{ll} \text{Re} \left( \begin{array}{ll} \sqrt {D_{\alpha } } \left( {\mathrm{e}^{{{\text{h}}_{1} {\text{M}}_{11}}} - \mathrm{e}^{{{\text{h}}_{2} {\text{M}}_{11} }} } \right)\left( {h_{1} - h_{2} } \right)M_{10} + \hfill \\ \left( {\mathrm{e}^{{{\text{h}}_{1} {\text{M}}_{11}}} + \mathrm{e}^{{{\text{h}}_{2} {\text{M}}_{11}}} } \right)\left( {h_{1} - h_{2} } \right)\sqrt {\text{Re} } \sqrt {R_{\text{m}} } S_{1} \alpha \sqrt {M_{1} } - 2\left( {\mathrm{e}^{{{\text{h}}_{1} {\text{M}}_{11} }} - \mathrm{e}^{{{\text{h}}_{2} {\text{M}}_{11}}} } \right)\alpha M_{1} \hfill \\ \end{array} \right) \hfill \\ \sqrt {N - M_{3} } \sqrt {Q_{0} } \left( {NM_{10} - M_{10} M_{3} - M_{1} Q_{0} } \right) \hfill \\ \end{array} \right)}}} \right\},$$
(44)
$$ \left. {h_{\text{x}} = \frac{1}{2}\left( \begin{array}{ll} C_{4} R_{\text{m}} \left( {h_{1} + h_{2} - 2y} \right) - ER_{\text{m}} \left( {h_{1} + h_{2} - 2y} \right) - \frac{{2G_{\text{r}} R_{\text{m}}\cosh \left( {M_{8} } \right)\text{Csch} \left( {M_{7} } \right)M_{2} \left( {N - M_{3} } \right)^{3/2} }}{{\text{Re} \sqrt {Q_{0} } \left( {M_{10} M_{9} + M_{1} Q_{0} } \right)}} + \hfill \\ \frac{{2\left( \begin{array}{ll} - \frac{{\mathrm{e}^{{ - {\text{M}}_{11} y}} \left( {C_{2} + C_{1} \mathrm{e}^{{2M_{11} {\text{y}}}} } \right)\sqrt {\text{Re} } M_{1} }}{{S_{1}^{2} }} + \frac{{\mathrm{e}^{{ - \left( {{\text{h}}_{1} + {\text{h}}_{2} } \right){\text{M}}_{11} }} \left( {\mathrm{e}^{{{\text{h}}_{1} {\text{M}}_{11} }} - \mathrm{e}^{{{\text{h}}_{2} {|text{M}}_{11} }} } \right)\left( {C_{2} + C_{1} \mathrm{e}^{{\left( {{\text{h}}_{1} + {\text{h}}_{2} } \right){\text{M}}_{11} }} } \right)M_{1}^{3/2} }}{{\left( {h_{1} - h_{2} } \right)\sqrt {R_{m} } S_{1}^{3} }} \hfill \\ + \frac{{G_{r} \sqrt {\text{Re} } R_{\text{m}} M_{2} \left( {N - M_{3} } \right)^{2} }}{{\left( {h_{1} - h_{2} } \right)Q_{0} \left( {M_{10} \left( { - N + M_{3} } \right) + M_{1} Q_{0} } \right)}} \hfill \\ \end{array} \right)}}{{\text{Re}^{3/2} }} \hfill \\ \end{array} \right)} \right\}, $$
(45)
$$j_{\text{z}} = \left. \begin{array}{ll} \frac{{\mathrm{e}^{{ - {\text{M}}_{11} {\text{y}}}} \left( { - C_{2} + C_{1} \mathrm{e}^{{2{\text{M}}_{11} {\text{y}}}} } \right)\sqrt {R_{{\text{m}}} } \sqrt {M_{1} } }}{{\sqrt {\text{Re} } S_{1} }} + \hfill \\ \frac{{R_{\text{m}} \left( {G_{\text{r}} \text{Csch} \left( {M_{7} } \right)\sinh \left( {M_{8} } \right)M_{2} \left( {N - M_{3} } \right) + \left( {C_{4} - E} \right)\text{Re} \left( {M_{10} \left( {N - M_{3} } \right) - M_{1} Q_{0} } \right)} \right)}}{{\text{Re} \left( {M_{10} \left( {N - M_{3} } \right) - M_{1} Q_{0} } \right)}} \hfill \\ \end{array} \right\},$$
(46)

where the constants M1–M13 are given by

$$\begin{aligned} & M_{1} = A = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},M_{2} = B = \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }},M_{3} = Kf = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }},M_{4} = \frac{{\sqrt {Q_{0} } }}{{\sqrt { - Kf + N} }} \\ & M_{5} = \frac{{\sqrt {Q_{0} } y}}{{\sqrt { - Kf + N} }},M_{6} = \frac{{h_{1} \sqrt {Q_{0} } }}{{\sqrt { - Kf + N} }},M_{7} = \frac{{\left( {h_{1} - h_{2} } \right)\sqrt {Q_{0} } }}{{\sqrt { - Kf + N} }},M_{8} = \frac{{\sqrt {Q_{0} } \left( {h_{1} - y} \right)}}{{\sqrt { - Kf + N} }} \\ & M_{9} = Kf - N,M_{10} = \text{Re} R_{\text{m}} S_{1}^{2} ,M_{11} = \frac{{\sqrt {\text{Re} } \sqrt {R_{\text{m}} } S_{1} }}{\sqrt A },M_{12} = R_{\text{m}} S_{1}^{2} \\ & M_{13} = \sqrt {Q_{0} } \left( {AQ_{0} + \left( {Kf - N} \right)\text{Re} R_{\text{m}} S_{1}^{2} } \right). \\ \end{aligned}$$
(47)

Discussion

Figures 2–7 illustrate the behavior of the resulting parameters, i.e., the nanoparticle volume fraction \(\phi\), magnetic Reynolds number \(R_{\text{m}}\), Strommer’s number \(S_{1}\), heat generation parameter \(Q_{0}\), and heat flux parameter \(N\) for CNTs of various shapes in salt water. The effect of \(\phi\) on the pressure gradient is illustrated in Fig. 2a. It is seen that an increase in the value of \(\phi\) results in an increasing trend in the pressure gradient. It is also observed from this figure that the impact of \(\phi\) on the pressure gradient is maximum for the zigzag shape but comparatively less for the chiral and minimum for the armchair shape. The effects of \(R_{\text{m}}\) and \(S_{1}\) on the pressure gradient are shown in Fig. 2b, c, revealing that the pressure gradient is enhanced for higher values of \(R_{\text{m}}\) and \(S_{1}\), for the CNTs of all three shapes (zigzag, chiral, and armchair). Meanwhile, Fig. 2d, e reveals that the pressure gradient decreases with an increase in the heat generation and heat flux parameter throughout the channel for the CNTs of different shapes.

Fig. 2
figure 2

a–e Variation of pressure gradient dp/dx for different flow parameters

Full size image
Fig. 3
figure 3

a–e Variation of pressure rise ∆p for different flow parameters

Full size image
Fig. 4
figure 4

a–c Variation of temperature profile θ for different flow parameters

Full size image
Fig. 5
figure 5

a, b Variation of axially induced magnetic field hx for different flow parameters

Full size image
Fig. 6
figure 6

a, b Variation of current density jz for different flow parameters

Full size image
Fig. 7
figure 7

a–f Variation of velocity profile u for different flow parameters

Full size image

Figure 3a–e shows the pumping characteristics in terms of the variation of the pressure rise per wavelength \(\Delta_{\text{p}}\) with the time-averaged flux \(\left( {Q = F + 1} \right)\). Figure 3a shows the impact of the volume fraction \(\phi\) on the pressure rise \(\Delta_{\text{p}}\), revealing that an increase of \(\phi\) throughout the domain results in an increase in the pressure rise. Figure 3b illustrates that an increase in the value of \(R_{\text{m}}\) results in a higher pressure rise in the region \(\left( {\Delta_{\text{p}} < 0,Q < 0} \right)\), but \(\Delta_{\text{p}}\) goes down in the pumping region \(\left( {\Delta_{\text{p}} > 0,Q > 0} \right)\). Figure 3c depicts the effect of \(S_{1}\) on the pressure rise, revealing a similar behavior to that found for \(R_{\text{m}}\). Figure 3d and e show the effects of \(Q_{0}\) and \(N\), respectively. Note that an increase in \(Q_{0} \,{\text{and}}\,N\) results in a decrease in the pressure rise for the CNTs with zigzag, chiral, and armchair shapes in the entire domain.

Figure 4a–c shows the temperature distributions for different values of \(\phi\), \(Q_{0}\), and \(N\). Figure 4a shows that \(\theta\) decreases when increasing \(\phi\) for the CNTs of zigzag, chiral, and armchair shape. In Fig. 4b, c, a similar trend is noted for \(Q_{0}\) and \(N\). Note that \(\theta\) increases when the values of \(Q_{0}\) and \(N.\) are raised.

Figure 5 depicts the effects of the magnetic Reynolds and Strommer’s numbers on \(h_{x}\). Here, the induced magnetic field is in one direction in a half-region of the channel but the opposite direction in the other half-region. In addition, Fig. 5a illustrates that the magnitude of \(h_{x}\) decreases with increasing \(R_{\text{m}}\) from the wall \(h_{1}\) to the middle of channel, whereas an increasing trend is seen in the other half of the channel. However, in Fig. 5b, the behavior of \(S_{1}\) on \(h_{x}\) is opposite compared with that found for \(R_{\rm m}\).

Figure 6a, b shows the current density \(j_{\text{z}}\) for different values of \(R_{\text{m}}\) and \(S_{1}\). In Fig. 6a, it is seen that, when increasing \(R_{\text{m}}\), \(j_{\text{z}}\) increases, but \(j_{\text{z}}\) decreases when increasing \(S_{1}\), as observed in Fig. 6b.

Figure 7a–e plots the velocity profile \(\left( u \right)\), showing an increase along the walls but a decrease in the middle of channel with increasing \(\phi\). Figure 7b, c illustrates \(R_{\text{m}}\) and \(S_{1}\) for the CNTs with zigzag, chiral, and armchair shape, revealing conflicting behavior in the middle of the channel. Figure 7d shows the effect of the heat generation parameter \(Q_{0}\) on the velocity profile \(u\), revealing that the velocity increases with rising \(Q_{0}\) in the middle of the channel, while the opposite behavior is seen at the channel walls.

Figure 7e demonstrates the effects of the Darcy number \(\left( { D_{\alpha } } \right)\) on the velocity profile. It is seen that, near the walls, the velocity profile increases when increasing \(D_{\alpha }\), but at the center of the channel, a quite opposite behavior on the velocity profile is observed. The impact of \(\alpha\) on the velocity profile is presented in Fig. 7f. Along the walls, the velocity profile decreases with increasing \(\alpha\), whereas at the center of the channel, a clear increase is observed.

To study the bolus phenomenon, streamlines of the Darcy number \(\left( { D_{\alpha } } \right)\) for the CNTs with zigzag, chiral, and armchair shape are plotted in Figs. 8 to 10. It is found that the bolus is small for larger values of \(D_{\text{a}}\).

Fig. 8
figure 8

a, b Streamlines for CNTs of zigzag shape for Dα = 0.1 and Dα = 0.2. The other parameters are \(Q = 2.0,\,\alpha = 2.0,\, a = 0.7,\, b = 0.8,\,S_{1} = 1.0, \,N = 0.02,\,D_{\alpha } = 0.002, \,Q_{0} = 0.5\)

Full size image
Fig. 9
figure 9

a, b Streamlines for CNTs of chiral shape for Dα = 0.1 and Dα = 0.2. The other parameters are \(Q = 2.0,\,\alpha = 2.0,\, a = 0.7,\, b = 0.8,\,S_{1} = 1.0, \,N = 0.02,\,D_{\alpha } = 0.002, \,Q_{0} = 0.5\)

Full size image
Fig. 10
figure 10

a, b Streamlines for CNTs of armchair shape for Dα = 0.1 and Dα = 0.2. The other parameters are \(Q = 2.0,\,\alpha = 2.0,\, a = 0.7,\, b = 0.8,\,S_{1} = 1.0, \,N = 0.02,\,D_{\alpha } = 0.002, \,Q_{0} = 0.5\)

Full size image

In addition, the effects of significant physical parameters such as the nanoparticle volume fraction, heat generation, and heat flux on the skin friction coefficient and Nusselt number are computed numerically using MATLAB software and presented in Tables 2 to 7. Tables 2 and 3 are formulated for the nanoparticles of zigzag shape at the walls \(h_{1}\) and \(h_{2}\), respectively. Tables 4 and 5 present the results for the nanoparticles of chiral shape at the walls \(h_{1}\) and \(h_{2}\), respectively. Tables 6 and 7 are prepared for the nanoparticles with armchair shape at the walls \(h_{1}\) and \(h_{2}\), respectively. The results presented in these tables indicate that the absolute value of the skin friction coefficient is enhanced with increases in the volume fraction, heat generation parameter \(Q_{0}\), and heat flux parameter \(N\) for the CNTs of all three shapes along both walls \(h_{1}\) and \(h_{2} .\)

Table 2 Numerical values of skin friction coefficient and Nusselt number at wall h1 when \(x = 0.2\) for zigzag-shaped nanoparticles
Full size table
Table 3 Numerical values of skin-friction coefficient and Nusselt number at wall h2 when x = 0.2 for zigzag-shaped nanoparticles
Full size table
Table 4 Numerical values of skin friction coefficient and Nusselt number at wall h1 when \(x = 0.2\) for chiral-shaped nanoparticles
Full size table
Table 5 Numerical values of skin friction coefficient and Nusselt number at wall h2 when \(x = 0.2\) for chiral-shaped nanoparticles
Full size table
Table 6 Numerical values of skin friction coefficient and Nusselt number at wall h1 when \(x = 0.2\) for armchair-shaped nanoparticles
Full size table
Table 7 Numerical values of skin friction coefficient and Nusselt number at wall h2 when \(x = 0.21\) for armchair-shaped nanoparticles
Full size table

Conclusions

The effects of addition of carbon nanotubes to a peristaltic flow in an induced magnetic field are studied, yielding the following key results:

  • The effect of the nanoparticle volume fraction \(\left( \phi \right)\) on the pressure gradient is least in the case of CNTs of armchair shape, being comparatively larger for chiral shape and maximum in case of zigzag shape.

  • The pressure gradient decreases with an increase in the heat generation parameter.

  • The pressure rise increases with an increase in the volume fraction or Reynolds and Strummer’s number. It is also seen that increasing the heat flux parameter and Nusselt number decreases the pressure rise for the CNTs of zigzag, chiral, or armchair shape.

  • The axial induced magnetic field decreases at the center of the right wall for higher values of the Strommer’s number.

  • The current density increases with increasing values of the magnetic Reynolds number, but declines with increasing Strommer’s number.

  • It is observed that the velocity profile increases with increase of the Darcy or Strommer’s number at the middle of channel.

  • The size of the bolus becomes small and the number of boluses reduces for higher values of the Reynold’s number and Darcy number, for CNTs of zigzag, chiral, and armchair shape.

  • The absolute value of the Nusselt number decreases when increasing \(\phi\) but decreases when increasing \(Q_{0}\) or N.