On Dual Solutions of an Unsteady Flow of Reiner-Rivlin Fluid Over a Stretchable Rotating Disk with Deceleration

Abstract

The goal of the current study is to investigate an unsteady flow and heat transfer over a stretchable rotating disk of a non-Newtonian Reiner-Rivlin (RR) fluid when the disk decelerates with an angular velocity that is inversely proportional to time. The partial differential equations (PDEs) for RR fluid that govern the flow and heat transfer are converted into a set of self-similar equations using appropriate similarity transformations. The numerical solutions of the self-similar equations are computed via Matlab solver “bvp4c". Dual solution branches are found only for negative values of the unsteadiness parameter. The effects of non-Newtonian parameter, stretching parameter and unsteadiness parameter on the velocity and temperature profiles and on the torque experienced by the disk are discussed in detail and shown graphically for both the branches. The results indicated that the effect of non-Newtonian parameter on the axial, tangential velocity and temperature fields is similar to the steady Kármán flow for slow deceleration in upper solution branch. However, opposite behavior is found for the fast deceleration on the axial, radial velocity and temperature fields.

Introduction

The study of rotating disk flows has gained considerable interest among the researchers due to the theoretical interest and practical significance in many areas, such as centrifugal force, spinning disk reactors, viscometers, turbo engines, atmospheric and oceanic circulations, food processing technologies and many more. In order to convert the complete Navier-Stokes (NS) equations into a collection of ODEs, Von Kármán [1] first addressed the important contribution of the steady flow induced by an infinite rotating disk with a constant angular velocity in a viscous fluid. The slight errors in Kármán’s analysis were fixed by Cochran [2]. In the extrusion processes of the metal and plastic industries, the flow created by a stretching sheet or disk is crucial (see Ref. [3]). In this field of research, Crane [4] first introduced the pioneering work, and later Wang [5] extended this problem into the three-dimensional (3D) case. After that Fang [6] studied the combined effects of disk rotating and disk stretching. Further, Turkyilmazoglu [7] extended Fang’s problem [6] by incorporating a magnetic field, joule heating and viscous dissipation effects. The flow between two parallel rotating discs are found in Refs. [8,9,10,11] with diverse physical effects.

In the past several decades, there has been a lot of research done on the non-uniqueness solutions for self-similar equations of various boundary layer flows. Libby [12] studied a general 3D stagnation point flow and found dual solutions for negative values of the velocity gradients ratio in a two-dimensional (2D) case. Miklavčič and Wang [13] considered the viscous flow over a shrinking sheet for both the 2D and axisymmetric cases. For the 2D case, they discovered dual solutions when the suction parameter value is more than 2, and for the axisymmetric case, an infinite number of solutions for a particular value of the suction parameter. Later, Wang [14] investigated the stagnation point flow towards a shrinking sheet and discovered that only the shrinking case depicts dual solutions structure. Very recently, Rehman et al. [15] analytically obtained dual solutions within a limite range of stretching/shrinking parameter through a novel least square method. Additionally, the review of the literature shows that an effort has been made to look into the possibility of dual solutions within the context of Von-Kármán flow (see Refs. [16, 17]). Recently, Naganthran et al. [18] obtained dual solutions on the swirling flow over a stretching/shrinking rotating disk.

The unsteady Kármán flow with deceleration was initially investigated by Watson and Wang [19]. Later, this problem was extended to a porous rotating disk by Watson et al. [20]. This issue was subsequently developed to include a porous rotating disc with a magnetic field by Chandrasekar and Nath [21]. They [21] formulated this problem into semi-similar and self-similar cases and discussed these cases in detail. Fang and Tao [22] combined the work of Ref. [19] and Ref. [6]. A recent investigation on the unsteady flow of nanofluid over a rotating disk with various flow parameters was conducted by Hayat et al. [23].

In all the above investigations, the fluid has been assumed as Newtonian fluid. Non-Newtonian fluids, however, have been found to be more useful in industries application. In general, fluids with heavy molecular weights which are frequently used in plastic and chemical industries do not obey the Newton’s law of viscosity. Paints, mud, oil, blood, egg whites, softened chocolate, nylon, lubricants, colloids and so on exhibit non-Newtonian fluid behaviour. These fluids show a unique feature known as memory effect. Due to the intermolecular nature inside viscoelastic fluids cause sustainable stress that does not allow it to disappear immediately upon evacuation. The non-Newtonian fluid behaviour derived by Reiner [24] and Rivlin [25] can satisfactorily predict flow behaviors of many ploymers, food products, biological and geological materials. For these several applications of non-Newtonian fluids in industries, we have considered Reiner-Rivlin fluid model in this present study. Several authors discussed the study of Von Kármán flow of various non-Newtonian fluids with various physical characteristics. In the review article, Rajagopal [26] discussed the flow up to 1991 of various non-Newtonian fluids caused by a revolving disk in detail. Also the unsteady flow of RR fluid over a rotating was first quantitatively explored by Attia [27] in 2003, and his work was further expanded by him [28] in 2005 with the inclusion of suction/injection effect. Further, Sahoo [29] investigated the steady Kármán flow of RR fluid with the effects of partial slip, joule heating and viscous dissipation. Recently, Tabassum and Mustafa [30] revisited the steady Kármán flow of RR fluid with the partial slip condition and corrected some inaccuracies of earlier reported momentum and heat equations. Very recently, Naqvi et al. [31] numerically studied the steady Kármán flow of RR nanofluid over a rough rotating disk with various slip conditions.

Keeping the applications in mind of stretchable surface in extrusion process and non-Newtonian fluids in chemical and plastic industries, the present study is devoted to investigate the unsteady flow and heat transfer of Reiner-Rivlin fluid over a stretchable rotating disk with deceleration. To the best of authors knowledge, not a single attempt has so far been communicated regarding our proposed flow model. Thus, our intention of this current study is to fill this gap. This new problem is an extension of Fang and Tao [22] with the inlcusion of Reiner-Rivlin fluid and heat transfer. The originality of this current study is shown in Table 1. We solve the self-similar equations numerically and scrutiny the dual solutions characteristics on the shear stresses, torque, nusselt number, velocity and temperature fields through graphs and tabular forms.

Table 1 Novelty of present study

Description of the Problem

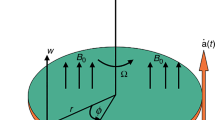
Consider an unsteady flow of RR fluid over a stretchable rotating disk that coincides with the plane $z=0$ and flow occupies in the area $z>0$. The physical sketch of the flow configuration is shown in Fig. 1. Let $u_r, u_\phi ~\text {and}~u_z$ be the velocity components in the directions of the cylindrical coordinate system $r, \phi ~\text {and}~z$ respectively. Assume that the angular velocity $\Omega (t)$ of the disk is inversely proportional to time and has the form $\Omega (t)=\frac{\omega }{1-ct}$, where c and $\omega (>0)$ are constants with dimension $(time)^{-1}$. Following, Fand and Tao [22], we consider $u_\phi (r,\phi ,0)=\Omega (t) r$ and $u_r(r,\phi ,0)=\Omega (t)\lambda r$, where $\lambda$ is a uniform stretching rate in radial direction and t is the time. The ambient fluid temperature $T_\infty$ and wall temperature $T_w$ are taken to be constants. The following equation is the constitutive equation for RR fluid:

$$\begin{aligned} \tau ^i_j=-p\delta ^i_j+\mu e^i_j+\mu _c e^i_k e^k_j; \quad e^j_j=0, \end{aligned}$$

(1)

Fig. 1

Flow configuration

where p denotes the pressure, $\delta ^i_j$ denotes the Kronecker symbol, $\mu$ and $\mu _c$ denote the coefficient of viscosity and cross viscosity respectively. Under these assumptions, the equation of continuity, momentum and linear heat transfer equations of an unsteady flow over a rotating disk are given below (see Refs. [27, 28, 30]):

$$\begin{aligned}{} & {} \frac{\partial }{\partial r}(ru_r)+\frac{\partial }{\partial z}(ru_z)=0, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \rho \left( \frac{\partial u_r}{\partial t}+u_r\frac{\partial u_r}{\partial r}+u_z\frac{\partial u_r}{\partial z}-\frac{u^2_\phi }{r}\right) =\frac{\partial \tau ^r_r}{\partial r}+\frac{\partial \tau ^r_z}{\partial z}+\frac{\tau ^r_r-\tau ^\phi _\phi }{r}, \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \rho \left( \frac{\partial u_\phi }{\partial t}+u_r\frac{\partial u_\phi }{\partial r}+u_z\frac{\partial u_\phi }{\partial z}+\frac{u_r u_\phi }{r}\right) =\frac{1}{r^2}\frac{\partial }{\partial r}\left( r^2\tau ^\phi _\phi \right) +\frac{\partial \tau ^z_\phi }{\partial z}+\frac{\tau ^r_\phi -\tau ^\phi _r}{r}, \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \rho \left( \frac{\partial u_z}{\partial t}+u_r\frac{\partial u_z}{\partial r}+u_z\frac{\partial u_z}{\partial z}\right) =\frac{1}{r}\frac{\partial (r\tau ^r_z)}{\partial r}+\frac{\partial \tau ^z_z}{\partial z}, \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \rho c_p\left( \frac{\partial T}{\partial t}+u_r\frac{\partial T}{\partial r}+u_z\frac{\partial T}{\partial z}\right) =k\frac{\partial ^2 T}{\partial z^2}, \end{aligned}$$

(6)

where $\rho$, $c_p$ and k are the fluid density, specific heat capacity and thermal conductivity respectively. The components of strain rate tensor are given below:

$$\begin{aligned} \left. \begin{aligned} e^r_r&=2\frac{\partial u_r}{\partial r},\quad e^\phi _\phi =2\frac{u_r}{r},\quad e^z_z=2\frac{\partial u_z}{\partial z},\\ e^r_\phi&=e^\phi _r=r\frac{\partial }{\partial r}\left( \frac{u_\phi }{r}\right) ,\quad e^z_\phi =e^\phi _z=\frac{\partial u_\phi }{\partial z},\quad e^r_z=e^z_r=\frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}. \end{aligned}\right\} \end{aligned}$$

(7)

From Eq. (1), the components of $\tau ^i_j$ are written as follow:

$$\begin{aligned}{} & {} \tau ^r_r=-p+\mu \left( 2\frac{\partial u_r}{\partial r}\right) +\mu _c\left\{ 4\left( \frac{\partial u_r}{\partial r}\right) ^2+\left( \frac{\partial u_\phi }{\partial r}-\frac{u_\phi }{r}\right) ^2+\left( \frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right) ^2\right\} , \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \tau ^z_r= \mu \left( \frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right) \nonumber \\{} & {} +\mu _c\left\{ \left( 2\frac{\partial u_r}{\partial r}\right) \left( \frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right) +\left( \frac{\partial u_\phi }{\partial r}-\frac{u_\phi }{r}\right) \left( \frac{\partial u_\phi }{\partial z}\right) +\left( \frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right) \left( 2\frac{\partial u_z}{\partial z}\right) \right\} \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \tau ^\phi _\phi = -p+\mu \left( \frac{2u_r}{r}\right) +\mu _c\left\{ \frac{4u_r^2}{r^2}+\left( \frac{\partial u_\phi }{\partial r}-\frac{u_\phi }{r}\right) ^2+\left( \frac{\partial u_\phi }{\partial z}\right) ^2 \right\} \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \begin{aligned} \tau ^r_\phi =&\mu \left( \frac{\partial u_\phi }{\partial r}-\frac{u_\phi }{r}\right) +\mu _c\left\{ \left( 2\frac{\partial u_r}{\partial r}\right) \left( \frac{\partial u_\phi }{\partial r}-\frac{u_\phi }{r}\right) \right. \\&\left. +\left( \frac{\partial u_\phi }{\partial r}-\frac{u_\phi }{r}\right) \left( \frac{2u_r}{r}\right) +\left( \frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right) \left( \frac{\partial u_\phi }{\partial z}\right) \right\} \end{aligned} \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \begin{aligned} \tau ^z_\phi =&\mu \left( \frac{\partial u_\phi }{\partial z}\right) \\&+\mu _c\left\{ \left( \frac{\partial u_\phi }{\partial r}-\frac{u_\phi }{r}\right) \left( \frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right) +2\left( \frac{u_r}{r}\right) \left( \frac{\partial u_\phi }{\partial z}\right) +2\left( \frac{\partial u_\phi }{\partial z}\right) \left( \frac{\partial u_z}{\partial z}\right) \right\} \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned}{} & {} \tau ^z_z= -p+\mu \left( 2\frac{\partial u_z}{\partial z}\right) +\mu _c\left\{ \left( \frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right) ^2 +\left( \frac{\partial u_\phi }{\partial z}\right) ^2+4\left( \frac{\partial u_z}{\partial z}\right) ^2\right\} \end{aligned}$$

(13)

subject to the boundary conditions (BCs)

$$\begin{aligned}{} & {} u_r=\Omega (t) \lambda r,\quad u_\phi =\Omega (t) r, \quad u_z=0, \quad T=T_w~~\text {at}~~z=0, \end{aligned}$$

(14a)

$$\begin{aligned}{} & {} u_r \rightarrow 0, \quad u_\phi \rightarrow 0, \quad T \rightarrow T_\infty ~~\text {as}~~z \rightarrow \infty . \end{aligned}$$

(14b)

Follwing Ref. [33], the angular velocity $\Omega (t)$ is defined by $\Omega (t)=\frac{\omega }{1-\beta t^*},$ where $t^*=\omega t,~ 1-\beta t^*>0$. Then we present the subsequent similarity transformations:

$$\begin{aligned} \left. \begin{aligned} \eta&=(\Omega (t)/\nu )^{1/2} z,\quad u_r=\Omega (t) r \mathcal {F}'(\eta ),\quad u_\phi =\Omega (t) r \mathcal {G}(\eta ),\\ u_z&=-2(\Omega (t) \nu )^{1/2} \mathcal {F}(\eta ), \quad p=-\Omega \rho \nu \mathcal {P}(\eta ), \quad T=T_\infty +(T_w-T_\infty ) \Theta (\eta ). \end{aligned}\right\} \end{aligned}$$

(15)

After substituting the stress tensors $\tau ^i_j$ and the similarity transformations (15) into the Eqs. (2) to (6), we obtain the following set of ODEs as follow:

$$\begin{aligned}{} & {} \mathcal {F}'''+2\mathcal {F}\mathcal {F}''-\mathcal {F}'^2+\mathcal {G}^2 +K\left( \mathcal {F}''^2-2\mathcal {F}'\mathcal {F}'''-\mathcal {G}'^2\right) -\beta \left( \frac{\eta }{2} \mathcal {F}''+\mathcal {F}'\right) =0, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \mathcal {G}''-2\mathcal {F}'\mathcal {G}+2\mathcal {F}\mathcal {G}' +2K\left( \mathcal {F}''\mathcal {G}'-\mathcal {F}'\mathcal {G}''\right) -\beta \left( \frac{\eta }{2} \mathcal {G}'+\mathcal {G}\right) =0, \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \Theta ''+Pr\left( 2\mathcal {F}-\beta \frac{\eta }{2}\right) \Theta '=0. \end{aligned}$$

(18)

and the relevant no-slip BCs (14) reduced to

$$\begin{aligned}{} & {} \mathcal {F}(0)=0,\quad \mathcal {F}'(0)=\lambda ,\quad \mathcal {G}(0)=1,\quad \Theta (0)=1, \end{aligned}$$

(19a)

$$\begin{aligned}{} & {} \mathcal {F}'(\infty )=0,\quad \mathcal {G}(\infty )=0,\quad \Theta (\infty )=0. \end{aligned}$$

(19b)

where $\beta =\frac{c}{\omega }$ and $K=\frac{\mu _c}{\mu }\Omega (t)$ denote the non-dimensional unsteadiness parameter and cross-viscous parameter respectively, $Pr=\frac{\mu c_p}{k}$ denotes the Prandtl number, $\lambda ~(>0)$ denotes the disk stretching parameter and $\beta >\text {or}<0$ corresponding to disk acceleration or deceleration.

It is noted that for $K=0$, Eqs. (16) and (17) with the BCs (19) recover the governing equations of Fang and Tao [22] for Newtonian fluid. On the other hand, $\beta =0$ recover the governing equations of Tabassum and Mustafa [30] for RR fluid. Thus our obtained self-similar Eqs. (16) to (18) are new and accurate.

From the point of engineering prospective, the most important physical quantities are the torque, skin friction coefficient and the rate of heat transfer. For a region of radius R, the torque ${\bar{T}}$ is defined by (Refs. [19, 30])

$$\begin{aligned} {\bar{T}}=2\pi \int _{0}^{R} \tau ^z_\phi |_{z=0} r^2 dr =\frac{\pi \rho (\nu )^{1/2}(\Omega (t))^{3/2}}{2}(1-2K\mathcal {F}'(0)) R^4 \mathcal {G}'(0). \end{aligned}$$

(20)

The skin friction coefficient $C_f$ is defined by (Ref. [30])

$$\begin{aligned} C_f=\frac{\sqrt{\tau ^2_r+\tau ^2_\phi }}{\rho (r\Omega (t))^2}, \end{aligned}$$

(21)

where $\tau _r$ and $\tau _\phi$ are radial and tangential shear stresses respectively. Using the similarity variables (15), we obtain

$$\begin{aligned} Re^{1/2}_xC_f=\sqrt{F''(0)^2+G'(0)^2}. \end{aligned}$$

(22)

The heat transfer rate from the wall surface of the disk to the fluid can be obtained using the Fourier’s law, $q=\left. -k\frac{\partial T}{\partial z}\right| _{z=0}$ and the local Nusselt number $Nu_x$ is defined by

$$\begin{aligned} Nu_x=\frac{rq}{k(T_w-T_\infty )}. \end{aligned}$$

(23)

Again using the similarity variables (15) into (23) yields

$$\begin{aligned} Re^{-1/2}_xNu_x=-\theta '(0), \end{aligned}$$

(24)

where $Re_x=\frac{\Omega (t) r^2}{\nu }$ is the local Reynolds number.

Numerical Method

The set of highly nonlinear ODEs (16) to (18) along with BCs (19) may solve either by some series solutions or by shooting method, but both methods are very tedious. The Matlab package “bvp4c” is one of the most popular modern-day software tools that can solve nonlinear BVPs with high accuracy with multi-point BCs. In fact, this code has capable to find multiple solutions (if exists) with the aid of appropriate initial guesses. The reader may consult with the brief note reported by Shampine et al. [34] for further details. In this study, Eqs. (16) to (19) are solved using the “bvp4c” Matlab solver. The infinite domain $[0, \infty )$ is replaced by a finite domain $[0, \eta ^*]$ and the relative tolerance is fixed to $10^{-7}$. Dual solutions exist of the obtained self-similar equations only for negative values of the unsteadiness parameter, $\beta$. The value of $\eta ^*\sim 8$ is found sufficient for both the solution branches to satisfy the far-field BCs (19b). To initiate the “bvp4c” routine in Matlab, we have to first convert the self-similar Eqs. (16) to (18) into a system of (3+2+2) first order ODEs given below:

$$\begin{aligned} \left. \begin{array}{ll} &{}f^{\prime }(1)=f(2),\\ &{}f^{\prime }(2)=f(3),\\ &{}f^{\prime }(3)=\frac{\beta \Big (\frac{\eta }{2}f(3)+f(2)\Big ) -2f(1)f(3)+f(2)^2-f(4)^2-K\Big (f(3)^2-f(5)^2\Big )}{1-2Kf(2)},\\ &{}f^{\prime }(4)=f(5),\\ &{}f^{\prime }(5)=\frac{\beta \Big (\frac{\eta }{2}f(5) +f(4)\Big )+2f(2)f(4)-2f(1)f(5)-2Kf(3)f(5)}{1-2Kf(2)},\\ &{}f^{\prime }(6)=f(7),\\ &{}f^{\prime }(7)=Pr\Big (\beta \frac{\eta }{2}-2f(1)\Big )f(7),\\ \end{array}\right\} \end{aligned}$$

(25)

where $\mathcal {F}=f(1),~\mathcal {F'}=f(2),~\mathcal {F''}=f(3), ~\mathcal {G}=f(4),~\mathcal {G'}=f(5),~\Theta =f(6),~\Theta '=f(7)$ and the BCs (19) are inserted in the following form

$$\begin{aligned} \left. \begin{array}{ll} &{}f_{a}(1),\\ &{}f_{a}(2)-\lambda ,\\ &{}f_{a}(4)-1,\\ &{}f_{a}(6)-1,\\ &{}f_{b}(2),\\ &{}f_{b}(4),\\ &{}f_{b}(6),\\ \end{array}\right\} \end{aligned}$$

(26)

where the subscripts “a” and “b” denote the initial and terminal points of the domain $[0, \eta ^*]$. To verify the accuracy of our numerical technique, comparative data for the Newtonian fluid ($K=0$) with the results published by Fang and Tao [22] have been shown in Table 2. It is discovered that the comparisons are in perfect agreement.

Results and Discussion

The variations of $\mathcal {F}''(0)$, $\mathcal {G}'(0)$ and $-\Theta '(0)$ with the unsteadiness parameter $\beta$ for several values of the stretching parameter $\lambda$ are depicted in Figs. 2, 3 and 4 when $K=0.2$ for both the solution branches. For better understanding, some numerical values are given in Table 3 for several combinations of the governing parameters. In upper solution branches (USB), each curve of $\mathcal {F}''(0)$ and $\mathcal {G}'(0)$ are monotonically increasing with an increase in $|\beta |$ for any fixed $\lambda$. Furthermore, it is observed that values of $\mathcal {G}'(0)$ decrease with an increase in stretching parameter $\lambda$ for all $\beta$. The values of $\mathcal {F}''(0)$ also decrease with an increase in $\lambda$ for small $|\beta |$; however, there are some crossovers for large $|\beta |$. In lower solution branches (LSB), each curve of $\mathcal {F}''(0)$ decreases with an increase in $|\beta |$ for any fixed $\lambda$; but for small $|\beta |$, each curve of $\mathcal {G}'(0)$ initially increase, and then decrease for large $|\beta |$. On the other hand, the values of $\mathcal {F}''(0)$ and $\mathcal {G}'(0)$ decrease with an increase in $\lambda$ for small $|\beta |$ but for large $|\beta |$, we have found complicated trends. However, each curve of $-\Theta '(0)$ is monotonically increasing for both the increase of $|\beta |$ and $\lambda$ in both the solution branches.

It is seen in Figs. 2 and 3 that there are some values of $\beta$ for which $\mathcal {F}''(0)=0$ and $\mathcal {G}'(0)=0$. The value of $\beta$ for which $\mathcal {F}''(0)=0$ is defined by $\beta _1^*$, which leads to a frictionless stretching disk as reported by Fang and Tao [22]. Again the value of $\beta$ for which $\mathcal {G}'(0)=0$ is defined by $\beta _2^*$. The torque ${\bar{T}}$ defined in Eq. (20) is related to the value of $\mathcal {G}'(0)$. The rotating disk experiences a resistance for $0\ge \beta >\beta _2^*$ because of the negative value of $\mathcal {G}'(0)$ as evident in Fig. 3. The disk experiences a torque in the rotation direction due to the positive value of $\mathcal {G}'(0)$ when $\beta <\beta _2^*$ as reported by Watson and ang [19]. But the torque becomes zero when $\beta =\beta _2^*$. This interesting feature can be related to the decay of a mass-free rotating disk. According to Watson and Wang [19], if an outside torque rotates a light solid disk, and after removing the torque, the disk still rotates because of the residual rotation of the fluid. The numerical values of $\beta _1^*$ and $\beta _2^*$ are given in Table 4 for several values of the controlling parameters. It is observed that both values increase in magnitude with the increase of $\lambda$ for some fixed K.

Figs. 5, 6, 7, 8, 9, 10, 11 and 12 respectively depict the variations of three velocity components $\mathcal {F}(\eta ),~\mathcal {F}'(\eta )~\text {and}~\mathcal {G}(\eta )$ in z, r and $\phi$ directions and the temperature profile $\Theta (\eta )$ for various pertinent parameters for both the branches. In USB in Fig. 5, it is observed that the axial velocity $\mathcal {F}(\eta )$ increases as the unsteadiness increase. Also, the value of $\mathcal {F}(\infty )$ increases with the increase of $|\beta |$, which is quite different with the results of Fang and Tao [22]. This may happen due to effect of cross-viscous parameter K, i.e. more fluid being pumped towards the disk surface for fast deceleration. The radial $\mathcal {F}'(\eta )$ and circumferential $\mathcal {G}(\eta )$ velocities increase with an increase in $|\beta |$ for small value of $\eta$ but decrease for large $\eta$. The radial velocity experiences an overshoot near the disk for fast deceleration and the similar trend is observed for Newtonian fluid (see Ref. [22].) But the temperature profile $\Theta (\eta )$ decreases when $|\beta |$ increases, which means the temperature reaches faster to the ambient fluid temperature for higher $|\beta |$. This result can be utilized in cooling process. On the other hand, the LSB in Fig. 6 shows some different characters than the USB. It is observed that each curve of axial velocity $\mathcal {F}(\eta )$ increases very near to the disk surface, then after a certain distance far away from the disk, they decrease. The values of $\mathcal {F}(\eta )$ decrease for higher deceleration (for large $|\beta |$). Each curve of radial and circumference velocity profiles $\mathcal {F}'(\eta )$ and $\mathcal {G}(\eta )$ decrease near the disk surface, and thereafter, they begin to increase far away from the disk and converge to zero. The unique difference between LSB with USB is that these three profiles show reversal flow. However, the temperature profile in LSB shows the same behaviour as the temperature profile in USB. The common feature for these four profiles is that the boundary layer and the thermal boundary layer thicknesses reduce for higher deceleration.

The effectiveness of $\lambda$ at $\beta =-2$ and $K=0.2$ are elucidated in Figs. 7 and 8 respectively for both the solution branches. In USB, the behaviour of axial velocity shows similar as discussed in Fig. 5. The radial velocity increase with the increase of $\lambda$, which means that more amounts of fluids are pumped towards the disk and the circumferential velocity decays faster to zero. The temperature profile decreases as $\lambda$ increases, which leading heat loss for large stretching. In such cases, stretching will play an important role in cooling a system. On the other hand, all four profiles in LSB show a similar trend, as discussed in Fig. 6.

Figs. 9 and 10 depicts the variations of velocity and temperature profiles for various values of non-Newtonian parameter K at $\lambda =1$ for slow deceleration (i.e., $\beta =-0.5$) for both the solution branches respectively. In USB, axial and radial velocities decrease with an increase in K, which means that less fluid is drawn axially and pushed away in the radial direction. The circumferential velocity and temperature profiles increase with an increase in K. It is observed that the behaviour of K on $\mathcal {F}(\eta )$, $\mathcal {G}(\eta )$ and $\Theta (\eta )$ profiles is qualitatively similar to steady Von Kármán flow of RR fluid (see Figs. 4 and 5 of Tabassum and Mustafa [30]). As was expected, the effect of K on these three profiles is preserved in the slow deceleration case. In LSB, all three velocity profiles increase near the disk and decrease away from it when K is incremented. But the $\Theta (\eta )$ profile decreases when K increases.

The effectiveness of K for fast deceleration (i.e., $\beta =-5$) on velocity and temperature profiles are shown in Figs. 11 and 12 for both branches respectively. In Fig. 11, the interesting observation in USB for fast deceleration is that all profiles except circumferential velocity profile $\mathcal {G}$ show the opposite behaviour than slow deceleration (see Fig. 9), which is a new finding of this current study. In Fig. 12, all three velocity profiles in LSB show similar variation trends, but the temperature profile shows the opposite trend compare to Fig. 10.

Fig. 13 demonstrates the influence of Prandtl number Pr on $\Theta (\eta )$ profile for both the branches at $\beta =-2$, $\lambda =1$ and $K=0.2$. In both the branches, it was expected that $\Theta (\eta )$ decrease with an increase in Pr, and thus the thermal boundary layer thickness gets decreased. The thermal boundary layer thickness in USB is lower than LSB.

Table 2 Comparison table of $\mathcal {F}''(0)$ and $\mathcal {G}'(0)$ with the available data in literature for various values of $\beta$ with $K=0$ and $\lambda =2$

Table 3 Numerical values of $\mathcal {F}''(0)$, $\mathcal {G}'(0)$ and $\Theta '(0)$ for several values $\lambda$, $\beta$ and K for both the solution branches

Table 4 Values of $\beta _1^*$ and $\beta _2^*$ for several values of K and $\lambda$

Fig. 2

Plot of $\mathcal {F}''(0)$ with $\beta$ for various $\lambda$ at $K=0.2$

Fig. 3

Plot of $\mathcal {G}'(0)$ with $\beta$ for various $\lambda$ at $K=0.2$

Fig. 4

Plot of $-\Theta '(0)$ with $\beta$ for various $\lambda$ at $K=0.2$

Fig. 5

Upper solution branch at $\lambda =1$ and $K=0.2$

Fig. 6

Lower solution branch at $\lambda =1$ and $K=0.2$

Fig. 7

Upper solution branch at $\beta =-2$ and $K=0.2$

Fig. 8

Lower solution branch at $\beta =-2$ and $K=0.2$

Fig. 9

Upper solution branch at $\beta =-0.5$ and $\lambda =1$

Fig. 10

Lower solution branch at $\beta =-0.5$ and $\lambda =1$

Fig. 11

Upper solution branch at $\beta =-5$ and $\lambda =1$

Fig. 12

Lower solution branch at $\beta =-5$ and $\lambda =1$

Fig. 13

Effects of Prandtl numbers in $\Theta (\eta )$ profile for (a) Upper and (b) Lower solution branches at $\beta =-2$, $\lambda =1$ and $K=0.2$

Conclusion

The unsteady flow induced by an infinite rotating stretchable disk with heat transfer of a non-Newtonian RR fluid with deceleration is studied. The similarity equations are obtained with the aid of similarity transformations. The self-similar solutions are obtained by employing an effective Matlab’s solver “bvp4c”. The following important aspects are drawn based on the present study:

• 1. Numerically dual solution branches are found of the Eqs. (16)–(19) when the unsteadiness parameter $\beta <0$. According to Fang and Tao [22], the LSB may not be practically reliable because the tangential velocity has negative direction as reflected in Figs. 6, 8, 12.

• 2. There exists some certain values $\beta _1^*$ for which $\mathcal {F}''(0)=0$, which leads to a frictionless stretching disk. The torque ${\bar{T}}$ is related to $\mathcal {G}'(0)$, and ${\bar{T}}$ becomes zero at some certain values $\beta _2^*$. The absolute values of $\beta _1^*$ and $\beta _2^*$ increase with an increase in $\lambda$ for some fixed K.

• 3. All three velocity profiles in LSB show reversal flow.

• 4. The momentum and thermal boundary layer thicknesses get reduced in both the branches with an increase in $|\beta |$ and $\lambda$.

• 5. For slow deceleration, the effect of K on $\mathcal {F}$, $\mathcal {G}$ and $\Theta$ profiles in USB is qualitatively similar to steady Kármán flow of RR fluid. But, for fast deceleration, the effect of K on $\mathcal {F}$, $\mathcal {F}'$ and $\Theta$ profiles in USB show opposite behavior corresponding to the profiles for slow deceleration.

• 6. Both the boundary layer thicknesses in USB are thinner than the LSB.

The present study may use as benchmark for further study of higher grade fluids. Also several thermal controlling effects like entropy generation, thermal radiation, Joule heating can be included in this present study to investigate thermal analysis. Literature survey indicates that nanofluids with various shape enhance the thermal conductivity and flow stability. Thus, the extension of present study on shape effects of nanofluids will be communicated in near future.