1 Introduction

The reliability analysis is to evaluate the probability that a product performs its intended performance under the given conditions. In the past decades, quite a lot of reliability analysis methods have been well developed such as the approximate methods, simulation methods and surrogate model-based methods [1, 2]. Most of the existing reliability analysis methods are based on the binary state assumption, where the boundary between the failure and safe domains is clearly defined. However, in some cases, this assumption may violate the reality. For example, different damage states are usually considered for seismic fragility analysis, such as slight damage, moderate damage, extensive damage and complete damage. And the failure threshold for each damage state is subjectively set [3]. For another example, the failure process of plastic materials often has four stages, i.e., elasticity, plasticity, necking, and fracture [4], which means that there is no clear distinction between success and failure, and the boundary between them is rather blurred. Under this context, the profust reliability theory was well established [5,6,7].

The profust reliability theory replaces the original binary state assumption by the fuzzy state assumption, i.e., there is a fuzzy failure domain between the failure and safe domains. The fuzzy state can be described by the membership function of the limit state function (LSF) to the fuzzy failure domain. However, the introduction of the membership function makes the profust reliability analysis (PRA) more complicated than the traditional reliability analysis. Some PRA methods [8, 9] based on the simple linear regression and numerical integral have been proposed, however they are not applicable to complicated problems. Feng et al. [10] transformed profust failure probability into an integral of classical failure probability. Then the profust failure probability was calculated by Gauss-Hermite quadrature in conjunction with crude Monte-Carlo simulation (MCS) or other smart simulation methods. This method is essentially a double-loop strategy, which was further improved by Ling et al. [11] by introducing the adaptive Kriging-based Monte Carlo simulation (AK-MCS) [12]. Zhang et al. [13] transformed this double-loop strategy into a single-loop version and proposed a more concise AK-MCS method. On basis of their works, Yang et al. [14] developed a novel active learning method based on the Kriging model to minimize the number of LSF evaluations in PRA.

However, most existing PRA methods are only applicable to time-independent problems. In fact, the performance of a structure will also vary with time when considering deterioration of structural resistance and material performance and the time-dependent environmental actions. Up to now, many effective time-dependent reliability analysis (TRA) methods have been developed under binary state assumption. The mainstream methods include the outcrossing rate-based methods [15,16,17], the extreme value methods [18,19,20], equivalent Gaussian process methods [21,22,23], and surrogate model-based methods [24,25,26,27]. Recently, Hu et al. [28] defined the time-dependent profust reliability analysis (TPRA) under fuzzy state based on the basic principle of PRA. Based on this new definition, it is imperative to develop an effective method for TPRA.

Therefore, the aim of this paper is to develop a novel TPRA method with fuzzy state. Firstly, a mixed efficient global optimization (MEGO) algorithm is developed to capture extreme values at all collocation points of sparse grid numerical integration (SGNI), where both collocation point and time variable are treated as input variables of Kriging model. Then, extreme value moments can be efficiently estimated by MEGO-based SGNI (MEGO-SGNI). Finally, the time-dependent profust failure probability is obtained by one-dimensional integral on the first four moments-based time-dependent failure probability. The innovations of this paper are concluded as follows:

  1. 1.

    Up to the authors’ knowledge, there is no work about estimating time-dependent profust failure probability using extreme value moments.

  2. 2.

    MEGO-SGNI algorithm is developed to estimate extreme value moments, which greatly saves the computational costs.

  3. 3.

    Time-dependent profust failure probability is reformulated as one-dimensional integral of the first four moments-based time-dependent failure probability, which permits estimating time-dependent profust failure probability by reusing the extreme value moment information.

Four numerical examples covering different types of membership functions, implicit LSFs and non-Gaussian random processes, are investigated, and the results indicate that the proposed method can equip engineers an effective tool to deal with time-dependent profust reliability problems with fuzzy state.

2 Time-dependent profust reliability analysis

For time-dependent problems, there are two kinds of probability inputs, i.e., random variable and random process, the latter of which is usually represented by standard normal random variables and time parameter based on the expansion optimal linear estimation (EOLE) method [29], the Karhunen–Loève (K–L) expansion [30, 31] or other strategies. Therefore, for the sake of simplicity, this paper unifies the input random variables and those random variables representing the input random process as input random vector X = [X1, X2, …, Xn]T. Let G(X, t) be the time-dependent LSF and its extreme value Ge(X) over the time interval of interests [0, T] can be expressed as follows [19, 20]:

$$G_{e} ({\mathbf{X}}) = \mathop {\min }\limits_{t \in [0,T]} G({\mathbf{X}},t)$$
(1)

In the traditional TRA, the state of the time-dependent structure is clearly classified as the safety one or the failure one. Let S = {G(X, t) > 0} denote the safe domain of time-dependent structure, F = {G(X, t) < 0} denote the failure domain of time-dependent structure, and B = {G(X, t) = 0} denote the boundary between safety domain S and failure domain F. Then, the time-dependent failure probability Pf(0, T) under binary state is defined by:

$$P_{f} (0,T) = \int {I[G_{e} ({\mathbf{x}}) < 0]f_{{\mathbf{X}}} ({\mathbf{x}})d{\mathbf{x}}}$$
(2)

where fX() is the joint probability density function (JPDF) of X; and I(·) is an indicator function of an event with value 1 if the event is true and 0 otherwise.

However, for some time-dependent structures, the boundary B between safety domain S and failure domain F may be time-dependent and fuzzy [28]. In this paper, the fuzzy domain \(\tilde{F}\) is assumed to be time-independent, whose degree of belonging to failure or safety is measured by a membership function \(u_{{\tilde{F}}} {[}G{(}{\mathbf{x}}{,}t{)]}\). Three types of commonly-used membership functions, including linear membership function \(u_{{\tilde{F}}}^{L} {[}G{(}{\mathbf{x}}{,}t{)]}\), normal membership function \(u_{{\tilde{F}}}^{N} {[}G{(}{\mathbf{x}}{,}t{)]}\) and Cauchy membership function \(u_{{\tilde{F}}}^{C} {[}G{(}{\mathbf{x}}{,}t{)]}\) are defined in Eqs.(3)–(5) and their specific diagrams are depicted in Fig. 1.

$$u_{{\tilde{F}}}^{L} [G{(}{\mathbf{x}}{,}t{)}] = \left\{ {\begin{array}{*{20}l} {1, \, G{(}{\mathbf{x}}{,}t{)} \le a_{1} } \hfill \\ {\frac{{a_{2} - G{(}{\mathbf{x}}{,}t{)}}}{{a_{2} - a_{1} }}{, }a_{1} \le G{(}{\mathbf{x}}{,}t{)} < a_{2} } \hfill \\ {0{, }G{(}{\mathbf{x}}{,}t{)} \ge a_{2} } \hfill \\ \end{array} } \right.$$
(3)
$$u_{{\tilde{F}}}^{N} [G{(}{\mathbf{x}}{,}t{)}] = \left\{ {\begin{array}{*{20}l} {1, \, G{(}{\mathbf{x}}{,}t{)} \le b_{1} } \hfill \\ {\exp \left[ { - \left( {\frac{{G{(}{\mathbf{x}}{,}t{)} - b_{1} }}{{b_{2} }}} \right)^{2} } \right]{, }G{(}{\mathbf{x}}{,}t{)} \ge b_{1} } \hfill \\ \end{array} } \right.$$
(4)
$$u_{{\tilde{F}}}^{C} [G{(}{\mathbf{x}}{,}t{)}] = \left\{ {\begin{array}{*{20}l} {1, \, G{(}{\mathbf{x}}{,}t{)} \le c_{1} } \hfill \\ {\frac{{c_{2} }}{{c_{2} + 10[G{(}{\mathbf{x}}{,}t{)} - c_{1} ]^{2} }}{, }G{(}{\mathbf{x}}{,}t{)} \ge c_{1} } \hfill \\ \end{array} } \right.$$
(5)

where a1 and a2, b1 and b2, and c1 and c2 are respectively the position and shape parameters of the linear, normal and Cauchy membership functions derived from the statistical data by the expert.

Fig. 1
figure 1

Three types of membership functions

Full size image

Based on the membership function \(u_{{\tilde{F}}} {[}G{(}{\mathbf{x}}{,}t{)]}\), Hu et al. [28] derived time-dependent profust failure probability as follows:

$$\tilde{P}_{f} (0,T) = \int {u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]}} f_{{\mathbf{X}}} ({\mathbf{x}})d{\mathbf{x}}$$
(6)

By introducing an auxiliary variable λ ∈ [0, 1], it can be proved that [9, 11]

$$u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]} = \int_{0}^{{u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]}}} 1 d\lambda + \int_{{u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]}}}^{1} 0 d\lambda = \int_{0}^{1} {I\{ \lambda - u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]\} }d\lambda }$$
(7)

Substituting Eq. (7) into Eq. (6) yields:

$$\tilde{P}_{f} (0,T) = \int_{0}^{1} {\int {I\{ \lambda - u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]\} }} f_{{\mathbf{X}}} ({\mathbf{x}})d{\mathbf{x}}} d\lambda = \int_{0}^{1} {P\{ \lambda < u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]}\} } d\lambda$$
(8)

Since \(u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}{)]}\) is a monotonically decreasing function with respect to Ge(x), it can be easily obtained that

$$\tilde{P}_{f} (0,T) = \int_{0}^{1} {P[G_{e} {(}{\mathbf{x}}{) < }u_{{\tilde{F}}}^{ - 1} (\lambda )]} d\lambda$$
(9)

If λ is treated as a standard uniform random variable, Eq. (9) can be rewritten as

$$\tilde{P}_{f} (0,T) = \int {I[G_{e} {(}{\mathbf{x}}{) < }u_{{\tilde{F}}}^{ - 1} (\lambda )]} f_{{\mathbf{X}}} ({\mathbf{x}})f_{\Lambda } (\lambda )d\lambda d{\mathbf{x}}$$
(10)

where \(f_{\Lambda } (\lambda )\) is the PDF of λ.

It can be seen from Eq. (10) that the time-dependent profust failure probability is transformed into a traditional time-dependent failure probability under binary state. According to Eqs. (6) and (10), there are two kinds of MCS methods available for estimating the time-dependent profust failure probability. The main procedures of the first kind of MCS method are shown as follows: Firstly, NMCS samples of X are generated according to fX(x). Then, evaluate extreme value at each sample by the time-discrete method, i.e., \(G_{e} {(}{\mathbf{x}}{)} = \mathop {\min }\limits_{{j = 1,2,\ldots,N_{T} }} G({\mathbf{x}},t_{j} )\), where NT is the number of discrete time nodes. Finally, the time-dependent profust failure probability is approximated by:

$$\tilde{P}_{f} (0,T) \approx \frac{1}{{N_{MCS} }}\sum\limits_{i = 1}^{{N_{MCS} }} {u_{{\tilde{F}}} {[}G_{e} {(}{\mathbf{x}}_{i} {)]}}$$
(11)

The first two steps of the second kind of MCS method are similar to those of the first kind, excluding that NMCS sample points of standard uniform variable λ are also required to generate. In the end, the time-dependent profust failure probabilities at all time nodes are given by:

$$\tilde{P}_{f} (0,T) \approx \frac{1}{{N_{MCS} }}\sum\limits_{i = 1}^{{N_{MCS} }} {I[G_{e} {(}{\mathbf{x}}_{i} {) < }u_{{\tilde{F}}}^{ - 1} (\lambda_{i} )]}$$
(12)

For either of these two kinds of MCS methods, its total number of LSF calls is Ncalls = NMCS × NT, which is computationally inefficient. Therefore, a more efficient method based on the extreme value moment information of LSF will be proposed in the next section.

3 Proposed approach for TPRA

3.1 Estimating extreme value moments using MEGO-SGNI

Routinely, the kth raw moment of extreme values can be defined as follows:

$$v_{{kG_{e} }} = \int {G_{e} ({\mathbf{x}})} f_{{\mathbf{X}}} ({\mathbf{x}})d{\mathbf{x}}$$
(13)

However, the multidimensional integral in Eq. (13) is intractably evaluated by direct numerical integration due to its complicated and multidimensional integral function. In this study, the sparse grid numerical integration (SGNI) [32, 33] is adopted herein to calculate it because of its good tradeoff between efficiency and accuracy. Based on the Smolyak algorithm [34], the sparse grid quadrature formulas for estimating \(v_{{kG_{e} }}\) can be derived as follows:

$$v_{{kG_{e} }} = \sum\limits_{{{\varvec{i}} \in H(q,n)}} {( - 1{)}^{q + n - |i|} \left( {\begin{array}{*{20}c} {n - 1} \\ {q + n - |{\varvec{i}}|} \\ \end{array} } \right)} \times \sum\limits_{{j_{1} = 1}}^{{m_{{i_{1} }} }} \cdots \sum\limits_{{j_{n} = 1}}^{{m_{{i_{n} }} }} {[G_{e} (x_{{j_{1} }}^{{i_{1} }} , \ldots ,x_{{j_{n} }}^{{i_{n} }} )]^{k} p_{{j_{1} }}^{{i_{1} }} \cdots p_{{j_{n} }}^{{i_{n} }} }$$
(14)

where \(G_{e} (x_{{j_{1} }}^{{i_{1} }} ,\ldots,x_{{j_{n} }}^{{i_{n} }} )\) is the extreme value at the collocation point \(x_{{j_{1} }}^{{i_{1} }} ,\ldots,x_{{j_{n} }}^{{i_{n} }}\) and given by:

$$G_{e} (x_{{j_{1} }}^{{i_{1} }} , \ldots ,x_{{j_{n} }}^{{i_{n} }} ) = \mathop {\min }\limits_{t \in [0,T]} G{(}x_{{j_{1} }}^{{i_{1} }} , \ldots ,x_{{j_{n} }}^{{i_{n} }} ,t)$$
(15)

and \(p_{{j_{i} }}^{{i_{i} }} = \frac{1}{\sqrt \pi }\zeta_{{j_{i} }}^{{i_{i} }}\) and \(x_{{j_{i} }}^{{i_{i} }} = \sqrt 2 \xi_{{j_{i} }}^{{j_{i} }}\) are the weights and abscissas, in which \(\zeta_{{j_{i} }}^{{i_{i} }}\) and \(\xi_{{j_{i} }}^{{i_{i} }}\) are the weights and abscissas in the Gauss-Hermite quadrature formula; ji = 1, …, \(m_{{i_{i} }}\); \({\varvec{i}} = (i_{1} , \ldots ,i_{n} ) \in N_{ + }^{n}\); q denotes the accuracy level; and the sparse gird H(q, n) is defined by:

$$H(q,n) = \left\{ {{\varvec{i}} \in N_{ + }^{n} ,{\varvec{i}} \ge 1:q + 1 \le \sum\limits_{i = 1}^{n} {i_{i} \le q + n} } \right\}$$
(16)

Let the number of all collocation points of SGNI be NSGNI, which depends on the accuracy level q and dimension n. Then, a total of NSGNI extreme values need to be evaluated at all collocation points. Recently, Zhao et al. [20] proposed an adaptive independent Kriging modelling method to approximate the extreme value responses at all collocation points of SGNI. In this method, time points are sampled independently from the collocation points, thus it does not consider the interaction effects of the collocation points and time during the Kriging modelling. Inspired by Hu and Du [25], a MEGO algorithm is proposed herein to evaluate these extreme values with high computational efficiency. Its main procedures are elaborated as follows:

Step 1: Generate a NSGNI-size initial time training set \({\mathbf{t}}^{s} = [t_{1} ,t_{2} , \ldots ,t_{{N_{SGNI} }} ]^{T}\) by Latin hypercube sampling (LHS) method [35]. The NSGNI-size collocation point set is regarded as the initial sample training set \({\mathbf{x}}^{s} = [{\mathbf{x}}_{1} ,{\mathbf{x}}_{2} ,\ldots,{\mathbf{x}}_{{N_{SGNI} }} ]^{T}\). Then, the following initial combined training set [xs, ts] can be obtained:

$$[{\mathbf{x}}_{s} ,{\mathbf{t}}_{s} ] = \left[ {\begin{array}{*{20}c} {{\mathbf{x}}_{1} } & {t_{1} } \\ {{\mathbf{x}}_{2} } & {t_{2} } \\ \vdots & \vdots \\ {{\mathbf{x}}_{{N_{SGNI} }} } & {t_{{N_{SGNI} }} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \cdots & {x_{1n} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{{N_{SGNI} 1}} } & {x_{{N_{SGNI} 2}} } & \cdots & {x_{{N_{SGNI} n}} } \\ \end{array} \begin{array}{*{20}c} {t_{1} } \\ {t_{2} } \\ \vdots \\ {t_{{N_{SGNI} }} } \\ \end{array} } \right]$$
(17)

Step 2: Evaluating LSF at the initial combined training set [xs, ts] yields a response set \({\mathbf{G}}^{s} = [G({\mathbf{x}}_{1} ,t_{1} ),G({\mathbf{x}}_{2} ,t_{2} ),\ldots,G({\mathbf{x}}_{{N_{SGNI} }} ,t_{{N_{SGNI} }} )]^{T}\).

Step 3: Regard Gs as the initial solution of \({\mathbf{G}}_{e} = [G_{e} ({\mathbf{x}}_{1} ),G_{e} ({\mathbf{x}}_{2} ),\ldots,G_{e} ({\mathbf{x}}_{{N_{SGNI} }} )]^{T}\).

Step 4: Let i = 1.

Step 5: Construct the mixed Kriging model \(\hat{G}({\mathbf{X}},t)\) based on [xs, ts] and Gs, where \(\hat{G}({\mathbf{X}},t)\) is called the mixed Kriging model because it is the function of X and t not just t.

Step 6: Based on the expected improvement (EI) function, identify the best training time point:

$$t^{ * } = \mathop {\arg \max }\limits_{t \in [0,T]} [EI(t)]$$
(18)

where the EI function EI (∙) is given by [36]:

$$EI(t) = [G_{e} ({\mathbf{x}}_{i} ) - \mu_{{\hat{G}}} ({\mathbf{x}}_{i} ,t)]\Phi \left( {\frac{{G_{e} ({\mathbf{x}}_{i} ) - \mu_{{\hat{G}}} ({\mathbf{x}}_{i} ,t)}}{{\sigma_{{\hat{G}}} ({\mathbf{x}}_{i} ,t)}}} \right) + \sigma_{{\hat{G}}} ({\mathbf{x}}_{i} ,t)\phi \left( {\frac{{G_{e} ({\mathbf{x}}_{i} ) - \mu_{{\hat{G}}} ({\mathbf{x}}_{i} ,t)}}{{\sigma_{{\hat{G}}} ({\mathbf{x}}_{i} ,t)}}} \right)$$
(19)

Step 7: Determine whether the following condition are fulfilled:

$$EI{(}t^{ * } ) \le |G_{e} ({\mathbf{x}}_{i} )|\varepsilon_{EI}$$
(20)

where εEI is the error coefficient and usually taken as 1% or 0.1%.

If the condition is met, terminate the training process, and output the current solution of Ge(xi). Otherwise, add [xi, t*] and G(xi, t*) into the current training set [xs, ts] and Gs, respectively, and update the current solution of Ge(xi) by:

$$G_{e} ({\mathbf{x}}_{i} ) = \left\{ {\begin{array}{*{20}l} {G({\mathbf{x}}_{i} ,t^{ * } )}, \hfill \\ {G_{e} ({\mathbf{x}}_{i} )}, \hfill \\ \end{array} } \right. \, \begin{array}{*{20}l} {{\text{if }}G({\mathbf{x}}_{i} ,t^{ * } ) < G_{e} ({\mathbf{x}}_{i} )} \hfill \\ {{\text{otherwise}}} \hfill \\ \end{array}$$
(21)

Then, go back to Step 5.

Step 8: Determine whether i = NSGNI. If so, output the current solution of Ge. Otherwise, let i = i + 1 and go back to Step 5.

After obtaining these extreme values, their first four raw moments, i.e., \(v_{{1G_{e} }}\), \(v_{{2G_{e} }}\), \(v_{{3G_{e} }}\) and \(v_{{4G_{e} }}\), can be evaluated based on Eq. (14) and further converted to its first four central moments by the following Eq. (22):

$$\left\{ {\begin{array}{*{20}l} {\mu_{{G_{e} }} = v_{{1G_{e} }} } \hfill \\ {\sigma_{{G_{e} }} = \sqrt {v_{{2G_{e} }} - v_{{1G_{e} }}^{2} } } \hfill \\ {\alpha_{{3G_{e} }} = {[}v_{{3G_{e} }} - 3v_{{2G_{e} }} v_{{1G_{e} }} + 2v_{{1G_{e} }}^{3} ]/\sigma_{{G_{e} }}^{3} } \hfill \\ {\alpha_{{4G_{e} }} = [v_{{4G_{e} }} - 4v_{{3G_{e} }} v_{{1G_{e} }} + 6v_{{2G_{e} }} v_{{1G_{e} }}^{2} - 3v_{{1G_{e} }}^{4} ]/\sigma_{{G_{e} }}^{4} } \hfill \\ \end{array} } \right.$$
(22)

For the optimization problem in Eq. (18), differential evolution algorithm [37] is used to find the global optimal solution. In MEGO-SGNI, the total number of LSF calls \(N_{calls} = N_{SGNI} + \sum\limits_{i = 1}^{{N_{SGNI} }} {N_{i} }\), where Ni is the number of LSF calls required in Step 4 to Step 7 for each collocation point.

3.2 Computation of time-dependent profust failure probability

For the given \(u_{{\tilde{F}}}^{ - 1} (\lambda )\), the first four moment-based time-dependent reliability index can be determined by:

$$\beta_{4M} (\lambda ) = - S^{ - 1} {[} - \beta_{2M} (\lambda )]$$
(23)

where \(\beta_{2M} (\lambda ) = \frac{{\mu_{{G_{e} }} - u_{{\tilde{F}}}^{ - 1} (\lambda )}}{{\sigma_{{G_{e} }} }}\) is the second order reliability index; and S–1[·] is the inverse Hermite polynomial model, whose detailed information is provided in Appendix 1.

Accordingly, the first four moment-based time-dependent failure probability is given:

$$P_{f} (0,T) = \Phi [ - \beta_{4M} (\lambda )]$$
(24)

Based on Eqs. (9) and (24), time-dependent profust failure probability can be reformulated as:

$$\tilde{P}_{f} (0,T) = \int_{0}^{1} {P_{f} (0,T)} d\lambda = \int_{0}^{1} {\Phi [ - \beta_{4M} (\lambda )]d\lambda }$$
(25)

It can be found that once the first four moments of extreme values are available, time-dependent profust failure probability can be easily estimated by one-dimensional numerical integral of Eq. (25) without any extra LSF evaluations. Thus, the effectiveness of the proposed method is independent of the fuzzy state described by membership function, only relying on using MEGO-SGNI to estimate extreme value moments.

3.3 Detailed procedures of the proposed method

The concrete steps of estimating time-dependent profust failure probability by the proposed method are summarized as follows. The corresponding flowchart is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the proposed method for TPRA

Full size image

Step 1: Choose the suitable accuracy level q. In general, the choice of q depends on the nonlinearity of the LSF considered. For slightly nonlinear problems, one may set q = 1. For strong nonlinear problems, it is usual to set 2 ≤ q ≤ 4 in practical applications to keep the balance between the numerical accuracy and computational efficiency [33].

Step 2: Generate NSGNI collocation points using the Smolyak algorithm.

Step 3: Evaluate extreme values at collocation points using MEGO.

Step 4: Estimate the first four moments of extreme values using SGNI.

Step 5: Compute the first four moments-based time-dependent failure probability using the inverse Hermite polynomial model.

Step 6: Integrating the first four moments-based time-dependent failure probability over [0, 1] yields time-dependent profust failure probability.

4 Numerical examples and investigations

In this section, four examples are provided to demonstrate the efficiency and accuracy of the proposed method for TPRA. Each of the examples is solved using the following five methods:

  • The first kind of MCS method: Eq. (11)

  • The second kind of MCS method: Eq. (12)

  • TD-EVMM: time-discrete-based extreme value moment method

  • MEGO-DL-AK: MEGO-based double-loop adaptive Kriging method (See Appendix 2)

  • Proposed: the method proposed in this paper

Their accuracy is measured by the relative error with respect to the solution from the first kind of MCS method.

4.1 Example 1: a numerical example

This numerical example considers the following time-dependent LSF:

$$G({\mathbf{X}},t) = X_{1}^{2} X_{2} - 5X_{1} t + (X_{2} + 1)t^{2} - 20$$
(26)

where X1 and X2 are two independent normal variables with mean values \(\mu_{{X_{1} }} = \mu_{{X_{2} }} = 3.5\) and standard deviations \(\sigma_{{X_{1} }} = \sigma_{{X_{2} }} = 0.3\).

In this example, the time interval of interest [0, T] is considered as [0, 1]. Five methods, including two kinds of MCS methods, TD-EVMM, MEGO-DL-AK and the proposed method, are used to solve time-dependent profust failure probability. In two kinds of MCS methods and TD-EVMM, [0, T] is discretized into 21 time nodes with time step Δt = 0.05. A total of 105 samples are used in these two kinds of MCS methods, thus both of their number of LSF calls is 21 × 105. In MEGO-DL-AK, the inner loop aims to estimate the extreme values using MEGO, and the outer loop solves time-dependent profust failure probability based on AK-MCS [12]. Thus, the total cost entailed in MEGO-DL-AK is from the functional evaluations required to evaluate extreme values at all training samples of X with MEGO. In TD-EVMM and the proposed method, the accuracy level q of SGNI is taken as 2 and a total of 17 collocation points are generated. In the former, LSF is evaluated at all discrete time nodes to estimate extreme value of each collocation point, thus the required LSF calls are 21 × 17 times. In the latter, extreme values at all collocation points are evaluated by the proposed MEGO, then the computational overhead is equal to \(17 + \sum\limits_{i = 1}^{17} {N_{i} }\). For comparison, the extreme values at collocation points evaluated by two methods are listed in Table 1. From Table 1, it can be seen that the results of the proposed method are totally the same as those of time-discrete method, but the former is much highly efficient than the latter.

Table 1 Extreme values at all collocation points in Example 1
Full size table

Firstly, fuzzy state is described by linear membership function (as shown in Eq. (3)), where three different sets of parameters a1 and a2 are considered. The results from five methods are shown in Table 2. For three different cases, the results of five methods are quite consistent. In terms of efficiency, the number of LSF calls required in the proposed method is the least among all methods.

Table 2 Time-dependent profust failure probability under \(u_{{\tilde{F}}}^{L} [G{(}{\mathbf{x}}{,}t{)}]\) in Example 1
Full size table

Next, normal membership function (as shown in Eq. (4)) is employed to describe fuzzy state. Again, three different sets of parameters b1 and b2 are considered, under which the results of five methods are presented in Table 3. It can be seen from Table 3 that the results of the proposed method are still consistent with those of other four methods, while the computational efficiency of the proposed method is higher than others.

Table 3 Time-dependent profust failure probability under \(u_{{\tilde{F}}}^{N} [G{(}{\mathbf{x}}{,}t{)}]\) in Example 1
Full size table

Finally, fuzzy state described by Cauchy membership function (as shown in Eq. (5)) with three different sets of parameters c1 and c2 is also investigated. Table 4 gives the time-dependent profust failure probabilities obtained by five methods. From Table 4, we can find that compared to other four methods, the proposed method has still desirable accuracy level with high efficiency.

Table 4 Time-dependent profust failure probability under \(u_{{\tilde{F}}}^{C} [G{(}{\mathbf{x}}{,}t{)}]\) in Example 1
Full size table

Through Tables 2, 3, 4, it is found that the results of TD-EVMM and the proposed method are highly consistent. This is because the accuracy of the proposed MEGO algorithm in capturing extreme values at all collocation points is comparable to that of the time-discrete method, as shown in Table 1. In addition, in terms of Ncalls, the proposed method is more robust than MEGO-DL-AK. These results reveal that the proposed method has a better performance than TD-EVMM and MEGO-DL-AK and no limitation for the type of membership function.

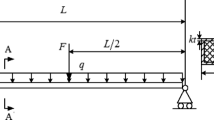
4.2 Example 2: a corrosion-forced beam structure

The second example presents a corrosion-forced beam under external load as shown in Fig. 3 [28]. Due to the influence of corrosion on the beam structure, the width b(t) and height h(t) of its cross-section has the following linear decaying with respect to time variable t:

$$b(t) = b_{0} - 2kt,\;h(t) = h_{0} - 2kt$$
(27)

where k = 0.25 mm/year is the decaying rate.

Fig. 3
figure 3

Corrosion-forced beam in Example 2

Full size image

The law of the external load subjected to the midpoint of the beam is sin(t/4)F, which varies with t. The failure event is considered as the bending moment M(t) at the midpoint of the beam exceeding its ultimate value Mu(t). Thus, the time-dependent LSF is defined as follows:

$$G({\mathbf{X}},t) = \frac{{M_{u} (t) - M(t)}}{1000} = \left[ {\frac{{b(t)h(t)^{2} \sigma_{u} }}{4} - \left( {\frac{\sin (t/4)FL}{4} + \frac{{\rho_{st} b_{0} h_{0} L^{2} }}{8}} \right)} \right] \times \frac{1}{1000}$$
(28)

where ρst = 78.5kN/m3 is the density of the beam; and L = 9 m is the total length of the beam (Table 5).

Table 5 Statistical information of input random variables in Example 2
Full size table

In this example, b0, h0, σu and F are regarded as random input variables, whose statistical information is given in Table 10. The linear membership function with the parameters a1 = 0 and a2 = 1 is used to describe fuzzy state here. The results from five methods are exhibited in Table 6. In two kinds of MCS methods and TD-EVMM, the time interval of interests [0, T] = [0, 10] years is divided into 101 time nodes with time step Δt = 0.1 year. It can be seen from Table 6 that time-dependent profust failure probabilities obtained by five methods are almost identical. However, the computational efficiency of the proposed method is greatly higher than other four methods. In the proposed method, once the extreme value moments are estimated by the proposed MEGO-SGNI, the profust failure probabilities can be evaluated by one-dimensional integral on the first four moments-based failure probability without any extra functional evaluation.

Table 6 Time-dependent profust failure probability in Example 2
Full size table

4.3 Example 3: the lower extremity exoskeleton

The lower extremity exoskeleton [38] is a wearable robotic derive, which can provide walking assistance and rehabilitation training for people with lower-limb dysfunction. The simplified model of the lower extremity exoskeleton is shown in Fig. 4. The knee joint is taken as the object of this study and further magnified in Fig. 5, where k1, k2, k3 and k4 are the lengths of the links and Lk(t) is the length of the hydraulic cylinder. The angle of the knee joint varies as the human body moves. To ensure the safety of the human body and the effectiveness of rehabilitation training, the motions of the knee joint should follow the ideal movement θ(t), whose value is given as follows:

$$\theta (t) = \frac{{\sum\limits_{i = 1}^{6} {a_{ki} \sin (b_{ki} t + c_{ki} )} }}{180}\pi$$
(29)

where aki, bki, cki, i = 1, …, 6, are coefficients given in Table 7.

Fig. 4
figure 4

Simplified model of the LEEX in Example 3

Full size image
Fig. 5
figure 5

Knee joint of the LEEX in Example 3

Full size image
Table 7 Coefficients aki, bki and cki in Example 3
Full size table

Considering the manufacturing error and assembly error, the practical angle α(t) of the knee joint can be presented by:

$$\alpha (t) = \pi - \arctan \frac{{k_{1} }}{{k_{2} }} - \arctan \frac{{k_{3} }}{{k_{2} }} - \arctan \frac{{k_{1}^{2} + k_{2}^{2} + k_{3}^{2} + k_{4}^{2} - [L_{k} (t)]^{2} }}{{2\sqrt {(k_{1}^{2} + k_{2}^{2} )(k_{3}^{2} + k_{4}^{2} )} }}$$
(30)

The length of the hydraulic cylinder is given by:

$$L_{k} (t) = \sqrt {1.3877 \times 10^{5} - 5.9722 \times 10^{4} \cos \left[ {\pi - 0.1246 - 0.9157 - \frac{{\sum\limits_{i = 1}^{6} {a_{ki} \sin (b_{ki} t + c_{ki} )} }}{180}\pi } \right]}$$
(31)

The failure event of the knee joint is defined as the difference between its practical and ideal angles exceeding the threshold ε = 10π/180. Thus, the time-dependent LSF is

$$G({\mathbf{X}},t) = \varepsilon - |\alpha (t) - \theta (t)|$$
(32)

In this example, k1, k2, k3 and k4 are regarded as four normal random variables and their statical information is listed in Table 8. The fuzzy state is described by Cauchy membership function with the parameters c1 = 0 and c2 = 10−4. The time-dependent profust failure probabilities obtained by five methods are shown in Table 9. The considered time interval is [0, 100] seconds, which is divided into 101 time nodes in two kinds of MCS methods and DT-EVMM. From Table 9, it can be seen that the results of five methods are very close to each other. In the proposed method, the number of collocation points of SGNI is 49, however the total number of LSF calls is only 2 times of it, which fully proves the computational efficiency of the proposed method for complicated engineering problems.

Table 8 Statistical information of input random variables in Example 3
Full size table
Table 9 Time-dependent profust failure probability in Example 3
Full size table

4.4 Example 4: a CRTS II track slab structure

The last example considers the bending failure mode of a CRTS II track slab structure (as shown in Fig. 6a) under train load and environmental actions [20, 23]. The corresponding time-dependent LSF is given as follows:

$$G({\mathbf{X}},t) = (1 - k_{1} t + k_{2} t^{2} )M_{R0} - M_{S} (t)$$
(33)
$$M_{R0} = (f_{s} A_{s} - f_{s}^{\prime } A_{s}^{\prime } + f_{p} A_{p} )[h_{0} - (f_{s} A_{s} - f_{s}^{\prime } A_{s}^{\prime } + f_{p} A_{p} )/2f_{c} b] + f_{s}^{\prime } A_{s}^{\prime } (h_{0} - a_{s}^{\prime } )$$
(34)
$$M_{S} (t) = M_{V} + M_{W} ,\;M_{W} = K_{t} T$$
(35)

where MR0 is the initial flexural bearing capacity of track slab; k1 = 0.015 and k2 = 5 × 10−5 are the linear decaying coefficients; MS(t) is the bending moment due to external loads, which consists of two parts: one is the bending moment MV under train load P(t), which is calculated by using a finite element model as shown in Fig. 6b, and another is the bending moment MW under temperature action; \(A_{s} = A^{\prime}_{s}\) = 201 mm2 are cross-sectional area of non-prestressed tendons in tension zone and compression zone, respectively; fs and \(f^{\prime}_{s}\) are the design values of tensile and compressive strength of non-prestressed tendons, respectively; fc is the design value of axial compressive strength of concrete; Ap = 471 mm2 and fp are the cross-sectional area and design value of tensile strength of prestressed tendons, respectively; b = 650 mm is the width of section of single sleeper; h0 = 130 mm is the sectional effective height; \(a^{\prime}_{s}\) = 60 mm is the distance between the resultant point of non-prestressed tendons in compression zone and the top surface of track slab; T is the temperature gradient; and Kt is the temperature bending moment coefficient.

Fig. 6
figure 6

CRTS II track slab structure in Example 4

Full size image

In this example, P(t) is assumed as a lognormal random process and simulated through a non-Gaussian process simulation technique [31]. The parameters fs,\(f_{s}^{\prime }\), fp, fc, Kt and T are regarded as random variables. The statistical information of these random variables and process is summarized in Table 10. The fuzzy state described by Normal membership function with the parameters b1 = 0 and b2 = 103 is considered here. The time-dependent profust failure probabilities estimated by two kinds of MCS methods, TD-EVMM, MEGO-DL-AK and the proposed method are shown in Table 11. In the first three methods, the time interval of interests [0, T] = [0, 60] years is divided into 61 nodes with equal interval length Δt = 0.6 year. As can be observed from Table 11, the results of TD-EVMM, MEGO-DL-AK and the proposed method are pretty consistent with those of two kinds of MCS methods. More importantly, the number of LSF calls required in the proposed method is only 118, while 6161 and 297 LSF calls are required in TD-EVMM and MEGO-DL-AK, respectively. Thus, for this problem with implicit LSF involved in finite element analysis, the proposed method still exhibits high computational efficiency and satisfactory accuracy.

Table 10 Statistical information of input random variables and processes in Example 4
Full size table
Table 11 Time-dependent profust failure probability in Example 4
Full size table

5 Concluding remarks

This paper develops a novel and efficient method to address time-dependent reliability problem with fuzzy state. In the proposed method, a MEGO algorithm is developed to evaluate extreme values at all collocation points of SGNI. Different from the previous methods, which treats collocation points and time variables independently, the proposed method regards both of them as input variables of Kriging model to ensure the highly efficient modelling. By introducing an auxiliary variable, time-dependent profust failure probability is reformulated as a one-dimensional integral of the first four moments-based time-dependent failure probability. Solving this integral requires no additional functional evaluation. Four examples are utilized to investigate the performance of the proposed method and some conclusions can be drawn:

  1. 1.

    Compared to TD-EVMM and MEGO-DL-AK, the proposed method requires less computational cost with comparable accuracy, thus its performance is more superior.

  2. 2.

    The effectiveness of the proposed method is insensitive to the fuzzy state described by different membership functions.

  3. 3.

    Without considering the fuzzy state assumption, this method can still be degraded to an effective method for traditional TRA.

It is well acknowledged that the probability distribution determined from the given first four central moments is not a unique one, and the Hermite polynomial model utilized in this study is applicable for only unimodal random variables. In addition, the higher order moment information facilitates a higher quality distribution model [39]. The future work will consider both the other distribution models and the higher moment information to deal with more complicated problems involving bimodal or even multi-peaked distributions. Moreover, Kriging model may show the poor approximation efficiency for high-dimensional problems. The applications of other kinds of surrogate models (such as support vector machine) in the proposed method will also be investigated in the future.