An efficient method for estimating time-dependent global reliability sensitivity

Abstract

Time-dependent global reliability sensitivity can quantify the effect of input variables in their whole distribution ranges on the time-dependent failure probability. To efficiently estimate it to help researchers control the time-dependent failure probability, a novel method is proposed. The proposed method transforms the estimation of unconditional-conditional time-dependent failure probabilities into that of the unconditional-conditional probability density functions (PDFs) of the minimum of time-dependent performance function. Firstly, the minimum of time-dependent performance function is evaluated by adaptive Kriging, and its unconditional-conditional fractional moments are estimated by multiplicative dimensional reduction method (M-DRM). Then, the maximum entropy (MaxEnt) constrained by these fractional moments is used to estimate the unconditional-conditional PDFs, on which the unconditional-conditional time-dependent failure probabilities can be obtained. Finally, the one-dimensional Gaussian quadrature is applied to estimate the time-dependent global reliability sensitivity indices. Due to the high efficiency of adaptive Kriging for estimating the minimum of time-dependent performance function, the avoidance of dimensional curse by M-DRM, and the high efficiency of MaxEnt constrained by fractional moments for estimating PDF, the proposed method can reduce the computational cost dramatically.

1 Introduction

Reliability is the probability that a structure performs its intended function over a specified period of time under specified service conditions. According to whether the performance of the structure is time-dependent or not, reliability can be classified into time-independent reliability and time-dependent one. Time-independent reliability, i.e., static reliability, does not consider the effect of time, in which the reliability (or failure probability) remains constant over time. In contrast, the time-dependent reliability analysis takes the effect of time under consideration. In engineering applications, for instance, over the service life of the Thermal Barrier Coating of aircraft engines, the stresses and strains of the Thermal Barrier Coating are time-variant (Miller 1997). Many structures also experience time-varying random motion errors due to random dimensions (tolerances), clearances, and deformations of structural components (Dubowsky et al. 1984; Dupac and Beale 2010). Other examples, such as the system of wind turbines, hydrokinetic turbines, and the aircraft turbine engines, the turbine blade loading always varies over time. Likewise, the wave loading acting on offshore structures fluctuates randomly with time (Nielsen 2010; Kuschel and Rackwitz 2000). For the above structures, the failure probability is a function of time and in general, increased with time, it is named as time-dependent failure probability, which can be used to measure the probability that a structure performs its designed function over its service time.

Time-dependent reliability analysis methodologies can be simply classified into two categories. The first one includes the extreme value methods (also named as quasi-static methods) (Chen and Li 2007; Li et al. 2007; Wang and Wang 2012), which firstly transforms the time-dependent problem into the time-independent one by estimating the extreme value of time-dependent performance function, then, uses the time-independent reliability analysis methods, such as the first-order reliability method, second-order reliability method and so on, to estimate the time-dependent failure probability. The second category consists of the first-passage methods (Jiang et al. 2017; Andrieu-Renaud et al. 2004; Hu and Du 2013), which directly uses the first-passage time or the first time to failure to judge whether the failure occurs or not over the time under consideration.

Recently, the surrogate model–based methods are a promising way to improve the accuracy and efficiency for estimating time-dependent failure probability, and the Kriging surrogate model is a well-used one. The Kriging model–based methods, for estimating the time-dependent failure probability, include the double-loop strategies and single-loop strategies. The technology of double-loop Kriging method (Wang and Wang 2015; Ling et al. 2019; Hu and Du 2015; Ling and Lu 2020) is constructing an inner loop Kriging model to estimate the minimum of time-dependent performance function with respect to the time parameter, and constructing an outer loop Kriging model for the extreme value surface of time-dependent performance function to estimate the time-dependent failure probability. The single-loop Kriging method (Ling and Lu 2020; Hu and Mahadevan 2016) treats the time parameter as a random variable distributed in the time interval, then, directly builds a Kriging model for the actual time-dependent performance function to estimate the time-dependent failure probability. The application results (Ling and Lu 2020) of these two methods show that the single-loop Kriging algorithm needs a smaller number of model evaluations than the double-loop Kriging algorithm. However, for complicated problems, extremely those with small failure probability or the time interval under consideration is too large, the single-loop Kriging algorithm is more time-consuming than the double-loop Kriging algorithm, because the candidate sample pool size of single-loop Kriging algorithm is larger than that of the double-loop Kriging algorithm. As aforementioned, the double-loop Kriging method for estimating time-dependent failure probability has to estimate the extreme value of time-dependent performance function with respect to the time parameter in the inner loop. Wang et al. (Wang and Wang 2015) used the one-dimensional Kriging model to approximate the time-dependent performance function at a specified sample, then, the well-trained one-dimensional Kriging model is applied to estimate the minimum of time-dependent performance function at this sample. Ling et al. (Ling et al. 2019) employed the derivative method to estimate the minimum of time-dependent performance function.

Sensitivity analysis aims at studying “how uncertainty in the model output can be apportioned to different source of uncertainty in the model input” (Saltelli et al. 2004), it can be sorted into two classes, i.e., local sensitivity analysis and global sensitivity analysis. Local sensitivity analysis (Campolongo et al. 2011) mainly focuses on estimating the partial derivative, therefore, it only provides sensitivity information at the nominal point where the derivative is calculated, and it cannot reflect the effect of input variables in their whole distribution domains on the model output. Compared with the local sensitivity analysis, global sensitivity analysis (Xiao et al. 2018; Aven 2016) can measure the effect of input variables in their entire distribution ranges on model output. According to the results of global sensitivity analysis, researchers can effectively reduce the uncertainty of model output by allocating more resources (people, time, and financial budges, etc.) to the most important input variable and simplify the model through fixing the unimportant input variables at their nominal values (Xiao and Lu 2017). In the past few decades, many global sensitivity analysis methods have been proposed. For example, Sobol and others used the variance-based global sensitivity indices (Sobol 2001; Yun et al. 2018a; Zhang et al. 2017; Yun et al. 2017a) to quantify the contributions of input variables’ variances to the variance of model output. Borgonovo and others developed the moment-independent global sensitivity indices (Borgonovo 2007; Feng et al. 2018; Yun et al. 2018b) to measure the effect of input uncertainty on the distribution of model output. Cui and others developed the global reliability sensitivity indices (Cui et al. 2010; Yun et al. 2017b; Wei et al. 2016; Shi et al. 2017) to measure the effect of input variables in their whole distribution domains on the probability of failure.

Structural reliability analysis is more interested in reliability or failure probability. Thus, it is necessary to study the effect of input variables in their whole uncertainty domains on the failure probability. Inspired by this idea, Cui et al. (Cui et al. 2010) proposed the failure probability–based global sensitivity analysis, i.e., global reliability sensitivity analysis, it is defined as the expectation of the square of the difference between the unconditional failure probability and conditional failure probability. The global reliability sensitivity technique is especially useful for reliability-based design. Wei et al. (Wei et al. 2016) and Shi et al. (Shi et al. 2017) extended the global reliability sensitivity technique to the time-dependent problem. Time-dependent global reliability sensitivity index is defined as the expectation of the square of the difference between the unconditional time-dependent failure probability and conditional time-dependent failure probability. Wei et al. (Wei et al. 2016) transformed the estimation of time-dependent global reliability sensitivity into that of the time-dependent variance-based global sensitivity about the indicator function of the failure region, then, used the envelope function method to estimate it. Shi et al. (Shi et al. 2017) estimated the time-dependent global reliability sensitivity based on the extreme value of time-dependent performance function, where the sparse grid technique combined with the fourth-moment method, and the dimensional reduction method combined with the maximum entropy are employed.

This paper aims at analyzing the time-dependent global reliability sensitivity to direct how to control the failure probability of structure effectively. The proposed method is a double-loop strategy, it is based on the Gaussian quadrature and transformation of the estimation of unconditional-conditional time-dependent failure probabilities into that of unconditional-conditional probability density functions (PDFs) of the minimum of time-dependent performance function. The inner loop of the proposed algorithm is to estimate the minimum of time-dependent performance function at the Gaussian grid point. Then, the unconditional-conditional fractional moments of the minimum are evaluated, on which the unconditional-conditional PDFs of the minimum of time-dependent performance function are solved. After that, the unconditional-conditional time-dependent failure probabilities can be estimated by taking univariate integral about the unconditional-conditional PDFs. Finally, the time-dependent global reliability sensitivity indices are obtained by the Gaussian quadrature in the outer loop. The proposed method includes three particular strategies:

• (1) The minimum of time-dependent performance function at the Gaussian grid point is solved by the one-dimensional adaptive Kriging method. A learning function, which is different from that in Ref. (Wang and Wang 2015), considering the local exploration and global exploration at the same time with a balance factor, is employed by this paper. It can efficiently select the significant sample point providing the maximum improvement to the prediction quality to update the Kriging model.

• (2) Based on the minimum of time-dependent performance function, the unconditional-conditional fractional moments of it are efficiently estimated by the multiplicative dimensional reduction method (M-DRM) (Zhang and Pandey 2013). The application of M-DRM makes the computational cost grow linearly with the dimensionality, hence, the dimensional curse is avoided to some extent.

• (3) The unconditional-conditional PDFs of the minimum of time-dependent performance function are estimated by the maximum entropy (MaxEnt) theory constrained by the unconditional-conditional fractional moments (Zhang and Pandey 2013).

The innovations of this paper are concluded as follows:

• (1) Up to the authors’ knowledge, there is no work about using adaptive Kriging to estimate the time-dependent global reliability sensitivity.

• (2) The M-DRM can estimate the unconditional-conditional fractional moments of the minimum of time-dependent performance function, simultaneously, by using the same group of Gaussian grids. This property reduces the total computational cost for estimating time-dependent global reliability sensitivity.

• (3) The learning function employed by this paper for constructing the Kriging model is different from that in Ref. (Wang and Wang 2015), which can construct a Kriging model quickly and precisely.

Obviously, the computational cost of the proposed method only consumes in the process for estimating the minimum of time-dependent performance function at the Gaussian grid point. Since the M-DRM releases the dimensional curse, the MaxEnt theory constrained by fractional moments can efficiently approximate the PDF, and the adaptive Kriging method can quickly estimate the minimum of time-dependent performance function, therefore, the proposed method reduces the computational cost for estimating time-dependent global reliability sensitivity dramatically.

This paper is organized as follows. Section 2 reviews the time-dependent global reliability sensitivity. The proposed strategy for efficiently estimating the time-dependent global reliability sensitivity is shown in section 3. Several examples are presented in section 4 to demonstrate the efficiency and accuracy of the proposed method for estimating time-dependent global reliability sensitivity. Section 5 gives the conclusions.

2 Time-dependent global reliability sensitivity

In the time-dependent problem, the performance function of the structure is not only determined by the stochastic uncertainties but also governed by the time-variant uncertainties such as loading conditions and component deterioration. Denote the performance function involving random variables X = {X₁, X₂, ⋯, X_n}^T (n represents the number of random input variables) and time parameter t as Y = g(X, t). The failure event occurs if the time-dependent performance function satisfies g(X, t) ≤ 0, and the structure is safe when g(X, t) > 0. The time-dependent failure probability over time interval [t₀, t_s] is defined as follows

$$ {P}_f\left({t}_0,{t}_s\right)=\boldsymbol{Prob}\left\{g\left(X,t\right)\le 0,\exists t\in \Big[{t}_0,{t}_s\Big]\right\} $$

(1)

where t₀ is the initial time when the structure is put into operation, and t_s denotes the endpoint of the investigated time-interval. Prob{·} represents the probability operator, and “∃” means “there exists.”

The time-dependent performance function g(X, t) can be seen as a compound function involving the random variables X in the probabilistic space Rⁿ and the time parameter t in the time interval [t₀, t_s]. When the input variables X are fixed at their realization values x ∈ Rⁿ, g(x, t) is a univariate function about t. Equation (1) shows that the structure is failed if there exists an instant t ∈ [t₀, t_s] satisfies g(x, t) ≤ 0. That is to say, the structure at realization x is failed if $\left(\underset{t\in \left[{t}_0,{t}_s\right]}{\mathit{\min}}g\left(x,t\right)\right)\le 0$, whereas for $\left(\underset{t\in \left[{t}_0,{t}_s\right]}{\mathit{\min}}g\left(x,t\right)\right)>0$ the structure is safe. Thus, the time-dependent failure probability can be expressed as follows

$$ {P}_f\left({t}_0,{t}_s\right)=\boldsymbol{Prob}\left\{\left(\underset{t\in \left[{t}_0,{t}_s\right]}{\mathit{\min}}g\left(X,t\right)\right)\le 0\right\} $$

(2)

Equation (2) implies that the key to estimate the time-dependent failure probability P_f(t₀, t_s) is to find the minimum of time-dependent performance function within [t₀, t_s] when X take their realization values x according to their joint PDF f_X(x). For the sake of concision, this paper denotes $\left(\underset{t\in \left[{t}_0,{t}_s\right]}{\mathit{\min}}g\left(X,t\right)\right)$ as g_min(X).

In order to measure the importance of model inputs X on the time-dependent failure probability P_f(t₀, t_s), define the time-dependent global reliability sensitivity index as follows

$$ {\displaystyle \begin{array}{c}{\delta}_{X_i}^{P_f}={\int}_{-\infty}^{+\infty }{\left\{{P}_f\left({t}_0,{t}_s\right)-{P}_{f\mid {X}_i}\left({t}_0,{t}_s\right)\right\}}^2{f}_{X_i}\left({x}_i\right)\mathrm{d}{x}_i\\ {}={E}_{X_i}{\left[{P}_f\left({t}_0,{t}_s\right)-{P}_{f\mid {X}_i}\left({t}_0,{t}_s\right)\right]}^2\end{array}} $$

(3)

where ${f}_{X_i}\left({x}_i\right)$ is the marginal PDF of variable X_i, ${E}_{X_i}\left[\cdotp \right]$ is the expectation operator about X_i, and ${P}_{f\mid {X}_i}\left({t}_0,{t}_s\right)$ is the conditional time-dependent failure probability when X_i is fixed, it can be expressed as

$$ {P}_{f\mid {X}_i}\left({t}_0,{t}_s\right)=\boldsymbol{Prob}\left\{\left(\underset{t\in \left[{t}_0,{t}_s\right]}{\mathit{\min}}g\left({X}_{-i},{X}_i,t\right)\right)\le 0\right\} $$

(4)

where X_−i = {X₁, X₂, ⋯, X_{i − 1}, X_{i + 1}, ⋯, X_n}^T denotes the vector of all input variables except X_i.

It is seen that the time-dependent global reliability sensitivity ${\delta}_{X_i}^{P_f}\left(i=1,2,\cdots, n\right)$ reflects the average effects of the input variables X_i(i = 1, 2, ⋯, n) over their distribution domains on the time-dependent failure probability. The higher ${\delta}_{X_i}^{P_f}$ is, the more important X_i is to the time-dependent failure probability.

3 Proposed method for estimating ${\delta}_{X_i}^{P_f}$

The unconditional and conditional time-dependent failure probabilities also can be estimated by Eqs. (5) and (6), respectively,

$$ {P}_f\left({t}_0,{t}_s\right)={\int}_{-\infty}^0{f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)\mathrm{d}{y}_{\mathrm{min}} $$

(5)

$$ {P}_{f\mid {X}_i}\left({t}_0,{t}_s\right)={\int}_{-\infty}^0{f}_{Y_{\mathrm{min}}\mid {X}_i}\left({y}_{\mathrm{min}}\right)\mathrm{d}{y}_{\mathrm{min}} $$

(6)

where Y_min = g_min(X) denotes the unconditional minimum of time-dependent performance function, Y_min ∣ X_i = g_min(X_−i, X_i) is the conditional minimum of time-dependent performance function when X_i is fixed. ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and ${f}_{Y_{\mathrm{min}}\mid {X}_i}\left({y}_{\mathrm{min}}\right)$ are the unconditional and conditional PDFs of unconditional minimum Y_min and conditional minimum Y_min ∣ X_i, respectively.

Substituting Eqs. (5) and (6) for Eq. (3), Eq. (7) can be obtained,

$$ {\delta}_{X_i}^{P_f}={\int}_{-\infty}^{+\infty }{\left\{{\int}_{-\infty}^0{f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)\mathrm{d}{y}_{\mathrm{min}}-{\int}_{-\infty}^0{f}_{Y_{\mathrm{min}}\mid {X}_i}\left({y}_{\mathrm{min}}\right)\mathrm{d}{y}_{\mathrm{min}}\right\}}^2{f}_{X_i}\left({x}_i\right)\mathrm{d}{x}_i $$

(7)

In this paper, the Gaussian quadrature is employed to estimate the one-dimensional integral with respect to X_i in the outer loop of Eq. (7). Suppose the N_i-point Gaussian quadrature is adopted for X_i, and the corresponding Gaussian points and weights of X_i are denoted as ${x}_i^{(m)}\left(m=1,2,\cdots, {N}_i\right)$ and ${p}_i^{(m)}\left(m=1,2,\cdots, {N}_i\right)$, respectively. Then, the time-dependent global reliability sensitivity index shown in Eq. (7) can be estimated by Eq. (8),

$$ {\displaystyle \begin{array}{c}{\delta}_{X_i}^{P_f}\approx \sum \limits_{m=1}^{N_i}\left\{{p}_i^{(m)}\times {\left[{\int}_{-\infty}^0{f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)d{y}_{\mathrm{min}}-{\int}_{-\infty}^0{f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)d{y}_{\mathrm{min}}\right]}^2\right\}\\ {}=\sum \limits_{m=1}^{N_i}\left\{{p}_i^{(m)}\times {\left[{P}_f\left({t}_0,{t}_s\right)-{P}_{f\mid {x}_i^{(m)}}\left({t}_0,{t}_s\right)\right]}^2\right\}\end{array}} $$

(8)

Equation (8) implies that the key to estimate the time-dependent global reliability sensitivity ${\delta}_{X_i}^{P_f}\left(i=1,2,\cdots, n\right)$ is to estimate the unconditional PDF ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and conditional PDF ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$ when X_i fixed at its Gaussian point ${x}_i^{(m)}\left(q=1,2,\cdots, {N}_i\right)$. To efficiently estimate the unconditional PDF ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and conditional PDF ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$, the MaxEnt theory constrained by fractional moments is employed.

3.1 MaxEnt constrained by fractional moments for estimating ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$

Combining the MaxEnt theory based on fractional moments constraint (Zhang and Pandey 2013) with the Lagrangian function and Kullback-Lerbler cross-entropy theory, the approximate unconditional PDF ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ is derived as

$$ {\hat{f}}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)=\mathit{\exp}\left\{-\sum \limits_{k=0}^r{\lambda}_k{\left({y}_{\mathrm{min}}\right)}^{\alpha_k}\right\} $$

(9)

in which λ = {λ₀, λ₁, λ₂, …, λ_r}^T and α = {α₀, α₁, α₂, …, α_r}^T are the Lagrangean multiplier vector and the fractional vector related to the fractional moments, respectively. α₀ = 0 and ${\lambda}_0=\mathit{\log}\left[{\int}_{Y_{\mathrm{min}}}\exp \left\{-\sum \limits_{k=1}^r{\lambda}_k{\left({y}_{\mathrm{min}}\right)}^{\alpha_k}\right\}\mathrm{d}{y}_{\mathrm{min}}\right]$. These parameters can be solved by the following optimization process

$$ \left\{\begin{array}{ll}\mathrm{Find}:& \lambda ={\left\{{\lambda}_0,{\lambda}_1,{\lambda}_2,\cdots, {\lambda}_r\right\}}^T\kern0.24em \mathrm{and}\kern0.24em \boldsymbol{\upalpha} ={\left\{{\alpha}_0,{\alpha}_1,{\alpha}_2,\dots, {\alpha}_r\right\}}^T\\ {}\operatorname{Minimize}:& I\left(\boldsymbol{\uplambda}, \boldsymbol{\upalpha} \right)=\log \left[{\int}_{Y_{\mathrm{min}}\left|{x}_i^{(m)}\right.}\exp \left\{-\sum \limits_{k=0}^r{\lambda}_k^{\prime}\left({y}_{\mathrm{min}}\right){\alpha}_k^{\prime}\right\}\mathrm{d}{y}_{\mathrm{min}}\right]+\sum \limits_{k=0}^r{\lambda}_k^{\prime }{M}_{Y_{\mathrm{min}}\left|{x}_i^{(m)}\right.}^{\alpha_k^{\prime }}\end{array}\right. $$

(10)

where ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ is the α_kth order fractional moment of Y_min.

Similarly, the approximate conditional PDF ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$ can be derived as

$$ {\hat{f}}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)=\mathit{\exp}\left\{-\sum \limits_{k=0}^r{\lambda}_k^{\prime }{\left({y}_{\mathrm{min}}\right)}^{\alpha_k^{\prime }}\right\} $$

(11)

in which the parameters can be estimated by Eq. (12),

$$ \left\{\begin{array}{cc}\boldsymbol{Find}:& {\boldsymbol{\uplambda}}^{\prime }={\left\{{\lambda}_0^{\prime },{\lambda}_1^{\prime },{\lambda}_2^{\prime },\dots, {\lambda}_r^{\prime}\right\}}^T\boldsymbol{and}{\boldsymbol{\alpha}}^{\prime }={\left\{{\alpha}_0^{\prime },{\alpha}_1^{\prime },{\alpha}_2^{\prime },\dots, {\alpha}_r^{\prime}\right\}}^T\\ {}\mathit{\operatorname{Minimize}}:& I\left({\boldsymbol{\lambda}}^{\prime },{\boldsymbol{\alpha}}^{\prime}\right)=\mathit{\log}\left[{\int}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\exp \left\{\sum \limits_{k=0}^r{\lambda}_k^{\prime }{\left({y}_{\mathrm{min}}\right)}^{\alpha_k^{\prime }}\mathrm{d}{y}_{\mathrm{min}}\right\}\right]+\sum \limits_{k=0}^r{\lambda}_k^{\prime }{M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}\end{array}\right. $$

(12)

where ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$ is the ${\alpha}_k^{\prime }$th order fractional moment of ${Y}_{\mathrm{min}}\mid {x}_i^{(m)}$.

Apparently, for estimating the unconditional-conditional PDFs ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$, it is necessary to evaluate the unconditional-conditional fractional moments ${M}_{Y_{\mathrm{min}}}^{\alpha_k}\left(k=1,2,\cdots, r\right)$ and ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}\left(k=1,2,\cdots, r\right)$ at the first.

3.2 M-DRM for estimating ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ and ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$

The multidimensional minimum function Y_min = g_min(X) can be expressed as a product of multiple univariate functions by employing the M-DRM strategy (Zhang and Pandey 2013),

$$ {\displaystyle \begin{array}{l}{g}_{\mathrm{min}}(X)\approx {\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{n-1}\prod \limits_{i=1}^n{g}_{\mathrm{min}}\left({\mu}_1,\dots, {\mu}_{i-1},{X}_i,{\mu}_{i+1},\dots, {\mu}_n\right)\\ {}\kern4em ={\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{n-1}\prod \limits_{i=1}^n{g}_{\mathrm{min}}\left({X}_i,{\mu}_{-i}\right)\end{array}} $$

(13)

in which μ = {μ₁, μ₂, ⋯, μ_n}^T is the mean vector of inputs X, μ_−i = {μ₁, …, μ_{i − 1}, μ_{i + 1}, …, μ_n}^T is the mean vector of all the input variables except X_i.

Suppose the input variables are independent with each other, so that the joint PDF of input variables can be expressed as ${f}_X(x)=\prod \limits_{i=1}^n{f}_{X_i}\left({x}_i\right)$. Then, the unconditional fractional moment ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ can be estimated by Gaussian quadrature,

$$ {\displaystyle \begin{array}{l}{M}_{Y_{\mathrm{min}}}^{\alpha_k}={\int}_X{\left[{g}_{\mathrm{min}}(x)\right]}^{\alpha_k}{f}_X(x)\mathrm{d}x\\ {}\kern3em \approx {\int}_X{\left[{g}_{\mathrm{min}}{\left(\mu \right)}^{1-n}\prod \limits_{l=1}^n{g}_{\mathrm{min}}\left({x}_l,{\mu}_{-l}\right)\right]}^{\alpha_k}\prod \limits_{l=1}^n\left\{{f}_{X_l}\left({x}_l\right)\mathrm{d}{x}_l\right\}\\ {}\begin{array}{l}\kern3em \approx {\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{\alpha_k-{\alpha}_kn}\prod \limits_{l=1}^n\left\{{\int}_{X_l}{\left[{g}_{\mathrm{min}}\left({x}_l,{\mu}_{-l}\right)\right]}^{\alpha_k}\ {f}_{X_l}\left({x}_l\right)\mathrm{d}{x}_l\right\}\\ {}\kern3em \approx {\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{\alpha_k-{\alpha}_kn}\prod \limits_{l=1}^n\left\{\sum \limits_{q=1}^{N_l}{p}_l^{(q)}{\left[{g}_{\mathrm{min}}\left({x}_l^{(q)},{\mu}_{-l}\right)\right]}^{\alpha_k}\right\}\end{array}\end{array}} $$

(14)

Substituting the fractional moments ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ estimated by Eq. (14) for Eq. (10), the parameters λ = {λ₀, λ₁, λ₂, …, λ_r}^T and α = {α₀, α₁, α₂, …, α_r}^T can be obtained, and the unconditional PDF ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ can be solved by Eq. (9).

The conditional fractional moment ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$ also can be estimated by Gaussian quadrature,

$$ {\displaystyle \begin{array}{l}{M}_{Y_{\left.\min \right|{x}_i^{(m)}}}^{\alpha_k}\approx {\int}_{X_{-i}}{\left[{\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{1-n}{g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)\prod \limits_{l=1,l\ne i}^n{g}_{\mathrm{min}}\left({x}_l,{\mu}_{-l}\right)\right]}^{a_k^{,}}{f}_{X_{-i}}\left({x}_{-i}\right){\mathrm{d}x}_{-i}\\ {}\kern4.75em ={\int}_{X_{-i}}{\left[{\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{1-n}{g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)\prod \limits_{l=1,l\ne i}^n{g}_{\mathrm{min}}\left({x}_l,{\mu}_{-l}\right)\right]}^{a_k^{,}}\prod \limits_{l=1,l\ne i}^n\left\{{f}_{X_l}\left({x}_l\right)\mathrm{d}{x}_{-l}\right\}\\ {}\begin{array}{l}\kern4.75em ={\left[{g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)\right]}^{a_k^{,}}{\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{a_k^{,}-{a}_k^{,}n}\prod \limits_{l=1,l\ne i}^n\left\{{\int}_{X_l}{\left[{g}_{\mathrm{min}}\left({x}_l,{\mu}_{-l}\right)\right]}^{a_k^{,}}\ {f}_{X_l}\left({x}_l\right)\mathrm{d}{x}_l\right\}\\ {}\kern4.75em \approx {\left[{g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)\right]}^{a_k^{,}}{\left[{g}_{\mathrm{min}}\left(\mu \right)\right]}^{a_k^{,}-{a}_k^{,}n}\prod \limits_{=1,l\ne i}^n\left\{\sum \limits_{q=1}^{N_l}{p}_l^{(q)}{\left[{g}_{\mathrm{min}}\left({x}_l^{(q)},{\mu}_{-l}\right)\right]}^{a_k^{,}}\right\}\end{array}\end{array}} $$

(15)

Comparing Eq. (14) with Eq. (15), it is seen that the terms g_min(μ) and ${g}_{\mathrm{min}}\left({x}_l^{(q)},{\mu}_{-l}\right)\left(l=1,2,\cdots, i-1,i+1,\cdots, n,q=1,2,\cdots, {N}_l\right)$ in Eq. (15) have been estimated in the process for estimating the unconditional fractional moments ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ in Eq. (14). That is to say, these terms in Eq. (15) can be obtained without any extra model evaluations. Thus, to estimate the conditional fractional moment ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$, it only needs to estimate ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)\left(i=1,2,\cdots, n,m=1,2,\cdots, {N}_i\right)$, and this term also has been evaluated in the process for estimating ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ in Eq. (14). Hence, the conditional fractional moments ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$ can be estimated by repeatedly using the results of the process for estimating ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$, i.e., this process can be completed and no extra model evaluation is needed. After obtaining ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$, the conditional PDF ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$ can be derived by the MaxEnt theory constrained by ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$.

The last issue that should be addressed is how to estimate the minimum of time-dependent performance function, and this paper adopts the adaptive Kriging to solve this problem.

3.3 Adaptive Kriging for estimating g_min(X)

Once the Gaussian points ${x}_i^{(m)}\left(i=1,2,\cdots, n,m=1,2,\cdots, {N}_i\right)$ of inputs are determined, it has to find the minimum response ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)$ at each point $\left({x}_i^{(m)},{\mu}_{-i}\right)=\left({\mu}_1,\dots, {\mu}_{i-1},{x}_i^{(m)},{\mu}_{i+1},\dots, {\mu}_n\right)$. To achieve this goal, the one-dimensional Kriging model ${g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)$ for the actual time-dependent performance function $g\left({x}_i^{(m)},{\mu}_{-i},t\right)$ at each point $\left({x}_i^{(m)},{\mu}_{-i}\right)$ is constructed.

3.3.1 One-dimensional Kriging model for approximating $g\left({x}_i^{(m)},{\mu}_{-i},t\right)$

Denote the samples of time parameter as $T={\left\{{t}_1={t}_0,{t}_2,\cdots, {t}_{n-1},{t}_{N_t}={t}_s\right\}}^{\mathrm{T}}$ (N_t is the number of time samples), which are evenly distributed over the time interval [t₀, t_s]. Given the point $\left({x}_i^{(m)},{\mu}_{-i}\right)$ in the probabilistic space, the responses of time-dependent performance function are $g\left({x}_i^{(m)},{\mu}_{-i},{t}_j\right)\left(j=1,2,\cdots, {N}_t\right)$. A one-dimensional response surface for the actual time-dependent performance function $g\left({x}_i^{(m)},{\mu}_{-i},t\right)$ can then be approximated using the Kriging method, it is expressed as follows

$$ {g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)=\beta \left({x}_i^{(m)},{\mu}_{-i}\right)+Z(t) $$

(16)

in which $\beta \left({x}_i^{(m)},{\mu}_{-i}\right)$ is the global mean of the one-dimensional Kriging model ${g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)$. Z(t) is the error term, it is a stationary Gaussian process with zero mean.

Suppose the training sample set is ${T}^{\left(\boldsymbol{train}\right)}={\left\{{t}_1^{\left(\boldsymbol{train}\right)},{t}_2^{\left(\boldsymbol{train}\right)},\cdots, {t}_M^{\left(\boldsymbol{train}\right)}\right\}}^{\mathrm{T}}$ (M is the number of training samples), the corresponding true responses of time-dependent performance function are ${g}^{\left(\boldsymbol{train}\right)}={\left\{g\left({x}_i^{(m)},{\mu}_{-i},{t}_j^{\left(\boldsymbol{train}\right)}\right),j=1,2,\cdots, M\right\}}^{\mathrm{T}}$. Construct the Kriging model ${g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)$ for actual time-dependent performance function $g\left({x}_i^{(m)},{\mu}_{-i},t\right)$ by using (T^(train), g^(train)), then, the prediction mean μ_K(t) and variance ${\sigma}_K^2(t)$ at an arbitrary point t ∈ T, obtained by the Kriging model ${g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)$, are shown in Eqs. (17) and (18), respectively,

$$ {\mu}_K(t)=\hat{\beta}\left({x}_i^{(m)},{\mu}_{-i}\right)+{r}^{\mathrm{T}}(t){R}^{-1}\left\{{g}^{\left(\boldsymbol{train}\right)}-\hat{\beta}\left({x}_i^{(m)},{\mu}_{-i}\right)1\right\} $$

(17)

$$ {\sigma}_K^2(t)={\hat{\sigma}}_Z^2\left\{1+{\left[{1}^{\mathrm{T}}{R}^{-1}r(t)-1\right]}^{\mathrm{T}}\left[{\left({1}^{\mathrm{T}}{R}^{-1}1\right)}^{-1}\right]\left[{1}^{\mathrm{T}}{R}^{-1}r(t)-1\right]-{r}^{\mathrm{T}}(t){R}^{-1}r(t)\right\} $$

(18)

where

$$ \hat{\beta}\left({x}_i^{(m)},{\mu}_{-i}\right)={\left({1}^{\mathrm{T}}{R}^{-1}1\right)}^{-1}{1}^{\mathrm{T}}{R}^{-1}{g}^{\left(\boldsymbol{train}\right)} $$

(19)

${\hat{\sigma}}_Z^2$ is the process variance for Z(t), it is shown as follows

$$ {\hat{\sigma}}_Z^2=\frac{{\left\{{g}^{\left(\boldsymbol{train}\right)}-\hat{\beta}\left({x}_i^{(m)},{\mu}_{-i}\right)1\right\}}^{\mathrm{T}}{R}^{-1}\left\{{g}^{\left(\boldsymbol{train}\right)}-\hat{\beta}\left({x}_i^{(m)},{\mu}_{-i}\right)1\right\}}{M} $$

(20)

1 is a M × 1 vector filled with 1, R is a M × M matrix of correlation function between each pair of points in the training sample set, and ${R}_{ij}=R\left({t}_i^{\left(\boldsymbol{train}\right)},{t}_j^{\left(\boldsymbol{train}\right)}\right)\left(i,j=1,2,\cdots, M\right)$ is shown in Eq. (21),

$$ R\left({t}_i^{\left(\boldsymbol{train}\right)},{t}_j^{\left(\boldsymbol{train}\right)}\right)=\mathit{\exp}\left\{-w{\left({t}_i^{\left(\boldsymbol{train}\right)}-{t}_j^{\left(\boldsymbol{train}\right)}\right)}^2\right\} $$

(21)

in which w is the unknown correlation parameter, it can be obtained by the maximum likelihood estimation method (Jones et al. 1998),

$$ \hat{w}=\mathit{\arg}\underset{w}{\mathit{\min}}\left({\left|R\right|}^{\frac{1}{M}}{\hat{\sigma}}_Z^2\right) $$

(22)

$r(t)={\left\{R\left(t,{t}_1^{\left(\boldsymbol{train}\right)}\right),R\Big(t,{t}_2^{\left(\boldsymbol{train}\right)}\Big),\cdots, R\Big(t,{t}_M^{\left(\boldsymbol{train}\right)}\Big)\right\}}^{\mathrm{T}}$ is a M × 1 vector of the correlations between candidate points t ∈ T and the M training points ${\left\{{t}_1^{\left(\boldsymbol{train}\right)},{t}_2^{\left(\boldsymbol{train}\right)},\cdots, {t}_M^{\left(\boldsymbol{train}\right)}\right\}}^{\mathrm{T}}$.

3.3.2 Adaptive sampling strategy

It is noted that the posterior distribution of Kriging model ${g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)$ is ${g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)\sim N\left({\mu}_K(t),{\sigma}_K^2(t)\right)$. Consider the following loss function L(t)

$$ L(t)={\left[g\left({x}_i^{(m)},{\mu}_{-i},t\right)-{g}_K\Big({x}_i^{(m)},{\mu}_{-i},t\Big)\right]}^2 $$

(23)

The expectation of the loss function L(t) is

(24)

where E[·] and Var[·] are respectively the expectation operator and variance operator.

The first term ${\left[g\left({x}_i^{(m)},{\mu}_{-i},t\right)-{\mu}_K(t)\right]}^2$ in Eq. (24) is the prediction bias, it represents the average difference between the true response and predicted response. The second term ${\sigma}_K^2(t)$ in Eq. (24) is the prediction variance of the Kriging model. The last term $\mathrm{Var}\left[g\left({x}_i^{(m)},{\mu}_{-i},t\right)\right]$ in Eq. (24) represents the intrinsic noise of the data, which is independent with the Kriging model, thus, it can be ignored when constructing the Kriging model. Therefore, the expected improvement EI(t) of the Kriging model at point t ∈ T can be expressed as follows

(25)

In the adaptive sampling process, the bias term acting as local exploitation is estimated by the leave-one-out cross-validation approach shown in Eq. (26), the variance term acting as global exploration is obtained directly by the constructed Kriging model.

$$ {\boldsymbol{bias}}^2(t)\approx \frac{1}{M}\sum \limits_{j=1}^M{\left[{\mu}_K(t)-{\mu}_K^{\left(-j\right)}(t)\right]}^2 $$

(26)

in which ${\mu}_K^{\left(-j\right)}(t)$ denotes the predicted response for $g\left({x}_i^{(m)},{\mu}_{-i},t\right)$ at point t ∈ T, it is obtained by the Kriging model fitted by all M training samples except ${t}_j^{\left(\boldsymbol{train}\right)}\in {T}^{\left(\boldsymbol{train}\right)}$.

Substituting Eq. (26) for Eq. (25) and introducing the balance factor α, the expected improvement of Kriging model at point t ∈ T can be reorganized as

$$ {\displaystyle \begin{array}{c}E{I}_{CV}^{\alpha }(t)=\alpha \cdotp {\boldsymbol{bias}}^2(t)+\left(1-\alpha \right)\cdotp {\sigma}_K^2(t)\\ {}=\alpha \cdotp \left\{\frac{1}{M}\sum \limits_{j=1}^M{\left[{\mu}_K(t)-{\mu}_K^{\left(-j\right)}(t)\right]}^2\right\}+\left(1-\alpha \right)\cdotp {\sigma}_K^2(t)\end{array}} $$

(27)

in which α is

$$ \alpha =\left\{\begin{array}{c}0.5\kern2.00em \begin{array}{cccc}& & & \end{array}q=1\\ {}0.99\times \mathit{\min}\left[0.5\times \frac{\left[g\left({x}_i^{(m)},{\mu}_{-i},{t}_{M+q-1}\right)-{\mu}_K\left({t}_{M+q-1}\right)\right]}{{\boldsymbol{bias}}^2\left({t}_{M+q-1}\right)}\right]q>1\end{array}\right. $$

(28)

where q denotes the qth iteration of the adaptive Kriging method.

The new training sample t_new for time parameter can be determined by the following optimization process, which will be evaluated and used to update the Kriging model.

$$ {t}_{\mathrm{new}}=\underset{t\in T}{\boldsymbol{argmax}}E{I}_{CV}^{\alpha }(t) $$

(29)

The Kriging model ${g}_K\left({x}_i^{(m)},{\mu}_{-i},t\right)$ will be updated iteratively until the maximum expected improvement is less than a critical value, and in this paper, the critical value is 0.01. Once the sufficiently precise Kriging model is obtained, the minimum of time-dependent performance function $g\left({x}_i^{(m)},{\mu}_{-i},t\right)$ can be obtained by ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)=\underset{t\in T}{\mathit{\min}}{\mu}_K(t)$.

To illustrate the difference between bias term in Eq. (26) and prediction variance, the Goldstein-price function shown in Eq. (30) is taken as an example.

$$ {\displaystyle \begin{array}{c}g\left({X}_1,{X}_2\right)=\left(1+{\left({X}_1+{X}_2+1\right)}^2\left(19-14{X}_1+3{X}_1^2-14{X}_2+6{X}_1{X}_2+3{X}_2^2\right)\right)\\ {}\times \left(30+{\left(2{X}_1-3{X}_2\right)}^2\left(16-32{X}_1+12{X}_1^2+48{X}_2-36{X}_1{X}_2+27{X}_2^2\right)\right)\end{array}} $$

(30)

in which X₁ and X₂ are mutually independent and the deign space is [−2, 2]².

In this example, 10 initial training samples are used to construct the initial Kriging model, the number of test points (the size of candidate sample pool) is 10⁵, and the learning function in Eq. (27) (extended to two-dimensional problem) is used to select the new training samples to update the Kriging model.

At different test points, the bias term and prediction variance term are different and it is unpractical to plot the bias term and prediction variance term at every test point, therefore, this paper only plots the maximum bias and maximum prediction variance varying with the number of training points. Just as demonstrated in Fig. 1, the number of initial training samples for constructing the initial Kriging model is 10, and the number of newly added training samples is 90. It is seen that at the early stage (the number of training samples is small), the bias term and prediction variance term are large, and the bias term is larger than the prediction variance term (except at the initial point). Then, the number of training samples is increasing and both of bias and prediction variance are decreasing.

Fig. 1

The variation of maximum bias and Kriging prediction variance

3.4 Implementation of the proposed method for estimating ${\delta}_{X_i}^{P_f}$

Step 1: Determine the samples $\left({x}_i^{(m)},{\mu}_{-i}\right)\left(i=1,2,\cdots, n,m=1,2,\cdots, {N}_i\right)$ where the minimum ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)$ of time-dependent performance function should be estimated. These samples are listed in Table 1, which are composed of the Gaussian quadrature grid points of inputs.

Table 1 Samples of inputs

It is noted that the total number of samples for input random variables is

$$ N=\left\{\begin{array}{ll}1+\sum \limits_{i=1}^o\left({N}_i-1\right)+{\Sigma}_{i=o+1}^n{N}_i& {N}_i=1,3,5,7,\cdots \\ {}1+{\Sigma}_{i=1}^n& {N}_i{N}_i=2,4,6,8,\cdots \end{array}\right. $$

(31)

where o is the number of inputs which have symmetric distributions, and n − o is the number of residual inputs with none-symmetric distributions.

Eq. (31) implies that the number of input samples N grows linearly with the dimensionality n, and this property avoids the curse of dimensionality to some extent.

Step 2: Estimate the minimum ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)$ of time-dependent performance function for samples in Table 1 by the adaptive Kriging method described in section 3.3. The flowchart of adaptive Kriging method for estimating ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)$ is shown in Fig. 2.

Fig. 2

The flowchart of adaptive Kriging for estimating ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)$

Step 3: Estimate the unconditional-conditional fractional moments ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ and ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$.

After obtaining the minimum ${g}_{\mathrm{min}}\left({x}_i^{(m)},{\mu}_{-i}\right)\left(i=1,2,\cdots, n,m=1,2,\cdots, {N}_i\right)$ by the adaptive Kriging method, the unconditional-conditional fractional moments (${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ and ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$) can be obtained by the M-DRM method demonstrated in section 3.2.

Step 4: Estimate the unconditional PDF ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and conditional PDF ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$ by the MaxEnt theory based on fractional moments ${M}_{Y_{\mathrm{min}}}^{\alpha_k}$ and ${M}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}^{\alpha_k^{\prime }}$, respectively.

Step 5: Estimate the unconditional-conditional time-dependent failure probabilities P_f(t₀, t_s) and ${P}_{f\mid {X}_i}\left({t}_0,{t}_s\right)$ by using the integral about the unconditional and conditional PDFs ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and ${f}_{Y_{\mathrm{min}}\mid {x}_i^{(m)}}\left({y}_{\mathrm{min}}\right)$ (Eqs. (5) and (6)), respectively.

Step 6: Estimate the time-dependent global reliability sensitivity ${\delta}_{X_i}^{P_f}\left(i=1,2,\cdots, n\right)$ by Eq. (8).

From the steps demonstrated above, it is seen that the model evaluations are produced in step 2 for estimating the minimum of time-dependent performance function. The flowchart of the proposed method for estimating time-dependent global reliability sensitivity ${\delta}_{X_i}^{P_f}\left(i=1,2,\cdots, n\right)$ is shown in Fig. 3.

Fig. 3

The flowchart of the proposed method for estimating ${\delta}_{X_i}^{P_f}\left(i=1,2,\cdots, n\right)$

4 Discussions

It is seen that the proposed algorithm depends on three specific technologies, i.e., adaptive Kriging, MaxEnt based on fractional moments and M-DRM. That is to say, the accuracy and efficiency of the proposed algorithm rely on these three methods.

• (1) Since the adaptive Kriging is responsible for estimating the minimum of time-dependent performance function, thus, if the minimum of time-dependent performance function is estimated precisely, it implies the adaptive Kriging is well-trained.

• (2) It is noted that the computational cost is only produced in constructing the Kriging model for estimating the minimum of time-dependent performance function, thus, the efficiency of adaptive Kriging determines the efficiency of the whole proposed algorithm.

• (3) The accuracy of M-DRM for estimating fractional moments affects the accuracy of the proposed algorithm for estimating time-dependent global reliability sensitivity. It is noted that the M-DRM only concerns the mean value term g_min(μ) and univariate terms g_min(X_i, μ_−i)(i = 1, 2, ⋯, n), it ignores the cross terms. Thus, if the cross-terms of the original function are important, the M-DRM will produce a large estimation error.

• (4) If the order of moment is larger than two, i.e., α > 2, although the M-DRM for estimating fractional moment introduces large estimation error, the PDF estimate maybe accurate, since the higher-order moment has little effect on the accuracy of PDF estimation. This issue will be demonstrated in the examples.

• (5) The fraction and Lagrangean multiplier in Eqs. (9) and (11) should be estimated by optimization strategy. It also affects the accuracy of the proposed algorithm. The selection of optimization strategy, initial point of the optimization strategy, etc., have a large impact on the final result.

• (6) The number of Gaussian grids influences the efficiency and accuracy of the proposed algorithm. Note that the k-point Gaussian quadrature will provide an exact answer if the integrand is a polynomial of order 2k − 1 or less. Theoretically, if k increases, the efficiency of the proposed algorithm will decrease, whereas the accuracy of the proposed algorithm will increase.

5 Examples

In this section, the proposed strategy is applied to several examples for the sake of illustration. The first example is a simple numerical example with two random variables. The second example is a case with respect to the transport aircraft wing structure, and the third one is an engineering case with implicit performance function.

5.1 Numerical example

The time-dependent performance function of the structure is characterized as follows,

$$ g\left(X,t\right)=\frac{X_1^2{X}_2-5{X}_1t+\left({X}_2+1\right){t}^2}{25} $$

(32)

in which the input variables X₁ and X₂ are independent normal variables, X₁~N(3.5, 0.2²) and X₂~N(4, 0.2²). The time interval under consideration is [0,5].

The samples $\left({x}_i^{(m)},{\mu}_{-i}\right)\left(i=1,2,m=1,2,\cdots, 5\right)$ of input variables of this example are listed in Table 2, which are obtained from the five-point Gaussian quadrature about the inputs. Since the input variables follow normal distributions, thus, the mean value point μ = {μ₁, μ₂}^T = {3.5, 4}^T is equivalent to the middle Gaussian point (samples 3 and 8 in Table 2), and it only needs to estimate arbitrary one sample of them to obtain g_min(μ). Therefore, the number of “useful” samples of this example is $N=1+\sum \limits_{i=1}^2\left(5-1\right)=9$.

Table 2 Input samples of numerical example

To evaluate the time-dependent global reliability sensitivity for this example, it has to estimate the minimum of time-dependent performance function at samples in Table 2. The estimated minimum value at each sample point is listed in Table 3, in which the values in the brackets denote the number of time-dependent performance function evaluations. Since the computational cost of the proposed algorithm only produces in the process for estimating the minimum of time-dependent performance function, thus, it can be seen that the total number of model evaluations of the proposed method for estimating time-dependent global reliability sensitivity is 54. It is obvious that the adaptive Kriging algorithm accurately estimates the minimum of time-dependent performance function with less computational cost compared with MCS.

Table 3 Minimum values at the samples in Table 2

After obtaining the minimum of time-dependent performance function, the unconditional-conditional PDFs ${f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)$ and ${f}_{Y_{\mathrm{min}}\mid {X}_i}\left({y}_{\mathrm{min}}\right)$ can be obtained by the MaxEnt theory based on the unconditional-conditional fractional moments constraint. To measure the approximation errors of the fractional moments using M-DRM, this paper lists the moments estimated by M-DRM and MCS at r ∈ {3, 4, 5} (r denotes the number of fractions). For r = 3, the fractions of fractional moments (the orders of the fractional moments) obtained by the optimization strategy are α = {−2.02, −0.06, 3.76}^T, for r = 4, the fractions of fractional moments obtained by the optimization strategy are α = {−1.02, 0.0056, 2.26, −0.87}^T, and for r = 5, the fractions of fractional moments obtained by the optimization strategy are α = {1.49, −0.002, 0.78, −6.40, 0.42}^T. The corresponding fractional moments ${M}_{Y_{\mathrm{min}}}^{\alpha_i}\left(i=1,2,\cdots, r\right)$ estimated by M-DRM and MCS for r ∈ {3, 4, 5} are listed in Table 4.

Table 4 The fractional moments estimated by M-DRM and MCS

It is seen that, at r = 3, the fractional moment ${M}_{Y_{\mathrm{min}}}^{3.76}$ estimated by MCS is 3.46, but the result obtained by M-DRM is 1.74, it means that the M-DRM estimates this fractional moment with large error. Comparing the results in Table 4, it also can be noted that, if the absolute value of the order of the moment is larger, the error of M-DRM for estimating the fractional moment tends to be larger.

Then, the unconditional-conditional time-dependent failure probabilities can be obtained by ${P}_f\left({t}_0,{t}_s\right)={\int}_0^1{f}_{Y_{\mathrm{min}}}\left({y}_{\mathrm{min}}\right)\mathrm{d}{y}_{\mathrm{min}}$ and ${P}_{f\mid {X}_i}\left({t}_0,{t}_s\right)={\int}_0^1{f}_{Y_{\mathrm{min}}\mid {X}_i}\left({y}_{\mathrm{min}}\right)\mathrm{d}{y}_{\mathrm{min}}$, respectively. Finally, the time-dependent global reliability sensitivity is shown in Table 5 (the value in the bracket represents the variation coefficient), in which MCS denotes the Monte Carlo simulation, DL-AK-MCS denotes the double-loop adaptive Kriging combined with MCS (Wang and Wang 2015), and SL-AK-MCS denotes the single-loop adaptive Kriging combined with MCS (Hu and Mahadevan 2016). N_eval denotes the total number of time-dependent performance function evaluations for estimating the time-dependent global reliability sensitivity.

Table 5 Result comparison for numerical example

To measure the effects of k (the number of Gaussian points) and r (the number of fractions) on computational efficiency and accuracy, the time-dependent global reliability sensitivity estimates under different k and r are provided. It is seen that the proposed method can obtain the similar results as the reference methods, and variable X₁ has larger contribution to the time-dependent failure probability compared with X₂.

It also can be concluded that the number of fractions r has no effect on computational efficiency, but has an effect on computational accuracy, the number of Gaussian points has an effect on computational efficiency and accuracy. At case k = 3 and r = 4, the proposed algorithm is the most efficient method compared with MCS, DL-AK-MCS and SL-AK-MCS.

It is seen from Table 4 that if the absolute value of the order of the moment is large, the estimation error of M-DRM will be large compared with MCS. At case r = 3, the orders of the moments are α = {−2.02, −0.06, 3.76}^T, the last one 3.76 is larger than two, thus, although the fractional moment obtained by M-DRM is far away from that obtained by MCS, the final result in Table 5 (including time-dependent failure probability and time-dependent global reliability sensitivity) is similar as that estimated by MCS.

5.2 A transport aircraft wing structure

This section considers a representative wing structure used in Refs. (Venter and Sobieszczanksi 2004; Acar and Haftka 2005). The wing is chosen as a typical long-range transport aircraft wing in the Boeing 767 class, the geometric details of it are obtained from Venter and co-workers (Venter and Sobieszczanksi 2004). A simple sketch of the transport aircraft wing geometry (Venter and Sobieszczanksi 2004) is given in Fig.4. Figure 5(a) is the cross-sectional view of the transport aircraft wing where T, h and c are the thickness, the depth and the chord of the wing, respectively. Figure 5(b) is the top view of the wing where b is the span and b = 40(m).

Fig. 4

Spar and rib configuration of the transport aircraft wing

Fig. 5

Transport aircraft wing. a Cross-sectional view. b Top view

The wing is subject to elliptical load (see Fig. 6) distribution of magnitude equal to the 40% (for each side, totally 80%) of 2.5 times (load factor) take-off gross weight of the aircraft. The effective (load carrying) chord length is taken as 45% of the actual chord corresponding to front spar located at 15% chord and the rear spar is located at 60% of the chord. The wing depth/chord ratio is taken as 85% of its maximum value since the depth/chord ratio changes chordwise (Acar and Haftka 2005).

Fig. 6

Loading on the wing

In this contribution, denote the input vector as X = {P_r, σ_f, c_r, c₀/c_r, h/c, T}^T, where X₁ = P_r is the loading at the root, X₂ = σ_f is the allowable stress, X₃ = c_r is the chord length of root, X₄ = c₀/c_r is the tip/chord ratio, X₅ = h/c is the depth/chord ratio and X₆ = T is the thickness of the wing. The parameters and distributions of input variables are listed in Table 6. In this transport aircraft wing example, the location in the x-axis can be viewed as time parameter t and t ∈ [10, 20], thus, this example can be viewed as a generalized time-dependent problem.

Table 6 Distribution parameters of input variables

To analyze the time-dependent global reliability sensitivity for the transport aircraft wing, it has to obtain the failure mode of the wing at the first. This contribution uses the maximum stress that does not exceed the allowable stress to construct the performance function of the wing.

The chord length c(X, t) of the wing is

$$ c\left(X,t\right)={c}_r\left[\left(\frac{c_0}{c_r}\right)+\left(1-\frac{c_0}{c_r}\right)\frac{t}{b/2}\right] $$

(33)

the wing depth h(X, t) is

$$ h\left(X,t\right)={c}_r\left(\frac{h}{c\left(X,t\right)}\right)\left[\left(\frac{c_0}{c_r}\right)+\left(1-\frac{c_0}{c_r}\right)\frac{t}{b/2}\right] $$

(34)

the moment of inertia I_Z(X, t) is

$$ {I}_Z\left(X,t\right)=\frac{1}{2}c\left(X,t\right)T{h}^2\left(X,t\right) $$

(35)

the wing loading P(t) and wing area A(t) are respectively shown in Eqs. (36) and (37),

$$ P(t)={P}_r\left[1-{\left(\frac{t}{b/2}\right)}^2\right] $$

(36)

$$ A(t)=\frac{1}{2}\left[c\left(X,t\right)+{c}_0\right]t $$

(37)

Then, the bending moment M(X, t) at any x-location can be expressed as

$$ M\left(X,t\right)=4{P}_r{c}_rb\left[\left(\frac{c_0}{c_r}\right)\frac{t^4}{12{b}^2}+\left(1-2\frac{c_0}{c_r}\right)\frac{t^5}{20{b}^3}+\left(\frac{c_0}{c_r}-1\right)\frac{t^6}{30{b}^4}\right] $$

(38)

Finally, the time-dependent performance function of this transport aircraft wing can be expressed as Eq. (36),

$$ g\left(X,t\right)=\frac{\sigma_f}{\frac{M\left(X,t\right)\left[h\left(X,t\right)/2\right]}{I_Z\left(X,t\right)}} $$

(39)

If g(X, t) ≤ 1, the wing structure is failed, and the wing structure is safe for others.

The samples $\left({x}_i^{(m)},{\mu}_{-i}\right)\left(i=1,2,\cdots, 6,m=1,2,\cdots, 5\right)$ of input variables of the transport aircraft wing are listed in Table 7 (takes the five-point Gaussian quadrature as an example). The number of “useful” samples of this transport aircraft wing example is $N=1+\sum \limits_{i=1}^6\left(5-1\right)=25$.

Table 7 Input samples of the transport aircraft wing

The estimated minimum of the time-dependent performance function at each sample point in Table 7 is listed in Table 8, it can be seen that the total number of model evaluations of the proposed method for estimating the time-dependent global reliability sensitivity is 270.

Table 8 Minimum values at the samples in Table 7

Then, the unconditional-conditional fractional moments and PDFs of the minimum of time-dependent performance function should be estimated. To measure the approximation errors of the fractional moments using M-DRM, the fractional moments estimated by M-DRM and MCS at r ∈ {3, 4, 5} are provided. For r = 3, the fractions of fractional moments obtained by the optimization strategy are α = {−0.04, −0.02, 5.3}^T, for r = 4, the fractions of fractional moments obtained by the optimization strategy are α = {1.55, −0.16, 1.82, −0.81}^T, and for r = 5, the fractions of fractional moments obtained by the optimization strategy are α = {0.96, −0.0018, 0.79, −4.14, 0.38}^T. The fractional moments estimated by M-DRM and MCS for these three cases are listed in Table 9. It also can be concluded that, generally, the estimation error of M-DRM for estimating the fractional moment is increase with the increase of the absolute value of the order of the moment.

Table 9 The moments estimated by M-DRM and MCS

Table 10 provides the results of time-dependent failure probability obtained by various methods, in which Cov[·] denotes the variation coefficient. According to the results in Table 10, it can be concluded that the proposed method is more efficient than the reference methods while the same accuracy is kept.

Table 10 Result comparison for transport aircraft wing

The time-dependent global reliability sensitivity results are listed in Fig. 7. It can be seen that the thickness T has the largest contribution to the time-dependent failure probability of the transport aircraft wing, followed by allowable stress σ_f and the loading at the root P_r. The chord length of the root c_r, the tip/chord ratio c₀/c_r, and the depth/chord length h/c have little effect on the time-dependent failure probability of the transport aircraft wing. For this example, the DL-AK-MCS and SL-AK-MCS methods have large estimation errors, but the proposed algorithm processes good approximation accuracy.

Fig. 7

Time-dependent global reliability sensitivity of transport aircraft wing structure

5.3 The undercarriage retraction and extension system

The main component of an undercarriage is demonstrated in Fig. 8. In retraction, if the load supported by the undercarriage retraction and extension system exceeds the driving force provided by the hydraulic system, the oil flux in the speed regulating valve of the hydraulic system will rapidly decrease to 0, and the velocity of the undercarriage retraction and extension system will decrease to 0, then, this system cannot complete the retraction task. According to this fact, the time-dependent performance function of the undercarriage retraction and extension system can be constructed as follows,

$$ g\left(X,t\right)={F}_{\mathrm{D}}-{F}_{\mathrm{L}}\left(X,t\right) $$

(40)

where X = {μ_A, μ_B, μ_C, μ_E, r₀}^T are the random inputs, in which μ_A, μ_B, μ_C and μ_E denotes the friction factors for joint points A, B, C, and E. r = r₀ − vt represents the radius of latch at point D, where r₀ is the initial radius of latch at point D, and the latch is gradual abrasion with time t, the abrasion velocity is v = 5 × 10⁻⁴(m/year), and the service time of this undercarriage structure is t ∈ [0, 10](year). F_D denotes the driving force provided by the hydraulic system, and F_L(X, t) represents the load subjected by the undercarriage retraction and extension system at the retraction process, it is obtained by the ADAMS software. The distribution types and parameters of the input variables are listed in Table 11.

Fig. 8

The undercarriage structure

Table 11 Distributions of input variables for the undercarriage structure

The evolution of the time-dependent performance function with the time parameter is shown in Fig. 9, in which the different curves denote the evolution of time-dependent performance function with the time parameter on the random variables fixed at different points. It is seen that, generally, the time-variant performance function is a non-linear function with single peak with respect to the time parameter.

Fig. 9

The evolution of time-dependent performance function with time parameter

The samples $\left({x}_i^{(m)},{\mu}_{-i}\right)\left(i=1,2,\cdots, 5,m=1,2,\cdots, 5\right)$ of input variables of the undercarriage retraction and extension system are listed in Table 12 (takes the five-point Gaussian quadrature as an example). The number of “useful” samples of this undercarriage retraction and extension system is $N=1+\sum \limits_{i=1}^5\left(5-1\right)=21$.

Table 12 Input samples of the undercarriage structure

The estimated minimum of time-dependent performance function at each sample point in Table 12 is listed in Table 13, it can be seen that the total number of model evaluations of the proposed method for estimating the time-dependent global reliability sensitivity is 187.

Table 13 Minimum values at the samples in Table 11

Then, the unconditional-conditional fractional moments and PDFs should be estimated by M-DRM and MaxEnt, respectively. To measure the approximation errors of the fractional moments using M-DRM, this paper lists the moments estimated by M-DRM and MCS at r ∈ {3, 4, 5}. For r = 3, the fractions of fractional moments obtained by the optimization strategy are α = {0.01, −2.43, −0.44}^T, for r = 4, the fractions of fractional moments obtained by the optimization strategy are α = {−1.80, 0.37, 0.72, 0.70}^T, and for r = 5, the fractions of fractional moments obtained by the optimization strategy are α = {0.82, −0.0013, 0.96, −5.13, 0.41}^T. The fractional moments estimated by M-DRM and MCS for these three cases are listed in Table 14.

Table 14 The fractional moments estimated by M-DRM and MCS

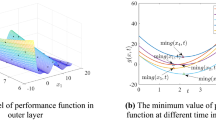
The estimation of unconditional PDF of the minimum of time-dependent performance function at different number of fractions (i.e., r = 3, r = 4, and r = 5) is shown in Fig. 10, which is obtained by MCS combined with MaxEnt. In Fig.10, the different curves in the same figure denote the PDF estimation of the minimum of time-dependent performance function at different initial values of the optimization process in Eq. (10). It is seen that the PDF estimation is sensitive to the initial value of the optimization process, and if the initial value is “bad”, the estimation of PDF may be far away from its true statistic characteristic. And the number of fractions also has impact on the accuracy of PDF estimation.

Fig. 10

The PDF estimation of the minimum of time-dependent performance function

Table 15 provides the results of time-dependent failure probability obtained by various methods. Figure 11 illustrates the time-dependent global reliability sensitivity obtained by different methods. It is seen that for this example, the time-dependent failure probability estimates obtained by DL-AK-MCS and the proposed algorithm at case k = 5 and r = 3 are close to the result estimated by MCS. The SL-AK-MCS and other cases of the proposed algorithm process large estimation error. The large error of the proposed algorithm mainly comes from: (1) The estimation error of M-DRM for estimating fractional moments. (2) The optimization process in MaxEnt for estimating PDF introduces large estimation error. Figure 11 implies that the friction factor μ_B has the largest impact on time-dependent failure probability.

Table 15 Result comparison for undercarriage retraction and extension system

Fig. 11

Time-dependent global reliability sensitivity of undercarriage structure

6 Conclusions

This contribution focuses on conducting the time-dependent global reliability sensitivity analysis, which can help researchers control the time-dependent failure probability. A novel method for estimating the time-dependent global reliability sensitivity is proposed. It firstly transforms the estimation of time-dependent unconditional-conditional failure probabilities into that of unconditional-conditional PDFs of the minimum of time-dependent performance function. The proposed method is a double-loop strategy. In the inner loop, the minimum of time-dependent performance function is efficiently estimated by adaptive Kriging, in which a new learning function is employed to iteratively select new training sample to update the Kriging model. Based on these minimum values, the unconditional-conditional fractional moments are obtained by M-DRM, and the unconditional-conditional PDFs are solved by MaxEnt constrained by these unconditional-conditional fractional moments. The unconditional-conditional time-dependent failure probabilities are evaluated by taking integral about the unconditional-conditional PDFs. Finally, the time-dependent global reliability sensitivity is obtained by the Gaussian quadrature in the outer loop.

The proposed method evaluates the time-dependent performance function only in the process for estimating the minimum of time-dependent performance function, and it can reduce the computational cost dramatically due to: (1) The adaptive Kriging is applied to estimate the minimum of time-dependent performance function. (2) The M-DRM can estimate the unconditional-conditional fractional moments simultaneously. (3) The MaxEnt based on fractional moments constraint can efficiently approximate the unconditional-conditional PDFs of the minimum of time-dependent performance function. The results of the examples illustrate that the proposed method can efficiently estimate the time-dependent global reliability sensitivity, but for highly nonlinear problem (M-DRM will ignore the cross term), or the number of fractions is large (the optimization process will introduce large approximation error), the result obtained by the proposed algorithm may have large approximation error.