1 Introduction

Reliability is the probability that a product performs its intended performance over a specified period of time under specified conditions (Hu and Du 2013). It can be classified into time-independent reliability and time-dependent reliability. Time-dependent reliability analysis quantifies the probability that a structure or system survives after it has worked for a certain time t or over the period [t 0, t f ] (Singh et al. 2010). When the time-dependent reliability analysis is performed at each time instant, it is said to be time-independent reliability analysis which is also called static reliability analysis.

The static reliability analysis aims at estimating the probability of structure or system matching specific requirement. In the past decades, many methods have been developed for reliability of static structure, such as the Monte Carlo Simulation (MCS) (Binder 1997), the First Order Reliability Method (FORM) (Hasofer and Lind 1974), the Second Order Reliability Method (SORM) (Zhao and Ono 1999), the Importance Sampling method (IS) (Au and Beck 2003) and the Line Sampling method (LS) (Schueller et al. 2004) etc. In engineering, the precise probability distributions of the inputs usually cannot be obtained. In such circumstances, some efficient approaches have been proposed, such as convex modeling analysis (Kang and Luo 2009), interval analysis (Moore 1966), possibility theory (Zadeh 1978) and probabilistic models (Kang and Luo 2010).

For the time-dependent reliability, Rice (Rice 2015; Lutes and Sarkani 2009) firstly developed the first-passage method and then this method was developed by several authors (Sudret 2008; Andrieu-Renaud et al. 2004). Now, the first-passage method becomes the most popular method for solving time-dependent reliability problem. The advantage of this method is its high efficiency, but its accuracy is poor for problem whose reliability is low and the accuracy is based on the assumption that all the up-crossings are independent. Extreme value method (Lutes and Sarkani 2004; Li and Mourelatos 2009) is another type procedure for time-dependent reliability analysis. This method uses the distribution of the extreme value of the limit state function under consideration to estimate the reliability. By introducing the envelope function and first order approximation of the motion error function, Du proposed an envelope method for the time-dependent reliability (Du 2014). This procedure is proved to be an accurate and efficient method for time-dependent reliability, but it is just suitable for the problem where the coefficient of variation of the input is small. Here are other studies on time-dependent reliability analysis (Mourelatos et al. 2015; Jiang et al. 2014). In this paper, we proposed two new strategies based on the moment of extreme value to efficiently estimate the failure probability for temporal and spatial multi-parameter dynamic reliability problem. By using the sparse grid technique (He et al. 2014) and dimensional reduction method (Rabitz 1999; Li and Artamonov 2003), we can efficiently estimate the extreme value moments. Then the temporal and spatial multi-parameter dynamic failure probability can be estimated by combining with the fourth-moment method (Zhao and Lu 2007) or the maximum entropy (Inverardi and Tagliani 2003).

The global sensitivity analysis can measure the overall effect of the uncertainty of each input on the variance or the distribution of the model outputs in consideration (Wei and Lu 2012). Many sensitivity analysis techniques are now available. Sobol and others proposed the variance-based global sensitivity indices (Sobol 2001; Song et al. 2015) to measure the effects of the uncertainty of input on the variance of model outputs. Borgonovo and others developed the moment-independent global sensitivity indices (Borgonovo 2007; Zhang et al. 2014b) to measure the effects of the uncertainty of each input on the distribution of model outputs. Cui, Li and Wei developed the global reliability sensitivity indices (Wei and Lu 2012; Cui and Lu 2010; Li et al. 2012) to measure the uncertainty of each input on the failure probability. The global reliability sensitivity indices (Li et al. 2012) proposed by Li is defined as the expectation of the square of the difference between the unconditional failure probability and conditional failure probability. The global reliability sensitivity technique is shown to be especially useful for reliability-based design. In this paper, we extend this global reliability sensitivity technique to the dynamic problem with the temporal and spatial multi-parameter. Based on the dynamic reliability analysis method we proposed, combining with the three-point estimation method (Zhang et al. 2014a), this paper develops two new efficient global reliability sensitivity approaches for temporal and spatial multi-parameter dynamic reliability problem.

This paper is organized as follows: Section 2 gives the definition of temporal and spatial multi-parameter dynamic reliability. Section 3 proposes two temporal and spatial multi-parameter dynamic reliability strategies by use of the extreme value moments to efficiently estimate the dynamic failure probability. Section 4 gives the definition of global reliability sensitivity indices for temporal and spatial multi-parameter dynamic problems and introduces two approaches to calculate the indices based on the proposed dynamic reliability strategies. Section 5 employs several examples for demonstrating the efficiency and precision of the proposed methods. Section 6 gives the conclusion.

2 The definition of temporal and spatial multi-parameter dynamic reliability

Considering the temporal and spatial limit state function is in the form of G = g(X, z), in which X = [X 1, X 2, …, X n ]T denotes the n-dimensional vector constructed by the independent random variables X i (i = 1, 2, …, n) and z = [z 1, z 2, …, z m ]T is temporal and spatial multi-parameter vector. In the discussed problem, we assume that the temporal and spatial parameter is in an interval, i.e. \( {z}_i\in \left[{\underset{\bar{\mkern6mu}}{z}}_i,{\overline{z}}_i\right] \), (i = 1, 2, …, m), and the random variables X i (i = 1, 2, …, n) are time independent and space position independent. As usual, the safe domain corresponds to positive values of g(⋅), and the failure domain corresponds to negative values of g(⋅). The temporal and spatial multi-parameter dynamic reliability over parameter intervals is defined by:

$$ R\left({z}_1,\dots, {z}_m\right)= P\left\{ g\left(\mathbf{X},\mathbf{z}\right)>0,\kern1em \forall \left({z}_1\in \left[{\underset{\bar{\mkern6mu}}{z}}_1,{\overline{z}}_1\right]\right)\cap \cdot \cdot \cdot \cap \left({z}_m\in \left[{\underset{\bar{\mkern6mu}}{z}}_m,{\overline{z}}_m\right]\right)\right\} $$
(1)

The failure probability for temporal and spatial multi-parameter dynamic problem can be defined as:

$$ {P}_f\left({z}_1,\dots, {z}_m\right)= P\left\{ g\left(\mathbf{X},\mathbf{z}\right)\le 0,\kern1em \exists \left({z}_1\in \left[{\underset{\bar{\mkern6mu}}{z}}_1,{\overline{z}}_1\right]\right)\cap \cdot \cdot \cdot \cap \left({z}_m\in \left[{\underset{\bar{\mkern6mu}}{z}}_m,{\overline{z}}_m\right]\right)\right\} $$
(2)

where \( \left({z}_1\in \left[{\underset{\bar{\mkern6mu}}{z}}_1,{\overline{z}}_1\right]\right)\cap \cdot \cdot \cdot \cap \left({z}_m\in \left[{\underset{\bar{\mkern6mu}}{z}}_m,{\overline{z}}_m\right]\right) \) means the value domain of the temporal and spatial multi-parameters.

The temporal and spatial multi-parameter dynamic limit state function Y = g(X, z) can be considered as a parametric function, where z is the parameter vector. That’s to say, the function represents a family of hyper-surfaces when z varies on the intervals. So the function g(⋅) can be regarded as the function of z when the input variables are fixed on their realization x ∗ over their distributions.

$$ h\left(\mathbf{z}\right)= g\left({\boldsymbol{x}}^{\ast },\mathbf{z}\right) $$
(3)

From the Eqs. (2) and (3), it is concluded that if the minimum value of the Eq. (3) is greater than zero, then the structure or system will be safe at the parameter intervals. Otherwise it will be failure if the minimum value is less than or equal to zero. Suppose the minimum value point is denoted as z ∗ = [z ∗1 , z ∗2 , …, z ∗ m ]T when x = x ∗, one method is proposed in next section to determine z ∗ at x = x ∗.

3 Temporal and spatial multi-parameter dynamic reliability analysis

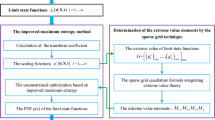
The moments on the minimum value of the dynamic limit state function is introduced to estimate the failure probability for temporal and spatial multi-parameter dynamic reliability problem. And the moments of the minimum value of g(X, z) is denoted as the extreme value moments. The key idea is to employ some point-estimation techniques to generate the samples and calculate the extreme value moments. After the extreme value moments are obtained, the failure probability of the temporal and spatial multi-parameter dynamic reliability problem can be estimated by the moment method and maximum entropy technique. The next subsections give two strategies about how to use different point-estimation techniques for estimating the extreme value moments and the dynamic failure probability.

3.1 A sparse grid technique combined with the fourth-moment method

The fourth-moment method (Zhao and Lu 2007) is an efficient method to estimate the failure probability for static reliability problem. We extend this method to calculate the failure probability of temporal and spatial multi-parameter dynamic reliability problem by using the extreme value moments. For estimating the extreme value moments, a sparse grid technique is employed.

A sparse grid stochastic collocation method (He et al. 2014) is an efficiently approach to compute the moment of limit state function in static reliability analysis. This method usually needs much fewer function evaluations than MCS method. In this paper, the input variables X = [X 1, X 2, …, X n ]T are assumed to be mutually independent standard normal random variables, if not so, one can use the Rosenblatt transformation (Rosenblatt 1952) to transform the input variables to be independent standard normal random variables.

For arbitrary input variables X, the minimum value function g S(X, z) of temporal and spatial multi-parameter dynamic limit state function g(X, z) can be expressed as follows.

$$ {g}^S\left(\mathbf{X},\mathbf{z}\right)=\underset{\underset{\bar{\mkern6mu}}{\mathbf{z}}\le \mathbf{z}\le \overline{\mathbf{z}}}{ \min}\left[ g\left(\mathbf{X},\mathbf{z}\right)\right] $$
(4)

Generally, the origin moments of the extreme value of the temporal and spatial multi-parameter dynamic reliability problem can be computed by the multivariate integration as follows.

$$ {M}_{\alpha_l{g}^S}={\displaystyle {\int}_{\mathbf{X}}{\left[{g}^S\left(\boldsymbol{x},\mathbf{z}\right)\right]}^{\alpha_l}{f}_{\mathbf{X}}\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}} $$
(5)

in which, α l (l = 1, 2, …, u) denotes the α l th moment, f X (x) is the joint probability density function (JPDF) of input variable vector. If the input variables are independent, then \( {f}_{\mathbf{X}}\left(\boldsymbol{x}\right)={\displaystyle \prod_{i=1}^n{f}_i\left({x}_i\right)} \), where f i (x i ) is the marginal PDF of X i (i = 1, 2, …, n). Furthermore, based on the hypothesis that input variables are independent standard normal random variables, Eq. (5) can be rewritten as:

$$ {M}_{\alpha_l{g}^S}={\displaystyle {\int}_{-\infty}^{+\infty}\cdot \cdot \cdot }{\displaystyle {\int}_{-\infty}^{+\infty }{\left[{g}^S\left({x}_1,\dots, {x}_n,\mathbf{z}\right)\right]}^{\alpha_l}\varphi \left({x}_1\right)\dots \varphi \left({x}_n\right) d{x}_1\dots d{x}_n} $$
(6)

where φ(⋅) is the PDF of a standard normal random variable.

With the Smolyak algorithm (Smolyak 1963), Eq. (6) can be derived as:

$$ {M}_{\alpha_l{g}^S}={\displaystyle \sum_{i\in H\left( q, n\right)}{\left(-1\right)}^{q+ n-\left| i\right|}}\left(\begin{array}{l}\kern1.5em n-1\\ {} q+ n-\left|\boldsymbol{i}\right|\end{array}\right)\times {\displaystyle \sum_{j_1=1}^{m_{i_1}}\cdots }{\displaystyle \sum_{j_n=1}^{m_{i_n}}{\left[{g}^S\left({x}_{j_1}^{i_1},\dots, {x}_{j_n}^{i_n},\mathbf{z}\right)\right]}^{\alpha_l}}{p}_{j_1}^{i_1}\cdots {p}_{j_n}^{i_n} $$
(7)

where the weights and abscissas are \( {p}_{j_i}^{i_i}=\frac{1}{\sqrt{\pi}}{\zeta}_{j_i}^{i_i} \) and \( {x}_{j_i}^{i_i}=\sqrt{2}{\xi}_{j_i}^{i_i} \), in which \( {\zeta}_{j_i}^{i_i} \) and \( {\xi}_{j_i}^{i_i} \) are the weights and abscissas in the Gauss-Hermite quadrature formula, \( {j}_i=1,\dots, {m}_{i_i} \), i = (i 1, …, i n ) ∈ N n+ , and the H(q, n) is defined by:

$$ H\left( q, n\right)=\left\{\boldsymbol{i}\in {N}_{+}^n,\boldsymbol{i}\ge 1: q+1\le {\displaystyle \sum_{l=1}^n{i}_l}\le q+ n\right\} $$
(8)

in which the choice of q depends on the nonlinearity of the g S(x, z).

In Eq. (7), the vector z represents the minimum value point corresponding to the input variable nodes \( {\left[{x}_{j_1}^{i_1},\dots, {x}_{j_n}^{i_n}\right]}^{\mathrm{T}} \). The input variable nodes \( {\left[{x}_{j_1}^{i_1},\dots, {x}_{j_n}^{i_n}\right]}^{\mathrm{T}} \) can be generated by the sparse grid technique, then we can determine the minimum value point z corresponding to the input variable nodes by the method proposed in subsection 3.3.

From above procedure, it is shown that the sparse grid method can generate much fewer interpolation nodes but most useful to calculate the extreme value moments. In this paper, the first four extreme value moments are combined with the fourth-moment method to estimate the dynamic failure probability. Before using the fourth-moment method, the origin moments should be converted to the central moments of the extreme value by the following Eq. (9).

$$ \left\{\begin{array}{l}{\gamma}_{1{g}^S}={M}_{1{g}^S}\\ {}{\gamma}_{2{g}^S}={\left({M}_{2{g}^S}-{M}_{1{g}^S}^2\right)}^{1/2}\\ {}{\gamma}_{3{g}^S}={\left({M}_{2{g}^S}-{M}_{1{g}^S}^2\right)}^{-3/2}\cdot \left({M}_{3{g}^S}-3{M}_{1{g}^S}{M}_{2{g}^S}+2{M}_{1{g}^S}^3\right)\\ {}{\gamma}_{4{g}^S}={\left({M}_{2{g}^S}-{M}_{1{g}^S}^2\right)}^{-2}\cdot \left({M}_{4{g}^S}-4{M}_{1{g}^S}{M}_{3{g}^S}+6{M}_{1{g}^S}^2{M}_{2{g}^S}-3{M}_{1{g}^S}^4\right)\end{array}\right. $$
(9)

in which \( {\gamma}_{k{ g}^S}\left( k=1,2,3,4\right) \) is the first four central moments of the extreme value function g S(⋅). Then the failure probability can be computed with the fourth-moment method as follows (Zhao and Lu 2007).

$$ \beta =\frac{\gamma_{3{g}^S}\left[{\left({\gamma}_{1{g}^S}/{\gamma}_{2{g}^S}\right)}^2-1\right]+3{\gamma}_{1{g}^S}\left({\gamma}_{4{g}^S}-1\right)/{\gamma}_{2{g}^S}}{\sqrt{\left(5{\gamma}_{3{g}^S}^2-9{\gamma}_{4{g}^S}+9\right)\left(1-{\gamma}_{4{g}^S}\right)}} $$
(10)
$$ {P}_f=\varPhi \left(-\beta \right) $$
(11)

in which β is the reliability index and Φ(⋅) is the standard normal cumulative distribution function (CDF).

3.2 Dimensional reduction method combined with the maximum entropy

In this subsection, the second strategy for the dynamic failure probability is presented. In this strategy, the fractional moments of the extreme value for the minimum value function g S(X, z) of g(X, z) is firstly estimated by the dimensional reduction method, then the maximum entropy approach is employed to estimate the dynamic failure probability.

For the static reliability analysis, it is efficient and accurate to compute the failure probability by using the multiplicative form of dimensional reduction method for estimating the fractional moments and the maximum entropy constrained by the fractional moments for estimating the failure probability (Zhang and Pandey 2013). In this paper, this approach is combined with the moments of the extreme value to analyze the temporal and spatial multi-parameter dynamic failure probability.

It is well known that multiplicative dimensional reduction method to compute the fractional moments is just appropriate for positive variables (Zhang and Pandey 2013). Therefore it should have some changes before computing the fractional moments of the extreme value. Suppose the dynamic response function is g L(X, z), and the corresponding threshold is Y L . Hence, the limit sate function can be expressed as:

$$ g\left(\mathbf{X},\mathbf{z}\right)=\frac{Y_L}{g^L\left(\mathbf{X},\mathbf{z}\right)} $$
(12)

For a multivariate function g(X, z), it can be expressed as a sum of functions of lower order in an increasing hierarchy as following.

$$ g\left(\boldsymbol{x},\mathbf{z}\right)= g\left(\boldsymbol{\upmu}, \mathbf{z}\right)+{\displaystyle \sum_{i=1}^n{g}_i\left({x}_i,\mathbf{z}\right)}+{\displaystyle \sum_{1\le i\le j\le n}{g}_{i j}\left({x}_i,{x}_j,\mathbf{z}\right)+}\cdot \cdot \cdot $$
(13)

Then after a series of derivation (Zhang et al. 2014c), a multiplicative approximation can be obtained as follows (Zhang and Pandey 2013):

$$ g\left(\boldsymbol{x},\mathbf{z}\right)\approx g{\left(\boldsymbol{\upmu}, \mathbf{z}\right)}^{1- n}{\displaystyle \prod_{i=1}^n g\left({x}_i,{\boldsymbol{\upmu}}_{- i},\mathbf{z}\right)} $$
(14)

in which μ = [μ 1, μ 2, …, μ n ]T is the mean value vector of the input variables, the sub-vector μ − i is (n − 1)-dimension vector that contains all the elements of μ except μ i . The minimum value function g S(X, z) can be written as the following by imitating the Eq. (14).

$$ {g}^S\left(\boldsymbol{x},\mathbf{z}\right)\approx {\left[{g}^S\left(\boldsymbol{\upmu}, \mathbf{z}\right)\right]}^{1- n}{\displaystyle \prod_{i=1}^n{g}^S\left({x}_i,{\boldsymbol{\upmu}}_{- i},\mathbf{z}\right)} $$
(15)

Then the α l th(l = 1, 2, …, u) order fractional moments of minimum value function g S(X, z) can be expressed as:

$$ \begin{array}{c}{M}_{\alpha_l{g}^S}={\displaystyle {\int}_{\mathbf{X}}{\left[{g}^S\left(\boldsymbol{x},\mathbf{z}\right)\right]}^{\alpha_l}{f}_{\mathbf{X}}\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}}\\ {}\approx {\displaystyle {\int}_{\mathbf{X}}{\left\{{\left[{g}^S\left(\boldsymbol{\upmu}, \mathbf{z}\right)\right]}^{1- n}{\displaystyle \prod_{i=1}^n{g}^S\left({x}_i,{\boldsymbol{\upmu}}_{- i},\mathbf{z}\right)}\right\}}^{\alpha_l}{f}_{\mathbf{X}}\left(\boldsymbol{x}\right)\mathrm{d}\boldsymbol{x}}\\ {}={\left[{g}^S\left(\boldsymbol{\upmu}, \mathbf{z}\right)\right]}^{\alpha_l-{\alpha}_l n}{\displaystyle \prod_{i=1}^n\left\{{\displaystyle {\int}_{{\mathrm{X}}_i}{\left[{g}^S\left({x}_i,{\boldsymbol{\upmu}}_{- i},\mathbf{z}\right)\right]}^{\alpha_l}{f}_i\left({x}_i\right)\mathrm{d}{x}_i}\right\}}\\ {}={\left[{g}^S\left(\boldsymbol{\upmu}, \mathbf{z}\right)\right]}^{\alpha_l-{\alpha}_l n}{\displaystyle \prod_{i=1}^n{M}_i}\end{array} $$
(16)

After using the dimensional reduction method, the original n-dimensional integration for the extreme value moments has been approximated by the product of n one-dimensional integrations. The first item of the right-hand of Eq. (16) can be calculated by Eq. (17). The one-dimensional integration can be efficiently computed by using the weight-points integration scheme such as five-point Gauss-Hermite integration scheme.

$$ {\left[{g}^S\left(\boldsymbol{\upmu}, \mathbf{z}\right)\right]}^{\alpha_l-{\alpha}_l n}={\left[ g\left(\boldsymbol{\upmu}, {\mathbf{z}}^{(0)\ast}\right)\right]}^{\alpha_l-{\alpha}_l n} $$
(17)
$$ {M}_i\approx {\displaystyle \sum_{s=1}^Q{w}_s{\left[{g}^S\left({x}_s,{\boldsymbol{\upmu}}_{- i},\mathbf{z}\right)\right]}^{\alpha_l}}={\displaystyle \sum_{s=1}^Q{w}_s{\left[ g\left({x}_s,{\boldsymbol{\upmu}}_{- i},{\mathbf{z}}^{(i)\ast}\right)\right]}^{\alpha_l}} $$
(18)

where the x s is the sth integration point, w s is the sth integration weight, Q is the sum of integration points, z (0) ∗ and z (i) ∗ are minimum value points which correspond to the input variable values μ and [x i , μ − i ]T respectively, and solving z (0) ∗ and z (i) ∗ is presented in subsection 3.3.

Denote the PDF of the minimum value function Y = g S(X, z) as f Y (y), then it can be obtained using MaxEnt (Inverardi 2003) in the following way.

$$ \left\{\begin{array}{l}\mathrm{find}:\kern3.5em {f}_Y(y)\\ {}\mathrm{Maximize}:\kern1em H\left[{f}_Y(y)\right]=-{\displaystyle {\int}_Y{f}_Y(y) \ln \left[{f}_Y(y)\right] dy}\\ {}\mathrm{Subject}\kern0.5em \mathrm{to}:\kern1em {\displaystyle {\int}_Y{y}^{\alpha_l}{f}_Y(y) dy={M}_{\alpha_l{g}^S}}\end{array}\right. $$
(19)

in which H[f Y (y)] is the entropy of the true PDF f Y (y). Under the constraint of the fractional moments of the extreme value, the estimate \( {\widehat{f}}_Y(y) \) can be obtained by maximizing the entropy of Y. After constructing the Lagrangian function associated with the MaxEnt problem, the estimate \( {\widehat{f}}_Y(y) \) is given as:

$$ {\widehat{f}}_Y(y)= \exp \left(-{\displaystyle \sum_{l=0}^u{\lambda}_l}{y}^{\alpha_l}\right) $$
(20)

where α 0 = 0, \( {\lambda}_0= \ln \left[{\displaystyle {\int}_Y \exp \left(-{\displaystyle \sum_{l=0}^u{\lambda}_l}{y}^{\alpha_l}\right)} dy\right] \), λ = [λ 0, λ 1, …, λ u ]T are the Lagrange multipliers and α = [α 1, α 2, …, α u ]T are the fractions associated with the fractional moments. One can refer (Inverardi and Tagliani 2003) for computing λ and α.

After getting the PDF \( {\widehat{f}}_Y(y) \) of the minimum value function Y = g S(X) based on the fractional moments of the extreme value, the failure probability can be obtained by an integral. Equation (12) indicates that, if the value of limit sate function is greater than one, the structure will be safe and if the value is greater than zero but less than or equal to one, the structure will be failure. Therefore, the failure probability of the temporal and spatial multi-parameter dynamic reliability problem can be estimated by the following integral.

$$ {P}_f={\displaystyle {\int}_0^1{\widehat{f}}_Y(y) dy} $$
(21)

The above discussions show that the proposed method only evaluates the temporal and spatial dynamic limit state function when estimating the extreme value moments. So it is an effective method for the temporal and spatial multi-parameter dynamic reliability problem.

3.3 Determination of the minimum value point z ∗ corresponding to x = x ∗

There are many methods to determine the minimum value point when x = x ∗, here we present one approach. For the sake of demonstration, the two-parameter case is used as an example to illustrate how to estimate the minimum value point z ∗ when x = x ∗, and this process can be easy to extend to the case where the parameter is greater than two. Before solving the minimum value point, the input variable is assumed to fix at x ∗. Such as the Fig. 1, the calculation contains three situations: the inner-interval (gray area), parameter boundary (blue line) and interval endpoints (red dot).

Fig. 1
figure 1

Dynamic limit state g(x, z) varying with z at x = x ∗

Full size image

Firstly consider the inner-interval situation. It is well known that the points satisfying that first partial derivative of one function equals to zero are the extreme points or inflection points of this function. So the minimum value point for this situation can be obtained by the following equations.

$$ \left\{\begin{array}{l}\frac{\partial g\left({\boldsymbol{x}}^{\ast },{z}_1,{z}_2\right)}{\partial {z}_1}=0\\ {}\frac{\partial g\left({\boldsymbol{x}}^{\ast },{z}_1,{z}_2\right)}{\partial {z}_2}=0\end{array}\right. $$
(22)

For the explicit and simple limit state function circumstance, the solution of the derivative equation can be obtained analytically. For the explicit and complicated limit state function circumstance, the modern heuristic algorithms, such as Simulated Annealing (SA) (Belisle 1992) and Genetic Algorithms (GA) (Malhotra et al. 2011) or the derivative equation solving function (e.g. Fsolve Function in MATLAB) can be used to calculate the solution of above equation. In this paper, we use the derivative equation solving function to calculate the derivative equation. Equation (22) is an equation set about vector [z 1, z 2]T and there may be multiple solutions [z ∗ (i)1 , z ∗ (i)2 ]T (i = 1, 2, …, k 1) (k 1 is the number of the solutions).

Secondly, we consider parameter boundary situation. At this situation, there is one parameter satisfying its boundary at least. For two parameters situation, z 1 and z 2 satisfy that \( \left({z}_1\in \left({\underset{\bar{\mkern6mu}}{z}}_1,{\overline{z}}_1\right),{\underset{\bar{\mkern6mu}}{z}}_2\right) \), \( \left({z}_1\in \left({\underset{\bar{\mkern6mu}}{z}}_1,{\overline{z}}_1\right),{\overline{z}}_2\right) \), \( \left({\underset{\bar{\mkern6mu}}{z}}_1,{z}_2\in \left({\underset{\bar{\mkern6mu}}{z}}_2,{\overline{z}}_2\right)\right) \) and \( \left({\overline{z}}_1,{z}_2\in \left({\underset{\bar{\mkern6mu}}{z}}_2,{\overline{z}}_2\right)\right) \). Here it is equivalent to the one-parameter situation. The solution can be obtained by solving differential equation \( \frac{\partial g\left({\boldsymbol{x}}^{\ast },\mathbf{z}\right)}{\partial {z}_j}=0 \) with \( {z}_{- j}={\underset{\bar{\mkern6mu}}{z}}_{- j} \) or \( {z}_{- j}={\overline{z}}_{- j} \) (j = 1, 2 and − j = 2 if j = 1, − j = 1 if j = 2) by the derivative equation solving function. Suppose the k 2 solutions are obtained at the parameter boundary situation. Add the solutions of the first situation, the total solutions are [z ∗ (i)1 , z ∗ (i)2 ]T (i = k 1 + 1, k 1 + 2, …, k 1 + k 2) (k 2 is the number of the solutions for this second situation).

Thirdly, we consider the interval endpoints situation. In this situation, the solutions for two parameters z 1 and z 2 are the combinations of the endpoints of z 1 and z 2 respectively as: \( {\left[{z}_1^{\ast \left({k}_1+{k}_2+1\right)},{z}_2^{\ast \left({k}_1+{k}_2+1\right)}\right]}^{\mathrm{T}}={\left[{\underset{\bar{\mkern6mu}}{z}}_1,{\underset{\bar{\mkern6mu}}{z}}_2\right]}^{\mathrm{T}} \), \( {\left[{z}_1^{\ast \left({k}_1+{k}_2+2\right)},{z}_2^{\ast \left({k}_1+{k}_2+2\right)}\right]}^{\mathrm{T}}={\left[{\underset{\bar{\mkern6mu}}{z}}_1,{\overline{z}}_2\right]}^{\mathrm{T}} \), \( {\left[{z}_1^{\ast \left({k}_1+{k}_2+3\right)},{z}_2^{\ast \left({k}_1+{k}_2+3\right)}\right]}^{\mathrm{T}}={\left[{\overline{z}}_1,{\underset{\bar{\mkern6mu}}{z}}_2\right]}^{\mathrm{T}} \) and \( {\left[{z}_1^{\ast \left({k}_1+{k}_2+4\right)},{z}_2^{\ast \left({k}_1+{k}_2+4\right)}\right]}^{\mathrm{T}}={\left[{\overline{z}}_1,{\overline{z}}_2\right]}^{\mathrm{T}} \).

With the above procedure of three situations (the inner-interval, parameter boundary and interval endpoints), all the solutions can be obtained. Comparing the g(x ∗, z) at [z ∗ (k)1 , z ∗ (k)2 ]T(k = 1, 2, …, k 1 + k 2 + 4), the minimum value point z ∗ = [z ∗1 , z ∗2 ]T can be obtained when x = x ∗. The minimum value g S(X, z) can be expressed as g S(x ∗, z) = g(x ∗, z ∗) at x = x ∗.

For the complicated problems involving implicit limit state function and high-fidelity analysis tools (e.g. FEA or CFD), the finite difference method (Brandimarte 2004; Tan and Liu 2006) can be employed to replace the derivative equation by the difference equation. In this circumstance, Eq. (22) can be rewritten as the following Eq. (23).

$$ \left\{\begin{array}{l}\frac{g\left({\boldsymbol{x}}^{\ast },{z}_1+{h}_1,{z}_2\right)- g\left({\boldsymbol{x}}^{\ast },{z}_1-{h}_1,{z}_2\right)}{2{h}_1}=0\\ {}\frac{g\left({\boldsymbol{x}}^{\ast },{z}_1,{z}_2+{h}_2\right)- g\left({\boldsymbol{x}}^{\ast },{z}_1,{z}_2-{h}_2\right)}{2{h}_2}=0\end{array}\right. $$
(23)

where h 1 and h 2 are difference step of z 1 and z 2 respectively. The Fsolve Function in MATLAB is an effective tool for solving the derivative equation and has no limitation on the form of the equation (explicit or implicit). By combining the Fsolve Function, the solution of above Eq. (23) can be obtained. For the parameter boundary situation and the interval endpoints situation, the procedure is the same as the explicit limit state function circumstance except replacing the derivative equation by the corresponding difference equation. Then the minimum value point z ∗ and the minimum value can be obtained.

Obviously, the computational cost of the proposed method for temporal and spatial multi-parameter dynamic reliability analysis is caused by estimating the minimum value with the derivative equation. In this paper, the derivative equation solving function (e.g. Fsolve Function in MATLAB) is employed to calculate the derivative equation. Comparing with the method which using heuristic optimization method to obtain the minimum value directly, the proposed method can reduce the computational cost for just solving several equations instead of searching the minimum value. Although the computational cost will has some increment for the reliability problems involving implicit limit state function than the explicit limit state function circumstance, the computational cost is also less than that of the heuristic optimization method to obtain the minimum value directly. Generally, above three strategies can guarantee to obtain the global minimum. For the complex non-convex function in which the solutions of derivation equations can not be found correctly, the heuristic optimization method is suggested. This will add significant computational cost.

4 Temporal and spatial multi-parameter global dynamic reliability sensitivity analysis

The temporal and spatial multi-parameter global dynamic reliability sensitivity analysis can distinguish the importance of the random inputs so as to provide reference for design and optimization of the structural system. One global sensitivity model is established for the temporal and spatial multi-parameter dynamic reliability problem in this section.

4.1 Definition of the global dynamic reliability sensitivity analysis

For a temporal and spatial multi-parameter dynamic reliability problem, the failure domain of this structure system is defined as:

$$ {\varOmega}_F=\left\{\mathbf{X}: g\left(\mathbf{X},\mathbf{z}\right)\le 0,\kern1em \exists {z}_1\in \left[{\underset{\bar{\mkern6mu}}{z}}_1,{\overline{z}}_1\right]\cap \cdot \cdot \cdot \cap {z}_m\in \left[{\underset{\bar{\mkern6mu}}{z}}_m,{\overline{z}}_m\right]\right\} $$
(24)

By extending the definition of static global reliability sensitivity indices (Li et al. 2012), the dynamic global reliability sensitivity index of the input variables on the failure probability is as follows:

$$ {S}_i=\frac{\delta_i^P}{V\left({I}_{\varOmega_F}\right)} $$
(25)

in which,

$$ {\delta}_i^P= E\left[{\left({P}_f-{P}_{f\Big|{X}_i}\right)}^2\right]={\displaystyle {\int}_{-\infty}^{+\infty }{\left({P}_f-{P}_{f\Big|{X}_i}\right)}^2{f}_i\left({x}_i\right) d{x}_i} $$
(26)
$$ V\left({I}_{\varOmega_F}\right)={P}_f\left(1-{P}_f\right) $$
(27)

where P f is the failure probability, \( {P}_{f\Big|{X}_i} \) is the failure probability conditional on X i , E(⋅) and V(⋅) represent the expectation operator and variance operator respectively. \( {I}_{\varOmega_F} \) is the indicator function of failure domain. It is defined as \( {I}_{\varOmega_F}\left(\boldsymbol{x}\right)=1 \) when x ∈ {Ω F }, or else \( {I}_{\varOmega_F}\left(\boldsymbol{x}\right)=0 \).

Furthermore, Eq. (26) can be simplified (Cui and Lu 2010) as:

$$ {\delta}_i^P= V\left({P}_{f\Big|{X}_i}\right) $$
(28)

It is shown that there are two loops for computing the δ P i . The inner loop is to calculate the conditional dynamic failure probability and the outer loop is for the variance estimation of the conditional dynamic failure probability.

So the procedure for analyzing global dynamic reliability sensitivity can be summed up in three steps. First of all, fix the input variable on its realization. Secondly, compute the conditional dynamic failure probability by above proposed reliability analysis method. Finally, calculate the variance of the conditional dynamic failure probability. In this contribution, the three-point estimation (Zhang et al. 2014a) is employed to estimate the variance of the conditional dynamic failure probability. After the input variable is fixed on its realization, the process for computing the conditional failure probability is similar with the process of calculating the unconditional failure probability. Refer to (Zhang et al. 2014a), we can obtain the dynamic failure probability P f and δ P i by the following equations.

$$ {P}_f={P}_{X_i^{(1)}}{P}_{f\Big|{L}_{X_i^{(1)}}}+{P}_{X_i^{(2)}}{P}_{f\Big|{L}_{X_i^{(2)}}}+{P}_{X_i^{(3)}}{P}_{f\Big|{L}_{X_i^{(3)}}} $$
(29)
$$ {\delta}_i^P={P}_{X_i^{(1)}}{\left({P}_{f\Big|{L}_{X_i^{(1)}}}-{P}_f\right)}^2+{P}_{X_i^{(2)}}{\left({P}_{f\Big|{L}_{X_i^{(2)}}}-{P}_f\right)}^2+{P}_{X_i^{(3)}}{\left({P}_{f\Big|{L}_{X_i^{(3)}}}-{P}_f\right)}^2 $$
(30)

in which \( {L}_{X_i^{(k)}} \) and \( {P}_{X_i^{(k)}}\left( k=1,2,3\right) \) represent nominal value and corresponding weights in the three-point estimation respectively, \( {P}_{f\Big|{L}_{X_i^{(k)}}}\left( k=1,2,3\right) \) is the conditional dynamic failure probability when input variable X i is fixed on its nominal value \( {L}_{X_i^{(k)}} \) (k = 1, 2, 3).

4.2 Steps of solving the global dynamic reliability sensitivity

The steps for solving the global dynamic reliability sensitivity are summarized as follows.

  1. Step 1

    Calculate the nominal value \( {L}_{X_i^{(k)}} \) and weight \( {P}_{X_i^{(k)}}\left( k=1,2,3\right) \) for three-point discrete distribution by the following equations (Zhang et al. 2014a).

    $$ {P}_{X_i^{(1)}}=\frac{1}{2}\left(\frac{1+{\gamma}_{3{X}_i}/\sqrt{4{\gamma}_{4{X}_i}-3{\gamma}_{3{X}_i}^2}}{\gamma_{4{X}_i}-{\gamma}_{3{X}_i}^2}\right) $$
    (31)
    $$ {P}_{X_i^{(2)}}=1-\frac{1}{\gamma_{4{X}_i}-{\gamma}_{3{X}_i}^2} $$
    (32)
    $$ {P}_{X_i^{(3)}}=\frac{1}{2}\left(\frac{1-{\gamma}_{3{X}_i}/\sqrt{4{\gamma}_{4{X}_i}-3{\gamma}_{3{X}_i}^2}}{\gamma_{4{X}_i}-{\gamma}_{3{X}_i}^2}\right) $$
    (33)
    $$ {L}_{X_i^{(1)}}={\gamma}_{1{X}_i}-\frac{\gamma_{2{X}_i}}{2}\left(\sqrt{4{\gamma}_{4{X}_i}-3{\gamma}_{3{X}_i}^2}-{\gamma}_{3{X}_i}\right) $$
    (34)
    $$ {L}_{X_i^{(2)}}={\gamma}_{1{X}_i} $$
    (35)
    $$ {L}_{X_i^{(3)}}={\gamma}_{1{X}_i}+\frac{\gamma_{2{X}_i}}{2}\left(\sqrt{4{\gamma}_{4{X}_i}-3{\gamma}_{3{X}_i}^2}+{\gamma}_{3{X}_i}\right) $$
    (36)

    in which \( {\gamma}_{j{ X}_i}\left( j=1,2,3,4\right) \) represents the first four central moments of input variable X i .

  2. Step 2

    Fix the input variable X i on nominal value \( {L}_{X_i^{(k)}}\left( k=1,2,3\right) \), and use the above proposed two reliability analysis methods in Section 3 to estimate the conditional dynamic failure probability \( {P}_{f\Big|{L}_{X_i^{(k)}}} \).

  3. Step 3

    Substitute the conditional dynamic failure probability \( {P}_{f\Big|{L}_{X_i^{(k)}}} \) into Eqs. (29)–(30) to calculate the dynamic failure probability P f and δ P i .

  4. Step 4

    Substitute the value of P f and δ P i into Eq. (25), then the global dynamic reliability sensitivity index S i can be obtained.

For limit state function G ω  = g ω (X, ω(t), z) of the temporal and spatial multi-parameter dynamic reliability problem involving stochastic process, where ω(t) = [ω 1(t), ω 2(t), …, ω M (t)]T is the stochastic process and t is the one-dimensional parameter, the proposed methods also can be extended to estimate the dynamic reliability and global dynamic reliability sensitivity indices. In this situation, the Karhunen-Loeve (KL) expansion (Sudret and Der Kiureghian 2000) is firstly employed to transform the stochastic process input ω(t) to random variable ξ = [ξ 1, ξ 2, …, ξ M ]T, in which \( {\boldsymbol{\upxi}}_i={\left[{\xi}_{i1},{\xi}_{i2},\dots, {\xi}_{i{ M}_i}\right]}^{\mathrm{T}}\left( i=1,2,\dots, M\right) \) and M i is the number of the random variable in the vector ξ i . After the transformation, the original dynamic limit state function can be transformed as G ω  = g ω (X, ξ, z), and the above proposed methods can be used to estimate the dynamic reliability and global dynamic reliability sensitivity indices.

5 Examples

Several examples are provided in this section to demonstrate the efficiency and accuracy of the presented method for temporal and spatial multi-parameter dynamic reliability and global reliability sensitivity analysis. The solutions by MCS method are applied as the reference results. For the dynamic reliability analysis, the procedure of the MCS method is to generate the samples of the random variables X and employ the proposed method in Section 3.3 to estimate the minimum value point z ∗ and the minimum value for every sample, and then the design fails or not corresponding to the negative or positive of these minimum values respectively. For the global dynamic reliability sensitivity analysis, the general double-loop MCS is used to estimate the global dynamic reliability sensitivity indices. In the process of estimating, the proposed method in Section 3.3 is employed to estimate the minimum value point z ∗ and the minimum value for every sample.

5.1 Numerical example

Consider the model with the dynamic limit state function is g(x, z) = Y L  − (x 1 cos 3z 1 + x 2 z 21  + x 3 z 1 +x 4 cos 4z 1 + 2x 5 z 1)sin z 2, where Y L is the threshold, and the input variables are independent normal variables, x i  ∼ N(10, 12)(i = 1, 2, 3, 4, 5), the parameter vector z = [z 1, z 2]T is defined as z 1 ∈ [0, 0.5] and z 2 ∈ [0, 5] (they are in radians when used with the sine and cosine functions). The dynamic failure probability is given in Table 1 and the numbers of function evaluations are shown in Table 2. The global dynamic reliability sensitivities of input variables are provided in Table 3.

Table 1 The dynamic failure probability for different thresholds
Full size table
Table 2 Numbers of function evaluations
Full size table
Table 3 The global dynamic reliability sensitivity indices
Full size table

In this numerical example, the numbers of function evaluation by the MCS method are shown in Table 2. It needs about 10 function evaluations to obtain the minimum value with the proposed method in Section 3.3 for each samples of the MCS method (e.g. when the threshold is set to be Y L  = 23, the samples of the MCS method is 1 × 105 and the total function evaluations are 1 × 105 × 10 = 1 × 106). The variance on dynamic failure probability of the MCS method states that the MCS solutions are precise enough to be the reference results. From Table 1, it is shown that when the failure threshold is set to be different value, the results estimated by the proposed two methods match well with the reference results. It proves definitively that the two proposed methods have enough accuracy in the temporal and spatial multi-parameter dynamic reliability analysis. From Table 2, one can see that the MCS procedure needs huge computational cost to obtain the dynamic failure probability. The two proposed methods just need several hundred times of function evaluations to gain an accurate solution. For the sparse grid stochastic technique combined with the fourth-moment method, here set q = 3, and it generates 61 samples of the random inputs. For arbitrary sample, it needs about 10 function evaluations to obtain the minimum value point with the proposed method in Section 3.3. Then the total function evaluations are 61 × (10 + 1) = 671. For the dimensional reduction method combined with the maximum entropy method, the five-point Gauss-Hermite integration scheme is used here. For one sample, it needs about 10 function evaluations to obtain the minimum value point. Then the total function evaluations are 10 × (1 + 5 × 4) + 5 × 4 + 1 = 231. So these two proposed methods have high efficiency for the temporal and spatial multi-parameter dynamic reliability analysis. Furthermore, when comparing the two proposed methods with each other, one can see that the dimensional reduction method combined with the maximum entropy is more efficient.

Table 3 shows that the two proposed global dynamic reliability sensitivity analysis methods can obtain the same importance ranking of input variables compared with MCS solution. The samples of the MCS method is 1 × 105. For one sample, it needs about 10 function evaluations to obtain the minimum value. The total function evaluations are (1 × 105 × 1 × 105 × 5 + 1 × 105) × 10 ≈ 5 × 1011. Compared with the MCS method, these two proposed methods can gain an accurate solution by less calculation cost. For the global dynamic reliability sensitivity analysis method based on the first proposed reliability method, set q = 3 and 41 samples will be generated by the sparse grid stochastic technique when one of the inputs is fixed at the realization every time. The number of the function evaluations for calculating the minimum value point with one sample is about 10. Then the total function evaluations are (41 × 10 + 41) × 3 × 5 = 6765. For the global dynamic reliability sensitivity analysis method based on the second proposed reliability method, fix one of the inputs at the realization and the response output will become a function of 4-dimension inputs. So the total function evaluations can be calculated as [10 × (1 + 4 × 4) + 4 × 4 + 1] × 3 × 5 = 2805. It shows that, x 1 has the largest global dynamic reliability sensitivity indices, followed by x 4, and then x 5, which indicates that these three input random variables are the most influential. That indicates that by reducing the uncertainties of the five input random variables, x 1 leads to the most increment of the time-dependent reliability, followed by x 4, and then x 5.

5.2 Engineering example

5.2.1 Automobile front axle

It is well-known that the automobile front axle beam is used to carry the weight of the front part of the vehicle (See Fig. 2a). Nowadays, the I-beam structure is popular in the design of front axle due to its high bend strength and light weight. As shown in Fig. 2b, the dangerous cross-section is in the I-beam part. The maximum normal stress and shear stress are \( \sigma =\frac{M}{W_x} \) and \( \tau =\frac{T}{W_{\rho}} \) respectively, where M and T are bending moment and torque, and they are time-varying, \( M={M}_0\left(\frac{1}{10} \cos \frac{1}{4} z+\frac{9}{10}\right) \), \( T={T}_0 \sin \frac{1}{3} z \), in which M 0 and T 0 is basic bending moment and torque, z is the time parameter and range is z ∈ [0, 10] (it is in radians when used with the sine and cosine functions). W x and W ρ are section factor and polar section factor which can be given respectively as follows:

$$ {W}_x=\frac{a{\left( h-2 c\right)}^3}{6 h}+\frac{b}{6 h}\left[{h}^3-{\left( h-2 c\right)}^3\right] $$
(37)
$$ {W}_{\rho}=0.8 b{c}^2+\frac{0.4{a}^3\left( h-2 c\right)}{c} $$
(38)
Fig. 2
figure 2

Diagram of an automobile front axle. a Diagram of front axle, b Cross section of front axle

Full size image

To check the strength of front axle, the limit state function can be represented as:

$$ g={\sigma}_S-\sqrt{\sigma^2+3{\tau}^2} $$
(39)

where σ S is the limit stress of yielding. The geometry variables of I-beam a, b, c, h and the loads M 0 and T 0 are independent normal variables with distribution parameters listed in Table 4. The dynamic failure probability is given in Table 5 and the numbers of function evaluations are shown in Table 6. The global dynamic reliability sensitivity of input variables are provided in Table 7.

Table 4 Distribution parameters of input variables
Full size table
Table 5 The dynamic failure probability for different limit stress
Full size table
Table 6 Numbers of function evaluations
Full size table
Table 7 The global dynamic reliability sensitivity indices
Full size table

Table 5 indicates that the proposed two methods can accurately estimate the dynamic failure probability for this time-dependent reliability problem. When the limit stress of yielding is defined as different values, the results estimated with the proposed two methods can match well with the reference solutions. From Table 6, one can see that, the MCS method needs huge computational cost (the procedure for calculating the total function evaluations is similar to the process in the first numerical example). These two proposed procedures can reduce the computational cost, especially the dimensional reduction method combined with the maximum entropy technology, which just needs a hundred times of function evaluations (the procedure for calculating the total function evaluation is similar to the process in the first numerical example). So these two proposed methods can save the computational cost.

From Table 7, when the limit stress of yielding is set to be 460MPa, the global dynamic reliability sensitivity indices ranking estimated by the proposed methods is the same as that of the MCS solution. And the importance ranking induced by the global dynamic reliability sensitivity is c > T 0 > b > a > h > M 0. It indicates that, by reducing the same amount of the uncertainties of the six input random variables individually, c produces the most increment in the time-dependent reliability, followed by T 0, and then b、 a、 h、 M 0 in sequence. It is also shown in Table 7 that the computational cost of MCS is enormous which is unpractical in engineering application (the procedure for calculating the total function evaluations is similar to the process in the first numerical example). Above solutions show that the proposed method can alleviate the computational burden (the procedure for calculating the total function evaluation is similar to the process in the first numerical example).

5.2.2 An aero engine turbine disk

Turbine disk is the key moving part of an aero engine, and it suffers huge centrifugal force and thermal stress during the initiate and accelerating process. Because of the complex structural shape, the stress concentration easily takes place in some parts during the working process, such as tongue and groove bottom, pin hole, etc. After working for some time, these parts may appear crack. Figure 3 shows the crack of the aero engine turbine disk. The load that an aero engine turbine disk is applied is F = (Cω 2/2π + 2ρω 2 J), in which ρ, C, ω and J are mass density, coefficient, a rotation angular velocity and moment of inertia. Here ω = 2πn, n is rotational frequency, and \( n={n}_0\left(\frac{1}{10} \sin {z}_1+\frac{6}{5}\right) \), wherein z 1 is the time parameter z 1 ∈ [0, 2π]. In this paper, we research the failure situation on the length direction of the turbine disk lateral view as is shown in Fig. 4. The ultimate strength of the turbine disk is σ s . Sectional area is related to location, and the relational expression is \( A={A}_0\left(-\frac{1}{60}{z}_2+2\right) \), in which z 2 is the location parameter and z 2 ∈ [0, 10] (they are in radians when used with the sine and cosine functions). So the multi-parameter dynamic limit state function of the turbine disk can be established as: g(σ s , ρ, C, A 0, J, n 0, z) = Aσ s  − F. The distribution parameters of input variables are listed in Table 8. The dynamic failure probability of this structure is given in Table 9. The global dynamic reliability sensitivity indices of input variables are provided in Table 10.

Fig. 3
figure 3

Diagram of crack of an aero engine turbine disk

Full size image
Fig. 4
figure 4

The profile of the aero engine turbine disk

Full size image
Table 8 Distribution parameters of input variables
Full size table
Table 9 The dynamic failure probabilities estimated by different methods
Full size table
Table 10 The global dynamic reliability sensitivity indices
Full size table

Table 9 shows that these two proposed methods can accurately estimate the dynamic failure probability for the temporal and spatial multi-parameter reliability problem. When compared with the MCS method, one can see that these two approaches can reduce the computational cost which is significant for engineering application (the procedure for calculating the total function evaluations is similar to the process in the first numerical example). When we consider these two methods with each other, we can see that the dimensional reduction method combined with the maximum entropy is more efficient in multi-parameter dynamic reliability analysis.

It is shown in Table 10 that, these three approaches have the same global dynamic reliability sensitivity indices ranking of input variables. The computational cost of these proposed global dynamic reliability sensitivity analysis methods is far less than that of the MCS method (the procedure for calculating the total function evaluations is similar to the process in the first numerical example). The importance ranking induced by the global dynamic reliability sensitivity is n 0 > ρ > σ s  > A 0 > J > C. That’s means by reducing the uncertainties of the six input random variables, n 0 leads to the most increment of the temporal and spatial multi-parameter dynamic reliability, followed by ρ.

6 Conclusions

Based on the extreme value theory of the dynamic reliability problem, this contribution develops two procedures to efficiently estimate dynamic failure probability with temporal and spatial multi-parameter. One employs the sparse grid stochastic collocation method to evaluate the extreme value moments, and then estimates the dynamic failure probability by the fourth-moment method. The other uses dimensional reduction method to compute the fractional moments of extreme value, and then combines the maximum entropy theory to estimate the PDF of the minimum value of the dynamic limit state function and obtain the dynamic failure probability by use of the estimated PDF. These two procedures inherit the advantage of sparse grid method and dimensional reduction method in high efficiency and accuracy, therefore with the proposed two methods to estimate the temporal and spatial multi-parameter dynamic failure probability, one can improve the computational efficiency which is very significant in engineering application.

For quantifying the effects of the uncertainties of the inputs on the temporal and spatial multi-parameter dynamic reliability, this paper develops two new efficient global sensitivity methods based on the proposed dynamic reliability analysis technology and three-point estimation method. These two proposed sensitivity methods can efficiently and precisely gain the temporal and spatial multi-parameter global dynamic reliability sensitivity indices which are useful for reliability-based design as they can efficiently identify the influential input variables.

Several examples are given for demonstrating the efficiency and precision of the proposed procedure for temporal and spatial multi-parameter dynamic reliability and global dynamic reliability sensitivity analysis. At the same time, the engineering problem of the temporal and spatial multi-parameter dynamic global reliability sensitivity indices is illustrated. In summary, the proposed methods provide some efficient ways to analyze temporal and spatial multi-parameter dynamic reliability and global dynamic reliability sensitivity problems.

The proposed methods also can be extended to analyze the reliability and global reliability sensitivity with the temporal and spatial multi-parameter dynamic reliability problem where the inputs are described by stochastic process. One feasible way is employing the existing methods such as KL expansion to transform the stochastic process input to random variable, and then the above proposed methods can be used to analyze the dynamic reliability and global dynamic reliability sensitivity.