Time-dependent reliability analysis method based on ARBIS and Kriging surrogate model

Abstract

Based on the existed idea of adaptive radial-based important sampling (ARBIS) method, a new method solving time-dependent reliability problems is proposed in this paper. This method is more widely used than the existed method combining importance sampling (IS) with time-dependent adaptive Kriging surrogate (AK) model, which is not only suitable for time-dependent reliability problems with single design point, but also for multiple design points, high nonlinearity, and multiple failure modes, especially for small failure probability problems. This method combines ARBIS with time-dependent AK model. First, at each sample point, the AK model of the performance function with regard to time t is established in the inner layer, and its minimum value is calculated as the performance function value of the outer layer to established time-independent AK model. Then, the optimal radius of the β-sphere is obtained with an efficient adaptive scheme. Excluding a β-sphere from the sample pool, there is no need to calculate the performance function value of the samples inside the β-sphere, which greatly improves the estimation efficiency of structural reliability analysis. Finally, three numerical examples are given to show the estimation efficiency, accuracy, and robustness of this method.

1 Introduction

In traditional reliability theory, time-dependent uncertainties such as load changing with time and strength degradation are often not considered. However, in many practical engineering problems, due to the influence of external environment, material properties, load size, structural strength, and other parameters are gradually changing with time. Therefore, the structural reliability is no longer a constant value under the static mechanical model, but shows time-dependent characteristic [1, 2].

The research on time-dependent reliability is a current research hotspot, and many classical analysis methods have been established. In general, time-dependent reliability analysis methods can be divided into three main methods: first crossing rate method [3], extreme value method [4,5,6], and surrogate model method [7,8,9]. Based on the surrogate models such as response surface method, artificial neural network, and support vector machine, Kriging surrogate model, an approximate model of the original time-dependent performance function is constructed; the number of calling commercial software to perform the numerical simulation is greatly reduced. Thus, the surrogate models have attracted more attentions in time-dependent reliability analysis of engineering practice.

Among all these surrogate models, AK model can not only provide the predicted value of performance function at the sample points, but also estimate the prediction variance. Thus, time-dependent reliability based on AK model has attracted great interest of researchers, and formed two kinds of classical analysis framework, including double-loop AK model method [10, 11] and single-loop AK model method [12]. Although the AK-MCS method reduces the number of calling original performance function, the calculation cost is still too large to meet the engineering requirements, especially for some small failure probability (less than 10^–5), multiple design points, high nonlinearity, and multiple failure modes problems [13].

To improve the estimation efficiency of AK model in reliability analysis, some methods combining AK model with advanced sampling methods are proposed. As the scale of advanced sample pool is smaller than MCS sample pool, the estimation efficiency of reliability analysis under small failure probability can be greatly improved. Echard et al. [14] proposed that AK model and IS generating the candidate sample pools are combined. Compared with AK-MCS method, AK-IS is more efficient, but it is not suitable for the problem of multiple design points. Dubourg et al. [15] proposed a method combining AK model with the metamodel-based IS, but the estimation of failure probability required an additional model to estimate the correction factor. Cadini et al. [16] proposed an improved AK-based IS method for multiple failure regions of low probability. However, the construction of the IS density function introduced not only extra computation, but also the corresponding approximation error. Huang et al. [13] proposed the method combining AK model with subset simulation (AK-SS). However, AK model and subset simulation were not coupled but independent and the essence of this method is also AK-MCS. Based on the AK-MCS, Yang [17] proposed the ALK-Pfst method which used a modified ERF as learning function and a new stopping criterion. Although improves the efficiency and robustness of Kriging model, it needs to search the efficient sampling methods for problem with small failure probabilities, because the AK model should make predictions at a larger population of candidate samples. Yang [18] proposed a method combining AK model with MAIS to address the system reliability analysis problem with small failure probability. It introduced EMO-MMO method to obtain all the potential MPPs on the surrogate LSS and the training points are only chosen from the IS located in the TCR. However, it is used to solve the system reliability problem which is complicated to time-dependent reliability problem with single system. To solve the single system reliability problem with small failure probability and multiple failure regions, Yang [19] proposed a novel method ALK-EMO-IS. According to several iterations, the surrogate LSS converges to the true LSS, and quasi MPPs converges to all the local and global true MPPs by EMO-MMO. IS method is used to improve the efficiency of sampling by the quasi MPPs in every iteration. However, repeated importance sampling will lead to unnecessary repeated sample pool. Other methods such as the hybrid algorithm for reliability analysis combining Kriging and subset simulation importance sampling [20] and AK-ARBIS method [21] can combine AK model with sampling method based on variance reduction. To solve the time-dependent reliability problem based on AK model under small failure probability, Ling [22] combined AK model with IS. Although it improved the estimation efficiency, it was only applicable to a single design point. Seeking all the design points at every instant and selecting the best point of them all as the final design point, the process was very complex. It could hardly solve the problem of highly nonlinear and multiple design points. Shi [23] proposed a time-dependent reliability analysis method based on single-loop AK model connecting with adaptive sampling method. Unfortunately, the optimal hypersphere radius of the adaptive sampling method was reduced according to a certain proportion, not based on the radial. At the same, the candidate sample pool of single-loop AK model is much larger than that of double-loop AK model, so its estimation efficiency is not very high. The combination of ARBIS and AK model for reliability analysis was proposed by Yun [21], but they were only used in time-independent reliability problems. Meanwhile, their method adding training points to candidate sample pool was different from that of traditional AK method. Their initial AK model was updated by the training samples of sample pool outside initial optimal hypersphere radius. However, the probability density of these training samples was so small that increased some useless training samples. As a result, the number of calling performance function is greatly increased.

Motivated by the existed methods mentioned above, we attempt to apply the ARBIS method to solve the estimation accuracy and efficiency in the time-dependent reliability analysis. In our method, the optimal radius of the sphere is searched by an iterative method. In every step of iterative process, the AK model is updated adaptively in a candidate sample pool composed of the samples between two adjacent hypersphere radii. The efficient time-dependent reliability analysis process is realized by searching the optimal hypersphere radius adaptively. To improve the estimation efficiency and accuracy of the reliability index, this method greatly reduces the number of calling the performance function under small failure probability, and generates as much as samples near the LSS.

The research of this paper is arranged as follows. In Sect. 2, the time-dependent reliability analysis principle and double-loop AK model are introduced, which is regard as a comparative verification for time-dependent reliability analysis method proposed in this paper. In Sect. 3, the basic principle of the time-dependent reliability analysis method based on ARBIS and double-loop AK model are discussed in detail. Three examples are given to verify the effectiveness of the proposed method in Sect. 4.

2 Existing time-dependent reliability analysis method based on double-loop AK model

2.1 Definition of time-dependent reliability

Generally, the time-dependent performance function can be expressed as $Z(t) = g({\mathbf{X}},{\mathbf{Y}}(t),t)$, where ${\mathbf{X}} = \{ X_{1} ,X_{2} , \ldots X_{n} \}^{T}$ is the n-dimensional random vector and does not change with time; ${\mathbf{Y}} = \{ Y_{1} (t),Y_{2} (t), \ldots Y_{m} (t)\}^{T}$ is the m-dimensional random process vector, which represents time-dependent load, temperature, and other variables related to time; t is a time variable with the time interval $[t_{0} ,t_{s} ]$. $Z(t) = g({\mathbf{X}},{\mathbf{Y}}(t),t) > 0$ means that the structure is reliable, while $Z(t) = g({\mathbf{X}},{\mathbf{Y}}(t),t) \le 0$, the structure is failed. Then, the reliability probability $R(t_{0} ,t_{1} )$ and failure probability $P_{{\text{f}}} (t_{0} ,t_{1} )$ in the time interval $[t_{0} ,t_{s} ]$ can be, respectively, defined as follows:

$$ R(t_{0} ,t_{1} ) = P\{ S\} = P\{ Z(t) > 0,\,\,\,\forall t \in [t_{0} ,t_{s} ]\} , $$

(1)

$$ P_{{\text{f}}} (t_{0} ,t_{1} ) = P\{ F\} = P\{ Z(t) \le 0,\,\,\,\exists t \in [t_{0} ,t_{s} ]\} . $$

(2)

To simplify the calculation of stochastic process Y(t), it can be approximately transformed into a combination of random variables and time variables through the EOLE [24, 25]. During this research, the combination of random variables and time variables are only considered, so the expression of performance function expression is $Z(t) = g({\mathbf{X}},t)$.

Assume Y(t) is a stationary Gaussian random process, we briefly introduce the expansion process of EOLE model as follows.

The time interval [t₀, t_s] is equally divided into N subintervals with N + 1 discrete time points $t_{i} = t_{0} + i\frac{{t_{s} - t_{0} }}{N}$$(i = 0, \ldots ,N)$, which is expanded according to the EOLE model

$$ {\mathbf{Y}}(t) \approx \mu_{Y} + \sigma_{Y}^{2} \sum\limits_{k = 1}^{r} {\frac{{{{\varvec{\upxi}}}_{k} }}{{\sqrt {\lambda_{k} } }}} {\mathbf{\varphi }}_{k}^{T} {{\varvec{\uprho}}}_{{\text{Y}}} (t), $$

(3)

where $\lambda_{k}$ and ${\mathbf{\varphi }}_{k} (k = 1,2 \ldots ,r)$ are the first r larger eigenvalues of the covariance matrix of the random process Y(t) and their corresponding eigenvectors, respectively.${{\varvec{\uprho}}}_{Y} (t) = \{ \rho_{Y} {(}t,t_{0} ), \, \rho_{Y} (t,t_{1} ), \ldots , \, \rho_{Y} (t,t_{N} )\}^{T}$ is the correlation coefficient vector. $\xi_{k} (k = 1,2, \ldots ,r)$ is the independent standard normal random variable. For convenience, the independent standard normal vector corresponding to Y(t) expansion is denoted as ${{\varvec{\upxi}}} = \{ {{\varvec{\upxi}}}_{1} ,{{\varvec{\upxi}}}_{2} , \ldots ,{{\varvec{\upxi}}}_{r} \} ^{{\text{T}}}$.

2.2 Time-dependent reliability analysis based on double-loop AK model

The time-dependent AK model has double loop. In the inner loop, the minimum value of performance function about time t can be obtained. While in the outer loop, the time-independent AK model can be used to solve the failure probability. The principle of reliability analysis of time-dependent AK model is shown in Fig. 1.

Fig. 1

Schematic diagram of reliability analysis principle of double-loop AK model

Take a realization value x* from input variable ${\mathbf{X}} \in R^{n}$, $Z(t) = g(x{*},t)$ is the function with respect to the time t, equally; the time-dependent failure domain in time interval $[t_{0} ,t_{s} ]$ can be expressed as

$$ F = \{ \mathop {\min }\limits_{{t \in [t_{0} ,t_{s} ]}} g(x*,t) \le 0\} . $$

(4)

Then, time-dependent failure probability $P_{{\text{f}}} (t_{{0}} ,t_{s} )$ in $[t_{{0}} ,t_{s} ]$ is given by

$$ P_{{\text{f}}} (t_{0} ,t_{s} ) = P\{ F\} = P\{ \mathop {\min }\limits_{{t \in [t_{0} ,t_{s} ]}} g(x*,t) \le 0\} . $$

(5)

According to this equation, time-dependent reliability problem can be transformed into time-independent reliability problem. The specific flow chart is presented as follows:

It can be seen from Fig. 2, at each sample $x{*}$, the minimum value of the performance function $Z(t) = g(x{*},t)$ in time interval $[t_{0} ,t_{s} ]$ is solved by inner loop AK model, and this minimum value ${\text{min}}_{{t \in [t_{{0}} ,t_{s} ]}} {\text{g(}}x{*,}t{)}$ is taken as the sample point of performance function in outer loop. Then, the time-independent AK model is established in the outer loop. Thus, the traditional methods of time-independent reliability analysis can be used to solve time-dependent reliability problem. In this paper, this classical double-loop AK method is employed to verify effectiveness and correctness of the method proposed in Sect. 3.

Fig. 2

Flowchart of double-loop AK model

3 The proposed time-dependent reliability analysis method

Since the proposed method in this paper is based on the traditional time-independent ARBIS method, to explain the difference between the proposed method and the ARBIS method, the basic principle and computational process of the ARBIS method is discussed first.

3.1 The basic principle of ARBIS method

Suppose that in an independent standard normal space, ${\mathbf{X}} = \{ X_{1} ,X_{2} , \cdots X_{n} \}^{T}$ is an n-dimensional independent standard normal variable; g(x) is the performance function. The optimal radius $\beta$ is the shortest distance from the origin to the LSS, which equals to the distance to the MPP, that is

$$ \left\{ \begin{gathered} \beta^{2} = \min \left( {\sum\limits_{i = 1}^{n} {x_{i}^{2} } } \right) \hfill \\ g(x_{1} ,x_{2} , \ldots x_{n} ) = 0, \hfill \\ \end{gathered} \right. $$

(6)

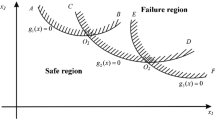
where $\sum\nolimits_{i = 1}^{n} {x_{i}^{2} }$ is a sample from the Chi-square distribution $\chi^{2} (n)$ with n degrees of freedom. In n-dimensional independent standard normal space, if the equation $X_{{1}}^{{2}} + X_{{2}}^{{2}} + \cdots + X_{n}^{{2}} = \beta^{{2}}$ defines n-dimensional $\beta {\text{ - sphere}}$ in Rⁿ, let ${||}x{||}^{{2}} { = }\sum\nolimits_{{i = {1}}}^{n} {x_{i}^{{2}} }$, then $\beta$-sphere divides the space Rⁿ into two parts: ${||}x{||}^{{2}} { < }\beta^{{2}}$ and ${||}x{||}^{{2}} { > }\beta^{{2}}$, as shown in Fig. 3.

Fig. 3

Schematic diagram of β-sphere in two dimensions

ARBIS was first proposed by Grooteman [26], which is an improvement of RBIS [27]. The basic idea of reliability analysis based on ARBIS is shown as follows. The optimal radius $\beta$ is adaptively searched based on the radial. The samples inside the $\beta$-sphere must be located in the security region. Thus, it avoids calculating the function values of those samples which can improve the estimation efficiency.

The advantage of this method is to adaptively calculate the optimal radius $\beta$. Without determining the unknown MPP first, this adaptive scheme is robust and efficient, and guarantees an optimal radius $\beta$.

3.2 Solution of reliability index $\beta$ under ARBIS method

Reliability index $\beta$ mentioned above is defined in the n-dimensional independent standard normal space. Using ARBIS method for reliability analysis, the original input variables need to be converted to the independent standard normal space. The detailed iterative process is shown in Fig. 4.

Fig. 4

Schematic diagram of β-sphere in bivariate dimensions

In this method, the performance function is denoted as G(x) in independent standard normal space, and the initial sample pool $S^{x}$ of independent standard normal space is randomly generated by MCS method. In the initial iteration, the initial radius $\beta_{0}$ of the sphere is determined by the formula

$$ \beta_{0} = \sqrt {\chi_{n}^{ - 2} (1 - p_{0} )} , $$

(7)

where number $p_{0}$ is the maximum failure probability for the first time, and $p_{0} = 10^{ - 6}$ is generally taken in small failure probability problem. The performance function value of the samples outside the initial β₀-sphere is calculated. Failure point is found out of the initial β-sphere, and the point calling approximate MPP on LSS is determined according to line search in this direction. The distance from this the approximate MPP to origin is recorded as $\tilde{\beta }_{{{\text{opt}}}}$, which is the closest point being searched to MPP for the first time. At the same time, this approximate MPP is used to determine the new radius $\beta_{1}$ of sphere, the value of $\beta_{1}$ can be obtained by Eq. (8)

$$ \left\{ \begin{gathered} p_{1} = 1 - \chi_{n}^{2} (\tilde{\beta }_{{{\text{opt}}}}^{2} ) \hfill \\ \beta_{1} = \sqrt {\chi_{n}^{ - 2} \left( {1 - \frac{{p_{1} }}{{p_{{{\text{step}}}} }}} \right){\kern 1pt} } ,\quad p_{{{\text{step}}}} = 0.8. \hfill \\ \end{gathered} \right. $$

(8)

In the next iteration, a new failure point is found in the region between $\beta_{1}$ and $\tilde{\beta }_{{{\text{opt}}}}$ to generate a new line search; the next approximate MPP is generated similarly. This process is repeated until there are no more samples between $\tilde{\beta }_{{{\text{opt}}}}$ and $\beta_{i}$ obtained by Eq. (8), or the distance between them is less than a convergence criterion ($\left| {\tilde{\beta }_{{{\text{opt}}}} - \beta_{i} } \right|$$< 0.01$); then, the iteration ends.

The ARBIS method is robust, no matter how the initial value of β is taken; it always tends to the MPP. Through the line search in the descending direction of the performance function gradient, the estimation efficiency can be greatly improved. The sample with lower value than the initial point can be quickly found, instead of iterating repeatedly through line search until the final MPP or optimal radius β of sphere is found.

The adaptive searching process of approximate MPP is shown in Fig. 5, which is one-dimensional searching process. It can be seen from the Fig. 5 that the value of the performance function at origin is known in a certain line searching process. Through the value at origin and the known failure point 1, a suitable linear function is determined to estimate the point of the first limit state surface (the value of point 2 in Fig. 5), and then, the convergence is judged. If the accuracy does not meet the requirements, repeat this process until the approximate MPP point is found. Higher calculation accuracy is not necessary, because Eq. (8) ensures that the MPP is always outside the sphere, and the number of iteration does not exceed 5 to avoid wasting a lot of analysis time.

Fig. 5

The process of adaptive searching MPP

3.3 Time-dependent reliability analysis method based on ARBIS method

The method proposed in this paper combines ARBIS method with AK model to transform time-dependent problem into time-independent problem. It is actually a double-loop AK model, which solves the minimum of each sample point about time t in the inner loop, and then constructs the AK model in each sample in the outer loop to solve the time-dependent reliability analysis problem.

3.3.1 Definition of β-hypersphere under time-dependent

In the time-dependent reliability analysis, if time interval ${[}t_{{0}} {,}t_{s} {]}$ is divided into n equal time points (namely $t_{1} ,t_{2} ,t_{3} , \ldots t_{n} ,$ where $t_{1} = t_{0} ,t_{n} = t_{s}$), then the LSS is different at different time. Each time point has a corresponding failure domain, which is recorded as $F_{i} = \{ G(x,t_{i} ) \le 0\} (i = 1,2 \ldots ,n)$. Here, the failure domain is the union of the failure domains composed of the performance functions at every time t_i (i = 1, 2…n) ($F = F_{1} \cup F_{2} \cup \cdots \cup F_{n}$). The limit state surface can also be regarded as the set of the limit state surface (LSSs) at all time points. Therefore, the selection of β-hypersphere radius should consider the LSSs at all time points. Then, the optimal radius β of the sphere is the shortest distance from the coordinate origin to all LSSs at all time points, as shown in Fig. 6.

Fig. 6

Schematic diagram of β-sphere of time-dependent performance function

3.3.2 Solution method of failure probability based on time-dependent ARBIS

In independent standard normal space composed of performance functions at all time points, the sample space is divided into $||x||^{2} < \beta^{2}$ and $||x||^{2} > \beta^{2}$ by β-sphere. The failure probability is expressed as

$$ \begin{aligned} P_{{\text{f}}} & = P\{ \mathop {\min {\kern 1pt} }\limits_{{t \in [t_{0} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le 0|x \in R^{n} \} \\ & = P\{ \mathop {\min {\kern 1pt} }\limits_{{t \in [t_{0} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le 0|||x||^{2} < \beta^{2} \} P\{ ||x||^{2} < \beta^{2} \} \\ & \quad + P\{ \mathop {\min {\kern 1pt} }\limits_{{t \in [t_{0} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le 0|||x||^{2} \ge \beta^{2} \} P\{ ||x||^{2} \ge \beta^{2} \} . \\ \end{aligned} $$

(9)

Because sample points inside $||{\kern 1pt} x{\kern 1pt} {\kern 1pt} {\kern 1pt} ||^{2} < \beta^{2}$ are absolutely safe, we have the equation $P\{ \mathop {\min {\kern 1pt} }\limits_{{t \in [t_{0} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le 0|{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\kern 1pt} {\kern 1pt} x{\kern 1pt} {\kern 1pt} ||^{2} < \beta^{2} \}$${ = 0}$.

Therefore, Eq. (10) is written as

$$ P\{ ||{\kern 1pt} {\kern 1pt} x{\kern 1pt} {\kern 1pt} ||^{2} \ge \beta^{2} \} = P\left\{ {\sum\limits_{i = 1}^{n} {x_{i}^{2} } \ge \beta^{2} } \right\} = 1 - F_{{\chi^{2} (n)}} (\beta^{2} ). $$

(10)

Therefore, the above equations can be obtained simultaneously

$$ P_{{\text{f}}} = [1 - F_{{\chi^{2} (n)}} (\beta^{2} )] \cdot P\{ \mathop {\min {\kern 1pt} }\limits_{{t \in [t_{0} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le 0|{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||x||^{2} \ge \beta^{2} \} . $$

(11)

The key to solve this probability is to find $P\{ \mathop {\min {\kern 1pt} }\limits_{{t \in [t_{{0}} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le {0}|{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||x||^{{2}} \ge \beta^{{2}} \}$. Meanwhile, the truncation probability density corresponding to the samples of ${\kern 1pt} ||x||^{2} \ge \beta^{2}$ is ${\kern 1pt} f_{x}^{{{\text{tr}}}} (x)$, and then, the above equation can be expanded into

$$ \begin{aligned} & \int\limits_{{\mathop {\min {\kern 1pt} }\limits_{{t \in [t_{{0}} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le {0}}} {f_{x} } (x)dx = [{1} - F_{{\chi^{{2}} (n)}} (\beta^{{2}} )] \cdot \int\limits_{g(x) \le 0} {f_{x}^{{{\text{tr}}}} } (x)dx \\ & \quad { = }\int\limits_{{\mathop {\min {\kern 1pt} }\limits_{{t \in [t_{{0}} ,t_{s} ]}} {\kern 1pt} {\kern 1pt} g(x,t) \le {0}}} {[{1} - F_{{\chi^{{2}} (n)}} (\beta^{{2}} )] \cdot f_{x}^{{{\text{tr}}}} } (x)dx. \\ \end{aligned} $$

(12)

Thus

$$ {\kern 1pt} f_{x}^{{{\text{tr}}}} (x) = \left\{ \begin{gathered} \frac{1}{{1 - F_{{\chi^{2} (n)}} (\beta^{2} )}}{\kern 1pt} f_{x} (x)\quad {\kern 1pt} || \, x{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||^{2} \ge \beta^{2} \hfill \\ {\kern 1pt} 0\quad ||x||{\kern 1pt}^{2} < \beta^{2} . \hfill \\ \end{gathered} \right. $$

(13)

Generate M samples ${\kern 1pt} \{ x_{1} ,x_{2} , \ldots x_{M} \}^{T}$ of input variable X according to the ${\kern 1pt} f_{x}^{{{\text{tr}}}} (x)$, and the estimated value of failure probability ${\kern 1pt} \hat{P}_{{\text{f}}}$ is

$$ \hat{P}_{{\text{f}}} = [1 - F_{{\chi^{2} (n)}} (\beta^{2} )] \cdot \frac{1}{M}\sum\limits_{j = 1}^{M} {I_{{\text{F}}} (\mathop {\min }\limits_{{t \in [t_{0} ,t_{s} ]}} g(x_{i} ,t))} . $$

(14)

To ensure the estimation accuracy, sufficient samples are needed to perform simulation. For example, the performance function whose failure probability is from 10–5 to 10–8 needs 5 × 10⁷ to 5 × 10¹⁰ samples to perform the MCS simulation. Therefore, for the time-dependent reliability problem of small failure probability (less than 10–5), although the AK-MCS method reduces the number of calling original performance function, the calculation cost is still too large to meet the engineering requirements. Meanwhile, it is still a challenging problem that how to improve the estimation efficiency of complex performance function and find the extremum in time interval.

3.3.3 Analysis procedure of the proposed time-dependent reliability method

The proposed method is based on ARBIS method and combined with double-loop AK model to transform the time-dependent reliability problem into a time-independent problem. The specific flowchart is shown in Fig. 7.

Fig.7

Flowchart of the proposed method

Step 1 The original variable is converted into standard normal space, and the converted performance function is marked as $g(x)$. Meanwhile, the sample pool ${\varvec{S}}^{x} = \left\{ {x_{1} ,x_{2} \ldots x_{{N^{x} }} } \right\}$ with sample size $N^{x}$ is generated.

Step 2 Set initial number of iterations $i_{\beta }$ = 1,$\beta_{1} { = }\sqrt {F_{{x^{2} (n)}}^{ - 1} (1 - p_{1} )}$, $p_{1} { = }10^{{{ - }6}}$, $\beta_{0} = + \infty$. where $F_{{x^{2} (n)}}^{ - 1} ( \cdot )$ is the inverse function of Chi-square distribution function (For small failure probability problem, $p_{1} { = }10^{{{ - }6}}$ is generally selected).

Step 3 $N_{0}$ initial samples from sample pool ${\varvec{S}}^{x}$ are randomly selected, and at a given value of x*, the performance function $g(x{*},t)$ is obtained with respect to t. In the inner loop, the AK model of performance function $g(x{*},t)$ with respect to t is established, and then, its minimum $G_{e} (x{*}) =$$\min_{{t \in [t_{0} ,t_{s} ]}} g_{k} (x*,t)$ is obtained. Because of $x^{ * } = x_{k}^{{\text{T}}}$, the initial training set is formed as $T =$ $\left\{ {(x_{k}^{T} ,G_{ek} (x_{k}^{T} )),k = 1,2 \ldots N_{0} } \right\}$ and AK model $G_{ek} (x)$ is established.

Step 4 The set of samples satisfying $\beta_{{i_{\beta } }} < \left\| x \right\| < \beta_{{i_{\beta } - 1}}$ in the sample pool ${\varvec{S}}^{x}$ is marked as ${\varvec{S}}_{{{\text{inside}}}}$.

Step 5 Samples inside ${\varvec{S}}_{{{\text{inside}}}}$ are used by outer loop AK model $G_{ek} (x)$ to judge the termination condition $C_{(K,MCS)} > C_{R}$, where the constant C_R ranges from 0.99 to 0.9999. If it holds, turn to Step 7; if not, turn to Step 6.

Especially, C_(K,MCS) is the parameter to judge the convergence condition constructing outer loop AK model $G_{ek} (x)$. Pr_c(x) is the probability that the validity of G_e(x) is judged by G_ek(x). The specific expression is as follows:

$$ C_{(K,MCS)} = E[\Pr_{c} ] = \frac{1}{{N^{x} }}\sum\limits_{i = 1}^{{N^{x} }} {\Pr_{c} (x_{i} )} , $$

(15)

$$ \Pr_{c} (x) = \Phi \left( {\frac{{|G_{eK} (x)|}}{{\sigma_{{G_{eK} (x)}} }}} \right). $$

(16)

Step 6 Combined with $x^{u} = \arg \max_{{x \in S_{{{\text{inside}}}} }} C_{{\text{A}}} (x)$, the update samples $(x^{u} ,G_{e} (x^{u} ))$ and the updated candidate training sample set $T = T \cup \left\{ {(x^{u} ,G_{e} (x^{u} ))} \right\}$ are obtained to update the AK model $G_{ek} (x)$. Then, turn to Step 4.

The expression of learning function C_A(x) is shown as follows:

$$ C_{{\text{A}}} (x) = (1 - \Pr_{c} (x)) \times f_{X} (x) \times \sigma_{{G_{eK} }} (x). $$

(17)

Step 7 In the $i_{\beta } {\text{th}}$ iteration, the updated AK model is used to count the value of failure samples and their indicator function is $I_{{\text{F}}} (x_{s}^{{i_{\beta } }} )(s = 1,2, \ldots N_{{i_{\beta } }} )$ in S_inside, then estimate the failure probability by $\sum\nolimits_{s = 1}^{{N_{{i_{\beta } }} }} {I_{{\text{F}}} (x_{s}^{{(i_{\beta } )}} )}$. Besides, calculate $\left| {\beta_{{i_{\beta } }} - \beta_{{i_{\beta } - 1}} } \right| \le \varepsilon$($\varepsilon = 0.01$). If it is satisfied, turn to Step 9; if not, turn to Step 8.

Step 8 Let $i_{\beta } = i_{\beta } + 1$. A new radius $\beta_{{i_{\beta } }}$ of the sphere is found by the $i_{\beta } {\text{th}}$ step of the ARBIS method. In all failure samples in ${\varvec{S}}_{{{\text{inside}}}}$, the sample with the highest probability density is found. In the direction of the line between this point and origin, a new radius $\beta_{{i_{\beta } }}$ of sphere is found by the linear search method. The previous $\beta_{{i_{\beta } }}$ is assigned to $\beta_{{i_{\beta } - 1}}$, and turn to step 4.

Step 9 Calculating failure probability $\hat{P}_{{\text{f}}} = [1 - F_{{\chi^{2} (n)}} (\beta_{{{\text{opt}}}}^{2} )] \cdot \frac{1}{{\sum\nolimits_{t = 1}^{{i_{\beta } }} {N_{t} } }}\sum\nolimits_{t = 1}^{{i_{\beta } }} {\sum\nolimits_{s = 1}^{{N_{{i_{\beta } }} }} {I_{F} (x_{s}^{(t)} )} }$, ${\text{Var}}[\hat{P}_{{\text{f}}} ] \approx \frac{{\hat{P}_{{\text{f}}} }}{{(\sum\nolimits_{t = 1}^{{i_{\beta } }} {N_{t} ) - 1} }}\{ [1 - F_{{\chi^{2} (n)}} (\beta_{{{\text{opt}}}}^{2} )] - \hat{P}_{{\text{f}}} \}$, and ${\text{Cov}}[\hat{P}_{{\text{f}}} ] = \sqrt {{\text{Var}}(\hat{P}_{{\text{f}}} )} /E(\hat{P}_{{\text{f}}} )$.

In the actual calculation, $1 - F_{{\chi^{2} (n)}} (\beta_{{{\text{opt}}}}^{2} ) \approx \frac{M}{N}$, where M is the number of samples outside the $\beta_{{{\text{opt}}}} {\text{ - sphere}}$, and N is the total number of samples.

Through the above steps, for the proposed method, the samples in the optimal β-sphere are absolutely safe, which avoids estimating the failure probability. On the contrary, only the samples outside the optimal β-sphere are regards as the candidate sample pool to update the AK model and estimate the failure probability. Therefore, the accuracy and efficiency of updating AK model are greatly improved. At the same time, especially for the small failure probability problem, the proposed method improves the efficiency of estimating the failure probability by reducing the capacity of the candidate sample pool. And this method is applicable to the problem with multiple MPPs.

4 Case study

In this section, three cases are analyzed. The first one is a two-dimensional numerical example, and its failure probability is about 10^–5. A four-bar function generator mechanism containing four variables. The third one is a wing structure; the performance function includes the variables of six dimensions and has a high degree of nonlinearity. The studies are carried out using the computer with a Inter (R) Core (TM) i7-8700 CPU processor, 8G RAM at 3.20 GHz and 3.19 GHz.

Five methods are used to provide the effectiveness of the proposed method:

• MCS: Monte Carlo Simulation method.

• Rice: the outcrossing rate method based on Rice’s formula.

• Double-loop AK: Double-loop adaptive Kriging surrogate model method.

• SILK: Single-loop adaptive Kriging surrogate model method.

• Prosed method: the method proposed in this paper.

4.1 Case 1: numerical example

The time-dependent performance function is characterized by Eq. (18)

$$ G(x,t) = x_{1}^{2} x_{2} - 5x_{1} t + 50\sin \left( \frac{t}{5} \right)(x_{2} + 1) - 18, $$

(18)

where the input variables $x_{1}$ and $x_{2}$ are independent normal variables, $x_{1} \sim N(3.5,0.3^{2} )$ and $x_{2}$$\sim N(3.5,0.3^{2} )$. The time interval is [0,5].

The comparison is shown in Table 1, N_call represents the number of calling the time-dependent performance function, and N_cand denotes the number of candidate samples and Runtime means the average runtime for estimating the time-dependent failure probability. Error stands for the relative error rate (%) compared with MCS method. Notations are suitable for all the following examples.

Table 1 Results of failure probability for Case 1

In this table, MCS method is listed for reference. The calculation results of the five methods are compared and analyzed. By comparing the results of the five methods, it can be seen that the error of the proposed method is the smallest of all the methods. In terms of computing time, the proposed method is more efficient than double-loop AK method. The number of calling performance function is analyzed, which shows that the proposed method is far less than that of MCS method. Although the calling number of the performance function of the proposed method is more than SILK, it is more efficient. Therefore, the proposed method is more suitable for time-dependent reliability analysis of complex engineering structures with small failure probability.

To illustrate the process of searching for the optimal radius β_opt of the sphere adaptively, the sample size of set S_inside and the corresponding radius β_i of the sphere in each iteration are listed in Table 2. It can be seen from this table that a total of three iterations have been carried out. The total number of samples in S_inside accounts for only 0.0556% of the initial sample pool. That is, 99.444% samples in the sample pool are unused in the estimation of failure probability, which is efficient for small failure probability.

Table 2 Record of the adaptive process

The process of searching for the optimal radius β_opt of the sphere is shown in Fig. 8. The training points added by updating AK model and all the approximate MPP are shown in Fig. 9.

Fig. 8

Adaptive sampling process

Fig. 9

The process of adaptively searching for MPP and adding training samples

4.2 Case 2: a four-bar function generator mechanism

This example is a function generator mechanism, as shown in Fig. 10. Where ${\mathbf{X}} = [R_{1} ,R_{2} ,R_{3} ,R_{4} ]$, the random variables R₁, R₂, R₃, R₄ are the normal distribution with mean value 53, 122, 66.5, and 100 respectively, and their standard deviation is all 0.1.

Fig. 10

A four-bar function generator mechanism

The relationship between the angles in the movement of four-bar function generator mechanism is as follows:

$$ \left\{ \begin{gathered} R_{1} \cos \theta + R_{2} \cos \delta - R_{3} \cos \varphi - R_{4} = 0 \hfill \\ R_{1} \sin \theta + R_{2} \sin \delta - R_{3} \sin \varphi = 0, \hfill \\ \end{gathered} \right. $$

(19)

where $\theta$ is input variable, and $\delta$ and $\varphi$ are output variables. Therefore, we get these equations

$$ \left\{ \begin{gathered} \varphi ({\mathbf{X}},\theta ) = 2\arctan \frac{{D \pm \sqrt {D^{2} + E^{2} - F^{2} } }}{E + F} \hfill \\ \varphi_{d} (\theta ) = 76^{ \circ } + 60^{ \circ } \sin (0.75(\theta - 95.5^{ \circ } )), \hfill \\ \end{gathered} \right. $$

(20)

where $D = - 2R_{1} R_{3} \sin \theta$,$E = 2R_{3} (R_{4} - R_{1} \cos \theta )$,$F = R_{2}^{2} - R_{1}^{2} - R_{3}^{2} - R_{4}^{2} + 2R_{1} R_{4} \cos \theta$.

Consequently, the performance function is given by

$$ G({\mathbf{X}},\theta ) = c - \varphi ({\mathbf{X}},\theta ) + \varphi_{d} (\theta ), $$

(21)

where failure threshold c is set as 0.8, $\theta$ under consideration is $[95.5^{ \circ } ,155.5^{ \circ } ]$ and the probability of failure $P_{{\text{f}}}$ is computed by

$$ P_{{\text{f}}} = \Pr \{ G({\mathbf{X}},\theta ) < 0,\exists \theta \in [95.5^{ \circ } ,155.5^{ \circ } ]\} = \Pr \{ \mathop {\min }\limits_{{\theta \in [95.5^{ \circ } ,155.5^{ \circ } ]}} G({\mathbf{X}},\theta ) < 0)\} . $$

(22)

The results are presented in Table 3.

Table 3 Results of failure probability for Case 2

From Table 3, we can find that the estimation efficiency of the proposed method is more efficient, and its running time is far less than any other methods. Although the number of calling performance function is higher than SILK method, its running time is less. The iterative process of searching for the optimal radius β_opt of the sphere is shown in Fig. 4.

According to Table 4, in the process of searching for the optimal radius β_opt of the sphere, nine times of iterations is conducted. The total number of the samples used to updating the AK model accounts for only 9.28% of the initial sample pool. This example also shows that the proposed method greatly reduces the calculation of the sample pool under small failure probability. Thus, it is more efficient than any other method listed in Table 3.

Table 4 Record of the adaptive process

4.3 Case 3: an aircraft wing structure

This example introduces an engineering application about the wing which is chosen as typical long-range transport aircraft wing in the Boeing 767 class [28]. The geometric details are obtained from Ref. [29]. A simple sketch of a reference wing geometric is given in Fig. 11

Fig.11

Reference wing: a cross-sectional view; b top view c loading on the wing [22]

Figure 11a shows the cross-sectional view of the reference wing, where T, h, and c are the thickness, the depth, and the chord of the wing, respectively. Figure 11b is the top view where b is the span and b = 40(m). Figure 11c shows the loading on the wing.

In this example, the location in the x-axis can be viewed as t parameter and t ∈ [0,20]. The input vector is denoted as X = $\{ P_{{\text{r}}} ,\sigma_{{\text{f}}} ,c_{{\text{r}}} ,c_{0} /c_{{\text{r}}} ,h/c,T\}^{T}$ and the corresponding distribution parameters are shown in Table 5.

Table 5 Distributions of inputs for case 3

The time-dependent performance function of the reference wing is represented by Eq. (21)

$$ G({\mathbf{X}},t){ = }\sigma_{{\text{f}}} - \frac{{M({\mathbf{X}},t)(h({\mathbf{X}},t)/{2})}}{{I_{{\text{Z}}} ({\mathbf{X}},t)}}, $$

(23)

where the chord length c, wing depth h, moment of inertia $I_{{\text{Z}}}$, and the bending moment M can be, respectively, expressed as

$$ c({\mathbf{X}},t){ = }c_{{\text{r}}} \left[ {\left( {\frac{{c_{0} }}{{c_{{\text{r}}} }}} \right) + \left( {{1} - \frac{{c_{0} }}{{c_{{\text{r}}} }}} \right)\frac{t}{{b/{2}}}} \right], $$

(24)

$$ h({\mathbf{X}},t) = c_{{\text{r}}} \left( \frac{h}{c} \right)\left[ {\left( {\frac{{c_{0} }}{{c_{{\text{r}}} }}} \right) + \left( {1 - \frac{{c_{0} }}{{c_{{\text{r}}} }}} \right)\frac{t}{b/2}} \right], $$

(25)

$$ I_{{\text{Z}}} ({\mathbf{X}},t){ = }\frac{{1}}{{2}}c({\mathbf{X}},t)Th^{{2}} ({\mathbf{X}},t), $$

(26)

$$ M({\mathbf{X}},t){ = 4}P_{{\text{r}}} c_{{\text{r}}} b\left[ {\left( {\frac{{c_{{0}} }}{{c_{{\text{r}}} }}} \right)\frac{{t^{{4}} }}{{{12}b^{{2}} }} + \left( {{1} - {2}\frac{{c_{{0}} }}{{c_{{\text{r}}} }}} \right)\frac{{t^{{5}} }}{{{20}b^{{3}} }} + \left( {\frac{{c_{{0}} }}{{c_{{\text{r}}} }} - {1}} \right)\frac{{t^{{6}} }}{{{30}b^{{4}} }}} \right]. $$

(27)

The results of the time-dependent failure probability estimated by referenced methods and the proposed method are shown in Table 6. Obviously, in the case of the same error, the proposed method is more efficient than other methods and the number of calling performance function is the least. Therefore, the proposed method is also suitable for high failure probability. Table 7 shows the iterative process of the proposed method in searching for MPP.

Table 6 Numerical results of failure probability for Case 3

Table 7 Record of adaptive process

From Table 7, the total number of samples in set S_inside accounts for 36.12% of the initial sample pool. Obviously, this ratio is much larger than 0.0556% and 3.25% of the previous two examples. The main reason is that optimal radius $\beta_{{{\text{opt}}}}$ of the sphere in this example is smaller than those in previous example, which leads to more samples used for updating the Kriging model outside $\beta_{{{\text{opt}}}}$-sphere. Therefore, the calculation is not significantly reduced compared with double-loop AK model method, but its estimation efficiency is still higher than that of the double-loop AK model and MCS method.

5 Conclusion

Through the analysis of cases above, we conclude that the proposed method can improve the estimation efficiency and accuracy of time-dependent reliability analysis. It is summarized as follows.

• 1. For the problem of small failure probability, the proposed method is more efficient than double-loop AK model and MCS method, and it has higher accuracy than double-loop AK model.

• 2. Compared with general AK model connecting with IS method, the proposed method does not need to calculate the MPP at first, but searching for it step by step adaptively, and it is also applicable to the case of multi MPPs and highly nonlinear performance function.

• 3. In some cases, the number of calling performance function of proposed method is more than double-loop AK model. The main reason is that, when AK model is updated initially, many useless training samples with low probability density are added. The solution to this problem is still under studying.

• 4. In the future study, three directions will be researched: (a) the research of improving the estimation efficiency of adaptive searching for the optimal radius β_opt of the sphere; (b) the influence of different initial radius β₀ of the sphere on the convergence speed and the number of calling performance function; (c) combining the ARBIS method with the single-loop time-dependent AK model.