1 Introduction

Uncertainties are unavoidable in a load-bearing structure, and it is crucial to conduct reliability analysis (RA) for the structure. In the conventional RA, a probability density function (PDF) is assigned to input variables and a performance function is defined to check whether the structure works or fails [1]. And then, the probability of failure, or the failure probability, is calculated. Practically, the performance function is frequently calculated by the finite element analysis and RA needs many function evaluations which is very time consuming. To minimize the number of function evaluations, quite a lot of methods have been proposed during the past decades.

Generally, those methods can be classified into three groups[2]. The first group includes the first-order and second-order reliability methods [3, 4]. Those methods are quite efficient while the accuracy is hard to be guaranteed if the performance function is highly nonlinear or has several failure regions. The second group comprises the crude Monte-Carlo simulation (MCS) method, the importance sampling (IS) methods [5,6,7] and the subset simulation (SS) method [8,9,10]. The main drawback of those methods is that they need quite a lot of function evaluations. The third group is the methods based on the surrogate models. The popularly used metamodels are the polynomial chaos expansion models [11, 12], the neural network models [13,14,15], and the Kriging model [16, 17].

State-of-the-art methods in the field of conventional RA are the active learning methods based on the Kriging (ALK) model [18,19,20]. By a learning function, optimal training points can be recognized and the prediction accuracy can be remarkably improved [2, 18, 21]. By a proper stopping condition, the learning process can be timely terminated without accuracy sacrifice [22,23,24]. The famous learning functions are U, the expected feasible function, and the expected risk function (ERF). The excellent works about the stopping conditions can be found in [22, 23, 25,26,27]. Abundant tests verify that ALK model can accurately estimate the failure probability with a pretty small number of function evaluations [27, 28].

Although great achievements have been obtained, one crucial issue exists in the conventional RA. As stated above, the binary state assumption is made to define the performance function. This means the state of a structure can only be eighter in the fully working state or complete failure state [29]. This assumption may violate the reality sometimes. For example, when evaluating the risk, it is often classified into several classes, such as no risk, weak risk, moderate risk, and large risk. And the threshold value between each pair of classes is subjectively set [30, 31]. For another example, the failure process of plastic materials often has four stages, i.e., elasticity, plasticity, necking, and fracture [32]. This means there is no distinct discrimination between success and failure and the boundary between them is quite ambiguous. In this context, the theory of profust RA is proposed [29, 33]. In profust RA, a membership function from the fuzzy set theory is assigned to the performance function [33]. The membership function measures the possibility that the state of a load-bearing structure belongs to the failure region. When compared with the traditional RA based on the binary-state assumption, the fuzzy-state assumption is introduced in profust RA that can reveal the degradation process of structure performance [34, 35]. In addition, the so-called nonprobabilistic RA with epistemic input uncertainties, described by convex set [21, 36], probability box [37], evidence theory [11], and fuzzy set [38,39,40], were also exploited by researchers. However, profust RA is different from the nonprobabilistic RA. In profust RA, epistemic uncertainty only exists in the output state of a structure. Contrarily, in nonprobabilistic RA, epistemic uncertainties are assumed in the input variables.

The introduction of fuzzy membership function makes the profust RA more complicated than the conventional RA. Primary studies on the evaluation of profust failure probability were conducted in [33, 41]. Those methods are based on the simple linear regression and numerical integral, which are not applicable to complicated problems [35]. The profust failure probability was transformed into the integration of failure probability at different thresholds of performance function. And then, it can be calculated by Gauss quadrature in conjunction with MCS or SS [35]. This is a double-layer process. The double-layer problem was transformed into a single layer problem and a more concise MCS method was presented in [42]. Considering the high efficiency of ALK model, the early exploration on how to adapt the ALK model to profust RA has been carried out. The active learning method combining Kriging model and MCS (AK-MCS), from the traditional RA, was integrated into the double-layer process and single-layer process in [31, 42, 43]. To make the ALK model applicable to estimate slightly small failure probability, the works of [44, 45] were extended to profust RA in [46] and a so-called dual-stage adaptive Kriging (DS-AK) method was proposed. Other works related to RA with fuzzy state can be seen from [47, 48].

This paper aims at proposing a more efficient method for profust RA based on the ALK model. The ERF given an arbitrary threshold of performance function is deduced and a new learning function is proposed for profust RA. The new learning function makes the learning process more robust than existing methods. The prediction error for profust failure probability is derived into a closed-form formula by making full use of the uncertain information of Kriging model and Central Limit Theorem. In this way, the learning process can be timely terminated compared with the existing methods. The proposed method is shorted as ALK-Pfst because it is an active learning method based on the Kriging model for the profust RA.

This paper is organized as follows. The theory of profust RA is briefly explained in Sect. 2. AK-MCS method is reviewed in Sect. 3. Section 4 is dedicated to our proposed method. The performance of the proposed method is demonstrated by four case studies in Sect. 5. Conclusions are made in the last section.

2 Profust reliability analysis

Denote the performance function of a structure as \(Y = G\left( {\mathbf{X}} \right)\), where \(\user2{X} = \left[ {X_{1} ,X_{2} , \ldots ,X_{{n_{X} }} } \right]\) is the vector of random variables. The joint PDF of random variables is \(f_{{\mathbf{X}}} \left( {\mathbf{x}} \right)\). In traditional RA, binary state is assumed and it is deemed that the structure belongs to the ‘fully working’ state or ‘completely failed’ state. The failure probability is defined as

$$P_{F} = \int_{{R^{n} }} {I\left[ {G\left( {\mathbf{x}} \right) < 0} \right]f_{{\mathbf{X}}} \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} ,$$
(1)

in which \(I\left[ \cdot \right]\) is an indicator function of an event with value 1 if the event is true and 0 otherwise.

In profust RA, a fuzzy state is introduced to describe the gradual transition from fully working state to completely failed state. A membership function \(\mu _{{\tilde{F}}} \left( Y \right)\) is used to measure the possibility of a structure belongs to the failure state. \(\mu _{{\tilde{F}}} \left( Y \right)\) monotonically decreases from 1 to 0 with respect to \(Y\). A larger \(\mu _{{\tilde{F}}} \left( Y \right)\) means a larger possibility that the structure belongs to the failure state. \(\mu _{{\tilde{F}}} \left( Y \right) = 0\) indicates that the structure is totally safe while \(\mu _{{\tilde{F}}} \left( Y \right) = 1\) means the structure completely fails. Several kinds of membership functions have been proposed so far. The most widely used ones are the linear membership function, the normal membership function, and the Cauchy membership function [43]. They are mathematically given in Eqs. (2)–(4).

  1. 1.

    Linear membership function

    $$\mu _{{\tilde{F}}} \left( Y \right) = \left\{ \begin{gathered} 1{\text{ }}Y \le a_{{\text{1}}} \hfill \\ {{\left( {y - a_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {y - a_{2} } \right)} {\left( {a_{1} - a_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {a_{1} - a_{2} } \right)}}{\text{ }}a_{{\text{1}}} < Y < a_{{\text{2}}} \hfill \\ 0{\text{ }}Y \ge a_{{\text{2}}} \hfill \\ \end{gathered} \right.$$
    (2)
  2. 2.

    Normal membership function

    $$\mu _{{\tilde{F}}} \left( Y \right) = \left\{ \begin{gathered} 1{\text{ }}Y \le b_{{\text{1}}} \hfill \\ \exp \left( { - \left( {Y - b_{1} } \right)^{2} /b_{2} } \right){\text{ }}Y{\text{ > }}b_{{\text{1}}} \hfill \\ \end{gathered} \right.$$
    (3)
  3. 3.

    Cauchy membership function

    $$\mu _{{\tilde{F}}} \left( Y \right) = \left\{ \begin{gathered} 1{\text{ }}Y \le c_{1} \hfill \\ {{c_{2} } \mathord{\left/ {\vphantom {{c_{2} } {\left[ {c_{2} + 10\left( {Y - c_{1} } \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {c_{2} + 10\left( {Y - c_{1} } \right)^{2} } \right]}}{\text{ }}Y{\text{ > }}c_{1} \hfill \\ \end{gathered} \right.$$
    (4)

where \(\left[ {a_{1} ,a_{2} } \right]\), \(\left[ {b_{1} ,b_{2} } \right]\), and \(\left[ {c_{1} ,c_{2} } \right]\) are parameters. The profust failure probability is defined as

$$P_{{\tilde{F}}} = \int_{{R^{n} }} {\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right]f_{{\mathbf{X}}} \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} .$$
(5)

Introduce an index variable \(\lambda\) with \(\lambda \in \left[ {0,1} \right]\), then it can be proved that [33, 43]

$$\begin{gathered} \int\limits_{0}^{1} {I\left( {\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right] < \lambda } \right)E\lambda } = \int\limits_{0}^{{\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right]}} {I\left( {\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right] < \lambda } \right){\text{d}}\lambda } + \int\limits_{{\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right]}}^{1} {I\left( {\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right] < \lambda } \right){\text{d}}\lambda } \hfill \\ = \int\limits_{0}^{{\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right]}} {1{\text{d}}\lambda } + \int\limits_{{\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right]}}^{1} {0{\text{d}}\lambda } = \int\limits_{0}^{{\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right]}} {1{\text{d}}\lambda } = \mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right]. \hfill \\ \end{gathered}$$
(6)

Because \(\mu _{{\tilde{F}}} \left( Y \right)\) is a monotonical function, it can be easily obtained that

$$\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right] = \int\limits_{0}^{1} {I\left( {\mu _{{\tilde{F}}} \left[ {G\left( {\mathbf{x}} \right)} \right] < \lambda } \right){\text{d}}\lambda } {\text{ = }}\int\limits_{0}^{1} {I\left[ {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right]{\text{d}}\lambda } ,$$
(7)

where \(\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)\) is the inverse function of \(\mu _{{\tilde{F}}} \left( Y \right)\). Substituting Eq. (7) into Eq. (5), there is

$$P_{{\tilde{F}}} {\text{ = }}\int_{{R^{n} }} {\left[ {\int\limits_{0}^{1} {I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right){\text{d}}\lambda } } \right]f_{{\mathbf{X}}} \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} .$$
(8)

In Refs. [35, 43, 46], the inner integration was put outside, i.e.,

$$P_{{\tilde{F}}} {\text{ = }}\int\limits_{0}^{1} {\left[ {\int_{{R^{n} }} {I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)f_{{\mathbf{X}}} \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} } \right]{\text{d}}\lambda } = \int\limits_{0}^{1} {E\left[ {I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)} \right]{\text{d}}\lambda } .$$
(9)

Then, the outer one-dimensional integral can be solved by Gauss quadrature.

$$P_{{\tilde{F}}} \approx \sum\limits_{{k = 1}}^{l} {\omega _{k} E\left[ {I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda _{k} } \right)} \right)} \right]} ,$$
(10)

where l is the number of Gauss points; \(\lambda _{k}\) and \(\omega _{k}\) are the kth quadrature point and weight. With MCS, one can obtain the first estimator of \(P_{{\tilde{F}}}\), i.e.,

$$\hat{P}_{{\tilde{F}}} \approx \sum\limits_{{k = 1}}^{l} {\left[ {\omega _{k} \frac{1}{{N_{{{\text{MC}}}} }}\sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {I\left( {G\left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda _{k} } \right)} \right)} } \right]} ,$$
(11)

in which \({\mathbf{x}}^{{\left( i \right)}}\) is the ith simulated sample of MCS.

However, the utilization of Gauss quadrature makes the calculation as a double-stage process. One must calculate the failure probability at \(l\) different thresholds. Moreover, the performance functions with \(l\) different thresholds are totally correlated which is detrimental for us to estimate the prediction error of \(\hat{P}_{{\tilde{F}}}\) according to the predication information of Kriging model.

Actually, Eq. (8) can be calculated in an integrated way by treating \(\lambda\) as a uniformly distributed variable in [0,1], i.e.,

$$\begin{gathered} P_{{\tilde{F}}} = \int\limits_{0}^{1} {\int_{{R^{n} }} {I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)f_{{\mathbf{X}}} \left( {\mathbf{x}} \right){\text{d}}{\mathbf{x}}} {\text{d}}\lambda } \hfill \\ = \int_{{R^{{n + 1}} }} {I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)f_{{\mathbf{X}}} \left( {\mathbf{x}} \right)f_{\Lambda } \left( \lambda \right){\text{d}}{\mathbf{x}}} {\text{d}}\lambda \hfill \\ {\text{ = }}E\left[ {I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)} \right], \hfill \\ \end{gathered}$$
(12)

in which \(f_{\Lambda } \left( \lambda \right)\) is the PDF of \(\lambda\). Then, another unbiased estimator can be obtained as [31, 42]

$$\tilde{P}_{{\tilde{F}}} = \frac{1}{{N_{{{\text{MC}}}} }}\sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {I\left[ {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]} ,$$
(13)

in which \(\lambda ^{{\left( i \right)}}\) is the ith simulated sample of \(\lambda\). This estimator is quite direct and the calculation is a single stage process.

3 Reminder of AK-MCS

To reduce the number of function evaluations, AK-MCS was investigated in [31, 42, 43], and is briefly presented in this section. AK-MCS was firstly proposed in the field of traditional RA. It can be easily adapted to the profust RA by modifying its learning function.

In Kriging model, \(G\left( {\mathbf{x}} \right)\) is expressed by a prior Gaussian process. Given a design of experiments (DoE), parameters of the Gaussian process can be updated and the posterior Gaussian process can be utilized to make predictions at unknown positions. At an unknown point, the prediction is given as \(G_{P} \left( {\mathbf{x}} \right) \sim N\left( {\mu _{G} \left( {\mathbf{x}} \right),\sigma _{G} \left( {\mathbf{x}} \right)} \right)\), in which \(\mu _{G} \left( {\mathbf{x}} \right)\) is the predicted mean and \(\sigma _{G}^{2} \left( {\mathbf{x}} \right)\) is the predicted variance.

The profust failure probability is mainly determined by \(I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)\), i.e., the sign of \(G\left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)\). Learning function U was modified in [31, 42, 43] to find the point at which the sign of \(G\left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)\) has the largest probability to be wrongly predicted according to the information \(G_{P} \left( {\mathbf{x}} \right) \sim N\left( {\mu _{G} \left( {\mathbf{x}} \right),\sigma _{G} \left( {\mathbf{x}} \right)} \right)\). The modified U is given as

$${\text{U}}\left( {\user2{x}\left| \lambda \right.} \right){\text{ = }}\left| {\frac{{\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}}{{\sigma _{G} \left( \user2{x} \right)}}} \right|.$$
(14)

Then, AK-MCS can be adapted to profust RA in the framework of double-stage MCS or single-stage MCS. For simplicity, AK-MCS in the framework of single-stage MCS is termed as AK-MCS#1 and in the framework of double-stage MCS is termed AK-MCS#2.

However, learning function U is very local [45, 49]. If the boundary between failure and working state has multiple branches, the ALK model based on the learning function U tends to sequentially approximate those branches. This generates potential risk that the learning process is terminated when only several branches are finely approximated. Moreover, because there is no estimation technique on the prediction error of \(P_{{\tilde{F}}}\), the stopping condition of AK-MCS must be defined very conservative. The learning process is not stopped until the minimum value of \({\text{U}}\left( {\user2{x}\left| \lambda \right.} \right)\) among the samples of MCS is larger than 2. As a result, quite a lot of training points are wasted by AK-MCS.

4 ALK-Profust

To overcome the drawbacks of AK-MCS, ALK-Profust is developed in this section. When compared with AK-MCS, twofold improvements exist in ALK-Profust. A learning criterion modified from ERF, which is more robust than U, is put forward. A new stopping criterion measuring the prediction error of \(\hat{P}_{{\tilde{F}}}\) is derived and the learning process can be timely terminated with little accuracy sacrifice.

4.1 Learning criterion

In this paper, ERF [21] is modified as the acquisition function. The profust failure probability is mainly determined by \(I\left( {G\left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)\). The predicted mean \(\mu _{G} \left( {\mathbf{x}} \right)\) is frequently utilized to replace \(G_{P} \left( {\mathbf{x}} \right)\) and a determinate prediction for \(I\left[ {G_{P} \left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right]\) is obtained. Actually, the prediction is uncertain because \(G_{P} \left( {\mathbf{x}} \right)\) is uncertain. Our goal is to find the point with the largest expectation of risk that \(I\left[ {\mu _{G} \left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right]\) violates \(I\left[ {G_{P} \left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right]\).

If \(\mu _{G} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) < 0\), we define a risk indicator function to measure the risk that \(G_{P} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) > 0\) as

$$R\left( {\user2{x}\left| \lambda \right.} \right) = \max \left( {\left( {G_{P} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right),0} \right).$$
(15)

Because \(R\left( {\user2{x}\left| \lambda \right.} \right)\) is also an uncertain variable, its expectation is calculated as follows.

$$E\left[ {R\left( {\user2{x}\left| \lambda \right.} \right)} \right] = \int\limits_{{\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}}^{{ + \infty }} {\left( {G_{P} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)f_{{G_{P} }} \left( {G_{P} \left( \user2{x} \right)} \right)} {\text{d}}G_{P} ,$$
(16)

in which \(f_{{G_{P} }} \left( {G_{P} \left( \user2{x} \right)} \right)\) is the PDF of \(G_{P} \left( \user2{x} \right)\). Let \(g = \frac{{G_{P} \left( \user2{x} \right) - \mu _{G} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}\), and we have

$$\begin{gathered} E\left[ {R\left( {\user2{x}\left| \lambda \right.} \right)} \right] = \int_{{\frac{{\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) - \mu _{G} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}}}^{{ + \infty }} {\left[ {\sigma _{G} \left( \user2{x} \right)g + \mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right]\phi \left( g \right){\text{d}}g} \hfill \\ = \int_{{\frac{{\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) - \mu _{G} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}}}^{{ + \infty }} {\sigma _{G} \left( \user2{x} \right)g\phi \left( g \right)dg} + \int_{{\frac{{\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) - \mu _{G} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}}}^{{ + \infty }} {\left( {\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)\phi \left( g \right){\text{d}}g} \hfill \\ = - \left. {\phi \left( g \right)\sigma _{G} \left( \user2{x} \right)} \right|_{{\frac{{\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) - \mu _{G} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}}}^{{ + \infty }} + \left. {\Phi \left( g \right)\left( {\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right)} \right|_{{\frac{{\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) - \mu _{G} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}}}^{{ + \infty }} \hfill \\ = \phi \left( {\frac{{\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}}{{\sigma _{G} \left( \user2{x} \right)}}} \right)\sigma _{G} \left( \user2{x} \right) + \Phi \left( {\frac{{\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}}{{\sigma _{G} \left( \user2{x} \right)}}} \right)\left( {\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right), \hfill \\ \end{gathered}$$
(17)

in which \(\phi \left( \cdot \right)\) and \(\Phi \left( \cdot \right)\) are the PDF and cumulative distribution function (CDF) of standard normal distribution. If \(\mu _{G} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) > 0\), the risk that \(G_{P} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) < 0\) is defined as

$$R\left( {\user2{x}\left| \lambda \right.} \right) = \min \left( {\left( {G_{P} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right),0} \right),$$
(18)

and the expected risk is obtained as

$$\begin{gathered} E\left[ {R\left( {\user2{x}\left| \lambda \right.} \right)} \right] = \int\limits_{{ - \infty }}^{{\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}} {\left( {\mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right) - G_{P} \left( \user2{x} \right)} \right)f_{{G_{P} }} \left( {G_{P} \left( \user2{x} \right)} \right)} {\text{d}}G_{P} \hfill \\ = \phi \left( {\frac{{\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}}{{\sigma _{G} \left( \user2{x} \right)}}} \right)\sigma _{G} \left( \user2{x} \right) - \Phi \left( { - \frac{{\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}}{{\sigma _{G} \left( \user2{x} \right)}}} \right)\left( {\mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right). \hfill \\ \end{gathered}$$
(19)

Combining Eqs. (16) and (19), the uniform expression of modified ERF can be obtained as:

$$E\left[ {R\left( {\user2{x}\left| \lambda \right.} \right)} \right] = - {\text{sign}}\left( {\mu _{{\tilde{G}}} \left( \user2{x} \right)} \right)\mu _{{\tilde{G}}} \left( \user2{x} \right)\Phi \left( { - {\text{sign}}\left( {\mu _{{\tilde{G}}} \left( \user2{x} \right)} \right)\frac{{\mu _{{\tilde{G}}} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}} \right) + \sigma _{G} \left( \user2{x} \right)\phi \left( {\frac{{\mu _{{\tilde{G}}} \left( \user2{x} \right)}}{{\sigma _{G} \left( \user2{x} \right)}}} \right),$$
(20)

in which \(\mu _{{\tilde{G}}} \left( \user2{x} \right) = \mu _{G} \left( \user2{x} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)\).

The modified ERF reveals the expected risk that the sign of \(G\left( {\mathbf{x}} \right)\) given an arbitrary threshold predicted by \(\mu _{G} \left( {\mathbf{x}} \right)\) violates that predicted by \(G_{P} \left( {\mathbf{x}} \right)\). The point at which the modified ERF is maximized should be added into the DoE. Among the candidate points \(\left( {{\mathbf{x}}^{{\left( i \right)}} ,\lambda ^{{\left( i \right)}} } \right)\left( {i = 1, \ldots ,N_{{{\text{MC}}}} } \right)\), the best next training point is obtained by

$${\mathbf{x}}_{{}}^{{\left( * \right)}} = {\mathbf{x}}_{{}}^{{\left( k \right)}} ,k = \arg \mathop {\max }\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} E\left[ {R\left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)} \right].$$
(21)

4.2 Stopping criterion

Denote the profust failure probability obtained from \(G_{P} \left( {\mathbf{x}} \right)\) as \(\hat{P}_{{\tilde{F}}}\) and that from \(\mu _{G} \left( {\mathbf{x}} \right)\) as \(\hat{P^{\prime}}_{{\tilde{F}}}\). Apparently, \(\hat{P}_{{\tilde{F}}}\) fully considers the prediction information of Kriging model, while \(\hat{P^{\prime}}_{{\tilde{F}}}\) only considers the predicted mean. The discrepancy between them can measure the prediction accuracy of profust failure probability. The prediction (relative) error of the profust failure probability can be given as

$$\varepsilon _{{\tilde{F}}} = \frac{{\left| {\hat{P}_{{\tilde{F}}} - \hat{P^{\prime}}_{{\tilde{F}}} } \right|}}{{\hat{P}_{{\tilde{F}}} }}{\text{ = }}\frac{{\left| {N_{{\tilde{F}}} - N^{\prime}_{{\tilde{F}}} } \right|}}{{N_{{\tilde{F}}} }},$$
(22)

in which \(N_{{\tilde{F}}}\) is the predicted number of failure samples considering prediction uncertainty of Kriging model and \(N^{\prime}_{{\tilde{F}}}\) is that without such consideration. They are given as

$$N_{{\tilde{F}}} = \sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {I\left[ {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]} ,$$
(23)

and

$$N^{\prime}_{{\tilde{F}}} = \sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {I\left[ {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]}$$
(24)

The numerator in Eq. (22) has an upper bound which is given as

$$\begin{gathered} \left| {N_{{\tilde{F}}} - N^{\prime}_{{\tilde{F}}} } \right| = \left| {\sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {\left( {I\left[ {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right] - I\left[ {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]} \right)} } \right| \hfill \\ \le \sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {\left| {I\left[ {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right] - I\left[ {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]} \right|} \hfill \\ = \sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {\left| {I\left\{ {\left[ {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]\left[ {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right] < 0} \right\}} \right|} \hfill \\ = N_{{{\text{WSP}}}}^{{}} , \hfill \\ \end{gathered}$$
(25)

in which \(N_{{{\text{WSP}}}}^{{}}\) is the number of points at which the signs of \(G_{P} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)\) and \(\mu _{G} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)\) are different, i.e., the number of points with wrong sign prediction (WSP).

Because \(G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right)\) is a random variable, \(I\left\{ {\left[ {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]\left[ {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right] < 0} \right\}\) is also random. Specifically, \(I\left\{ {\left[ {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right]\left[ {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right] < 0} \right\}\) follows the Bernoulli distribution.

According to the prediction information that \(G_{P} \left( {\mathbf{x}} \right) \sim N\left( {\mu _{G} \left( {\mathbf{x}} \right),\sigma _{G} \left( {\mathbf{x}} \right)} \right)\), the probability of a point with WSP can be obtained as [22]

$$P_{{{\text{WSP}}}} \left( {{\mathbf{x}}\left| \lambda \right.} \right) = \Phi \left( { - \frac{{\left| {\mu _{G} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right|}}{{\sigma _{G} \left( {\mathbf{x}} \right)}}} \right).$$
(26)

Then, the expectation and variance of \(I\left[ {\left( {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right)\left( {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right) < 0} \right]\) can be obtained as:

$$E\left\{ {I\left[ {\left( {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right)\left( {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right) < 0} \right]} \right\} = P_{{{\text{WSP}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| \lambda \right.^{{\left( i \right)}} } \right),$$
(27)
$$Var\left\{ {I\left[ {\left( {G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right)\left( {\mu _{G} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( {\lambda ^{{\left( i \right)}} } \right)} \right) < 0} \right]} \right\} = P_{{{\text{WSP}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)\left( {1 - P_{{{\text{WSP}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)} \right).$$
(28)

Recall that \(N_{{{\text{WSP}}}}^{{}}\) is the summation of \(N_{{{\text{MC}}}}\) random variables obeying the Bernoulli distribution. According to the Central Limit Theorem [50], if \(N_{{{\text{MC}}}} \to \infty\) and \(G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right)\left( {i = 1,2, \ldots ,N_{{{\text{MC}}}} } \right)\) are mutually independent, \(N_{{{\text{WSP}}}}^{{}}\) in distribution converges to such a normal distribution as

$$N_{{{\text{WSP}}}}^{{}} \sim N\left( {\mu _{{N_{{{\text{WSP}}}} }}^{{}} ,\left( {\sigma _{{N_{{{\text{WSP}}}} }}^{{}} } \right)^{2} } \right),$$
(29)

with the mean and variance

$$\left\{ \begin{gathered} \mu _{{N_{{{\text{WSP}}}} }}^{{}} {\text{ = }}\sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {P_{{{\text{WSP}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)} \hfill \\ \left( {\sigma _{{N_{{{\text{WSP}}}} }}^{{}} } \right)^{2} {\text{ = }}\sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {P_{{{\text{WSP}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)\left( {1 - P_{{{\text{WSP}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)} \right)} \hfill \\ \end{gathered} \right..$$
(30)

Similarly, if \(N_{{{\text{MC}}}} \to \infty\) and \(G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right)\left( {i = 1,2, \ldots ,N_{{{\text{MC}}}} } \right)\) are totally independent,\(N_{{\tilde{F}}}^{{}}\) in distribution will also converges to such a normal distribution as:

$$N_{{\tilde{F}}}^{{}} \sim N\left( {\mu _{{N_{{\tilde{F}}} }}^{{}} ,\left( {\sigma _{{N_{{\tilde{F}}} }}^{{}} } \right)^{2} } \right),$$
(31)

with the mean and variance

$$\left\{ \begin{gathered} \mu _{{N_{{\tilde{F}}}^{{}} }}^{{}} {\text{ = }}\sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {P_{{{\text{fail}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)} \hfill \\ \left( {\sigma _{{N_{{\tilde{F}}} }}^{{}} } \right)^{2} {\text{ = }}\sum\limits_{{i = 1}}^{{N_{{{\text{MC}}}} }} {P_{{{\text{fail}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)\left( {1 - P_{{{\text{fail}}}} \left( {{\mathbf{x}}^{{\left( i \right)}} \left| {\lambda ^{{\left( i \right)}} } \right.} \right)} \right)} \hfill \\ \end{gathered} \right.,$$
(32)

in which \(P_{{{\text{fail}}}}^{{}} \left( {{\mathbf{x}}\left| \lambda \right.} \right)\) is the probability of \(G_{P} \left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)\), which is given as:

$$P_{{{\text{fail}}}}^{{}} \left( {{\mathbf{x}}\left| \lambda \right.} \right) = P\left\{ {G_{P} \left( {\mathbf{x}} \right) < \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)} \right\} = \Phi \left( { - \frac{{\mu _{G} \left( {\mathbf{x}} \right) - \mu _{{\tilde{F}}}^{{ - 1}} \left( \lambda \right)}}{{\sigma _{G} \left( {\mathbf{x}} \right)}}} \right).$$
(33)

In summary, the upper bound of Eq. (22) is obtained as:

$$\varepsilon _{{\tilde{F}}} \le \frac{{N_{{{\text{WSP}}}}^{{}} }}{{N_{{\tilde{F}}} }} = \hat{\varepsilon }_{{\tilde{F}}} ,$$
(34)

and the error limit \(\hat{\varepsilon }_{{\tilde{F}}}\) on the right hand has two normal variables. At a confidence level \(1 - \alpha\), the confidence interval is given as:

$$\hat{\varepsilon }_{{\tilde{F}}} \in \left[ {F^{{ - 1}} \left( {\frac{\alpha }{2}} \right),F^{{ - 1}} \left( {1 - \frac{\alpha }{2}} \right)} \right],$$
(35)

in which \(F^{{ - 1}} \left( \cdot \right)\) is the inverse CDF of \(\hat{\varepsilon }_{{\tilde{F}}}\). It is hard to obtain the confidence interval in an analytic way. MCS can be utilized instead. The upper bound of \(\hat{\varepsilon }_{{\tilde{F}}}\) can be estimated by the following procedures [51].

(A1) Generate \(N_{\varepsilon }\) independently and identically distributed samples for \(N_{{{\text{WSP}}}}^{{}}\) and \(N_{{\tilde{F}}}^{{}}\).

(A2) Calculate \(\hat{\varepsilon }_{{\tilde{F}}}^{{\left( i \right)}}\) \(\left( {i = 1, \ldots ,N_{\varepsilon } } \right)\) at the samples of \(N_{{{\text{WSP}}}}^{{}}\) and \(N_{{\tilde{F}}}^{{}}\).

(A3) Sort \(\hat{\varepsilon }_{{\tilde{F}}}^{{\left( i \right)}}\) from the smallest to the largest. Let \(\hat{\varepsilon }_{{s:l}}^{{\left( i \right)}}\) \(\left( {i = 1, \ldots ,N_{\varepsilon } } \right)\) be the sorted values. And the upper bound of confidence interval can be estimated as

$$\bar{\varepsilon }_{{\tilde{F}}}^{{}} = \hat{\varepsilon }_{{s:l}}^{{\left( {N_{\alpha } } \right)}} ,$$
(36)

and there is

$$N_{\alpha } = \left\lfloor {N_{\varepsilon } \left( {1 - \frac{\alpha }{2}} \right)} \right\rfloor ,$$
(37)

in which \(\left\lfloor \cdot \right\rfloor\) is the ceiling (or round-up) function.

In theory, if \(\bar{\varepsilon }_{{\tilde{F}}}^{{}}\) is smaller than a prescribed threshold \(\gamma\), i.e., \(\bar{\varepsilon }_{{\tilde{F}}}^{{}} \le \gamma\), the learning process can be stopped. However, it should be reminded that the correlation among \(G_{P} \left( {{\mathbf{x}}^{{\left( i \right)}} } \right)\left( {i = 1,2, \ldots ,N_{{{\text{MC}}}} } \right)\) is neglected. If the correlation is considered, \(N_{{{\text{WSP}}}}^{{}}\) and \(N_{{\tilde{F}}}^{{}}\) in distribution “asymptotically” converge to normal distribution as \(N_{{{\text{MC}}}} \to \infty\) [10, 52]. This means the estimator in Eq. (36) is a little biased. Therefore, a more conservative criterion is utilized in this paper. At the kth iteration, the stopping condition is given as:

$$\sum\limits_{{l = \left( {k - N_{r} + 1} \right)}}^{k} {I\left[ {\bar{\varepsilon }_{{\tilde{F}}}^{{\left( l \right)}} \le \gamma } \right]} = N_{r} ,$$
(38)

in which \(N_{r}\) is a constant and \(k \ge N_{r}\); \(\bar{\varepsilon }_{{\tilde{F}}}^{{\left( l \right)}}\) is the value of \(\bar{\varepsilon }_{{\tilde{F}}}^{{}}\) in the lth iteration. If Eq. (38) is satisfied, it means \(\bar{\varepsilon }_{{\tilde{F}}}^{{}}\) has been consistently smaller than \(\gamma\) during the last \(N_{r}\) iterations and the estimated error is very stable. In this paper, \(\gamma = 2\%\) and \(N_{r} = 5\) are used.

5 Summary of ALK-Pfst

The flowchart of the proposed method is shown in Fig. 1, and the concrete procedures are explained as follows.

  1. (B1)

    Generate \(N_{{{\text{MC}}}}\) samples for \({\mathbf{x}}\) and \(\lambda\).

  2. (B2)

    Define the initial DoE.

    1. 1.

      The number of initial training points is defined 12. The number should be enlarged for high-dimensional problems.

    2. 2.

      Latin hypercube sampling is utilized to generate those training points. The lower and upper bounds are chosen as \(\left[ {\varvec{\mu }}_{X} - 5{\varvec{\sigma }}_{X} {\text{, }}{\varvec{\mu} }_{X} + 5{\varvec{\sigma }}_{X} \right]\) with \({\varvec{\mu }}_{X}\) and \({\varvec{\sigma }}_{X}\) the mean and standard variation of \({\mathbf{x}}\).

    3. 3.

      Evaluate the performance function at those points and construct an initial Kriging model with the DoE.

  3. (B3)

    Obtain the optimal training point by Eq. (21).

  4. (B4)

    According to the prediction information of Kriging model, obtain the distributions of \(N_{{{\text{WSP}}}}^{{}}\) and \(N_{{\tilde{F}}}^{{}}\).

  5. (B5)

    Based on the procedures in (A1)– (A3), obtain the upper bound of \(\hat{\varepsilon }_{{\tilde{F}}}\) in the current stage.

  6. (B6)

    If the stopping condition in Eq. (38) is satisfied, continue to Step (B8). Otherwise, evaluate the performance function at \({\mathbf{x}}^{{\left( * \right)}}\). Add \({\mathbf{x}}^{{\left( * \right)}}\) into the DoE and update the Kriging model. Go to Step (B3).

  7. (B7)

    Estimate the profust failure probability based on the Kriging model.

Fig. 1
figure 1

Flowchart of ALK-Pfst

Full size image

6 Numerical examples

6.1 A mathematical problem

The first example has four unconnected failure regions and it is employed to demonstrate the performance of ALK-Pfst for problems with multiple failure regions. The performance function is defined as

$$G\left( {\mathbf{x}} \right) = \min \left\{ \begin{gathered} 3 + \frac{{\left( {x_{1} - x_{2} } \right)^{2} }}{{10}} \pm \frac{{\left( {x_{1} - x_{2} } \right)}}{{\sqrt 2 }} \hfill \\ \frac{7}{{\sqrt 2 }} \mp \left( {x_{1} - x_{2} } \right) \hfill \\ \end{gathered} \right.,$$
(39)

in which \({\mathbf{x}} = \left[ {x_{1} ,x_{2} } \right]\) are two independent random variables obeying the standard normal distribution. Fuzzy failure state is assumed and is described by a linear membership function (as shown in Eq. (2)) with parameters a1 = − 0.1, a2 = 0.

The results of different methods are given in Table 1. The results of DS-AK and AK-MCS are duplicated from [46]. The proposed method is performed 20 times and the data are averaged results. It can be seen that the proposed method is more efficient than other methods. Note that the number of candidate points of the proposed method is kept the same as MCS. The Cov of ALK-Pfst (3.28%) is a little larger than DS-AK and AK-MCS while it is acceptable in practice.

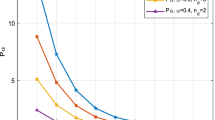
Table 1 Results of different methods (Sect. 5.1)
Full size table

To demonstrate the robustness of ALK-Pfst, the efficiency and accuracy varying with the prescribed error threshold \(\gamma\) is illustrated by boxplots (Fig. 2). At each value of \(\gamma\), ALK-Pfst is tested 20 independent times. The best, mean, and worst performances of the proposed method can be clearly seen in the figure. Generally, along with the decreasing of \(\gamma\), the number of function evaluations increases and the accuracy becomes higher. The proposed method is quite robust if \(\gamma\) is set as 2%.

Fig. 2
figure 2

Boxplots of true relative error and Ncall VS error threshold γ (Example 5.1)

Full size image

Also note that learning function U can also be utilized in ALK-Pfst. However, U is not robust which may cause the early stop of learning process. In one test, learning function U is utilized in the ALK-Pfst method and the comparison of training points obtained by U and ERF is given in Fig. 3. It can be seen that the boundary of failure and safety has four branches and the upper left one is coarsely approximated by U. This may be because rare initial training points are placed around the upper left branch. U is too local which tends to find new training points around existing training points. In contrast, all the four branches are finely approximated by the modified ERF in this test. The modified ERF is more robust than U and is more proper to ALK-Pfst.

Fig. 3
figure 3

DoE of training points obtained by U and modified ERF in an extreme situation

Full size image

According to the membership function, the region in which \(G\left( {\mathbf{x}} \right) > 0\) is the totally safe region, the region in which \(G\left( {\mathbf{x}} \right) < - 0.1\) is the complete failure region and the region where \(- 0.1 \le G\left( {\mathbf{x}} \right) \le 0\) is the fuzzy failure region. As shown in Fig. 3, the region bounded by \(G\left( {\mathbf{x}} \right) + 0.1 = 0\) and \(G\left( {\mathbf{x}} \right) = 0\) is the fuzzy failure region. The existence of fuzzy failure region is the main difference between the profust RA and the traditional RA. If the fuzzy failure region is ignored and treated as the failure region, the failure probability of \(G\left( {\mathbf{x}} \right) < 0\) calculated by MCS will be 0.0022. That is larger than the profust failure probability.

6.2 A nonlinear oscillator

The second example is a nonlinear oscillator taken from [46, 53]. Several methods have been used to solve this problem. The performance of the proposed method is compared with other methods to show its advantage. The performance function is defined as:

$$G\left( {\mathbf{x}} \right) = 3r - \left| {\frac{{2F_{1} }}{{m\omega _{0}^{2} }}\sin \left( {\frac{{\omega _{0}^{2} t_{1} }}{2}} \right)} \right|,$$
(40)

where \(\omega _{0} = \sqrt {\left( {w_{1} + w_{2} } \right)/m}\). Six variables exist in this example and they are given in Table 2. The membership function of the failure state is assumed as the Cauchy form with parameters \(c_{1} = - 0.1\) and \(c_{2} = 0.001\).

Table 2 Random variables of the nonlinear oscillator
Full size table

The results of different methods are given in Table 3. Again, it can be seen that the proposed method is apparently more efficient than other methods in this example. Only about 35 function evaluations are cost while very accurate results are obtained by ALK-Pfst. Although the performance function is very simple, DS-AK and AK-MCS#2 need quite a lot of function calls. That is because they should approximate the boundary of failure and safety at different thresholds. With the same size of candidate points, about 20 more function evaluations are needed by AK-MCS#1 than ALK-Pfst. That is because the stopping condition of AK-MCS#1 is very conservative.

Table 3 Results of the nonlinear oscillator with different methods
Full size table

The learning processes of ALK-Pfst and AK-MCS#1 are given in Fig. 4. It can be seen that along with the absorption of new training points, the prediction accuracy of both methods is improved. However, after absorbing 20 ones, little improvement occurs. However, AK-MCS#1 continues learning and a quantity of training points are added. The prediction error estimated by Eq. (36) during the learning process is given in Fig. 4. It can be seen that the proposed technique properly estimates the error of Kriging model. Aided by the error estimated technique, the proposed method timely terminates the learning process and only several additional points are added.

Fig. 4
figure 4

Evolution of predicted failure probability and estimated error (Example 5.2)

Full size image

Also note that randomness exists in the proposed method. In addition, the parameter of prescribed error threshold γ will influent the accuracy and efficiency of the proposed method. To demonstrate the robustness and variation, the performance variation of 20 runs along with different error thresholds is offered in Fig. 5. In this figure, the information on the mean and worst accuracy (efficiency) can be obtained. It can be seen that, the efficiency will degenerate if the stopping condition becomes stricter. In general, the estimated error is smaller than the true error. However, the fact reverses sometimes in the worst case. Therefore, it is recommended to set the error threshold as a little small for conservation.

Fig. 5
figure 5

Boxplots of true relative error and Ncall VS error threshold γ (Example 5.2)

Full size image

6.3 A creep–fatigue failure problem

The third example is obtained from [42]. The proposed method is compared with methods in [42] in efficiency and accuracy. The performance function in this example describes the creep- and fatigue behaviors of a material. It is obtained from fitting the experimental data which is given as[42, 54]

$$G\left( {\mathbf{x}} \right) = 2 - \exp \left( { - \theta _{1} D_{{\text{c}}} } \right) + \frac{{\exp \left( {\theta _{1} } \right) - 2}}{{\exp \left( { - \theta _{2} } \right) - 1}}\left( {\exp \left( { - \theta _{2} D_{{\text{c}}} } \right) - 1} \right) - D_{{\text{f}}} ,$$
(41)

where \(D_{{\text{c}}}\) is the amount of creep damage and \(D_{{\text{f}}}\) is that of fatigue damage; \(\theta _{1}\) and \(\theta _{2}\) are parameters which can be obtained by experimental data. Only one level of creep and fatigue loading is assumed in this example. Therefore, the damage can be computed by

$$D_{{\text{c}}} = \frac{{n_{{\text{c}}} }}{{N_{{\text{c}}} }},$$
(42)

in which \(n_{{\text{c}}}\) is the number of creep loading cycles and \(N_{{\text{c}}}\) is the total number of cycles to creep failure at the creep loading level. Similarly, the fatigue damage can be obtained by

$$D_{{\text{f}}} = \frac{{n_{{\text{f}}} }}{{N_{{\text{f}}} }},$$
(43)

in which \(n_{{\text{f}}}\) is the number of fatigue loading cycles and \(N_{{\text{f}}}\) is the total number of cycles to fatigue failure at the fatigue loading level. Six random variables exist in this example, and they are given in Table 4. The failure state is assumed to be fuzzy. Three kinds of membership functions are considered, as shown in Table 5.

Table 4 Random variables of the creep–fatigue failure problem
Full size table
Table 5 Results of Example 5.3 with different methods
Full size table

The results of different methods are given in Table 5. ALK-Pfst is performed 10 times and average results are listed in this table. Advanced sampling methods, i.e., SS and IS, offers very accurate results with fewer function evaluations than MCS. In addition, the proposed method is remarkably more efficient than other methods. Especially, ALK-Pfst saves 60–150 function evaluations than AK-MCS#1.

In one test of Case 3, ALK-Pfst and AK-MCS#1 are implemented with the same candidate points and initial training points. The varying processes of the predicted \(\tilde{P}_{{\tilde{F}}}\) are given in Fig. 6. It can be seen that both methods in accuracy can converge to the true value along with the involvement of new training points. However, in AK-MCS#1, after the predicted accuracy has been very high, a very large number of redundant training points are involved. In contrast, only several additional training points are added by the proposed method. The evolutionary process of estimated error in the proposed method is also given in the figure. The estimated error gradually becomes smaller and smaller during the process. By monitoring the prediction error of \(\tilde{P}_{{\tilde{F}}}\), the learning process can be timely terminated and a large quantity of function calls can be saved without loss of accuracy.

Fig. 6
figure 6

Evolution of predicted \(\tilde{P}_{{\tilde{F}}}\) and estimated error (Example 5.3)

Full size image

6.4 Engineering application: a missile wing

A missile wing[49], comprising ribs, spars, and skins, is investigated in this example. The performance function is implicit and the finite element software is required to solve it. The application of the proposed method to practical engineering problems can be verified in this example. The detailed geometry and finite element model of the wing are shown in Fig. 7. The Young’s modulus of the skins is 70 GPa and that of the ribs and spars is 120 GPa. The wing is fixed on the main boy of missile by a mount. During cruise of the missile, the upper skin of the wing is subject to a uniform air pressure P. The thicknesses of the skins, the ribs from No. 3 to 5, and the spars are denoted as si (i = 1, 2), ri(i = 3, 4, 5, 6), and ti(i = 1, 2,⋯, 5).

Fig. 7
figure 7

Geometry model and finite element model of the missile wing [49]

Full size image

To maintain the flight accuracy of the missile, the maximum deflection of the wing should not exceed 11 mm according to the design requirement. Therefore, the performance function of this problem is defined as

$$G\left( \user2{x} \right) = 11 - \Delta \left( \user2{x} \right),$$
(44)

in which \(\user2{x = }\left[ {s_{1} ,s_{2} ,r_{3} , \ldots ,r_{6} ,t_{1} , \ldots ,t_{5} ,P} \right]\) is the vector of random variables and \(\Delta\) is the maximum deflection of the wing. Considering that the design requirement—the deflection should not exceed 11 mm—is subjectively prescribed, fuzzy failure state is assumed in this problem. A linear membership functions with parameters a1 = 0 and a2 = 0.1 are used here to describe the failure state. The distributions of the twelve random variables are listed in Table 6.

Table 6 Random variables of the missile wing structure
Full size table

The results of different methods are given in Table 7. Note that, one time of finite element analysis needs about 27 s on a workstation with an Intel® Xeon E5-2650 v4 CPU and 32 GB RAM. Therefore, it is very hard to obtain the true \(\tilde{P}_{{\tilde{F}}}\) by MCS. Therefore, 500 training points uniformly distributed throughout a rather large space are generated and a “global” Kriging model is built to approximate the true performance function. MCS with 105 samples is used to estimate \(\tilde{P}_{{\tilde{F}}}\) based on the global Kriging model. In addition, the solution is regarded as the benchmark of other methods. AK-MCS#1 and ALK-Pfst are run ten independent times, and the average results are outlined in the table. Table 7 shows that both methods have very high accuracy while ALK-Pfst doubles the efficiency compared with AK-MCS#1.

Table 7 Results of Example 5.4 with different methods
Full size table

The traditional RA is also performed based on the global Kriging model. If the epistemic uncertainty in the failure state is ignored, the failure probability will be 0.0107 which is smaller than \(\tilde{P}_{{\tilde{F}}}\) in this example. If the epistemic uncertainty exists while the wing is designed according to the traditional RA, the design may be a little ideal which may not satisfy the requirement of profust RA.

7 Conclusion

Profust RA is researched and a new method based on the ALK model is proposed in this paper. The new method is termed ALK-Pfst. In ALK-Pfst, two main contributions are made: (1) a modified ERF is proposed as the learning function. The new learning function measures the expected risk that Kriging model wrongly predicts the sign of performance function given an arbitrary threshold. The new learning function makes the learning process more robust. (2) The prediction error of profuse failure probability is deduced based on the Kriging prediction information and the Central Limit Theorem. With the prediction error, the accuracy of Kriging model can be monitored in real time and the learning process can be timely stopped.

Four examples are utilized to investigate the performance of the proposed method and other state-of-the-art methods. The results validate the efficiency and robustness of ALK-Pfst outperform other methods with little loss of accuracy. However, it should be noted that high-dimensional problems and problems with small failure probabilities are not tested in this paper. For high-dimensional problems, exploring the optimal parameters of Kriging model by a global optimization algorithm will take a long time [55]. For problems with small failure probabilities, Kriging model should make predictions at a large population of candidate samples [49], which is also pretty time demanding. To overcome those problems, the fusion of the ALK model with dimensionality reduction techniques [55] and importance sampling methods [49] will be our future research emphases.