An efficient Kriging-based subset simulation method for hybrid reliability analysis under random and interval variables with small failure probability

Abstract

This paper proposes an efficient Kriging-based subset simulation (KSS) method for hybrid reliability analysis under random and interval variables (HRA-RI) with small failure probability. In this method, Kriging metamodel is employed to replace the true performance function, and it is smartly updated based on the samples in the first and last levels of subset simulation (SS). To achieve the smart update, a new update strategy is developed to search out samples located around the projection outlines on the limit-state surface. Meanwhile, the number of samples in each level of SS is adaptively adjusted according to the coefficients of variation of estimated failure probabilities. Besides, to quantify the Kriging metamodel uncertainty in the estimation of the upper and lower bounds of the small failure probability, two uncertainty functions are defined and the corresponding termination conditions are developed to control Kriging update. The performance of KSS is tested by four examples. Results indicate that KSS is accurate and efficient for HRA-RI with small failure probability.

1 Introduction

Hybrid reliability analysis under both aleatory and epistemic uncertainties has attracted great attention over the past two decades (Zhang and Huang 2010; Liu et al. 2017; Brevault et al. 2016; Jiang et al. 2018; Alvarez et al. 2018; Wang et al. 2018a, b). Generally, the classical probability theory is often employed to quantify aleatory uncertainty while epistemic uncertainty is described by some other methods, such as possibility theory (Mourelatos and Zhou 2005), probability box (Jiang et al. 2012), evidence theory (Jiang et al. 2013; Li et al. 2013; Xiao et al. 2015; Zhang et al. 2015, 2018b), and interval theory (Du et al. 2005; Guo and Du 2009; Wu et al. 2013; Wang et al. 2016, 2017; Jiang et al. 2018). In practical engineering, a structure is fortunately designed with codified rules leading to a large safety margin, which means that failure is a small probability event (Echard et al. 2013). In reliability analysis with small failure probability, the sample populations generated by the simulation methods, such as Monte Carlo simulation (MCS), need to be very large, which leads to huge computational burden in terms of the evaluations of true performance functions, especially when the true performance functions involve expensive and time-consuming computer simulation codes. Therefore, assessing small failure probabilities (lower than 10⁻³) (Balesdent et al. 2013) is quite a challenging task (Lelièvre et al. 2018). In this paper, hybrid reliability analysis under both aleatory and epistemic uncertainties with small failure probability is investigated, in which aleatory and epistemic uncertainties are quantified by probability theory and interval theory, respectively.

Specifically, in hybrid reliability analysis under random and interval variables (HRA-RI), the failure probability P_f is an interval value due to the existence of interval variables. The upper and lower bounds of P_f can be respectively estimated by Du (2008):

$$ {P}_f^U=P\left(\underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min }G\left(\mathbf{X},\mathbf{Y}\right)\le 0\right) $$

(1)

$$ {P}_f^L=P\left(\underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\max }G\left(\mathbf{X},\mathbf{Y}\right)\le 0\right) $$

(2)

where G(X,Y) is the performance function with a vector of random variables $X={\left[{x}_1,{x}_2,...,{x}_{n_x}\right]}^{\mathrm{T}}$ and a vector of interval variables $Y={\left[{y}_1,{y}_2,...,{y}_{n_y}\right]}^{\mathrm{T}}$. P(∙) represents the probability of an event. ${P}_f^U$ is the upper bound of the failure probability related to the minimum value of the performance function in terms of interval variables. ${P}_f^L$ is the lower bound of the failure probability corresponding to the maximum value of the performance function in terms of interval variables. Y^L and Y^U are the lower and upper bounds of interval variables, respectively.

For HRA-RI, some methods have been developed to estimate the upper and lower bounds of the failure probability. MCS is a basic sampling method and easy to implement. However, a large number of calls to the actual performance function are required when MCS is utilized to deal with reliability analysis problems, especially in cases with small failure probabilities. Unified uncertainty analysis (UUA) method based on the first-order reliability method (FORM), termed as the FORM-UUA method (Du 2008), can be employed to evaluate the upper and lower bounds of the failure probability in HRA-RI. In terms of calculation efficiency, FORM-UUA shows greater advantages in cases with small failure probabilities compared with MCS. However, the application of FORM-UUA is limited by FORM, which may generate unstable and unacceptable results for reliability analysis problems with highly nonlinear performance functions or multiple design points (Yang et al. 2015).

To alleviate the computational burden in reliability analysis by MCS, advanced variance reduction-based simulation methods, such as importance sampling (IS) and subset simulation (SS), are adopted to reduce the total number of samples involved in MCS for accurate estimation of the upper and lower bounds of the failure probability. SS is a well-known and efficient method for reliability analysis, especially for estimating small failure probabilities. Alvarez et al. (2018) developed a combination method of SS and random set theory to estimate the upper and lower bounds of the failure probability. However, this method still needs a large computational effort when handling practical problems with time-consuming performance functions.

Up to now, metamodel techniques have been extensively employed in reliability analysis to reduce the computational cost (Shan and Wang 2006; Basudhar and Missoum 2010; Picheny et al. 2010; Zhu and Du 2016; Sadoughi et al. 2018). However, a majority of metamodel-assisted techniques handle reliability analysis only with random variables and their applications to HRA-RI are few. For HRA-RI, Yang et al. (2015) proposed an efficient method based on an active learning Kriging metamodel and MCS, in which Kriging metamodel is built to replace the performance function with locally refining the limit-state surface by adding update training points in its vicinity. To refine the limit-state surface in HRA-RI, Brevault et al. (2016) developed a modification of the generalized max–min method to search out update points for refining Kriging metamodel. Though well approximating the limit-state surface can obtain accurate estimation of the upper and lower bounds of failure probability, it is determined that projection outlines on the limit-state surface are crucial rather than the whole limit-state surface in HRA-RI (Zhang et al. 2018a). Compared with the whole limit-state surface, the region of projection outlines is much smaller. Hence, refining the whole limit-state surface may cause unnecessary computational cost. With refining the projection outlines, an efficient projection outline-based active learning method combined with Kriging and MCS is proposed for HRA-RI. Though this method is successfully employed in HRA-RI and the computational cost can be reduced, a large number of samples are involved in MCS to estimate the upper and lower bounds of failure probability, which could provoke computer memory problems. Especially, in cases with small failure probabilities, the sample populations need to be very large (Lelièvre et al. 2018), which will incur greater computational burden. This drawback of the method limits its applications in the cases with small failure probabilities.

As mentioned above, relatively fewer samples are involved in reliability analysis to estimate small failure probabilities by SS compared with MCS; meanwhile, the metamodel-assisted techniques can alleviate the computational burden by substituting easy-to-evaluate mathematical functions for expensive simulation-based models. Thus, an efficient Kriging-based subset simulation (KSS) method is proposed in this paper. In KSS, the performance function is replaced by Kriging metamodel, which is constructed by using initial design of experiments (DoE) and then smartly refined based on the samples in the first and last levels of SS. Because candidate samples in the first level of SS are distributed in the whole random variable space, Kriging update based on these samples has high contribution to the exploration of failure domain. On the other hand, samples in the last level of SS are located around the separation surface between the failure and safety domains. Hence, the Kriging update based on these samples benefits the exploitation of failure domain. To achieve the above update, a new update strategy is developed to search out samples located around the projection outlines on the limit-state surface from those in the first and last levels of SS. Meanwhile, the number of samples in each level of SS is adaptively adjusted according to the coefficients of variation of estimated ${P}_f^U$ and ${P}_f^L$. Besides, in consideration of the influence of metamodel uncertainty (Apley et al. 2006; An and Choi 2012; Zhang et al. 2013; Wang and Wang 2014) on estimation of ${P}_f^U$ and ${P}_f^L$, two uncertainty functions are defined and new termination conditions are developed for Kriging update. Four examples are presented to test the performance of KSS.

The remainder of this paper is outlined as follows. The subset simulation method is introduced in Section 2. In Section 3, a new update strategy, termination conditions of Kriging update, and the proposed KSS method for HRA-RI with small failure probability are elaborated. Four examples are employed to test the proposed KSS method in Section 4. Section 5 provides the conclusions and future work.

2 Subset simulation method

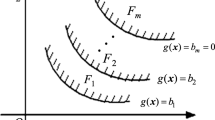
In HRA-RI, for the upper bound of the failure probability, the failure domain can be described as ${F}^U=\left\{\mathbf{X}|\underline{g}\left(\mathbf{X}\right)\le 0\right\}$ and the safe domain is ${S}^U=\left\{\mathbf{X}|\underline{g}\left(\mathbf{X}\right)>0\right\}$, where $\underline{g}\left(\mathbf{X}\right)$ is calculated by (3). The separation surface between F^U and S^U can be represented by $\underline{g}\left(\mathbf{X}\right)=0$. Similarly, for the lower bound of the failure probability, the failure and safe domains are ${F}^L=\left\{\mathbf{X}|\overline{g}\left(\mathbf{X}\right)\le 0\right\}$ and ${S}^L=\left\{\mathbf{X}|\overline{g}\left(\mathbf{X}\right)>0\right\}$, where $\overline{g}\left(\mathbf{X}\right)$ is evaluated by (4). The separation surface between F^L and S^L is $\overline{g}\left(\mathbf{X}\right)=0$. Figure 1 schematically displays the failure domains for the upper and lower bounds of the failure probability.

$$ \underline{g}\left(\mathbf{X}\right)=\underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min }G\left(\mathbf{X},\mathbf{Y}\right) $$

(3)

$$ \overline{g}\left(\mathbf{X}\right)=\underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\max }G\left(\mathbf{X},\mathbf{Y}\right) $$

(4)

Fig. 1

Failure regions in the design space of two random variables

The basic idea of SS is that a rare failure event with a small probability is expressed as a sequence of multiple intermediate failure events with larger probabilities. Taking the upper bound of the failure probability in HRA-RI as an example, the application of SS will be introduced in the following sections.

2.1 Principle of SS

In SS, the failure event E^U is expressed as a sequence of multiple intermediate failure events ${E}_i^U\left(i=1,2,\dots, \overline{m}\right)$, where $\overline{m}$ denotes the number of simulation levels in SS. These intermediate failure events ${E}_i^U$ are defined by a series of threshold values ${b}_i^U$, which are formulated as:

$$ {E}_i^U=\left\{\underline{g}\left(\mathbf{X}\right)\le {b}_i^U\right\},\kern0.5em i=1,2,\dots, \overline{m} $$

(5)

These threshold values and intermediate failure events should satisfy the following conditions:

$$ {b}_1^U>{b}_2^U>\cdots >{b}_{\overline{m}}^U=0 $$

(6)

$$ {E}_1^U\supset {E}_2^U\supset \cdots \supset {E}_{\overline{m}}^U={E}^U $$

(7)

where ${b}_i^U\left(i=1,2,\dots, \overline{m}-1\right)$ are adaptively determined in SS.

Then, the upper bound of the failure probability can be estimated by using the product of conditional probabilities $P\left({E}_i^U|{E}_{i-1}^U\right)$ and $P\left({E}_1^U\right)$ in (8).

$$ {P}_f^U=P\left({E}_{\overline{m}}^U\right)=P\left({E}_1^U\right)\prod \limits_{i=2}^{\overline{m}}P\left({E}_i^U|{E}_{i-1}^U\right) $$

(8)

Define ${P}_1^U=P\left({E}_1^U\right)$ and ${P}_i^U=P\left({E}_i^U|{E}_{i-1}^U\right)$ (i = 2, 3,…,$\overline{m}$). The upper bound of the failure probability in (8) can be rewritten as:

$$ {P}_f^U=\prod \limits_{i=1}^{\overline{m}}{P}_i^U $$

(9)

${P}_1^U$ in the first level of SS is evaluated by MCS, i.e.,

$$ {P}_1^U\approx {\widehat{P}}_1^U=\frac{1}{N_1^U}\sum \limits_{k=1}^{N_1^U}{I}_1^U\left({\mathbf{X}}_k^{(1)}\right) $$

(10)

where ${\mathbf{X}}_k^{(1)}\ \left(k=1,2,\dots, {N}_1^U\right)$ are independent and identically distributed samples generated based on the joint probability density function (PDF). ${I}_1^U\left({\mathbf{X}}_k^{(1)}\right)$ is the intermediate failure indicator function as:

$$ {I}_1^U\left({\mathbf{X}}_k^{(1)}\right)=\Big\{1,\kern0.87em \underline{g}\left({\mathbf{X}}_k^{(1)}\right)\le {b}_1^U0,\kern0.62em \underline{g}\left({\mathbf{X}}_k^{(1)}\right)>{b}_1^U $$

(11)

To assess the conditional probability ${P}_i^U\left(i=2,3,\dots, \overline{m}\right)$ in the ith level of SS, Markov chain Monte Carlo (MCMC) can be employed. In this study, modified Metropolis-Hastings (MMH) (Au and Wang 2014) is used to implement the MCMC. The ${P}_i^U\left(i=2,3,\dots, \overline{m}\right)$ can be calculated by:

$$ {P}_i^U\approx {\widehat{P}}_i^U=\frac{1}{N_i^U}\sum \limits_{k=1}^{N_i^U}{I}_i^U\left({\mathbf{X}}_k^{(i)}\right),\kern0.36em i=2,3,...,\overline{m} $$

(12)

where ${\mathbf{X}}_k^{(i)}\ \left(k=1,2,\dots, {N}_i^U,i=2,3,\dots, \overline{m}\right)$ are MCMC samples obtained according to the conditional PDF $q\left(\mathbf{X}|{F}_{i-1}^U\right)={I}_{i-1}^U\left(\mathbf{X}\right)f\left(\mathbf{X}\right)/P\left({F}_{i-1}^U\right)$. The indicator function ${I}_i^U\left({\mathbf{X}}_k^{(i)}\right)$ is represented as:

$$ {I}_i^U\left({\mathbf{X}}_k^{(i)}\right)=\Big\{1,\kern0.62em \underline{g}\left({\mathbf{X}}_k^{(i)}\right)\le {b}_i^U0,\kern0.62em \underline{g}\left({\mathbf{X}}_k^{(i)}\right)>{b}_i^U,\kern0.75em i=2,3,...,\overline{m} $$

(13)

In practice, the value of ${P}_i^U\left(i=1,2,\dots, \overline{m}-1\right)$ is usually set as a fixed conditional probability p₀. It is demonstrated that choosing any p₀∈[0.1, 0.3] will have the similar computational efficiency (Zuev et al. 2012). Thus, in this paper, p₀ is set to 0.1. Then, the conditional probability ${\widehat{P}}_{\overline{m}}^U$ is not less than 0.1. Thresholds ${b}_i^U\left(i=1,2,\dots, \overline{m}-1\right)$ will be adaptively evaluated based on the fixed p₀. The upper bound of the failure probability in (9) can be rewritten as:

$$ {P}_f^U\approx {\widehat{P}}_f^U={p}_0^{\overline{m}-1}{\widehat{P}}_{\overline{m}}^U={p}_0^{\overline{m}-1}\frac{1}{N_{\overline{m}}^U}\sum \limits_{k=1}^{N_{\overline{m}}^U}{I}_{\overline{m}}^U\left({\mathbf{X}}_k^{\left(\overline{m}\right)}\right) $$

(14)

2.2 Statistical property of SS

According to the reference Au and Beck (2001), the coefficient of variation of ${P}_1^U=P\left({E}_1^U\right)$ in the first level of SS is calculated by ${\delta}_1^U=\sqrt{\left(1-{P}_1^U\right)/{P}_1^U{N}_1^U}$. The coefficient of variation of ${P}_i^U$ in the ith level of SS (i = 2, 3,…,$\overline{m}$) is evaluated by:

$$ {\delta}_i^U=\sqrt{\frac{1-{P}_i^U}{P_i^U{N}_i^U}\left(1+{\gamma}_i^U\right)},i=2,3,\dots, \overline{m} $$

(15)

$$ {\gamma}_i^U=2\sum \limits_{k=1}^{N_i^U/{N}_{ci}^U-1}\left(1-\frac{k{N}_{ci}^U}{N_i^U}\right){\rho}_i^U(k) $$

(16)

in which ${N}_{ci}^U$ is the number of initial samples in MCMC, and ${\rho}_i^U(k)$ is the correlation coefficient. The coefficient of variation of ${P}_f^U$ can be calculated by:

$$ \delta \left({P}_f^U\right)=\sqrt{\sum \limits_{i=1}^{\overline{m}}{\left({\delta}_i^U\right)}^2} $$

(17)

Similarly, when the lower bound of the failure probability ${P}_f^L$ is estimated by SS, the corresponding coefficient of variation can be evaluated by:

$$ \delta \left({P}_f^L\right)=\sqrt{\sum \limits_{i=1}^{\underset{\_}{m}}{\left({\delta}_i^L\right)}^2} $$

(18)

where $\underline{m}$ is the number of simulation levels in SS for estimation of ${P}_f^L$. ${\delta}_i^L$ is the coefficient of variation of the conditional probability ${P}_i^L$ in the ith simulation level of SS.

3 The proposed method: Kriging-based subset simulation

The concept of projection outlines on the limit-state surface is first proposed in reliability analysis by Zhang et al. (2018a), which can be respectively represented by point sets shown as follows:

$$ \left\{\left({\mathbf{X}}^{\prime },{\mathbf{Y}}^{\prime}\right)\ |\ G\left({\mathbf{X}}^{\prime },{\mathbf{Y}}^{\prime}\right)=0\kern0.37em \mathrm{and}\kern0.5em {\mathbf{Y}}^{\prime }=\arg \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min }G\left({\mathbf{X}}^{\prime },\mathbf{Y}\right)\right\} $$

(19)

$$ \left\{\left({\mathbf{X}}^{{\prime\prime} },{\mathbf{Y}}^{{\prime\prime}}\right)\ |\ G\left({\mathbf{X}}^{{\prime\prime} },{\mathbf{Y}}^{{\prime\prime}}\right)=0\kern0.37em \mathrm{and}\kern0.5em {\mathbf{Y}}^{{\prime\prime} }=\arg \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\max }G\left({\mathbf{X}}^{{\prime\prime} },\mathbf{Y}\right)\right\} $$

(20)

The relationship between projection outlines and the failure probability in HRA-RI has been illustrated in Zhang et al. (2018a). Namely, if the projection outlines in (19) and (20) are accurately approximated by a metamodel, the upper and lower bounds of the failure probability can be accurately assessed. The detailed introduction can be referred to (Zhang et al. 2018a).

In this paper, the Kriging metamodel is employed to approximate the actual performance function. A new update strategy is developed for refining Kriging. Meanwhile, two uncertainty functions are defined to quantify the influence of Kriging metamodel uncertainty on the estimation of the upper and lower bounds of failure probability by SS. Accordingly, the new termination conditions of Kriging update are developed. Based on the new update strategy and termination conditions, a Kriging-based subset simulation method, termed as KSS, is proposed to evaluate the upper and lower bounds of small failure probability in HRA-RI.

3.1 Update strategy of Kriging metamodel

With the substitution of the performance function by a Kriging metamodel, the upper bound of the failure probability in (1) can be represented as:

$$ {P}_f^U=\iint \cdots \int {\widehat{I}}_F^U\left(\mathbf{X}\right)f\left(\mathbf{X}\right)d\mathbf{X} $$

(21)

where ${\widehat{I}}_F^U\left(\mathbf{X}\right)$ is the failure indicator function associated with the minimum response of the approximate performance function by the Kriging metamodel. It can be expressed by:

$$ {\widehat{I}}_F^U\left(\mathbf{X}\right)=\Big\{{\displaystyle \begin{array}{l}1,\kern0.62em \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min}\widehat{G}\left(\mathbf{X},\mathbf{Y}\right)\le 0\\ {}0,\kern0.62em \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min}\widehat{G}\left(\mathbf{X},\mathbf{Y}\right)>0\end{array}} $$

(22)

Given a set Ω^U with a large number of random variable samples ${\mathbf{X}}_i^U$ (i = 1, 2,…, N^U), the value of $\widehat{G}\left({\mathbf{X}}_i^U,{\mathbf{Y}}_i^U\right)$ requires to be evaluated in order to calculate the value of ${\widehat{I}}_F^U\left({\mathbf{X}}_i^U\right)$, where ${\mathbf{Y}}_i^U$ can be solved by:

$$ {\mathbf{Y}}_i^U=\arg \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min}\widehat{G}\left({\mathbf{X}}_i^U,\mathbf{Y}\right) $$

(23)

The above minimization problem can be solved by some alternative methods, such as the vertex method, the interior-point algorithm, and the sampling method (Alvarez et al. 2018). The vertex method is efficient for linear performance functions, while calculation error will be caused by the vertex method for highly nonlinear performance functions. The interior-point algorithm may be easily trapped into a local optimal solution. Furthermore, it may be time-consuming if a constrained optimization problem is solved for each random variable sample. In this paper, the sampling method is employed to solve (23) by uniformly sampling 200 points within the range of interval variables.

Using the Kriging metamodel, the probability of making a wrong prediction about the actual sign of $G\left({\mathbf{X}}_i^U,{\mathbf{Y}}_i^U\right)$ is $\varPhi \left(-U\left({\mathbf{X}}_i^U,{\mathbf{Y}}_i^U\right)\right)$, in which Φ(⋅) is the cumulative distribution function of a standard normal distribution. U(⋅) is a learning function formulated as (Echard et al. 2011):

$$ U\left(\mathbf{X},\mathbf{Y}\right)=\frac{\mid \widehat{G}\left(\mathbf{X},\mathbf{Y}\right)\mid }{\sigma_{\widehat{G}}\left(\mathbf{X},\mathbf{Y}\right)} $$

(24)

where ${\sigma}_{\widehat{G}}\left(\mathbf{X},\mathbf{Y}\right)$ is the prediction variance of the Kriging metamodel. It can be seen that the smaller $U\left({\mathbf{X}}_i^U,{\mathbf{Y}}_i^U\right)$ is, the larger the probability of making a wrong prediction about the sign of $G\left({\mathbf{X}}_i^U,{\mathbf{Y}}_i^U\right)$. Hence, in this study, an update point is chosen by minimizing $U\left({\mathbf{X}}_i^U,{\mathbf{Y}}_i^U\right)$. Namely, the update point is defined as:

$$ \left({\mathbf{X}}_{\ast}^U,{\mathbf{Y}}_{\ast}^U\right)=\arg \underset{i=1,2,\dots, {N}^U}{\min }U\left({\mathbf{X}}_i^U,{\mathbf{Y}}_i^U\right) $$

(25)

Based on (24) and (25), the point, which is closer to the approximate limit-state surface $\widehat{G}\left(\mathbf{X},\mathbf{Y}\right)=0$ and has a larger prediction variance, will have more chance to be selected as the update one. Note that the chosen update point satisfies (23). According to the projection outlines described in (19) and (20), the selection of an update point based on (25) actually focuses on the region in the vicinity of the approximate projection outlines on the limit-state surface.

Similarly, the lower bound of the failure probability in (2) can be rewritten as:

$$ {P}_f^L=\iint \cdots \int {\widehat{I}}_F^L\left(\mathbf{X}\right)f\left(\mathbf{X}\right)d\mathbf{X} $$

(26)

where ${\widehat{I}}_F^L\left(\mathbf{X}\right)$ is the failure indicator function related to the maximum response of the approximate performance function by the Kriging metamodel. It is depicted as:

$$ {\widehat{I}}_F^L\left(\mathbf{X}\right)=\Big\{{\displaystyle \begin{array}{l}1,\kern0.62em \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\max}\widehat{G}\left(\mathbf{X},\mathbf{Y}\right)\le 0\\ {}0,\kern0.62em \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\max}\widehat{G}\left(\mathbf{X},\mathbf{Y}\right)>0\end{array}} $$

(27)

Given a set Ω^L with a large number of random variable samples ${\mathbf{X}}_i^L$ (i = 1, 2,…, N^L), it requires to estimate the value of $\widehat{G}\left({\mathbf{X}}_i^L,{\mathbf{Y}}_i^L\right)$ in order to evaluate ${\widehat{I}}_F^L\left({\mathbf{X}}_i^L\right)$, where ${\mathbf{Y}}_i^L$ is calculated by:

$$ {\mathbf{Y}}_i^L=\arg \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\max}\widehat{G}\left({\mathbf{X}}_i^L,\mathbf{Y}\right) $$

(28)

Then, a design point with the minimization of $U\left({\mathbf{X}}_i^L,{\mathbf{Y}}_i^L\right)$ can be chosen as an update one to improve the approximation accuracy of projection outlines on the limit-state surface. The update point is searched out by:

$$ \left({\mathbf{X}}_{\ast}^L,{\mathbf{Y}}_{\ast}^L\right)=\arg \underset{i=1,2,\dots, {N}^L}{\min }U\left({\mathbf{X}}_i^L,{\mathbf{Y}}_i^L\right) $$

(29)

3.2 Termination conditions of Kriging update

In HRA-RI, the conditional probabilities ${P}_{\overline{m}}^U$ and ${P}_{\underline{m}}^L$ in the last level of SS need to be computed and the others are set as the fixed value p₀. When the performance function is substituted by the Kriging metamodel, the influence of metamodel uncertainty on the calculation of the two conditional probabilities needs to be considered. To quantify this influence, two uncertainty functions under random and interval variables are developed for the estimation of the upper and lower bounds of the failure probability by SS.

For the condition probability ${\widehat{P}}_{\overline{m}}^U$ in the estimation of ${P}_f^U$, the uncertainty function is defined as:

$$ {\mathrm{UF}}^U=\int \varPhi \left(-U\left(\mathbf{X},{\mathbf{Y}}^U\right)\right)q\left(\mathbf{X}|{E}_{\overline{m}-1}^U\right)d\mathbf{X},\kern0.37em \mathrm{where}\kern0.37em {\mathbf{Y}}^U=\arg \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min}\widehat{G}\left(\mathbf{X},\mathbf{Y}\right) $$

(30)

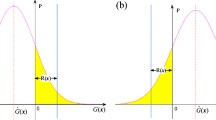
where $q\left(\mathbf{X}|{E}_{\overline{m}-1}^U\right)$ is the conditional PDF of the intermediate failure event ${E}_{\overline{m}-1}^U$. When U(X, Y^U) > 2, the probability of making a wrong prediction on the sign of G(X, Y^U) will be less than Φ(− 2) = 0.0228. Hence, within the domain of {X| U(X, Y^U) > 2}, a high prediction accuracy of the sign of G(X, Y^U) can be ensured (Echard et al. 2011). Then, UF^U can be approximated as:

$$ {\mathrm{UF}}^U=\int R\left(\mathbf{X},{\mathbf{Y}}^U\right)q\left(\mathbf{X}|{E}_{\overline{m}-1}^U\right)d\mathbf{X},\kern0.37em \mathrm{where}\kern0.37em {\mathbf{Y}}^U=\arg \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min}\widehat{G}\left(\mathbf{X},\mathbf{Y}\right) $$

(31)

where R(·) is evaluated by

$$ R\left(\mathbf{X},\mathbf{Y}\right)=\Big\{{\displaystyle \begin{array}{l}\varPhi \left(-U\left(\mathbf{X},\mathbf{Y}\right)\right),U\left(\mathbf{X},\mathbf{Y}\right)\le 2\\ {}0\kern2.28em ,U\left(\mathbf{X},\mathbf{Y}\right)>2\;\end{array}} $$

(32)

Based on samples in the last level of SS, UF^Ucan be calculated by:

$$ {\mathrm{UF}}^U\approx {\widehat{\mathrm{UF}}}^U=\frac{1}{N_{\overline{m}}^U}\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right) $$

(33)

The variance of ${\widehat{\mathrm{UF}}}^U$ is estimated by:

$$ {\displaystyle \begin{array}{l}\operatorname{var}\left({\widehat{\mathrm{UF}}}^U\right)\approx \frac{1}{{\left({N}_{\overline{m}}^U\right)}^2}\operatorname{var}\left(\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)\right)=\frac{1}{N_{\overline{m}}^U}\operatorname{var}\left(R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)\right)\\ {}\approx \frac{1}{N_{\overline{m}}^U}\left(\frac{1}{N_{\overline{m}}^U}\sum \limits_{k=1}^{N_{\overline{m}}^U}{R}^2\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)-{\left(\frac{1}{N_{\overline{m}}^U}\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)\right)}^2\right)\\ {}\kern1.8em <\frac{1}{2{\left({N}_{\overline{m}}^U\right)}^2}\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)\\ {}\kern1.68em \end{array}} $$

(34)

Hence,

$$ \sqrt{\operatorname{var}\left({\widehat{\mathrm{UF}}}^U\right)}<\frac{1}{\sqrt{2}{N}_{\overline{m}}^U}\sqrt{\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)} $$

(35)

According to the central limit theorem (Sun et al. 2017), the following condition will be satisfied, namely:

$$ P\left({\mathrm{UF}}^U<{\widehat{\mathrm{UF}}}^U+1.65\sqrt{\operatorname{var}\left({\widehat{\mathrm{UF}}}^U\right)}\right)\approx 0.95 $$

(36)

The influence of metamodel uncertainty on the estimation of ${\widehat{P}}_{\overline{m}}^U$ is defined as:

$$ \frac{{\mathrm{UF}}^U}{{\widehat{P}}_{\overline{m}}^U}\approx \frac{{\widehat{\mathrm{UF}}}^U}{{\widehat{P}}_{\overline{m}}^U}=\frac{\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)}{N_{\overline{m}}^U{\widehat{P}}_{\overline{m}}^U} $$

(37)

Considering the influence of Kriging uncertainty on the estimation of ${\widehat{P}}_{\overline{m}}^U$, a termination condition of Kriging update is set as:

$$ \frac{{\widehat{\mathrm{UF}}}^U}{{\widehat{P}}_{\overline{m}}^U}\le {t}^u $$

(38)

where t^u is a prescribed convergence value of ${\widehat{\mathrm{UF}}}^U/{\widehat{P}}_{\overline{m}}^U$.

Based on (35)–(38), it can be derived that:

$$ {\displaystyle \begin{array}{l}\frac{1.65\sqrt{\operatorname{var}\left({\widehat{\mathrm{UF}}}^U\right)}}{{\widehat{P}}_{\overline{m}}^U}<\frac{1.65}{\sqrt{2}{N}_{\overline{m}}^U{\widehat{P}}_{\overline{m}}^U}\sqrt{\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)}\\ {}\kern2.759999em =\frac{1.65}{\sqrt{2}\sqrt{N_{\overline{m}}^U{\widehat{P}}_{\overline{m}}^U}}\sqrt{\frac{\sum \limits_{k=1}^{N_{\overline{m}}^U}R\left({\mathbf{X}}_k^{\left(\overline{m}\right)},{\mathbf{Y}}_k^U\right)}{N_{\overline{m}}^U{\widehat{P}}_{\overline{m}}^U}}\\ {}\kern2.759999em \le \frac{1.65}{\sqrt{2}\sqrt{N_{\overline{m}}^U{\widehat{P}}_{\overline{m}}^U}}\sqrt{t^u}\end{array}} $$

(39)

Then, (40) can be derived from (36) and (39).

$$ P\left(\frac{{\mathrm{UF}}^U}{{\widehat{P}}_{\overline{m}}^U}<\frac{{\widehat{\mathrm{UF}}}^U}{{\widehat{P}}_{\overline{m}}^U}+\frac{1.65}{\sqrt{2}\sqrt{N_{\overline{m}}^U{\widehat{P}}_{\overline{m}}^U}}\sqrt{t^u}\right)>0.95 $$

(40)

Because the conditional probability ${\widehat{P}}_m^U$ ≥ 0.1, when ${N}_{\overline{m}}^U$ in the last level of SS is not less than 10⁴ and stopping condition in (38) is satisfied, (40) can be rewritten as:

$$ P\left(\frac{{\mathrm{UF}}^U}{{\widehat{P}}_{\overline{m}}^U}<{t}^u+0.0369\sqrt{t^u}\right)>0.95 $$

(41)

When t^u is set to 0.05, (41) can be written as (42). It can be observed that a narrow interval can be determined under 95% confidence value when t^u is set to 0.05. Thus, t^u is set to 0.05 in this paper.

$$ P\left(\frac{{\mathrm{UF}}^U}{{\widehat{P}}_{\overline{m}}^U}<0.0583\right)>0.95 $$

(42)

Similarly, the uncertainty function for the condition probability ${\widehat{P}}_{\underset{\_}{m}}^L$ is defined as:

$$ {\mathrm{UF}}^L=\int R\left(\mathbf{X},{\mathbf{Y}}^L\right)q\left(\mathbf{X}|{E}_{\underline{m}-1}^L\right)d\mathbf{X},\mathrm{where}\kern0.37em {\mathbf{Y}}^L=\arg \underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\max}\widehat{G}\left(\mathbf{X},\mathbf{Y}\right) $$

(43)

where $q\left(\mathbf{X}|{E}_{\underline{m}-1}^L\right)$ is the conditional PDF of the intermediate failure event ${E}_{\underline{m}-1}^U$. After setting a prescribed convergence value t^l, a stopping condition of Kriging update during calculating ${\widehat{P}}_{\underline{m}}^L$ in the estimation of ${P}_f^L$ is set as:

$$ \frac{{\mathrm{UF}}^L}{{\widehat{P}}_{\underline{m}}^L}\approx \frac{\sum \limits_{k=1}^{N_{\underline{m}}^L}R\left({\mathbf{X}}_k^{\left(\underline{m}\right)},{\mathbf{Y}}_k^L\right)}{N_{\underline{m}}^L{\widehat{P}}_{\underline{m}}^L}\le {t}^l $$

(44)

In this paper, t^l is also set to 0.05.

3.3 The KSS method

Based on the update strategy and termination conditions for Kriging metamodel, an efficient KSS method is proposed for HRA-RI with small failure probability. In KSS, the Kriging metamodel is first built by using initial design of experiments (DoE) and then smartly updated based on the samples in the first and last levels of SS. In this paper, the toolbox DACE (Lophaven et al. 2002) is employed to build the Kriging metamodel and the first-order polynomial regression model is selected for the Kriging construction. To take the estimation of the upper bound of the small failure probability as an example, the flowchart of KSS is given in Fig. 2, and the procedure is elaborated as follows:

• 1. Generate M^U initial samples in the first level of SS in random variable space. These samples are simulated by MCS according to the joint PDF of random variables. The set of these samples is denoted as ${\varOmega}_{mc}^U$. The number of samples in the first level of SS in random variable space is adaptively added during the procedure. Hence, it is not necessary to assign a very large value to M^U. In this paper, M^U is set to 10⁴.

• 2. Define the initial DoE. Some alternative techniques, such as random sampling and Latin Hypercube Sampling (LHS), can be employed. For random variables, the bounds of the sampling domain are defined as ${F}_i^{-1}\left(\varPhi \left(\pm 5\right)\right)\ \left(i=1,2,...,{n}_x\right)$, where ${F}_i^{-1}\left(\cdot \right)$ is the inverse cumulative distribution function of random variable x_i and n_x is the number of random variables. For interval variables, their intervals are taken as the sampling domain. According to the experience in Echard et al. (2011), the number of points N_i in the initial DoE is set to the maximum value between n_x + n_y + 2 and 12 to build an initial Kriging, where n_x is the number of random variables and n_y is the number of interval variables. The response of the actual performance function is then calculated for each of these points. The iteration information iter is set to 1.

• 3. Establish an initial Kriging metamodel based on the DoE.

• 4. Search out an update point $\left({\mathbf{X}}_{\ast}^U,{\mathbf{Y}}_{\ast}^U\right)$ based on ${\varOmega}_{mc}^U$ and the update strategy in (23)–(25).

• 5. Judge the stopping condition of Kriging update. In consideration of the uncertainty of current Kriging metamodel, based on (38), the stopping condition is defined as:

Fig. 2

KSS flowchart

$$ \frac{{\widehat{\mathrm{UF}}}_{mc}^U}{{\widehat{P}}_f^U}\le {t}^u $$

(45)

where ${\widehat{\mathrm{UF}}}_{mc}^U$ and ${\widehat{P}}_f^U$ are respectively calculated by:

$$ {\widehat{\mathrm{UF}}}_{mc}^U=\frac{1}{N_{mc}^U}\sum \limits_{k=1}^{N_{mc}^U}R\left({\mathbf{X}}_k^U,{\mathbf{Y}}_k^U\right) $$

(46)

$$ {\widehat{P}}_f^U=\frac{1}{N_{mc}^U}\sum \limits_{k=1}^{N_{mc}^U}{I}_F^U\left({\mathbf{X}}_k^U\right) $$

(47)

${\mathbf{X}}_k^U$ (k = 1, 2, …, ${N}_{mc}^U$) denotes the samples in ${\varOmega}_{mc}^U$. ${N}_{mc}^U$ is the total number of samples in ${\varOmega}_{mc}^U$. Note that the above Kriging update is based on the samples in the first level of SS and the ${\widehat{P}}_f^U$ in (47) is not the ultimate output result of KSS. If the condition in (45) is not satisfied, go to the next step; otherwise, go to step 7.

• 6. Rebuild Kriging. The response of the performance function is calculated for the update point $\left({\mathbf{X}}_{\ast}^U,{\mathbf{Y}}_{\ast}^U\right)$ and then DoE is augmented with the data of this update point. Kriging metamodel is rebuilt by using the updated DoE. After that, the procedure goes back to step 4.

• 7. Implement the ith (i = 2, 3,…, $\overline{m}$) level of SS. The current Kriging metamodel is denoted by ${\widehat{G}}^{(0)}$. Because each level of SS has the same number of samples and the number of samples in the first level of SS is ${N}_{mc}^U$, the number of samples ${N}_i^U$ in the ith (i = 2, 3, …, $\overline{m}$) level of SS is equal to ${N}_{mc}^U$. The first threshold b₁ is determined based on all samples in ${\varOmega}_{mc}^U$. Then, the ith (i = 2, 3, …, $\overline{m}$) level of SS is performed based on ${\widehat{G}}^{(0)}$, and the thresholds ${b}_i^U$ (i = 1, 2, …, $\overline{m}$) are recorded. In addition, the set of samples ${\mathbf{X}}_k^{\left(\overline{m}\right)}$ (k = 1, 2, …,${N}_{\overline{m}}^U$) in the last level of SS is denoted as ${\varOmega}_{SS}^U$. The coefficient of variation of ${\widehat{P}}_i^U$ in the ith level of SS (i = 2, 3,…,$\overline{m}$) is evaluated by (15) and (16), and then the coefficient of variation $\delta \left({\widehat{P}}_f^U\right)$ is estimated by (17).

• 8. Identify an update point $\left({\mathbf{X}}_{\ast}^U,{\mathbf{Y}}_{\ast}^U\right)$ based on ${\varOmega}_{SS}^U$ and the update strategy in (23)–(25).

• 9. Judge the stopping condition of Kriging update. To control the influence of metamodel uncertainty on estimation of ${P}_{\overline{m}}^U$, the stopping condition in (38) is employed. If the stopping condition is not satisfied, go to step 10; otherwise, the current Kriging metamodel is denoted as ${\widehat{G}}^{(1)}$, and go to step 11.

• 10. Rebuilt Kriging. The response of the performance function is calculated for the update point $\left({\mathbf{X}}_{\ast}^U,{\mathbf{Y}}_{\ast}^U\right)$ and DoE is augmented with the data of update point. Then, the Kriging metamodel is rebuilt by using the updated DoE. After that, the procedure goes back to step 8.

• 11. Calculate the upper bound of the failure probability and the corresponding coefficient of variation based on sample ${\mathbf{X}}_k^{\left(\overline{m}\right)}$ (k = 1, 2, …, ${N}_{\overline{m}}^U$) and ${\widehat{G}}^{(1)}$. The response of ${\widehat{G}}^{(1)}$ at each ${\mathbf{X}}_k^{\left(\overline{m}\right)}$ is estimated. Then, the upper bound of the failure probability ${P}_f^{U(iter)}$ is calculated by:

$$ {\widehat{P}}_f^{U(iter)}={p}_0^{\overline{m}-1}\frac{1}{N_{\overline{m}}^U}\sum \limits_{k=1}^{N_{\overline{m}}^U}{I}_{\overline{m}}^U\left({\mathbf{X}}_k^{\left(\overline{m}\right)}\right) $$

(48)

where p₀ is fixed conditional probability and set to 0.1 in this work. The coefficient of variation of ${\widehat{P}}_{\overline{m}}^U$ is recalculated based on responses of ${\widehat{G}}^{(1)}$ at ${\mathbf{X}}_k^{\left(\overline{m}\right)}$ (k = 1, 2, …, ${N}_{\overline{m}}^U$), and hence, the coefficient of variation $\delta \left({\widehat{P}}_f^U\right)$ is also recalculated.

• 12. Judge the validity of ${\widehat{P}}_f^U$. Based on the rule of SS, the condition probability ${\widehat{P}}_f^U$ needs to be larger than p₀. In addition, an intermediate failure event should include its latter intermediate failure events. Thus, it is necessary to determine whether ${E}_{\overline{m}}^U=\left\{{\underset{\_}{g}}^{(1)}\left(\mathbf{X}\right)\le {b}_{\overline{m}}^U\right\}$ is included in ${E}_{\overline{m}-1}^U=\left\{{\underset{\_}{g}}^{(0)}\left(\mathbf{X}\right)\le {b}_{\overline{m}-1}^U\right\}$, where:

$$ {\underline{g}}^{(1)}\left(\mathbf{X}\right)=\underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min }{\widehat{G}}^{(1)}\left(\mathbf{X},\mathbf{Y}\right) $$

(49)

$$ {\underline{g}}^{(0)}\left(\mathbf{X}\right)=\underset{{\mathbf{Y}}^L\le \mathbf{Y}\le {\mathbf{Y}}^U}{\min }{\widehat{G}}^{(0)}\left(\mathbf{X},\mathbf{Y}\right) $$

(50)

To implement the judgment, MCMC is employed to generate ${N}_{\overline{m}}^U$ samples in ${E}_{\overline{m}}^U$ based on ${\widehat{G}}^{(1)}$. Then, the responses of ${\widehat{G}}^{(0)}$ at these samples are calculated. If all responses are less than ${b}_{\overline{m}-1}^U$, and ${\widehat{P}}_{\overline{m}}^U$ is not less than p₀, ${\widehat{P}}_f^{U(iter)}$ is taken as a valid value, and then the procedure goes to step 13. Otherwise, the procedure goes back to step 4.

• 13. Judge the termination condition of the procedure. If the condition in (51) is satisfied and iter is not equal to 1, the procedure will go to step 15; otherwise, go to step 14.

$$ \delta \left({\widehat{P}}_f^U\right)<{\delta}_{\ast}^U\kern0.37em \mathrm{and}\kern0.37em \mid \frac{{\widehat{P}}_f^{U(iter)}-{\widehat{P}}_f^{U\left( iter-1\right)}}{{\widehat{P}}_f^{U\left( iter-1\right)}}\mid <0.1 $$

(51)

where ${\delta}_{\ast}^U$ is the prescribed convergence value of the coefficient of variation of ${\widehat{P}}_f^U$. It is used to ensure whether the number of samples in SS is sufficiently large to obtain a small coefficient of variation. Based on the experience in Echard et al. (2011), ${\delta}_{\ast}^U$ is set to 0.05 in this study.

• 14. Generate M^U new random variable samples and add them into ${\varOmega}_{MC}^U$ in the first level of SS. Then, iter = iter + 1, and the procedure goes back to step 4.

• 15. Terminate the procedure and output ${P}_f^{U(iter)}$.

Note that when the lower bound of the failure probability ${\widehat{P}}_f^L$ is estimated by KSS, all MCS samples in ${\varOmega}_{MC}^U$ are chosen as the samples in the first level of SS in the first iteration, and all sample points in DoE during estimating ${\widehat{P}}_f^U$ is used to build the initial Kriging. The other steps in estimating ${\widehat{P}}_f^L$ are similar to those in the estimation of ${\widehat{P}}_f^U$. Hence, the detail procedure of estimating ${\widehat{P}}_f^L$ by KSS is not introduced. In this paper, t^u and t^l are set to 0.05.

4 Test examples

In this section, four examples are employed to validate the efficiency and accuracy of KSS for HRA-RI with small failure probability. In example 1 for a nonlinear mathematical problem, the performance function is highly nonlinear, which is used to validate the performance of the proposed method in the case with nonlinear performance functions. In examples 2 and 3 for a roof structure and a 23-bar planar truss, traditional civil engineering structures are tested. In example 4, a piezoelectric energy harvester is presented to test the proposed method in real-world mechanical engineering applications.

4.1 Example 1: a nonlinear mathematical example

A mathematical example with small failure probability is modified from Yang et al. (2015), in which the nonlinear performance function is formulated as:

$$ G\left({x}_1,{x}_2,y\right)=\sin \left(\frac{5\left({x}_1+1.5\right)}{2}\right)-\frac{\left({\left({x}_1+1.5\right)}^2+4\right)\left({x}_2+1.5\right)}{20}+y $$

(52)

where x₁ and x₂ are two random variables obeying independent standard normal distribution. y is an interval variable bounded in [3, 4].

In this example, the comparison among MCS, SS, FORM-UUA, and KSS is performed. Meanwhile, to analyze the influence of N_i (i.e., the number of points in the initial DoE) on the performance of the proposed KSS method, different cases under N_i = 6, 12, 20, and 30 are tested. The results of MCS are gained with 200 × 10⁶ performance function evaluations, where 10⁶ random variable samples are simulated based on the joint PDF of random variables, and 200 interval variable samples are selected to evaluate the maximum and minimum values of the performance function over the range of interval variables. The upper and lower bounds of the failure probability assessed by MCS are considered as reference values. For MCS, SS, and KSS, 10 independent runs of each of them for this example are conducted. The average results of each method are obtained. Comparative results are listed in Table 1. In Table 1, N_call is the total number of the true performance function evaluations. ${\widehat{P}}_f^{\mathrm{max}}$ and ${\widehat{P}}_f^{\mathrm{min}}$ denote the estimated values of the upper and lower bounds of failure probability, respectively. $\varepsilon \left({\widehat{P}}_f^{\mathrm{max}}\right)$ and $\varepsilon \left({\widehat{P}}_f^{\mathrm{min}}\right)$ are the relative errors of ${\widehat{P}}_f^{\mathrm{max}}$ and ${\widehat{P}}_f^{\mathrm{min}}$ compared with the references obtained by MCS, respectively. $ci\left({\widehat{P}}_f^{\mathrm{max}}\right)$ and $ci\left({\widehat{P}}_f^{\mathrm{min}}\right)$ stand for the 95% confidence intervals of ${\widehat{P}}_f^{\mathrm{max}}$ and ${\widehat{P}}_f^{\mathrm{min}}$ over 10 independent runs for MCS, SS, and KSS.

Table 1 Comparative results in example 1

As shown in Table 1, for the estimated values of the upper and lower bounds of the failure probability, the relative errors of FORM-UUA are the largest. The relative errors of SS and KSS in each case are smaller. Besides, the confidence interval of KSS in each case is narrower than that of SS. As N_i increases, the number of update points in KSS decreases while N_call increases. The reason is that the sample points in the initial DoE are usually scattered in the uncertain design space while the update points are located around the projection outlines. Thus, more sample points in the initial DoE may not be beneficial to cut down the total number of performance function evaluations. However, from Table 1, it can be observed that KSS in each case needs much fewer performance function evaluations than the other methods. Hence, KSS is an accurate and efficient method for HRA-RI with small failure probability.

Figure 3 respectively presents the update samples during estimating ${\widehat{P}}_f^U$ by KSS under N_i = 12, samples in the last level of SS at the last iteration of KSS, the true separation surface $\underset{\_}{g}=0$, and the approximate separation surface by Kriging metamodel. As shown in Fig. 3, it can be seen that the true separation surface is well approximated in the region where the random variables have a high probability density. Besides, a majority of update samples are located in the vicinity of the true separation surface, which indicates that the update strategy in KSS can well search out update samples to refine the approximate separation surface. To estimate the lower bound of the failure probability, 4 update points are added into the initial DoE. Figure 4 respectively shows these update points, samples in the last level of SS at the last iteration of KSS, the true separation surface $\overline{g}=0$, and the approximate separation surface by Kriging metamodel. It can be also found that the true separation surface is well approximated in the region where the random variables have a high probability density, and the update points are close to the true separation surface. Figure 5 displays the iterative curves of estimating ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ by KSS under N_i = 12 in one independent run. It can be seen that ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ are very close to the reference values at the end of iterations. Therefore, it is illustrated that KSS is an accurate and efficient method for HRA-RI with small failure probability.

Fig. 3

Update points during estimating ${\widehat{P}}_f^U$ by KSS under N_i = 12 in example 1

Fig. 4

Update points during estimating ${\widehat{P}}_f^L$ by KSS under N_i = 12 in example 1

Fig. 5

Iterative curves of estimating ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ by KSS under N_i = 12 in example 1

4.2 Example 2: a roof structure

This example is associated with a roof structure with small failure probability (Yang et al. 2015) shown in Fig. 6. The tension bars and the bottom boom are made by steel while the top boom and compression bars are reinforced by concrete. A uniformly distributed load q is imposed on this roof structure. It can be equivalently transformed into the nodal load P = ql/4. At node C, the vertical deflection can be calculated by:

$$ {\Delta}_C=\frac{q{l}^2}{2}\left(\frac{3.81}{A_C{E}_C}+\frac{1.13}{A_S{E}_S}\right) $$

(53)

where E_C and E_S respectively denote the Young’s moduli of the concrete and steel bars. A_C and A_S respectively represent their cross-sectional areas. The allowable value of the vertical deflection at node C is 0.027 m. In this example, the performance function is formulated as G(X, Y) = 0.027 − Δ_C. The random and interval variables in this example are given in Table 2.

Fig. 6

Schematic view of the roof structure

Table 2 Random and interval variables in example 2

For MCS, SS, and KSS with 12 sample points in initial DoE, 10 independent runs of each method for this example are conducted. The average results of each method are obtained. Comparative results of MCS, SS, FORM-UUA, and KSS are presented in Table 3. As shown in Table 3, FORM-UUA shows the largest relative errors for the upper and lower bounds of the failure probability, while the relative errors of SS and KSS are smaller and KSS has the smallest relative errors. Furthermore, the 95% confidence intervals of KSS are narrower than those of SS. In terms of N_call, about 38 evaluations of the actual performance function are required in KSS to obtain the final ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$, which is the fewest among the comparative methods. Figure 7 presents the iterative curves of estimating ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ by KSS in one independent run. It can be seen that the estimated values of ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ by KSS are very close to the reference values at the end of iterations. Accordingly, KSS can accurately and efficiently estimate the upper and lower bounds of the failure probability in HRA-RI with small failure probabilities.

Table 3 Comparative results in example 2

Fig. 7

Iterative curves of estimating ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ by KSS in example 2

4.3 Example 3: 23-bar planar truss

A planar 23-bar truss structure shown in Fig. 8 with small failure probability (Dai et al. 2014) is selected. The six loads are taken as random variables. The cross-sectional areas of the main members and diagonal members, and Young’s modulus E are taken as interval variables. All uncertain variables are introduced in Table 4. The performance function of the 23-bar planar truss is formulated by:

$$ g\left(\mathbf{X},\mathbf{Y}\right)={v}_a-{v}_1 $$

(54)

where v₁ represents the vertical deflection at node 1, which is computed through finite element analysis. The response of the truss is assumed to be linear elastic. v_a is the allowable deflection, which is set to 0.08 m.

Fig. 8

Schematic view of the planar 23-bar truss structure

Table 4 Random and interval variables in example 3

For MCS, SS, and KSS with 12 sample points in initial DoE, 10 independent runs of each method for this example are performed. The average results of each method are gained. Comparative results of MCS, SS, FORM-UUA, and KSS are listed in Table 5. As seen in Table 5, for the estimation of upper and lower bounds of the failure probability, large relative errors are caused by FORM-UUA. However, the relative errors of SS and KSS are smaller and KSS has the smallest relative errors. In addition, the 95% confidence interval of ${\widehat{P}}_f^U$ in KSS is similar to that in SS, while the 95% confidence interval of ${\widehat{P}}_f^L$ in KSS is narrower than that in SS. In terms of N_call, it can be observed that KSS requires the fewest true performance function evaluations. Figure 9 shows the iterative curves of estimating ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ by KSS in one independent run. As seen in Fig. 9, it can be seen that the final ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ obtained by KSS are very close to the reference values. Overall, it is illustrated that KSS is accurate and efficient for HRA-RI with small failure probability.

Table 5 Comparative results in example 3

Fig. 9

Iterative curves of estimating ${\widehat{P}}_f^U$ and ${\widehat{P}}_f^L$ by KSS in example 3

4.4 Example 4: a piezoelectric energy harvester

The structural reliability of a piezoelectric energy harvester (Sadoughi et al. 2018; Seong et al. 2017) is assessed in this example. As shown in Fig. 10, it consists of a tip mass attached at one end and a shim laminated by piezoelectric materials at the other end. The shim and tip mass are constructed from blue steel and tungsten/nickel alloy, respectively. Mechanical strain is transferred into voltage or current with the piezoelectric effect. Thirty-one modes are taken into account in this example, where higher longitudinal strain is allowed when the energy harvester is subject to small input forces. Voltage is produced along the thickness direction with longitudinal stress/strain. The piezoelectric energy harvester can be modeled by a transformer circuit. According to the Kirchhoff’s voltage Law, the circuit can be represented by the coupled differential equations that characterize the transformation from mechanical stress/strain to voltage. The conversion process can be simulated by Matlab Simulink. The details of this piezoelectric energy harvester can be found in Sadoughi et al. (2018).

Fig. 10

A piezoelectric energy harvester

In this example, the length of shim l_b, piezoelectric strain coefficient v, Young’s modulus for PZT-5A E₁, Young’s modulus for the shim E₂, the length of tip mass l_m, and the height of tip mass h_m are uncertain variables. The distributions of l_b, v, E₁, and E₂ are known while only bounds can be obtained for l_m and h_m. Table 6 provides all these variables. The performance function is expressed as:

$$ G={P}_0-P\left({l}_b,v,{E}_1,{E}_2,{l}_m,{h}_m\right) $$

(55)

where P is the harvester output power, and P₀ is the minimum required power, which is set to 28 mW.

Table 6 Random and interval variables in example 4

In this example, the number of sample points in initial DoE in KSS is set to 12 since 6 uncertain variables exist. The performance function evaluation in this example is expensive and time-consuming. Meanwhile, a large number of true performance function evaluations are required by MCS for reliability analysis with small failure probability. Thus, the lower and upper bounds of failure probability estimated by SS with 3 × 10⁴ random samples in each level are taken as reference values in this real-world example. Table 7 shows the comparative results between SS and KSS. As shown in Table 7, the relative errors of KSS are small and it needs much fewer evaluations of the true performance function compared with KSS. Hence, KSS is accurate and efficient in support of HRA-RI with small failure probability.

Table 7 Comparative results in example 4

5 Conclusions and future work

In this paper, an efficient KSS method is proposed for HRA-RI with small failure probability. In this method, the number of samples in each level of SS is adaptively adjusted according to the coefficients of variation of estimated failure probability. Kriging metamodel is first built by using initial DoE to replace the actual performance function and then smartly updated based on the samples in the first and last levels of SS, in which a new update strategy is developed to refine Kriging by searching out the samples around the approximate projection outlines on the limit-state surface. Because the candidate samples in the first level of SS are distributed in the whole random variable space and samples in the last level of SS are located around the separation surface between the failure and safety domains, the Kriging update based on these samples can benefit from the exploration and exploitation of the failure domain. In addition, to control the influence of Kriging metamodel uncertainty on the estimation of the upper and lower bounds of the small failure probability, two uncertainty functions are defined and corresponding termination conditions are developed for Kriging update. Finally, four examples are provided to validate the advantages of the proposed KSS method. The prominent performance of KSS is illustrated by comparative results in terms of accuracy and efficiency for HRA-RI with small failure probability.

Kriging metamodels may show the poor approximation efficiency for high-dimensional functions, i.e., large-scale problems. When high-dimensional performance functions are involved in HRA-RI with small failure probability, the proposed method will be unsuitable. The applications of other kinds of surrogate models (such as support vector machine) in HRA-RI with small failure probability for large-scale problems can be investigated in the future.