1 Introduction

In practical engineering design, computer simulation models have often been employed to replace the costly controlled real-life experiments. However, running simulation models, e.g., computational fluid dynamics (CFD) and finite-element analysis (FEA), for complex engineering system with multiple inputs and outputs can be computationally prohibitive [1,2,3]. Just take the airfoil simulation case as an example, it is reported that it takes the designer about 7–10 h to produce a single output using the CFD model [4]. It is unrealistic to directly use these simulation models to evaluate a large number of design solutions when optimizing the design space. A promising way to address this issue is to adopt the surrogate model, also called the metamodel or approximation model, to replace the computational expensive simulation model [5,6,7,8]. There are several commonly used surrogate models, such as Kriging model [9,10,11], Support Vector Regression (SVR) model [12,13,14], Polynomial Response Surface (PRS) model [15], and Radial Basis Function (RBF) model [16, 17]. Among these surrogate models, Kriging model is the most thoroughly studied surrogate model to improve the computational efficiency of engineering design optimization, because it has several interesting characteristics compared to other surrogate models [18, 19]. First, the Kriging model can provide the prediction bias of each un-sampled point. The prediction bias obtained can reflect the level of prediction confidence at the un-sampled point. The lower the prediction bias, the higher the degree of confidence in the prediction, and vice versa. Second, although different surrogate models perform well under different situations, preliminary results illustrate that in most cases, Kriging model performs better than other surrogate models regarding modeling accuracy, especially when the number of sample points is small and the black-box functions exhibit strong nonlinearity [20,21,22,23].

As reported in the literature, the Kriging model-assisted engineering design optimization can be classified into two types: off-line type and on-line type. In the off-line type, a pre-specified amount of sample points is employed to build a Kriging model, which is used for replacing the simulation analysis in the engineering optimization subsequently [24]. The main shortcoming of the off-line type is that it is difficult to predetermine the proper sample size for obtaining an accurate Kriging model [25, 26]. On the other hand, the on-line type generates an initial Kriging model first and then adaptively updates the Kriging model following certain metrics, the distance criteria [27], prediction variance [28, 29], cross-validation error [30], etc. Compared with the off-line type, the on-line type can make use of the knowledge from the previous iterations and is reported to be more efficient for engineering design optimization. So far, most of the existing on-line Kriging model-assisted engineering design optimization focus on sequential updating of the objective function. The most famous method, called efficient global optimization (EGO), was proposed by Jones et al. [31], where the Kriging surrogate model is updated by selecting the point that maximizes the expected improvement (EI) over the present best solution. Furthermore, Sóbester et al. [32] proposed a weighted expected improvement criterion, which is designed to allow a more flexible way to balance the exploration and exploitation in global searching. Wang et al. [33] developed a boundary and best neighbor searching (BBNS) approach for selecting sampling points that are not only in the neighborhood of the present best solution but also near the boundary of the design space. Zhan et al. [34] proposed a parallel EGO algorithm, where multiple updating points were selected in each cycle by dynamically controlling the number of EI maxima and points around each EI maximum. Dong et al. [35] proposed a hybrid surrogate-based optimization algorithm, in which the update points need to satisfy a defined distance criterion. While a limited number of approaches consider the updating strategy for the constraints [36]. Schonlau et al. [37] proposed a probability of feasibility (PoF) approach to identify regions of feasibility, i.e., the probability of the prediction at design alternatives will be larger or smaller than a constant limit. Li et al. [38] applied the PoF approach to finding initial feasible sample points in a Kriging-based constrained global optimization algorithm. Wang et al. [39] extended the PoF approach for the design optimization of the black-box stochastic systems. Zhang et al. [40] adopted the PoF approach to address the global constraint optimization, where multi-fidelity analysis models are available. Parr et al. [41] provided a review of three typical updating strategies for handling constraints and made a comparative among them, concluding that further improvements are needed, since these methods may discard solutions if the PoF of design alternatives close or equal to zero. Sasena et al. [42] illustrated that the expected violation (EV) method could address the shortcoming of the PoF approach. Bichon et al. [43] proposed an efficient global reliability analysis (EGRA) approach, which shares a similar idea with EV, for updating constraints with the value likely to be zero. Furthermore, Li et al. [44] adjusted it from the global design region to the local one in a honeycomb material design problem. However, it is reported that EV method evaluates design points from a finite set, which may not be able to locate the optimum of the original problem as accurately as solving the constrained one [42]. Recently, Shu et al. [45] developed a weighted accumulative error sampling (WAE) strategy for updating metamodels and then applied it to improve the quality of global optimization. Liu et al. [46] proposed a DIRECT-type constraint-handling technique that can separately handle feasible and infeasible cells. Dong et al. [47] developed a novel multi-start space reduction (MSSR) algorithm for solving computationally expensive black-box global optimization problems with bound constrains and nonlinear constrains. Shi et al. [48] developed a filter-based adaptive Kriging method, in which a probability of constrained improvement (PCI) criterion is developed based on the notion of filter to sequentially generate new samples for updating Kriging metamodels of objective and constraints. Wu et al. [49] extended the adaptive metamodel-based global optimization algorithm (EAMGO) to handle constrained global optimization problems, in which the updating strategy for the constraints can be used for different surrogate models. However, because the interpolation uncertainties are not considered in all updating iterations, the feasibility of the design alternatives that changed due to these interpolation uncertainties will mislead the global searching direction.

To address the issue-mentioned above, a general sequential constraint-updating approach based on the confidence intervals from the Kriging surrogate model (SCU-CI) is proposed. In the developed SCU-CI approach, an objective switching and sequential updating strategy is introduced to determine, (1) whether the actual simulation models or the Kriging metamodel should be used to evaluate the feasibility of the design alternatives and (2) which design alternatives would be selected to improve the prediction accuracy of the Kriging metamodel. The developed updating strategy is mainly based on whether the feasibility status of the design alternatives would be changed because of the interpolation uncertainty from the Kriging surrogate model or not. The performance of the proposed approach is illustrated using nine numerical cases and two real-world engineering examples. The comparisons between the proposed approach and some existing approaches considering the quality of the obtained optimum and computational efficiency are made. The merits of the proposed approach are analyzed and summarized.

The rest of this paper is organized as follows. In Sect. 2, the background of the Kriging model and several typical constraint-updating strategies are presented. Details of the proposed are introduced in Sect. 3. In Sect. 4, the comparison results between the proposed approach and some existing approaches on a numerical benchmark case and two real-world engineering design problems are presented. Finally, the concluding remarks are given in Sect. 5.

2 Background

2.1 Kriging model

Kriging model is a kind of interpolation model, which was developed by Danie G. Krige for forecasting the mining holes. Then, it was introduced to approximate the computer experiments by Sacks et al. [50]. Supposing that there are N sample points \(X = \left\{ {x^{(1)} ,x^{(2)} , \ldots ,x^{(N)} } \right\}\) with \(\varvec{x}^{(1)} = \left\{ {x_{1}^{(1)} ,x_{2}^{(1)} , \ldots ,x_{k}^{(1)} } \right\}\) and the corresponding response is \(y = \left\{ {y^{(1)} ,y^{(2)} , \ldots ,y^{(N)} } \right\}\). The Kriging model can be expressed as

$$\hat{f}(x) = p(x) + Z(x),$$
(1)

where \(p(x)\) denotes the mean of the Gaussian process, indicating the global property, \(Z(x)\) represents the local property with the mean value being equal to zero, and the variance is \(\sigma\).

The variables of the Kriging model were considered to be correlated with each other through the basis function:

$$\begin{aligned} R\left[ {y(x^{(i)} ),y(x^{(j)} )} \right] & = {\text{Cor}}\left[ {y(x^{(i)} ),y(x^{(j)} )} \right] \\ &= \exp \left( { - \sum\limits_{m = 1}^{k} {\theta_{m} \left| {x_{m}^{i} - x_{m}^{j} } \right|^{{p_{m} }} } } \right), \\ \end{aligned}$$
(2)

where R is the correlation coefficient, \(R\left[ {y(x^{(i)} ),y(x^{(j)} )} \right]\) denotes the correlation between \(x^{(i)}\) and \(x^{(j)}\), \(\theta_{m}\), and \(p_{m}\) are the hyper-parameters that influence the correlation of the sample points and the smoothness of the surrogate model.

The hyper-parameters can be obtained by the maximum likelihood estimation:

$$L\left( {y^{(1)} ,y^{(2)} , \ldots ,\left. {y^{(N)} } \right|\sigma ,\mu } \right) = \frac{1}{{(2\pi \sigma^{2} )^{{{\raise0.7ex\hbox{$n$} \!\mathord{\left/ {\vphantom {n 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}\exp \left[ { - \frac{{\sum {(y^{(i)} - \mu )^{2} } }}{{2\sigma^{2} }}} \right].$$
(3)

The value of \(\mu\) and \(\sigma\) can be obtained by setting the derivate of Eq. (3) to be zero

$$\hat{\mu } = \frac{{1^{T} R^{ - 1} y}}{{1^{T} R^{ - 1} 1}},$$
(4)
$$\hat{\sigma }^{2} = \frac{{(y - 1\hat{\mu })R^{ - 1} (y - 1\hat{\mu })}}{N}.$$
(5)

Substituting Eqs. (4) and (5) to Eq. (3), an expression can be got for parameters are \(\theta\) and \(p\)

$$\ln (L) = - \frac{n}{2}\ln (\frac{{(y - 1\hat{\mu })R^{ - 1} (y - 1\hat{\mu })}}{N}) - \frac{1}{2}\ln \left| R \right|.$$
(6)

The maximum likelihood estimation should be maximized, so that the hyper-parameters can be got, which is the best fit to the Kriging model. It is difficult to get an analytical solution of Eq. (6); therefore, a global search algorithm, e.g., genetic algorithm, is used for finding the optimum of \(\theta\) and \(p\).

Then, the predicted value at an un-sampled point x can be calculated as

$$\hat{f}(x) = \hat{\mu } + r^{T} R^{ - 1} (y - 1\hat{\mu }),$$
(7)

where \(y\) is the response value of the sample points, R is the correlation matrix of the sample points, and r is a vector, whose dimension is N × 1. The elements of the vector r are \(r_{i} = {\text{Cor}}\left[ {y(x),y(x^{(i)} )} \right]\).

The advantage of the Kriging model compared with other surrogate models is that it can provide the variance value of the predict points, which can be expressed as

$$s^{2} (x) = \hat{\sigma }^{2} \left[ {1 - r^{T} R^{ - 1} r + \frac{{(1 - 1^{T} R^{ - 1} r)^{2} }}{{1^{T} R^{ - 1} 1}}} \right].$$
(8)

The variance function can be calculated in every predicted point, so that a confidence interval can be got to forecast the range of forecasting. A one-dimensional example is presented in Fig. 1. The function which is approximated has an expression of \(f(x) = (6x - 2)^{2} \sin (12x - 4)\). The sample points are \(X = \left[ {0,0.25,0.5,0.75,1} \right]^{\text{T}}\). In Fig. 1, the solid line represents the real response value of the function, and the dashed line represents the predicted value through the Kriging surrogate model; the dot lines denote the upper bound and lower bound. The predict response at sample points equal to the real response and the errors equal to zero. The bounds consist of the confidence interval of the Kriging model, of which has 95.5% probability that the points would fall into it.

Fig. 1
figure 1

Illustration of the Kriging model with its confidence interval

Full size image

2.2 Descriptions of five typical constraint-updating strategies

A general formulation of a constraint optimization problem is given as:

$$\begin{array}{l} \mathop {\hbox{min} }\limits_{x} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(x) \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{j} (x) \le 0,j = 1,2 \ldots J \\ {\kern 1pt} x_{\text{lb}} \le x \le x_{\text{ub}} , \end{array}$$
(9)

where \(f(\varvec{x})\) is the objective function, \(x = (x_{1} ,x_{2} , \ldots x_{N} )^{\text{T}}\) is the design variable vector, \(x_{\text{lb}}\) and \(x_{\text{ub}}\) are the lower and upper bounds of \(x\), respectively, and \(g = (g_{1} ,g_{2} , \ldots ,g_{J} )\) are the constraints.

In this work, we focus on the constraints, which involve expensive simulations, i.e., we assume that the evaluation of the objective is cheap. This is common in the design of engineering structure, i.e., the minimum weight design of structures. Therefore, in this section, brief introductions of five typical constraint-updating strategies, including EV, PoF, maximum MSE (MAX-MSE) method, WAE, and EAMGO methods, are introduced.


(1) EV method

EV method is one of the most commonly used constraint-handling strategies. The typical characteristic of this method is that the constraints are checked before the sampling criterion is taken into consideration. For every candidate point, the expected violation is calculated as [42]

$${\text{EV}}_{i} = \left\{ {\begin{array}{*{20}c} {(\hat{g}_{i} - 0)\varPhi \left( {\frac{{\hat{g}_{i} - 0}}{{\hat{s}_{i} }}} \right) + \hat{s}_{i} \phi \left( {\frac{{\hat{g}_{i} - 0}}{{\hat{s}_{i} }}} \right),\;\;{\text{if}}\;\;\hat{s}_{i} > 0} \\ {0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{if}}\;\;\hat{s}_{i} \; = \;0} \\ \end{array} } \right.,$$
(10)

where \(\hat{g}_{i}\) refers to the predicted mean of constraint \(i\), and \(\hat{s}_{i}\) is the standard deviation. It is worth mentioning that the expected violation plays a similar role as the EI function. When the constraint has prominent uncertainty or is likely to be violated, the expected violation trends to be large. As to the problem with several constraints, the EV can be a vector.


(2) PoF method

The PoF approach is based on the feasible probability of the candidate design points, and the constraint functions are classified into two types (i.e., “inexpensive” and “expensive”) according to computing time. The feasible probability of inexpensive constraints is 0 or 1, because it is quite easy to verify whether the candidate points satisfy the constraints or not. It can be expressed as [41]

$$P_{\text{inexp}} = \left\{ {\begin{array}{*{20}c} {1,} & \quad {{\text{if }}g(x) \le 0} \\ {0,} & \quad {\text{otherwise}} \\ \end{array} } \right..$$
(11)

As to expensive constraint functions, the feasible probability needs to be estimated from the statistical models. The estimated the feasible probability could be expressed as

$$P_{\exp } = \varPhi \left( {\frac{{0 - \hat{g}(x)}}{{\hat{s}(x)}}} \right),$$
(12)

where \(\varPhi\) refers to the Gaussian cumulative distribution function. \(\hat{g}(x)\) and \(\hat{s}_{i} (x)\) are Kriging predicted mean and standard deviation, which are obtained from Eqs. (7) and (8), respectively.


(3) MAX-MSE method

The MAX-MSE method is a general updating strategy not only for handling constraints but also for objective functions. The main idea of The MAX-MSE method is that adding the sample point with the largest variance is the most beneficial to improve the prediction accuracy of the Kriging model. Since the Kriging model assumes that the correlations between the design points are dependent on their distances, the accuracy of the Kriging model for the constraints in the neighborhood of the selected samples will also increase obviously. The formula can be expressed as [51]

$$\text{max} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s^{2} (x),$$
(13)

where \(s^{2} (\varvec{x})\) is the variance value, which can be obtained by Eq. (9). The MAX-MSE value is found through an optimization method such as Direct Search when dealing with practical problems.


(4) WAE method

In the WAE method, the optimization objective is to find a sample point with the maximum weighted accumulative predicted error obtained by analyzing data from the previous iterations, and a space-filling criterion is also introduced and treated as a constraint to avoid generating clustered sample points. To some extent, the WAE method is an extension of the MAX-MSE method, which can be expressed as

$$e_{\text{WAES}} (x) = \sqrt {\sum\limits_{i = 1}^{n} {w_{i} (\hat{y}_{ - i} (x) - \hat{y}(x))^{2} } }$$
(14)

where \(\hat{y}(\varvec{x})\) denotes the Kriging model constructed using the current sample set, while \(\hat{y}_{ - i} (\varvec{x})\) is the Kriging model constructed using the current sample set without the \(i{\text{th}}\) sample. The value of \(w_{i}\) reflects the influence of different sample points on the error on x.

In addition, the WAE method limits the minimum distance between a new point and existing points by the following criterion:

$$\hbox{min} \left\| {x - x_{i} } \right\| \ge d,$$
(15)

where d denotes the threshold distance, which is calculated by the average value of the minimum distance between each pair of the sample points.


(5) EAMGO method

EAMGO is different from adaptive metamodel-based global optimization (AMGO) for its constrains updating strategy. During each iteration, the updating point is obtained by minimizing the summation of predicted constraint values subject to the approximate constraints and the distance limitation. The constraints updating strategy in the EAMGO method can be described as

$$\begin{aligned} \mathop {\hbox{min} }\limits_{x} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^{J} {\hat{g}_{j}^{k} (x)} \hfill \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat{g}_{j}^{k} (x) \le 0,j = 1,2 \ldots J \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\| {x - x_{i} } \right\| \ge \zeta_{\text{iter}} d_{\text{max} } \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{\text{lb}} \le x \le x_{\text{ub}} , \hfill \\ \end{aligned}$$
(16)

where k is the current iteration number, dmax denotes the maximum distance between two sample points in the current sampling set, \(\zeta_{\text{iter}}\) is a distance coefficient obtained from a constant array, and \(x_{i}\) denotes the \(i{\text{th}}\) sample in the current sample set.

3 Proposed approach

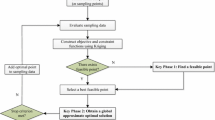
In this work, a genetic algorithm (GA) from Coello [52] is used to solve the optimization problems. If the constraints are calculated by running the computational expensive simulation models, it will be unrealistic to directly use these simulation models to evaluate a large number of design solutions when optimizing the design space. To improve the effectiveness of solving this problem, the Kriging surrogate model instead of the actual constraints can be used. As mentioned in Sect. 2.1, there are prediction errors between the Kriging surrogate model and the real constraint values, which may lead to infeasible optimal solutions. The purpose of the proposed approach is to sequentially update the Kriging surrogate models to ensure the feasibility of the optimization solutions. The flowchart of SCU-CI approach is demonstrated in Fig. 2. The Step 4 and Step 5 are the cores of SCU-CI and will be described in details in Sects. 3.1 and 3.2.

Fig. 2
figure 2

Flowchart of the proposed approach

Full size image

3.1 The developed objective switching criterion

Prediction values from Kriging surrogate models have prediction uncertainty, which may lead to infeasible optimization solutions. Therefore, the SCU-CI approach is presented to take the interpolation uncertainty of the Kriging surrogate model into consideration. Note that as long as the feasibilities of the design alternatives may not change due to the Kriging surrogate model uncertainty, the feasibilities of the individuals can be predicted by the Kriging surrogate models instead of expensive simulation models. However, if the feasibilities of the design alternatives may change, then the feasibilities of the individuals should be evaluated by simulation models. Thus, an objective switching criterion is introduced in SCU-CI to determine whether the simulation models or the Kriging surrogate models should be used to evaluate the feasibilities of individuals.

In each generation of GA, when the effects of interpolation uncertainty from the Kriging surrogate model are taken into consideration, there are four possible scenarios for a design alternative, as shown in Fig. 3.

Fig. 3
figure 3

Four possible scenarios for a design alternative

Full size image

In the first scenario, as shown in Fig. 3a, point A is a feasible design alternative and the confidence interval does not intersect the constraint boundary. It means that point A would be feasible at the given confidence probability. Similarly, in the fourth scenario, point D would be an infeasible solution at the given confidence probability, as shown in Fig. 3d. In summary, for these two scenarios, although the Kriging surrogate model has prediction errors at point A and point D, these prediction errors do not affect the feasibilities of the two points. Therefore, there is no need to add these points as new sample points for updating the Kriging surrogate model in the subsequent optimization process.

In the second scenario, as shown in Fig. 3b, point B is feasible, while its confidence interval intersects the constraint boundary. This means that point B may be infeasible at the given confidence probability. Similarly, in the third scenario, point C is infeasible, while it may become feasible due to the prediction error from the Kriging surrogate model. For these two scenarios, the feasibilities of points B and C are uncertain. Therefore, the new sample points should be selected from the points, whose feasibilities are uncertain. The conditions that these points satisfy can be described as:

$$\begin{aligned} \hat{g}_{i} (x_{j} ) \le 0\,\&\, \hat{g}_{i} (x_{j} ) + 2s(x_{j} ) \ge 0\;\;\;\;\;i = 1,2, \ldots ,J \hfill \\ \hat{g}_{i} (x_{j} ) \ge 0\,\&\, \hat{g}_{i} (x_{j} ) - 2s(x_{j} ) \le 0{\kern 1pt} \;\;\;\;i = 1,2, \ldots ,J, \hfill \\ \end{aligned}$$
(17)

where \(\hat{g}_{i} (x)\) are the predicted constraint value of the optimization problem; \(s(x)\) is the standard deviation of the corresponding Kriging surrogate model.

3.2 Distance metric

It is noted that it may cause unnecessary computational cost if the points selected according to the criterion in Sect. 3.1 are all evaluated by simulation models. This is because (1) these sample points may be very close in the design space, resulting in the oversampling for Kriging surrogate model [45, 53] and (2) when a new sample point is used to update the Kriging surrogate model, the prediction error at an unobserved point near the new sample point will be significantly reduced. It indicates that the points, which are very close to other existing sample points, should not be selected as new sample points.

To prevent the cluster of sample points, the points that satisfy the following constraint are selected as new sample points:

$$\begin{aligned} d(x) > \frac{{\bar{d}}}{\delta } \hfill \\ d(x) = \hbox{min} \left( {\sqrt {\big(x - x_{i}^{(n)} \big)^{T} \big(x - x_{i}^{(n)} \big)} } \right)(i = 1,2, \ldots ,N^{(n)} ) \hfill \\ \bar{d} = \sum\limits_{i = 1}^{n} {\hbox{min} \left( {\sqrt {\big(x_{i} - x_{j}^{(n)} \big)^{T} \big(x_{i} - x_{j}^{(n)} \big)} } \right)} j = 1,2, \ldots ,i - 1,i + 1, \ldots ,n, \hfill \\ \end{aligned}$$
(18)

where \(\delta\) is the distance threshold control parameter which is set to be 2 in this work, x is the sample points to be judged, and \(x_{i}^{(n)}\) is the nth sample point in the current sample points set. The algorithm for determining new sample points that meet the requirements is listed in Table 1.

Table 1 Algorithm for determining new sample points satisfying the distance constraint
Full size table

3.3 Steps of the proposed approach

The detailed steps of the proposed approach are described as follows.

Begin

Step 1: Generate initial sample points and obtain the response values. The essential requirement of initial sampling is that sample points should distribute uniformly in whole design space. In this paper, the optimal Latin hypercube design (OLHD) is used for initial sampling.

Step 2: Construct the initial Kriging surrogate model.

Step 3: Initialize the population of GA, Set gen = 1, evaluate the fitness values of initial individuals by Kriging surrogate model.

Step 4: Select the individuals whose feasibility may change due to the interpolation uncertainty from the Kriging surrogate model according to Eq. (17).

Step 5: Determine the new sample points by a distance criterion according to Eq. (18).

Step 6: Update the Kriging surrogate model. Generate the new population and update the count number gen = gen + 1.

Step 7: Evaluate the responses of the new individuals by Kriging model

Step 8: Check whether the stopping criterion is satisfied: If yes, go to Step 9; otherwise, go back to Step 4. The stopping criterion satisfies one of the following conditions:

$$\left\{ \begin{array}{l} \left| {y_{\text{gen}} - y_{{{\text{gen}} - 1}} } \right| \le \varepsilon_{y} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {y_{{{\text{gen}} - 1}} - y_{{{\text{gen}} - 2}} } \right| \le \varepsilon_{y} \hfill \\ {\text{gen}} = {\text{MAXGEN}} \hfill \\ \end{array} \right.,$$
(19)

where \(y_{{{\text{gen}} - 2}}\), \(y_{{{\text{gen}} - 1}}\), and \(y_{\text{gen}}\) are the optimal solutions obtained in the \(({\text{gen}} - 2){\text{th}}\), \(({\text{gen}} - 1){\text{th}}\), and \({\text{genth}}\) generation, \(\varepsilon_{y}\) is the relaxation factor, and \({\text{MAXGEN}}\) is the maximum generation of GA.

Step 9: Output the optimization solutions.

End

4 Examples and results

In this section, nine numerical examples and two practical engineering cases are used to demonstrate the effectiveness and merits of the proposed approach. In the test cases, all the five updating strategies are used in the framework of GA as the proposed SCU-CI strategy. A Kriging model with the same sample points is built in the initial stage of the GA method. Then, the Kriging model is used to evaluate the fitness value during the evolution process. The difference among all the approaches is the updating strategy, where the alternatives are selected. To provide a detailed description of the implementation process of the proposed SCU-CI approach, one of the numerical examples is used as an illustrative example. The parameters set for the GA are as follows: the population size and max iterations are 40 and 100, respectively. The crossover probability and mutation probability are 0.80 and 0.15, respectively. The generation gap is 0.95 to keep the elites in each generation.

4.1 Illustration example

A numerical case from Zhou et al. [54] is used to describe the proposed approach steps by steps. The object is to find the minimum value of the objective function subject to two constraints. The expression of this optimization problem is given as

$$\begin{array}{ll} \hbox{min} & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = x_{1}^{3} \sin (x_{1} + 4) + 10x_{1}^{2} + 22x_{1} + 5x_{1} x_{2} + 2x_{2}^{2} + 3x_{2} + 12\\ s.t. & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{1} = x_{1}^{2} + 3x_{1} - x_{1} \sin (x_{1} ) + x_{2} - 2.75 \le 0 \\ &{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\\ &g_{2} = - \log_{2} (0.1x_{1} + 0.41) + x_{2} {\text{e}}^{{ - x_{1} + 3x_{2} - 4}} + x_{2} - 3 \le 0 \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}\\ &- 3 \le x_{1} \le 1.5,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 4 \le x_{2} \le 1.5. \hfill \end{array}$$
(20)

In this example, it is assumed that the original nonlinear constraint \(g_{2}\) is an expensive cost model, while the objective function f and g1 can be expressed explicitly. Two metrics, the obtained optimal solution and the required number of sample points (NS), are employed in this work to evaluate the accuracy and efficiency of the proposed method. Both of these two metrics are expected to be smaller values. For illustration, the proposed approach is compared with five approaches: (1) EV method [42], (2) MAX-MSE method, (3) PoF method [37, 40], (4) WAE method [45], and (5) EAMGO method [49]. Since the true optimal solution for a numerical example can be obtained, the stopping criteria used for the numerical example are different from those for the engineering problems for a better comparison of the performance of different approaches. The stopping criterion satisfying one of the following conditions:

$$\left\{ \begin{aligned} \left| {\frac{{y_{\text{gen}} - y*}}{y*}} \right| \le \varepsilon \hfill \\ n = {\text{MAXGEN}} \hfill \\ \end{aligned} \right.,$$
(21)

where \(y_{\text{gen}}\) is the optimal solution obtained in the genth generation; \(y *\) is the true optimal solution of the numerical example, and \({\text{MAXGEN}}\) is the maximum generation of GA. \(\varepsilon\) is set to be 0.02 in this example.

For the initial Kriging surrogate model, 20 initial sample points are generated by OLHD for different approaches. The comparison results are summarized in Table 2.

Table 2 Comparison results of the different approaches for the illustration example
Full size table

As can be seen in Table 2, although the proposed SCU-CI approach required more sample points than those of EV, PoF, and WAE approaches, it can obtain the best optimal solution at the same time satisfying the constraints. Compared to EAMGO, SCU-CI can obtain better optimal solution while requires fewer sample points. In addition, EV, PoF, and WAE approaches violate the constraint and lead to an infeasible optimal solution. The obtained optimal solutions of the six methods are described in Fig. 4. From Fig. 4, it can be seen that only the optimal solutions obtained by the proposed SCU-CI approach and EAMGO fall into the feasible region and are very close to the constraint boundary, while the optimal solutions obtained by other approaches are infeasible.

Fig. 4
figure 4

Optimal solutions from different approaches

Full size image

To demonstrate the sequential updating process of the proposed SCU-CI approach, Fig. 5 provides the sample points and their confidence intervals of the constraint in different generations of GA.

Fig. 5
figure 5

Individuals, selected sample points, and their confidence level in different generations of GA

Full size image

As shown in Fig. 5a, the individuals in the first generation are randomly distributed in the design space, and the confidence intervals of the Kriging model of the constraint are large for most individuals. With the optimization process goes on, the new sample points are added around the constraint boundary. It can be seen in Fig. 5b that the individuals in the sixth generation are closer to the constraint boundary and the confidence intervals are becoming smaller. As shown in Fig. 5c, all the individuals are near the constraint boundary with small confidence intervals (most of them close to being 0) in the last generation of GA. The newly added sample points of the proposed SCU-CI approach are plotted in Fig. 6. In Fig. 6, the red triangles represent the newly added sample points, the black dash line and the red dash-and-dot line denote the two constraints, and the blue domain is the feasible region of the optimization problem. As illustrated in Fig. 6, the newly added sample points of the proposed SCU-CI approach are distributed around the constrained boundary.

Fig. 6
figure 6

Added sample point diagram of the proposed sequential sampling method

Full size image

It can be concluded from Figs. 5 and 6 that the searching space of the proposed SCU-CI approach can adaptively locate the regions, in where the feasibility states of the individuals could be changed due to the prediction uncertainty from the Kriging surrogate model. This can result in a large probability to get a more desirable solution.

4.2 Additional numerical test cases

In this section, eight additional numerical test cases from Wang et al. [55] are used to illustrate the effectiveness of the proposed SCU-CI approach. The formulations of these test cases are described as follows. A more detailed description of these examples, e.g., characteristics, actual optimal solutions, can be found in Wang et al. [55]:

Gomez

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = \Bigg(4 - 2.1x_{1}^{2} + \frac{1}{3}x_{1}^{4} \Bigg)x_{1}^{2} + x_{1} x_{2} + \Bigg( - 4 + 4x_{2}^{2} \Bigg)x_{2}^{2} \hfill \\ s.t. \hfill \\ g = - \sin (4\pi x_{1} ) + 2\sin^{2} (2\pi x_{2} ) \le 0 \hfill \\ - 1 \le x_{i} \le 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} for{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2. \hfill \\ \end{array}$$
(22)

Constrained Branin

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = \frac{1}{51.95}((ax_{2} - bx_{1}^{2} + cx_{1} - d)^{ 2} + h(1 - ff)\cos (x_{1} ) - 44.81) \hfill \\ s.t. \hfill \\ g = \mathop {\text{max} }\limits_{{j \in \{ 1,2\} }} \{ g_{j} \} \le 0 \hfill \\ g_{1} = \frac{1}{10}(x_{1} (1 - x_{2} ) - x_{2} ) \hfill \\ g_{2} = \frac{1}{10}\left( {1 - \left( {\frac{{(x_{1} - 5)^{2} }}{8} + \frac{{(x_{2} - 15)^{2} }}{4}} \right)} \right) \hfill \\ a = 1,b = \frac{5.1}{{4\pi^{2} }},c = \frac{5}{\pi },d = 6,h = 10,ff = \frac{1}{8\pi } \hfill \\ - 5 \le x_{1} \le 10,0 \le x_{2} \le 15. \hfill \\ \end{array}$$
(23)

New Branin

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = \frac{1}{80}\left( { - (x_{1} - 10)^{2} - (x_{2} - 15)^{2} } \right) \hfill \\ s.t. \hfill \\ g = \frac{1}{51.95}((ax_{2} - bx_{1}^{2} + cx_{1} - d)^{ 2} + h(1 - ff)\cos (x_{1} ) - 5 + h) \le 0 \hfill \\ a = 1,b = \frac{5.1}{{4\pi^{2} }},c = \frac{5}{\pi },d = 6,h = 10,ff = \frac{1}{8\pi } \hfill \\ - 5 \le x_{1} \le 10,0 \le x_{2} \le 15. \hfill \\ \end{array}$$
(24)

Sasena

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = - (x_{1} - 1)^{2} - (x_{2} - 0.5)^{2} \hfill \\ s.t. \hfill \\ g = \mathop {\text{max} }\limits_{{j \in \{ 1,2,3\} }} \{ g_{j} \} \le 0 \hfill \\ g_{1} = ((x_{1} - 3)^{2} + (x_{2} + 2)^{2} )e^{{ - x_{2}^{7} }} - 12 \hfill \\ g_{2} = 10x_{1} + x_{2} - 7 \hfill \\ g_{3} = (x_{1} - 0.5)^{2} + (x_{2} - 0.5)^{2} - 0.2 \hfill \\ 0 \le x_{i} \le 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} for{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2. \hfill \\ \end{array}$$
(25)

Qcp4

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = - 2x_{1} + x_{2} - x_{3} \hfill \\ s.t. \hfill \\ g = \mathop {\text{max} }\limits_{{j \in \{ 1,2,3\} }} \{ g_{j} \} \le 0 \hfill \\ g_{1} = x_{1} + x_{2} + x_{3} - 4 \hfill \\ g_{2} = 3x_{2} + x_{3} - 6 \hfill \\ g_{3} = - \varvec{x^{\prime}A^{\prime}Ax} + 2\varvec{y^{\prime}Ax} - \varvec{y}^{2} + 0.25\varvec{b} - \varvec{z}^{2} \hfill \\ \varvec{A} = [0,0,1;0, - 1,0; - 2,1, - 1], \hfill \\ \varvec{b} = [3;0; - 4],\varvec{y} = [1.5; - 0.5; - 5],\varvec{z} = [0; - 1; - 6] \hfill \\ \varvec{x} = [x_{1} ;x_{2} ;x_{3} ].0 \le x_{1} \le 2,0 \le x_{i} \le 3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 2,3. \hfill \\ \end{array}$$
(26)

G4

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = \frac{{5.3578547x_{3}^{2} + 0.8356891x_{1} x_{5} + 37.293239x_{1} - 40792.141}}{2000} \hfill \\ s.t. \hfill \\ g = \mathop {\text{max} }\limits_{{j \in \{ 1,2,3,4,5,6\} }} \{ g_{j} \} \le 0 \hfill \\ g_{1} = 0 - u \hfill \\ g_{2} = u - 92 \hfill \\ g_{3} = 90 - v \hfill \\ g_{4} = v - 110 \hfill \\ g_{5} = 20 - w \hfill \\ g_{6} = w - 25 \hfill \\ u = 85.334407 + 0.0056858x_{2} x_{5} + 0.0006262x_{1} x_{4} - 0.0022053x_{3} x_{5} \hfill \\ v = 80.51249 + 0.0071317x_{2} x_{5} + 0.0029955x_{1} x_{2} + 0.00 2 1 8 1 3x_{ 3}^{ 2} \hfill \\ w = 9.300961 + 0.0047026x_{3} x_{5} + 0.0012547x_{1} x_{3} + 0.0019085x_{3} x_{4} \hfill \\ 78 \le x_{1} \le 102,33 \le x_{2} \le 45,27 \le x_{i} \le 45{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 3,4,5. \hfill \\ \end{array}$$
(27)

G24

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = \frac{5}{7}( - x_{1} - x_{2} ) \hfill \\ s.t. \hfill \\ g = \mathop {\text{max} }\limits_{{j \in \{ 1,2\} }} \{ g_{j} \} \le 0 \hfill \\ g_{1} = \frac{1}{4}( - 2x_{1}^{4} + 8x_{1}^{3} - 8x_{1}^{2} + x_{2} - 2) \hfill \\ g_{2} = \frac{1}{4}( - 4x_{1}^{4} + 32x_{1}^{3} - 88x_{1}^{2} + 96x_{1} + x_{2} - 36) \hfill \\ 0 \le x_{1} \le 3,0 \le x_{2} \le 4. \hfill \\ \end{array}$$
(28)

Angun

$$\begin{array}{l} \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} f = \frac{5}{34.8}(5(x_{1} - 1)^{2} + (x_{2} - 5)^{2} + 4x_{1} x_{2} ) \hfill \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ g = \mathop {\text{max} }\limits_{{j \in \{ 1,2\} }} \{ g_{j} \} \le 0 \hfill \\ g_{1} = \frac{5}{17.1544}((x_{1} - 3)^{2} + x_{2}^{2} + x_{1} x_{2} - 4) \hfill \\ g_{2} = \frac{5}{17.1544}(x_{1}^{2} + 3(x_{2} + 1.061)^{2} - 9) \hfill \\ 0 \le x_{1} \le x_{3} , - 2 \le x_{2} \le 1. \hfill \\ \end{array}$$
(29)

Since the actual optimal solutions for these numerical examples are known, the stopping criteria used are the same as that of the illustration example, i.e., the max iterations reach or the difference between the optimal solution and the true solution is in the predefined domain, the algorithm will stop. To consider the randomness of the GA, 30 different runs are carried out for each numerical example. As mentioned before, the obtained optimal solution may violate the actual constraints due to the interpolation uncertainties from the Kriging surrogate models. For constrained optimization problems, it is known that satisfying the constraints is the first condition followed by the optimal objective function and solving efficiency. Therefore, the ratios of the feasibility in 30 runs for each numerical case are recorded and compared. A high ratio of the feasibility denotes a greater ability to guarantee the feasibility of the solutions in surrogate model-assisted optimization design problems. Table 3 summaries the ratios of the feasibility of the different approaches for the additional numerical test cases. An intuitive conclusion can be made from Table 3 that the proposed SCU-CI approach can ensure the feasibility of the solution for most numerical test cases, which is not the case for other five approaches. Table 4 summarizes the average ranking results for the six approaches considering the additional numerical test cases. As observed in Table 4, the average ranking of the proposed SCU-CI approach is 1.375, which is the best among all approaches. EV ranks the second, followed by the MAX-MSE. The average rank of WAE is the worst.

Table 3 Ratios of the feasibility of the different approaches for the additional numerical test cases
Full size table
Table 4 Average ranking results for the six approaches for the additional numerical test cases
Full size table

In addition, p values are used to test the differences between approaches over multiple data sets regarding the ratio of the feasibility. The Bergmann–Hommel procedure is adopted to calculate adjusted p values [56], as listed in Table 5. The p values for WAE vs. SCU-CI, EAMGO vs. SCU-CI, and PoF vs. SCU-CI are less than 0.05, indicating that there are significant differences in the ability to guarantee the feasibility of the solutions between the proposed SCU-CI approach and these three constraint-updating techniques. The differences between the proposed SCU-CI and the rest two approaches (MAX-MSE and EV) are not significant.

Table 5 Adjusted p values for ratios of the feasibility obtained in the additional numerical test cases by Bergmann–Hommel’s dynamic procedure
Full size table

To further compare the efficiency of MAX-MSE, EV, and the proposed SCU-CI, the mean values of NS are recorded. Notice that the quality of the optimal solution (objective function value) is considered in the convergence conditions. The comparison results of the NS are summarized in Table 6. As shown in Table 6, the proposed SCU-CI approach required the smallest NS in six of the eight test cases, indicating that SCU-CI approach is the most effective approach among these three constraint-updating techniques. The p values are also used to test the differences between approaches over multiple data sets regarding the efficiency. The adjusted p values are listed in Table 7. It is concluded from Table 7 that there are significant differences in efficiency between the proposed SCU-CI approach and MAX-MSE and EV.

Table 6 NS of the EV, MAX-MSE, and SCU-CI for the additional numerical test cases
Full size table
Table 7 NS of the EV, MAX-MSE, and SCU-CI for the additional numerical test cases
Full size table

4.3 Design optimization of lattice structure design of an L-shaped bracket

The proposed SCU-CI approach is applied to the design optimization of lattice structure design of an L-shaped bracket. The bracket is a simplified version of a proprietary aircraft component. The bracket consists of three vertical walls and a base. There are four support beams between the three walls. The bracket is fixed along the back side and subjected to a distributed load of 0.065 N/mm2 at the bottom surface. The structure and the loading of the bracket are plotted in Fig. 7.

Fig. 7
figure 7

Structure and the loading of the bracket

Full size image

The lattice model of the bracket is established using a cross lattice type with a size of 10 mm. In this paper, the ANSYS 18.0 is used for getting the simulation results, and the computational platform with a 3.70 GHz AMD Ryzen 7 2700X Eight-Core Processor and 8 GB RAM is used. The lattice model and the simulation result can be seen in Fig. 8. The material properties are listed in Table 8.

Fig. 8
figure 8

Lattice model and the simulation results of the bracket

Full size image
Table 8 Material properties of the bracket
Full size table

In this design optimization problem, the objective is to minimize the total volume of the bracket while keeping the maximal stress and displacement below the threshold values. The mathematical formulation of the problem is given as

$$\begin{array}{l} {\text{find}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} d_{1} ,d_{2} ,d_{3} ,d_{4} ,d_{5} ,d_{6} \hfill \\ \hbox{min} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} V \hfill \\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} u \le 5mm \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S_{\text{max} } \le 36MPa \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.7\;{\text{mm}} \le d_{1} \le 1.5\;{\text{mm}},0.3\;{\text{mm}} \le d_{2} \le 1.0\;{\text{mm}},0.1\;{\text{mm}} \le d_{3} \le 0.7\;{\text{mm}} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.0\;{\text{mm}} \le d_{4} \le 2.5\;{\text{mm}},0.5\;{\text{mm}} \le d_{5} \le 2.0\;{\text{mm}},0.1\;{\text{mm}} \le d_{6} \le 1.5\;{\text{mm,}} \hfill \\ \end{array}$$
(30)

where \(u\) is the maximal displacement of the bracket, and \(S_{\text{max} }\) is the maximum equivalent stress. \(d_{1} ,d_{2} ,d_{3} ,d_{4} ,d_{5}\) and \(d_{6}\) are the design variables, where \(d_{1}\) represents the radius of the frame pillar, \(d_{2}\) represents the radius of the frame cross pillar, \(d_{3}\) represents the radius of the cross pillar, and \(d_{4} ,d_{5} ,d_{6}\) represent the radius of the frame cross, pillars cross, and upper beams, respectively.

In this case, the constraints are obtained from the expensive simulation models, while the objective function can be calculated by arithmetic expression. The proposed SCU-CI approach and the existing five approaches are used to solve this design optimization problem. For the engineering problem, we also compare the proposed SCU-CI approach with the direct simulation-based approach (DSBA), in which simulation model instead of Kriging surrogate model is directly used during the design optimization process. 60 initial sample points are generated for the initial Kriging metamodel. The comparison results are listed in Table 9.

Table 9 Comparison results of the different approaches for the engineering case
Full size table

As shown in Table 9, the proposed approach can obtain a feasible solution, which is very close to the solution obtained by DSBA. However, the computation cost of simulation-based approach is about 17 times more than the proposed approach, which is unacceptable for complex engineering problems. The EV approach and PoF approach can also obtain feasible solutions. However, the obtained solutions are inferior to that from the proposed SCU-CI. Concerning computational efficiency, the computational cost of these two approaches is 146 and 150% higher than the proposed approach, respectively. In addition, the MAX-MSE approach, EAMGO approach, and the WAE approach failed to obtain a feasible solution. The results indicate that the SCU-CI shows a better ability to handing the constrained optimization problem.

4.4 Lightweight design optimization of conical shell with longitudinal and circumferential stiffeners

In this section, the proposed approach is applied to the design optimization of a conical shell with longitudinal and circumferential stiffeners. The conical shell is a non-pressures underwater structure. Figure 9 plots the structure profile.

Fig. 9
figure 9

Structured profile of the conical shell

Full size image

As illustrated in Fig. 9, the structure of the conical shell consists of an outer plate and the inner stiffened ribs. In this work, the fixed parameters are the radius of the small end of the conical shell R1 = 500 mm, the radius of the big end of the conical shell R2 = 2000 mm, and the length of the conical shell is 600 mm. The number and the distribution of the stiffeners are fixed. The geometry model constructed by ANSYS 18.0 is shown in Fig. 10.

Fig. 10
figure 10

Geometry model constructed by ANSYS

Full size image

The design variables are the dimension of the longitudinal and circumferential stiffeners which are T section, the thickness of the shell plate for the former five rib space t1, and the thickness of the remainder shell plate t2. In this work, the optimizing problem is a constrained problem that minimizes the weight of the conical shell and the design constrains are the vibration performance of the conical shell and the dimensions’ matches of the ribs. Thus, the optimization problem of the shell can be specified as

$$\begin{array}{l} {\text{find}}\varvec{ x} = \left[ {x_{1} ,x_{2} ,,,x_{10} } \right] \hfill \\ {\text{minimize}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} w(\varvec{x}) \hfill \\ {\text{subject}}{\kern 1pt} {\kern 1pt} {\text{to}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{1} = 180Hz - f \le 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{2} = a_{z} - 90\;{\text{dB}} \le 0 \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{3} = \frac{{x_{1} }}{{20x_{2} }} - 1 \le 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{4} = \frac{{x_{3} }}{{8x_{4} }} - 1 \le 0 \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{5} = \frac{{x_{5} }}{{20x_{6} }} - 1 \le 0;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} g_{6} = \frac{{x_{7} }}{{8x_{8} }} - 1 \le 0, \hfill \\ \end{array}$$
(31)

where x1–x10 are the design variables, whose physical meaning and boundaries are presented in Table 10. \(w(x)\) denotes the total weight of this conical shell, \(f\) is the frequency of the first-order modal in the air, and \(a_{z}\) is the gross stage of the acceleration ranging from 100 Hz to 250 Hz at the small end of the conical shell, which can be calculated as

$$a_{z} = 10\log \left[ {f_{w} \sum\limits_{1}^{k} {\left( {\frac{{a_{i} }}{{a_{0} }}} \right)^{2} } } \right],$$
(32)

where k is the number of the calculated frequencies, \(a_{i}\) is the acceleration response under the ith order calculated frequency, \(a_{0} = 10^{ - 6}\)m/s2 is the basis acceleration, and \(f_{w}\) is the interval of sweep frequency. In this case, the constraints \(g_{1}\) and \(g_{2}\) are obtained from the expensive simulation models, while the objective function and the rest constraints can be calculated by arithmetic expression.

Table 10 Design variables and their ranges for the design optimization of conical shell
Full size table

The frequency of the first-order modal and the gross stage of the acceleration are assumed to be expensive to be obtained. In this simulation, the elastic modulus is \(E = 2.11 \times 10^{11} {\text{Pa}}\), the Poisson ratio is \(\mu = 0.3\), and the density of the material is \(\rho { = }7850\) kg/m3. A downward unit harmonic force is applied at the small end of the conical shell. Element Beam 188 and Shell 181 are used to simulate the geometry model of this conical shell structure. The mapped grid model with 6180 elements is used for this problem. The FEA model and simulation results are shown in Fig. 11.

Fig. 11
figure 11

FEA model and simulation results for the design optimization of the conical shell

Full size image

The proposed SCU-CI approach is compared with five existing approaches. 60 initial sample points are generated for constructing the initial Kriging metamodel. The optimal solutions of different approaches are summarized in Table 11. The corresponding objective functions, constraints, and the number of simulation calls are listed in Table 12.

Table 11 Optimal design points of different approaches
Full size table
Table 12 Corresponding objective functions, constraints, and the number of simulation calls for different approaches
Full size table

As observed in Table 12, only the DSBA approach and proposed SCU-CI approach can obtain feasible solutions for this engineering case. The other approaches failed to obtain feasible solutions. In terms of the computational cost, the number of total sample points of DSBA is 5050, which is actually a computation-prohibitive process for complex engineering problems. The total sample points of SCU-CI approach are about 20 times less than that of DSBA, indicating that the proposed SCU-CI approach can obtain feasible optimal solution while significantly reduce the computational cost.

5 Conclusion

In this work, general sequential constraints updating approach based on the confidence intervals from the Kriging surrogate model, SCU-CI, is proposed, in which an objective switching and sequential updating strategy is introduced to address two issues in the updating of Kriging surrogate model. One issue is whether the actual simulation models or the Kriging metamodel should be used to evaluate the feasibility of the design alternatives. The other one is which design alternatives would be selected to improve the prediction accuracy of the Kriging metamodel. The core idea is based on whether the feasibility status of the design alternatives would be changed because of the interpolation uncertainty from the Kriging surrogate model or not.

To demonstrate the applicability and efficiency of the proposed SCU-CI approach, nine numerical examples and two practical engineering cases are tested. The observations are summarized as follows, (a) the proposed SCU-CI approach can generally obtain the optimum that meets the requirements of the actual feasibility, while it is not the case in other five existing approaches due to the prediction uncertainty from the Kriging surrogate model and (b) in terms of the computational efficiency, the proposed SCU-CI approach shows obvious advantages compared to DSBA and is more efficient than EV, PoF, MAX-MSE, WAE, and EAMGO approaches when all of them can obtain the feasible solutions. It should be pointed out that the proposed SCU-CI approach is general in the sense that it can be integrated with any efficient global optimization approaches. As part of future work, combining the proposed approach with different sequential objective functions updating strategies for complex engineering optimization design problems will be investigated.