Global sensitivity analysis-enhanced surrogate (GSAS) modeling for reliability analysis

Abstract

An essential issue in surrogate model-based reliability analysis is the selection of training points. Approaches such as efficient global reliability analysis (EGRA) and adaptive Kriging Monte Carlo simulation (AK-MCS) methods have been developed to adaptively select training points that are close to the limit state. Both the learning functions and convergence criteria of selecting training points in EGRA and AK-MCS are defined from the perspective of individual responses at Monte Carlo samples. This causes two problems: (1) some extra training points are selected after the reliability estimate already satisfies the accuracy target; and (2) the selected training points may not be the optimal ones for reliability analysis. This paper proposes a Global Sensitivity Analysis enhanced Surrogate (GSAS) modeling method for reliability analysis. Both the convergence criterion and strategy of selecting new training points are defined from the perspective of reliability estimate instead of individual responses of MCS samples. The new training points are identified according to their contribution to the uncertainty in the reliability estimate based on global sensitivity analysis. The selection of new training points stops when the accuracy of the reliability estimate reaches a specific target. Five examples are used to assess the accuracy and efficiency of the proposed method. The results show that the efficiency and accuracy of the proposed method are better than those of EGRA and AK-MCS.

1 Introduction

Reliability analysis predicts the reliability of a product based on available knowledge about the relationship between system response, inputs, and variations in the inputs (Haldar and Mahadevan 2000). In engineering applications, the relationship between system response and inputs is often available through computer simulation models, such as finite element analysis (FEA) and computational fluid dynamics (CFD) models. Since physics simulation models are computationally intensive, a crucial issue in reliability analysis is how to predict reliability with fewer function evaluations, i.e., fewer runs of the expensive physics simulations. Two classical and widely used methods are the First-Order Reliability Method (FORM) and Second-Order Reliability Method (SORM) (Haldar and Mahadevan 2000; Du and Hu 2012). These two methods approximate the system performance function at a single point called the Most-Probable Point (MPP). For response functions with highly nonlinear behaviors or multimodal distribution properties, the accuracy of FORM and SORM may not be acceptable. In this situation, Monte Carlo sampling based on the surrogate model is a promising way (Faravelli 1989; Simpson et al. 2001), where surrogate models are inexpensive substitutes for the original expensive physics simulation models.

During the past decades, various surrogate model-based reliability analysis methods have been developed and may be roughly classified into three groups. The first group consists of methods based on the polynomial chaos expansion (PCE) (Xiu and Karniadakis 2002; Xiu and Karniadakis 2003). For example, Paffrath and Wever proposed a shifted and windowed Hermite polynomial chaos method to enhance the accuracy of small failure probability analysis (Paffrath and Wever 2007). Blatman and Sudret developed an adaptive algorithm to efficiently build a sparse polynomial chaos expansion of a mechanical model with random inputs (Blatman and Sudret 2010). To reduce the number of bivariate basis functions in expansion, Hu and Youn integrated sparse polynomial chaos expansion with dimension reduction techniques (Vinh et al. 2011). The second group of methods relies on Kriging or Gaussian process (GP) models. Examples of Kriging-based methods include the Efficient Global Reliability Analysis (EGRA) method proposed by Bichon et al. (Bichon et al. 2008), the Adaptive Kriging Monte Carlo simulation (AK-MCS) method developed by Echard et al. (Echard et al. 2011), combined importance sampling and adaptive Kriging (Echard et al. 2013; Dubourg et al. 2013), and Kriging-based quasi-optimal importance sampling (Dubourg and Sudret 2014). The third group is based on Support Vector Machines (SVM). In this group, samples are classified into safe or failed using SVM. For instance, Basudhar and Missoum applied SVM to construct explicit limit state boundaries (Basudhar and Missoum 2008), and also to identify disjoint failure domains and limit state boundaries for continuous response (Basudhar et al. 2008). Bourinet et al. combined subset simulation and SVMs to assess small failure probabilities (Bourinet et al. 2011). Along with the above three types of surrogate model techniques, other types of surrogate models such as quadratic response surfaces (Gomes and Awruch 2004) and neural networks (Gomes and Awruch 2004) have also been studied in reliability analysis.

In this paper, we focus on the Kriging-based method. Since being proposed in the area of geosciences (Stein 1999) in the middle of the nineteenth century, Kriging models have been intensively studied in many other fields during the past decades. Reliability analysis using Kriging models has been investigated in (Echard et al. 2011, 2013; Dubourg et al. 2013; Dubourg and Sudret 2014) as mentioned above. Amongst these methods, EGRA and AK-MCS methods are two representative approaches that dramatically improve the efficiency of reliability analysis. These two methods implement a similar procedure. An initial surrogate model is constructed first by using Kriging with a few initial training points. Then new training points are identified adaptively based on learning functions. In the EGRA method, an Expected Feasibility Function (EFF) is defined as the learning function. In the AK-MCS method, a U function is defined. Both the EFF and U functions are used to quantify how close the training point is to the limit state. By adding more training points in the region of the limit state, the required number of training points for reliability analysis is reduced. However, in these two methods, it is observed that some unnecessary training points (those points that bring no change to the results of reliability analysis as shown in the numerical examples (the points labeled as red “+” in Figs. 8, 9, 16, and 17)) are identified close to the limit state for two reasons. The first one is that the convergence criterion of the learning function (i.e., EFF and U) is defined from single system responses of individual MCS samples but not from the aspect of reliability analysis accuracy. Even if the response of one single sample cannot satisfy the requirement of learning function defined in AK-MCS and EGRA, it does not mean that the reliability analysis accuracy cannot satisfy the requirement. As indicated in Fig. 6, after iteration 18, the reliability analysis result is already very close to the true value, but EGRA keeps adding new training points. The added new training points, however, almost bring no change to the reliability analysis results. After removing those unnecessary training points, it can be seen in Fig. 8 that the limit state learned from EGRA almost does not change. Similar phenomenon is observed for AK-MCS. The other reason is the way of selecting new training points. In both AK-MCS and EGRA, a new training point is selected independently without considering its correlation with other training points (points used to construct surrogate model) and samples (candidate points from which the training point is selected) around it. The selected training points without considering this correlation may not be the optimal ones. This phenomenon comes from the definition of learning functions defined in EGRA and AK-MCS. More detailed discussions about the limitation of AK-MCS and EGRA are given in Sec. 3.1.1.

This paper proposes a Global Sensitivity Analysis enhanced Surrogate (GSAS) model method for reliability analysis. The method is based on two main ideas: (1) Uncertainty quantification of the reliability estimate. The uncertainty in the prediction of the Kriging model is propagated through the failure indicator model to quantify the uncertainty in the failure probability estimate. (2) Selection of new training points by analyzing their contributions to the uncertainty of the reliability estimate. Correlation between samples from which new training points are selected is considered during the uncertainty contribution analysis of each sample point. Based on these two ideas, training points are selected such that they have the most significant impact on the ultimate objective — estimation of reliability. Based on these two ideas, unnecessary training points identified in EGRA and AK-MCS are effectively eliminated. The efficiency of reliability analysis is therefore improved.

The paper is organized as follows. Section 2 provides a brief review of the Kriging surrogate model method and reliability analysis approaches based on adaptive Kriging models. Section 3 introduces the proposed surrogate model method based on global sensitivity analysis. Section 4 summaries the main procedure and algorithms of the proposed method. Five examples are used to demonstrate the effectiveness of the proposed method in Section 5. Following that, conclusions remarks are given in Section 6.

2 Kriging-based reliability analysis

2.1 A brief review of Kriging models

In Kriging models, the performance function g(x) is assumed to be a realization of a Gaussian process (GP), G(x), given by (Rasmussen 2006)

$$ G\left(\mathbf{x}\right)=\mathbf{f}{\left(\mathbf{x}\right)}^T\boldsymbol{\upbeta} +\varepsilon \left(\mathbf{x}\right) $$

(1)

where β = [β ₁, β ₂, ⋯, β _p ]^T is a vector of unknown coefficients, f(x) = [f ₁(x), f ₂(x), ⋯, f _p (x)]^T is a vector of regression functions, f(x)^T β is the trend of prediction or mean of the GP, and ε(x) is assumed to be a GP with zero mean and covariance Cov[ε(x ⁽ⁱ⁾), ε(x ^(j))].

Cov[ε(x ⁽ⁱ⁾), ε(x ^(j))] is given by

$$ Cov\left[\varepsilon \left({\mathbf{x}}^{(i)}\right),\kern0.5em \varepsilon \left({\mathbf{x}}^{(j)}\right)\right]={\sigma}_{\varepsilon}^2R\left({\mathbf{x}}^{(i)}-{\mathbf{x}}^{(j)},\kern0.5em \boldsymbol{\uptheta} \right) $$

(2)

in which σ ² _ε is the constant variance of the GP, θ is a vector of unknown parameters, and R(⋅, ⋅) is the correlation function. There are a variety of correlation functions available. The most commonly used one is the Gaussian correlation function given by (Rasmussen 2006; Kaymaz 2005; Xiong et al. 2007; Kbiob 1951; Kleijnen 2009; Santner et al. 2003)

$$ R\left({\mathbf{x}}^{(i)}-{\mathbf{x}}^{(j)},\kern0.5em \boldsymbol{\uptheta} \right)= \exp \left[-{\displaystyle \sum_{k=1}^{n_d}{\theta}_k{\left|{\mathbf{x}}_k^{(i)}-{\mathbf{x}}_k^{(j)}\right|}^2}\right] $$

(3)

where n _d is the dimension of design variables and x ⁽ⁱ⁾ _k is the k-th element of x ⁽ⁱ⁾.

With k training points, [x ⁽ⁱ⁾, g(x ⁽ⁱ⁾)] _{i = 1, 2, ⋯, k} , the coefficients β is estimated by (Lophaven et al. 2002)

$$ \boldsymbol{\upbeta} ={\left({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}{\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{g} $$

(4)

where R is a correlation matrix with elements, R(x ⁽ⁱ⁾ − x ^(j), θ), i, j = 1, 2, ⋯, k, F = [f(x ⁽¹⁾)^T, f(x ⁽²⁾)^T, ⋯, f(x ^(k))^T]^T, and g = [g(x ⁽¹⁾), g(x ⁽²⁾), ⋯, g(x ^(k))]^T.

For a new point x, the mean prediction (ĝ(x)) and mean square error (MSE) (MSE(ĝ(x))) of the prediction of G(x) are estimated using the best linear unbiased estimation (BLUE) as follows (Lophaven et al. 2002):

$$ \widehat{g}\left(\mathbf{x}\right)=\mathbf{f}{\left(\mathbf{x}\right)}^T\boldsymbol{\upbeta} +\mathbf{r}{\left(\mathbf{x}\right)}^T{\mathbf{R}}^{-1}\left(\mathbf{g}-\mathbf{F}\boldsymbol{\upbeta } \right) $$

(5)

$$ MSE\left(\widehat{g}\left(\mathbf{x}\right)\right)={\sigma}_{\varepsilon}^2\left\{1-\mathbf{r}{\left(\mathbf{x}\right)}^T{\mathbf{R}}^{-1}\mathbf{r}\left(\mathbf{x}\right)+{\left[{\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{r}\left(\mathbf{x}\right)-\mathbf{f}\left(\mathbf{x}\right)\right]}^T{\left({\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}\left[{\mathbf{F}}^T{\mathbf{R}}^{-1}\mathbf{r}\left(\mathbf{x}\right)-\mathbf{f}\left(\mathbf{x}\right)\right]\right\} $$

(6)

where

$$ \mathbf{r}\left(\mathbf{x}\right)=\left[R\left(\mathbf{x}-{\mathbf{x}}^{(1)},\kern0.5em \boldsymbol{\uptheta} \right),\kern0.5em R\left(\mathbf{x}-{\mathbf{x}}^{(2)},\kern0.5em \boldsymbol{\uptheta} \right),\kern0.5em \cdots, \kern0.5em R\left(\mathbf{x}-{\mathbf{x}}^{(k)},\kern0.5em \boldsymbol{\uptheta} \right)\right] $$

(7)

and

$$ {\sigma}_{\varepsilon}^2=\frac{{\left(\mathbf{g}-\mathbf{F}\boldsymbol{\upbeta } \right)}^T{\mathbf{R}}^{-1}\left(\mathbf{g}-\mathbf{F}\boldsymbol{\upbeta } \right)}{k} $$

(8)

For the sake of illustration, in the following sections, all the hyper-parameters of the GP model, which include β, the variance σ ² _ε , and parameters θ of correlation function, are denoted as Θ. Besides, we define a new random variable G _p (x) as the prediction at point x conditioned on current training points and ${G}_p\left(\mathbf{x}\right)\sim N\left(\widehat{g}\left(\mathbf{x}\right),\kern0.5em {\sigma}_{G_p}^2\left(\mathbf{x}\right)\right)$, where N(⋅, ⋅) is normal distribution and ${\sigma}_{G_p}\left(\mathbf{x}\right)=\sqrt{MSE\left(\widehat{g}\left(\mathbf{x}\right)\right)}$. The proposed method developed in this paper is based on an available Kriging toolbox called DACE (Lophaven et al. 2002). When the roughness parameters θ are overestimated, the uncertainty of prediction may be overestimated. As a result, the reliability analysis methods will increase the number of training points in the surrogate modeling.

2.2 Reliability analysis based on Kriging models

Once a Kriging model is built, the reliability estimation can simply be based on Monte Carlo sampling (MCS) with the Kriging model, since function evaluation of the Kriging model is inexpensive. A common way is to estimate the probability of failure based on mean predictions, ĝ(x), as follows:

$$ {\widehat{p}}_f\approx \frac{1}{N}{\displaystyle \sum_{i=1}^NI\left(\widehat{g}\left({\mathbf{x}}^{(i)}\right)\right)} $$

(9)

where N is the number of samples in MCS, and I(ĝ(x ⁽ⁱ⁾)) = 1, if μ _g (x ⁽ⁱ⁾) ≤ 0, otherwise I(ĝ(x ⁽ⁱ⁾)) = 0.

The boundary ĝ(x) = 0 is commonly used to classify the samples into safe and failed samples. This implies that the accuracy of the failure probability estimate ${\widehat{p}}_f$ is mainly affected by the limit state or boundary ĝ(x) = 0. By generating more training points near the limit state or in the region of interest, accuracy and efficiency of reliability analysis can be improved. Inspired by this idea, a group of methods have been proposed, such as EGRA (Bichon et al. 2008) and AK-MCS (Echard et al. 2011), which construct the Kriging model G(x) adaptively based on learning functions. In EGRA, the learning function is called the expected feasibility function (EFF) and is defined as

$$ \begin{array}{l} EFF\left(\mathbf{x}\right)=\left(\widehat{g}\left(\mathbf{x}\right)-e\right)\left[2\varPhi \left(\frac{e-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)-\varPhi \left(\frac{e^L-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)-\varPhi \left(\frac{e^U-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)\right]\\ {}\left.\kern0.5em -{\sigma}_{G_p}\left(\mathbf{x}\right)\left[2\phi \left(\frac{e-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)\right.-\phi \left(\frac{e^L-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)-\phi \left(\frac{e^U-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)\right]-\left[\varPhi \left(\frac{e^L-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)-\varPhi \left(\frac{e^U-\widehat{g}\left(\mathbf{x}\right)}{\sigma_{G_p}\left(\mathbf{x}\right)}\right)\right]\end{array} $$

(10)

in which e ^U = e + ε, e ^L = e − ε, e is the failure threshold, ε is usually chose as $\varepsilon =2{\sigma}_{G_p}\left(\mathbf{x}\right)$, and Φ(⋅) and ϕ(⋅) are the cumulative density function (CDF) and probability density function (PDF) of a standard normal random variable. The EFF quantifies how well the true value (g(x)) of G _p (x) at x is expected to be at the limit state (Bichon et al. 2008).

In AK-MCS, a U function is defined as the learning function as below

$$ U\left(\mathbf{x}\right)=\frac{\left|\widehat{g}\left(\mathbf{x}\right)\right|}{\sigma_{G_p}\left(\mathbf{x}\right)} $$

(11)

The U value computed from Eq. (11) is associated with the probability (Φ(−U)) of making a mistake on the sign of g(x) by substituting g(x) with ĝ(x) (Echard et al. 2011). In AK-MCS, the U value of each sample is computed using Eq. (11) and a new training point is selected by arg min{U(x)}. The algorithm stops when min{U(x)} > 2.

3 GSAS method for reliability analysis

3.1 Basic principles of the GSAS method

In this section, we first investigate the drawbacks of EGRA and AK-MCS. Based on that, we propose the basic idea of GSAS.

3.1.1 Limitation analysis of EGRA and AK-MCS

Recall that in surrogate model-based reliability analysis methods, the probability of failure ${\widehat{p}}_f$ is estimated based on Monte Carlo sampling as

$$ {\widehat{p}}_f\approx {\displaystyle \sum_{i=1}^NI\left({G}_p\left({\mathbf{x}}^{(i)}\right)\right)}/N $$

(12)

where x ⁽ⁱ⁾, i = 1, 2, ⋯, N are sampling points from MCS.

In above equation, I(G _p (x ⁽ⁱ⁾)) = 1, if G _p (x ⁽ⁱ⁾) ≤ 0, otherwise, I(G _p (x ⁽ⁱ⁾)) = 0. For a point x ⁽ⁱ⁾, from a Kriging surrogate model, we have ${G}_p\left({\mathbf{x}}^{(i)}\right)\sim N\left(\widehat{g}\left({\mathbf{x}}^{(i)}\right),\kern0.5em {\sigma}_{G_p}^2\left({\mathbf{x}}^{(i)}\right)\right)$, where ĝ(x ⁽ⁱ⁾) and ${\sigma}_{G_p}^2\left({\mathbf{x}}^{(i)}\right)$ are obtained from Eqs. (5) and (6).

Due to the uncertainty in G _p (x ⁽ⁱ⁾), there is also uncertainty in ${\widehat{p}}_f$. Based on Eq. (12), the variance of ${\widehat{p}}_f$ is computed by

$$ Var\left({\widehat{p}}_f\right)\approx \frac{1}{N^2}\left({\displaystyle \sum_{i=1}^NVar\left(I\left({G}_p\left({\mathbf{x}}^{(i)}\right)\right)\right)}+{\displaystyle \sum_{i\ne j}Cov\left(I\left({G}_p\left({\mathrm{x}}^{(i)}\right)\right),I\left({G}_p\left({\mathrm{x}}^{(j)}\right)\right)\right)\kern0.5em }\right) $$

(13)

where Var(⋅) stands for variance and Cov(⋅, ⋅) is the covariance.

The variance of ${\widehat{p}}_f$ as indicated in Eq. (13) consists of two parts: ${\displaystyle \sum_{i=1}^NVar\left(I\left({G}_p\left({\mathbf{x}}^{(i)}\right)\right)\right)}$ and ${\displaystyle \sum_{i\ne j}Cov\left(I\left({G}_p\Big({\mathbf{x}}^{(i)}\right)\right),\kern0.5em I\left({G}_p\left({\mathbf{x}}^{(j)}\right)\right)}$. The first part comes from responses of individual MCS samples while the second part comes from the mutual effects between these individual responses. From Eq. (13), it is found that the learning function defined in EGRA and AK-MCS mainly focuses on reducing the individual variances in the first part. There are therefore two limitations common to both of them, which are explained as follows.

• (1) The convergence criteria of AK-MCS and EGRA are defined from the aspect of individual samples and not from the aspect of reliability analysis. For instance, in the AK-MCS method, even though the U values of some samples are less than two, which do not satisfy the convergence criterion, min{U(x)} > 2, it does not mean that the samples cannot meet the accuracy requirement of reliability analysis. Also, as presented in Eq. (13), even if the variance of some individual inputs Var(I(G _p (x ⁽ⁱ⁾))) cannot satisfy the requirement of AK-MCS or EGRA, it does not imply that the uncertainty of ${\widehat{p}}_f$ cannot satisfy the requirement. From results presented in the numerical examples, it can be seen that adding more training points will not change the failure probability estimate too much after certain iterations (Figs. 6, 14, 19, 21).

• (2) The new training point is selected independently without considering its effects on other samples and reliability analysis. The sample with the minimum U value is selected as the new training point in AK-MCS. This sample, however, may not be the optimal one when it is evaluated from the aspect of reliability analysis (as indicated in Eq. (13)). The optimal point should be the one which affects the reliability analysis result most significantly.

  Motivated by overcoming these two limitations, a Global Sensitivity Analysis enhanced Surrogate (GSAS) model method is developed in this work, which further improves the efficiency of AK-MCS and EGRA for reliability analysis.

3.1.2 Basic idea of GSAS

In surrogate model-based reliability analysis methods, a widely used method is to directly use the mean prediction ĝ(x ⁽ⁱ⁾) to substitute for G _p (x ⁽ⁱ⁾) in Eq. (12). The direct use of mean value will inevitably result in error in the reliability estimate if the surrogate model is not well trained.

The basic idea of the proposed GSAS method is treating the probability of failure estimate (${\widehat{p}}_f$) in a manner similar to the system output or response; and the system inputs are the random system responses predicted from Kriging model (as indicated in Fig. 1). By propagating the uncertainty in the inputs of Fig. 1 through Eq. (12), the uncertainty in the failure probability estimate is quantified. Based on that, a new convergence criterion is defined. In order to select a new training point, GSA is used to quantify the contributions of uncertainty in G _p (x ⁽ⁱ⁾), i = 1, 2, ⋯, N on the uncertainty of ${\widehat{p}}_f$. Since G _p (x ⁽ⁱ⁾), i = 1, 2, ⋯, N are correlated, correlation between G _p (x ⁽ⁱ⁾), i = 1, 2, ⋯, N is considered during the GSA. A new training point is selected such that the reduction of uncertainty in ${\widehat{p}}_f$ is the most significant.

Fig. 1

Probability of failure estimate as a system response

3.2 A new convergence criterion

In this section, we first present a conservative formula for the error estimation of reliability prediction. We then discuss how to estimate the error based on the uncertainty quantification of ${\widehat{p}}_f$.

3.2.1 Formula for error estimation of reliability prediction

In AK-MCS method, a U function is defined as in Eq. (11). A large value of U indicates a low probability of making an error on the sign of ĝ(x). The error of reliability prediction based on the surrogate model, therefore, mainly comes from those sampling points with small values of U. For U(x) > 3.1, the probability of making a mistake in the sign of samples is less than 0.001. We therefore assume that the error in the reliability estimate mainly comes from the group of samples with U(x) ≤ 3.1. This assumption holds since the value of 3.1 is larger than the value of 2 used in AK-MCS (Echard et al. 2011). Based on this assumption, we divide the samples x ^MCS = [x ⁽¹⁾, x ⁽²⁾, ⋯, x ^(N)] into two groups x ^MCS _g1 and x ^MCS _g2 . The group-one samples (x ^MCS _g1 ) correspond to those samples with U values larger than 3.1 and the group-two samples are the remaining samples in x ^MCS.

Based on the group-one and group-two samples, Eq. (12) is rewritten as

$$ {\widehat{p}}_f=\frac{N_{f1}+{N}_{f2}}{N} $$

(14)

where N _f1 = ∑I(G _p (x ^MCS _g1 )) and N _f2 = ∑I(G _p (x ^MCS _g2 )).

In surrogate model-based method, the mean predictions ĝ(x ^MCS _g1 ) and ĝ(x ^MCS _g2 ) are usually used to substitute for G _p (x ^MCS _g1 ) and G _p (x ^MCS _g2 ); therefore the probability of failure estimate is given by

$$ {\widehat{p}}_f^{\hbox{'}}=\frac{{\widehat{N}}_{f1}+{\widehat{N}}_{f2}}{N} $$

(15)

where ${\widehat{N}}_{f1}={\displaystyle \sum I\left(\widehat{g}\left({\mathbf{x}}_{g1}^{MCS}\right)\right)}$ and ${\widehat{N}}_{f2}={\displaystyle \sum I\left(\widehat{g}\left({\mathbf{x}}_{g2}^{MCS}\right)\right)}$.

Since we assume that the error or uncertainty of ${\widehat{p}}_f$ comes from the group-two samples, we can use ĝ(x ^MCS _g1 ) to approximate G _p (x ^MCS _g1 ) in Eq. (14). Based on that, Eq. (14) is rewritten as

$$ {\widehat{p}}_f=\frac{{\widehat{N}}_{f1}+{N}_{f2}}{N} $$

(16)

Based on Eqs. (15) and (16), the percentage error of the probability of failure estimate given in Eq. (15) is computed as

$$ {\varepsilon}_r=\frac{\left|{\widehat{p}}_f-{\widehat{p}}_f^{\hbox{'}}\right|}{{\widehat{p}}_f}\times 100\%=\frac{\left|{\widehat{N}}_{f2}-{N}_{f2}\right|}{{\widehat{N}}_{f1}+{N}_{f2}}\times 100\% $$

(17)

Equation (14) indicates that N _f2 is a random variable bounded in the interval [0, N ₂], where N ₂ is the number of samples in x ^MCS _g2 . The maximum percentage error of failure probability estimate given in Eq. (15) is obtained as

$$ {\varepsilon}_r^{\max }=\underset{N_{f2}\in \left[0,\kern0.5em {N}_2\right]}{ \max}\left\{\frac{\left|{\widehat{N}}_{f2}-{N}_{f2}\right|}{{\widehat{N}}_{f1}+{N}_{f2}}\times 100\%\right\} $$

(18)

Based on the error estimation of reliability analysis, we can stop the training of the surrogate model when the percentage error of reliability estimate satisfies our accuracy requirement.

3.2.2 Error estimation based on uncertainty quantification of ${\widehat{p}}_f$

The above error estimation is easy to compute but may be too conservative even if it is better than just using min{U(x)} > 2 in AK-MCS. From Eq. (16), we have

$$ {\widehat{p}}_f=\frac{N_{f1}+{N}_{f2}}{N}\approx \frac{{\widehat{N}}_{f1}+{\displaystyle \sum I\left({G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\right)}}{N} $$

(19)

It implies that ${\widehat{p}}_f$ is a system response with random inputs of ${G}_p\left({\mathbf{x}}_{g2}^{MCS(i)}\right)\sim N\left(\widehat{g}\left({\mathbf{x}}_{g2}^{MCS(i)}\right),\kern0.5em {\sigma}_{G_p}^2\left({\mathbf{x}}_{g2}^{MCS(i)}\right)\right)$, i = 1, 2, ⋯, N ₂, where N ₂ is the number of samples in group-two samples x ^MCS _g2 (as indicated in Fig. 2).

Fig. 2

Failure probability estimate with random inputs of group two samples

The uncertainty in ε _r (Eq. (17)) can be quantified based on the uncertainty quantification of ${\widehat{p}}_f$. Since the dimensionality of G _p (x ^MCS (i) _g2 ), i = 1, 2, ⋯, N ₂ may be high, analytically solving Eq. (19) may be difficult. In this paper, sampling-based method is used.

G _p (x ^MCS (i) _g2 ), i = 1, 2, ⋯, N ₂ are N ₂ correlated normal variables according to the property of Kriging model. We therefore analyze the correlation between these random variables first. Let the current training points be x ^s and g(x ^s), for given hyper-parameters, Θ, the covariance matrix of G _p (x ^MCS _g2 ) conditioned on the training points, x ^s and g(x ^s), is given by

$$ {\varSigma}_{\left.p\right|t}={\varSigma}_{pp}-{\varSigma}_{pt}{\varSigma}_{tt}^{-1}{\varSigma}_{pt}^T $$

(20)

where Σ _pp , Σ _pt , and Σ _tt are the covariance matrixes between G _p (x ^MCS _g2 ) and $\begin{array}{cc}\hfill {G}_p\left({\mathbf{x}}_{g2}^{MCS}\right),\hfill & \hfill {G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\hfill \end{array}$ and $\begin{array}{cc}\hfill {G}_p\left({\mathbf{x}}^s\right),\hfill & \hfill {G}_p\left({\mathrm{x}}^{\mathrm{s}}\right)\hfill \end{array}$ and G _p (x ^s), respectively.

$\begin{array}{cc}\hfill {\displaystyle {\sum}_{pp},}\hfill & \hfill {\displaystyle {\sum}_{pt}}\hfill \end{array}$ and Σ _tt are estimated by inputting the elements of the normalized $\begin{array}{cc}\hfill {\mathbf{x}}_{g2}^{MCS},\hfill & \hfill {\mathrm{x}}^{\mathrm{s}}\hfill \end{array}$ and Θ into Eqs. (2) and (3). Based on the covariance matrix ∑ _p/t , the correlation matrix ρ _p|t of G _p (x ^MCS _g2 ) is obtained as

$$ {\boldsymbol{\uprho}}_{\left.p\right|t}={\left[\begin{array}{cccc}\hfill 1\hfill & \hfill {\rho}_{12}\hfill & \hfill \cdots \hfill & \hfill {\rho}_{1{N}_2}\hfill \\ {}\hfill {\rho}_{21}\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill {\rho}_{2{N}_2}\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill {\rho}_{N_21}\hfill & \hfill {\rho}_{N_22}\hfill & \hfill \cdots \hfill & \hfill 1\hfill \end{array}\right]}_{N_2\times {N}_2} $$

(21)

where ρ _ij is the correlation between G _p (x ^MCS(i) _g2 ) and G _p (x ^MCS(j) _g2 ), i, j = 1, 2, ⋯, N ₂, conditioned on current training points.

In order to generate samples for $\begin{array}{cc}\hfill {G}_p\left({\mathbf{x}}_{g2}^{MCS}\right),\hfill & \hfill {G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\hfill \end{array}$ are then represented as independent standard normal variables ξ based on eigenvalue and eigenvector analyses of ρ _p|t as below (Sudret and Der Kiureghian 2000).

$$ {G}_p\left({\mathbf{x}}_{g2}^{MCS(i)}\right)=\widehat{g}\left({\mathbf{x}}_{g2}^{MCS(i)}\right)+{\sigma}_{G_p}\left({\mathbf{x}}_{g2}^{MCS(i)}\right){\displaystyle \sum_{j=1}^{N_2}\frac{\xi_j}{\sqrt{\eta_j}}{\boldsymbol{\upvarphi}}_j^T}{\boldsymbol{\uprho}}_{:\kern0.5em i} $$

(22)

where η _i and φ ^T _i are the eigenvalues and eigenvectors of ρ _p|t and ${\boldsymbol{\uprho}}_{:\kern0.5em i}={\left[{\rho}_{i1},\kern0.5em {\rho}_{i2},\kern0.5em \cdots, {\rho}_{i{N}_2}\right]}^T$.

Based on Eq. (22), samples are generated for G _p (x ^MCS _g2 ). Denoting the samples of G _p (x ^MCS _g2 ) as ${\mathbf{g}}_{N_2\times {n}_r}$, we have

$$ {\mathbf{g}}_{N_2\times {n}_r}={\left[\begin{array}{cccc}\hfill g\left(1,\kern0.5em 1\right)\hfill & \hfill g\left(1,\kern0.5em 2\right)\hfill & \hfill \cdots \hfill & \hfill g\left(1,\kern0.5em {n}_r\right)\hfill \\ {}\hfill g\left(2,\kern0.5em 1\right)\hfill & \hfill g\left(2,\kern0.5em 2\right)\hfill & \hfill \cdots \hfill & \hfill g\left(2,\kern0.5em {n}_r\right)\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill & \hfill \ddots \hfill & \hfill \vdots \hfill \\ {}\hfill g\left({N}_2,\kern0.5em 1\right)\hfill & \hfill g\left({N}_2,\kern0.5em 2\right)\hfill & \hfill \cdots \hfill & \hfill g\left({N}_2,\kern0.5em {n}_r\right)\hfill \end{array}\right]}_{N_2\times {n}_r} $$

(23)

where n _r is the number of samples.

Combining Eq. (23) with Eq. (19), samples of ${\widehat{p}}_f$ are obtained as

$$ {\widehat{p}}_f(i)=\frac{{\widehat{N}}_{f1}+{\displaystyle \sum_{j=1}^{N_2}I\left(g\left(j,\kern0.5em i\right)\right)}}{N},\kern1em i=1,\kern0.5em 2,\kern0.5em \cdots, \kern0.5em {n}_r $$

(24)

Similar as Eq. (17), samples are obtained for ε _r as follows

$$ \begin{array}{cc}\hfill {\varepsilon}_r(i)=\frac{{\displaystyle \sum_{j=1}^{N_2}I\left(g\left(j,\kern0.5em i\right)\right)}-{\widehat{N}}_{f2}}{{\widehat{N}}_{f1}+{\displaystyle \sum_{j=1}^{N_2}I\left(g\left(j,\kern0.5em i\right)\right)}},\hfill & \hfill i=1,2,\cdots, {n}_r\hfill \end{array} $$

(25)

Once samples of ε _r (i) , i = 1, 2, ⋯, n _r , are available, the error distribution of current reliability estimate is approximated. In this paper, the Kernel Smoothing function (Wand and Jones 1994) with a bandwidth of 0.005 is employed to fit the distribution. Based on the fitted distribution, the maximum error, ε ^max _r is approximated as

$$ {\varepsilon}_r^{\max }= \max \left\{\left|{F}_{\varepsilon_r}^{-1}(0.99)\right|,\kern0.5em \left|{F}_{\varepsilon_r}^{-1}(0.01)\right|\right\} $$

(26)

where ${F}_{\varepsilon_r}^{-1}\left(\cdot \right)$ is the inverse CDF of ε _r .

The above approximation corresponds to a probability that the actual estimation error of ${\widehat{p}}_f$ is larger than ε ^max _r is 0.02. Since a conservative estimation of ε ^max _r is given in Eq. (18), to avoid the situation that the estimation given in Eq. (26) is larger than that given in Eq. (18), we can rewrite Eq. (26) as

$$ {\varepsilon}_r^{\max }= \min \left\{ \max \left\{\left|{F}_{\varepsilon_r}^{-1}(0.99)\right|,\kern0.5em \left|{F}_{\varepsilon_r}^{-1}(0.01)\right|\right\},\underset{N_{f2}\in \left[0,\kern0.5em {N}_2\right]}{ \max}\left\{\frac{\left|{\widehat{N}}_{f2}-{N}_{f2}\right|}{{\widehat{N}}_{f1}+{N}_{f2}}\right\}\right\} $$

(27)

The percentage error of reliability estimates is checked using Eq. (27) every time the surrogate model is updated. When the requirement of accuracy is satisfied, the training process stops. In the next sub-section, we will discuss how to select new training points when the accuracy requirement cannot be satisfied. In addition, when the number of samples in group-two is very large, a sampling-based method to estimate ε ^max _r may be computationally expensive. A large number (e.g., larger than 1 × 10⁴) of group-two samples indicates high uncertainty in ${\widehat{p}}_f$. In this situation, Eq. (18) is used directly to estimate ε ^max _r .

3.3 Selection of new training points based on GSA

3.3.1 Principle of selecting new training points

Equation (19) indicates that ${\widehat{p}}_f$ is uncertain due to the uncertainty in G _p (x ^MCS _g2 ). The uncertainty in ${\widehat{p}}_f$ will decrease and will approach its true value when more training points are added. The optimal training points should reduce the uncertainty in ${\widehat{p}}_f$ in the most effective way.

In AK-MCS and EGRA, the sample which has the lowest U value or highest EFF value is selected as the new training point. When all sample responses (G _p (x ^MCS _g2 )) predicted from the surrogate model are completely independent, the point with the lowest U value or the highest EFF value is also the point that reduces the uncertainty of ${\widehat{p}}_f$ most effectively (as indicated in Eq. (13)). The reason for this is: ${\widehat{p}}_f$ is a function of the sign of responses and the U and EFF functions are computed only based on the local mean and variance at each point. In the Kriging surrogate model method, however, the sample response (G _p (x ^MCS _g2 )) are not completely independent. This implies that, the training of one sample point may also affect the signs of responses of other sample points around it. As indicated in Fig. 3, for two candidate training points (Points A and B) with the same or very close U or EFF values identified from MCS samples, it is apparent that Point B has a higher priority than Point A since it may reduce the uncertainty of ${\widehat{p}}_f$ more effectively.

Fig. 3

Illustration of candidate new training points

Based on this observation, we propose to select new training points based on their contributions to the uncertainty of ${\widehat{p}}_f$. There are several possible ways to analyze contributions of uncertainty in G _p (x ^MCS _g2 ) to uncertainty of ${\widehat{p}}_f$, such as global sensitivity analysis and analytically derive variance of ${\widehat{p}}_f$ based on Eq. (19). In this paper, the analysis of contributions of sample points are achieved through global sensitivity analysis of G _p (x ^MCS _g2 ) with respect to ${\widehat{p}}_f$. Since G _p (x ^MCS _g2 ) are correlated random variables, GSA methods based on variance decomposition (i.e., Sobol indices) are not applicable (Sobol’ 2001; Sudret 2008). In the subsequent sections, GSA method with correlated random variables used in this work is introduced first. Following that, selection of new training points based on GSA is discussed.

3.3.2 GSA with correlated random variables

Variance-based global sensitivity analysis of models with independent input variables has been intensively studied during the past decades (Sobol’ 2001; Wagner 1995; Saltelli et al. 1999). In terms of GSA with correlated random variables, a few studies have been reported. For example, Borgonovo proposed a δ-sensitivity measure method (Borgonovo 2007). Li and Rabitz developed an ANalysis of COVAriance (ANCOVA) method for GSA with independent and/or dependent inputs (Li et al. 2010). Jacques, et.al. presented a GSA method for models with model uncertainty and correlated inputs using the group sensitivity analysis method (Jacques et al. 2006). Sudret computed the GSA analytically by post-processing the Polynomial Chaos Expansion (PCE) coefficients (Sudret 2008). Xu and Gertner extended the Fourier Amplitude Sensitivity Test (FAST) to models with correlated parameters (Xu and Gertner 2007). Mara and Tarantola proposed a set of variance-based sensitivity indices to perform sensitivity analysis of models with dependent inputs (Mara and Tarantola 2012).

In this paper, the extended FAST method developed by Xu and Gertner (Xu and Gertner 2007) is employed to facilitate the selection of new training points. The basic principle of FAST is to assign each random variable with a characteristic frequency through a periodic sampling function. The variance contribution of a specific variable is then analyzed through a Fourier transform (Xu and Gertner 2007; McRae et al. 1982). FAST was originally developed for models with independent variables. Xu and Gertner (Xu and Gertner 2007) extended it to models with correlated variables, by reordering the samples generated from FAST to capture the correlation between variables and then shifting the system outputs to compute the partial variance of each variable. More details of the extended FAST method are available in Ref. (Xu and Gertner 2007). However, the proposed GSAS method is not limited to the extended FAST; any other GSA method could also be employed.

3.3.3 Selection of new training points based on GSA

As discussed in Sec. 3.3.1, the system response is ${\widehat{p}}_f$ and inputs are G _p (x ^MCS(i) _g2 ), i = 1, 2, ⋯, N ₂, in GSA. For some problems, N ₂ will be very large, which results in a very high-dimensional GSA problem. GSA with high-dimensional correlated random variables is computationally expensive. In order to reduce the dimensionality of the problem, we further divide the group-two samples x ^MCS _g2 into two groups, namely candidates of new training points (x ^Can) and the other set (x ^Other) of samples in x ^MCS _g2 . The first n _can samples with the lowest U values in x ^MCS _g2 are selected as x ^Can since samples with low U values have high probabilities of having wrong signs or high probability of being the new training point. For the other set of samples in x ^MCS _g2 (i.e., x ^Other), we use ĝ(x ^Other)|G _p (x ^Can), g(x ^s) (i.e., mean predictions, ĝ(x ^Other), at x ^Other conditioned on realizations of G _p (x ^Can) and current training points g(x ^s)) instead of ĝ(x ^Other) to substitute G _p (x ^Other) in GSA. The purpose of doing so is to preserve the correlation between responses of samples, x ^Can and x ^Other, and to account for effects of realizations of G _p (x ^Can) on ĝ(x ^Other).

After the above partition, for given realizations of $\begin{array}{cc}\hfill {G}_p\left({\mathbf{x}}^{Can}\right),\hfill & \hfill {\widehat{p}}_f\left({G}_p\left({\mathbf{x}}^{Can}\right)\right)\hfill \end{array}$ is computed as

$$ {\widehat{p}}_f\left({G}_p\left({\mathbf{x}}^{Can}\right)\right)=\frac{{\widehat{N}}_{f1}+{\displaystyle \sum I\left(\left.\widehat{g}\left({\mathbf{x}}^{Other}\right)\right|{G}_p\left({\mathbf{x}}^{Can}\right),\kern0.5em g\left({\mathbf{x}}^s\right)\right)}+{\displaystyle \sum I\left({G}_p\left({\mathbf{x}}^{Can}\right)\right)}}{N} $$

(28)

Figure 4 illustrates inputs and output of the failure probability estimate in GSA.

Fig. 4

Illustrate of failure probability estimate in GSA

For given realizations of G _p (x ^Can) and values of $\begin{array}{cc}\hfill g\left({\mathbf{x}}^s\right),\hfill & \hfill \left.\widehat{g}\left({\mathbf{x}}^{Other}\right)\right|{G}_p\left({\mathbf{x}}^{Can}\right),\kern0.5em g\left({\mathbf{x}}^s\right)\hfill \end{array}$ is computed based on the conditional probability and current Kriging model as follows

$$ \left.\widehat{g}\left({\mathbf{x}}^{Other}\right)\right|{G}_p\left({\mathbf{x}}^{Can}\right),\kern0.5em g\left({\mathbf{x}}^s\right)=\mathbf{f}{\left({\mathbf{x}}^{Other}\right)}^T\boldsymbol{\upbeta} +{\mathbf{r}}_{new}{\left({\mathbf{x}}^{Other}\right)}^T{\mathbf{R}}_{new}^{-1}\left({\mathbf{g}}^{temp}-{\mathbf{F}}_{new}\boldsymbol{\upbeta} \right) $$

(29)

where g ^temp = [G _p (x ^Can); g(x ^s)], β are from the hyper-parameters $\begin{array}{cc}\hfill \varTheta, \hfill & \hfill \mathrm{f}{\left(\mathrm{x}\right)}^T\hfill \end{array}$ are the trend functions as discussed in Sec. 2.1, r _new (x ^Other) are obtained by inputting $\begin{array}{cc}\hfill {\mathbf{x}}^{Other},\hfill & \hfill {\mathbf{x}}^{temp}=\left[{\mathbf{x}}^{Can};\kern0.5em {\mathbf{x}}^s\right]\hfill \end{array}$ and Θ into Eq. (3), R _new is the correlation matrix between x ^temp and x ^temp, which is obtained by inputting x ^temp and Θ into Eq. (3), and F _new are obtained by inputting x ^temp into f(x)^T. The main purpose of using Eq. (29) is to investigate how the uncertainty in G _p (x ^Can) may result in the variability of mean predictions of ĝ(x ^Other). In the above equation, the hyper-parameters Θ need to be recalculated for each realization of G _p (x ^Can). Repeatedly recalculating Θ, however, may increase the computational burden significantly. In this paper, we directly use current hyper-parameters instead of recalculating them repeatedly. This works well as indicated in the numerical examples. Recalculating the hyper-parameters for each realization of G _p (x ^Can) may further improve the accuracy of the proposed method, and needs to be investigated in future work. Note that all samples points x and responses g(x) may need to be normalized depending on the Kriging algorithms used in above computations.

Equation (28) implies that the response is ${\widehat{p}}_f\left({G}_p\left({\mathbf{x}}^{Can}\right)\right)$ and inputs are random variables G _p (x ^Can) for GSA. Following the procedure of the extended FAST method (Xu and Gertner 2007), the main steps of GSA for ${\widehat{p}}_f\left({G}_p\left({\mathbf{x}}^{Can}\right)\right)$ are summarized as below.

• (1) Generate n _F independent samples g ^F for G _p (x ^Can) based on the characteristic frequencies ${\boldsymbol{\upomega}}_{1\times {n}_{can}}$ obtained from FAST.

• (2) Obtain the conditional covariance matrix of G _p (x ^Can) as follows

  $$ {\varSigma}_{\left.c\right|t}={\varSigma}_{cc}-{\varSigma}_{ct}{\varSigma}_{tt}^{-1}{\varSigma}_{ct}^T $$

  (30)

  where $\begin{array}{cc}\hfill {\displaystyle {\sum}_{ct},}\hfill & \hfill {\displaystyle {\sum}_{tt}}\hfill \end{array}$ and ∑ _cc stand for covariance matrixes between G _p (x ^Can) and $\begin{array}{cc}\hfill {G}_p\left({\mathbf{x}}^s\right),\hfill & \hfill {G}_p\left({\mathbf{x}}^s\right)\hfill \end{array}$ and G _p (x ^s), and G _p (x ^Can) and G _p (x ^Can). The correlation matrix, ρ _c|t , of G _p (x ^Can) is then obtained from Σ _c|t . n _F correlated samples ${\mathbf{w}}_{n_F\times {n}_{can}}$ with mean of zero and standard deviation of one are generated based on the eigenvalue and eigenvector analysis of ρ _c|t .

• (3) Samples of ${\mathbf{w}}_{n_F\times {n}_{can}}$ are then sorted in ascending order. According to the indices of sorted $\begin{array}{cc}\hfill {\mathbf{w}}_{n_F\times {n}_{can}},\hfill & \hfill {g}^F\hfill \end{array}$ are reordered so that the reordered g ^F has the same rank correlation as ${\mathbf{w}}_{n_F\times {n}_{can}}$. Here, we denote the reordered samples of g ^F as ${\overline{\mathbf{g}}}^F$. ${\overline{\mathbf{g}}}^F$ is a n _F  × n _Can sampling matrix. Each row of the matrix is a realization of ĝ(x ^Can).

• (4) With samples (i.e., ${\overline{\mathbf{g}}}^F$) of G _p (x ^Can), the corresponding samples of response $\begin{array}{cc}\hfill {\widehat{p}}_f(i),\hfill & \hfill i=1,\kern0.5em 2,\kern0.5em \cdots, \kern0.5em {n}_F\hfill \end{array}$ are obtained using Eq. (28).

  Based on samples of $\begin{array}{cc}\hfill {\widehat{p}}_f(i),\hfill & \hfill i=1,\kern0.5em 2,\kern0.5em \cdots, \kern0.5em {n}_F\hfill \end{array}$ partial variances, $\begin{array}{cc}\hfill {V}_j,\hfill & \hfill j=1,\kern0.5em 2,\kern0.5em \cdots, \kern0.5em {n}_{can}\hfill \end{array}$ of each variable in ĝ(x ^Can) are obtained using the extended FAST method.

  Then, the new training point is identified by finding the sample point that corresponds to the maximum variance:

  $$ {i}_{\max }= \arg \max \left(\mathbf{V}\right) $$

  (31)

  The new training point x _new is thus selected as x ^Can(i _max, :). After the new training point is identified, the surrogate model is updated and percentage error is verified. This process continues until the accuracy requirement is satisfied.

4 Algorithms for implementation

In this section, algorithms to implement the proposed GSAS method are first summarized. Following that, further development of GSAS by incorporating GSAS with importance sampling (IS) is discussed.

4.1 Implementation procedure

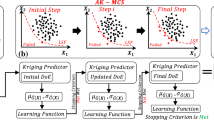
The overall numerical procedure is depicted in Fig. 5. Table 1 gives the overall procedure of the GSAS method. Following that, Tables 2 and 3 present algorithms for the error estimation of reliability estimate (Algorithm 1) and selection of a new training point based on GSA (Algorithm 2), respectively.

Fig. 5

Flowchart of the proposed GSAS method

Table 1 Overview of the GSAS method

Table 2 Main procedures of algorithm 1

Table 3 Main procedures of algorithm 2

4.2 GSAS based on importance sampling (GSAS-IS)

The GSAS method is based on MCS. It can be further improved by incorporating importance sampling (IS). The main procedure of the resulting method GSAS-IS is the same as that of original GSAS. The following changes need to be made to GSAS when it is combined with IS.

• (1) The most probable point (MPP) needs to be identified first. After the MPP point is obtained, in Step 3 of Table 1, the sample points are generated from IS instead of MCS.

• (2) Due to the IS, the equation for ${\widehat{p}}_f$ given in Eq. (12) is modified as

  $$ {\widehat{p}}_f\approx {\displaystyle \sum_{i=1}^{N_{IS}}I\left({G}_p\left({\mathbf{x}}^{(i)}\right)\right)w\left({\mathbf{x}}^{(i)}\right)}/{N}_{IS} $$

  (32)

  where N _IS is the number of samples in IS and w(x ⁽ⁱ⁾) is the weight of sample x ⁽ⁱ⁾ given by

  $$ w\left({\mathbf{x}}^{(i)}\right)=f\left({\mathbf{x}}^{(i)}\right)/h\left({\mathbf{x}}^{(i)}\right) $$

  (33)

  in which f(x ⁽ⁱ⁾) and h(x ⁽ⁱ⁾) are the original joint PDF and the instrumental probability density function, respectively.

  In Step 9 of Table 1, the way of computing ${\widehat{N}}_{f1}$ and ${\widehat{N}}_{f2}$ (Eq. (15)) is modified as

  $$ {\widehat{N}}_{f1}={\displaystyle \sum I\left(\widehat{g}\left({\mathbf{x}}_{g1}^{MCS}\right)\right)}w\left({\mathbf{x}}_{g1}^{MCS}\right) $$

  (34)
  $$ {\widehat{N}}_{f2}={\displaystyle \sum I\left(\widehat{g}\left({\mathbf{x}}_{g2}^{MCS}\right)\right)}w\left({\mathbf{x}}_{g2}^{MCS}\right) $$

  (35)

  Similarly, the way of computing the error of reliability analysis (Eqs. (16) and (25)) is modified by adding the weights of samples into the equations.

• (3) In Step 1 of Table 3, the method of selecting the candidate samples is different for GSAS and GSAS-IS. In GSAS, the n _can samples of x ^MCS _g2 with the lowest U(x ^MCS _g2 ) values are selected as x ^Can. In GSAS-IS, the n _can samples of x ^MCS _g2 with the largest Var _I (x ^MCS _g2 ) are selected as x ^Can, where Var _I (x ^MCS _g2 ) is the variance of indicator function at sample x ^MCS _g2 .

  If ĝ(x ^MCS _g2 ) > 0, we have

  $$ \left\{\begin{array}{l} \Pr \left\{I\left({G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\right)w\left({\mathbf{x}}_{g2}^{MCS}\right)=0\right\}=\varPhi \left(\left|\widehat{g}\left({\mathbf{x}}_{g2}^{MCS}\right)\right|/{\sigma}_{G_p\left({\mathbf{x}}_{g2}^{MCS}\right)}\right)=\varPhi \left(U\left({\mathbf{x}}_{g2}^{MCS}\right)\right)\\ {} \Pr \left\{I\left({G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\right)w\left({\mathbf{x}}_{g2}^{MCS}\right)=w\left({\mathbf{x}}_{g2}^{MCS}\right)\right\}=\varPhi \left(-U\left({\mathbf{x}}_{g2}^{MCS}\right)\right)\end{array}\right. $$

  (36)

  Var _I (x ^MCS _g2 ) is then computed by

  $$ \begin{array}{l}Va{r}_I\left({\mathbf{x}}_{g2}^{MCS}\right)=Var\left\{I\left({G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\right)w\left({\mathbf{x}}_{g2}^{MCS}\right)\right\}\\ {}\kern8em =E\left({I}^2\left({G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\right){w}^2\left({\mathbf{x}}_{g2}^{MCS}\right)\right)-E\left(I\left({G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\right)w\left({\mathbf{x}}_{g2}^{MCS}\right)\right)E\left(I\left({G}_p\left({\mathbf{x}}_{g2}^{MCS}\right)\right)w\left({\mathbf{x}}_{g2}^{MCS}\right)\right)\end{array} $$

  (37)

  After simplification, we have

  $$ Va{r}_I\left({\mathbf{x}}_{g2}^{MCS}\right)=\varPhi \left(-U\left({\mathbf{x}}_{g2}^{MCS}\right)\right)\varPhi \left(U\left({\mathbf{x}}_{g2}^{MCS}\right)\right){w}^2\left({\mathbf{x}}_{g2}^{MCS}\right) $$

  (38)

  Same expression is obtained for the case ĝ(x ^MCS _g2 ) < 0.

• (4) In Step 13 of Table 1, the coefficient of variation of ${\widehat{p}}_f$ is computed in GSAS-IS as

  $$ CO{V}_{p_f}=\frac{1}{N_{IS}-1}\left(\frac{1}{N_{IS}}{\displaystyle \sum_{i=1}^{N_{IS}}\left(I\left({G}_p\left({\mathbf{x}}^{(i)}\right)\right){w}^2\left({\mathbf{x}}^{(i)}\right)\right)}-{\widehat{p}}_f^2\right) $$

  (39)

  Note that the function evaluations used to find the MPP points are also used to construct the surrogate model. The way of finding the MPP can be FORM-based method or metamodel-based method.

5 Numerical examples

In this section, five numerical examples, which have been employed in other studies to verify the effectiveness of surrogate model-based reliability analysis methods, are used to demonstrate the effectiveness of the proposed GSAS method. In each example, the GSAS method is compared with EGRA and AK-MCS methods and other methods if results are available. The result of Monte Carlo simulation (MCS) with a large sample size is used as a benchmark for accuracy comparison. The percentage error of each method is analyzed. The percentage error ε (%) is defined as

$$ \varepsilon \kern0.5em \left(\%\right)=\frac{\left|{\widehat{p}}_f-{p}_f^{MCS}\right|}{p_f^{MCS}}\times 100\% $$

(40)

where ${\widehat{p}}_f$ stands for the estimation of a method (i.e., GSAS, EGRA, AK-MCS, or others) and p ^MCS _f is the estimation of MCS.

The parameters of GSAS, EGRA, and AK-MCS methods are the same for all the five examples. A squared exponential correlation function is used. The initial training points are also the same for GSAS, EGRA, and AK-MCS. The Hammersley sampling approach is employed to generate initial training points in the standard normal space in the interval [−4, 4]. The training points are then transformed from the standard normal space to original space to get the initial training points. The parameters of the GSAS method are n _can  = 1 × 10⁴ (population size of MCS, step 3 of Table 1), n = 5 × 10⁴ (step 3 of Table 2), n _can  = 40 (step 1 of Table 3), and n _F  = 2.5 × 10⁴ + 1 (step 2 of Table 3, number of samples for GSA in extended FAST). These parameters remain consistent for all numerical examples.

5.1 Example 1: A multimodal function

A multimodal function used in (Bichon et al. 2008) is taken as our first example. The limit state function is given by

$$ g\left(\mathbf{X}\right)=\frac{\left({\left(1.5+{X}_1\right)}^2+4\right)\left(\left(2.5+{X}_2\right)-1\right)}{20}- \sin \frac{5\left(1.5+{X}_1\right)}{2}-2 $$

(41)

where X ₁ and X ₂ are two independent standard normal variables.

The probability of failure of Eq. (41) is analyzed using the GSAS, EGRA, and AK-MCS methods. The initial Kriging model is constructed using seven initial training points. The Kriging model is then updated in GSAS, EGRA, and AK-MCS when new training points are added. Figure 6 shows ${\widehat{p}}_f$ obtained from different methods with respect to the number of added new training points. It illustrates that EGRA and AK-MCS keep adding new training points after ${\widehat{p}}_f$ can satisfy the accuracy requirement while the proposed GSAS method stops adding training points when the estimation of ${\widehat{p}}_f$ is accurate. Figures 7 and 9 depict the true limit state, the limit state from the surrogate model, the initial training points, and the added training points of the GSAS, EGRA, and AK-MCS methods. It illustrates that the GSAS method effectively reduces the number of training points used in the EGRA and AK-MCS methods. In Figs. 8a and 9a, we label some added training points which may not be necessary from the reliability analysis perspective since they will not result in any change in the estimation of ${\widehat{p}}_f$ (as indicated in Fig. 6). These points are labeled as red “+” in Figs. 8a and 9a. In Figs. 8b and 9b, we plot the limit states obtained from EGRA and AK-MCS after removing the unnecessary training points. The plots indicate that removing the unnecessary training points almost bring no change to the shape of the limit state. Note that the training points from GSAS, AK-MCS, and EGRA are different due to the differences in the learning functions and the way of selecting new training points. The unnecessary training points in Figs. 8 and 9 are therefore also different for AK-MCS and EGRA.

Fig. 6

${\widehat{p}}_f$ vs number of added new training points

Fig. 7

Initial and added training points of the GSAS method

Fig. 8

Initial and added training points of the EGRA method (a) With unnecessary training points (red “+” denotes unnecessary training point), (b) Without unnecessary training points

Fig. 9

Initial and added training points of the AK-MCS method (red “+” denotes unnecessary training point) (a) With unnecessary training points (red “+” denotes unnecessary training point), (b) Without unnecessary training points

Table 4 gives the result comparison between the GSAS, EGRA, and AK-MCS methods (Bichon et al. 2008). The result of the EGRA method is also available in (Bichon et al. 2008). The results provided in Table 4 include the number of function evaluation (NOF) of the limit state function, the estimated probability of failure (${\widehat{p}}_f$), percentage error (ε (%)) of each method, and the computational time required in addition to the number of function evaluations. The computational times were based on a Dell computer with Intel (R) Core (TM) i7-2600 CPU and 8 GB system memory that we used. Figure 10 gives the convergence history of ${\widehat{p}}_f$ with respect to the number of samples in MCS.

Table 4 Results of Example 1

Fig. 10

${\widehat{p}}_f$ vs number of MCS samples

The results in Table 4 imply that the GSAS method requires much less NOF than the EGRA and AK-MCS methods to achieve the acceptable accuracy level shown in Fig. 5 (i.e., error < 3 %). Further analysis showed that GSAS method needs only 24 training points to get a more accurate result (pf = 0.03125 and error = 0.16 %) than AK-MCS, which produced an error of 0.31 % with 31 training points. The EGRA result is very accurate for this particular problem; however, the accuracy of GSAS is better than EGRA in the subsequent examples. Besides, the GSAS method improved the additional computational time as indicated in Table 4, which is common to other advanced sampling approaches. This increase is acceptable comparing to expensive computer simulation models. Some steps of the proposed method (i.e., GSA in algorithm 2) can be further parallelized and optimized to reduce the additional computational time.

5.1.1 Parameter study

In the proposed method, there are some parameters that may affect the accuracy and efficiency of the proposed method, such as the number of candidate samples (n _can ), the threshold for the error of failure probability estimate (ε ^max _r ), and the coefficient of variation ($CO{V}_{p_f}$). We also performed parameter study for the proposed method in this example. Figures 11 and 13 give the comparison of the number of function evaluations (NOF) and percentage error of failure probability estimate under different values of $\begin{array}{cc}\hfill {n}_{Can},\hfill & \hfill {\varepsilon}_r^{\max}\hfill \end{array}$ and $CO{V}_{p_f}$, respectively. The results show that increasing the value of n _can can reduce the number of function evaluations and improve the accuracy of overall failure probability estimate. Increasing the value of ε ^max _r will improve the efficiency and sacrificing the accuracy (as indicated in Fig. 12). Increasing the value of $CO{V}_{p_f}$ has the same effect as ε ^max _r (as indicated in Fig. 13). Recommended values for these parameters are given at the beginning of Sec. 5. The recommended values remain the same for all the five examples in this paper.

Fig. 11

Comparison of the number of function (NOF) evaluations and percentage errors under different values of n _Can (ε ^max _r  = 0.02, COV _pf  = 0.01)

Fig. 12

Comparison of the number of function (NOF) evaluations and percentage errors under different values of ε ^max _r (n _Can  = 40, COV _pf  = 0.01)

Fig. 13

Comparison of the number of function (NOF) evaluations and percentage errors under different values of $CO{V}_{p_f}$ (n _Can  = 40, ε ^max _r  = 0.02)

5.1.2 Discussion

It is observed that some of the training points (accumulated over the iterations) are clustered together in the GSAS, EGRA, and AK-MCS methods. Some of the clustered training points may be unnecessary, i.e., the clustered training points will not significantly change the shape of the limit state surrogate. There are mainly two reasons that the GSAS method does not remove all the clustered training points. First, the region with the clustered training points (as indicated in Fig. 7) is close to the origin, which implies that the signs of samples in that region will affect the reliability analysis result more significantly than those of samples in other regions. In order to guarantee the accuracy of reliability analysis, the limit state in that region needs to be well-trained. From the true limit state in the clustered region, it can be seen that the nonlinearity of the true limit state in the clustered region is high, which also requires more training points to get an accurate learning of the true limit state. Second, in all the methods (AK-MCS, EGRA, and GSAS), the training points are selected adaptively. In the first several iterations, the surrogate model is not well-trained and there is large uncertainty in the prediction. Since the clustered training points are close to the limit state and in the high probability density region, they are selected in the first several iterations. Even if these selected clustered training points seem to be unnecessary in the last iteration, they are still “necessary” training points for the iterations when they are selected. For instance, the clustered training points in Fig. 7 are selected in iterations 1 to 5. These clustered training points may appear to be unnecessary when they are assessed from the point of view of the final iteration (iteration 12). But they are necessary and useful in iterations 1 to 5 (when the surrogate model is not well-trained) when they are selected. This implies that when the initial quality of the surrogate model is quite poor, EGRA, GSAS, and AK-MCS may face the issue of clustered- training points. One possible way of avoiding clustering is to require a minimum distance between the new and old training points. This improvement may be considered in future work.

5.2 Example 2: Series system with four branches

A series system with four limit state functions as given in Eq. (42) is employed as the second example. This example is taken from (Echard et al. 2011; Schueremans and Van Gemert 2005).

$$ g\left(\mathbf{X}\right)= \min \left\{\begin{array}{l}3+0.1{\left({X}_1-{X}_2\right)}^2\pm \frac{\left({X}_1+{X}_2\right)}{\sqrt{2}}\\ {}\left({X}_1-{X}_2\right)+\frac{6}{\sqrt{2}}\kern0.5em \\ {}\left({X}_2-{X}_1\right)+\frac{6}{\sqrt{2}}\end{array}\right\} $$

(42)

where X ₁ and X ₂ are independent standard normal variables.

Similar to Example 1, the probability of failure is first analyzed using the GSAS, EGRA, and AK-MCS methods. The results are then compared with the other surrogate model methods available in the literature. Twelve initial training points are generated for the GSAS, EGRA, and AK-MCS methods. Based on the initial Kriging model, new training points are added. Figure 14 gives the value of ${\widehat{p}}_f$ with respect to the number of added new training points. Figures 15 and 17 show the true limit state, the limit-state from surrogate model, the initial training points, and the added training points used in the GSAS, EGRA, and AK-MCS, respectively. It is seen that the EGRA and AK-MCS methods added many more training points than the GSAS method. Some of these added training points are not necessary from the aspect of reliability analysis. Most of the unnecessary training points are successfully eliminated in the GSAS method. Similar to Example one, we label the unnecessary training points using red “+” in Figs. 16 and 17. In Figs. 16 and 17, we also show the limit state obtained from EGRA and AK-MCS after removing the unnecessary training points. Table 5 gives the results comparison of Example 2. The GSAS method is compared with the EGRA method, the AK-MCS method, the importance sampling + spline method (IS + Spline), and the importance sampling + Neural Network (IS + Neural Network). The results of IS + Spline and IS + Neural Network are taken from (Echard et al. 2011; Schueremans and Van Gemert 2005).

Fig. 14

${\widehat{p}}_f$ vs number of added new training points

Fig. 15

Initial and added training points of the GSAS method

Fig. 16

Initial and added training points of the EGRA method (a) With unnecessary training points (red “+” denotes unnecessary training point), (b) Without unnecessary training points

Fig. 17

Initial and added training points of the AK-MCS method (a) With unnecessary training points (red “+” denotes unnecessary training point), (b) Without unnecessary training points

Table 5 Results of Example 2

The results show that the GSAS, EGRA, and AK-MCS methods can estimate the probability of failure very accurately and GSAS has a smaller percentage error than both EGRA and AK-MCS. The GSAS method is much more efficient than the EGRA and AK-MCS method. In addition, the GSAS method is also much more efficient than the IS + Spline method and IS + Neural Network method.

Further analysis showed that EGRA and AK-MCS need 99 and 78 training points respectively to get the same accuracy as GSAS.

5.3 Example 3: Nonlinear undamped one-degree-of-freedom system

As shown in Fig. 18, a nonlinear undamped one-degree-of-freedom system is taken from (Echard et al. 2011; Schueremans and Van Gemert 2005; Rajashekhar and Ellingwood 1993; Gayton et al. 2003) as the third example. The limit state function of the non-linear oscillator is given in Eq. (43). Table 6 gives the distributions and parameters of the six random variables in the limit state function.

$$ g\left(\mathbf{X}\right)=3r-\left|\frac{2F}{m{\omega}_0^2} \sin \left(\frac{\omega_0{t}_1}{2}\right)\right| $$

(43)

where X = [m, c ₁, c ₂, r, F, t ₁] and ${\omega}_0=\sqrt{\frac{c_1+{c}_2}{m}}$.

Fig. 18

A non-linear oscillator

Table 6 Random Variables of Example 3

Similar to Example 2, the GSAS method is compared with the EGRA, AK-MCS, IS + Spline, and IS + Neural Network method. The results of IS + Spline and IS + Neural Network are taken from (Echard et al. 2011; Schueremans and Van Gemert 2005). Table 7 presents the results comparison of these methods. Similar conclusions can be obtained as that from Examples 1 and 2. The GSAS method is more efficient than the EGRA, AK-MCS, IS + Spline, and IS + Neural Network methods. Figure 19 gives the value of ${\widehat{p}}_f$ with respect to the number of added new training points for different methods. It shows that GSAS stops adding new training points effectively when the estimate is close to the true value while other methods keep adding new training points. This is due to the fact that the convergence criterion in GSAS is defined directly from the reliability estimate perspective while those of AK-MCS and EGRA are defined from the variance of single sample perspective. In order to investigate the fluctuation of the GSAS estimate beyond reaching the stopping criterion, we continue to add more training points in GSAS. Figure 20 gives the value of ${\widehat{p}}_f$ with respect to the number of added new training points. It indicates that the estimate does not fluctuate too much after the stopping criterion is reached (within the 1.5 % error bounds of the true value).

Table 7 Results of Example 3

Fig. 19

${\widehat{p}}_f$ vs number of added new training points

Fig. 20

${\widehat{p}}_f$ vs number of added new training points in GSAS

5.4 Example 4: Roof truss

A roof truss structure given in Fig. 21 is used as the fourth example. This example is modified from (Zhao et al. 2014; Song et al. 2009). In the truss structure, the top chords and compression bars are made of steel reinforced concrete and the bottom chords and tension bars are made of steel. A failure event is defined as the vertical deflection of the roof top being larger than 0.03 m. The limit state function is given in Eq. (44). Table 8 presents the distributions and parameters of the six random variables in the limit state function. The original distributions of random variables were assumed to be normal in (Zhao et al. 2014; Song et al. 2009). In this paper, the distributions are modified to be non-normal to examine the effectiveness of GSAS in solving problems with non-normal inputs.

$$ g\left(\mathbf{X}\right)=0.03-\frac{q{l}^2}{2}\left(\frac{3.81}{A_C{E}_C}+\frac{1.13}{A_S{E}_S}\right) $$

(44)

where X = [q, l, A _S , A _C , E _S , E _C ].

Fig. 21

A roof truss structure

Table 8 Random Variables of Example 4

The probability of failure is estimated using GSAS, EGRA, and AK-MCS. Table 9 shows the results comparison between different methods. Figure 22 gives the value of ${\widehat{p}}_f$ with respect to the number of added new training points for different methods. It indicates that the GSAS method is more efficient than the EGRA and AK-MCS methods. The accuracy of GSAS is the same as AK-MCS and better than EGRA for this problem. Similar to Example 3, Fig. 23 gives the value of ${\widehat{p}}_f$ with respect to the number of added new training points from GSAS by continue adding new training points after stopping criterion is satisfied.

Table 9 Results of Example 4

Fig. 22

${\widehat{p}}_f$ vs number of added new training points

Fig. 23

${\widehat{p}}_f$ vs number of added new training points in GSAS

5.5 Example 5: Two-degree-of-freedom primary/secondary damped oscillator

A two-degree-of-freedom primary/secondary damped oscillator example originally proposed by Der Kiureghian (Kiureghian and Stefano 1991) is used as the fifth example. This example has also been studied by Dubourg et al. (Dubourg et al. 2013) and Bourinet et al. (Bourinet et al. 2011). There are eight independent random variables in this example. The limit state function is given by

$$ g\left(\mathbf{X}\right)={F}_s-3{k}_s{\left(\frac{\pi {S}_0}{4{\xi}_s{\omega}_s^3}\left[\frac{\xi_a{\xi}_s}{\xi_p{\xi}_s\left(4{\xi}_a^2+{\theta}^2\right)+\gamma {\xi}_a^2}\frac{\left({\xi}_p{\omega}_p^3+{\xi}_s{\omega}_s^3\right){\omega}_p}{4{\xi}_a{\omega}_a^4}\right]\right)}^{1/2} $$

(45)

where $\begin{array}{cccccc}\hfill \mathbf{X}=\left[{k}_p,\kern0.5em {k}_s,\kern0.5em {m}_p,\kern0.5em {m}_s,\kern0.5em {\xi}_p,\kern0.5em {\xi}_s,\kern0.5em {F}_s,\kern0.5em {S}_0\right],\hfill & \hfill {\omega}_p=\sqrt{k_p/{m}_p},\hfill & \hfill {\omega}_s=\sqrt{k_s/{m}_s},\hfill & \hfill {\omega}_a=\left({\omega}_p+{\omega}_s\right)/2,\hfill & \hfill {\xi}_a=\left({\xi}_p+{\xi}_s\right)/2,\hfill & \hfill \gamma ={m}_s/{m}_p\hfill \end{array}$ and θ = (ω _p  − ω _s )/ω _a .

Table 10 gives the distributions and parameters of the eight random variables.

Table 10 Random Variables in Example 5

The results of the GSAS method are compared with the EGRA, AK-MCS method, the Meta-IS method (Dubourg et al. 2013), and the Support Vector Machine + Subset simulation (SVM + Subset) method (Bourinet et al. 2011). The results comparison is given in Table 11. Figure 24 gives the value of ${\widehat{p}}_f$ with respect to the number of added new training points for different methods. The results illustrate that the GSAS method is more efficient and accurate than the EGRA and AK-MCS methods. The computational time required by GSAS in addition to the NOF is less than that required by EGRA and higher than its counterpart needed by AK-MCS. The NOF of the GSAS method is higher than that of the Meta-IS method. One possible reason for this phenomenon is that the training points are selected from the MCS sampling pool in the GSAS method whereas the training points of Meta-IS method are selected from the sampling pool of importance sampling. Combining the proposed method with importance sampling (IS) approach will further improve the efficiency of the proposed method. The integration of GSAS with IS however will change the equations given in Sec. 3 and algorithms presented in Sec. 4. The main steps of the combination of GSAS and IS have been briefly discussed in Sec.4.2. Since it belongs to another kind of method, here, we only give the results of GSAS-IS. Table 12 shows the comparison of GSAS-IS with Meta-IS. The results given in Table 12 are based on FORM-based IS. The NOF of GSAS-IS includes both the NOFs required by FORM and GSAS. Combining Meta-IS with GSAS may further improve the efficiency. Integration of GSAS with Meta-IS is another direction that may be pursued in future research.

Table 11 Results of Example 5

Fig. 24

${\widehat{p}}_f$ vs number of added new training points

Table 12 Comparison of GSAS-IS and Meta-IS

6 Conclusion

Monte Carlo sampling based on a surrogate model is a widely used approach of reliability analysis when the physics model evaluation is expensive. Adaptive Kriging-based methods have been studied in recent years to select training points for the surrogate model, by focusing on the region of interest using learning functions. In previous methods, the stopping criterion and learning function are defined from the aspect of individual training points. The effects of training points on the overall accuracy of reliability estimate are not considered. As a result, some un-important sampling points, which have weak contributions to the failure probability estimate, are selected as training points.

A Global Sensitivity Analysis enhanced Surrogate (GSAS) modeling method is developed in this work to improve the efficiency of adaptive Kriging, by considering a new stopping criterion and a new way of selecting new training points. The main idea is to treat the probability of failure estimated from the surrogate model similar to system response and prediction variance as the random input in GSA. The sampling pool, from which the training points are selected, is first divided into two groups. The error distribution of current failure probability estimate is then analyzed by propagating the uncertainty of prediction through a failure indicator function. The training points are selected to reduce the uncertainty in the failure probability estimate in the most effective way.

An overall implementation framework and two algorithms are provided for implementation of the proposed GSAS method. Five numerical examples, which include two mathematical examples and three engineering-related examples, demonstrate that the GSAS method can effectively improve the efficiency of surrogate model-based reliability analysis. Another way of improving the efficiency of surrogate modeling might be to maximize distance of the candidate point with the training points, which is a popular strategy used in SVM-based reliability analysis methods (Basudhar and Missoum 2008). This method, however, has not yet been integrated with the learning functions widely used in Kriging-based reliability analysis methods. Integration of the distance criterion with the learning functions needs to be studied in future work. The developed method presented in this paper increases the computational overhead required by the algorithm selecting the training points (even though it reduces the number of training points), which is common to all kinds of advanced sampling approaches. Optimizing the computer implementation of the proposed method needs to be investigated in future work. As indicated in the results of Example 5, the computational efficiency of the proposed method can be further improved by integrating the proposed method with importance sampling. This is another direction that needs to be investigated to improve the effectiveness of the developed method.