1 Introduction

Uncertainties commonly accompany a product in reality. Reliability analysis is required so that the safety under uncertainty can be quantitatively assessed. According to the number of failure modes, reliability analysis can be divided into the component reliability analysis (CRA) and the system reliability analysis (SRA). Only a single failure mode is considered in CRA, and multiple failure modes are simultaneously considered in SRA.

Generally, reliability analysis should be transformed into numerous times of deterministic analysis. If the performance functions should be computed by finite element (FE) analysis, the whole process of reliability analysis will be prohibitively time-consuming. Therefore, developing a method which can minimize the number of function evaluations has consistently been the pursuit of researchers.

Generally, methods for CRA can be extended to SRA. The first-order reliability method (FORM) is popularly used in CRA. However, it is not unwise to directly apply FORM to SRA. The system performance function (SPF) usually has multiple failure regions, and the direct application of FORM will generate a large error. Therefore, the first-order bounding theory was proposed (Ditlevsen 1979; Deb et al. 2009). In this theory, the system failure probability is bounded in a bilateral closed interval, and the bounds can be obtained from the component failure probability. In this manner, FORM can be used to obtain each component failure probability and then the bounds of system failure probability can be obtained. The saddle-point approximation method was also extended to SRA based on the first-order bounding theory (Du 2010). To improve the accuracy and efficiency, the second-order bound method (Ditlevsen 1979), and the linear programming bound method (Kang et al. 2008) were successively proposed. However, examples have shown that the bounds obtained by those techniques can be fairly wide, and reliable assessment of system failure probability cannot be achieved according to the bounds (Sues and Cesare 2005). In addition, if all the most probable points (MPPs) have been located by FORM, linear approximation or quadratic response surface can be conducted at those MPPs, and approximate failure probability can be obtained by the Monte Carlo simulation (MCS) method (Sues and Cesare 2005; Pandey 1998; Li and Mourelatos 2009; Hu and Du 2018). Other relevant methods can be seen in (Youn and Wang 2009; Wang et al. 2011).

Kinds of sampling methods, such as MCS method and important sampling (IS) method, can also be applied into SRA. SRA based on the IS method can be seen from (Dey and Mahadevan 1998). However, the number of function evaluations required by those methods is very large. Additionally, the SRA problem can be efficiently solved by building faster-evaluated surrogate models for SPF. The frequently used surrogate models are polynomial response surface method (Shayanfar et al. 2017), polynomial chaos expansion model (Sudret 2008), support vector machine (Bourinet et al. 2011), and Kriging model. The SRA method based on traditional response surface model is reported in (Sues and Cesare 2005). The method based on support vector machine can be seen in (Hu and Du 2018). It should be noted that the way of deploying training points determines the efficiency and accuracy of a surrogate model. From this perspective, the advent of active learning Kriging (ALK) model is a major step forward.

In the ALK model, a learning function that takes the full advantage of predicted mean and variance of a Kriging model is defined. Using the learning function, the point at which the sign of performance function has the largest “probability” to be located around the limit state surface (LSS) can be recognized. By iteratively exploring such a kind of training points, the sign-prediction ability of a Kriging model can be remarkably improved, and accurate failure probability can be obtained. Most of the obtained training points are accumulated around the region of interest rather than throughout a prescribed space. This is the main advantage of ALK model over other traditional surrogate models.

The basic idea of ALK model was first proposed and realized in Ref. (Bichon et al. 2008), where the so-called efficient global reliability analysis (EGRA) method was proposed. EGRA was improved in (Echard et al. 2011), where the so-called active learning method combining Kriging and MCS (AK-MCS) was proposed. Afterwards, diverse strategies were proposed to make the ALK model more efficient and robust (Hu and Mahadevan 2016; Wen et al. 2016; Jiang et al. 2019). In addition, several solutions were proposed by coupling ALK model with IS to estimate small failure probability. The methods combining the ALK model with single-MPP-based IS were proposed in (Echard et al. 2013; Gaspar et al. 2017). The methods reported in (Yang et al. 2018a; Cadini and Santos 2014; Razaaly and Congedo 2018) can solve problems with several failure regions in CRA.

The research of ALK model for SRA was also in a gradually deepening process. EGRA was adapted in Ref. (Bichon et al. 2011), and a method known as EGRA-SYS was proposed. AK-MCS was adapted in (Fauriat and Gayton 2014) and the method termed AK-SYS was proposed. In (Wang and Wang 2015), a so-called integrated performance measure approach was proposed. In (Sadoughi et al. 2018; Wei et al. 2018; Hu et al. 2017), the multivariate Gaussian process was introduced. It should be noted that a new task was posed to SRA compared with CRA: The training points should be cleared from the component LSSs that rarely contribute to system failure (Bichon et al. 2011; Fauriat and Gayton 2014; Hu et al. 2017). However, the methods in (Wang and Wang 2015; Wei et al. 2018) do not have such ability, and all the LSSs are finely approximated. Sometimes, EGRA-SYS and AK-SYS may fail to recognize the unimportant components correctly, and thus, the ALK model with a truncated candidate region (TCR) was proposed in (Yang et al. 2018b). The method is termed ALK-TCR. ALK-TCR was further improved in (Yang et al. 2019a).

Although extensive studies have been conducted in the field of SRA based on ALK model, one important issue remains unsolved: the estimation of small failure probability. ALK model is popularly coupled with MCS in the existing methods. If the failure probability is very small (like 10−6~10−9), numerous simulated samples (108~1011) will be required. The Kriging model should provide predictions at all the simulated samples in each iteration so that one training point is obtained. Then, the learning process will become very time-demanding.

This paper systemically investigates the method fusing ALK model and multimodal adaptive important sampling (MAIS) to address the rare-event estimation issue of SRA. An innovative scheme is proposed to build the ALK models of system: In each iteration, MPPs on the surrogate LSS are explored, important samples are generated and treated as the candidate points of ALK model; the system surrogate LSS is iteratively updated until it unbiasedly converges to the true LSS. A recently proposed multimodal optimization algorithm, called the evolutionary multi-objective optimization-based multimodal optimization (EMO-MMO) (Cheng et al. 2018), is first utilized to obtain all the MPPs on the system surrogate LSS. In this manner, the unbiasedness of the proposed scheme is guaranteed. Improper solutions of EMO-MMO are excluded, and the weighted instrumental sampling density function is formulated. Finally, the basic idea of ALK-TCR (Yang et al. 2018b) is introduced and training points are chosen from the important samples located in the TCR. The proposed method is termed ALK-MAIS-TCR.

This paper is outlined as follows. SRA based on the IS method is reviewed in Sect. 2. Our ALK-MAIS-TCR method is systematically expounded in Sect. 3. Four case studies are investigated to demonstrate the performance of our method. Conclusions are provided in the final section.

2 SRA based on IS method

When importance sampling method is involved, researchers prefer to expound the theory in the standard normal space. This space can be transformed from the original space by Nataf or Rosenblatt transformation (Der Kiureghian and Dakessian 1998). In addition, the values of component performance functions (CPFs) might be different by several magnitudes. The numerical difference of components may influence our search for MPPs. Therefore, it is recommended to normalize the value of every CPF in this paper. One way of doing such normalization is offered in Sect. 3.6.

In the standard normal space, denote the vector of random variables as u = [u1, ⋯, un], and the ith (normalized) CPF as gi(u). The failure probability of a series system and that of a parallel system are respectively defined as

$$ {P}_f=P\left\{\underset{i=1}{\overset{p}{\cup }}{g}_i\left(\mathbf{u}\right)<0\right\}=P\left\{\underset{i=1}{\overset{p}{\min }}{g}_i\left(\mathbf{u}\right)<0\right\} $$
(1)

and

$$ {P}_f=P\left\{\underset{i=1}{\overset{p}{\cap }}{g}_i\left(\mathbf{u}\right)<0\right\}=P\left\{\underset{i=1}{\overset{p}{\max }}{g}_i\left(\mathbf{u}\right)<0\right\} $$
(2)

in which P{·} is the probability of an event. Define \( G\left(\mathbf{u}\right)=\underset{i=1}{\overset{p}{\min }}{g}_i\left(\mathbf{u}\right) \) or \( G\left(\mathbf{u}\right)=\underset{i=1}{\overset{p}{\max }}{g}_i\left(\mathbf{u}\right) \), and G(u) is the SPF. The integration form of failure probability is given as

$$ {P}_f={\int}_{R^n}{I}_F\left(\mathbf{u}\right)\phi \left(\mathbf{u}\right)d\mathbf{u}=E\left[{I}_F\left(\mathbf{u}\right)\right] $$
(3)

in which E[·] is the expectation operator; ϕ(·) is the probability density function (PDF) of the standard normal distribution, and IF(·) is the failure indication function which is given as

$$ {I}_F\left(\mathbf{u}\right)=\left\{\begin{array}{l}1\kern1.5em G\left(\mathbf{u}\right)\le 0\\ {}0\kern1.25em G\left(\mathbf{u}\right)>0\end{array}\right. $$
(4)

Equation (3) can be directly estimated by the MCS method. However, a huge number of calls to G(u) are required for a small failure probability. By introducing an instrumental PDF (iPDF) h(u), the failure probability integral can be rewritten as

$$ {P}_f={\int}_{R^n}{I}_F\left(\mathbf{u}\right)\frac{\phi \left(\mathbf{u}\right)}{h\left(\mathbf{u}\right)}h\left(\mathbf{u}\right)d\mathbf{u}={E}_h\left[{I}_F\left(\mathbf{u}\right)\right] $$
(5)

Then, we can obtain another estimator for Pf, i.e.,

$$ {\hat{P}}_f^{\mathrm{IS}}=\frac{1}{N_{\mathrm{IS}}}\sum \limits_{i=1}^{N_{\mathrm{IS}}}{I}_F\left({\mathbf{u}}^{(i)}\right)\frac{\phi \left({\mathbf{u}}^{(i)}\right)}{h\left({\mathbf{u}}^{(i)}\right)} $$
(6)

where {u(i), i = 1, ⋯, NIS} are the important samples generated from h(u). The coefficient of variation (Cov) is given as

$$ Cov\left({\hat{P}}_f^{\mathrm{IS}}\right)\approx \frac{\sqrt{Var\left({\hat{P}}_f^{\mathrm{IS}}\right)}}{{\hat{P}}_f^{\mathrm{IS}}} $$
(7)

in which Var(·) is the variance operator, and we have

$$ Var\left({\hat{P}}_f^{\mathrm{IS}}\right)\approx \frac{1}{N_{\mathrm{IS}}}\left(\frac{1}{N_{\mathrm{IS}}}\sum \limits_{i=1}^{N_{\mathrm{IS}}}I\left({u}^{(i)}\right){\left(\frac{\phi \left({\mathbf{u}}^{(i)}\right)}{h\left({\mathbf{u}}^{(i)}\right)}\right)}^2-{\left({\hat{P}}_f^{\mathrm{IS}}\right)}^2\right) $$
(8)

The real art of IS lies in the development of h(u). By properly developing an iPDF, the estimator \( {\hat{P}}_f^{\mathrm{IS}} \)can be unbiased, and its Cov can be remarkably smaller than that of MCS. A proper iPDF should be able to guide the samples to cover all the failure regions with large probability density. The most classic technique is building a Gaussian mixture function centered on the MPPs. Other techniques can be found in Refs. (Kurtz and Song 2013; Au and Beck 1999).

3 ALK-MAIS-TCR

The basic ideas of our proposed method are shown as follows:

  1. 1.

    Separately build a Kriging model for each component

  2. 2.

    According to the prediction information of current Kriging models, obtain the surrogate LSS of system

  3. 3.

    Obtain multiple MPPs on the surrogate LSS by the evolutionary multimodal optimization (MMO) algorithm

  4. 4.

    Formulate an iPDF based on the “quasi” MPPs and generate important samples

  5. 5.

    Treat the important samples located in TCR as candidate points, choose training points, and update the Kriging models

  6. 6.

    Repeat steps (2)–(5) until the Kriging models of components are accurate enough

Then, we will expound our method step-by-step.

3.1 Surrogate LSS of a system

If multiple components exist in a system, it is desirable to separately build a Kriging model for each CPF rather than to build a single Kriging model for the SPF (Bichon et al. 2011). This is because the SPF often has several sharp corners, and those sharp corners will cost a lot of training points. Given a design of experiments (DoE), a Kriging model predicts gi(u) as a Gaussian process, i.e., \( {\hat{g}}_i\left(\mathbf{u}\right)\sim N\left({\mu}_{g_i}\left(\mathbf{u}\right),{\sigma}_{g_i}^2\left(\mathbf{u}\right)\right) \). In the prediction, \( {\mu}_{g_i}\left(\mathbf{u}\right) \) is the Kriging mean and \( {\sigma}_{g_i}^2\left(\mathbf{u}\right) \) is the Kriging variance. \( {\mu}_{g_i}\left(\mathbf{u}\right) \) represents the most probable value of gi(u), and \( {\sigma}_{g_i}^2\left(\mathbf{u}\right) \) can be regarded as the uncertainty that gi(u) has such a value. Such uncertainty is epistemic and can be reduced along with the enrichment of DoE (Dubourg et al. 2011).

By making full use of the prediction information of all component Kriging models, a proper surrogate LSS can be obtained for the system. In Ref. (Yang et al. 2019a), two measures of failure regions were proposed. They are known as the “plausibility” measure and the “belief” measure of failure regions. Along with the enrichment of DoE, both of them will converge to the true failure regions. The “plausibility” measure of failure regions is defined as \( {\tilde{\varOmega}}_{\mathrm{P}}=\left\{u\left|{\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)<0\right.\right\} \), and we have

$$ {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=\left\{\begin{array}{l}\underset{i=1}{\overset{p}{\min }}\left({\mu}_{g_i}\left(\mathbf{u}\right)-\alpha {\sigma}_{g_i}\left(\mathbf{u}\right)\right)\kern0.5em \mathrm{series}\ \mathrm{system}\\ {}\underset{i=1}{\overset{p}{\max }}\left({\mu}_{g_i}\left(\mathbf{u}\right)-\alpha {\sigma}_{g_i}\left(\mathbf{u}\right)\right)\kern0.5em \mathrm{parallel}\ \mathrm{system}\end{array}\right. $$
(9)

in which α is a constant which controls the confidence level. By setting α = 1.96, the confidence level will be 95%. In \( {\tilde{\varOmega}}_{\mathrm{P}} \), both the region with a very large confidence level and the region remaining uncertain to be failure regions are included. That means, all potential failure regions are taken into consideration. Therefore, the boundary of \( {\tilde{\varOmega}}_{\mathrm{P}} \), denoted as \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=0 \), is taken as the system surrogate LSS in this paper.

People may take it for granted that \( \underset{i=1}{\overset{p}{\min }}{\mu}_{g_i}\left(\mathbf{u}\right)=0 \) or \( \underset{i=1}{\overset{p}{\max }}{\mu}_{g_i}\left(\mathbf{u}\right)=0 \)can also be used as a surrogate LSS for a system. Unfortunately, neither of them is qualified enough. The Kriging variance is not taken into account, and several potential failure regions are excluded by them. In SRA, multiple failure regions exist and the system LSS often has multiple branches. It is frequently encountered that only several branches of the system LSS are finely approximated while others are not. Biased estimation often occurs when using them as the surrogate LSS.

3.2 Evolutionary multimodal optimization algorithm

The MPPs on \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=0 \) will be explored and utilized to formulate an iPDF for the IS method. For distinction with the true MPPs, they are called the quasi MPPs in this paper. The quasi MPPs can be obtained by solving such an optimization problem as

$$ \left\{\begin{array}{l}\kern1.25em \underset{\mathbf{u}}{\min}\left\Vert \mathbf{u}\right\Vert \\ {}s.t.{\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)\le 0,\mathbf{u}\in \left[\underset{\_}{\mathbf{u}},\overline{\mathbf{u}}\right]\end{array}\right. $$
(10)

in which \( \left[\underset{\_}{\mathbf{u}},\overline{\mathbf{u}}\right] \) is a prescribed searching space (like [− 6,6]n). \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right) \) is combined by multiple components, and hence, multiple optimal solutions frequently exist. Note that the optimal solutions include the global ones and local ones, and both of them should be found. Ignoring the local optima will cause \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right) \) to biasedly converge to the true LSS. Traditional optimization algorithms, such as the genetic algorithm and differential evolution algorithm (Wang et al. 2015), can only obtain one single optimum. To obtain all the optima of one optimization problem, the MMO algorithm is needed.

The MMO approaches can be coarsely classified into two groups: the niching ones and those based on the multi-objective optimization (MOO). The naïve idea of niching approaches has been applied to MPPs exploration in (Li and Mourelatos 2009; Der Kiureghian and Dakessian 1998), where a bulge-adding approach and a niching genetic algorithm were respectively proposed. Other early studies of niching approaches can be seen from (Shir 2012). However, the feasibility of those approaches is pretty sensitive to parameter settings, and it is hard to tune them. Some of the optima can be easily neglected by those methods (Cheng et al. 2018; Wang et al. 2015).

The approaches based on MOO attempted to transform an MMO problem into an MOO problem. Several excellent techniques along this direction have been proposed recently (Cheng et al. 2018; Wang et al. 2015; Yao et al. 2010). Their great performances have been verified by quite a lot of very complicated case studies (Cheng et al. 2018; Wang et al. 2015; Yao et al. 2010). However, the application of such advanced methods into SRA has not been reported so far. In this paper, the EMO-MMO algorithm (Cheng et al. 2018) is introduced into SRA for the first time.

Equation (10) can be transformed into such an unconstrained optimization problem as

$$ {\displaystyle \begin{array}{l}\min\ P\left(\mathbf{u}\right)=\left\Vert \mathbf{u}\right\Vert +\lambda \max {\left({\hat{G}}_S\left(\mathbf{u}\right),0\right)}^2\\ {}s.t.\kern0.5em \mathbf{u}\in \left[\underset{\_}{\mathbf{u}},\overline{\mathbf{u}}\right]\end{array}} $$
(11)

in which λ is a penalty factor with a very large value, like 2 × 1010. To preserve the diversity of solutions, a diversity function d(u) can be introduced into (11), and thus, we obtain such an bi-objective optimization problem as

$$ {\displaystyle \begin{array}{l}\min\ F\left(\mathbf{u}\right)=\left(P\left(\mathbf{u}\right),d\left(\mathbf{u}\right)\right)\\ {}s.t.\kern0.5em \mathbf{u}\in \left[\underset{\_}{\mathbf{u}},\overline{\mathbf{u}}\right]\end{array}} $$
(12)

By solving the Pareto front of (12), optimal solutions with remarkable diversity can be obtained. The Pareto front can be solved by quite a lot of MOO algorithms, and the most popular one, i.e., the non-dominated sorting genetic algorithm II (NSGA-II) was utilized in EMO-MMO. EMO-MMO is a population-based metaheuristic and d(u) is defined according to the current population of solutions.

In generation t(t ∈ [1, ⋯, tmax]), denote the population of solutions as \( \left[{\mathbf{u}}_{t,1},{\mathbf{u}}_{t,2},\cdots, {\mathbf{u}}_{t,{N}_{\mathrm{pop}}}\right] \). d(u) was defined as

$$ d\left(\mathbf{u}\right)=\left|{\mathbf{K}}_t\right|-\frac{1}{\delta_t}\left(\sum \limits_{k\in {\mathbf{K}}_t}{\left\Vert \mathbf{u}-{\mathbf{u}}_{t,k}\right\Vert}_1\right) $$
(13)

where Kt contains the indices of solutions in a niche, i.e.,

$$ {\mathbf{K}}_t=\left\{j\in \left[1,\cdots, {N}_{\mathrm{pop}}\right]:{\left\Vert \mathbf{u}-{\mathbf{u}}_{t,j}\right\Vert}_1<{\delta}_t\right\} $$
(14)

|Kt| is the number of elements in Kt, and δt is the radius of the niche which was defined as

$$ {\delta}_t=\left(1-\frac{t-1}{t_{\mathrm{max}}}\right)\times \underset{1\le i\le {N}_{\mathrm{pop}}}{\max}\left\{\underset{j\ne i}{\min }{\left\Vert {\mathbf{u}}_{t,i}-{\mathbf{u}}_{t,j}\right\Vert}_1\right\} $$
(15)

Note that ‖·‖1 is the Manhattan distance (L1 norm) of two points, and the distance is calculated in a grid-based normalized coordinate system in (Cheng et al. 2018). Equation (13) shows that, in a generation, a candidate solution having more neighbors or closer distances to those neighbors will have a larger value of d(u). As a consequence, offspring candidates will be attracted to the region with rare points and the diversity of solutions is maintained. The interested readers can refer to (Cheng et al. 2018) for more details.

In EMO-MMO, the candidate solutions in all generations of NSGA-II are stored in an archive. From the historical candidate solutions, we can mine multiple approximate optimal solutions. The approximate solutions can be further refined by a local optimizer. The procedure is listed as follows.

  • Among the historical candidates, choose the points satisfying \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)<0 \). Denote the set of them as D.

  • Divide D into Nclust clusters \( \left\{{\mathbf{D}}_1,{\mathbf{D}}_2,\cdots, {\mathbf{D}}_{N_{clust}}\right\} \) by the K-means clustering algorithm (Jain 2010). In Di(i = 1, ⋯, Nclust), obtain the point with a minimal value of ‖u‖. Denote it as \( {\mathbf{u}}_F^{(i)} \).

  • Set \( \left({\mathbf{u}}_F^{(1)},{\mathbf{u}}_F^{(2)},\cdots, {\mathbf{u}}_F^{\left({N}_{clust}\right)}\right) \) as the starting points, perform Nclust times of independent local search by gradient-based optimization method. The sequential quadratic programming (SQP) algorithm is adopted here.

3.3 Weighted iPDF

The number of quasi MPPs is not known in prior and Nclust is assigned a value just according to experience. The set of solutions obtained by EMO-MMO probably blend spurious solutions. Moreover, in one failure region, there exist a crowd of solutions. Therefore, improper solutions should be eliminated. Otherwise, important samples will cover the unimportant regions or overly indulge in certain failure regions.

Geometrically, the position vector of a quasi MPP and the gradient of \( {\hat{G}}_S \) at the quasi MPP should be collinear (Li and Mourelatos 2009). Therefore, a point u can be treated as a quasi MPP only if

$$ {\lambda}_{\theta }=\left|\frac{\left\langle \mathbf{u},{\left(\nabla {\hat{G}}_S\right)}_{\mathbf{u}}\right\rangle }{\left\Vert \mathbf{u}\right\Vert \left\Vert {\left(\nabla {\hat{G}}_S\right)}_{\mathbf{u}}\right\Vert}\right|\approx 1 $$
(16)

If λθ < 0.8, the point should be eliminated. In this manner, spurious optimal solutions can be excluded.

If two points ui, uj are very close to each other, their position vectors should be almost the same. Mathematically, there is

$$ {\rho}_{ij}=\frac{\left\langle {\mathbf{u}}_i,{\mathbf{u}}_j\right\rangle }{\left\Vert {\mathbf{u}}_i\right\Vert \left\Vert {\mathbf{u}}_j\right\Vert}\approx 1 $$
(17)

ρij is named the correlation coefficient of two points in (Deb et al. 2009; Li and Mourelatos 2009). If ρij ≥ 0.95, the point with a larger value of ‖u‖ should be eliminated. In this way, the solutions will not be crowded in one failure region.

After wiping out the inferior solutions, an iPDF can be formulated. Denote the quasi MPPs as \( \left\{{\mathbf{u}}_{\mathrm{MPP}}^{(k)},k=1,\cdots, {N}_{\mathrm{MPP}}\right\} \), and the iPDF can be given as

$$ \tilde{h}\left(\mathbf{u}\right)=\sum \limits_{k=1}^{N_{\mathrm{MPP}}}{w}_k\varphi \left(\mathbf{u}\left|{\mathbf{u}}_{\mathrm{MPP}}^{(k)}\right.\right) $$
(18)

in which

$$ \varphi \left(\mathbf{u}\left|{\mathbf{u}}_{\mathrm{MPP}}^{(k)}\right.\right)=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{{\left(\mathbf{u}-{\mathbf{u}}_{\mathrm{MPP}}^{(k)}\right)}^2}{2}\right) $$
(19)

and wk is the weight of each quasi MPP. wk is introduced to take the contribution of each potential failure region to the system failure probability into account. For the sake of simplicity, those potential failure regions are considered to be mutually independent, and FORM can give an approximate failure probability for each of them. Then, wkcan be given as

$$ {w}_k=\frac{\varPhi \left(-\left\Vert {\mathbf{u}}_{\mathrm{MPP}}^{(k)}\right\Vert \right)}{\sum \limits_{i=1}^{N_{\mathrm{MPP}}}\varPhi \left(-\left\Vert {\mathbf{u}}_{\mathrm{MPP}}^{(i)}\right\Vert \right)} $$
(20)

in which Φ(·) is the cumulative distribution function (CDF) of standard normal distribution and \( \varPhi \left(-\left\Vert {\mathbf{u}}_{\mathrm{MPP}}^{(k)}\right\Vert \right) \) is the approximate failure probability of the kth failure region by FORM. Then, NIS important samples obeying \( \tilde{h}\left(\mathbf{u}\right) \) can be generated by the sampling method offered in (Au and Beck 1999). Denote the set of important samples as ΩIS.

3.4 Truncated candidate region

Training points can be chosen from ΩIS by a learning function. Note that several learning functions have been proposed, such as the learning function U (Echard et al. 2011), the expected risk function (ERF) (Yang et al. 2015), and the expected feasibility function (EFF) (Bichon et al. 2008). In this paper, ERF is adopted. For the ith Kriging model, ERF was defined as

$$ ER{F}_{g_i}\left(\mathbf{u}\right)=-\operatorname{sign}\left({\mu}_{g_i}\left(\mathbf{u}\right)\right){\mu}_{g_i}\left(\mathbf{u}\right)\varPhi \left(-\operatorname{sign}\left({\mu}_{g_i}\left(\mathbf{u}\right)\right)\frac{\mu_{g_i}\left(\mathbf{u}\right)}{\sigma_{g_i}\left(\mathbf{u}\right)}\right)+{\sigma}_G\left(\mathbf{u}\right)\phi \left(\frac{\mu_{g_i}\left(\mathbf{u}\right)}{\sigma_{g_i}\left(\mathbf{u}\right)}\right) $$
(21)

in which sign(·) is the sign function, and ϕ(·) is the PDF of the standard normal distribution. For a single component, the point maximizing EFR should be chosen as the training point. For a system, one can directly choose the point with the maximal value among the p ERFs, i.e.,

$$ {\mathbf{u}}^{\ast }=\underset{\mathbf{u},1\le i\le p}{\max } ER{F}_{g_i}\left(\mathbf{u}\right) $$
(22)

However, in this way, training points will finally be populated around all component LSSs including the unimportant ones. Take a 2D series system with three components as an example. As shown in Fig. 1, the region covered by ΩIS may also cover the unimportant LSSs, i.e., \( {\mathrm{O}}_1\mathrm{C} \), \( {\mathrm{O}}_1\mathrm{B} \), \( {\mathrm{O}}_2\mathrm{E} \), and\( {\mathrm{O}}_2\mathrm{D} \). If the training points are directly chosen by (22), those unimportant LSSs will also attract training points. As a result, a certain number of function evaluations are wasted.

Fig. 1
figure 1

A 2D series system with three components

Full size image

Therefore, it is recommended to choose training points in a systematic way. Several advanced strategies have been proposed to assist training points to get away from the unimportant component LSSs (Bichon et al. 2011; Fauriat and Gayton 2014; Hu et al. 2017; Yang et al. 2018b, 2019b). In this paper, the method based on the so-called TCR is adopted (Yang et al. 2018b, 2019b). In this method, the unimportant region is cut off from the original candidate region, and training points are only chosen from the TCR.

For a series system, the TCR was defined as

$$ {\tilde{\varOmega}}_{\mathrm{T}}\left(\mathbf{u}\right)=\left\{\mathbf{u}\left|\underset{i=1}{\overset{p}{\min }}\left({\mu}_{g_i}\left(\mathbf{u}\right)+\alpha {\sigma}_{g_i}\left(\mathbf{u}\right)\right)>0\right.\right\} $$
(23)

and for a parallel system, the TCR was defined as

$$ {\tilde{\varOmega}}_{\mathrm{T}}\left(\mathbf{u}\right)=\left\{\mathbf{u}\left|\underset{i=1}{\overset{p}{\max }}\left({\mu}_{g_i}\left(\mathbf{u}\right)-\alpha {\sigma}_{g_i}\left(\mathbf{u}\right)\right)<0\right.\right\} $$
(24)

The optimal training point can be obtained by

$$ {\displaystyle \begin{array}{l}{\mathbf{u}}^{\ast }=\underset{\mathbf{u},1\le i\le p}{\max } ER{F}_{g_i}\left(\mathbf{u}\right)\\ {}s.t.\kern0.75em \mathbf{u}\in {\tilde{\varOmega}}_{\mathrm{T}}\end{array}} $$
(25)

Another issue is how many training points should be chosen from ΩIS in each sequence. If only one is chosen from one set of important samples, EMO-MMO will be executed for many times, which is quite time-demanding. Executing the learning process multiple times and choosing multiple training points from the current ΩIS are recommend. The number is assigned as NSeq in this paper.

3.5 Stopping condition

The difference between the “plausibility” measure and the “belief” measure of the system failure region was utilized to judge the accuracy of component Kriging models in (Yang et al. 2019a). Recall that \( {\tilde{\varOmega}}_{\mathrm{P}} \) is the plausibility measure. By setting the parameter α in \( {\tilde{\varOmega}}_{\mathrm{P}} \) as − 1.96, the “belief” measure of system failure region can be obtained. The belief measure is denoted as \( {\tilde{\varOmega}}_{\mathrm{B}} \).

Along with the enrichment of DoE, the epistemic uncertainty of a Kriging model can be gradually reduced, and \( {\tilde{\varOmega}}_{\mathrm{P}} \) will gradually approach to \( {\tilde{\varOmega}}_{\mathrm{B}} \). Thus, the stopping condition can be defined by the following expression:

$$ {\varepsilon}_{P_f}=\frac{\left|{\tilde{P}}_{f\mathrm{P}}^{\mathrm{IS}}-{\tilde{P}}_{f\mathrm{B}}^{\mathrm{IS}}\right|}{{\tilde{P}}_{f\mathrm{P}}^{\mathrm{IS}}}<\gamma $$
(26)

in which \( {\tilde{P}}_{f\mathrm{P}}^{\mathrm{IS}} \) is the plausibility measure of failure probability, and \( {\tilde{P}}_{f\mathrm{B}}^{\mathrm{IS}} \) is the belief measure of failure probability. Thus,

$$ {\tilde{P}}_{f\mathrm{B}}^{\mathrm{IS}}=\frac{1}{N_{\mathrm{IS}}}\sum \limits_{i=1}^{N_{\mathrm{IS}}}{I}_F\left({\mathbf{u}}^{(i)}\in {\tilde{\varOmega}}_{\mathrm{B}}\right)\frac{\phi \left({\mathbf{u}}^{(i)}\right)}{\tilde{h}\left({\mathbf{u}}^{(i)}\right)} $$
(27)
$$ {\tilde{P}}_{f\mathrm{P}}^{\mathrm{IS}}=\frac{1}{N_{\mathrm{IS}}}\sum \limits_{i=1}^{N_{\mathrm{IS}}}{I}_F\left({\mathbf{u}}^{(i)}\in {\tilde{\varOmega}}_{\mathrm{P}}\right)\frac{\phi \left({\mathbf{u}}^{(i)}\right)}{\tilde{h}\left({\mathbf{u}}^{(i)}\right)} $$
(28)

Note that, for convenience, \( {\tilde{P}}_{f\mathrm{P}}^{\mathrm{IS}} \) and \( {\tilde{P}}_{f\mathrm{B}}^{\mathrm{IS}} \) are estimated from the same set of important samples. The important samples are obtained in Sect. 3.3, i.e., those generated for \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=0 \). However, such convenience cannot vitally disturb the convergence of our method. If \( {\tilde{\varOmega}}_{\mathrm{P}} \) and \( {\tilde{\varOmega}}_{\mathrm{B}} \) are different from each other, the important samples of \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=0 \) definitely cannot generate two similar estimations in (27) and (28). Only when \( {\tilde{\varOmega}}_{\mathrm{P}} \) and \( {\tilde{\varOmega}}_{\mathrm{B}} \)are very close to each other, they share the same set of important samples and generate the same estimation of failure probability. In addition, γ = 5% is adopted in this paper.

3.6 Summarization of ALK-MAIS-TCR

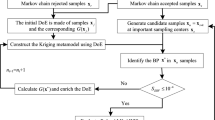
The proposed method is shown in Fig. 2. It consists of 11 steps:

  1. 1.

    Transform the random variables into the standard normal space.

  2. 2.

    Draw a small number of training points by the Latin hypercube sampling method. Those points are uniformly distributed in the region [−5, 5]n, and the number is assigned 12. Denote the set of initial training points as Ω0.

  3. 3.

    Obtain the normalized CPFs by \( {g}_k\left(\mathbf{u}\right)={Y}_k\left(\mathbf{u}\right)/{\mu}_{Y_k}\left(k=1,\cdots, p\right) \), where Yk(u) is the original value of the kth CPF, and \( {\mu}_{Y_k}=\underset{\mathbf{u}\in {\varOmega}_0}{mean}\left({Y}_k\left(\mathbf{u}\right)\right) \). Build p Kriging models for gk(u)(k = 1, ⋯, p). Denote the kth Kriging model as \( {\hat{g}}_k\left(\mathbf{u}\right) \).

  4. 4.

    With the prediction information of \( {\hat{g}}_k\left(\mathbf{u}\right)\left(k=1,\cdots, p\right) \), formulate the surrogate LSS of the system by (9).

  5. 5.

    Obtain multiple quasi MPPs on \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=0 \) by the EMO-MMO algorithm.

  6. 6.

    Remove the unqualified solutions and formulate a weighted iPDF by (18). GenerateNIS important samples and denote the set of them as ΩIS.

  7. 7.

    If \( {\varepsilon}_{P_f}<\gamma \) and m ≥ Nmin, which means the Kriging models of components have been accurate enough, step out to step (11). Otherwise, set NSeq = 0 and continue.

  8. 8.

    In ΩIS, obtain the points located in the TCR. Among the points in the TCR, choose the optimal training point u∗ by (25).

  9. 9.

    If \( {N}_{Seq}>{N}_{Seq}^{\mathrm{max}} \) or \( {\varepsilon}_{P_f}<\gamma \), return to Step (4).

  10. 10.

    Otherwise, add u∗ into the DoE and evaluate the (normalized) CPFs at u∗. Update all the Kriging models and set NSeq = NSeq + 1. Return to Step (8).

  11. 11.

    Obtain the system failure probability based on all the Kriging models.

Fig. 2
figure 2

Flowchart of ALK-MAIS-TCR

Full size image

Note that, m ≥ Nmin is introduced in step (7) to guarantee that at least m − Nmin times of learning are executed. The learning process of our method without this condition may be terminated in the beginning by sheer coincidence. That is because the size of initial training points is very small and randomly generated. The surrogate LSS might regard all the prescribed searching space as the safety region and EMO-MMO cannot obtain any feasible solution. Under this situation, we take the point among the candidates of EMO-MMO closest to \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=0 \) as the quasi MPP. Such a last resort might result in the early termination of learning process. m ≥ Nmin is introduced to prevent this from happening. A similar measure can also be seen in (Cadini and Santos 2014).

4 Test examples

In this section, four examples will be investigated to examine our method. In each example, the parameter settings of our method are outlined in Table 1. The method will be independently executed ten times. The averaged result and the bounds of each quantity will be extracted.

Table 1 Parameter settings of ALK-MAIS-TCR
Full size table

4.1 System with four failure regions

Four components exist in this system, and the ith one is defined as

$$ {g}_i(u)=\min \left\{\begin{array}{l}\frac{k_i}{2}+\frac{{\left({u}_1-{u}_2\right)}^2}{10}\pm \frac{\left({u}_1+{u}_2\right)}{\sqrt{2}}\\ {}\frac{k_i}{\sqrt{2}}\pm \left({u}_1-{u}_2\right)\end{array}\right. $$
(29)

in which u = [u1, u2] are two independent random variables obeying standard normal distribution and ki = 9 + i. Note that each of them is a complicated black-box function with four failure regions. Two cases are considered in this example.

4.1.1 Case I series system

In case I, the four CPFs are assumed to form a series system. Note that only g1 = 0contributes to system failure. Results of different methods are collected in Table 2. The true failure probability is 9.13 × 10−7, which is obtained by MCS with 1 × 109. EMO-MMO + IS refers to the method combining the EMO-MMO algorithm with IS method: EMO-MMO described in Sect. 3.2 is used to calculate all MPPs of the true SPF, and the IS method offered in Sect. 3.3 is used to estimate the true failure probability. FERUM#11 + IS uses the famous reliability analysis software FERUM (method 11) to obtain all the MPPs and IS method offered in Sect. 3.3 to estimate the true failure probability. In the FERUM software (Bourinet et al. 2009), method 11 refers to the bulge-adding approach for multi-MPP calculation proposed in (Der Kiureghian and Dakessian 1998). In (Der Kiureghian and Dakessian 1998), after one MPP is obtained, a bulge is added to the performance function around the MPP so that the optimizer can be forced to explore another region. The optimizer is implemented several times until multiple MPPs are obtained. However, FERUM#11 + IS provides a biased estimation and only two MPPs are obtained. That is because the size of the bulge is very hard to be determined, and some MPPs are concealed by the bulge. By contrast, EMO-MMO obtains all the MPPs, and unbiased estimation is offered by EMO-MMO + IS.

Table 2 Results of Example 4.1 with different methods (case I)
Full size table

Using 67.6 function evaluations, the proposed method accurately estimates such a small failure probability. The DoE of the proposed method is shown in Fig. 3. Note that the SPF has four failure regions, and all of them contribute to the failure probability integration. In addition, only the first component contributes to system failure. It can be seen that the training points are mainly accumulated around the LSS of the first component. By fusing the TCR strategy into our method, little portion of training points is deployed to the unimportant LSSs, and thus, the waste of training points is avoided.

Fig. 3
figure 3

DoE comparison. a ALK-MAIS. b ALK-MAIS-TCR#1. c ALK-MAIS-TCR

Full size image

The learning process of the proposed method is shown in Fig. 4. The system surrogate LSS, the obtained quasi MPPs, the generated important samples, and the chosen training points are offered. It can be seen that, along with the enrichment of DoE, the surrogate LSS converges to the true one. In each sequence, the quasi MPPs are all correctly found by the EMO-MMO algorithm. The quasi MPPs gradually converge to the true ones, and redundant ones are rarely kept during this process. From those figures, the rationality of the proposed method can be revealed. Figure 5 shows the historical populations of EMO-MMO in sequence (1) and sequence (6). It can be seen that all the surrogate failure regions are densely covered by the candidate solutions. With them, it is pretty easy to mine all the global and local quasi MPPs by the technique offered in this paper. The effectiveness of EMO-MMO guarantees the unbiasedness of the proposed method.

Fig. 4
figure 4

Learning process of ALK-MAIS-TCR: green line is the surrogate LSS of system; black line is the true system LSS; black star is the MPP; the blue dot is the initial training point, the red dot represents the added training point, and the black dot is the important samples

Full size image
Fig. 5
figure 5

Populations stored by EMO-MMO: left, Sequence 1; right, Sequence 6

Full size image

People may also doubt that \( \underset{i=1}{\overset{p}{\min }}{\mu}_{g_i}\left(\mathbf{u}\right)=0 \) which does not take the Kriging variance into account can also serve as the surrogate LSS of this system. However, in this manner, it takes a huge risk that several branches of the system LSS are never approximated throughout the learning process. As shown in Fig. 6, the learning process is terminated early before all branches of the system LSS are accurately approximated. Throughout the learning process, the lower right branch does not attract any training point. Because no failure training points are located around this region initially, \( \underset{i=1}{\overset{p}{\min }}{\mu}_{g_i}\left(\mathbf{u}\right)=0 \) rashly holds that there is no failure region here. As a result, no candidate points are generated in this region and no training points will be chosen in the next sequences. By contrast, the Kriging variance here is quite large, and \( {\hat{G}}_{\mathrm{S}}\left(\mathbf{u}\right)=0 \) regards this region as a potential failure region. Therefore, training points will also be deployed into this region, and unbiased estimation is guaranteed.

Fig. 6
figure 6

Failed learning process without considering Kriging variance

Full size image

To demonstrate the effect of weighted iPDF and TCR on the proposed method, two methods ALK-MAIS and ALK-MAIS-TCR#1 are introduced. If the training points are directly chosen from all the candidate points rather than from the TCR, the method is termed ALK-MAIS. If all the quasi MPPs obtained by EMO-MMO are kept and an equally weighted iPDF is formulated based on those MPPs, the method is termed ALK-MAIS-TCR#1. The other conditions of those methods are kept the same with ALK-MAIS-TCR. The results of those methods are also given in Table 2. It can be seen that ALK-MAIS-TCR is apparently more efficient than the other two methods. The DoEs of the other two methods are also given in Fig. 3. It can be seen that (I) if the quasi MPPs are not filtered, some portion of the failure regions with little contribution will also have training points; (II) if the TCR is not introduced, the unimportant components will also attract training points. Both cases should be avoided while building ALK models.

4.1.2 Case II parallel system

In case II, the four CPFs are assumed to form a parallel system. In this case, only g4 = 0 contributes to the system and the system failure probability is very small. By the EMO-MMO + IS method, the estimated failure probability is 1.24 × 10−10. Such an estimation is unbiased because the four MPPs on g4 = 0 are obtained by EMO-MMO. Therefore, the estimation of EMO-MMO + IS is regarded as the benchmark.

Table 3 gives the results of this case. Both ALK-MAIS-TCR and ALK-MAIS obtain very accurate results. Their efficiency is very distinct: A considerable number of training points are saved by ALK-MAIS-TCR. In one test, the DoEs of them are offered in Fig. 7. It can be seen that most attention of ALK-MAIS-TCR is paid to the system LSS. On the contrary, all the four component LSSs distract the attention of ALK-MAIS. To sum up, introducing the TCR can reduce the waste of training points for complicated SRA.

Table 3 Results of Example 4.1 with different methods (case II)
Full size table
Fig. 7
figure 7

DoE comparison: left, ALK-MAIS; right, ALK-MAIS-TCR

Full size image

4.2 Series system with 10 components

This example is a series system modified from Refs. (Bichon et al. 2011; Fauriat and Gayton 2014). It has ten failure modes related to the impact crash-worthiness of a vehicle. The system failure probability is defined as

$$ {P}_f=P\left\{\begin{array}{l}{g}_1\left(\mathbf{x}\right)\ge 1\cup {g}_2\left(\mathbf{x}\right)\ge 4.55\cup {g}_3\left(\mathbf{x}\right)\ge 32.5\cup {g}_4\left(\mathbf{x}\right)\ge 34.6\cup {g}_5\left(\mathbf{x}\right)\ge 34.5\cup \\ {}{g}_6\left(\mathbf{x}\right)\ge 0.32\cup {g}_7\left(\mathbf{x}\right)\ge 0.32\cup {g}_8\left(\mathbf{x}\right)\ge 0.32\cup {g}_9\left(\mathbf{x}\right)\ge 10.1\cup {g}_{10}\left(\mathbf{x}\right)\ge 15.89\end{array}\right\} $$
(30)

in which x = [x1, x2, ⋯, x11] is the random variables and gk is the kth CPF. x and gk(k = 1, ⋯, 10) are kept the same with Refs. (Bichon et al. 2011; Fauriat and Gayton 2014), and details about them can be seen there. Only the thresholds of those CPFs are modified so that the true failure probability of the system is very small.

The results of this example are given in Table 4. The true failure probability of this system is 6.13 × 10−6, which is obtained by MCS with 2 × 108 simulations. EMO-MMO + IS is also used to calculate the small failure probability. The population size of EMO-MMO is 500, and the number of generations is 100. A total of 5 × 104 candidates are stored by EMO-MMO, and the K-means algorithm divides them into 10 clusters. Ten times of local optimization take 7687 function evaluations. Three inferior solutions are eliminated and seven MPPs are finally obtained. IS with 104 samples is performed based on the seven MPPs, and the obtained failure probability is very close to the true one. FORM can also be applied to calculate a small failure probability. By FORM, the MPP of each component is calculated, and multiple linear approximation can be constructed at the ten MPPs (Hu and Du 2018). Then, MCS can be executed based on the linear approximation. However, the accuracy of FORM cannot be assured. For this problem, FORM takes 1160 function evaluations while the error is quite large. Also note that, at one point, all those CPFs can be obtained by one time of FE analysis in practice. However, FORM has to be executed in a component-by-component way. That is why it takes so many function evaluations. FERUM#11 + IS only obtains one MPP and the estimation is a little biased. With ALK-MAIS-TCR, only 37.8 function evaluations are needed, and a very accurate result is obtained. This reveals the advantage of the proposed method. Without considering the TCR, ALK-MAIS needs about four more function evaluations. It is beneficial to exclude the unimportant components during building ALK models in SRA.

Table 4 Results of Example 4.2 with different methods
Full size table

4.3 A cantilever beam

A cantilever beam from (Du 2010; Hu and Du 2018) is investigated here. As shown in Fig. 8, the beam is subjected to two moments, two concentrated forces, and two distributed loads. The geometric parameters of the beam are given in Table 5. Twelve random variables exist, and details about them can be seen in Table 6. Three main failure modes are considered here. The first failure mode occurs if the maximal stress exceeds the yield strength (σs), and its CPF is given by

$$ {g}_1\left(\mathbf{x}\right)={\sigma}_s-\frac{6M}{w{h}^2} $$
(31)

in which Mis calculated by

$$ {\displaystyle \begin{array}{l}M=\sum \limits_{i=1}^2{M}_i+\sum \limits_{i=1}^2{F}_i{b}_i+\sum \limits_{i=1}^2{q}_{Li}\left({d}_i-{c}_i\right)\left({d}_i+{c}_i\right)/2+\\ {}\sum \limits_{i=1}^2\left[\left({q}_{Ri}-{q}_{Li}\right)\left({d}_i-{c}_i\right)/2\right]\left[{c}_i+2\left({d}_i-{c}_i\right)/3\right]\end{array}} $$
(32)
Fig. 8
figure 8

A cantilever beam (Hu and Du 2018)

Full size image
Table 5 Geometric parameters of cantilever beam
Full size table
Table 6 Random variables of cantilever beam
Full size table

The second failure mode occurs if the maximal deflection is larger than 35 mm, and its CPF is defined as

$$ {g}_2\left(\mathbf{x}\right)=35-\delta $$
(33)

in which δ is computed by

$$ \delta =\frac{1}{EI}\left[\begin{array}{l}\frac{M{L}^2}{2}+\frac{R{L}^3}{6}+\sum \limits_{i=1}^2\frac{M_i{\left(L-{a}_i\right)}^2}{2}-\sum \limits_{i=1}^2\frac{F_i{\left(L-{b}_i\right)}^3}{6}-\sum \limits_{i=1}^2\frac{q_{Li}{\left(L-{c}_i\right)}^4}{24}\\ {}-\sum \limits_{i=1}^2\frac{\left({q}_{Ri}-{q}_{Li}\right){\left(L-{c}_i\right)}^5}{120\left({d}_i-{c}_i\right)}+\sum \limits_{i=1}^2\frac{q_{Ri}{\left(L-{d}_i\right)}^4}{24}+\sum \limits_{i=1}^2\frac{\left({q}_{Ri}-{q}_{Li}\right){\left(L-{d}_i\right)}^5}{120\left({d}_i-{c}_i\right)}\end{array}\right] $$
(34)

where E is the Young’s modulus, I is the moment inertia, and R is the reaction force at the fixed end. E = 200GPa and I = wh3/12.R is given by

$$ R=\sum \limits_{i=1}^2{F}_i+\sum \limits_{i=1}^2{q}_{Li}\left({d}_i-{c}_i\right)+\sum \limits_{i=1}^2\left({q}_{Ri}-{q}_{Li}\right)\left({d}_i-{c}_i\right)/2 $$
(35)

The third failure mode occurs because the shear stress exceeds the shear strength (τa), and its CPF is given by

$$ {g}_3\left(\mathbf{x}\right)={\tau}_a-\frac{3R}{2 wh} $$
(36)

Any of the three failure modes is not allowed, and the three failure modes compose a series system.

The results of different methods are given in Table 7. The failure probability obtained by MCS is 4.26 × 10−7, which is very small. EMO-MMO + IS obtains a pretty accurate result by about 105 function evaluations. This time, FERUM#11 + IS successfully obtains all the MPPs, and an unbiased estimation is obtained. By FORM, 331 function evaluations are needed while the result is quite inaccurate. However, by the proposed method, only 48 training points are used to build three Kriging models and a very accurate estimation is obtained for the system.

Table 7 Results of Example 4.3 with different methods
Full size table

Note that the CPF g1(x) is remarkably smaller than the other two CPFs. To obtain all the MPPs by EMO-MMO, one should normalize the values of the three CPFs into a similar magnitude. Otherwise, several dominant MPPs will not be obtained. That is because a uniform penalty factor is used for all the CPFs in this paper. EMO-MMO will always deem the region around g1(x) superior to that around the other two CPFs. However, such a kind of normalization does not need to be very strict. Just unifying the values of CPFs into a similar magnitude has been able to meet the requirement.

4.4 A 3D truss

A space truss with 25 bars, as shown in Fig. 9, is investigated to demonstrate the application of the proposed method to practical engineering. The truss has 10 nodes, and their coordinates are listed in Table 8. The number of bars, the nodes of each bar, and individual area are shown in Table 9. Five loads are exerted on nodes 1, 2, 4 and 6. The Young’s modulus of bars 1~13 is 120 GPa and that of bars 14~25 is 70 GPa. Random variables are given in Table 10. After several times of FE analysis, it can be found that bars 6, 8, 23, and 24 are subjected to a remarkably larger tensile stress than other bars. The CPFs are defined as

$$ \left\{\begin{array}{l}{g}_1\left(\mathbf{x}\right)=230-{\sigma}_6\left(\mathbf{x}\right)\\ {}{g}_2\left(\mathbf{x}\right)=230-{\sigma}_8\left(\mathbf{x}\right)\\ {}{g}_3\left(\mathbf{x}\right)=210-{\sigma}_{23}\left(\mathbf{x}\right)\\ {}{g}_4\left(\mathbf{x}\right)=210-{\sigma}_{24}\left(\mathbf{x}\right)\end{array}\right. $$
(37)

in which σi(x)(i = 6, 8, 23, 24) are the tensile stresses of the four vulnerable bars, and their unit is MPa. The four CPFs form a series system. The four CPFs are calculated by FE analysis, and one time of FE analysis can obtain all their values.

Fig. 9
figure 9

A 3D truss

Full size image
Table 8 Nodes coordinates of 3D truss
Full size table
Table 9 Details of bars of 3D truss
Full size table
Table 10 Random variables of 3D truss
Full size table

Results of different methods are offered in Table 11. The true result is obtained by the EMO-MMO + IS method. In this method, the population size of EMO-MMO is 105, 1018 function evaluations are cost by four times of local optimization, and 104 important samples are used to estimate the small failure probability. FERUM#11 + IS also successfully solves this problem. FORM is independently executed four times to obtain the MPPs of the four CPFs, and a linear approximation is conducted at the MPPs. And the obtained failure probability is very close to the true one. However, 357 times of FE analysis are consumed by the four times of MPP exploration. By the proposed method, only 95.5 times of FE analysis are required, and an unbiased estimation is obtained.

Table 11 Results of Example 4.4 with different methods
Full size table

5 Conclusions

This paper proposes a new method combining ALK model and MAIS to address the SRA problem with small failure probability. In each iteration, training points are chosen among the important samples predicted by a so-called surrogate LSS, and the surrogate LSS is updated. After several iterations, the system surrogate LSS converges to the true LSS. To obtain all the MPPs on the surrogate LSS, a brilliant MMO algorithm (EMO-MMO) is introduced. After filtering the quasi MPPs, a weighted iPDF is constructed, and important samples considering the contribution of failure region are generated. To further save the training points, TCR is introduced, and training points are only chosen from the important samples located in the TCR.

Through four complicated examples, the characteristics of the proposed method are demonstrated. The method can approximate all the branches of system LSS and obtain all the main MPPs of the system. The training points of the proposed method pays much attention to the LSSs of components which really contribute to system failure. These two important features guarantee the unbiasedness and high efficiency of the proposed method.