1 Introduction

As a matter of fact, as well as improving the properties of the applicable structures [1, 2] in the different engineering fields [3,4,5] by employing the various methods in the last decades, researchers have found a novel and excellent method for enhancing the static and dynamic responses of the low-density plate, beam, shell, and disk [6,7,8,9,10,11,12]. Based on this matter, honeycombed structures are presented for use in the related industry. Mukhopadhyay et al. [13]. investigated the vibrational characteristics of the sandwich panel with honeycomb core with the aid of Hamilton’s principle. They reported that the honeycomb core could improve the natural frequency and, finally, the stiffness of the sandwich panel. Ref. [14] studied the effects of various defects that occur for building honeycomb composite beams and obtained the mechanical performance of honeycomb beams in different vibration modes using finite element analysis and fast Fourier transform analyzer. Significant results of this study showed that the natural frequency of the structure decreases with increasing defect percentage. Mozafari et al. [15] studied the vibrational frequencies of honeycomb sandwich panels with different cores. Using experimental testing, they determined the mechanical properties of polyurethane foams. They examined the effect of the first resonant frequency, the shape of the state, and the impact of the foams on the vibrational response of the core. The free vibration of the graded corrugated lattice core structure and the analytical method to solve the governing equations were examined by Ref. [16]. They analyzed the effect of beam length, graded parameters, and facial leaf thickness on the frequency responses of the mentioned structure. Amini et al. [17] controlled the amplitude of the vibrations of a solar panel that is made of a honeycomb core and smart layers. With Hamilton’s principle and thin plate theory, they developed the motion equations and boundary conditions. Finally, they found that the elastoelectric effects have an essential role in the frequency responses of the solar panel. Ref [18]. evaluated the post-buckling behavior of panels with honeycomb cores and reinforced by graphene particles. The researchers' findings show that core thickness, GPL weight fraction, and geometric parameters related to the panel have an essential role in the post-buckling behavior of the sandwich panel. The bending behavior of a curved beam with graphene nanoplatelets and honeycomb core was studied by Sobhy [19]. Using DQM, they solved the complex motion equations and associated boundary conditions. Wang et al. [20] conducted research about frequency responses of a sandwich panel with honeycomb core using experimental and finite element outcomes. Finally, their essential work found that the thickness ratio of the face sheet and filling foam density had a vital role in the frequency of the sandwich panel with a honeycomb core. Ref [21]. presented a frequency analysis of a sandwich beam with honeycomb hybrid core with the aid of finite element and experimental techniques. Nonlinear frequency responses of a honeycomb sandwich shell were presented by Zhang et al. [22]. They solved the governing equations of the structure with simply supported boundary conditions via the homotopy perturbation method. In recent years, the use of CNTs as reinforcement has got a lot of attention. For this issue, Keleshteri et al. [23] analyzed major bending responses of an FG annular plate, which is enhanced through employing CNTs and surrounded by an elastic foundation. They believe that in their mathematical approach, the von Karman and thick shear deformation models are utilized for reporting more accuracy when it comes to presenting results. Furthermore, to solve the equations obtained via energy methods, they employed the GDQ model along with Newton–Raphson. Their emphasized outcome is that the thickness and the value fraction of CNT may play a prominent role when it comes to the investigation of the annular disk’s nonlinear frequency. Ansari and Torabi [24] analyzed nonlinear forced and free dynamics of an FG disk by using the von Kármán method as well as thin SDT. They mainly emphasized the modified GDQ model to solve the FG disk’s governing equation and reported a structure’s large amplitude vibration. Keleshteri et al. [25, 26] conducted a study on the frequency of the CNT-reinforced circular sector plate considering a piezoelectric layer utilizing GDQM and FSDT. By taking into account the same process, Keleshtary et al. [27] investigated the FG-CNT reinforced circular plate’s amplitude performance covered by the piezoelectric layer and sitting on an elastic medium. Torabi and Ansari [28] reported that it is essential to extend motion equations of the FG-CNT reinforced circular plate’s large amplitude vibration based on the relations of general asymmetry in the existence of primary thermal stress for achieving accurate results. Also, many studies reported the application of applied soft computing method for prediction of the behavior of the complex system [29,30,31,32,33,34,35,36].

Vinyas and Harursampath [37] performed geometrically nonlinear free vibration behaviour of higher-order shear deformable carbon nanotube-reinforced magneto-electro-elastic doubly curved shells. Dat et al. [38] presented an analytical approach on the nonlinear magneto-electro-elastic vibration of a smart sandwich plate. They modeled the sandwich plate consisting of a carbon nanotube-reinforced nanocomposite core integrated with two magneto-electro-elastic face sheets. Mahesh and Harursampath [39, 40] investigated the nonlinear deflection problem of magneto-electro-elastic shells reinforced with carbon nanotubes subjected to multiphysics loads such as mechanical, electric and magnetic loads. In this regard, they derived a mathematical model based on higher-order shell theory, von Karman’s nonlinearity using finite element platform. Vinyas [41] explored the vibrational behavior of porous functionally graded magneto-electro-elastic circular and annular plates through finite element procedures.

Based on the extremely detailed exploration in the literature by the authors, no one can claim there is a research on the frequency analysis of the sandwich disk with a honeycomb core and imperfect MHLC face sheets rested on an elastic foundation. First-order shear deformation theory (FSDT) is applied to formulate the stresses–strains relation. Rule of the mixture and modified Halpin–Tsai model are engaged to provide the effective material constant of the MHC disk. By employing Hamilton’s principle, the governing equations of the structure are derived. Finally, the outcomes of the presented study show that some geometrical and physical parameters have an important role in the frequency responses of the sandwich disk.

2 Mathematical modeling

2.1 The homogenization process of MHC

The procedure of homogenization is made of two main steps based upon the Halpin–Tsai model, together with a micromechanical theory [6,7,8,9,10,11,12, 42]. The first stage is engaged with computing the effective characteristics of the composite reinforced with CF as follows [43]:

$$E_{11} = V_{{\text{F}}} E_{11}^{{\text{F}}} + V_{{{\text{NCM}}}} E^{{{\text{NCM}}}} ,$$
(1)
$$\frac{1}{{E_{22} }} = \frac{{V_{{\text{f}}} }}{{E_{22}^{{\text{F}}} }} + \frac{{V_{{{\text{NCM}}}} }}{{E^{{{\text{NCM}}}} }} - V_{{\text{F}}} V_{{{\text{NCM}}}} \times \frac{{\left( {\nu^{{\text{F}}} } \right)^{2} \frac{{E^{{{\text{NCM}}}} }}{{E_{22}^{{\text{F}}} }} + \left( {\nu^{{{\text{NCM}}}} } \right)^{2} \frac{{E_{22}^{{\text{F}}} }}{{E^{{\text{M}}} }} - 2\nu^{{\text{F}}} \nu^{{{\text{NCM}}}} }}{{V_{{\text{F}}} E_{22}^{{\text{F}}} + V_{{{\text{NCM}}}} E^{{{\text{NCM}}}} }},$$
(2)
$$\frac{1}{{G_{12} }} = \frac{{V_{{\text{F}}} }}{{G_{12}^{{\text{F}}} }} + \frac{{V_{{{\text{NCM}}}} }}{{G^{{{\text{NCM}}}} }},$$
(3)
$$\rho = V_{{{\text{NCM}}}} \rho^{{{\text{NCM}}}} + V_{{\text{F}}} \rho^{{\text{F}}} ,$$
(4)
$$\nu_{12} = V_{NCM} \nu^{NCM} + V_{F} \nu^{F} .$$
(5)

The volume fraction of the fiber and nanocomposite matrixes can be given by [43]:

$$V_{{\text{F}}} + V_{{{\text{NCM}}}} = 1.$$
(6)

The second step is organized to obtain the effective characteristics of the nanocomposite matrix reinforced with CNTs with the aid of the extended Halpin–Tsai micromechanics as follows:

$$E^{{{\text{NCM}}}} = E^{{\text{M}}} \left( {\frac{5}{8}\left( {\frac{{1 + 2\beta_{{{\text{dd}}}} V_{{{\text{CNT}}}} }}{{1 - \beta_{{{\text{dd}}}} V_{{{\text{CNT}}}} }}} \right) + \frac{3}{8}\left( {\frac{{1 + 2\left( {l^{{{\text{CNT}}}} /d^{{{\text{CNT}}}} } \right)\beta_{{{\text{dl}}}} V_{{{\text{CNT}}}} }}{{1 - \beta_{{{\text{dl}}}} V_{{{\text{CNT}}}} }}} \right)} \right).$$
(7)

Here, βdd and βdl are computed as the following expression:

$$\begin{aligned} \beta_{{{\text{dl}}}} & = \frac{{(E_{11}^{{{\text{CNT}}}} /E^{{\text{M}}} )}}{{(l^{{{\text{CNT}}}} /2t^{{{\text{CNT}}}} ) + (E_{11}^{{{\text{CNT}}}} /E^{{\text{M}}} )}} - \frac{{(d^{{{\text{CNT}}}} /4t^{{{\text{CNT}}}} )}}{{(l^{{{\text{CNT}}}} /2t^{CNT} ) + (E_{11}^{{{\text{CNT}}}} /E^{{\text{M}}} )}}, \, \\ \beta_{{{\text{dd}}}} & = \frac{{(E_{11}^{CNT} /E^{M} )}}{{(d^{{{\text{CNT}}}} /2t^{{{\text{CNT}}}} ) + (E_{11}^{{{\text{CNT}}}} /E^{M} )}} - \frac{{(d^{{{\text{CNT}}}} /4t^{CNT} )}}{{(d^{CNT} /2t^{{{\text{CNT}}}} ) + (E_{11}^{{{\text{CNT}}}} /E^{{\text{M}}} )}}. \\ \end{aligned}$$
(8)

The volume fraction of CNTs can be formulated as below [44,45,46]:

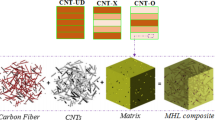
$$V_{{{\text{CNT}}}}^{ * } = \frac{{W_{{{\text{CNT}}}} }}{{W_{{{\text{CNT}}}} + \left( {\frac{{\rho^{{{\text{CNT}}}} }}{{\rho^{{\text{M}}} }}} \right)\left( {1 - W_{{{\text{CNT}}}} } \right)}}.$$
(9)

Also, various kinds of MHC distribution along with thickness direction can be given by (see Fig. 1):

$$\begin{gathered} V_{{{\text{CNT}}}} = 4V_{{{\text{CNT}}}}^{*} \frac{{\left| {\xi_{j} } \right|}}{h} \, \,\,\,\,{\text{FG } - \text{ X}} \hfill \\ V_{{{\text{CNT}}}} = 2V_{{{\text{CNT}}}}^{*} \left( {1 - 2\frac{{\left| {\xi_{j} } \right|}}{h}} \right){\text{ FG } - \text{ O}} \hfill \\ V_{{{\text{CNT}}}} = V_{{{\text{CNT}}}}^{*} \, \,\,\,\,\,{\text{FG } - \text{ UD}}{.} \hfill \\ \end{gathered}$$
(10)
Fig. 1
figure 1

Distribution of CNT and CF through the thickness of the MHL composite

Full size image

Here, \(\xi_{j} = \left( {\frac{1}{2} + \frac{1}{{2N_{t} }} - \frac{j}{{N_{t} }}} \right)h \quad j = 1,2, \ldots ,N_{t}\).

Furthermore, the sum of VM and VCNT is equal to one as follows [6,7,8,9,10,11,12, 42]:

$$V_{{{\text{CNT}}}} + V_{{\text{M}}} = 1.$$
(11)

Finally, the mechanical properties of the MHC face sheets can be given by [44,45,46]:

$$\rho^{{{\text{NCM}}}} = V_{{{\text{CNT}}}} \rho^{{{\text{CNT}}}} + V_{{\text{M}}} \rho^{{\text{M}}} ,$$
(12)
$$\nu^{{{\text{NCM}}}} = \nu^{{\text{M}}} ,$$
(13)
$$G^{{{\text{NCM}}}} = \frac{{E^{{{\text{NCM}}}} }}{{2\left( {1 + \nu^{{{\text{NCM}}}} } \right)}}.$$
(14)

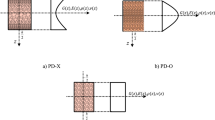
In Fig. 2, various kinds of porosity distributions, namely, uniform, X, and O, are presented. The Young's modulus, shear modulus, and mass density are as below:

$$\tilde{E}_{11} = E_{11} \left( {1 - e_{0} s\left( z \right)} \right),$$
(15a)
$$\tilde{E}_{22} = E_{22} \left( {1 - e_{0} s\left( z \right)} \right),$$
(15b)
$$\tilde{G}_{12} \left( z \right) = \frac{{\tilde{E}_{11} }}{{2\left( {1 - v\left( z \right)} \right)}},$$
(15c)
$$\tilde{\rho }\left( z \right) = \rho \left( z \right)\left[ {1 - e_{{\text{m}}} s\left( z \right)} \right] + V_{{{\text{ncm}}}} \rho_{{{\text{ncm}}}} ,$$
(15d)
Fig. 2
figure 2

Patterns of porosity distribution through the thickness of MHC

Full size image

where:

$$s = \left\{ {\begin{array}{*{20}l} {s_{{\text{o}}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{PD}} - {\text{UD}}} \hfill \\ {s_{{\text{o}}} \cos \left( {\frac{\pi }{4} + \frac{\pi z}{{2h}}} \right)\,\,\,\,\,\,\,\,\,\,\,\,{\text{PD}} - {\text{X}}} \hfill \\ {s_{{\text{o}}} {\cos}\left( {\frac{\pi z}{h}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{PD}} - {\text{O}}} \hfill \\ \end{array} } \right.$$
(16)

Based on the Gaussian random field scheme, we have:

$$e_{{\text{m}}} = \frac{{1.121\left[ {1 - \left( {1 - e_{0} s\left( z \right)} \right)^{{\frac{1}{2.3}}} } \right]}}{s\left( z \right)}.$$
(17)

The Poisson's ratio of the porous disk corresponding to the closed-cell Gaussian random field can be written as:

$$\tilde{v}_{12} = 0.221\left( {1 - \frac{{\tilde{\rho }\left( z \right)}}{\rho }} \right) + v_{12} \left[ {1 + 0.342\left( {1 - \frac{{\tilde{\rho }\left( z \right)}}{\rho }} \right)^{2} - 1.21\left( {1 - \frac{{\tilde{\rho }\left( z \right)}}{\rho }} \right)} \right],$$
(18a)
$$\tilde{v}_{21} = \tilde{v}_{12} \frac{{\tilde{E}_{11} }}{{\tilde{E}_{22} }}.$$
(18b)

Also, when the total masses of the disk with different porosity distributions are the same, the value of S0 can be formulated as:

$$s_{0} = \frac{1}{{e_{0} }}\left[ {1 - \left( {\frac{{\frac{1}{h}\int\nolimits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\frac{{\tilde{\rho }\left( z \right)}}{\rho }{\text{d}}z + 0.121} }}{1.121}} \right)^{2.3} } \right].$$
(19)

2.2 Modeling of honeycomb cores

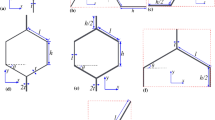
The hexagonal cell geometry is illustrated in Fig. 3. According to the Gibson model, we have [47]:

$$E_{11}^{*} = \frac{{\sigma_{1} }}{{\varepsilon_{1} }} = E_{\rm S} \left( \frac{t}{l} \right)\frac{{\cos \left( {\theta_{\rm h} } \right)}}{{\left( {h/1 + \sin \left( {\theta_{\rm h} } \right)} \right)\sin^{2} \left( {\theta_{\rm h} } \right)}}\frac{1}{{1 + \left( {t/1} \right)^{2} \cot^{2} \left( {\theta_{\rm h} } \right)}},$$
(20-a)
$$E_{22}^{*} = \frac{{\sigma_{2} }}{{\varepsilon_{2} }} = E_{\rm S} \left( \frac{t}{l} \right)^{3} \frac{{\left( {h/1 + \sin \left( {\theta_{\rm h} } \right)} \right)}}{{\cos^{3} \left( {\theta_{\rm h} } \right)}}\frac{1}{{1 + \left( {t/1} \right)^{2} \cot^{2} \left( {\theta_{\rm h} } \right)}},$$
(20-b)
$$\nu_{12}^{*} = - \frac{{\varepsilon_{2} }}{{\varepsilon_{1} }} = \frac{{\cos^{2} \left( {\theta_{\rm h} } \right)}}{{\left( {h/1 + \sin \left( {\theta_{\rm h} } \right)} \right)\sin \left( {\theta_{\rm h} } \right)}}\frac{{1 - \left( {t/1} \right)^{2} }}{{1 + \cot^{2} \left( {\theta_{\rm h} } \right)\left( {t/1} \right)^{2} }},$$
(20-c)
$$\nu_{21}^{*} = - \frac{{\varepsilon_{1} }}{{\varepsilon_{2} }} = \frac{{\left( {h/1 + \sin \left( {\theta_{\rm h} } \right)} \right)\sin \left( {\theta_{\rm h} } \right)}}{{\cos^{2} \left( {\theta_{\rm h} } \right)}}\frac{{1 - \left( {t/1} \right)^{2} }}{{1 + \left( {\left( {h/1} \right)\sec^{2} \left( {\theta_{\rm h} } \right) + \tan^{2} \left( {\theta_{\rm h} } \right)} \right)\left( {t/1} \right)^{2} }},$$
(20-d)
$$G_{12}^{*} = E_{\rm S} \left( \frac{t}{l} \right)^{3} \frac{{\left( {h/1 + \sin \left( {\theta_{\rm h} } \right)} \right)}}{{\left( {h/1} \right)^{2} \cos \left( {\theta_{\rm h} } \right)}}\frac{1}{R}$$
(20-e)
$$R = \left( {1 + 2\frac{h}{l} + \left( \frac{t}{l} \right)^{2} \frac{{h/1 + \sin \left( {\theta_{\rm h} } \right)}}{{\left( {h/1} \right)^{2} }}\left[ {\left( {h/1 + \sin \left( {\theta_{\rm h} } \right)} \right)\tan^{2} \left( {\theta_{\rm h} } \right) + \sin \left( {\theta_{\rm h} } \right)} \right]} \right),$$
(20-f)
$$\frac{{\rho^{*} }}{{\rho_{S} }} = \frac{{\left( \frac{t}{l} \right)\left( {\frac{h}{l} + 2} \right)}}{{2\cos \left( {\theta_{\rm h} } \right)\left( {\frac{h}{l} + \sin \left( {\theta_{\rm h} } \right)} \right)}}.$$
(20-i)
Fig. 3
figure 3

The hexagonal cell geometry

Full size image

Figure 4 is presented for the geometry of the imperfect honeycomb core sandwich disk with MHC face sheets.

Fig. 4
figure 4

The geometry of honeycomb core sandwich disk with MHC face sheet

Full size image

Based on FSDT, the displacement fields can be defined by the below relations [48,49,50]:

$$\begin{gathered} u^{\eta } = u_{0}^{\eta } + zu_{1}^{\eta } \hfill \\ v^{\eta } = v_{0}^{\eta } + zv_{1}^{\eta } \hfill \\ w^{\eta } = w_{0}^{\eta } . \hfill \\ \end{gathered}$$
(21)

In Eq. (21), η defines the core, top, and bottom layers.

2.3 Strain–stress of the honeycomb core

Based on FSDT, the strain–stress formulation can be written as [44,45,46, 48,49,50,51,52,53,54,55,56,57]:

$$\begin{gathered} \left[ \begin{gathered} \sigma_{RR} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{R\theta } \hfill \\ \sigma_{Rz} \hfill \\ \sigma_{\theta z} \hfill \\ \end{gathered} \right]^{\rm c} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{44} } \\ \end{array} } \right]^{\rm c} \left[ \begin{gathered} \varepsilon_{RR} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \varepsilon_{R\theta } \hfill \\ \varepsilon_{Rz} \hfill \\ \varepsilon_{\theta z} \hfill \\ \end{gathered} \right]^{\rm c} \hfill \\ Q_{11}^{\rm c} = \frac{{E_{11}^{*} }}{{1 - \nu_{12}^{*} \nu_{21}^{*} }},\,\,\,\,Q_{22}^{\rm c} = \frac{{E_{22}^{*} }}{{1 - \nu_{12}^{*} \nu_{21}^{*} }},\,\,\,Q_{12}^{\rm c} = \frac{{\nu_{21}^{*} E_{22}^{*} }}{{1 - \nu_{12}^{*} \nu_{21}^{*} }}, \hfill \\ Q_{44}^{\rm c} = G_{12}^{*} ,\,\,Q_{55}^{\rm c} = G_{13}^{*} ,\,\,\,Q_{66}^{\rm c} = G_{23}^{*} ,\,\,\,G_{13}^{*} = G_{23}^{*} = G_{12}^{*} . \hfill \\ \end{gathered}$$
(22)

So, the strain components would be written as:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR} } \\ {\varepsilon_{\theta \theta } } \\ {\gamma_{R\theta } } \\ {\gamma_{Rz} } \\ {\gamma_{\theta z} } \\ \end{array} } \right\}^{\psi } = \left\{ {\begin{array}{*{20}c} {\varepsilon_{RR}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\gamma_{R\theta }^{0} } \\ {\gamma_{Rz}^{0} } \\ {\gamma_{\theta z}^{0} } \\ \end{array} } \right\}^{\psi } + z\left\{ {\begin{array}{*{20}c} {\kappa_{RR} } \\ {\kappa_{\theta \theta } } \\ {\kappa_{R\theta } } \\ {\kappa_{Rz} } \\ {\kappa_{\theta z} } \\ \end{array} } \right\}^{\psi }$$
(23a)
$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\gamma_{R\theta }^{0} } \\ {\gamma_{Rz}^{0} } \\ {\gamma_{\theta z}^{0} } \\ \end{array} } \right\}^{\rm c} = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial R}}} \\ {\frac{u}{R} + \frac{\partial v}{{R\partial \theta }}} \\ {\frac{\partial u}{{R\partial \theta }} + \frac{\partial v}{{\partial R}} - \frac{v}{R}} \\ {\phi_{R} + \frac{\partial w}{{\partial R}}} \\ {\phi_{\theta } + \frac{\partial w}{{R\partial \theta }}} \\ \end{array} } \right\}^{\rm c} ,\,\,\,\,\,\,\left\{ {\begin{array}{*{20}c} {\kappa_{RR} } \\ {\kappa_{\theta \theta } } \\ {\kappa_{R\theta } } \\ {\kappa_{Rz} } \\ {\kappa_{\theta z} } \\ \end{array} } \right\}^{\rm c} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \phi_{R} }}{\partial R}} \\ {\frac{{\phi_{R} }}{R} + \frac{{\partial \phi_{\theta } }}{R\partial \theta }} \\ {\frac{{\partial \phi_{R} }}{R\partial \theta } + \frac{{\partial \phi_{\theta } }}{\partial R} - \frac{{\phi_{\theta } }}{R}} \\ 0 \\ 0 \\ \end{array} } \right\}^{\rm c} .$$
(23b)

Stress–strain relations of MHC angle-ply-laminated disk can be written as follows [58,59,60,61,62,63,64,65]:

$$\left[ \begin{gathered} \sigma_{RR} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{R\theta } \hfill \\ \sigma_{Rz} \hfill \\ \sigma_{\theta z} \hfill \\ \end{gathered} \right]^{\psi } = \left[ {\begin{array}{*{20}c} {\hat{\overline{Q}}_{11} } & {\hat{\overline{Q}}_{12} } & 0 & 0 & {\hat{\overline{Q}}_{16} } \\ {\hat{\overline{Q}}_{21} } & {\hat{\overline{Q}}_{22} } & 0 & 0 & {\hat{\overline{Q}}_{26} } \\ 0 & 0 & {\hat{\overline{Q}}_{44} } & {\hat{\overline{Q}}_{45} } & 0 \\ 0 & 0 & {\hat{\overline{Q}}_{45} } & {\hat{\overline{Q}}_{55} } & 0 \\ {\hat{\overline{Q}}_{16} } & {\hat{\overline{Q}}_{26} } & 0 & 0 & {\hat{\overline{Q}}_{66} } \\ \end{array} } \right]^{\psi } \left[ \begin{gathered} \varepsilon_{RR} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \varepsilon_{R\theta } \hfill \\ \varepsilon_{Rz} \hfill \\ \varepsilon_{\theta z} \hfill \\ \end{gathered} \right]^{\psi } .$$
(24)

The above equation \(\psi\) defines the top and bottom layers, where

$$\hat{\overline{Q}}^{\psi }_{11} = \cos^{4} \theta_{{\text{f}}} \tilde{Q}^{\psi }_{11} + 2\sin^{2} \theta_{{\text{f}}} \cos^{2} \theta_{{\text{f}}} \,\left( {\tilde{Q}^{\psi }_{12} + 2\tilde{Q}^{\psi }_{66} } \right) + \sin^{4} \theta_{{\text{f}}} \tilde{Q}^{\psi }_{22} ,$$
(25a)
$$\hat{\overline{Q}}^{\psi }_{12} = \sin^{2} \theta_{{\text{f}}} \cos^{2} \theta_{{\text{f}}} \left( {\tilde{Q}^{\psi }_{11} + \tilde{Q}^{\psi }_{22} - 4\tilde{Q}^{\psi }_{66} } \right)\, + \left( {\sin^{4} \theta_{{\text{f}}} + \cos^{4} \theta_{{\text{f}}} } \right)\tilde{Q}^{\psi }_{12} ,$$
(25b)
$$\hat{\overline{Q}}^{\psi }_{16} = \cos^{3} \theta_{{\text{f}}} \sin \theta_{{\text{f}}} \left( {2\tilde{Q}^{\psi }_{11} - 2\tilde{Q}^{\psi }_{12} - \tilde{Q}^{\psi }_{66} } \right) + \cos \theta_{{\text{f}}} \sin^{3} \theta_{{\text{f}}} \left( {\tilde{Q}^{\psi }_{66} + 2\tilde{Q}^{\psi }_{12} - 2\tilde{Q}^{\psi }_{22} } \right),$$
(25c)
$$\hat{\overline{Q}}^{\psi }_{22} = \sin^{4} \theta_{{\text{f}}} \tilde{Q}^{\psi }_{11} + 2\sin^{2} \theta_{{\text{f}}} \cos^{2} \theta_{{\text{f}}} \tilde{Q}^{\psi }_{12} + \cos^{4} \theta_{{\text{f}}} \tilde{Q}^{\psi }_{22} + 2\sin^{2} \theta_{{\text{f}}} \cos^{2} \theta_{{\text{f}}} \left( {\tilde{Q}^{\psi }_{12} + 2\tilde{Q}^{\psi }_{66} } \right),$$
(25d)
$$\hat{\overline{Q}}^{\psi }_{26} = \cos^{3} \theta_{{\text{f}}} \sin \theta_{{\text{f}}} \,\left( {2\tilde{Q}^{\psi }_{12} - 2\tilde{Q}^{\psi }_{22} + \tilde{Q}^{\psi }_{66} } \right) + \cos \theta_{{\text{f}}} \sin^{3} \theta_{\rm f} \left( {2\tilde{Q}^{\psi }_{11} - 2\tilde{Q}^{\psi }_{12} - \tilde{Q}^{\psi }_{66} } \right),$$
(25e)
$$\hat{\overline{Q}}^{\psi }_{44} = \cos^{2} \theta_{\rm f} \tilde{Q}^{\psi }_{44} + \sin^{2} \theta_{\rm f} \tilde{Q}^{\psi }_{55} ,$$
(25f)
$$\hat{\overline{Q}}^{\psi }_{45} = \cos \theta_{\rm f} \sin \theta_{\rm f} \left( {\tilde{Q}^{\psi }_{55} - \tilde{Q}^{\psi }_{44} } \right),$$
(25g)
$$\hat{\overline{Q}}^{\psi }_{55} = \cos^{2} \theta_{\rm f} \tilde{Q}^{\psi }_{55} + \sin^{2} \theta_{\rm f} \tilde{Q}^{\psi }_{44} ,$$
(25h)
$$\hat{\overline{Q}}^{\psi }_{66} = \tilde{Q}^{\psi }_{66} \left( {\cos^{2} \theta_{\rm f} - \sin^{2} \theta_{\rm f} } \right)^{2} \, + 4\sin^{2} \theta_{\rm f} \cos^{2} \theta_{\rm f} \left( {\tilde{Q}^{\psi }_{11} + \tilde{Q}^{\psi }_{22} - 2\tilde{Q}^{\psi }_{12} } \right).$$
(25i)

The terms involved in Eq. (25) would be obtained as [45, 66,67,68,69,70,71,72,73,74,75,76]

$$\tilde{Q}^{\psi }_{11} = \frac{{\tilde{E}_{11} }}{{1 - \tilde{\nu }_{12} \tilde{\nu }_{21} }},\,\,\tilde{Q}^{\psi }_{12} = \frac{{\tilde{\nu }_{12} \tilde{E}_{22} }}{{1 - \tilde{\nu }_{12} \tilde{\nu }_{21} }},\,\,\tilde{Q}^{\psi }_{22} = \frac{{\tilde{E}_{22} }}{{1 - \tilde{\nu }_{12} \tilde{\nu }_{21} }},\,\,\tilde{Q}^{\psi }_{44} = \tilde{G}_{12} ,\,\,\tilde{Q}^{\psi }_{55} = \tilde{G}_{23} ,\,\,\tilde{Q}^{\psi }_{66} = \tilde{G}_{13} .$$

So, the strain components would be written as:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR} } \\ {\varepsilon_{\theta \theta } } \\ {\gamma_{R\theta } } \\ {\gamma_{Rz} } \\ {\gamma_{\theta z} } \\ \end{array} } \right\}^{\psi } = \left\{ {\begin{array}{*{20}c} {\varepsilon_{RR}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\gamma_{R\theta }^{0} } \\ {\gamma_{Rz}^{0} } \\ {\gamma_{\theta z}^{0} } \\ \end{array} } \right\}^{\psi } + z\left\{ {\begin{array}{*{20}c} {\kappa_{RR} } \\ {\kappa_{\theta \theta } } \\ {\kappa_{R\theta } } \\ {\kappa_{Rz} } \\ {\kappa_{\theta z} } \\ \end{array} } \right\}^{\psi }$$
(26)

Equation (26) can be rewritten as

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{RR}^{0} } \\ {\varepsilon_{\theta \theta }^{0} } \\ {\gamma_{R\theta }^{0} } \\ {\gamma_{Rz}^{0} } \\ {\gamma_{\theta z}^{0} } \\ \end{array} } \right\}^{\psi } = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial R}}} \\ {\frac{u}{R} + \frac{\partial v}{{R\partial \theta }}} \\ {\frac{\partial u}{{R\partial \theta }} + \frac{\partial v}{{\partial R}} - \frac{v}{R}} \\ {\phi_{R} + \frac{\partial w}{{\partial R}}} \\ {\phi_{\theta } + \frac{\partial w}{{R\partial \theta }}} \\ \end{array} } \right\}^{\psi } ,\,\,\,\,\left\{ {\begin{array}{*{20}c} {\kappa_{RR} } \\ {\kappa_{\theta \theta } } \\ {\kappa_{R\theta } } \\ {\kappa_{Rz} } \\ {\kappa_{\theta z} } \\ \end{array} } \right\}^{\psi } = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \phi_{R} }}{\partial R}} \\ {\frac{{\phi_{R} }}{R} + \frac{{\partial \phi_{\theta } }}{R\partial \theta }} \\ {\frac{{\partial \phi_{R} }}{R\partial \theta } + \frac{{\partial \phi_{\theta } }}{\partial R} - \frac{{\phi_{\theta } }}{R}} \\ 0 \\ 0 \\ \end{array} } \right\}^{\psi }$$
(27)

2.4 Compatibility equations

The compatibility conditions assuming perfect bonding between the core and the composite layers can be defined as follows [54, 58, 62, 77,78,79,80,81,82,83,84]:

$$\begin{gathered} u^{{\text{c}}} (z_{{\text{c}}} = - h_{{\text{c}}} /2) = u^{{\text{b}}} (z_{{\text{b}}} = h_{{\text{b}}} /2), \hfill \\ v^{{\text{c}}} (z_{{\text{c}}} = - h_{{\text{c}}} /2) = v^{{\text{b}}} (z_{{\text{b}}} = h_{{\text{b}}} /2), \hfill \\ w^{{\text{c}}} (z_{{\text{c}}} = - h_{{\text{c}}} /2) = w^{{\text{b}}} (z_{{\text{p}}} = h_{{\text{b}}} /2), \hfill \\ u^{{\text{c}}} (z_{{\text{c}}} = h_{{\text{c}}} /2) = u^{{\text{t}}} (z_{{\text{t}}} = - h_{{\text{t}}} /2), \hfill \\ v^{{\text{c}}} (z_{{\text{c}}} = h_{{\text{c}}} /2) = v^{{\text{t}}} (z_{{\text{t}}} = - h_{{\text{t}}} /2), \hfill \\ w^{{\text{c}}} (z_{{\text{c}}} = h_{{\text{c}}} /2) = w^{{\text{t}}} (z_{{\text{t}}} = - h_{{\text{t}}} /2). \hfill \\ \end{gathered}$$
(28)

2.5 Extended Hamilton’s principle

Based on energy methods known as the Hamilton principle, there are relations between boundary conditions and motion equations which can be written as [53,54,55, 85,86,87,88,89,90]:

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta T^{*} - \delta U^{*} + \delta W^{*} } \right)}^{\eta } {\text{ d}}t = 0\,.$$
(29)

The corresponding kinetic energy of the rotating system would be formulated as [91,92,93,94,95,96,97]:

$$T^{*\eta } = \int\limits_{V} {\frac{1}{2}\rho^{\eta } \left[ {\left( {\frac{\partial U}{{\partial t}}} \right)^{2} + \left( {\frac{\partial V}{{\partial t}}} \right)^{2} + \left( {\frac{\partial W}{{\partial t}}} \right)^{2} } \right]}^{\eta } \,{\text{d}}V,$$
(30)
$$\begin{gathered} \delta T^{*\eta } = \int\limits_{V} {\rho^{\eta } \left( {\frac{\partial U}{{\partial t}}\frac{\partial \delta U}{{\partial t}} + \frac{\partial V}{{\partial t}}\frac{\partial \delta V}{{\partial t}} + \frac{\partial W}{{\partial t}}\frac{\partial \delta W}{{\partial t}}} \right)}^{\eta } \,{\text{d}}V: \hfill \\ \delta T^{*\eta } = \int\limits_{{R_{1} }}^{{R_{2} }} {\int\limits_{0}^{\theta } {\left[ \begin{gathered} \left\{ { - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{R} }}{{\partial t^{2} }}} \right\}\delta u + \left\{ { - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{R} }}{{\partial t^{{2u_{1} }} }}} \right\}\delta \phi_{R} \hfill \\ + \left\{ { - I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }}} \right\}\delta v + \left\{ { - I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }}} \right\}\delta \phi_{\theta } \hfill \\ + \left\{ { - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right\}\delta w \hfill \\ \end{gathered} \right]^{\eta } R{\text{d}}R{\text{d}}\theta ,} } \hfill \\ \end{gathered}$$
(31)

where:

$$\left\{ {I_{i} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\rho^{\eta } \left( z \right)\left\{ {z^{i} } \right\}dZ} ,\quad i = 0:6.$$
(32)

Also, the strain energy of the current composite structure would be obtained as:

$$\begin{aligned} \delta U^{*\eta } & = \frac{1}{2}\iiint\limits_{V} {\sigma_{ij}^{\eta } \delta \varepsilon_{ij}^{\eta } {\text{d}}V} \\ & = \int\limits_{A} {\left[ \begin{gathered} \left( {N_{RR} \frac{{\partial \delta u_{\,0\,} }}{\partial R} + M_{RR} \frac{{\partial \delta u_{1\,} }}{\partial R}} \right) + \left( \begin{gathered} N_{\theta \theta } \frac{{\partial \delta v_{0} }}{R\partial \theta } + M_{\theta \theta } \frac{{\partial \delta v_{1} }}{R\partial \theta } \hfill \\ + N_{\theta \theta } \frac{{\delta u_{0\,} }}{R} + M_{\theta \theta } \frac{{\delta u_{1\,} }}{R} \hfill \\ \end{gathered} \right) \hfill \\ + \left( \begin{gathered} N_{R\theta } \frac{{\partial \delta v_{0} }}{\partial R} + M_{R\theta } \frac{{\partial \delta v_{1} }}{\partial R} + N_{R\theta } \frac{{\partial \delta u_{0} }}{R\partial \theta } \hfill \\ + M_{R\theta } \frac{{\partial \delta u_{1} }}{R\partial \theta } - N_{R\theta } \frac{{\delta v_{0} }}{R} - M_{R\theta } \frac{{\delta v_{1} }}{R} \hfill \\ \end{gathered} \right) \hfill \\ + \left( {N_{Rz} \left( {\delta u_{1\,} + \frac{{\partial \delta w_{0\,} }}{\partial R}} \right)} \right) + \left( {N_{\theta z} \left( {\delta v_{1\,} + \frac{{\partial \delta w_{0\,} }}{R\partial \theta }} \right)} \right) \hfill \\ \end{gathered} \right]}^{\eta } \,{\text{d}}A, \\ \end{aligned}$$
(33)

where

$$\begin{gathered} \left\{ {N_{RR} ,M_{RR} } \right\}^{\eta } = \int_{z} {\left\{ {\sigma_{RR} ,z\sigma_{RR} } \right\}}^{\eta } {\text{d}}z; \hfill \\ \left\{ {N_{\theta \theta } ,M_{\theta \theta } } \right\}^{\eta } = \int_{z} {\left\{ {\sigma_{\theta \theta } ,z\sigma_{\theta \theta } } \right\}^{\eta } } {\text{d}}z;\, \hfill \\ \left\{ {N_{Rz} ,M_{Rz} } \right\}^{\eta } = \int_{z} {\left\{ {\sigma_{Rz} ,z\sigma_{Rz} } \right\}^{\eta } } {\text{d}}z;. \hfill \\ \left\{ {N_{R\theta } ,M_{R\theta } } \right\}^{\eta } = \int_{z} {\left\{ {\sigma_{R\theta } ,z\sigma_{R\theta } } \right\}^{\eta } } {\text{d}}z; \hfill \\ \left\{ {N_{\theta z} ,M_{\theta z} } \right\}^{\eta } = \int_{z} {\left\{ {\sigma_{\theta z} ,z\sigma_{\theta z} } \right\}^{\eta } } {\text{d}}z. \hfill \\ \end{gathered}$$
(34)

Furthermore, the first variation of work done due to the elastic substrate can be formulated as follows:

$$\delta W^{*\eta } = \int {\left( { - K_{{\text{w}}} w\delta w + K_{{\text{p}}} \left[ {\left( {\frac{\partial w}{{\partial R}}} \right)\left( {\frac{\partial }{\partial R}\delta w} \right) + \frac{1}{{R^{2} }}\left( {\frac{\partial w}{{\partial \theta }}} \right)\left( {\frac{\partial }{\partial \theta }\delta w} \right)} \right]} \right)^{\eta } {\text{d}}A} .$$
(35)

Eventually, the governing equations and the corresponding boundary conditions can be derived by substituting Eqs. (35), (33), and (31) in Hamilton’s principle (Eq. (29)) that can be given by the following equations:

$$\delta u_{0}^{\eta } :\frac{\partial }{\partial R}N_{RR}^{\eta } - \frac{{N_{\theta \theta }^{\eta } - N_{RR}^{\eta } }}{R} + \frac{\partial }{R\partial \theta }N_{R\theta }^{\eta } = I_{0}^{\eta } \frac{{\partial^{2} u_{0}^{\eta } }}{{\partial t^{2} }} + I_{1}^{\eta } \frac{{\partial^{2} u_{1}^{\eta } }}{{\partial t^{2} }},$$
(36a)
$$\delta v_{0}^{\eta } :\,\frac{\partial }{R\partial \theta }N_{\theta \theta }^{\eta } + \frac{{2N_{R\theta }^{\eta } }}{R} + \frac{\partial }{\partial R}N_{R\theta }^{\eta } = I_{0}^{\eta } \frac{{\partial^{2} v_{0}^{\eta } }}{{\partial t^{2} }} + I_{1}^{\eta } \frac{{\partial^{2} v_{1}^{\eta } }}{{\partial t^{2} }},$$
(36b)
$$\delta w^{\eta } :\frac{{\partial S_{RZ} }}{\partial R} + \frac{1}{R}\frac{{\partial S_{\theta Z} }}{\partial \theta } - K_{{\text{W}}} w\,{ + }K_{{\text{P}}} \frac{{\partial^{2} w}}{{\partial R^{2} }}{ + }\frac{{K_{{\text{P}}} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}\, = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }},$$
(36c)
$$\delta \phi_{R}^{\eta } :\frac{{\partial M_{RR} }}{\partial R} - \frac{{M_{\theta \theta } }}{R} + \frac{1}{R}\frac{{\partial M_{R\theta } }}{\partial \theta } - S_{RZ} = \,I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \phi_{R} }}{{\partial t^{2} }},$$
(36d)
$$\delta \phi_{\theta } :\,\frac{\partial }{R\partial \theta }M_{\theta \theta } + \frac{2}{R}M_{R\theta } + \frac{\partial }{\partial R}M_{R\theta } - M_{\theta z} = I_{1}^{\eta } \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + I_{2}^{\eta } \frac{{\partial^{2} v_{1} }}{{\partial t^{2} }}.$$
(36e)

Also, general associated boundary conditions can be given by:

$$\delta u^{\eta } = 0{\text{ or }}N_{RR}^{\eta } \hat{n}_{R} + \frac{{N_{R\theta }^{\eta } }}{R}\hat{n}_{\theta } = 0\,\,\,,$$
(37a)
$$\delta v = 0{\text{ or }}N_{R\theta }^{\eta } \hat{n}_{R} + \frac{{N_{\theta \theta }^{\eta } }}{R}\hat{n}_{\theta } = 0 \, \,,$$
(37b)
$$\delta w^{\eta } = 0{\text{ or }}\left[ {S_{RZ} - K_{{\text{p}}} \frac{\partial w}{{\partial R}}} \right]^{\eta } \hat{n}_{R} + \left[ {\frac{{S_{\theta Z} }}{R} - \frac{{K_{{\text{p}}} }}{R}\frac{\partial w}{{\partial \theta }}} \right]^{\eta } \hat{n}_{\theta } = 0,$$
(37c)
$$\delta \phi_{R}^{\eta } = 0{\text{ or }}\left[ {M_{RR} } \right]^{\eta } \hat{n}_{R} + \left[ {\frac{{M_{R\theta } }}{R}} \right]^{\eta } \hat{n}_{\theta } = 0,$$
(37d)
$$\delta \phi_{\theta }^{\eta } = 0{\text{ or }}\left[ {M_{R\theta } } \right]^{\eta } \hat{n}_{R} + \left[ {\frac{{M_{\theta \theta } }}{R}} \right]^{\eta } \hat{n}_{\theta } = 0.$$
(37e)

It is noted that, based on the compatibility equations (Eq. (28)), the numbers of unknown variables are declined from 15 to 9. So, the total number of unknowns in the face sheets and core is decreased to 9.

2.6 Solution procedure

In this part of the present work, we displayed an FE-based [51, 52] solution procedure which is called GDQM for solving the formulation of the current problem. The first assumption in this is as follows:

$$\,\left. {\frac{\partial f}{{\partial r}}} \right|_{{r = r_{i} ,\,\theta = \theta_{j} }} = \sum\limits_{m = 1}^{{N_{r} }} {\sum\limits_{n = 1}^{{N_{\theta } }} {A_{im}^{r} } } I_{jn}^{\theta } f_{mn} ,$$
(38a)
$$\,\left. {\frac{\partial f}{{\partial \theta }}} \right|_{{r = r_{i} ,\,\theta = \theta_{j} }} = \sum\limits_{m = 1}^{{N_{r} }} {\sum\limits_{n = 1}^{{N_{\theta } }} {I_{im}^{r} } } A_{jn}^{\theta } f_{mn} ,$$
(38b)
$$\frac{\partial }{\partial r}\,\left( {\left. {\frac{\partial f}{{\partial \theta }}} \right|_{{r = r_{i} ,\,\theta = \theta_{j} }} } \right) = \sum\limits_{m = 1}^{{N_{r} }} {\sum\limits_{n = 1}^{{N_{\theta } }} {A_{im}^{r} } } A_{jn}^{\theta } f_{mn} ,$$
(38c)
$$\,\left. {\frac{{\partial^{2} f}}{{\partial r^{2} }}} \right|_{{r = r_{i} ,\,\theta = \theta_{j} }} = \sum\limits_{m = 1}^{{N_{r} }} {\sum\limits_{n = 1}^{{N_{\theta } }} {B_{im}^{r} } } I_{jn}^{\theta } f_{mn} ,$$
(38d)
$$\,\left. {\frac{{\partial^{2} f}}{{\partial \theta^{2} }}} \right|_{{r = r_{i} ,\,\theta = \theta_{j} }} = \sum\limits_{m = 1}^{{N_{r} }} {\sum\limits_{n = 1}^{{N_{\theta } }} {I_{im}^{r} } } B_{jn}^{\theta } f_{mn} .$$
(38e)

Also, \(I_{im}^{r}\) and \(I_{jn}^{\theta }\) are equal to one when i = m and j = n, otherwise are equal to zero. Also, \(A_{im}^{r}\), \(A_{jn}^{\theta }\), \(B_{im}^{r}\) and \(B_{jn}^{\theta }\) are weighting coefficients of the first- and second-order derivatives along with the r and θ directions, respectively, and may be considered as

$$A_{im}^{r} = \left\{ {\begin{array}{*{20}l} {\frac{{\xi \left( {r_{i} } \right)}}{{\left( {r_{i} - r_{m} } \right)\xi \left( {r_{m} } \right)}}\,\,\,\,\,\,{\text{when}}\,\,\,\,i \ne m} \hfill \\ { - \sum\limits_{k = 1,k \ne i}^{{N_{r} }} {A_{ik} \,\,\,\,\,{\text{when}}\,\,\,\,i = m} } \hfill \\ \end{array} } \right.\,\,\,\,\,\,\,\,\,i,m = 1,2, \ldots ,N_{r} ,$$
(39a)
$$A_{jn}^{\theta } = \left\{ {\begin{array}{*{20}l} {\frac{{\xi \left( {\theta_{j} } \right)}}{{\left( {\theta_{j} - \theta_{n} } \right)\xi \left( {\theta_{n} } \right)}}\,\,\,\,\,\,{\text{when}}\,\,\,\,j \ne n} \hfill \\ { - \sum\limits_{k = 1,k \ne j}^{{N_{\theta } }} {A_{jk} \,\,\,\,{\text{when}}\,\,\,\,j = n} } \hfill \\ \end{array} } \right.\,\,\,\,\,\,\,\,\,j,n = 1,2, \ldots ,N_{\theta } ,$$
(39b)

in which

$$\xi \left( {r_{i} } \right) = \prod\limits_{k = 1,k \ne i}^{{N_{r} }} {\left( {r_{i} - r_{k} } \right)} ,$$
(40a)
$$\xi \left( {\theta_{j} } \right) = \prod\limits_{k = 1,k \ne j}^{{N_{\theta } }} {\left( {\theta_{j} - \theta_{k} } \right)} ,$$
(40b)

and

$$B_{im}^{r} = 2\left( {A_{ii}^{r} A_{im}^{r} - \frac{{A_{im}^{r} }}{{\left( {r_{i} - r_{m} } \right)}}} \right)\,\,\,\,\,i,m = 1,2, \ldots ,N_{r} \,\,,\,\,i \ne m,$$
(41a)
$$B_{jn}^{\theta } = 2\left( {A_{jj}^{\theta } A_{jn}^{\theta } - \frac{{A_{jn}^{\theta } }}{{\left( {\theta_{j} - \theta_{n} } \right)}}} \right)\,\,\,\,\,j,n = 1,2, \ldots ,N_{\theta } \,\,,\,\,j \ne n,$$
(41b)
$$B_{ii}^{r} = - \sum\limits_{k = 1,k \ne i}^{{N_{r} }} {B_{ik}^{r} \,\,\,\,,\,i = 1,2, \ldots ,N_{r} } ,\,\,i = m,$$
(41c)
$$B_{jj}^{\theta } = - \sum\limits_{k = 1,k \ne j}^{{N_{\theta } }} {B_{jk}^{\theta } \,\,\,\,,\,j = 1,2, \ldots ,N_{j} } ,\,\,j = n.$$
(41d)

Also, using Chebyshev polynomials greed points, the seed along with the r-axis and \(\theta\)-axis can be distributed as [98]:

$$r_{i} = \frac{{R_{0} - R_{i} }}{2}\left( {1 - \cos \left( {\frac{{\left( {i - 1} \right)}}{{\left( {N_{r} - 1} \right)}}\pi } \right)} \right) + R_{i} \quad i = 1,2,3, \ldots ,N_{r} ,$$
(42a)
$$\theta_{j} = \frac{\chi }{2}\left( {1 - \cos \left( {\frac{{\left( {j - 1} \right)}}{{\left( {N_{\theta } - 1} \right)}}\pi } \right)} \right)\quad j = 1,2,3, \ldots ,N_{\theta } .$$
(42b)

The following equation can give the GDQ form of the structure:

$$\left\{ {\left[ {\begin{array}{*{20}c} {\left[ {M_{{{\text{dd}}}} } \right]} & {\left[ {M_{{{\text{db}}}} } \right]} \\ {\left[ {M_{{{\text{bd}}}} } \right]} & {\left[ {M_{{{\text{bb}}}} } \right]} \\ \end{array} } \right]\omega_{n}^{2} + \left[ {\begin{array}{*{20}c} {\left[ {K_{{{\text{dd}}}} } \right]} & {\left[ {K_{{{\text{db}}}} } \right]} \\ {\left[ {K_{{{\text{bd}}}} } \right]} & {\left[ {K_{{{\text{bb}}}} } \right]} \\ \end{array} } \right]} \right\}\left\{ \begin{gathered} \delta_{{\text{d}}} \hfill \\ \delta_{{\text{b}}} \hfill \\ \end{gathered} \right\} = 0.$$
(43)

Finally, with the aid of Eq. (43), the new system is

$$\left[ {K_{{{\text{db}}}} } \right]\delta_{{\text{b}}} + \left[ {K_{{{\text{dd}}}} } \right]\delta_{{\text{d}}} = 0,$$
(44a)
$$\left[ {K_{{{\text{bb}}}} } \right]\delta_{{\text{b}}} + \left[ {K_{{{\text{bd}}}} } \right]\delta_{{\text{d}}} = 0,$$
(44b)

where the vector of the freedom degrees can be defined as:

$$\delta_{{\text{b}}} = - \frac{{\left[ {K_{{{\text{dd}}}} } \right]}}{{\left[ {K_{{{\text{db}}}} } \right]}}\delta_{{\text{d}}} .$$
(45)

By substituting Eq. (45) in Eq. (44b), we have:

$$\left( {\left[ {K_{{{\text{bd}}}} } \right] - \left[ {K_{{{\text{bb}}}} } \right]\left[ {K_{{{\text{db}}}} } \right]^{ - 1} \left[ {K_{{{\text{dd}}}} } \right]} \right)\delta_{{\text{d}}} = 0.$$
(46)

So,

$$K^{*} = \left[ {K_{{{\text{bd}}}} } \right] - \left[ {K_{{{\text{bb}}}} } \right]\left[ {K_{{{\text{db}}}} } \right]^{ - 1} \left[ {K_{{{\text{dd}}}} } \right]$$
(47)

and

$$\left[ {M_{{{\text{bd}}}} } \right]\delta_{{\text{d}}} + \left[ {M_{{{\text{bb}}}} } \right]\delta_{{\text{b}}} = 0.$$
(48)

Also, by substituting Eqs. (45) in (48), we have:

$$\left( {\left[ {M_{{{\text{bd}}}} } \right] - \left[ {M_{{{\text{bb}}}} } \right]\left[ {K_{{{\text{db}}}} } \right]^{ - 1} \left[ {K_{{{\text{dd}}}} } \right]} \right)\delta_{{\text{d}}} = 0.$$
(49)

So,

$$M^{*} = \left[ {M_{{{\text{bd}}}} } \right] - \left[ {M_{{{\text{bb}}}} } \right]\left[ {K_{{{\text{db}}}} } \right]^{ - 1} \left[ {K_{{{\text{dd}}}} } \right].$$
(50)

Finally, by solving the below equation, frequency information and displacement fields of the structure can be extracted using GDQM.

$$K^{*} + M^{*} \omega^{2} = 0.$$
(51)

3 Results and discussion

The data in Table 1 provide details about the properties of the reinforcements and epoxy. The thermomechanical constants of the used reinforcements are given in Table 1. Also, carbon fiber, epoxy, and carbon nanotube are used to make a reinforced sandwich disk with honeycomb core and multiscale hybrid nanocomposite face sheets and core.

Table 1 The properties of MHC [99] and core [19]
Full size table

Convergence conditions of the GDQ method for having independent outcomes with respect to the three boundary conditions are shown in Table 2. Based on Table 2, when the number of grid points in the GDQ method is more than 11, the error for calculating the natural frequency of the disk becomes zero, and this matter is a fact for all boundary conditions.

Table 2 Convergence number of grid points for having independent results with respect to the three kinds of boundary conditions
Full size table

The influence of the number of layers (\({\text{Nt}}\)) and various functionally graded distribution on the frequency of the disk with respect to the porosity patterns are depicted in Table 3. If we have a glance at the Table 3 can claim that not only the structure will have the best dynamic response, which is considered the FG-O and PD-X patterns, but also the number of layers should not be more than nine for all porosity and FG patterns, because of that for \(Nt \ge 9\) we cannot see any changes in the frequency of the structure.

Table 3 Convergence number of layers in the compositionally face sheets and various functionally graded distribution effects on the frequency of the disk with respect to the porosity patterns
Full size table

They analyze the effects of three types of methods for reinforcing the structure on the frequency of the system with consideration of three porosity coefficient and boundary conditions, which are discussed in Table 3. The ends of Table 4 show that not only CNTs/HC/CNTs reinforced disk has the highest natural frequency in comparison with MHC/HC/MHC, but also the imperfection effect is a reason to increase the frequency of the system. If we have a glance at the given information in Table 4, we can conclude that employing the honeycomb network as the core of the structure will improve the dynamic response of the structure impressively.

Table 4 Effects of three types of methods for reinforcing the structure on the frequency of the system with consideration of three porosity coefficient and boundary conditions
Full size table

The provided information in Fig. 5 gives results about the frequency behavior of the disk by considering the angle of the honeycomb network effect. The more critical conclusion in Fig. 5 is that when the angle of the fibers is close to the horizon, the frequency of the system improves.

Fig. 5
figure 5

Frequency of the clamped–clamped honeycomb reinforced disk versus the outer to inner radius ratio for various \(\theta_{{\text{h}}}\)

Full size image

The provided information in Fig. 6 gives results about the frequency behavior of the disk considering \(V_{{\text{f}}}\) effect. The more important conclusion in Fig. 6 is that when the sandwich disk is made of the higher value fraction of carbon fibers, the frequency of the system could be improved.

Fig. 6
figure 6

Frequency of the clamped–clamped honeycomb reinforced disk versus radius ratio for various \(V_{{\text{f}}}\)

Full size image

The provided information in Fig. 7 gives results about the frequency behavior of the disk considering the value fraction of CNTs (\(W_{{{\text{CNT}}}}\)) effect. The more important conclusion in Fig. 7 is that when the sandwich disk is made of a higher value fraction of CNTs, the frequency of the system could be improved.

Fig. 7
figure 7

Frequency of the clamped–clamped honeycomb-reinforced disk versus the radius ratio for various \(W_{{{\text{CNT}}}}\)

Full size image

The presented diagrams in Fig. 8 give the results about the frequency behavior of the disk considering the thickness to length ratio of the honeycomb network (\(t_{{\text{h}}} /l_{{\text{h}}}\)) effect. Concerning Fig. 8, the thicker the honeycomb core, the better is the dynamic provided for the sandwich disk.

Fig. 8
figure 8

Frequency of the clamped–clamped honeycomb-reinforced disk versus the radius ratio for various \(t_{{\text{h}}} /l_{{\text{h}}}\)

Full size image

Figure 9 presents some information for analyzing the impacts of the orientation of fibers (\(\theta_{{\text{f}}} /\pi\)) in the epoxy matrix and thickness to length ratio of the honeycomb network (\(t_{{\text{h}}} /l_{{\text{h}}}\)) on the vibrational information of a sandwich disk with consideration of three kinds of boundary conditions. The main point in this part of the presented study is that for the structure with C–C and C–S edges and each \(t_{{\text{h}}} /l_{{\text{h}}}\), the lowest frequency response is for a disk which is reinforced by the carbon fibers with \(\theta_{{\text{f}}} /\pi\) = 0.5, and this fiber angle is called the critical angle. Also, for S–S boundary conditions, the critical fiber angles are 0.34 and 0.68. Besides, as the \(t_{{\text{h}}} /l_{{\text{h}}}\) increases, the frequency of the structure with critical fiber angles increases. Furthermore, when there is an ever increase in \(\theta_{{\text{f}}} /\pi\), before and after critical fiber angles, the dynamic response of the disk increases and falls, respectively. The last result from Fig. 9 is that employing the thicker honeycomb core will enhance the stability of the structure.

Fig. 9
figure 9

Frequency of the honeycomb-reinforced disk versus \(\theta_{{\text{f}}} /\pi\) for various \(t_{{\text{h}}} /l_{{\text{h}}}\) and three kinds of boundary conditions

Full size image

Figure 10 presents some data for analyzing the impacts of the orientation of fibers (\(\theta_{{\text{f}}} /\pi\)) in the epoxy matrix, Winkler–Pasternak constants (\(K_{{\text{w}}}\) and \(K_{{\text{p}}}\)), and three kinds of boundary conditions on the vibrational information of a sandwich disk. As \(K_{{\text{w}}}\) and \(K_{{\text{p}}}\) increase, the frequency of the disk increases. In addition, it is true that the roles of \(K_{{\text{w}}}\) and \(K_{{\text{p}}}\) are the same as enhancements, but the impact of \(K_{{\text{w}}}\) could be much more considerable than the effect of \(K_{{\text{p}}}\) on the stability of the structure.

Fig. 10
figure 10

Frequency of the honeycomb-reinforced disk versus to \(\theta_{{\text{f}}} /\pi\) for three values of \(K_{{\text{w}}}\) and \(K_{{\text{p}}}\) with three kinds of boundary conditions

Full size image

4 Conclusion

For the first time, the vibrational characteristics of a sandwich disk rested on the elastic foundation is investigated. The stresses and strains are obtained using FSDT. Rule of the mixture and modified Halpin–Tsai model are engaged to provide the effective material constant of the multi-hybrid laminated nanocomposite face sheets of the sandwich disk. Finally, the most bolded results of this paper are as follows:

Not only CNTs/HC/CNTs reinforced disk have the highest natural frequency compared with MHC/HC/MHC, but also growing the imperfection effect is a reason to decline the frequency of the systems.

We can conclude that employing the honeycomb network as the core of the structure improves the dynamic response of the design impressively.

When the angle of the fibers is close to the horizon, the frequency of the system improves.

For the structure with C–C and C–S edges and each value of \(t_{{\text{h}}} /l_{{\text{h}}}\), the lowest frequency response is for a disk which is reinforced by the carbon fibers with \(\theta_{{\text{f}}} /\pi\) = 0.5, and this fiber angle is called the critical fiber angle.

For S–S boundary conditions, the critical fiber angles are 0.34 and 0.68. Also, as the \(t_{{\text{h}}} /l_{{\text{h}}}\) increases, the frequency of the structure with critical fiber angles increases.