1 Introduction

Up to now, huge research is proved that the compositionally structures have a marvelous thermo-electro-mechanical property [1,2,3] and this issue is being an important reason to take the attention of all engineering fields for having efficient productions with the aid of composite structure, especially carbon-based nanofillers reinforced structure [4,5,6,7,8,9,10]. In addition to what is mentioned owing to the wide applications of wave propagation analysis in structural health monitoring, most recently, an interesting field of research has been started in scholar which is called wave propagation response [11,12,13]. In addition, the properties of reinforcements make them an appropriate choice to be used in chemistry, physics, electrical engineering [14,15,16,17,18,19,20,21,22,23,24,25,26], materials science [10], and engineering applications [27,28,29,30,31,32,33,34,35].

By considering the mentioned necessities and in the field of wave propagation in composite beams and plates, Ebrahime et al. [36] could present a paper to investigate the wave propagation of the sandwich plate in which the structure is embedded in a nonlinear foundation. Also, they considered a magnetic environment in their model and used the classical theory for doing their computational formulation. Based on their result, as the magnetic layer will play the most important role on the wave response of the sandwich plate [37]. presented a comprehensive formulation on the wave dispersion of a high speed rotating 2D-FG nanobeam. They used nonlocal theory for consideration of the couple stress in the nanomechanics effect on the wave response of the structure. They could solve their complex formulation via an analytical method and they reported that the rotating speed is the most effective parameter. By employing the new version couple stress theory, Global matrix, and Legendre orthogonal polynomial methods, and, Liu et al. [38] had a try for reporting the characteristics of the propagated wave in a micro FG plate. They reported that by controlling the couple stress, we will have the grater phase velocity in the aspect of wave propagation. Ebrahimi et al. [39] succeeded in publishing a paper in which a computational framework is developed for investigation wave behavior in a thermally affected nonlocal beam which is made by FG materials. One of their assumptions was that the nanobeam is under high-speed rotation and is located in a thermal environment. They presented a lot of results but the most significant one was that changing the rotating speed can provide some novel results on the wave propagation in the nanostructure. In a novel work, Barati [40] showed the behavior of propagated wave in the porous nanobeam with attention to the nonlocality via strain–stress gradient theory. Gao et al. [41] could report a mathematical framework to analyze the propagated wave in a GPLs reinforced porous FG plate via a well-known mixture method. Based on their result, porosity and GPLs weight fraction are two important parameters in the field of structural health monitoring via wave propagation method. Ebrahimi et al. [42] were able to provide results on the characteristics propagated waves in a compositionally nonlocal plate in which the structure located in a high-temperature environment. Also, they consider the shear deformation in each element of the structure. They found that without doubt the nonlocal effect has a bolded role on the characteristics of propagated waves. Safaei et al. [43] tried to report characteristics of the propagated waves in a CNTs reinforced FG thermoelastic plate via the high order ready plat theory and Mori–Tanaka method. Their important achievement was that the thermal stress and adding small amount of CNTs can make a remarkable effect on the wave velocity in the structure. The static and dynamic stabilities of the reinforced nanocomposite structures are presented in some researches [44,45,46,47,48,49,50] by having attention to the impacts of honeycomb core, porosity distributions, and transverse dynamic loads via higher-order theories. Many researchers [51,52,53,54,55,56] studied the behavior and stability of the FG multilayer composite and isotropic materials.

In the field of characteristics propagated waves in the shell, Bakhtiari et al. [57] provided some results on the wave propagation of the FG shell in which fluid flow through the shell is considered. Ebrahimi et al. [58] studied the wave response in a high-speed rotating nanoshell with a GPLs reinforced compositionally core and patched piezoelectric face sheet. They claimed that if the rotating should be controlled for improving the phase velocity of the nanoshell. The dispersion behavior of the wave in the MHC reinforced shell is investigated by Ebrahimi et al. [59]. They used the lowest order shear deformation theory and eigenvalue problem for providing their formulation and results. They found out that the impact of nanosize reinforcements is more effective than the macro size reinforcements for improving the phase velocity of the compositionally shell. Karami et al. [60] developed a mathematical model for literature in which wave dispersion in an imperfect nanoshell via NSG and HSD theories is analyzed. They provided some evidences that sensitivity of the prospected waves to the nonlocal effects, temperature, and humidity in the porous material should be considered. The vibration and buckling/post-buckling responses of the curved structures are investigated in some researches [61,62,63,64,65,66,67]. A key issue in various engineering field is that the prediction of the properties, behavior, and performance of different systems is an important aspect [68,69,70,71,72,73,74,75,76,77]. Also, some researchers tried to predict the static and dynamic properties of different structures and materials via neural network solution [78,79,80,81,82,83,84]. In addtion, many studies reported the application of applied soft computing method for prediction of the behavior of complex system [85,86,87,88,89,90,91,92].

In the field of analysis, the wave propagation in the smart structure, Li et al. [93] succeeded in publishing an article in which they examined the wave propagation of a smart plate via a semi-analytical method. They modeled a GPLs reinforced plate which is covered with a piezoelectric actuator. They used the Reissner–Mindlin plate theory and Hamilton’s principle for developing their computational approach and did the formulation. The application of their result is that GPLs in a matrix can play a positive role in structural health monitoring and improve wave propagation in the structures, especially smart structures. Ebrahimi et al. [94] developed a mathematical model for literature in which wave dispersion of a smart sandwich nanoplate by considering the nanosize effect via nonlocal strain gradient theory and the sandwich structure is made of ceramic face sheets and magnetostrictive core. Abad et al. [95] published an article in which they presented a formulation about the wave propagation problem of a somewhat sandwich thick plate. They smarted the plate by patching a piezoelectric layer on the top face of the structure and they considered Maxwell's assumptions in their computational approach. Habibi et al. [96] studied the wave response in a nanoshell with a GPLs reinforced compositionally core and patched piezoelectric face sheet. When they compared their result with molecular simulation, it can be seen that the nonlocality should be considered via NSGT. As a practical outcome they reported that the thickness of the smart layer will have more effect on the characteristics propagated waves in the nanoshell.

Based on the extremely detailed exploration in the literature by the authors, no one can claim that there is a study on the wave propagation of the doubly curved panel.

Therefore, characteristics of the propagated wave in a sandwich structure with a soft core and multi-hybrid nanocomposite face sheets are investigated. The HSDT is applied to formulate the stresses and strains. Rule of the mixture and modified Halpin–Tsai model are engaged to provide the effective material constant of the multi-hybrid nanocomposite face sheets of the sandwich panel. By employing Hamilton’s principle, the governing equations of the structure are derived. Via the compatibility rule, the bonding between the smart layer and the soft core is modeled. The results show that, CNT’s weight fraction, core to total thickness ratio, various FG face sheet patterns, small radius to total thickness ratio, and carbon fiber angel have an important role in the phase velocity of the FML panel.

2 Mathematical modeling

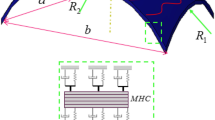
Figure 1 shows a sandwich doubly curved panel. The effective thickness (hb + hc + ht) and the middle surface radius of the doubly curved panel are presented by heff and R, respectively. Besides, hb hc, and hp are the thickness of the multi-hybrid nanocomposite reinforcement at the top layer, the core layer, and the multi-hybrid nanocomposite reinforcement at the bottom layer, respectively.

Fig. 1
figure 1

A schematic of a sandwich doubly curved panel

Full size image

2.1 MHC reinforcement

The procedure of homogenization is made of two main steps based upon the Halpin–Tsai model together with a micromechanical theory. The first stage is engaged with computing the effective characteristics of the composite reinforced with CF as following [97]:

$$E_{11} = V_{\rm{F}} E_{11}^{\rm{F}} + V_{\rm{NCM}} E^{\rm{NCM}} ,$$
(1)
$$\begin{gathered} \frac{1}{{E_{22} }} = {1 \mathord{\left/ {\vphantom {1 {E_{22}^{\rm{F}} }}} \right. \kern-\nulldelimiterspace} {E_{22}^{\rm{F}} }} + {{V_{\rm{NCM}} } \mathord{\left/ {\vphantom {{V_{\rm{NCM}} } {E^{\rm{NCM}} }}} \right. \kern-\nulldelimiterspace} {E^{\rm{NCM}} }} - V_{\rm{F}} V_{\rm{NCM}} \hfill \\ - \frac{{(\nu^{\rm{F}} )^{2} {{E^{\rm{NCM}} } \mathord{\left/ {\vphantom {{E^{\rm{NCM}} } {E_{22}^{\rm{F}} }}} \right. \kern-\nulldelimiterspace} {E_{22}^{\rm{F}} }} + (\nu^{\rm{NCM}} )^{2} {{E_{22}^{\rm{F}} } \mathord{\left/ {\vphantom {{E_{22}^{\rm{F}} } {E^{M} }}} \right. \kern-\nulldelimiterspace} {E^{M} }} - 2\nu^{\rm{NCM}} \nu^{\rm{F}} }}{{V_{\rm{F}} E_{22}^{\rm{F}} + V_{\rm{NCM}} E^{\rm{NCM}} }}, \hfill \\ \end{gathered}$$
(2)
$$\frac{1}{{G_{12} }} = \frac{{V_{\rm{NCM}} }}{{G^{\rm{NCM}} }} + \frac{{V_{\rm{F}} }}{{G_{12}^{\rm{F}} }},$$
(3)
$$\rho = V_{\rm{F}} \rho^{\rm{F}} + V_{\rm{NCM}} \rho^{\rm{NCM}} ,$$
(4)
$$\nu_{12} = V_{\rm{F}} \nu^{\rm{F}} + V_{\rm{NCM}} \nu^{\rm{NCM}} .$$
(5)

Here, elasticity modulus, mass density, Poisson’s ratio, and shear modulus are symbolled via \(\rho ,\,\,E,\,\,G\) and \(\nu\). The superscripts of the matrix and fiber are NCM and F, respectively. Add the carbon fiber volume fraction ( \(V_{\rm{F}}\)) to the nanocomposite matrix volume fraction ( \(V_{\rm{NCM}}\)) is one.

$$V_{\rm{F}} + V_{\rm{NCM}} = 1.$$
(6)

The second step is organized to obtain the effective characteristics of the nanocomposite matrix reinforced with CNTs with the aid of the extended Halpin–Tsai micromechanics as follows [97]:

$$E^{j} = \frac{5}{8}\left(\frac{{1 + 2\beta_{dd} V_{\rm{CNT}} }}{{1 - \beta_{dd} V_{\rm{CNT}} }}\right)E^{M} + \frac{3}{8}\left(\frac{{\beta_{dl} V_{\rm{CNT}} (2l^{CNT} /d^{CNT}) + 1}}{{1 - \beta_{dl} V_{\rm{CNT}} }}\right ).$$
(7)

Here, \(\beta_{dd}\) and \(\beta_{dl}\) would be computed as the following expression:

$$\begin{gathered} \beta_{dl} = {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} \mathord{\left/ {\vphantom {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} {(E_{11}^{CNT} /E^{M} ) + (l^{CNT} /2t^{CNT} )}}} \right. \kern-\nulldelimiterspace} {(E_{11}^{CNT} /E^{M} ) + (l^{CNT} /2t^{CNT} )}}, \hfill \\ \beta_{dd} = {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} \mathord{\left/ {\vphantom {{(E_{11}^{CNT} /E^{M} ) - (d^{CNT} /4t^{CNT} )} {(E_{11}^{CNT} /E^{M} ) + (d^{CNT} /2t^{CNT} )}}} \right. \kern-\nulldelimiterspace} {(E_{11}^{CNT} /E^{M} ) + (d^{CNT} /2t^{CNT} )}}, \hfill \\ \end{gathered}$$
(8)

volume fraction, thickness, length, elasticity modulus, weight fraction, and diameter of CNTs are \(V_{\rm{CNT}}\), \(t^{CNT}\), \(l^{CNT}\), \(E^{CNT}\),\(W_{\rm{CNT}}\), and \(d^{CNT}\). Also, the volume fraction of the matrix and elasticity modulus of the matrix are \(V_{M}\) and \(E^{M}\). So, The CNTs volume fraction can be formulated as below:

$$V_{\rm{CNT}}^{ * } = \frac{{W_{\rm{CNT}} }}{{W_{\rm{CNT}} +\left (\frac{{\rho^{CNT} }}{{\rho^{M} }}\right)(1 - W_{\rm{CNT}} )}}.$$
(9)

Also, the effective volume fraction of CNTs can be formulated as follows:

$$\begin{gathered} V_{\rm{CNT}} = V_{\rm{CNT}}^{*} \frac{{\left| {\xi_{j} } \right|}}{h}{\text{ FG - X,}} \hfill \\ V_{\rm{CNT}} = V_{\rm{CNT}}^{*} \left( {1 + \frac{{2\xi_{j} }}{h}} \right){\text{ FG - V,}} \hfill \\ V_{\rm{CNT}} = V_{\rm{CNT}}^{*} \left( {1 - \frac{{2\xi_{j} }}{h}} \right){\text{ FG } - \text{ A}}{.} \hfill \\ V_{\rm{CNT}} = V_{\rm{CNT}}^{*} {\text{ FG - UD,}} \hfill \\ \end{gathered}$$
(10)

where \(\xi_{j} = \left( {\frac{1}{2} + \frac{1}{{2N_{t} }} - \frac{j}{{N_{t} }}} \right)h{\text{ j = 1,2,}}...{,}N_{t}\). Furthermore, the sum of \(V_{M}\) and \(V_{\rm{CNT}}\) as the two constituents of the nanocomposite matrix is equal to 1.

$$V_{\rm{CNT}} + V_{M} = 1.$$
(11)

Also, Poisson’s ratio, mass density, and shear modulus will be calculated as

$$\rho^{j} = V_{\rm{CNT}} \rho^{CNT} + V_{M} \rho^{M} ,$$
(12)
$$\nu^{j} = \nu^{M} ,$$
(13)
$$G^{j} = \frac{{E^{j} }}{{2\left( {1 + \nu^{j} } \right)}}.$$
(14)

2.2 Kinematic relations

The displacement fields of the core can be given by [98]

$$\begin{gathered} u^{c} (x,y,z,t) = u_{0}^{c} (x,y,t) + z_{c} \phi_{x}^{c} (x,y,t) - c_{1} z_{c}^{3} \left[ {\phi_{x}^{c} (x,y,t) + \frac{{\partial w_{0}^{c} (x,y,t)}}{\partial x}} \right], \hfill \\ v^{c} (x,y,z,t) = v_{0}^{c} (x,y,t) + z_{c} \phi_{y}^{c} (x,y,t) - c_{1} z_{c}^{3} \left[ {\phi_{y}^{c} (x,y,t) + \frac{{\partial w_{0}^{c} (x,y,t)}}{\partial y}} \right], \hfill \\ w^{c} (x,y,z,t) = w_{0}^{c} (x,y,t). \hfill \\ \end{gathered}$$
(15)

The strain components can be given by [98, 99]

$$\left\{ \begin{gathered} \varepsilon_{xx}^{c} \hfill \\ \varepsilon_{yy}^{c} \hfill \\ \gamma_{xy}^{c} \hfill \\ \gamma_{xz}^{c} \hfill \\ \gamma_{yz}^{c} \hfill \\ \end{gathered} \right\} = \left[ \begin{gathered} \frac{{\partial u_{0}^{c} }}{\partial x} + z_{c} \frac{{\partial \phi_{x}^{c} }}{\partial x} - z_{c}^{3} c_{1} \left( {\frac{{\partial \phi_{x}^{c} }}{\partial x} + \frac{{\partial^{2} w_{0}^{c} }}{{\partial x^{2} }}} \right) + \frac{{w_{0}^{c} }}{{R_{1} }} \hfill \\ \frac{{\partial v_{0}^{c} }}{\partial y} + z_{c} \frac{{\partial \phi_{x}^{c} }}{\partial y} - z_{c}^{3} c_{1} \left( {\frac{{\partial \phi_{y}^{c} }}{\partial y} + \frac{{\partial^{2} w_{0}^{c} }}{{\partial y^{2} }}} \right) + \frac{{w_{0}^{c} }}{{R_{2} }} \hfill \\ \frac{{\partial u_{0}^{c} }}{\partial y} + \frac{{\partial v_{0}^{c} }}{\partial x} + z_{c} \left( {\frac{{\partial \phi_{x}^{c} }}{\partial y} + \frac{{\partial \phi_{y}^{c} }}{\partial x}} \right) - z_{c}^{3} c_{1} \left( {\frac{{\partial \phi_{x}^{c} }}{\partial y} + \frac{{\partial \phi_{y}^{c} }}{\partial x} + 2\frac{{\partial^{2} w_{0}^{c} }}{\partial x\partial y}} \right) \hfill \\ (1 - 3z_{c}^{2} c_{1} )\left( {\phi_{x}^{c} + \frac{{\partial w_{0}^{c} }}{\partial x}} \right) \hfill \\ (1 - 3z_{c}^{2} c_{1} )\left( {\phi_{y}^{c} + \frac{{\partial w_{0}^{c} }}{\partial y}} \right) \hfill \\ \end{gathered} \right].$$
(16)

Also, the strain–stress equations of the metal structure can be given as

$$\left[ \begin{gathered} \sigma_{xx}^{c} \hfill \\ \sigma_{yy}^{c} \hfill \\ \sigma_{xy}^{c} \hfill \\ \sigma_{xz}^{c} \hfill \\ \sigma_{yz}^{c} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{21} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{44} } \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon_{xx}^{c} \hfill \\ \varepsilon_{yy}^{c} \hfill \\ \varepsilon_{xy}^{c} \hfill \\ \varepsilon_{xz}^{c} \hfill \\ \varepsilon_{yz}^{c} \hfill \\ \end{gathered} \right].$$
(17)

In which [100,101,102,103]:

$$Q_{11} = Q_{22} = \frac{{E_{c} }}{{1 - \nu_{c}^{2} }},\,\,\,Q_{12} = Q_{21} = \frac{{E_{c} \nu_{c} }}{{1 - \nu_{c}^{2} }},\,\,\,\,\,\,\,Q_{44} = Q_{55} = Q_{66} = \frac{{E_{c} }}{{2(1 + \nu_{c} )}}.$$

In the Eq. (17) \(E_{c}\), and \(\nu_{c}\) are Young’s module and poison ratio of the metal, respectively.

2.3 Face sheets

In the present structural model for the sandwich panel, the HSDT is adopted for the face sheets. Hence, the displacement components of the top and bottom face sheets (j = t, b) are represented as

$$\begin{gathered} u^{j} (x,y,z,t) = u_{0}^{j} (x,y,t) + z_{j} \phi_{x}^{j} (x,y,t) - c_{1} z_{j}^{3} \left[ {\phi_{x}^{j} (x,y,t) + \frac{{\partial w_{0}^{j} (x,y,t)}}{\partial x}} \right], \hfill \\ v^{j} (x,y,z,t) = v_{0}^{j} (x,y,t) + z\phi_{y}^{j} (x,y,t) - c_{1} z_{j}^{3} \left[ {\phi_{y}^{j} (x,y,t) + \frac{{\partial w_{0}^{j} (x,y,t)}}{\partial y}} \right], \hfill \\ w^{j} (x,y,z,t) = w_{0}^{j} (x,y,t). \hfill \\ \end{gathered}$$
(18)

The strain components can be given by

$$\left\{ \begin{gathered} \varepsilon_{xx}^{j} \hfill \\ \varepsilon_{yy}^{j} \hfill \\ \gamma_{xy}^{j} \hfill \\ \gamma_{xz}^{j} \hfill \\ \gamma_{yz}^{j} \hfill \\ \end{gathered} \right\} = \left[ \begin{gathered} \frac{{\partial u_{0}^{j} }}{\partial x} + z_{j} \frac{{\partial \phi_{x}^{j} }}{\partial x} - z_{j}^{3} c_{1} \left( {\frac{{\partial \phi_{x}^{j} }}{\partial x} + \frac{{\partial^{2} w_{0}^{j} }}{{\partial x^{2} }}} \right) + \frac{{w_{0}^{j} }}{{R_{1} }} \hfill \\ \frac{{\partial v_{0}^{j} }}{\partial y} + z_{j} \frac{{\partial \phi_{x}^{j} }}{\partial y} - z_{j}^{3} c_{1} \left( {\frac{{\partial \phi_{y}^{j} }}{\partial y} + \frac{{\partial^{2} w_{0}^{j} }}{{\partial y^{2} }}} \right) + \frac{{w_{0}^{j} }}{{R_{2} }} \hfill \\ \frac{{\partial u_{0}^{j} }}{\partial y} + \frac{{\partial v_{0}^{j} }}{\partial x} + z_{j} \left( {\frac{{\partial \phi_{x}^{j} }}{\partial y} + \frac{{\partial \phi_{y}^{j} }}{\partial x}} \right) - z_{j}^{3} c_{1} \left( {\frac{{\partial \phi_{x}^{j} }}{\partial y} + \frac{{\partial \phi_{y}^{j} }}{\partial x} + 2\frac{{\partial^{2} w_{0}^{j} }}{\partial x\partial y}} \right) \hfill \\ (1 - 3z_{j}^{2} c_{1} )\left( {\phi_{x}^{j} + \frac{{\partial w_{0}^{j} }}{\partial x}} \right) \hfill \\ (1 - 3z_{j}^{2} c_{1} )\left( {\phi_{y}^{j} + \frac{{\partial w_{0}^{j} }}{\partial y}} \right) \hfill \\ \end{gathered} \right].$$
(19)

Also, the strain–stress equations of the metal structure can be given as [9, 104,105,106,107,108,109,110,111,112,113,114,115,116,117,118]

$$\left[ \begin{gathered} \sigma_{xx}^{j} \hfill \\ \sigma_{yy}^{j} \hfill \\ \sigma_{xy}^{j} \hfill \\ \sigma_{xz}^{j} \hfill \\ \sigma_{yz}^{j} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {Q^{j}_{11} } & {Q^{j}_{12} } & 0 & 0 & 0 \\ {Q^{j}_{21} } & {Q^{j}_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q^{j}_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q^{j}_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q^{j}_{44} } \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon_{xx}^{j} \hfill \\ \varepsilon_{yy}^{j} \hfill \\ \varepsilon_{xy}^{j} \hfill \\ \varepsilon_{xz}^{j} \hfill \\ \varepsilon_{yz}^{j} \hfill \\ \end{gathered} \right],$$
(20)

where [119]

$$\begin{gathered} \overline{Q}^{j}_{11} = Q^{j}_{11} \cos^{4} \theta + 2Q^{j}_{12} \sin^{2} \theta \cos^{2} \theta + Q^{j}_{22} \sin^{4} \theta , \hfill \\ \overline{Q}^{j}_{12} = \left( {Q^{j}_{11} + Q_{22} } \right)\sin^{2} \theta \cos^{2} \theta + Q^{j}_{12} \left( {\sin^{4} \theta + \cos^{4} \theta } \right), \hfill \\ \overline{Q}^{j}_{22} = Q^{j}_{11} \sin^{4} \theta + 2Q^{j}_{12} \sin^{2} \theta \cos^{2} \theta + Q^{j}_{22} \cos^{4} \theta , \hfill \\ \overline{Q}^{j}_{55} = Q^{j}_{55} \cos^{2} \theta . \hfill \\ \end{gathered}$$
(21)

The terms involved in Eq. (21) would be obtained as [114, 120,121,122,123]

$$Q^{j}_{11} = Q^{j}_{22} = \frac{{E^{j} }}{{1 - (\nu^{j} )^{2} }},\,\,\,Q^{j}_{12} = Q^{j}_{21} = \frac{{E^{j} \nu^{j} }}{{1 - (\nu^{j} )^{2} }},\,\,\,\,\,\,\,Q^{j}_{44} = Q^{j}_{55} = Q^{j}_{66} = \frac{{E^{j} }}{{2(1 + \nu^{j} )}}.$$

Therefore, the face sheets are assumed as in-plane flexible and transversely rigid panels. Also, the core is assumed as an in-plane and transversely flexible layer. Finally, in this model, there are fifteen displacement unknowns: five unknowns for each face sheet and five unknowns for the core.

2.4 Compatibility equations

The compatibility conditions assuming perfect bonding between the core and the composite layers that can be defined as follows:

$$\begin{gathered} u^{c} (z_{c} = - h_{c} /2) = u^{b} (z_{b} = h_{b} /2), \hfill \\ v^{c} (z_{c} = - h_{c} /2) = v^{b} (z_{b} = h_{b} /2), \hfill \\ w^{c} (z_{c} = - h_{c} /2) = w^{b} (z_{p} = h_{b} /2), \hfill \\ u^{c} (z_{c} = h_{c} /2) = u^{t} (z_{t} = - h_{t} /2), \hfill \\ v^{c} (z_{c} = h_{c} /2) = v^{t} (z_{t} = - h_{t} /2), \hfill \\ w^{c} (z_{c} = h_{c} /2) = w^{t} (z_{t} = - h_{t} /2). \hfill \\ \end{gathered}$$
(22)

2.5 Extended Hamilton’s principle

For obtaining the governing equation and associated boundary conditions, we can apply extended Hamilton’s principle as follows [24,25,26, 98, 124,125,126]:

$$\int\limits_{{t_{1} }}^{{t_{2} }} {(\delta U - \delta W){\text{d}}t = 0} .$$
(23)

The components of strain energy can be expressed as below:

$$\begin{gathered} \delta U = \frac{1}{2}(\iiint\limits_{V} {\sigma^{c}_{mn} \delta \varepsilon^{c}_{mn} dV^{c} } + \iiint\limits_{V} {\sigma^{j}_{mn} \delta \varepsilon^{j}_{mn} dV^{j} }) = \hfill \\ = \iint\limits_{A} {\left[ \begin{gathered} N^{c}_{xx} (\frac{{\partial \delta u_{0}^{c} }}{\partial x} - \frac{{\delta w_{0}^{c} }}{{R_{1} }}) + M^{c}_{xx} \frac{{\partial \delta \phi u_{x}^{c} }}{\partial x} - P^{c}_{xx} c_{1} \left( {\frac{{\partial \delta \phi_{x}^{c} }}{\partial x} + \frac{{\partial^{2} \delta w_{0}^{c} }}{{\partial x^{2} }}} \right) \hfill \\ + N^{c}_{yy} (\frac{{\partial \delta v_{0}^{c} }}{\partial y} - \frac{{\delta w_{0}^{c} }}{{R_{2} }}) + M^{c}_{yy} \frac{{\partial \delta \phi_{x}^{c} }}{\partial y} - P^{c}_{yy} c_{1} \left( {\frac{{\partial \delta \phi_{y}^{c} }}{\partial y} + \frac{{\partial^{2} \delta w_{0}^{c} }}{{\partial y^{2} }}} \right) \hfill \\ + N^{c}_{xy} \frac{{\partial \delta u_{0}^{c} }}{\partial y} + N^{c}_{xy} \frac{{\partial \delta v_{0}^{c} }}{\partial x} + M^{c}_{xy} \left( {\frac{{\partial \delta \phi_{x}^{c} }}{\partial y} + \frac{{\partial \delta \phi_{y}^{c} }}{\partial x}} \right) \hfill \\ - P^{c}_{xy} c_{1} \left( {\frac{{\partial \delta \phi_{x}^{c} }}{\partial y} + \frac{{\partial \delta \phi_{y}^{c} }}{\partial x} + 2\frac{{\partial^{2} \delta w_{0}^{c} }}{\partial x\partial y}} \right) \hfill \\ + (Q^{c}_{xz} - 3S^{c}_{xz} c_{1} )\left( {\delta \phi_{x}^{c} + \frac{{\partial \delta w_{0}^{c} }}{\partial x}} \right) + (Q^{c}_{yz} - 3S^{c}_{yz} c_{1} )\left( {\delta \phi_{y}^{c} + \frac{{\partial \delta w_{0}^{c} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]\,}(1 + \frac{{z^{c} }}{{R_{1} }})(1 + \frac{{z^{c} }}{{R_{2} }})dA^{c} + \hfill \\ \iint\limits_{A} {\left[ \begin{gathered} N^{j}_{xx} (\frac{{\partial \delta u_{0}^{j} }}{\partial x} - \frac{{\delta w_{0}^{j} }}{{R_{1} }}) + M^{j}_{xx} \frac{{\partial \delta \phi_{x}^{j} }}{\partial x} - P^{j}_{xx} c_{1} \left( {\frac{{\partial \delta \phi_{x}^{j} }}{\partial x} + \frac{{\partial^{2} \delta w_{0}^{j} }}{{\partial x^{2} }}} \right) \hfill \\ + N^{j}_{yy} (\frac{{\partial \delta v_{0}^{j} }}{\partial y} - \frac{{\delta w_{0}^{j} }}{{R_{2} }}) + M^{j}_{yy} \frac{{\partial \delta \phi_{x}^{j} }}{\partial y} - P^{j}_{yy} c_{1} \left( {\frac{{\partial \delta \phi_{y}^{j} }}{\partial y} + \frac{{\partial^{2} \delta w_{0}^{j} }}{{\partial y^{2} }}} \right) \hfill \\ + N^{j}_{xy} \frac{{\partial \delta u_{0}^{j} }}{\partial y} + N^{j}_{xy} \frac{{\partial \delta v_{0}^{j} }}{\partial x} + M^{j}_{xy} \left( {\frac{{\partial \delta \phi_{x}^{j} }}{\partial y} + \frac{{\partial \delta \phi_{y}^{j} }}{\partial x}} \right) \hfill \\ - P^{j}_{xy} c_{1} \left( {\frac{{\partial \delta \phi_{x}^{j} }}{\partial y} + \frac{{\partial \delta \phi_{y}^{j} }}{\partial x} + 2\frac{{\partial^{2} \delta w_{0} }}{\partial x\partial y}} \right) \hfill \\ + (Q^{j}_{xz} - 3S^{j}_{xz} c_{1} )\left( {\delta \phi_{x}^{j} + \frac{{\partial \delta w_{0}^{j} }}{\partial x}} \right) + (Q^{j}_{yz} - 3S^{j}_{yz} c_{1} )\left( {\delta \phi_{y}^{j} + \frac{{\partial \delta w_{0}^{j} }}{\partial y}} \right) \hfill \\ \end{gathered} \right]\,}(1 + \frac{{z^{j} }}{{R_{1} }})(1 + \frac{{z^{j} }}{{R_{2} }})dA^{j} , \hfill \\ \end{gathered}$$
(24a)

which

$$\begin{gathered} \left\{ {N^{\lambda }_{xx} ,N^{\lambda }_{yy} ,N^{\lambda }_{xy} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma^{\lambda }_{xx} ,\sigma^{\lambda }_{yy} ,\sigma^{\lambda }_{xy} } \right\}} dz_{\lambda } , \hfill \\ \left\{ {M^{\lambda }_{xx} ,M^{\lambda }_{yy} ,M^{\lambda }_{xy} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma^{\lambda }_{xx} ,\sigma^{\lambda }_{yy} ,\sigma^{\lambda }_{xy} } \right\}} z_{\lambda } dz_{\lambda } , \hfill \\ \left\{ {P^{\lambda }_{xx} ,P^{\lambda }_{yy} ,P^{\lambda }_{xy} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma^{\lambda }_{xx} ,\sigma^{\lambda }_{yy} ,\sigma^{\lambda }_{xy} } \right\}} z_{{_{\lambda } }}^{3} dz_{\lambda } , \hfill \\ \left\{ {Q^{\lambda }_{xz} ,Q^{\lambda }_{yz} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma^{\lambda }_{xz} ,\sigma^{\lambda }_{xy} } \right\}} dz_{\lambda } , \hfill \\ \left\{ {S^{\lambda }_{xz} ,S^{\lambda }_{yz} } \right\} = \int_{{z_{\lambda } }} {\left\{ {\sigma^{\lambda }_{xz} ,\sigma^{\lambda }_{xy} } \right\}z_{{_{\lambda } }}^{2} } dz_{\lambda } . \hfill \\ \end{gathered}$$
(24b)

where \(\lambda = b,\,t,\,c\).

Also, the kinetic energy [4,5,6, 8, 127,128,129,130,131,132] of each layer of the structure can be defined as bellow:

$$\begin{gathered} \delta K = \int\limits_{{Z^{j} }} {\iint\limits_{{A^{j} }} {\rho^{j} \left\{ {(\frac{{\partial u^{j} }}{\partial t}\frac{{\partial \delta u^{j} }}{\partial t}) + \frac{{\partial v^{j} }}{\partial t}\frac{{\partial \delta v^{j} }}{\partial t} + \frac{{\partial w^{j} }}{\partial t}\frac{{\partial \delta w^{j} }}{\partial t}} \right\}}} (1 + \frac{{z^{j} }}{{R_{1} }})(1 + \frac{{z^{j} }}{{R_{2} }})dA^{j} \hfill \\ + \int\limits_{{Z^{c} }} {\iint\limits_{{A^{c} }} {\rho^{c} \left\{ {(\frac{{\partial u^{c} }}{\partial t}\frac{{\partial \delta u^{c} }}{\partial t}) + \frac{{\partial v^{c} }}{\partial t}\frac{{\partial \delta v^{c} }}{\partial t} + \frac{{\partial w^{c} }}{\partial t}\frac{{\partial \delta w^{c} }}{\partial t}} \right\}}} (1 + \frac{{z^{c} }}{{R_{1} }})(1 + \frac{{z^{c} }}{{R_{2} }})dA^{c} . \hfill \\ \end{gathered}$$
(25)

Finally, the motion equations are derived as follows:

$$\begin{gathered} \delta u_{0}^{c} :\frac{{\partial N^{c}_{xx} }}{\partial x} + \frac{{\partial N^{c}_{xy} }}{\partial y} = I_{0}^{c} \frac{{\partial^{2} u_{0}^{c} }}{{\partial t^{2} }} + I_{1}^{c} \frac{{\partial^{2} \phi_{x}^{c} }}{{\partial t^{2} }} - I_{3}^{c} c_{1} \left( {\frac{{\partial^{2} \phi_{x}^{c} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{c} }}{{\partial t^{2} \partial x}}} \right), \hfill \\ \delta v_{0}^{c} :\frac{{\partial N^{c}_{yy} }}{\partial y} + \frac{{\partial N^{c}_{xy} }}{\partial x} = I_{0}^{c} \frac{{\partial^{2} v_{0}^{c} }}{{\partial t^{2} }} + I_{1}^{c} \frac{{\partial^{2} \phi_{y}^{c} }}{{\partial t^{2} }} - I_{3}^{c} c_{1} \left( {\frac{{\partial^{2} \phi_{y}^{c} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{c} }}{{\partial t^{2} \partial y}}} \right), \hfill \\ \delta w_{0}^{c} :c_{1} \frac{{\partial^{2} P^{c}_{xx} }}{{\partial x^{2} }} + c_{1} \frac{{\partial^{2} P^{c}_{yy} }}{{\partial y^{2} }} + 2c_{1} \frac{{\partial^{2} P^{c}_{xy} }}{\partial x\partial y} + \frac{{\partial Q^{c}_{xz} }}{\partial x} - 3c_{1} \frac{{\partial S^{c}_{xz} }}{\partial x} + \frac{{\partial Q^{c}_{yz} }}{\partial y} - 3c_{1} \frac{{\partial S^{c}_{yz} }}{\partial y} \hfill \\ + \frac{{N^{c}_{xx} }}{{R_{1} }} + \frac{{N^{c}_{yy} }}{{R_{2} }} = c_{1} I_{3}^{c} \frac{{\partial^{3} u_{0} }}{{\partial x\partial t^{2} }} + c_{1} I_{4}^{c} \frac{{\partial^{3} \phi_{x}^{c} }}{{\partial x\partial t^{2} }} - I_{6}^{c} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{x}^{c} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{4} w_{0}^{c} }}{{\partial t^{2} \partial x^{2} }}} \right) \hfill \\ + c_{1} I_{3}^{c} \frac{{\partial^{3} v_{y}^{c} }}{{\partial y\partial t^{2} }} + c_{1} I_{3}^{c} \frac{{\partial^{3} \phi_{y}^{c} }}{{\partial y\partial t^{2} }} - I_{6}^{c} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{y}^{c} }}{{\partial y\partial t^{2} }} + \frac{{\partial^{4} w_{0}^{c} }}{{\partial t^{2} \partial y^{2} }}} \right) + \left( {I_{0}^{c} \frac{{\partial^{2} w_{0}^{c} }}{{\partial t^{2} }}} \right), \hfill \\ \delta \phi_{x}^{c} :\frac{{\partial M^{c}_{xx} }}{\partial x} - c_{1} \frac{{\partial P^{c}_{xx} }}{\partial x} + \frac{{\partial M^{c}_{xy} }}{\partial y} - c_{1} \frac{{\partial P^{c}_{xy} }}{\partial y} - Q^{c}_{xz} + 3c_{1} S^{c}_{xz} = \hfill \\ + I_{1}^{c} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{2}^{c} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - I_{4}^{c} c_{1} \left( {\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}} \right) \hfill \\ - c_{1} I_{3}^{c} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - c_{1} I_{4}^{c} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + I_{6}^{c} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{x}^{c} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{c} }}{{\partial t^{2} \partial x}}} \right), \hfill \\ \delta \phi_{y}^{c} :\frac{{\partial M^{c}_{yy} }}{\partial y} - c_{1} \frac{{\partial P^{c}_{yy} }}{\partial y} + \frac{{\partial M^{c}_{xy} }}{\partial x} - c_{1} \frac{{\partial P^{c}_{xy} }}{\partial x} - Q^{c}_{yz} + 3c_{1} S^{c}_{yz} = \hfill \\ I_{1}^{c} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + I_{2}^{c} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - I_{4}^{c} c_{1} \left( {\frac{{\partial^{2} \phi_{y}^{c} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{c} }}{{\partial t^{2} \partial y}}} \right) \hfill \\ - c_{1} I_{3}^{c} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} - c_{1} I_{4}^{c} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + I_{6}^{c} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{y}^{c} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{c} }}{{\partial t^{2} \partial y}}} \right). \hfill \\ \end{gathered}$$
(26)

Also, the motion equations for the nanocomposite face sheets are as follows:

$$\begin{gathered} \delta u_{0}^{j} :\frac{{\partial N^{j}_{xx} }}{\partial x} + \frac{{\partial N^{j}_{xy} }}{\partial y} = I_{0}^{j} \frac{{\partial^{2} u_{0}^{j} }}{{\partial t^{2} }} + I_{1}^{j} \frac{{\partial^{2} \phi_{x}^{j} }}{{\partial t^{2} }} - I_{3}^{j} c_{1} \left( {\frac{{\partial^{2} \phi_{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right), \hfill \\ \delta v_{0}^{j} :\frac{{\partial N^{j}_{yy} }}{\partial y} + \frac{{\partial N^{j}_{xy} }}{\partial x} = I_{0}^{j} \frac{{\partial^{2} v_{0}^{j} }}{{\partial t^{2} }} + I_{1}^{j} \frac{{\partial^{2} \phi_{y}^{j} }}{{\partial t^{2} }} - I_{3}^{j} c_{1} \left( {\frac{{\partial^{2} \phi_{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right), \hfill \\ \delta w_{0}^{j} :c_{1} \frac{{\partial^{2} P^{j}_{xx} }}{{\partial x^{2} }} + c_{1} \frac{{\partial^{2} P^{j}_{yy} }}{{\partial y^{2} }} + 2c_{1} \frac{{\partial^{2} P^{j}_{xy} }}{\partial x\partial y} + \frac{{\partial Q^{j}_{xz} }}{\partial x} - 3c_{1} \frac{{\partial S^{j}_{xz} }}{\partial x} + \frac{{\partial Q^{j}_{yz} }}{\partial y} - 3c_{1} \frac{{\partial S^{j}_{yz} }}{\partial y} \hfill \\ + \frac{{N^{j}_{xx} }}{{R_{1} }} + \frac{{N^{j}_{yy} }}{{R_{2} }} = c_{1} I_{3}^{j} \frac{{\partial^{3} u_{0}^{j} }}{{\partial x\partial t^{2} }} + c_{1} I_{4}^{j} \frac{{\partial^{3} \phi_{x}^{j} }}{{\partial x\partial t^{2} }} - I_{6}^{j} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{x}^{j} }}{{\partial x\partial t^{2} }} + \frac{{\partial^{4} w_{0}^{j} }}{{\partial t^{2} \partial x^{2} }}} \right) \hfill \\ + c_{1} I_{3}^{j} \frac{{\partial^{3} v_{0}^{j} }}{{\partial y\partial t^{2} }} + c_{1} I_{4}^{j} \frac{{\partial^{3} \phi_{y}^{j} }}{{\partial y\partial t^{2} }} - I_{6}^{j} c_{1}^{2} \left( {\frac{{\partial^{3} \phi_{y}^{j} }}{{\partial y\partial t^{2} }} + \frac{{\partial^{4} w_{0}^{j} }}{{\partial t^{2} \partial y^{2} }}} \right) + \left( {I_{0}^{j} \frac{{\partial^{2} w_{0}^{j} }}{{\partial t^{2} }}} \right), \hfill \\ \delta \phi_{x}^{j} :\frac{{\partial M^{j}_{xx} }}{\partial x} - c_{1} \frac{{\partial P^{j}_{xx} }}{\partial x} + \frac{{\partial M^{j}_{xy} }}{\partial y} - c_{1} \frac{{\partial P^{j}_{xy} }}{\partial y} - Q^{j}_{xz} + 3c_{1} S^{j}_{xz} = \hfill \\ + I_{1}^{j} \frac{{\partial^{2} u_{0}^{j} }}{{\partial t^{2} }} + I_{2}^{j} \frac{{\partial^{2} \phi_{x}^{j} }}{{\partial t^{2} }} - I_{4}^{j} c_{1} \left( {\frac{{\partial^{2} \phi_{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right) \hfill \\ - c_{1} I_{3}^{j} \frac{{\partial^{2} u_{0}^{j} }}{{\partial t^{2} }} - c_{1} I_{4}^{j} \frac{{\partial^{2} \phi_{x}^{j} }}{{\partial t^{2} }} + I_{6}^{j} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{x}^{j} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{j} }}{{\partial t^{2} \partial x}}} \right), \hfill \\ \delta \phi_{y}^{j} :\frac{{\partial M^{j}_{yy} }}{\partial y} - c_{1} \frac{{\partial P^{j}_{yy} }}{\partial y} + \frac{{\partial M^{j}_{xy} }}{\partial x} - c_{1} \frac{{\partial P^{j}_{xy} }}{\partial x} - Q^{j}_{yz} + 3c_{1} S^{j}_{yz} = \hfill \\ I_{1}^{j} \frac{{\partial^{2} v_{0}^{j} }}{{\partial t^{2} }} + I_{2}^{j} \frac{{\partial^{2} \phi_{y}^{j} }}{{\partial t^{2} }} - I_{4}^{j} c_{1} \left( {\frac{{\partial^{2} \phi_{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right) \hfill \\ - c_{1} I_{3} \frac{{\partial^{2} v_{0}^{j} }}{{\partial t^{2} }} - c_{1} I_{4} \frac{{\partial^{2} \phi_{y}^{j} }}{{\partial t^{2} }} + I_{6} c_{1}^{2} \left( {\frac{{\partial^{2} \phi_{y}^{j} }}{{\partial t^{2} }} + \frac{{\partial^{3} w_{0}^{j} }}{{\partial t^{2} \partial y}}} \right). \hfill \\ \end{gathered}$$
(27)

It is worth mentioning that, according to compatibility equations (Eq. 22), the numbers of unknown variables are decreased from 15 to 9. Therefore, the total number of unknowns in the core and the face sheet is reduced to 9.

2.6 Solution procedure

Displacement fields for investigation the wave propagation analysis of the structure defined as follow [24,25,26, 109]:

$$\left\{ \begin{gathered} u_{0}^{c} \hfill \\ v_{0}^{c} \hfill \\ w_{0}^{c} \hfill \\ \phi_{x}^{c} \hfill \\ \phi_{y}^{c} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} U_{0}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ V_{0}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ W_{0}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi_{x}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi_{y}^{c} \exp (sx + n\theta - \omega t)i \hfill \\ \end{gathered} \right\},\,\,\left\{ \begin{gathered} u_{0}^{j} \hfill \\ v_{0}^{j} \hfill \\ w_{0}^{j} \hfill \\ \phi_{x}^{j} \hfill \\ \phi_{y}^{j} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} U_{0}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ V_{0}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ W_{0}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi_{x}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ \Phi_{y}^{j} \exp (sx + n\theta - \omega t)i \hfill \\ \end{gathered} \right\}.$$
(28)

where s and n are wave number along with the directions of x and y, respectively, also \(\omega\) is called frequency. With replacing Eq. (28) into governing equations achieve to [133,134,135,136,137]:

$$(\left[ K \right] - \omega^{2} [M])\left\{ d \right\} = \left\{ 0 \right\},$$
(29)

where

$$\left\{ d \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{0} } & {v_{0} } \\ \end{array} } & {w_{0} } & {\psi_{{x_{0} }} } & {\psi_{{\theta_{0} }} } \\ \end{array} } \right\}.$$
(30)

Also, the phase velocity of wave dispersion can be calculated by Eq. (29):

$$c = \frac{\omega }{s}.$$
(31)

In the Eq. (31), c and s are called phase velocity and wavenumber of a laminated nanocomposite cylindrical shell. These parameters are propagation speeds of the particles in a sandwich panel.

2.7 Validation

The obtained results for the perfect panel are compared with the results of Refs.[138, 139]. These results are listed in Table 1 and 2. From these tables, it can be seen that the present results have a good agreement with the obtained results in the literature. Note that, the dimensionless form of the frequency can be calculated using the below relation:

$$\Omega = \omega \frac{{a^{2} }}{h}\sqrt {\frac{{\rho_{M} }}{{E_{M} }}} .$$
(32)
Table 1 Comparison of the first dimensionless natural frequency of simply supported CNT reinforced composite square perfect panel (a/h = 10)
Full size table
Table 2 Non-dimensional fundamental frequency of SSSS cross-ply laminated square plate with G12/E2 = 0.6, G13/E2 = 0.6, G23/E2 = 0.5, a = b = 1, \(\upsilon\)=0.25
Full size table

For more verification, the fundamental frequencies of the FML moderately thick plates resting on partial elastic foundations are calculated by the free vibration Eq. (21) as an eigenvalue problem. In Table 2, non-dimensional fundamental frequencies of the symmetrically laminated cross-ply plate \(({0}^{^\circ },{90}^{^\circ },9{0}^{^\circ },{0}^{^\circ })\) are shown as compared for different E1/E2.

3 Results

In this part, a comprehensive investigation is carried out to demonstrate the effects of various parameters on the phase velocity response of a multi-hybrid nanocomposite doubly curved panel. The geometrical and material characteristics of constituent materials would be presented in Table 3.

Table 3 Material properties of the multiscale hybrid nanocomposite annular plate [122]
Full size table

With pay attention to Fig. 1 can find an investigation about the impacts of the various CNTs weight fraction (\({W}_{\rm{CNT}}\)) and core to total thickness ratio (\({h}_{c}/h\)) of the FML panel on the wave responses of the doubly carved panel.

As stated by Fig. 2, the impact of \({W}_{\rm{CNT}}\) on the phase velocity is obvious and considerable if the \({h}_{c}/h\) is less than 0.8. in another word for \({0\le h}_{c}/h\le 0.8\), the phase velocity can improve due to increasing the CNTs' weight fraction and this enhancement will be weakened by increasing the core thickness of the FML panel. Also, when the thickness of the core is small, the phase velocity falling down owning to increasing the \({h}_{c}/h\), but if we consider the thicker core, we can find an indirect relation between \({h}_{c}/h\) and phase velocity. Accordingly, the sensitivity of the phase velocity of the FML panel to the \({W}_{\rm{CNT}}\) can decrease when we consider the core of the panel thicker.

Fig. 2
figure 2

Phase velocity versus \({h}_{c}/h\) with having attention to the impact of \({W}_{\rm{CNT}}\)

Full size image

From Fig. 3, we can find research about the effects of the various FG face sheet patterns and core to total thickness ratio (\({h}_{c}/h\)) of the FML panel on the wave responses of the MHC reinforced doubly carved panel.

Fig. 3
figure 3

Phase velocity versus \({h}_{c}/h\) with having attention to the impact of different FG face sheet patterns

Full size image

The most obvious result in Fig. 3 is that for having an impact from FG face sheet patterns on the phase velocity we should consider the \({h}_{c}/h\) less than 0.2. As another explanation, considering different FG face sheet patterns will be ineffective at the higher value of the \({h}_{c}/h\). As a practical result, according to Fig. 3, it can be stated that the sensitivity of the phase velocity of the FML panel to the different FG face sheet patterns can decrease when the thickness of the core of the FML panel increases. Generally, for each \({h}_{c}/h\), when the face sheet is made by Pattern 1 and Pattern 3, we can see the lowest and highest phase velocity in the sandwich panel.

With the aid of Fig. 4, presented the effects of the wavenumber and small radius to total thickness ratio (\({R}_{1}/h\)) of the FML panel on the wave responses of the FML reinforced doubly carved panel.

Fig. 4
figure 4

Phase velocity versus wavenumber by having attention to the impact of \({R}_{1}/h\)

Full size image

The most evident outcome in Fig. 4 is that boosting the wave number can be an encouragement for improving the phase velocity of the FML panel and this impact from wavenumber on the wave propagation of the sandwich structure will change to be ineffective when the wavenumber is more than 11e4. As a practical result, if the small radius of the FML doubly curved panel is rising, the phase velocity of the system can increase and this impact will be ineffectual at the higher value of the wavenumber.

With attention to Fig. 5 can see an investigation for analysis the impacts of the various CNTs weight fraction (\({W}_{\rm{CNT}}\)) and wavenumber on the wave responses of the FML doubly carved panel.

Fig. 5
figure 5

Phase velocity versus wavenumber by having attention to the impact of \({W}_{\rm{CNT}}\)

Full size image

The apparent and the most important result in Fig. 5 is that if there is more distribution of CNTs in the matrix of the face sheet of the FML panel, we will find that the phase velocity or wave response of the system can improve and without a doubt, this issue is considerable at the higher wavenumber.

Presented diagrams in Fig. 6 are drawn to have an explanation about the effects of the wavenumber and different FG face sheet patterns of the FML panel on the wave responses of the FML reinforced doubly carved panel.

Fig. 6
figure 6

Phase velocity versus wavenumber by having attention to the impact of different FG face sheet patterns

Full size image

The bolded result in Fig. 6 is that boosting the wave number can be an encouragement for improving the phase velocity of the FML panel and this impact from wavenumber on the wave propagation of the sandwich structure will change to be ineffective in the higher value of the wavenumber. As a practical result and at the lower wavenumber, when the face sheet is made by Pattern 1 and Pattern 3, we can see the lowest and highest phase velocity in the sandwich panel. Also, the wave propagation response of the FML panel with Pattern 2, 3, and 4 is similar when the wavenumber is great enough.

With the aid of Fig. 7, the effects of the fibers angel and different FG face sheet patterns on the wave responses of the FML reinforced doubly carved panel are presented.

Fig. 7
figure 7

Phase velocity versus fibers angel by having attention to the impact of different FG face sheet patterns

Full size image

The most general result in Fig. 7 is that for each FG face sheet patterns when the fibers angel is less than \(\pi /2\), the phase velocity is decreasing and this trend will be revers for the fibers angel more than \(\pi /2\). As the most interesting result from Fig. 7 is that when the fiber angel is \(0.3\le \theta /\pi \le 0.7\), employing different FG patterns for making the FML cannot provide any change on the phase velocity of the structure. As another explanation, if the fibers are distributed in the matrix vertically, changing the FG patterns cannot play any roles on the wave response of the FML panel and as the fibers become horizontal, the effect of the FG patterns on the phase velocity becomes more dramatic. Reported data in Fig. 8 are shown to have a deep presentation about the effects of the wavenumber, fibers angel of the FML panel, and small radius to total thickness ratio (\({R}_{1}/h\)) of the FML panel on the wave responses of the doubly carved panel.

Fig. 8
figure 8

Phase velocity versus fibers angel for two value of wavenumber

Full size image

If we have excellent attention to Fig. 8, it could be seen that within a certain range of the core to total thickness ratio, there is no effect from the small radius to total thickness ratio of the FML panel on the phase velocity, and this range will be wider if the wave number rises. Also, for the lower wavenumber, when the fiber angel is 0 and 1 radians, the pick of the phase velocity of the system will happen but as the wave number increases, the maximum value of the phase velocity will be seen at 0.25 and 0.75 radians.

With the aid of Fig. 9, the effects of the fibers angel and weight fraction of CNTs (\({W}_{\rm{CNT}}\)) on the wave responses of the FML doubly carved panel are presented.

Fig. 9
figure 9

Phase velocity versus \(\theta /\pi\) for different value of \({W}_{\rm{CNT}}\)

Full size image

The most interesting result from Fig. 9 is that when the fiber angel is \(0.4\le \theta /\pi \le 0.6\), increasing \({W}_{\rm{CNT}}\) cannot provide any change on the phase velocity of the structure. As another explanation, if the fibers are distributed in the matrix vertically, changing the \({W}_{\rm{CNT}}\) cannot play any roles on the wave response of the FML panel and as the fibers become horizontal, the effect of \({W}_{\rm{CNT}}\) on the phase velocity becomes more dramatic. With pay attention to Fig. 10, we can see a study about the effects of the fibers angel and core to total thickness ratio (\({h}_{c}/h\)) of the FML panel on the wave responses of the doubly carved panel.

Fig. 10
figure 10

Phase velocity versus \(\theta /\pi\) for different value of \({h}_{c}/h\)

Full size image

as stated by Fig. 10 when the fiber angel is 0 \(\le \theta /\pi \le\) 0.42 and 0.58 \(\le \theta /\pi \le\) 1, the phase velocity will be improved by having each decline in the core to total thickness ratio but this relation between fiber angel and \({h}_{c}/h\) change to direct as the fibers angel is 0.42 \(<\theta /\pi <\) 0.58. The reported 3D diagram in Figs. 11 and 12 are shown to have a comparative study about the effects of the wavenumber, core to total thickness ratio (\({h}_{c}/h\)) of the FML panel, and fiber angle on the wave responses of the doubly carved panel.

Fig. 11
figure 11

Phase velocity of the FML panel with respects to the impact of wavenumber and fibers angel

Full size image
Fig. 12
figure 12

Phase velocity of the FML panel by concerning the impacts of wavenumber and core to total thickness ratio

Full size image

The most principal and evident result in Figs. 11 and 12 are that as the wave number increases, the changes in phase velocity of the MHC reinforced sandwich panel which is caused by increasing the fibers angel and core to total thickness ratio become much more dramatic. In the simpler word, the effects of fibers angel and core to total thickness ratio on the phase velocity of the FML panel are highly dependent on the wavenumber.

4 Conclusion

Wave propagation characteristics of a sandwich structure with the soft core and multi-hybrid nanocomposite face sheets is investigated. The stresses and strains are obtained using HSDT. Rule of the mixture and modified Halpin–Tsai model are engaged to provide the effective material constant of the multi-hybrid nanocomposite face sheets of the sandwich panel. Via the compatibility rule, the bonding between the smart layer and a soft core is modeled. Finally, the most bolded results of this paper are as follow:

  • it is true that when the thickness of the core is small, the phase velocity falling down owning to increasing the \({h}_{c}/h\), but if we consider the thicker core, we can find an indirect relation between \({h}_{c}/h\) and phase velocity;

  • the sensitivity of the phase velocity of the FML panel to the \({W}_{\rm{CNT}}\) and different FG face sheet patterns can decrease when we consider the core of the panel thicker;

  • boosting the wave number can be an encouragement for improving the phase velocity of the FML panel and this impact from wavenumber on the wave propagation of the sandwich structure will change to be ineffective when the wavenumber is more than 11e4;

  • as a practical result, if the small radius of the FML doubly curved panel is rising, the phase velocity of the system can increase and this impact will be ineffectual at the higher value of the wavenumber;

  • if the fibers are distributed in the matrix vertically, changing the FG patterns cannot play any role on the wave response of the FML panel and as the fibers become horizontal, the effect of the FG patterns on the phase velocity becomes more dramatic;

  • when the fiber angel is 0 and 1 radians, the pick of the phase velocity of the system will happen but as the wave number increases, the maximum value of the phase velocity will be seen at 0.25 and 0.75 radians;

  • when the fiber angel is 0 \(\le \theta /\pi \le\) 0.42 and 0.58 \(\le \theta /\pi \le\) 1, the phase velocity will be improved by having each decline in the core to total thickness ratio but this relation between fiber angel and \({h}_{c}/h\) changes to direct as the fiber angel is 0.42 \(<\theta /\pi <\) 0.58;

  • the effects of fibers angel and core to total thickness ratio on the phase velocity of the FML panel is hardly dependent on the wavenumber.