1 Introduction

Owing to the recent advancement in mechanical and material sciences [1,2,3], FG and laminated composites have attracted in plenty of applications [4,5,6,7,8,9,10,11,12,13,14]. Many researches show that [15,16,17,18,19] the laminated composite structures have a better dynamic response in comparison with the isotropic and other materials. Safarpour et al. [20] modeled a laminated nanoshell in a thermal environment and investigated the wave dispersion of the structure. They analyzed the size effects with the aid of NSGT. They found that it is not accepted which by increasing the number of layers of the laminated structure the dynamic stability improves. They reported that the number of layers has an optimum number. Zeighampour et al. [21] presented a mathematical modeling for investigation of wave dispersion of the laminated nanoshell MSGT and thin theory. They claimed that MSGT encounter us with accurate result in comparison with classical theory. Sahmani et al. [22] presented the dynamic and static response of the laminated beams which are reinforced with GPLs. They modeled the structure with the aid of NSGT. They found that initial load decreases the frequency of the structure. Nonlocal effects on the dynamic and static responses of the micro-/nanostructure are presented in Refs [23,24,25,26,27,28,29].

In the scope of dynamic behavior of the piezoelectric cylindrical shell [30,31,32], Shojaeefard et al. [33] dealt with frequency analysis for different boundary conditions on a rotary cylindrical piezoelectric nanoshell surrounded by an elastic foundation. Also, they used GDQ method for solving the problems. Dehkordi et al. [34] studied vibrational behavior of a piezoelectric conic nanotube using moderately thin model and a size-dependent theory. They investigated the effects of flex electric on the frequency of the nanosmart tube. Arefi [35] employed nonlocal elasticity theory and FSDT for investigation of bending behavior of a doubly curved piezoelectric nanoshell. The nanostructure is exposed to transverse loads, voltage and surrounded with Winkler–Pasternak foundation. They in this work examined the effects of nonlocal parameter, applied voltage, viscoelastic parameters on the electromechanic behaviors of the piezonanostructure. Razavi et al. [36] modeled a piezoelectric nanoshell which is composed with functionally graded (FG) and piezoelectric materials. They presented influences of dimensional parameters on the frequency behavior of the piezoelectric nanostructures. Ninh and Bich [37] demonstrated the nonlinear dynamic behavior of the electrically FG nanocylindrical shells in the thermal conditions. A FG shell reinforced with carbon nanotube is modeled in a condition that outer and inner surfaces were surrounded by piezolayers. Fangand et al. [38] engaged with thick theory and electromechanic theory for investigation of nonlinear frequency of a nanoshell surrounded by a piezolayer. They studied the amplitude frequency curves of the nanoshell. Eftekhari et al. [39] investigated vibrational property of a FG cylindrical shell reinforced with carbon nanotube and the structure surrounded by PIAC in an orthotropic elastic medium and thermal site. They in this work employed an analytical method and DQ method in other to figure out the equations, and they presented influences of electromagnetic field and various patterns of CNT ratio on dynamic behaviors of the system. Vinyas [40] encountered with FE modeling for frequency analysis of a plate which this structure has an MEE property. He considered moderately thick theory for modeling the problem. He emphasized that CNT pattern and volume of the reinforcement have a significant impact on the free vibration of the structure. Zhu et al. [41] did a study on the free vibration of a PIAC nanocylindrical shell, and by employing the perturbation method, they solved the governing equations. They investigated the impact of surface energy on the dynamic behaviors of the nanosmart structure. Singh et al. [42] with the aid of a numerically method modeled curved panel. The structure covered with the PIAC. Their results showed the effect of piezolayer on the frequency of the nanostructure. Fan et al. [43] conducted research into free vibration of a conical nanostructure. Inner and outer layers of a conical CNTRC are surrounded by piezolayers. In the field of critical temperature of the cylindrical shell structures, Refs [20, 44] presented thermal static and dynamic behaviors of FG shells beneath some geometrical imperfection and various load conditions. Their results demonstrate that the behavior of the cylindrical structure beneath the nonlinear change of temperature is more stable in comparison with a linear change in temperature through thickness. Vibration, buckling, wave propagation and bending responses of the nanocomposite-reinforced structures are investigated in Refs [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60].

Also, Wang et al. [61] carried out research into critical thermal loading for a shell based on a theoretical method. The main conclusion of the paper reported a theoretical method for finding the critical temperature of that structure. Safarpour et al. [62] presented an exact numerical method for investigation buckling, free and forced vibration of a FG nanoshell in a thermal site. Some theories with consideration thickness stretching effect are employed in Refs [63,64,65,66,67,68,69,70] for investigation vibrational behavior of the composite structures. In the field of stability analysis of the structures, Safarpour et al. [30, 33, 71,72,73,74,75,76,77,78,79,80,81,82] presented buckling and vibrational analysis of the structures with various geometrical parameters.

For the first time, the presented study investigates the thermodynamic analysis of a laminated composite cylindrical nanoshell based on NSGT considering the exact values of nonlocal constants and material length scale parameters. The thermodynamic equations of the laminated cylindrical nanoshell are based on FSDT, and GDQEM is implemented to solve these equations and obtain natural frequency and critical temperature of the current model. Finally, using mentioned continuum mechanics theory, the investigation has been made into the influence of the temperature difference and the different types of the laminated composites on the critical temperature difference and dynamic stability of the laminated composite nanostructure.

2 Theory and formulation

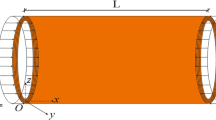
In Fig. 1, a laminated composite nanoshell with consideration of thermal effects is sketched, where R is the radius of tube’s middle surface and h is the thickness of the nanoshell. Also, \(\bar{\theta }\) is the ply angle of each layer. The material of the nanostructure is considered as a laminated composite.

Fig. 1
figure 1

The geometry of a laminated composite nanoshell

Full size image

2.1 NSG model

The fundamental equation can be expressed as follows due to the NSG model [83]:

$$(1 - \mu^{2} \nabla^{2} )t_{ij} = C_{ijck} (1 - l^{2} \nabla^{2} )\varepsilon_{ck}$$
(1)

where \(\nabla^{2} = \partial^{2} /\partial x^{2} + \partial^{2} /R^{2} \partial \theta^{2}\); \(t_{ij}\), \(C_{ijck}\) and \(\varepsilon_{ck}\), respectively, are the NSG stress, elasticity tensors and strain. The tensor of NSG stress can be defined as follows [83]:

$$t_{ij} = \sigma_{ij} - \nabla \sigma_{ij}^{\left( 1 \right)}$$
(2)

where \(\sigma_{ij}\) and \(\sigma_{ij}^{\left( 1 \right)}\) presented the components of basic and nanosize stresses, respectively. The l and µ are constant values standing for the higher-order strain gradient stress and noninvariant influence. Recent experimental researches also demonstrated the calibrated values of the size-dependent factors. The strain tensor could be written as:

$$\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)$$
(3)

where \(u_{i}\) stands for the elements of the displacement vector. Due to Eq (2), the relation between stress and strain of the mentioned structure would be presented as [84]:

$$\begin{aligned} \left[ \begin{aligned} t_{xx} \hfill \\ t_{\theta \theta } \hfill \\ t_{x\theta } \hfill \\ \end{aligned} \right] & = \frac{{(1 - l^{2} \nabla^{2} )}}{{(1 - \mu^{2} \nabla^{2} )}}\left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right]^{(L)} \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} - \alpha \Delta T} \\ {\varepsilon_{\theta \theta } - \alpha \Delta T} \\ {\varepsilon_{x\theta } } \\ \end{array} } \right], \\ \left[ \begin{aligned} t_{\theta z} \hfill \\ t_{xz} \hfill \\ \end{aligned} \right] & = \frac{{(1 - l^{2} \nabla^{2} )}}{{(1 - \mu^{2} \nabla^{2} )}}\left[ {\begin{array}{*{20}c} \begin{aligned} C_{44} \hfill \\ 0 \hfill \\ \end{aligned} & \begin{aligned} 0 \hfill \\ C_{55} \hfill \\ \end{aligned} \\ \end{array} } \right]^{(L)} \left[ \begin{aligned} \varepsilon_{\theta z} \hfill \\ \varepsilon_{xz} \hfill \\ \end{aligned} \right] \\ \end{aligned}$$
(4)

Equation (4) defines temperature changes as well as thermal expansion as \(\Delta T\) and \(\alpha\), respectively. In the case of laminated composites, the elements of the tensor of elasticity are defined as the orthotropic material’s lessened elastic constants of the Lth layer, and the next equations express the mentioned relations [84]:

$$\begin{aligned} C_{11} & = Q_{11} \cos^{4} \bar{\theta } + 2(Q_{12} + 2Q_{44} )\sin^{2} \bar{\theta }\cos^{2} \bar{\theta } \\ & \quad + Q_{22} \sin^{4} \bar{\theta } \\ C_{12} & = (Q_{11} + Q_{22} - 4Q_{44} )\sin^{2} \bar{\theta }\cos^{2} \bar{\theta } \\ & \quad + Q_{12} (\sin^{4} \bar{\theta } + \cos^{4} \bar{\theta }) \\ C_{22} & = Q_{11} \sin^{4} \bar{\theta } + 2(Q_{12} + 2Q_{44} )\sin^{2} \bar{\theta }\cos^{2} \bar{\theta } \\ & \quad + Q_{22} \cos^{4} \bar{\theta } \\ C_{44} & = Q_{44} \cos^{4} \bar{\theta } + Q_{55} \sin^{4} \bar{\theta } \\ C_{55} & = Q_{55} \cos^{4} \bar{\theta } + Q_{66} \sin^{4} \bar{\theta } \\ C_{66} & = (Q_{11} + Q_{22} - 2Q_{12} )\sin^{2} \bar{\theta }\cos^{2} \bar{\theta } \\ & \quad + Q_{66} (\cos^{2} \bar{\theta } - \sin^{2} \bar{\theta })^{2} \\ \end{aligned}$$
(5)

The aforementioned equations express the relation between stress and strain components for the Lth orthotropic lamina referred to the lamina’s principal material axes x, \(\theta\), and z. In Eq (5), \(Q_{ij }\) components are expressed by the following equations:

$$\begin{aligned} Q_{11} & = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{12} = \frac{{\nu_{12} E_{2} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{22} = \frac{{E_{2} }}{{1 - \nu_{12} \nu_{21} }} \\ Q_{66} & = G_{12} ,\quad Q_{44} = G_{23} ,\quad Q_{55} = G_{13} \\ \end{aligned}$$
(6)

2.2 Displacement field

FSDT enables us to define the displacement field of a laminated nanoshell in the following equations [16, 47, 50, 53, 85,86,87,88,89,90,91]:

$$\begin{aligned} U(x,\theta ,z,t) & = u(x,\theta ,z) + z\psi_{x} (x,\theta ,t) \\ V(x,\theta ,z,t) & = v(x,\theta ,z) + z\psi_{\theta } (x,\theta ,t) \\ W(x,\theta ,z,t) & = w(x,\theta ,t) \\ \end{aligned}$$
(7)

Also, \(u(x,\theta ,t)\), \(v(x,\theta ,t)\) and \(w(x,\theta ,t)\), respectively, demonstrate the displacements of the neutral surface in x and \(\theta\) axes. \(\psi_{x} (x,\theta ,t)\) and \(\psi_{\theta } (x,\theta ,t)\) illustrate the cross section rotations around \(\theta\) and x directions. By inserting Eq (7) into Eq (3), the strain tensor’s components can be obtained by the following equations:

$$\begin{aligned} \varepsilon_{xx} & = \frac{\partial u}{\partial x} + z\frac{{\partial \psi_{x} }}{\partial x},\,\varepsilon_{\theta \theta } = \frac{1}{R}\frac{\partial v}{\partial \theta } + \frac{z}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta } + \frac{w}{R} \\ \varepsilon_{xz} & = \frac{1}{2}\left( {\psi_{x} + \frac{\partial w}{\partial x}} \right),\,\varepsilon_{\theta z} = \frac{1}{2}\left( {\psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R}} \right) \\ \varepsilon_{x\theta } & = \frac{1}{2}\left( {\frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x}} \right) + \frac{z}{2}\left( {\frac{1}{R}\frac{{\partial \psi_{x} }}{\partial \theta } + \frac{{\partial \psi_{\theta } }}{\partial x}} \right) \\ \end{aligned}$$
(8)

2.3 Governing equations and boundary conditions

The motion equations along with the possible BCs related to the mentioned structure would be extracted applying energy methods (Hamilton principle) based on FSDT and the NSG model by the following equation:

$$\int_{{t_{1} }}^{{t_{2} }} {(\delta K - \delta \varPi_{\text{s}} + \delta W)} {\text{ d}}t = 0$$
(9)

where K illustrates the kinetic energy, \(\varPi_{s}\) defines strain energy and the work done by forces imposed can be shown as \(\varPi_{\text{w}}\). For a usual nanoshell exposed to high level of temperature situation, it is suggested that the temperature distributes through its thickness.

Based on NSG model, Eq (10) defines the strain energy [83]:

$$\delta K = \int\limits_{Z} {\iint\limits_{A} {\rho \left\{ \begin{array}{l} \left( {\frac{\partial u}{\partial t} + z\frac{{\partial \psi_{x} }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta u + z\frac{\partial }{\partial t}\delta \psi_{x} } \right) \hfill \\ \quad+ \left( {\frac{\partial v}{\partial t} + z\frac{{\partial \psi_{\theta } }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta v + z\frac{\partial }{\partial t}\delta \psi_{\theta } } \right) \hfill \\ \quad+ \left( {\frac{\partial w}{\partial t}} \right)\frac{\partial }{\partial t}\delta w \hfill \\ \end{array} \right\}}} {\text{d}}V$$
(10)

And also, the strain energy can be defined as the following equation due to the NSG model [83]:

$$\begin{aligned} \varPi_{s} & = \frac{1}{2}\iiint\limits_{V} {\left( {\sigma_{ij} \varepsilon_{ij} + \sigma_{ij}^{\left( 1 \right)} \nabla \varepsilon_{ij} } \right){\text{dV}}} \, \\ & \quad \Rightarrow \, \delta \varPi_{s} { = }\iiint\limits_{S} {t_{ij} \delta \varepsilon_{ij} {\text{dV}}} + \iint\limits_{A} {\sigma_{ij}^{\left( 1 \right)} }\delta \varepsilon_{ij} \left| {_{0}^{L} } \right.{\text{d}}S \\ \end{aligned}$$
(11)

For a typical isotropic cylindrical shell which is in the high-temperature environment, it is assumed that the temperature can be distributed across its thickness. Hence, the work done depended on the temperature change can be obtained as:

$$\delta W = \iint\limits_{A} {\left[ {\left( {N_{2}^{T} } \right)\left( {\frac{{\delta w_{0} }}{\partial x}} \right)\frac{{\partial w_{0} }}{\partial x} + \left( {N_{1}^{T} } \right)\left( {\frac{{\delta v_{0} }}{\partial x}} \right)\frac{{\partial v_{0} }}{\partial x}} \right]}R{\text{d}}x\,{\text{d}}\theta$$
(12)

where \(N_{1}^{T}\) and \(N_{2}^{T}\) are the thermal resultants which can be obtained as follows:

$$\begin{aligned} N_{1}^{T} & = \int_{{ - h_{c} /2}}^{{h_{c} /2}} {(\bar{Q}_{11} + \bar{Q}_{12} )\,\alpha (T - T_{0} ){\text{d}}z_{c} ,} \\ N_{2}^{T} & = \int_{{ - h_{c} /2}}^{{h_{c} /2}} {(\bar{Q}_{21} + \bar{Q}_{22} )\,\alpha (T - T_{0} ){\text{d}}z_{c} .} \\ \end{aligned}$$
(13)

It is assumed that the temperature varies linearly along the thickness from \(T_{m}\) at the outer surface to \(T_{c}\) at the inner surface. Governing motion equations for a nanoshell due to the FSDT as well as NSG model are presented inserting Eqs. (10), (12), and (13) into Eq (9) and integrating as follows:

$$\begin{aligned} & \delta u: \, A_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + l^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }}} \right) + B_{11} \left( {\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }}} \right) + B_{12} \frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } \\ & \quad A_{12} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } + \frac{1}{R}\frac{\partial w}{\partial x} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right) - N_{h} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } - \frac{1}{{R^{2} }}\frac{{\partial^{2} u}}{{\partial \theta^{2} }}} \right) \\ & \quad + \frac{{A_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }}} \right) + B_{12} \left( { - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) \\ & \quad + \frac{{B_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) = (1 - \mu^{2} \nabla^{2} )\left( {I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right) \\ \end{aligned}$$
(14)
$$\begin{aligned} & \delta v: \, \frac{{A_{12} }}{R}\left( {\frac{{\partial^{2} u}}{\partial x\partial \theta } + l^{2} \frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }}} \right) + \frac{{B_{12} }}{R}\left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }}} \right) - (1 - \nabla^{2} l^{2} )N_{1}^{T} \frac{{\partial^{2} v}}{{\partial x^{2} }} \\ & \quad \frac{{A_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} v}}{{\partial \theta^{2} }} + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }}} \right) - A_{66} \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }} \\ & \quad + \frac{{B_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} + \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial \theta^{4} }}} \right) + A_{66} \left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } + \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }}} \right) \\ & \quad + B_{66} \left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }}} \right) \\ & \quad + \frac{{K_{s} A_{44} }}{R}\left( {\psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R} - l^{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) = \left( {1 - \mu^{2} \nabla^{2} } \right)\left( {I_{0} \left[ {\frac{{\partial^{2} v}}{{\partial t^{2} }}\,\,} \right] + I_{1} \left[ {\frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }}} \right]} \right) \\ \end{aligned}$$
(15)
$$\begin{aligned} & \delta w: \, \frac{{A_{12} }}{R}\left(\frac{\partial u}{\partial x} + l^{2} \frac{{\partial^{3} u}}{{\partial x^{3} }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} u}}{{\partial x\partial \theta^{2} }}\right) + \frac{{B_{12} }}{R}\left( {\frac{{\partial \psi_{x} }}{\partial x} + l^{2} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial \theta^{2} }}} \right) \\ & \quad - (1 - \nabla^{2} l^{2} )N_{2}^{T} \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{A_{22} }}{R}\left( { - \frac{1}{R}\frac{\partial v}{\partial \theta } - \frac{w}{R} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} v}}{{\partial \theta^{3} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) \\ & \quad + \frac{{B_{22} }}{R}\left( { - \frac{1}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta } + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{\theta } }}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} \psi_{\theta } }}{{\partial \theta^{3} }}} \right) \\ & \quad + K_{s} A_{55} \left( {\frac{{\partial \psi_{x} }}{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }} - l^{2} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} - l^{2} \frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }}} \right) \\ & \quad + \frac{{K_{s} A_{44} }}{R}\left( {\frac{{\partial \psi_{\theta } }}{\partial \theta } - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{\partial v}{\partial \theta } - l^{2} \frac{{\partial^{3} \psi_{\theta } }}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }} + \frac{{l^{2} }}{R}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{\theta } }}{{\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} w}}{{\partial \theta^{4} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} v}}{{\partial \theta^{3} }}} \right) = \left( {1 - \mu^{2} \nabla^{2} } \right)\left( {I_{0} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }}} \right)} \right) \\ \end{aligned}$$
(16)
$$\begin{aligned} & \delta \psi_{x} : \, B_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} - l^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }}} \right) + D_{11} \left( {\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} - l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }}} \right) \\ & \quad + B_{12} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } + \frac{1}{R}\frac{\partial w}{\partial x} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right) + D_{12} \left( { - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }}} \right) \\ & \quad + D_{12} \left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) + \frac{{B_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }}} \right) \\ & \quad + \frac{{D_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) \\ & \quad - K_{s} A_{55} \left( {\psi_{x} + \frac{\partial w}{\partial x} - l^{2} \frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} - l^{2} \frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right) = (1 - \mu^{2} \nabla^{2} )\left( {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right) \\ \end{aligned}$$
(17)
$$\begin{aligned} & \delta \psi_{\theta } : \, \frac{{B_{12} }}{R}\left( {\frac{{\partial^{2} u}}{\partial x\partial \theta } - l^{2} \frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }}} \right) + \frac{{D_{12} }}{R}\left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } - l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }}} \right) \\ & \quad + \frac{{B_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} v}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }}} \right) + \frac{{D_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }}} \right) \\ & \quad + B_{66} \left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } - \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }}} \right) - \frac{{D_{22} }}{R}\frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial \theta^{4} }} \\ & \quad + D_{66} \left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } - \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }}} \right) \\ & \quad - k_{s} A_{44} \left( {\psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R} - l^{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{R}\frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) = \left( {1 - \mu^{2} \nabla^{2} } \right)\left[ {I_{1} \left( {\frac{{\partial^{2} v}}{{\partial t^{2} }}} \right) + I_{2} \left( {\frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }}} \right)} \right] \\ \end{aligned}$$
(18)

where the defined elements in Eqs. (14) - (18) are explained as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{22} } & {A_{66} } & {A_{44} } & {A_{55} } \\ \end{array} } \right\} & = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{22} } & {C_{66} } & {C_{44} } & {C_{55} } \\ \end{array} } \right\}} {\text{ d}}z \\ \left\{ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & {B_{22} } & {B_{66} } \\ \end{array} } \right\} & = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{22} } & {C_{66} } \\ \end{array} } \right\}} \, z{\text{d}}z \\ \left\{ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & {D_{22} } & {D_{66} } \\ \end{array} } \right\} & = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{22} } & {C_{66} } \\ \end{array} } \right\} \, } z^{2} {\text{d}}z \\ \left\{ {\begin{array}{*{20}c} {I_{0} } & {I_{1} } & {I_{2} } \\ \end{array} } \right\} & = \int\limits_{ - h/2}^{h/2} {\rho (z,T)\left\{ {\begin{array}{*{20}c} 1 & z & {z^{2} } \\ \end{array} } \right\}} \, z{\text{d}}z \\ \end{aligned}$$
(19)

3 Solution procedure

One of the best numerical methods which is well known for its accuracy and convergence is differential quadrature method (DQM) [92,93,94]. In this method, it is really important that the numbers of seed should be optimal; it means that due to an increase in the computational charge, too many seeds or elements are not applicable; and employing the few seeds, however, would lead to a negative impact on accuracy of the results [95,96,97,98,99,100,101,102,103,104,105]. At first, this method encounters its users with a limitation which they could not use too many seed owning to the weighting function was algebraic. GDQEM is employed with the aim of finding the solutions of governing equations beneath various boundary conditions (Fig. 2). The flowchart of the aforementioned solution method is as below:

Fig. 2
figure 2

The flowchart of GDQEM

Full size image

With a view of this method, the estimated rth is defined by f(x) as follows:

$$\left. {\frac{{\partial^{r} f(x)}}{{\partial x^{r} }}} \right|_{{x = x_{p} }} = \sum\limits_{j = 1}^{n} {C_{ij}^{(r)} f(x_{i} )}$$
(20)

n and Cij are the number of seeds and weighting coefficients in order that the second one is computed as below:

$$\begin{aligned} C_{ij}^{\left( 1 \right)} & = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}, \\ \,i,j & = 1,2, \ldots ,n\,\,\,\,{\text{and}}\,\,\,\,i \ne j \\ C_{ij}^{\left( 1 \right)} & = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( 1 \right)} } ,\,i = j \\ \end{aligned}$$
(21)

where

$$M\left( {x_{i} } \right) = \prod\limits_{j = 1,j \ne i}^{n} {\left( {x_{i} - x_{j} } \right)}$$
(22)

Also, these higher-order weight coefficients are as follows:

$$\begin{aligned} C_{ij}^{\left( r \right)} & = r\left[ {C_{ij}^{{\left( {r - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right] \\ i,j & = 1,2, \ldots ,n,i \ne j\,\,\,{\text{and}}\,\,\,2 \le r \le n - 1 \\ C_{ii}^{\left( r \right)} & = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( r \right)} } \\ i,j & = 1,2, \ldots ,n\,\,\,{\text{and}}\,\,\,1 \le r \le n - 1 \\ \end{aligned}$$
(23)

In the present research investigation, a seeds’ nonuniform set is chosen along x and \(\theta\) excess:

$$x_{i} = \frac{L}{2}\left( {1 - \cos \left( {\frac{{\left( {i - 1} \right)}}{{\left( {N_{i} - 1} \right)}}\pi } \right)} \right),\quad i = 1,2,3, \ldots ,N_{i}$$
(24)

The freedom degrees can be taken into consideration as follows:

$$\begin{aligned} u(x,\theta ,t) = U(x)\cos (n\theta )e^{i\omega t} , \hfill \\ v(x,\theta ,t) = V(x)\sin (n\theta )e^{i\omega t} , \hfill \\ w(x,\theta ,t) = W(x)\cos (n\theta )e^{i\omega t} , \hfill \\ \psi_{x} (x,\theta ,t) = \varPsi_{x} (x)\cos (n\theta )e^{i\omega t} , \hfill \\ \psi_{\theta } (x,\theta ,t) = \varPsi_{\theta } (x)\sin (n\theta )e^{i\omega t} . \hfill \\ \end{aligned}$$

Reorganizing the quadrature analogs of boundary conditions along with field equations into the generalized eigenvalue problem’s fabric, we obtain:

$$\left\{ {\left[ {\begin{array}{*{20}c} {\left[ {M_{dd} } \right]} & {\left[ {M_{db} } \right]} \\ {\left[ {M_{bd} } \right]} & {\left[ {M_{bb} } \right]} \\ \end{array} } \right]\omega^{2} + \left[ {\begin{array}{*{20}c} {\left[ {K_{dd} } \right]} & {\left[ {K_{db} } \right]} \\ {\left[ {K_{bd} } \right]} & {\left[ {K_{bb} } \right]} \\ \end{array} } \right]} \right\}\left\{ \begin{aligned} \delta_{d} \hfill \\ \delta_{b} \hfill \\ \end{aligned} \right\} = 0$$
(25)

where the subscripts d and b are pertained to the grid points’ domain and boundary, respectively. Also, displacement vector is shown by \(\delta\). Equation (25), however, may be changed to a basic problem of eigenvalue:

$$\begin{aligned} {[K^{*}]}\{ \delta_{i} \} = \left( {\omega^{2} } \right)[M^{ * } ]\{ \delta_{i} \} \hfill \\ [K^{ * } ] = [K_{dd} - K_{db} K_{bb}^{ - 1} K_{bd} ] \hfill \\ [M^{ * } ] = [M_{dd} - M_{db} K_{bb}^{ - 1} K_{bd} ] \hfill \\ \end{aligned}$$
(26)

Also, dimensionless natural frequency and dimensionless temperature difference are defined as follows:

$$\varOmega = 10 \times \omega L(\sqrt {\frac{\rho }{E}} )$$
(27)

4 Results section

In this paper, the laminated composite nanoshell’s material properties are given in Table 1. The most prominent superiority of AS/3501 composite compared with conventional composites is their higher stiffness and strength as well as less density [106].

Table 1 The effect of the number of grid points on the results convergence for the dimensionless frequency of the GNPRC micropanel with respect to different patterns and boundary conditions (B. Cs) when a/b = 6.5, h = a/9, R1 = R2 = 10a, \(\Delta\) T = 10 (K), gGPL = 0.5%
Full size table

4.1 Convergence

A sufficient number of grid points are necessary to achieve accurate results in GDQM [20, 44, 107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127]. The convergence studies are conducted for different boundary conditions as well as different materials. Moreover, it can be seen that the structure with (C–C) boundary conditions is stiffer than the structure with C–F boundary conditions which will lead to a smaller natural frequency. Also, GPLRC cylindrical nanoshell, due to the addition of GPL reinforcing nanofillers, has a higher natural frequency in comparison with pure epoxy. According to Table 2, for results convergence, thirteen grid points are suitable.

Table 2 The material properties of AS/3501 graphite–epoxy layers [84]
Full size table

4.2 Validation

For results verification of this work with other articles, Table 3 gives a comparison of results for dimensionless natural frequency of the nanostructure with the results of Ref [128], for different geometrical parameters. Moreover, the results reveal that the decrease in dimensionless length scale parameter (h/l) would lead to the reduction of the dimensionless natural frequency. In order to validate the proposed formulation, some comparative studies are conducted between the obtained results in this study and those available in the literature. Table 3 shows that there is a very good agreement between the results.

Table 3 Comparison of dimensionless first three natural frequencies of isotropic homogeneous nanostructure, with different thicknesses
Full size table

5 The effects of length scale parameter and temperature on the frequency for different boundary conditions

Figures 3, 4 and 5 present the effect of length scale parameter (l) on the dimensionless frequency with different boundary conditions. In this study, for reliability of result four quantities are considered for l (l = 0.1, 0.15, 0.2 and 0.25 nm). It is observed that for l = 0.25 nm dimensionless frequency was higher in all the boundary conditions that evaluated; also, for this among of l critical temperature was more, compare other one. It can be seen from figures that an increase in the l causes an increase in the critical temperature and increases the stability of the nanostructure. Also, it can be observed that by increasing temperature, frequency has been decreased. This is because increasing the temperature is eventuated to decrease the stiffness and frequency of the nanostructure. When one draws a comparison between Figs. 3, 4 and 5, it can be inferred that while a boundary condition changes from clamp to simply, both frequencies and critical temperature decrease. This results in a decrease in the stability of the nanostructure.

Fig. 3
figure 3

The effects of \(l\) and temperature of environment on the frequency for C–C boundary conditions

Full size image
Fig. 4
figure 4

The effects of \(l\) and temperature of environment on the frequency for C–S boundary conditions

Full size image
Fig. 5
figure 5

The effects of \(l\) and temperature of environment on the frequency for S–S boundary conditions

Full size image

6 The effects of nonlocal parameter and temperature on the frequency for different boundary conditions

The dimensionless temperature versus the dimensionless natural frequency for different nonlocal parameters and S–S, C–S and C–C boundary conditions is depicted in Figs. 6, 7 and 8, respectively. It can be observed that by increasing temperature, dynamic stability of the nanostructure has been decreased as long as critical temperature is seen. As a best result for the literature, it is seen that increasing in the dimensionless nonlocal parameter doesn’t have any effects on the critical temperature for each boundary condition. The difference between Figs. 6, 7 and 8 is that, for a specific value of dimensionless nonlocal parameter, the critical temperature and dimensionless frequency of C–C boundary conditions are higher than S–S and C–S boundary conditions. It is clear from these figures that nonlocal parameter and temperature have a same or direct effect on the dynamic stability (dimensionless frequency) of the nanostructure but nonlocal parameter doesn’t show any effects on the static stability (critical temperature) of the cylindrical nanoshell.

Fig. 6
figure 6

The effects of \(\mu\) and temperature of environment on the frequency for C–C boundary conditions

Full size image
Fig. 7
figure 7

The effects of \(\mu\) and temperature of environment on the frequency for C–S boundary conditions

Full size image
Fig. 8
figure 8

The effects of \(\mu\) and temperature of environment on the frequency for S–S boundary conditions

Full size image

6.1 The effects of different length to radius ratio on the frequency for different boundary conditions and between odd- and even-layered laminates

From Figs. 9, 10 and 11, it can be observed that three-layered [0° 90° 0°] laminated composite has the lowest value of the critical dimensionless temperature. In addition, the highest value of the critical temperature occurs in the six-layered [0° 90° 0° 90° 0° 90°] laminated composite. Another significant result is that four-layered [0° 90° 0° 90°] has the higher critical temperature than five-layered [0° 90° 0° 90° 0°] laminated composite nanostructure. It can be seen that increasing the number of layers causes the critical temperature to increase. It can be concluded from the results that the number of layers has a significant effect on the critical temperature of the laminated composite nanostructure.

Fig. 9
figure 9

The effects of \(L/R\) and the number of layers on the frequency for C–C boundary conditions

Full size image
Fig. 10
figure 10

The effects of \(L/R\) and the number of layers on the frequency for C–S boundary conditions

Full size image
Fig. 11
figure 11

The effects of \(L/R\) and the number of layers on the frequency for S–S boundary conditions

Full size image

6.2 Influences of length scale parameter on the frequency of the laminated composite nanostructure

Figures 12, 13, 14, 15, 16, 17, 18 and 19 show the effect of the different symmetric laminate angle, the number of layers and length scale parameter on the frequency for different boundary conditions. The intended model is a laminated composite cylindrical nanoshell in a thermal environment with \(\Delta T = 100\), R = 1 nm and h = R/10. The size-dependent parameters are assumed to be µ = 0.55 nm, l = 0.35 nm in the relevant theories [83].

Fig. 12
figure 12

The effects of l and even layers’ number on the frequency for C–C boundary conditions

Full size image
Fig. 13
figure 13

The effects of l and even layers’ number on the frequency for C–S boundary conditions

Full size image
Fig. 14
figure 14

The effects of l and even layers’ number on the frequency for S–S boundary conditions

Full size image
Fig. 15
figure 15

The effects of l and even layers’ number on the frequency for C–F boundary conditions

Full size image
Fig. 16
figure 16

The effects of l and odd layers’ number on the frequency for C–C boundary conditions

Full size image
Fig. 17
figure 17

The effects of l and odd layers’ number on the frequency for C–S boundary conditions

Full size image
Fig. 18
figure 18

The effects of l and odd layers’ number on the frequency for S–S boundary conditions

Full size image
Fig. 19
figure 19

The effects of l and odd layers’ number on the frequency for C–F boundary conditions

Full size image

6.3 The comparison between the even-layered laminates

According to Figs. 12, 13, 14 and 15, for C–C, C–S and S–S boundary conditions, increasing the length scale parameter, all the figures demonstrate a similar behavior. By increasing the length scale parameter, the frequency of the nanostructure increases. These figures present that by boosting the even layers’ number of the laminated composite, the frequency of the structure increases. This increment is remarkable for C–C boundary conditions and improves the structure stability. The difference between Figs. 12, 13 and 14 is that the dimensionless frequency of C–C boundary condition is higher than S–S and C–S boundary conditions. This is because C–C boundary condition improves the nanostructure stability. In addition, for C–F boundary condition, Fig. 15 presents a new result. For this regard, it can be seen that the effect of length scale parameter on the frequency is much more changeable. Moreover, for every even layers’ number, in the lower value of length scale parameter, by increasing the length scale parameter, the frequency of the structure decreases but in the higher value of length scale parameter this matter is inverse. In addition, this figure shows that even layers’ number effect on the frequency, change in l = 0.872 nm. So, for length scale parameter less than 0.872 nm, by increasing the number of the composite layers, the frequency increases, while for \(l > 0.872\,{\text{nm}}\) the reverse is true.

6.4 The comparison between the odd-layered laminates

The dimensionless frequency versus the length scale parameter for different odd layers’ numbers of the laminated composite and S–S, C–S, C–C and C–F boundary conditions is depicted in Figs. 16, 17, 18 and 19. It is seen that increasing length scale parameter causes the frequency of the system to increase. It is clear from Figs. 16, 17, 18 and 19 that because of an increase in stiffness of structure with rising odd layers’ number, the variation of frequency with an increase in odd layers’ number decreases. As mentioned earlier, by increasing the length scale parameter, the dynamic stability is enhanced. This enhancement is more significant in C–C boundary condition. The difference between these figures is that the effects of odd layers’ number on the frequency of the structure with C–F boundary condition are much less than in comparison with others boundary conditions. For more comprehensive, it is true that the odd layers’ number has a positive effect on the frequency of the cylindrical nanoshell with C–F boundary condition, but this effect is very little and can be ignored.

7 Conclusion

This article investigated the thermal buckling and stability analysis of a size-dependent laminated composite cylindrical nanoshell in thermal environment using NSGT. The governing equations of the laminated composite cylindrical nanoshell in thermal environment have been derived using Hamilton’s principle and solved with the assistance of the GDQEM. In the current study and for the first time, the critical temperature and dynamic stability analysis of a laminated composite cylindrical nanoshell in thermal environment are examined based on an exact continuum theory. Finally, using mentioned continuum mechanics theory, the investigation has been made into the influence of the temperature difference and the different types of the laminated composite on the vibrational characteristics of the nanostructure. In this work, the following main results have been achieved.

  1. 1.

    For C–F boundary conditions and every even layers’ number, in the lower value of length scale parameter, by increasing the length scale parameter, the frequency of the structure decreases but in the higher value of length scale parameter this matter is inverse.

  2. 2.

    For C–F boundary conditions and even layers’ number, the effects of length scale parameter on the frequency is much more changeable.

  3. 3.

    For C–C, C–S and S–S boundary conditions and every even and odd layers’ number, by increasing the length scale parameter and layers’ number, the frequency of the structure increases.

  4. 4.

    The results show that the odd layers’ number has a positive effect on the frequency of the cylindrical nanoshell with C–F boundary conditions, but this effect is very little and can be ignored.

  5. 5.

    Nonlocal parameter and temperature have a direct effect on the natural frequency of the cylindrical nanoshell, but nonlocal parameter doesn’t show any effects on the critical temperature of the cylindrical nanoshell.

  6. 6.

    The number of layers has a positive effect on the critical temperature of the laminated composite cylindrical nanoshell.