Bi-directional thermal buckling and resonance frequency characteristics of a GNP-reinforced composite nanostructure

Abstract

In this article, thermal buckling and resonance frequency of a composite cylindrical nanoshell reinforced with graphene nanoplatelets (GNP) under bi-directional thermal loading are presented. The temperature-dependent material properties of piece-wise GNP-reinforced composites (GNPRC) are assumed to be graded in the thickness direction of a cylindrical nanoshell. Also, Halphin-Tsai nanomechanical model is used to surmise the effective material properties of each layer. The size-dependent GNPRC nanoshell is analyzed using modified couple stress parameter (FMCS). For the first time, in the presented study show that bi-directional thermal buckling occurs if the percent of relative frequency change tends to 30%. The novelty of the current study is in considering the effects of bi-directional thermal loading in addition of FMCS on relative frequency, resonance frequencies, thermal buckling, and dynamic deflection of the GNPRC nanoshell. The governing equations and boundary conditions are developed using Hamilton’s principle and solved with the aid of analytical method. The results show that, various bi-directionasl thermal loading and other geometrical and mechanical properties have important role on resonance frequency, relative frequency change, thermal buckling, and dynamic deflection of the GNPRC cylindrical nanoshell. The results of the current study are useful suggestions for design of materials science, micro-mechanical and nano-mechanical systems such as microactuators and microsensors.

1 Introduction

According to the recent progressions in science and technology [1,2,3,4,5,6,7,8], novel and new research aspects have considerable attention [9,10,11,12,13,14,15,16,17]. Some applications of GPL reinforcement are reported in Ref. [18]. In addition, the properties of GPL reinforcements make them an appropriate choice to be used in chemistry, physics, electrical engineering, materials science [19] and engineering applications [20,21,22,23,24,25,26,27,28,29].

Rafiee et al. [30] compared the mechanical properties of epoxy nanocomposites refined with 1% value fraction of single-walled carbon nanotubes (SWNT), multi-walled carbon nanotube (MWNT) and GPL with each other. Their results show that, Young’s modulus, ultimate tensile strength, fracture toughness, fracture energy, and fatigue resistance of the GPLs are greater than the other materials. So, GPL reinforcement can be replaced by SWNTs and MWNTs in many applications (Fig. 1).

Fig. 1

Ultimate tensile strength and Young modulus for the baseline epoxy and GNP/epoxy, MWNT/epoxy, and SWNT/epoxy nanocomposites [30]

In addition, Yavari et al. [31] reported microstructure of epoxy/GNP nanocomposites. The grains with the Brighter background is epoxy and the bounded which reinforcement the epoxy is GNP (Fig. 2).

Fig. 2

Microstructure of epoxy nanocomposites refined with GNP [31]

Researches demonstrated that subjoining very meager amount of graphene into primary polymer matrix can desperately improve its mechanical, thermal and electrical properties. It is worth to mention that nanostructures reinforced by GPL are more applicable in engineering design, so focus on dynamic modeling of the nanostructure with GPL reinforcement is useful and important. In addition, this material can be used in electrical devices such as those mentioned in Refs. [32,33,34,35]. Furthermore, polymer matrix reinforced by various types of nanofillers has a wide range of applications such as field effect transistors, electromechanical actuators, biosensors and chemical sensors, solar cells, photoconductor and superconductor devices. Therefore, investigation of their mechanical characteristics is of great interest for engineering design and manufacture. Many researchers [36,37,38,39,40,41] studied the behavior and stability of the FG multilayer composite and isotropic materials. Feg et al. [42] investigated nonlinear bending behavior of a novel glass made of multi-layer polymer composite beams reinforced by GPLs. They reported that beams with a high weight fraction of GPLs and symmetric distribution are less sensitive to the nonlinear deformation. In addition, current nanostructure can be used in smart systems. The experiments and researches show that size effects play an important role in mechanical properties. Thus, neglecting these effects may lead to inaccurate responses. It should be mentioned that, the size effect is not considered in the classical continuum theories, so these theories are not appropriate for micro and nano scales. Therefore, some methods, such as: molecular dynamic (MD) simulations, FE method and non-classical continuum theory are used to study nanostructures. MD simulation includes complicated and time-consuming calculations which are not efficient. In contrast, simple and efficient, higher order continuum mechanic theories, have recently attracted researcher’s attentions. As studying the mechanical behaviors of nanoshells relate to submicron dimensions, they could not be correctly predicted by the classical theory. Thus taking into consideration the size effect, higher order continuum theories are used. These theories include the nonlocal elasticity theory, the modified couple stress theory, and nonlocal strain gradient theory. A Bernoulli–Euler nanobeam model considering nonhomogeneous temperature fields, based on Eringen’s nonlocal elasticity theory was proposed by Ref. [43]. They presented a thermodynamically consistent and reliable nonlocal nanobeam model that can be used in non-homogenous and non-isothermal environments. Bending analysis of armchair carbon nanotubes using gradient elasticity theory was examined by Ref. [44]. In this article, as an important result, influences of small-size effects on the Young’s modulus were investigated. Exact solutions of inflected functionally graded nanobeams with integral elasticity were investigated by Ref. [45]. The solutions of the stress-driven integral method indicate that the stiffness of nanobeams increases at smaller scales due to size effects.

A key issue in various engineering field is that the prediction of the properties, behavior, and performance of different systems is an important aspect [46,47,48,49,50,51,52,53,54,55]. For this regard, in field of the dynamic/static responses of the size-dependent GPLRC nanostructures, sahmani et al. [56] studied nonlinear instability of GPLRC nanoshells under the hydrostatic pressure using nonlocal elasticity theory and MSGT. In another work [57], they investigated nonlinear instability of axially loaded GPLRC nanoshells based on nonlocal strain gradient elasticity theory. It should be noted that, MSGT is an high order continuum theory which employs three length scale parameters [58]. These parameters are very useful in modeling of nano structures which are introduced in results section. In addition, in the field of forced vibration analysis of structures, Song et al. [59] investigated free and forced vibration of FG polymer composite plates reinforced by GPLs. They studied the effects of GPL distribution pattern, weight function, geometry and size, as well as, the total number of layers on the dynamic characteristics of the plates. Forced vibration of an orthotropic double-nanoplate system using nonlocal theory was examined by Atanasov et al. [60]. In their research, employing an analytical method the dynamic responses of the orthotropic double-nanoplate system for different external transversal loads were studied. Also, Du et al. [61] investigated nonlinear forced vibration of infinitely long FG cylindrical shells using the Lagrangian theory and multiple scale method. An interesting result of their work is that, power-law exponents have important role on the amplitude response of the FG cylindrical shells. Li et al. [62] focused on the coupled vibration characteristics of a spinning and axially moving composite thin-walled beam. In their work, some interesting conclusions about the critical axial speed and critical spinning angular speed were drawn. Another important factor in the design of composite nanostructures is porosity which occurs during manufacturing process. Therefore, these phenomena must be considered in the simulation and modeling of nanostructures. Barati et al. [63] studied forced vibration analysis of heterogeneous nanoporous plates using generalized nonlocal strain gradient theory. They showed that the forced vibration characteristics of a nanoplate are strongly influenced by the excitation frequency, porosities, nonlocal parameter and dynamic load location. Free and forced vibration characteristics of FG porous beams with non-uniform porosity distribution were studied by Chen et al. [64]. They examined both symmetric and asymmetric porosity distributions in this work. Chen et al. [65] conducted a study on nonlinear free vibration behavior of a porous moderately thick beam. They used Ritz method and von Kármán type nonlinear strain–displacement relations for deriving the equation system. According to their results, porosity coefficient, slenderness ratio, thickness ratio and other parameters play important roles in the nonlinear vibration characteristics of the porous moderately thick beam. In another work, Chen et al. [66] examined nonlinear vibration and post-buckling behaviors of GPLRC porous nanocomposite beam. Moreover, the influences of both porosity coefficient and GPL weight fraction on static and dynamic behaviors of the GPLRC porous nanocomposite were shown in their work. Y.H. Dong et al. [67] studied free vibration characteristics of a GPLRC porous nanocomposite cylindrical shell with spinning motion. Finally, they represented the effect of initial hoop tension on vibration characteristics of the spinning GPLRC porous nanocomposite cylindrical shell. Yang et al. [68] investigated buckling and free vibration characteristics of GPLRC nanocomposite plates with porosity. Recently, Chen et al. [69] focused on dynamic response and energy absorption of FG two-dimensional porous structures in the framework of finite element analysis. Li et al. [70] investigated free vibration characteristics of a spinning composite thin-walled beam under the hydrothermal environment. Their governing equations and boundary conditions were solved using Galerkin’s method. In their result, the effects of spinning motion and hydrothermal environment on natural frequency and critical spinning angular speed of the beam were examined. In another work, Li et al. [71] investigated parametric instability of a FG cylindrical thin shell under the thermal environment. In other work [72], they studied parametric resonance of a FG cylindrical thin shell with periodic rotating angular speeds in the thermal environment. They also demonstrated that constant of rotating angular speed, material heterogeneity and thermal effects have remarkable influence on vibration characteristics, instability regions and critical rotating speeds of the shell. Nonlinear vibration of FG cylindrical shells in thermal environments was studied by Ref. [73]. Du et al. [74] analyzed nonlinear vibration of FG circular cylindrical shells in thermal environment. Their results showed that, temperature and volume fractions of composition play an important role in the exact resonance condition and bifurcation characteristics of FG cylindrical shells. Also, some researchers tried to predict the static and dynamic properties of different structures and materials via neural network solution [75,76,77,78,79,80,81,82,83,84,85,86,87,88,89].

To the best of our knowledge, no studies have been reported in the literature for investigation of bi-directional thermal buckling using relative frequency changes. For the first time, in the present study show that bi-directional thermal buckling occurs if the percent of relative frequency change tends to 30%. The novelty of the current study is consideration of GNPRC, bi-directional, thermal loading, dynamic load and size effects implemented on proposed model using FMCS. Because of high accuracy and efficiency of the analytical method, it is employed to solve the governing equations of the problem. The governing equations and boundary conditions have been developed using minimum potential energy which solved with the aid of the analytical method. Finally, using the mentioned continuum mechanics theory, the investigation has been made into the influence of the bi-directional thermal loading and GNP distribution pattern on the thermal buckling, resonance frequency, relative frequency change and dynamic deflection.

2 Multilayer polymer composites reinforced GNPs formulation

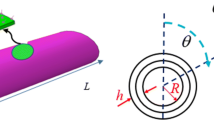
A cylindrical nanoshell in bi-directional thermal environment and under dynamic load is modeled. The thickness, length, and the middle surface radius of the cylindrical shell are denoted by h, L, and R, respectively. In addition, q₀ is the transverse force due to applied dynamic load (Fig. 3).

Fig. 3

Geometry of cylindrical FG nanoshell under dynamic load and thermal environment

The cylindrical nanoshell is made of composite material. The volume fraction functions of these four patterns of GPL are represented by [90, 91]

$${\text{Pattern 1}}:\;U - GPLRC\,(UD):\,\,\,\,\,V_{GPL} (k) = V_{GPL}^{*}$$

(1)

$${\text{Pattern 2}}:\;X - GPLRC\,(FG - X):\,\,\,\,\,\,\,V_{GPL} (k) = 2V_{GPL}^{*} \left| {2k - N_{L} - 1} \right|/N_{L}$$

(2)

$${\text{Pattern 3}}:O - GPLRC\,(FG - O):\,\,\,\,\,\,V_{GPL} (k) = 2V_{GPL}^{*} \left[ {1 - \left( {\left| {2k - N_{L} - 1} \right|/N_{L} } \right)} \right]$$

(3)

$${\text{Pattern 4}}:\;A - GPLRC\,(FG - A):\,\,\,\,\,\,\,\,V_{GPL} (k) = 2V_{GPL}^{*} (2k - 1)/N_{L}$$

(4)

where k is number of layers of the nanoshell, ${N}_{L}$ is the total number of layers and ${V}_{GPL}^{*}$ is the total volume fraction of GNPs. The relation between ${V}_{GPL}^{*}$ and their weight fraction ${g}_{GPL}$ can be expressed by [92,93,94,95,96,97]:

$$V_{GPL}^{*} = \frac{{g_{GPL} }}{{g_{GPL} + (\rho_{GPL} /\rho_{m} )(1 - g_{GPL} )}}$$

(5)

in which ${\rho }_{GPL}$ and ${\rho }_{m}$ are the mass densities of GNPs and the polymer matrix. Based on Halpin–Tsai model, the elastic modulus of composites reinforced randomly with GNPs approximated by [98,99,100]:

$$\begin{gathered} E = \frac{3}{8}E_{L} + \frac{5}{8}E_{T} , \hfill \\ E_{L} = \frac{{1 + \xi_{L} n_{L} V_{GPL} }}{{1 - n_{L} V_{GPL} }}E_{m} ,\,\,\,\,\,\,E_{T} = \frac{{1 + \xi_{T} n_{T} V_{GPL} }}{{1 - n_{T} V_{GPL} }}E_{m} \,\,\,\,\,\,\, \hfill \\ \end{gathered}$$

(6)

where E is effective modulus of composites reinforced with GNPs and E_L and E_T are the longitudinal and transverse module for a unidirectional lamina. In Eq. (6) the GNP geometry factors (${\xi }_{L}$ and ${\xi }_{T})$ and other parameters are given by [101, 102]:

$$\begin{gathered} \xi_{L} = 2({\mathbb{Z}}_{GPL} /h_{GPL} ),\,\,\,\,\xi_{t} = 2(b_{GPL} /h_{GPL} ), \hfill \\ n_{L} = \frac{{(E_{GPL} /E_{m} ) - 1}}{{(E_{GPL} /E_{m} ) + \xi_{L} }},\,\,\,n_{T} = \frac{{(E_{GPL} /E_{m} ) - 1}}{{(E_{GPL} /E_{m} ) + \xi_{T} }} \hfill \\ \end{gathered}$$

(7)

where ${\mathbb{Z}}_{GPL}{\mathbb{Z}}_{GPL}$,${h}_{GPL}$,${b}_{GPL}$ are the average length, thickness and width of the GNPs. Using rule of mixture, mechanical properties of the GNP/ polymer nanocomposite are expressed as [103]:

$$\begin{gathered} \overline{E} = E_{GPL} V_{GPL} + E_{M} V_{M} , \hfill \\ \overline{\rho } = \rho_{GPL} V_{GPL} + \rho_{M} V_{M} , \hfill \\ \overline{\nu } = \nu_{GPL} V_{GPL} + \nu_{M} V_{M} , \hfill \\ \overline{\alpha } = \alpha_{GPL} V_{GPL} + \alpha_{M} V_{M} . \hfill \\ \end{gathered}$$

(8)

The mechanical properties of the FG-GNPR cylindrical shell with different types of distributions can be obtained by [104]:

3 Mathematical modelling

Based on the first order shear deformation theory [105] (FSDT), the displacement field of cylindrical shell along the three directions of x, θ, z is as follows:

$$\begin{aligned} u(x,\theta ,z,t) & = u_{0} (x,\theta ,t) + z\psi _{x} (x,\theta ,t) \\ v(x,\theta ,z,t) & = v_{0} (x,\theta ,t) + z\psi _{\theta } (x,\theta ,t) \\ w(x,\theta ,z,t) & = w_{0} (x,\theta ,t) \\ \end{aligned}$$

(9)

where,$u_{0} (x,\theta ,z)$, $v_{0} (x,\theta ,z))$ and $w_{0} (x,\theta ,z))$ represent the displacements in axial-, circumferential- and radial-directions, respectively. $\psi_{x} (x,\theta ,t)$ and $\psi_{\theta } (x,\theta ,t)$ are the rotations of the normal to the element middle plane about the circumferential and axial-directions. In addition, the three-dimensional stress–strain relations can be expressed as follows [106,107,108,109]:

$$\left[ \begin{gathered} \sigma_{xx} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{zz} \hfill \\ \sigma_{x\theta } \hfill \\ \sigma_{xz} \hfill \\ \sigma_{\theta z} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{13} } & 0 & 0 & 0 \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & {\overline{Q}_{23} } & 0 & 0 & 0 \\ {\overline{Q}_{13} } & {\overline{Q}_{23} } & {\overline{Q}_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\overline{Q}_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {\overline{Q}_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {\overline{Q}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon_{xx} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ \varepsilon_{zz} \hfill \\ \varepsilon_{x\theta } \hfill \\ \varepsilon_{xz} \hfill \\ \varepsilon_{\theta z} \hfill \\ \end{gathered} \right]$$

(10)

In Eq. (10) the stiffness coefficients are obtained by Ref. [110,111,112]. Also, $\alpha_{i}$ and $\Delta T$ are thermal expansions (in x,$\theta$ and z directions) and temperature changes, respectively. For the equations of the motion and boundary conditions, the extended Hamilton’s principle states that [113,114,115,116,117]:

$$\int_{{t_{1} }}^{{t_{2} }} {(\delta T - \delta U + \delta W_{1} - \delta W_{2} )dt = 0}$$

(11)

Strain energy of FMCS parameter cylindrical nanoshell is expressed as follows [118, 119]:

$$U = \frac{1}{2}\iiint\limits_{V} {(\sigma_{ij} \varepsilon_{ij} + m_{ij}^{s} \chi_{ij}^{s} )R\,dxd\theta dz}$$

(12)

In Eq. (12) ${\varepsilon }_{\mathrm{ij}}$ and ${\sigma }_{\mathrm{ij}}$ represent the components of a strain tensor and stress tensor, which are expressed in Ref. [110]. In addition, ${\chi }_{ij}^{s}$ and ${m}_{ij}$ are the components of a symmetric rotation gradient tensor and higher order stress tensor, which can be expressed as:

$$\begin{aligned} \chi _{{ij}}^{s} & = \frac{1}{2}(\varphi _{{i,j}} + \varphi _{{j,i}} )\,\,\,\,\,\, \\ m_{{ij}}^{s} & = 2l^{2} \mu \chi _{{ij}}^{s} \\ \end{aligned}$$

(13)

where $\varphi_{i}$ and $ll$ respectively represent the extremely small rotation vector and MCS parameter, which is related to symmetric rotation gradients can be expressed as follows:

$$l = l_{GPL} V_{GPL} + l_{M} V_{M} \,\,\,$$

(14)

Moreover, the non-zero components of symmetric rotation gradient tensor are obtained as follows:

$$\begin{aligned} \chi _{{xx}}^{s} & = - \frac{1}{2}\left( {\frac{{\partial \psi _{\theta } }}{{\partial x}} + \,\frac{1}{R}\frac{{\partial v}}{{\partial x}} - \frac{1}{R}\frac{{\partial ^{2} w}}{{\partial x\partial \theta }}} \right) \\ \chi _{{\theta \theta }}^{s} & = - \frac{1}{{2R}}\left( {\frac{1}{R}\frac{{\partial u}}{{\partial \theta }} - \frac{{\partial v}}{{\partial x}} - z\frac{{\partial \psi _{\theta } }}{{\partial x}}} \right) - \frac{1}{2}\left( {\frac{1}{R}\frac{{\partial ^{2} w}}{{\partial x\partial \theta }} - \frac{1}{R}\frac{{\partial \psi _{x} }}{{\partial \theta }}} \right) \\ \chi _{{zz}}^{s} & = - \frac{1}{2}\left( {\frac{1}{R}\frac{{\partial \psi _{x} }}{{\partial \theta }} - \frac{{\partial \psi _{\theta } }}{{\partial x}} - \frac{1}{{R^{2} }}\frac{{\partial u}}{{\partial \theta }}} \right)\,\, \\ \chi _{{x\theta }}^{s} & = \, - \frac{1}{4}\left( {\frac{1}{{R^{2} }}\frac{{\partial v}}{{\partial \theta }} + \frac{{\partial ^{2} w}}{{\partial x^{2} }} - \frac{1}{{R^{2} }}\,\frac{{\partial ^{2} w}}{{\partial \theta ^{2} }} - \,\frac{{\partial \psi _{x} }}{{\partial x}} + \frac{1}{R}\frac{{\partial \psi _{\theta } }}{{\partial \theta }}} \right) \\ \chi _{{xz}}^{s} & = - \frac{1}{4}\left( {\frac{1}{R}\frac{{\partial ^{2} u}}{{\partial x\partial \theta }} - \frac{{\partial ^{2} v}}{{\partial x^{2} }} - \frac{v}{{R^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial w}}{{\partial \theta }} + \frac{{\psi _{\theta } }}{R}} \right) - \frac{z}{4}\left( {\frac{1}{R}\frac{{\partial ^{2} \psi _{\theta } }}{{\partial x\partial \theta }} - \frac{{\partial ^{2} \psi _{\theta } }}{{\partial x^{2} }}} \right) \\ \chi _{{\theta z}}^{s} & = - \frac{1}{4}\left( {\frac{1}{{R^{2} }}\frac{{\partial ^{2} u}}{{\partial \theta ^{2} }} - \frac{1}{R}\frac{{\partial ^{2} v}}{{\partial x\partial \theta }} - \frac{1}{R}\frac{{\partial w}}{{\partial x}} + \frac{{\psi _{x} }}{R}} \right) - \frac{z}{4}\left( {\frac{1}{{R^{2} }}\frac{{\partial ^{2} \psi _{x} }}{{\partial \theta ^{2} }} - \frac{1}{R}\frac{{\partial ^{2} \psi _{\theta } }}{{\partial x\partial \theta }}} \right) \\ \end{aligned}$$

(15)

Finally, the classical and non-classical strain energies of the current study based on FMCS parameter are expressed as follows:

$$\begin{gathered} \frac{1}{2}\iiint\limits_{V} {(\sigma_{ij} \delta \varepsilon_{ij} )}dV = \iint\limits_{A} {\left\{ \begin{array}{l} \left( {N_{xx} \frac{\partial }{\partial x}\delta u + M_{xx} \frac{\partial }{\partial x}\delta \psi_{x} } \right) + N_{\theta \theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta v + \frac{\delta w}{R}} \right) + \hfill \\ M_{\theta \theta } \frac{1}{R}\frac{\partial }{\partial \theta }\delta \psi_{\theta } + Q_{xz} \left( {\delta \psi_{x} + \frac{\partial }{\partial x}\delta w} \right) + \hfill \\ N_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta u + \frac{\partial }{\partial x}\delta v} \right) + M_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta \psi_{x} + \frac{\partial }{\partial x}\delta \psi_{\theta } } \right) \hfill \\ + Q_{z\theta } \left( {\delta \psi_{\theta } + \frac{1}{R}\frac{\partial }{\partial \theta }\delta w - \frac{\delta v}{R}} \right) \hfill \\ \end{array} \right\}}Rdxd\theta \hfill \\ \frac{1}{2}\iiint\limits_{V} {(m_{ij}^{s} \delta \chi_{ij}^{s} )}dV = \iint\limits_{A} {\left\{ \begin{array}{l} \left( { - \frac{{Y_{\theta \theta } }}{{2R^{2} }} + \frac{{Y_{zz} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta u - \left( {\frac{{Y_{\theta z} }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} }}\delta u \hfill \\ - \left( {\frac{{Y_{zx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta u \hfill \\ + \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2R}} \right)\frac{\partial }{\partial x}\delta v + \left( {\frac{{Y_{xz} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta v \hfill \\ - \left( {\frac{{Y_{\theta x} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta v \hfill \\ + \left( {\frac{{Y_{\theta z} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta v + \left( {\frac{{Y_{xz} }}{{2R^{2} }}} \right)\delta v + \left( {\frac{{Y_{\theta z} }}{2R}} \right)\frac{\partial }{\partial x}\delta w \hfill \\ - \left( {\frac{{Y_{\theta x} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta w \hfill \\ - \left( {\frac{{Y_{zx} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta w + \left( {\frac{{Y_{x\theta } }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} }}\delta w + \hfill \\ \left( { - \frac{{Y_{\theta \theta } }}{2R} + \frac{{Y_{xx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta w \hfill \\ + \left( {\frac{{Y_{x\theta } }}{2}} \right)\frac{\partial }{\partial x}\delta \psi_{x} + \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2R}} \right)\frac{\partial }{\partial \theta }\delta \psi_{x} \hfill \\ - \left( {\frac{{T_{zx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta \psi_{x} \hfill \\ - \left( {\frac{{Y_{z\theta } }}{2R}} \right)\delta \psi_{x} - \left( {\frac{{Y_{x\theta } }}{2R}} \right)\frac{\partial }{\partial \theta }\delta \psi_{\theta } + \hfill \\ \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2} + \frac{{Y_{zz} }}{2}} \right)\frac{\partial }{\partial x}\delta \psi_{\theta } \hfill \\ + \left( {\frac{{T_{z\theta } }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta \psi_{\theta } - \left( {\frac{{T_{z\theta } }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} \,}}\delta \psi_{x} \hfill \\ + \left( {\frac{{T_{xz} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta \psi_{\theta } - \left( {\frac{{Y_{xz} }}{2R}} \right)\delta \psi_{\theta } \hfill \\ \end{array} \right\}}Rdxd\theta \hfill \\ \end{gathered}$$

(16)

where parameters used in above equation are defined as:

$$\begin{gathered} (N_{xx} ,N_{\theta \theta } ,N_{x\theta } ) = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } )dz,} \hfill \\ (M_{xx} ,M_{\theta \theta } ,M_{x\theta } ) = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } )zdz} , \hfill \\ (Q_{xz} ,Q_{z\theta } ) = \int_{ - h/2}^{h/2} {k_{s} (\sigma_{xz} ,\sigma_{z\theta } )dz} , \hfill \\ (Y_{xx} ,Y_{\theta \theta } ,Y_{zz} ,Y_{x\theta } ,Y_{xz} ,Y_{z\theta } ) = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } )dz,} \hfill \\ (T_{xx} ,T_{\theta \theta } ,T_{zz} ,T_{x\theta } ,T_{xz} ,T_{z\theta } ) = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } )zdz} \hfill \\ \end{gathered}$$

(17)

Furthermore, the kinetic energy of the FG-GRCs cylindrical nanoshell using MCS parameter can be expressed as [120]:

$$\delta T = \int\limits_{Z} {\iint\limits_{A} {\rho \left\{ \begin{gathered} \left( {\frac{\partial u}{{\partial t}} + z\frac{{\partial \psi_{x} }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta u + z\frac{\partial }{\partial t}\delta \psi_{x} } \right) \hfill \\ + \left( {\frac{\partial v}{{\partial t}} + z\frac{{\partial \psi_{\theta } }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta v + z\frac{\partial }{\partial t}\delta \psi_{\theta } } \right) + \left( {\frac{\partial w}{{\partial t}}} \right)\frac{\partial }{\partial t}\delta w \hfill \\ \end{gathered} \right\}}} R\,dz\,dx\,d\theta$$

(18)

For the composite layer reinforced with uniform (UD) of FG distribution of GPLs, Fourier heat conduction relation can be formulated as:

$$\begin{gathered} \frac{1}{z}k_{z} \frac{\partial }{\partial z}\left( {z\frac{\partial T}{{\partial z}}} \right) + k_{x} \frac{{\partial^{2} T}}{{\partial x^{2} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for}}\,\,UD \hfill \\ \frac{1}{z}\frac{\partial }{\partial z}\left( {k_{z} z\frac{\partial T}{{\partial z}}} \right) + k_{x} \frac{{\partial^{2} T}}{{\partial x^{2} }} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for}}\,\,FG \hfill \\ \end{gathered}$$

(19)

In addition, thermal surface boundary conditions are as follows:

$$T(x,\theta , - h/2) = T_{i} ,\,\,\,T(x,\theta ,h/2) = T_{0} ,\,\,T\left( {0,\theta ,z} \right) = T\left( {L,\theta ,z} \right) = 0$$

(20)

The work done by applied forces can be written as:

$$W_{2} = \frac{1}{2}\left\{ {q_{{{\text{dynamic}}}} w^{2} } \right\}\,R\,dV$$

(21)

In which q_dynamic is the transverse force due to applied dynamic load. Substituting Eqs. (10), (16), (17) into Eq. (9) and integrating by part, the equations of motion and boundary conditions of the GNP cylindrical nanoshell in thermal environment using MCS parameter can be obtained as follows:

$$\begin{gathered} \,\left[ {\frac{{\partial N_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } + \frac{1}{{2R^{2} }}\left( { - \frac{{\partial Y_{\theta \theta } }}{\partial \theta } + \frac{{\partial Y_{zz} }}{\partial \theta }} \right) + \frac{1}{2R}\frac{{\partial^{2} Y_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y_{\theta z} }}{{\partial \theta^{2} }}} \right]\delta u \hfill \\ + \left[ {\frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{\partial }{\partial \theta }N_{\theta \theta } + \frac{{Q_{z\theta } }}{R} + \frac{1}{2}\left\{ {\frac{1}{R}\frac{\partial }{\partial x}( - Y_{xx} + Y_{\theta \theta } ) - \frac{1}{{R^{2} }}\frac{{\partial Y_{\theta x} }}{\partial \theta } - \frac{{\partial^{2} Y_{xz} }}{{\partial x^{2} }} - \frac{{Y_{xz} }}{{R^{2} }} - \frac{1}{R}\frac{{\partial^{2} Y_{z\theta } }}{\partial \theta \,\partial x}} \right\}} \right]\delta v \hfill \\ - N_{2}^{T} \frac{{\partial^{2} v}}{{\partial x^{2} }}\delta v + \left[ {\frac{{\partial Q_{xz} }}{\partial x} + \frac{1}{R}\frac{{\partial Q_{z\theta } }}{\partial \theta } - \frac{{N_{\theta \theta } }}{R} - \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y_{\theta x} }}{{\partial \theta^{2} }} - \frac{1}{{2R^{2} }}\frac{{\partial Y_{zx} }}{\partial \theta } + \frac{1}{2R}\frac{{\partial Y_{\theta z} }}{\partial x} + \frac{{\partial^{2} Y_{x\theta } }}{{2\partial x^{2} }}} \right]\delta w_{0} \hfill \\ + \left[ { - \frac{1}{2R}\frac{{\partial^{2} }}{\partial \theta \,\partial x}(Y_{xx} - Y_{\theta \theta } ) - N_{1}^{T} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right]\delta w_{0} + \left[ {\frac{{\partial M_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } - Q_{xz} + \frac{1}{2}\frac{{\partial Y_{\theta x} }}{\partial x} - \frac{1}{2R}\frac{\partial }{\partial \theta \,}(Y_{zz} - Y_{\theta \theta } )} \right]\delta \psi_{x} \hfill \\ + \left[ {\frac{{Y_{zz} }}{R} + \frac{1}{2R}\frac{{\partial^{2} T_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} T_{\theta z} }}{{\partial \theta^{2} }}} \right]\delta \psi_{x} + \left[ {\frac{1}{R}\frac{{\partial M_{\theta \theta } }}{\partial \theta } + \frac{{\partial M_{x\theta } }}{\partial x} - Q_{z\theta } + \frac{1}{2}\frac{\partial }{\partial x}\left( {Y_{zz} - Y_{xx} + \frac{{T_{\theta \theta } }}{R}} \right)} \right]\delta \psi_{\theta } \hfill \\ + \left[ { - \frac{1}{2}\frac{{\partial Y_{\theta x} }}{\partial \theta } + \frac{{Y_{xz} }}{2R} - \frac{1}{2R}\frac{{\partial^{2} T_{\theta z} }}{\partial \theta \,\partial x} - \frac{1}{2}\frac{{\partial^{2} T_{zx} }}{{\,\partial x^{2} }}} \right]\delta \psi_{\theta } = \,\left\{ {I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right\}\delta u + \left\{ {I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }}} \right\}\delta v \hfill \\ + I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }}\delta w_{0} + \left\{ {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right\}\delta \psi_{x} + \left\{ {I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }}\,} \right\}\delta \psi_{\theta } + q_{{{\text{dynamic}}}} \delta w \hfill \\ \end{gathered}$$

(22)

In addition, governing equations and boundary conditions are given in Appendix A.

4 Solution procedure

In this section, analytical method is implemented to solve the governing equations of MSGT-based on GPLRC nanoshell. In addition, in this research, the proposed model is simply supported in x = 0, L and $\theta = \pi /2,\,3\pi /2\,\,$. Thus, the displacement fields can be calculated as:

$$\left\{ \begin{gathered} u_{0} (x,\theta ,t) \hfill \\ v_{0} (x,\theta ,t) \hfill \\ w_{0} (x,\theta ,t) \hfill \\ \psi _{x} (x,\theta ,t) \hfill \\ \psi _{\theta } (x,\theta ,t) \hfill \\ \end{gathered} \right\} = \sum\limits_{{m = 1}}^{\infty } {\sum\limits_{{n = 1}}^{\infty } {\left\{ \begin{gathered} U_{{0mn}} \,\cos \,\left( {\frac{{m\pi }}{L}x} \right)\,\cos \,(n\theta ) \hfill \\ V_{{0mn}} \,\sin \,\left( {\frac{{m\pi }}{L}x} \right)\,\sin \,(n\theta ) \hfill \\ W_{{0mn}} \sin \,\left( {\frac{{m\pi }}{L}x} \right)\,\cos \,(n\theta ) \hfill \\ \psi _{{xmn}} \,\cos \,\left( {\frac{{m\pi }}{L}x} \right)\,\cos \,(n\theta ) \hfill \\ \psi _{{\theta mn}} \,\sin \left( {\frac{{m\pi }}{L}x} \right)\,\sin \,(n\theta ) \hfill \\ \end{gathered} \right\}} } \sin (\omega t)$$

(23)

where $\left\{ {U_{0mn} ,V_{0mn} ,W_{0mn} ,\Psi_{xmn} ,\Psi_{\theta mn} } \right\}$ are the unknown Fourier coefficients that need to be determined for each n and m values. Also, n and m are the circumferential and axial wave numbers, respectively. For vibration analysis of the structure, by substituting Eq. (21) into governing equations, one obtains [121,122,123,124,125,126]:

$$\left( {\left\{ {\begin{array}{*{20}c} {K_{11} } & {K_{12} } & {K_{13} } & {K_{14} } & {K_{15} } \\ {K_{21} } & {K_{22} } & {K_{23} } & {K_{24} } & {K_{25} } \\ {K_{31} } & {K_{32} } & {K_{33} } & {K_{34} } & {K_{35} } \\ {K_{41} } & {K_{42} } & {K_{43} } & {K_{44} } & {K_{45} } \\ {K_{51} } & {K_{52} } & {K_{53} } & {K_{54} } & {K_{55} } \\ \end{array} } \right\} - \omega_{ex}^{2} \left\{ {\begin{array}{*{20}c} {M_{11} } & {M_{12} } & {M_{13} } & {M_{14} } & {M_{15} } \\ {M_{21} } & {M_{22} } & {M_{23} } & {M_{24} } & {M_{25} } \\ {M_{31} } & {M_{32} } & {M_{33} } & {M_{34} } & {M_{35} } \\ {M_{41} } & {M_{42} } & {M_{43} } & {M_{44} } & {M_{45} } \\ {M_{51} } & {M_{52} } & {M_{53} } & {M_{54} } & {M_{55} } \\ \end{array} } \right\}} \right)\left( \begin{gathered} U_{0} \hfill \\ V_{0} \hfill \\ W_{0} \hfill \\ \psi_{x} \hfill \\ \psi_{\theta } \hfill \\ \end{gathered} \right) = \left[ \begin{gathered} 0 \hfill \\ 0 \hfill \\ q_{{{\text{dynamic}}}} \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right]\left( \begin{gathered} U_{0} \hfill \\ V_{0} \hfill \\ W_{0} \hfill \\ \psi_{x} \hfill \\ \psi_{\theta } \hfill \\ \end{gathered} \right)$$

(24)

It should be noted that stiffness and mass components are given in Appendix A. In Eq. (22), $\omega_{ex}$ is the excitation frequency and applied dynamic load ($q_{{{\text{dynamic}}}}$) is defined as:

$$q_{dynamic} = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {q_{0} \sin \,\left( {\frac{m\pi }{L}x} \right)\,\cos \,(n\theta )} } \sin (\omega t),$$

(25)

Solution of Eq. (23) gives the dynamic deflection and excitation frequency of the porous FG-GPLRC cylindrical nanoshell. The dimensionless excitation frequency and forced vibration amplitude are defined as:

$$\Omega = 10 \times \omega_{ex} L\sqrt {\rho /E} ,\,\,\,\,\,\,\,\,\,\overline{W}_{{{\text{uniform}}}} = W_{0mn} \frac{{10Eh^{3} }}{{L^{4} q_{0} }}$$

(26)

5 Temperature field

To satisfy temperature boundary conditions, Eq. (18), following Fourier series solution to Eqs. (30), (31) is assumed

$$T = \sum\limits_{m = 1}^{\infty } {\sin \left( {P_{m} x} \right)} \cos (n\theta )$$

(27)

where $P_{m} = \frac{{m\pi }}{L}$. Thermal conductivity coefficients regarding to each GPLs distribution pattern can be determined as

$$\frac{{k_{i} }}{{k_{m} }} = 1 + D_{i} \quad {\text{for UD}}$$

(28)

$$\frac{{k_{i} }}{{k_{m} }} = 1 + 2D_{i} \left( {\frac{{z - r_{i} }}{h}} \right)\quad {\text{for FG } - \text{ A}}$$

(29)

$$\frac{{k_{i} }}{{k_{m} }} = 1 + 2D_{i} \left| {1 - \frac{{2\left( {z - r_{i} } \right)}}{h}} \right|\quad {\text{for FG } - \text{ X}}$$

(30)

$$\begin{gathered} \frac{{k_{i} }}{{k_{m} }} = 1 + 2D_{i} \left( {\frac{{z - r_{i} }}{\frac{h}{2}}} \right)\quad \mathrm{for} \, z\,{ \le}\,r_{i} + \frac{h}{2}\quad {\text{for FG } - \text{ O}} \hfill \\ \frac{{k_{i} }}{{k_{m} }} = 1 + 2D_{i} \left( {\frac{{r_{o} - h_{p} - z}}{\frac{h}{2}}} \right)\quad \mathrm{for}\quad {\text{z}}\,{\ge}\,r_{i} + \frac{h}{2}\quad {\text{for}}\quad {\text{FG } - \text{ O}} \hfill \\ \end{gathered}$$

(31)

where ${\text{D}}_{i} = \frac{{P_{3} V_{GPL} }}{3} \times \frac{{\frac{{k_{iGPL} }}{{k_{m} }}}}{{P_{3} + \left( {\frac{{2a_{k} }}{d} \times \frac{{k_{iGPL} }}{{k_{m} }}} \right)}}{ ; }\left( {i = z,x} \right){ ;}a_{k} = R_{k} k_{m}$. Temperature gradient of radial coordinate for UD pattern of GPLs can be obtained by implementing Eqs. (25) and (26) in Eq. (17) as follows

$$T_{m} \left( z \right) = B_{1} I_{o} \left( {qz} \right) + C_{1} K_{o} \left( {qz} \right)$$

(32)

where $q = P_{m} \sqrt {\frac{{k_{x} }}{{k_{z} }}} {\text{ and }}B_{1} \, ,C_{1}$ are constants of integration which can be obtained from thermal surface boundary conditions at the inner and outer surfaces of layer reinforced with UD pattern of GPLs (More information is presented in Appendix B). From Eqs. (25), (27, 28, 29), heat conduction differential equation, Eq. (17) would be reduced to Heun’s differential equation as following

$$\left( {A_{1} z^{2} + A_{2} z^{3} } \right)\frac{{\partial^{2} T}}{{\partial z^{2} }} + \left( {2A_{2} z^{2} + A_{1} z} \right)\frac{\partial T}{{\partial z}} + \left( {A_{3} z^{2} + A_{4} z^{3} } \right)T = 0$$

(33)

Here ${\text{A}}_{{1}} {\text{ ,A}}_{{2}} { ,}...{\text{ ,A}}_{{6}}$ are constant coefficients depending on the pattern of GPLs distribution (see Appendix B). Analytical solution is determined for Eq. (31) according to subsequent relation

$$\begin{gathered} T\left( z \right) = HeunC\left( {\frac{{2A_{1} }}{{A_{2} }}\sqrt { - \frac{{A_{4} }}{{A_{2} }}} ,0,0,\frac{{A_{1} }}{{A_{2}^{3} }}\left( {A_{1} A_{4} - A_{2} A_{3} } \right),0, - \frac{{A_{2} }}{{A_{1} }}r} \right)e^{{ - \sqrt { - \, \frac{{A_{4} }}{{A_{2} }}} }} \times \hfill \\ \left\{ {B_{2} \int_{{r_{i} }}^{{r_{o} }} {\frac{{e^{{2\sqrt { - \, \frac{{A_{4} }}{{A_{2} }}} {\text{z}}}} }}{{z\left( {A_{2} z + A_{1} } \right)\left( {HeunC\left( {\frac{{2A_{1} }}{{A_{2} }}\sqrt { - \frac{{A_{4} }}{{A_{2} }}} ,0,0,\frac{{A_{1} }}{{A_{2}^{3} }}\left( {A_{1} A_{4} - A_{2} A_{3} } \right),0, - \frac{{A_{2} }}{{A_{1} }}z} \right)} \right)^{2} }}dz + C_{2} } } \right\} \hfill \\ \end{gathered}$$

(34)

where $B_{2} {\text{ and }}C_{2}$ are constant coefficients of integration which would be computed from thermal surface boundary conditions applied at the inner and outer surface of the layer reinforced with FG distribution patterns of GPLs (see Appendix B). By employing Eq. (25) and (32) leads to the following heat conduction equation in the form of modified Bessel differential equation

$$z^{2} \frac{{\partial^{2} T_{a} }}{{\partial z^{2} }} + z\frac{{\partial T_{a} }}{\partial z} - \left( {m_{a}^{2} z^{2} } \right)T_{a} = 0$$

(35)

Here $m_{a} = p_{m} \sqrt {\frac{{k_{ax} }}{{k_{az} }}}$. Solution to Eq. (33) for the actuator layers are as

$$T_{a} \left( z \right) = B_{3} I_{o} \left( {m_{a} z} \right) + C_{3} K_{o} \left( {m_{a} z} \right)$$

(36)

where $I_{o} , \, K_{o}$ are modified Bessel function of the first kind and second kind of zero order, respectively; $B_{3} , \, C_{3}$ are constant of integration which are determined from surface temperature boundary condition (Appendix B).

6 Results and discussion

In the result section, the GNP cylindrical nanoshell in a thermal environment under various thermal loading is modeled for the simply supported boundary conditions. After the modeling of the current structure using FMCS parameter, the effects of GNP distribution pattern, modified couple stress parameter, length to radius ratio, mode number, and thermal environment on resonance frequency and dynamic deflection are studied. In the next section will be shown that, these elements have important role on the dynamic behavior of the presented structure. However, results section of our paper are divided into two sections. In the first section, validation of our model with the aid of previous papers of the literature is presented. In the second section, effects of various thermal loading and some various parameters on the resonance frequency, thermal buckling and dynamic deflection of a GNP nanoshell in thermal environments are presented.

6.1 Model validation

Table 1 illustrates a comparison study between the results of this paper and literatures of the simply supported nanoshell with considering modified couple stress theory. Beni et al. [127] investigated vibrational analysis of the FG cylindrical thin nanoshell using modified couple stress theory. It can be seen there is good agreement between the dimensionless natural frequency of the current study and the results of Ref. [127]. As another verification for this work, according to Fig. 4, it is revealed that the suggested modeling can provide good agreement with MD simulation. Figure 4 shows that, as l = R/3, the results of the current research are very similar to those of MD simulation. The material properties of SWNT are presented in Table 2.

Table 1 Comparison of dimensionless first three natural frequencies of isotropic homogeneous nanoshells, with different thicknesses, L/R = 10 and m = 1

Fig. 4

Comparison of the natural frequency of cylindrical nanoshell with the results obtained by MD simulation [128]

Table 2 The material properties of single-walled carbon nanotube

6.2 Parametric results

In this section, analytical results are indicated for simply supported a GNP cylindrical nanoshell in thermal environments under various thermal loadings. In the present paper, the GNP nanostructure with a total thickness h_GNP = 1.5 nm, length of a_GNP = 2.5 m$\upmu$ and Radius of R_GNP = 0.75 m$\upmu$. Table 3 is included mechanical properties of GNP. Now, in this section, the effects of different parameters on the excitation frequency, dimensionless amplitude and relative frequency changes of the structure are investigated.

Table 3 Material properties of the epoxy and GNP [129]

Temperature dependent of the GNP materials is shown as follow [129]:

$\alpha_{m} = 45(1 + 0.0005\Delta T) \times 10^{ - 6} /K$ and E = (3.52 − 0.0034T) GPa, in which T = T₀ + $\Delta T$.

Figure 5 shows thermal buckling mode shape of GNP CNTRC cylindrical nanoshell versus the dimensionless cylindrical shell length. To have a better view of the mode shapes, the vertical displacement of the nanoshell is normalized according to the maximum displacement of the thermal buckling mode shape.

Fig. 5

The thermal buckling mode shapes of the cylindrical microshell in this study

6.3 The effect of different parameters on relative frequency change

The percentage value in parentheses denotes the relative frequency increase $(\omega_{C} - \omega_{M} )$, where $\omega_{C}$ and $\omega_{M}$ are natural frequencies with and without GPL, respectively. Figure 6 shows the relative frequency changes of the FG-GPLRC cylindrical nanoshell with different total number of layers (N_L). As expected, the fundamental frequencies of the structure with GPL distribution pattern 1 are not affected by N_L since they are homogeneous. For the cylindrical nanoshells with pattern 2 in which GPLs are non-uniformly dispersed, their fundamental frequencies decrease with increasing the total number of layers to N_L = 7, then they remain almost unchanged when N_L is further increased. In contrast, this trend is reversed for GPL distribution pattern 3. Among the three non-uniform patterns considered, the fundamental frequency of the structure with GPL patterns 1 and 4 is least affected by the change in N_L. According to this figure by increasing the number of layers (1 < N_L < 7) the natural frequency and stability of the nanostructure change (for non-uniform GPL distribution patterns 2 and 3). It is observed that, in the non-uniform GPL distribution pattern 3, by increasing of the number of layers, the natural frequency and stability of the nanostructure increase. Also, for the other uniform and non-uniform distribution patterns, number of layers of the GPL is not important. The other amazing result is that, by increasing the number of layers in the non-uniform GPL distribution pattern 2, the natural frequency and stability decrease.

Fig. 6

Effect of total number of layers NL on the percentage fundamental frequency change for different patterns of GNP/epoxy ($\Delta T = 10K$, l = R/3, Pattern2, L/R = 10, R/h = 10 and n = m = 1)

Figure 7 shows the effects of mode number and weight function on the relative frequency change of the GNP cylindrical nanoshell. Based on Fig. 7, an increase in the mode number causes to improve in the relative frequency and decreases the stability of the structure. The amazing results is that; weight function has direct effect on relative frequency change of the GNP cylindrical nanoshell. This is because, by increasing the weight function, the structure become softer and it is a reason for increasing the relative frequency change.

Fig. 7

Effect of weight function on the percentage fundamental frequency change for different mode numbers ($\Delta T = 10K$, l = R/3, Pattern2, L/R = 10, R/h = 10)

In Table 4, the effects of different GNP distribution pattern, FMCS parameter, and thermal distribution on natural frequency of the GNP-nanosturacture are shown. It can be seen from the table that as GNP distribution pattern increases from 1 to 4, the behavior of the natural frequency depends on the type of pattern. For example, the patterns 2 and 3 of the GNP have the higher and lower natural frequency. For better comprehensive, the GPL with pattern 2 has higher stability in comparison with other patterns. It is observed that by increasing the FMCS parameter to radius ratio (l/R), the natural frequency increases. Also, the results show that the nonlinear temperature change (NLT) has higher effect on natural frequency in comparison with the linear temperature change (LT).

Table 4 The effects of different FMCS parameter to radius ratio, pattern of GNP and temperature on natural frequency (GHz) of the GNPRC nanoshell with L/R = 10, R/h = 10, g_GPL = 1% and different thermal distributions

Figures 8 and 9 show the effects of MCS and classic theories on the relative frequency changes of the GNP cylindrical nanoshell, respectively. According to these figures, an increase in the temperature change causes to improve in the relative frequency and decrease the stability of the structure. Relative frequency increases smoothly when the temperature change increases. At a certain value of temperature change, a notable increase in relative frequency of the structure is observed. The reason of this phenomena is that, the buckling at this temperature occurs. The amazing results is that, MCS theory has higher effect on critical temperature of the structure in comparison with classic theory. So, for modelling of the nanostructures should be attention to the size-dependent theories specially MCS theory. Also, weight function has direct effect on relative frequency changes of the GNP cylindrical nanoshell. This is because, by increasing the weight function, the structure become softer and it is a reason for increasing the relative frequency change.

Fig. 8

The effects of temperature change and classical theory on the relative frequency change for different weight function and linear temperature change (LT) (Pattern4, L/R = 10, R/h = 10 and n = m = 1)

Fig. 9

The effects of temperature change and MCS theory on the relative frequency change for different weight function and linear temperature change (LT) (Pattern4, L/R = 10, R/h = 10 and n = m = 1)

6.4 The effects of different parameter on excitation frequency and dimensionless amplitude

In Fig. 10, the effect of weight function on dynamic deflection and resonance frequency was presented for the GNP/nanostructure. Also, in this figure, different values’ function (g_GNP) effects are examined. It is evident that, dynamic deflection of the GNP cylindrical nanoshell is affiliated by the value of excitation frequency of dynamic load. By increasing the excitation frequency can see smoothly increase for dynamic deflection. At a specific value of excitation frequency, a remarkable increase in deflection of GNP cylindrical nanoshell is observed. The reason is that the resonance phenomena occurs if the dynamic deflection tends to infinity. With decreasing the weight function, it is observed that, resonance frequency of the GNP cylindrical nanoshell decreases. The reason for this issue is that, stiffness, resonance frequency and stability of a structure improved due to increasing weight function.

Fig. 10

Dynamic deflection and resonance frequency of the cylindrical nanoshell for different weight function ($\Delta T = 20K$, l = R/3, Pattern2, L/R = 10, R/h = 10 and n = m = 1)

In Fig. 11, the effect of different GNP distribution pattern on dynamic deflection and resonance frequency of the GNP nanosturacture is shown. It can be seen from the graph that as GNP distribution pattern increases from 1 to 4, the resonance frequency increases, this leads to an increase in the instability of structure. In other words, A-GNPRC gives larger resonance frequency than other patterns. Also, the resonance frequency of the structure, in the pattern 4 is more similar to pattern 3. The reason of this issue is in the mathematical function which is presented in previous section.

Fig. 11

Dynamic deflection and resonance frequency of the cylindrical nanoshell for different GNP distribution patterns ($\Delta T = 20K$, l = R/3, L/R = 10, R/h = 10 and n = m = 1)

In Fig. 12, the effects of FMCS parameter on forced vibration of GNP cylindrical nanoshell for X-GNPRC pattern are presented. As an important result, can see that the FMCS parameter has significantly effect on the resonance frequency of the structure. It can be seen from the diagram, by improving the FMCS parameter the resonance frequency of the structure increases. Also, this phenomenon improves the stability of the GNP cylindrical nanoshell. It should be mentioned that, as the FMCS parameter is equal to zero, the classic theory occurs.

Fig. 12

Dynamic deflection and resonance frequency of the cylindrical nanoshell for different modified couple stress parameter ($\Delta T = 20K$, Pattern2, L/R = 10, R/h = 10 and n = m = 1)

For investigation of radius-to-thickness ratio (R/h) and temperature change effects on resonance frequency of the GNP cylindrical nanoshell Figs. 13 and 14 is drawn, respectively. According to Fig. 13, it can be observed that by increasing the R/h ratio, the resonance frequency and stability decline. As it mentioned earlier, by increasing the temperature difference, the stability and resonance frequency decrease.

Fig. 13

Dynamic deflection and resonance frequencies of the cylindrical nanoshell for different radius to thickness ratios ($\Delta T = 0K$, l = R/3, Pattern4, L/R = 10 and n = m = 1)

Fig. 14

Dynamic deflection and resonance frequencies of the cylindrical nanoshell for different temperature changes (l = R/3, Pattern4, L/R = 10, R/h = 10 and n = m = 1)

7 Conclusion

This article presents the size-dependent free and forced vibration characteristics of a composite cylindrical nanoshell reinforced with GNP under bi-directional thermal loading. The size-dependent GNP nanoshell is analyzed using FMCS parameter. The equations of motion and non-classic boundary conditions are derived using the Hamilton’s principle. Also, the results of current model were validated with those obtained by molecular dynamics (MD) simulation. The influence of some key parameters such as, various thermal loading, GNP distribution pattern, modified couple stress parameter, length to radius ratio, mode number and thermal environment on the resonance frequency, relative frequency change and dynamic deflection of the GNP nanoshell were studied. In this study, the following main results can be achieved:

• (1) The results show that the nonlinear temperature changes (NLT) have higher effect on the natural frequency in comparison with the linear temperature changes (LT).1) The results show that the nonlinear temperature changes (NLT) have higher effect on the natural frequency in comparison with the linear temperature changes (LT).

• (2) It was observed that the resonance frequency is increased when the modified couple stress parameter and weight function increase and decreased when the temperature difference increases.

• (3) The results show that A-GNP gives larger resonance frequency than other patterns.

• (4) The results show that an increase in the temperature change causes an increase in the relative frequency change and decrease the stability of the structure.

• (5) With an increase in the radius-to-thickness ratio the resonance frequency and stability of the GNP cylindrical nanoshell tends to increase.

Appendices

Appendix A

The components of the matrices in Eq. (24):

$$K_{11} = \left\{ \begin{gathered} A_{11} ( - m^{2} ) - A_{66} \left( \frac{n}{R} \right)^{2} + \frac{{A_{77} l^{2} n^{2} }}{{4R^{2} }}( - m^{2} ) \hfill \\ + \left( { - \frac{{A_{77} l^{2} n^{4} }}{{4R^{4} }}} \right) - \frac{{A_{77} l^{2} n^{2} }}{{R^{4} }} \hfill \\ \end{gathered} \right\}$$

$$K_{12} = \left\{ \begin{gathered} \frac{{A_{12} n}}{R}(m) + \frac{{A_{66} n}}{R}(m) + \frac{{A_{77} l^{2} n}}{4R}( - m^{3} ) \hfill \\ + \left( {\frac{{A_{77} l^{2} ( - n - n^{3} )}}{{4R^{3} }}} \right)(m) \hfill \\ \end{gathered} \right\}$$

$$K_{13} = \left\{ {\frac{{A_{12} }}{R}(m) - \left( {\frac{{A_{77} l^{2} n^{2} }}{{2R^{3} }}} \right)(m)} \right\}$$

$$K_{14} = \left\{ \begin{gathered} B_{11} ( - m^{2} ) - B_{66} \frac{{n^{2} }}{{R^{2} }} + \frac{{B_{77} l^{2} n^{2} }}{{4R^{2} }}( - m^{2} ) \hfill \\ + \left( {\frac{{5A_{77} l^{2} n^{2} }}{{4R^{3} }} - \frac{{B_{77} l^{2} n^{4} }}{{4R^{4} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{15} = \left\{ \begin{gathered} \frac{{B_{12} n}}{R}(m) + \frac{{B_{66} n}}{R}(m) + \frac{{B_{77} l^{2} n}}{4R}( - m^{3} ) \hfill \\ - \left( {\frac{{(B_{77} )l^{2} n}}{{2R^{3} }} + \frac{{A_{77} l^{2} n}}{{4R^{2} }} - \frac{{B_{77} l^{2} n^{3} }}{{4R^{3} }}} \right)(m) \hfill \\ \end{gathered} \right\}$$

$$K_{21} = - \left\{ \begin{gathered} + \frac{{A_{12} n}}{R}( - m) + \frac{{A_{66} n}}{R}( - m) + \frac{{A_{77} l^{2} n}}{4R}(m^{3} ) \hfill \\ + \left( {\frac{{A_{77} l^{2} ( - n - n^{3} )}}{{4R^{3} }}} \right)( - m) \hfill \\ \end{gathered} \right\}$$

$$K_{22} = \left\{ \begin{gathered} A_{66} \sum\limits_{k = 1}^{i} {( - m^{2} )} - A_{11} \left( \frac{n}{R} \right)^{2} - \frac{{k_{s} A_{66} }}{{R^{2} }} - \frac{{A_{77} l^{2} }}{4}(m^{4} ) \hfill \\ + \left( {\frac{{A_{77} l^{2} (2 + n^{2} )}}{{4R^{2} }}} \right)( - m^{2} ) \hfill \\ + \left( { - \frac{{A_{77} l^{2} (1 + n^{2} )}}{{4R^{4} }}} \right) - N_{h} \frac{n}{{R^{2} }} \hfill \\ \end{gathered} \right\}$$

$$K_{23} = \left\{ \begin{gathered} - A_{11} \frac{n}{{R^{2} }} - k_{s} A_{66} \frac{n}{{R^{2} }} + \left( {\frac{{A_{66} l^{2} n}}{{4R^{2} }}} \right)( - m^{2} ) \hfill \\ + \left( { - \frac{{A_{566} l^{2} (n^{3} + n)}}{{4R^{4} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{24} = \left\{ \begin{gathered} - \frac{{B_{66} n}}{R}( - m) - \frac{{B_{12} n}}{R}( - m) - \frac{{B_{77} l^{2} n}}{4R}(m^{3} ) \hfill \\ - \left( {\frac{{A_{77} l^{2} n}}{{2R^{2} }} + \frac{{B_{77} l^{2} ( - n^{3} + n)}}{{4R^{3} }}} \right)( - m) \hfill \\ \end{gathered} \right\}$$

$$K_{25} = \left\{ \begin{gathered} B_{66} ( - m^{2} ) - B_{11} \left( \frac{n}{R} \right)^{2} + \frac{{k_{s} A_{55} }}{R} - \frac{{B_{77} l^{2} }}{4}(m^{4} ) \hfill \\ - \left( {\frac{{ - 3A_{77} l^{2} }}{4R} - \frac{{B_{77} l^{2} }}{2R} - \frac{{B_{77} l^{2} (n^{2} - 1)}}{{4R^{2} }}} \right)( - m^{2} ) \hfill \\ + \left( {\frac{{A_{77} l^{2} (1 - n^{2} )}}{{4R^{3} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{31} = - \left\{ { + \frac{{A_{12} }}{R}( - m) - \left( {\frac{{A_{77} l^{2} n^{2} }}{{2R^{3} }}} \right)( - m)} \right\}$$

$$K_{32} = \left\{ \begin{gathered} - A_{11} \frac{n}{{R^{2} }} - k_{s} A_{66} \frac{n}{{R^{2} }} + \left( {\frac{{A_{77} l^{2} n}}{{4R^{2} }}} \right)( - m^{2} ) \hfill \\ + \left( { - \frac{{A_{77} l^{2} (n^{3} + n)}}{{4R^{4} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{33} = \left\{ \begin{gathered} k_{s} A_{55} ( - m^{2} ) - k_{s} A_{66} \left( \frac{n}{R} \right)^{2} - \frac{{A_{11} }}{{R^{2} }} - \frac{{A_{77} l^{2} }}{4}(m^{4} ) + \hfill \\ \left( {\frac{{A_{77} l^{2} (2n^{2} + 1)}}{{4R^{2} }}} \right)( - m^{2} ) \hfill \\ \left( { - \frac{{A_{77} l^{2} (n^{2} + n^{4} )}}{{4R^{4} }}} \right) - N_{h} \frac{{n^{2} }}{{R^{2} }} \hfill \\ \end{gathered} \right\}$$

$$K_{34} = \left\{ \begin{gathered} k_{s} A_{66} ( - m) - \frac{{B_{12} }}{R}( - m) + \frac{{A_{77} l^{2} }}{4}(m^{3} ) \hfill \\ - \left( {\frac{{A_{77} l^{2} (n^{2} + 1)}}{{4R^{2} }}} \right)( - m) \hfill \\ \end{gathered} \right\}$$

$$K_{35} = \left\{ \begin{gathered} \frac{{k_{s} A_{55} n}}{R} - \frac{{B_{11} n}}{{R^{2} }} + \left( {\frac{{B_{77} l^{2} n}}{{2R^{2} }} - \frac{{A_{77} l^{2} n}}{4R}} \right)( - m^{2} ) \hfill \\ + \left( {\frac{{A_{77} l^{2} (n - n^{3} )}}{{4R^{3} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{41} = \left\{ \begin{gathered} + B_{11} ( - m^{2} ) - B_{66} \frac{{n^{2} }}{{R^{2} }} + \frac{{B_{77} l^{2} n^{2} }}{{4R^{2} }}( - m^{2} ) \hfill \\ + \left( {\frac{{5A_{77} l^{2} n^{2} }}{{4R^{3} }} - \frac{{B_{77} l^{2} n^{4} }}{{4R^{4} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{42} = - \left\{ \begin{gathered} - \frac{{B_{66} n}}{R}(m) - \frac{{B_{12} n}}{R}(m) - \frac{{B_{77} l^{2} n}}{4R}( - m^{3} ) \hfill \\ - \left( {\frac{{A_{77} l^{2} n}}{{2R^{2} }} + \frac{{B_{77} l^{2} ( - n^{3} + n)}}{{4R^{3} }}} \right)(m) \hfill \\ \end{gathered} \right\}$$

$$K_{43} = - \left\{ \begin{gathered} k_{s} A_{66} (m) - \frac{{B_{12} }}{R}(m) + \frac{{A_{77} l^{2} }}{4}( - m^{3} ) \hfill \\ - \left( {\frac{{A_{77} l^{2} (n^{2} + 1)}}{{4R^{2} }}} \right)(m) \hfill \\ \end{gathered} \right\}$$

$$K_{44} = \left\{ \begin{gathered} - D_{66} \left( \frac{n}{R} \right)^{2} - k_{s} A_{66} + \left( {\frac{{D_{77} l^{2} n^{2} }}{{4R^{2} }} + \frac{{A_{77} l^{2} }}{4}} \right)( - m^{2} ) \hfill \\ + \left( { - \frac{{D_{77} l^{2} n^{4} }}{{4R^{4} }} + \frac{{2B_{77} l^{2} n^{2} }}{{4R^{3} }} - \frac{{A_{77} l^{2} (1 + 4n^{2} )}}{{4R^{2} }}} \right)D_{11} ( - m^{2} ) \hfill \\ \end{gathered} \right\}$$

$$K_{45} = \left\{ \begin{gathered} \frac{{D_{12} n}}{R}(m) + D_{66} \frac{n}{R}(m) + \frac{{D_{77} l^{2} n}}{4R}( - m^{3} ) \hfill \\ + \left( { - \frac{{D_{77} l^{2} n^{3} }}{{4R^{3} }} + \frac{{B_{77} l^{2} n}}{2R} - \frac{{3A_{77} l^{2} n}}{4R}} \right)(m) \hfill \\ \end{gathered} \right\}$$

$$K_{51} = \left\{ \begin{gathered} + \frac{{B_{12} n}}{R}( - m) + \frac{{B_{66} n}}{R}( - m) + \frac{{B_{77} l^{2} n}}{4R}\sum\limits_{k = 1}^{i} {C_{i,k}^{\left( 3 \right)} } \hfill \\ - \left( {\frac{{(B_{77} )l^{2} n}}{{2R^{3} }} + \frac{{A_{77} l^{2} n}}{{4R^{2} }} - \frac{{B_{77} l^{2} n^{3} }}{{4R^{3} }}} \right)( - m) \hfill \\ \end{gathered} \right\}$$

$$K_{52} = \left\{ \begin{gathered} B_{66} ( - m^{2} ) - B_{11} (\frac{n}{R})^{2} + \frac{{k_{s} A_{66} }}{R} - \frac{{B_{77} l^{2} }}{4}(m^{4} ) \hfill \\ - \left( {\frac{{ - 3A_{77} l^{2} }}{4R} - \frac{{B_{77} l^{2} }}{2R} - \frac{{B_{77} l^{2} (n^{2} - 1)}}{{4R^{2} }}} \right)( - m^{2} ) \hfill \\ + \left( {\frac{{A_{77} l^{2} (1 - n^{2} )}}{{4R^{3} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{53} = \left\{ \begin{gathered} \frac{{k_{s} A_{77} n}}{R} - \frac{{B_{11} n}}{{R^{2} }} + \left( {\frac{{B_{77} l^{2} n}}{{2R^{2} }} - \frac{{A_{77} l^{2} n}}{4R}} \right)( - m^{2} ) \hfill \\ + \left( {\frac{{A_{77} l^{2} (n - n^{3} )}}{{4R^{3} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$K_{54} = - \left\{ \begin{gathered} + \frac{{D_{12} n}}{R}( - m) + D_{66} \frac{n}{R}( - m) + \frac{{D_{77} l^{2} n}}{4R}(m^{3} ) \hfill \\ + \left( { - \frac{{D_{77} l^{2} n^{3} }}{{4R^{3} }} + \frac{{B_{77} l^{2} n}}{2R} - \frac{{3A_{77} l^{2} n}}{4R}} \right)( - m) \hfill \\ \end{gathered} \right\}$$

$$K_{55} = \left\{ \begin{gathered} - D_{11} (\frac{n}{R})^{2} + D_{66} ( - m^{2} ) - k_{s} A_{55} - \frac{{D_{77} l^{2} }}{4}(m^{4} ) \hfill \\ + \left( {\frac{{D_{77} l^{2} n^{2} }}{{4R^{2} }} + \frac{{B_{77} l^{2} }}{2R} + A_{77} l^{2} + \frac{{D_{77} l^{2} }}{2R}} \right)( - m^{2} ) \hfill \\ + \left( { - \frac{{A_{77} l^{2} n^{2} }}{{4R^{2} }} - \frac{{A_{77} l^{2} }}{{4R^{2} }}} \right) \hfill \\ \end{gathered} \right\}$$

$$\begin{gathered} M_{11} = I_{0} ,M_{14} = I_{1} ,M_{22} = I_{0} ,M_{25} = I_{1} ,M_{33} = I_{0} ,M_{41} = I_{1} ,\,M_{44} = I_{2} ,\,M_{52} = I_{1} ,\,M_{55} = I_{2} \hfill \\ \,M_{12} = M_{13} = M_{15} = M_{21} = M_{23} = M_{24} = M_{31} = M_{32} = M_{34} = M_{35} = M_{42} = M_{43} = M_{45} = \,M_{51} = M_{53} = M_{54} = 0\, \hfill \\ \end{gathered}$$

Appendix B

$$B_{1} = \frac{1}{\Delta F}\left| {\begin{array}{*{20}c} {T_{i} } & {K_{o} \left( {q\left( {r_{i} } \right)} \right)} \\ {T_{o} } & {K_{o} \left( {q\left( {r_{o} } \right)} \right)} \\ \end{array} } \right| \, C_{1} = \frac{1}{\Delta F}\left| {\begin{array}{*{20}c} {I_{o} \left( {q\left( {r_{i} } \right)} \right)} & {T_{i} } \\ {I_{o} \left( {q\left( {r_{o} } \right)} \right)} & {T_{o} } \\ \end{array} } \right| \, \Delta F = \left| {\begin{array}{*{20}c} {I_{o} \left( {q\left( {r_{i} } \right)} \right)} & {K_{o} \left( {q\left( {r_{i} } \right)} \right)} \\ {I_{o} \left( {q\left( {r_{o} } \right)} \right)} & {K_{o} \left( {q\left( {r_{o} } \right)} \right)} \\ \end{array} } \right|$$

2.1 FG-V:

$${\text{A}}_{1} = 1 - \frac{{2D_{z} r_{i} }}{h},{\text{ A}}_{2} = \frac{{2D_{z} }}{h},{\text{ A}}_{3} = P_{m}^{2} \left( {\frac{{2D_{x} r_{i} }}{h} - 1} \right),{\text{ A}}_{4} = - 2P_{m}^{2} \frac{{D_{x} }}{h}, \, \frac{{k_{i} }}{{k_{m} }} = 1 + 2D_{i} \left( {\frac{{z - r_{i} }}{h}} \right)$$

2.2 FG-X:

$$\begin{gathered} {\text{when: z }}\langle {\text{ r}}_{i} { + }\frac{h}{2} \hfill \\ {\text{A}}_{1} = 1 + 2D_{z} \left( {1 + \frac{{2r_{i} }}{h}} \right),{\text{ A}}_{2} = - \frac{{4D_{z} }}{h},{\text{ A}}_{3} = - P_{m}^{2} \left( {1 + 2D_{x} \left( {1 + \frac{{2r_{i} }}{h}} \right)} \right),{\text{ A}}_{4} = 4P_{m}^{2} \frac{{D_{x} }}{h} \hfill \\ \frac{{k_{i} }}{{k_{m} }} = 1 + 2D_{i} \left( {1 - \frac{{2\left( {z - r_{i} } \right)}}{h}} \right) \hfill \\ {\text{when: z }}\rangle {\text{ r}}_{i} { + }\frac{h}{2} \hfill \\ {\text{A}}_{1} = 1 - 2D_{z} \left( {1 + \frac{{2r_{o} }}{h}} \right),{\text{ A}}_{2} = \frac{{4D_{z} }}{h},{\text{ A}}_{3} = - P_{m}^{2} \left( {1 - 2D_{x} \left( {1 + \frac{{2r_{o} }}{h}} \right)} \right),{\text{ A}}_{4} = - 4P_{m}^{2} \frac{{D_{x} }}{h} \hfill \\ \frac{{k_{i} }}{{k_{m} }} = 1 + 2D_{i} \left( { - 1 + \frac{{2\left( {z - r_{i} } \right)}}{h}} \right) \hfill \\ \end{gathered}$$

2.3 FG-O:

$$\begin{gathered} {\text{when: z}}\langle {\text{ r}}_{i} { + }\frac{h}{2} \hfill \\ {\text{A}}_{1} = 1 - \frac{{4D_{z} r_{i} }}{h},{\text{ A}}_{2} = \frac{{4D_{z} }}{h},{\text{ A}}_{3} = P_{m}^{2} \left( {\frac{{4D_{x} r_{i} }}{h} - 1} \right),{\text{ A}}_{4} = - 4P_{m}^{2} \frac{{D_{x} }}{h} \hfill \\ \frac{{k_{i} }}{{k_{m} }} = 1 + 4D_{i} \left( {\frac{{z - r_{i} }}{h}} \right) \hfill \\ {\text{when: z }}\rangle {\text{ r}}_{i} { + }\frac{h}{2} \hfill \\ {\text{A}}_{1} = 1 + \frac{{4D_{z} r_{o} }}{h},{\text{ A}}_{2} = - \frac{{4D_{z} }}{h},{\text{ A}}_{3} = - P_{m}^{2} \left( {\frac{{4D_{x} r_{o} }}{h} + 1} \right),{\text{ A}}_{4} = 4P_{m}^{2} \frac{{D_{x} }}{h} \hfill \\ \frac{{k_{i} }}{{k_{m} }} = 1 + 4D_{i} \left( {\frac{{r_{o} - z}}{h}} \right) \hfill \\ \end{gathered}$$

$$\begin{gathered} B_{2} = \frac{1}{{\int_{{r_{i} }}^{{r_{o} }} {\frac{{e^{{2\sqrt { - \, \frac{{A_{4} }}{{A_{2} }}} {\text{ z}}}} }}{{z\left( {A_{2} z + A_{1} } \right)H_{z}^{2} }}dz} }} \times \left\{ {\frac{{T_{o} }}{{H_{o} \times e^{{ - \sqrt { - \, \frac{{A_{4} }}{{A_{2} }}} \, r_{o} }} }} - \frac{{T_{i} }}{{H_{i} \times e^{{ - \sqrt { - \, \frac{{A_{4} }}{{A_{2} }}} {\text{ r}}_{i} }} }}} \right\} \hfill \\ C_{2} = \frac{{T_{i} }}{{HeunC\left( {\frac{{2A_{1} }}{{A_{2} }}\sqrt { - \frac{{A_{4} }}{{A_{2} }}} ,0,0,\frac{{A_{1} }}{{A_{2}^{3} }}\left( {A_{1} A_{4} - A_{2} A_{3} } \right),0, - \frac{{A_{2} }}{{A_{1} }}r_{i} } \right) \times e^{{ - \sqrt { - \, \frac{{A_{4} }}{{A_{2} }}} \, r_{i} }} }} \hfill \\ \end{gathered}$$

$$\begin{gathered} H_{z} = HeunC\left( {\frac{{2A_{1} }}{{A_{2} }}\sqrt { - \frac{{A_{4} }}{{A_{2} }}} ,0,0,\frac{{A_{1} }}{{A_{2}^{3} }}\left( {A_{1} A_{4} - A_{2} A_{3} } \right),0, - \frac{{A_{2} }}{{A_{1} }}z} \right) \hfill \\ H_{o} = HeunC\left( {\frac{{2A_{1} }}{{A_{2} }}\sqrt { - \frac{{A_{4} }}{{A_{2} }}} ,0,0,\frac{{A_{1} }}{{A_{2}^{3} }}\left( {A_{1} A_{4} - A_{2} A_{3} } \right),0, - \frac{{A_{2} }}{{A_{1} }}r_{o} } \right) \hfill \\ H_{i} = HeunC\left( {\frac{{2A_{1} }}{{A_{2} }}\sqrt { - \frac{{A_{4} }}{{A_{2} }}} ,0,0,\frac{{A_{1} }}{{A_{2}^{3} }}\left( {A_{1} A_{4} - A_{2} A_{3} } \right),0, - \frac{{A_{2} }}{{A_{1} }}r_{i} } \right) \hfill \\ \end{gathered}$$

$$\begin{gathered} B_{3} = \frac{1}{\Delta A}\left| {\begin{array}{*{20}c} {T_{2} } & {K_{o} \left( {m_{a} z} \right)} \\ {T_{ai} } & {K_{o} \left( {m_{a} \left( {r_{o} - h_{p} } \right)} \right)} \\ \end{array} } \right| \, C_{3} = \frac{1}{\Delta A}\left| {\begin{array}{*{20}c} {I_{o} \left( {m_{a} z} \right)} & {T_{2} } \\ {I_{o} \left( {m_{a} \left( {r_{o} - h_{p} } \right)} \right)} & {T_{ai} } \\ \end{array} } \right| \hfill \\ \Delta A = \left| {\begin{array}{*{20}c} {I_{o} \left( {m_{a} z} \right)} & {K_{o} \left( {m_{a} z} \right)} \\ {I_{o} \left( {m_{a} \left( {r_{o} - h_{p} } \right)} \right)} & {K_{o} \left( {m_{a} \left( {r_{o} - h_{p} } \right)} \right)} \\ \end{array} } \right| \hfill \\ Where{\text{ T}}_{ai} = \left. {T_{a} } \right|_{{z = r_{o} - h_{p} }} \hfill \\ \end{gathered}$$